最新第1章 静电场(1)
第一章 静电场
电场强度的定义式能否改为 E F q ? 0 答:当场源电荷分布不受正的试验点电 荷q0电场的影响时,该定义式成立。
从上述定义式可知,电场中任一点的电场强度在 数值上相当于单位正点电荷在该点所受之力,其 方向则为正点电荷的受力方向。
3、点电荷产生电场强度
E (r)
q e 2 r 4 0r
①以上算式的运用前提:电荷连续分布。 注意: ②电场强度的矢量积分一般先转化为各坐标轴上的标 量积分, 然后再合成。
例:
真空中长为L的均匀带电非导电棒,电荷线密度为τ,试 求P点的场强.
解:采用直角坐标系,令Y轴经过P点,导线与X轴重合 Y dEdEY dEx P ·
d E ( x, y ) d Ex
rr2 r 1
2
r2 r1 d cos
d cos ( ) 2 4 0 r q
令:
P qdez
电偶极距,方向由负电荷指向正 电荷,单位:C.m
qdez er P er 2 4 0 r 4 0 r 2
当=90时,=0. 说明偶极子平分面上的任意一点电位为0,在这个 平面上移动电荷不做功
§1.1
电场强度点位
杰明· 富兰克林的实验
一、电荷 1、正电荷
用丝绸摩擦玻璃棒,将玻璃棒上带的电荷叫做正电荷
2、负电荷
用毛皮摩擦火漆,并将火漆所带的电荷称为负电荷 自然界中最小的“自由”电荷是电子或质子所带的电荷
e=1.602×10-19 C
二、电场
电荷的周围,存在着一种特殊形式的物质,称为电场。 其基本特征是对于被引入场中的电荷有力的作用。
2 2 3 2
2
1 x a x
第一章静电场

真 空 容 器
光 杠 杆 系 统
环 型 磁 芯
实验图片
电量单位 -MKSA制
1库仑:当导线中通过1安培稳恒电流
时,一秒钟内通过导线某一给定截面 的电量为
1C=1A· S
若F=1N, q1= q2 = 1C, r =1m 则 k = 8.9880×109N· m2/C2
≈ 9.00×109N· m2/C2
电 磁 学
Electronmagnetism
奥妙无穷的电现象
知识结构:
基本内容:
电磁学基本概念和规律
相关内容:
电磁学基本原理的应用 拓展内容:
与电磁学相关的科学前沿 的有关内容
教师讲授重点
“三二一”讲授结构
三个实验定律 两个基本方程 一个方程组
库仑 定律
安培 定律
法拉第电 磁感定律
通量 方程
真空条件(Vacuum) :
作用:为了除去其它电荷的影响,使两 个点电荷只受对方作用。 如果真空条件破坏会如何? 总作用力比真空时复杂些,但由于力的 独立作用原理,两个点电荷之间的力仍 遵循库仑定律 因此库仑定律可以推广到介质、导体
点电荷 (Point charge) :
理想模型(已学过的) 质点 刚体 理想流体 平衡态(热学) 点电荷:忽略了带电体形状、大小 以及电荷分布情况的电荷。
美国帝国大厦 (地上102层,高 448.5m)在大风之 下只会摇摆八英尺 左右。为什么?
Coulomb定律具有丰富、深刻的内 涵和外延,是培养科学素质的重要载体 之一。
Coulomb定律的内涵是什么? Coulomb定律是怎样发现的? Coulomb定律成立的条件是什么? Coulomb定律的使用范围是什么? Coulomb定律的理论地位是什么?
第一章静电场

第一章 静电场本章内容研究静电场的基本性质和规律。
主要讨论四个问题。
● 静电场的基本规律(库仑定律)● 描述静电场性质的两个物理量(U ,)● 静电场中的导体● 一些重要电场的分布学习要求:掌握“三基”:基本概念静电场 电场强度 电势 电通量基本理论和规律● 库仑定律(221041r q q F πε=) ● 高斯定理(∑⎰⎰=⋅E q ds E 01ε)● 环路定理(0=⋅⎰dl E )基本方法● 场强的电场线描述法● 电场强度、电势叠加法● 应用高斯定理求对称电场场强第二章 恒磁场电与磁经常是联系在一起并互相转化的。
本章讨论不随时间变化电流(或运动电荷)产生的稳定磁场(恒磁场)的基本性质和规律以及对载流导线和带电粒子的作用。
主要讨论四个问题:● 恒磁场的基本规律(库仑定律、安培定律)● 描述磁场的几个物理量(H 、B 、A )● 磁场对载流导线的作用——安培力()B l d I F d ⨯= ● 带电粒子在磁场中所受的力(洛伦磁力 F B U q ⨯=)及运动学习要求:掌握“三基”基本概念:● 磁场强度()H ; ● 磁感应强度()B ; ● 安培力基本理论(规律):●磁的库仑定律(磁荷观点);●安培定律(电流观点);●安培环路定理;●磁场的“高斯定理”;基本方法:●类比法:将恒磁场与静电场类比,可得两者相似(对应)的概念,规律和公式。
●磁感应强度B 、安培力、洛伦磁力、磁力功的一般计算方法。
●应用安培环路定理计算对称磁场B 的方法。
●载流长直细导线、圆柱、圆线圈、螺线管、螺绕环等重要磁场分布的计算方法。
第三章 电磁感应 电磁场的相对论变换电磁感应现象是电磁学中最重大的发现之一,在科学上和技术上都具有划时代的意义。
它揭示了电与磁相互联系和转化的重要方面,不仅丰富了人类对于电磁学理论的发展,而且在实践上开拓了广泛应用的前途。
例如在电子、电工、电磁测量和自动化等技术领域中都有广泛的应用。
本章内容介绍电磁感应的基本规律和有关问题以及电磁场在不同参考系的变换。
第一章静电场

51014 (个)
返回
例2:
两个相距很远的带电金属小球A和B所带 电量分别为+4×10-5C 和- 6×10-5C, 用和它们完全一样的金属小球C先后分 别与A、B各接触一下后拿走,A、B之 间的静电力变成原来的多少倍?
返回
AC ++ ++
AC ++ ++
A ++
BC
----- ++
BC
-- --
B
--
F
k
4 61010 r2
F'
k
2 21010 r2
F’=F / 6
物体带电 小
带电的现象
带电的本质
起电的方法 带电的特点
电荷守恒定律
结 库仑定律
定律的发现
定律的内容
定律的条件 定律的应用
条件: 真空中、点电荷
公式: F k Qq r2
常量:k 9.0109 Nm2 / c2
应用
例题1
某带电体带正电,且所带电量是 8×10-5C,则该带电体 ——(填 “失 去”或“得到”)了 ———— 个电 子。
例题1
分析与解答
带正电
失去了电子
失去电子数为: 8105 1 61019
e=1.6×10-19 c
电荷守恒定律
电荷既不能创造,也不能消 灭,它们只能从一个物体转移 到另一个物体,或者从物体的一 个部分转移到另一个部分。在 转移的过程中,电荷的代数和 不变。
电荷之间的相互作用力
猜 想: 与带电体的电量有关
与带电体之间的距离有关 与带电体自身的大小及形状有关 与带电体所处的空间物质即介质有关
定性实验: 控制变量法
第一章 静电场

电势差与电场强度的关系
结论一
匀强电场中,两点间的电势差,等于电场强度与 这两点沿电场方向的距离的乘积。
UAB = E ·dAB
UAB = E ·dAB
U AB E d AB
匀强电场中,电场强度等于两点间的 电势差与两点沿电场方向距离的比值。
电势差与电场强度的关系
结论一
匀强电场中,两点间的电势差,等于电场强度与 这两点沿电场方向的距离的乘积。Biblioteka 结论二UAB = E ·dAB
U AB E d AB
匀强电场中,电场强度等于两点间的电势差与两 点沿电场方向距离的比值。
结论三
沿电场线,电势下降最快。 等差等势面越密的区域,电场强度越大。
总结
电荷受到的力F
公式
名称
适用范围
q1 q 2 F k 2 r
F=qE
库仑定律 /库仑力或静电力
用于计算真空中 两个静止点电荷 之间的作用力
特点四:静电平衡状态的导体,净电荷只分布在 导体的外表面上,导体内部没有净电荷。
应用:静电屏蔽 实验一 实验二
(1)对外电场的屏蔽
E 0
(2)接地空腔导体屏蔽腔内电荷对外界的影响
A
A
静电平衡状态: 导体中(包括表面)没有电荷的定向移动 的状态,叫做静电平衡状态。
E0 E' E E0 E ' 0
E
静电平衡状态
静电平衡状态的导体的特点 特点一:处于静电平衡状态的导体, E=E’,故内部的场强处处为零。 特点二:处于静电平衡状态的导体是等势体, 导体表面是等势面。(电势不为零) 特点三:处于静电平衡状态的导体,其外部表面 场强不为零,且表面上任何一点的场强 方向跟该点的表面垂直
第一章 静电场 ppt 电磁学课件

E
•
A
E
Ax
E p
1 E r3
理学院大学物理教研室
结论: 1.电偶极子延长线上一点的场强与
电偶极子电矩的二倍成正比,与该点离 中心的距离的三次方成反比,方向与电 矩方向相同。
2. 电偶极子中垂线上距离中心较远处 一点的场强,与电偶极子的电矩成正比, 与该点离中心的距离的三次方成反比,方 向与电矩方向相反。
本节主要内容: 一、 电场线及其数密度 二、电通量 三、高斯定理及应用
理学院大学物理教研室
§3.1电场线及其数密度
1、电场线(电力线)electric line of force 定义:在电场中画一组曲线,曲线上每一点的切线方向
与该点的电场方向一致,这一组曲线称为电场线。
电场线上各点的切线方向表示电场中该点场强的 方向,在垂直于电场线的单位面积上的电场线的条 数(数密度)等于该点的场强的大小。
例题1:求点电荷q所产生的电场中各点的电场强度
p 在真空O点有一静止的点电荷q,在空间p放置一试探电荷q0
q0所受力:
F
1
qq0
rˆ
1
qq0
r
场点
4 r 2
4 r 3
位矢
r
r q E
F q0
0
q
4 0r3
r
0
O 场源 ( 的方向O指向P的方向)
1)球对称场。 2)非均匀场
理学院大学物理教研室
即均匀带电圆环轴线上一点的场强
E
1
4 0
(x2
qx R2
)3/ 2
R
x dE
r
方向沿轴线方向,
讨论: 1)当x=0 时,E=0,即环心处的场强为0。
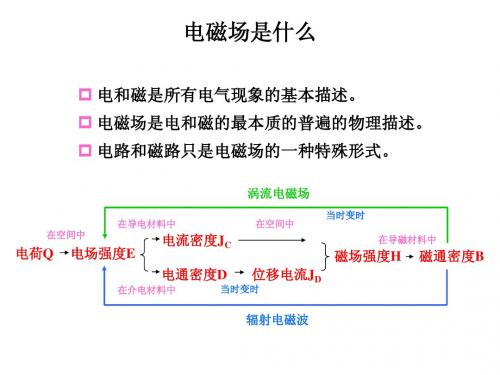
工程电磁场——静电场——第1讲PPT课件

演讲人:XXXXXX 时 间:XX年XX月XX日
边值问题
电位
解析法
有限差分法 镜像法,电轴法 分离变量法 直接积分法
静电参数(电容及部分电容) 静电场知识结构
静电能量与力
第一章
静电场
1.1 电场强度和电位
1.1.1 电场强度 1.1.2 叠加积分法求电场强度
库仑定律:
F21
q1q2
4π 0
e12 R2
F21 F12
N (牛顿)
图
两点电荷间的作用力
第一章
第一章 静电场
静电场
序 电场强度和电位 环路定律、 基本方程、分界面上的衔接条件 边值问题、惟一性问题 分离变量法 有限差分法 镜像法和电轴法 电容和部分电容 静电能量与力 静电场的应用
第一章
1.0 序
静电场
静电场是相对观察者静止且量值不随时间变化的 电荷所产生的电场。
它是电磁理论最基本的内容。由此建立的物理概念、 分析方法在一定条件下可应用推广到恒定电场,恒定 磁场及时变场。
q
(r)
4π 0 r r'
(r)
q
C
4π 0 r r '
点电荷群
(r) 1 N qi C
4π 0 i1 r ri '
连续分布电荷 (r) 1
dq C
4π 0 V ' r r'
式中dq dV , dS , dl相应的积分原域 V ', S ', l '。
第一章
1.第一章 静电场1

r
库仑力满足牛顿第三定律
0
此定律只能用于真空中的点电荷(空气中也近 似应用)
电子和质子之间的静电力与万有引力的比值为
2.261039
1库仑=1安培×秒,量纲为:[q]=TI
2、静电力的叠加原理: 两个以上的点电荷之间 的作用力并不因为第三个电 荷的存在而有所改变,等于 每个电荷单独存在时对该电 荷作用力的矢量和。 对分立带电体
电磁学
简介电磁学发展史
电与磁关系探密 2500多年前(周朝)人类历 史上第一次记载了电与磁的现象:古希腊著名哲学 家泰勒斯在爱琴海的海滩上散步时,被一种黄褐色 石块(琥珀)吸引了,他发现使劲摩擦它以后能吸 引麦杆碎渣和羽毛碎片,之后他又仔细观察魔石 (天然磁石)吸引小铁片的现象,泰勒斯将这两种 现象当作一回事,他把观察到的现象说得头头是道, 以至这一错误见解被科学界奉为金科玉律长达2200 年左右。 直到1600年,英国一位叫吉伯的著名医生兼物 理学家,写了一本《论磁石》的书,书中把物体经 摩擦后产生对其他物体的吸引力或斥力称为电力, 而把磁石对铁的引力称为磁力,明确指出电力与磁 力是两码事。
O
Q
qQ F 2 2 0 R 2
方向如图向右
§2 电场 电场强度
2.1 电场(电场是种特殊形式的物质) 历史上两种观点: (1)沿袭牛顿力学“超距作用” (2)法拉第场论观点 电场: 带电体周围存在的一种特殊物质 静电场: 相对观测者静止的电荷周围存在的电场 电荷 电场 电荷
电场的最重要的表现
在不同的参照系内观察,同一个带电粒子的电量不变。
1.5 库仑定律
1、 库仑定律
q1q2 F e 2 r 40 r
q1q2 r 3 40 r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一篇 题文第1章 静电场1.1 选择题11001 一点电荷与放在相距为3cm 处的另一个点电荷的电相互作用力为F , 若两点电荷之间的距离增加到6cm ,此时它们之间的静电力为:A.F/4;B.F/2;C.F ;D.4F 。
11002 一个带电体要能够被看成点电荷,必须: A.其线度很小; B.其线度与它到场点的距离相比足够小;C.其带电量很小;D.其线度及带电量都很小。
11003 电量为q 的三个点电荷,分别放在正三角形的三个顶点,在三角形中心处有另一点电荷Q ,欲使作用在每个点电荷上的合力均为零,则Q 的电量为:A.-2q ;B.2q ;C.33-q ; D.32-q 。
11004 只要场源电荷的大小和分布确定,则: A.场中各点的场强就确定;B.场中各点的电位就确定;C.任意带电体在场中各点受到的电场力就确定;D.电荷在各点的电位能就确定。
11005 对电荷概念有下述四种说法: A.电荷是指带电体的一种属性; B.电荷是指带电体上所带的电量;C.电荷是指带电体;D.电荷是一切实体物质固有的一种属性。
11006 边长为a 的正方形的四个顶点上,放置如题图11006所示的点电荷, 则中心P 点处的场强p E 的大小为: A.20a qπε;B.2022aqπε;C. 20223a qπε; D. 203a q πε。
11007 真空中两块互相平行的无限大均匀带电平板,其中一块的面电荷密度为+σ,另一块的面电荷密度为+2σ,两板间的距离为d ,则两板间的电位差为:A.0;B.d 023εσ; C.d 0εσ; D.d 02εσ。
11008 半径为R 的均匀带电球面上,电荷面密度为σ,在球面上取ΔS ,则ΔS 上的电荷受到的电场力为:A.0;B.022εσS ∆;C. 02εσS ∆;D. 2024RS πεσ∆。
11009 在静电场中,下列说法正确的是:-q2q-2q qaa a a P●题图 11006A.若场的分布不具有对称性,则高斯定理不成立;B.点电荷在电场力作用下,一定沿电力线运动;C.两点电荷q1,q2间的作用力为F ,当第三个点电荷q3移近时,q1、q2间的作用力仍为F ;D.有限长均匀带电直线的场具有轴对称性,因此可以用高斯定理求出空间各点的场强E 。
11010 电场中任意高斯面上各点的电场强度是由: A.分布在高斯面内的电荷决定的; B.分布在高斯面外的电荷决定的;C.空间所有电荷决定的;D.高斯面内电荷代数和决定的。
11011 在静电场中通过高斯面S 的通量为零,则: A.S 内必无电荷;B.S 内必无净电荷;C.S 外必无电荷;D.S 上E 处处为零。
11012 在静电场中过高斯面S 的通量为零,则:A.S 上E 处处为零;B.S 上E 处处不为零;C.S 上处处E ⊥n ;D.只说明0=•⎰⎰SdS E 。
11013 对高斯定理i Sq dS E ∑=⋅⎰⎰1ε的理解如下:A.E 仅由S 内电荷产生;B.它说明静电场是有源场;C.通过S 的通量为正时,S 内必无负电荷;D.当S 上E 改变时,S 内电荷的位置必然改变 。
11014 据高斯定理i Sq dS E ∑=⋅⎰⎰1ε可以说明以下几点:A.通过闭合曲面的总通量仅由面内电荷决定;B.通过闭合曲面的总通量为正时,面内一定没有负电荷;C.闭合曲面上各点的场强仅由面内电荷决定;D.闭合曲面上各点的场强为零时,面内一定没有电荷。
11015 空间有一非匀强电场,其电力线分布如题图11015所示,若电场中取一半径为R 的球面(面内无电荷),已知通过球面ΔS 的电通量为ΔΦe ,则通过球面其余部分的电通量为: A.-ΔΦe ;B.SR e∆∆Φ24π;C. SS R e ∆∆Φ∆-)4(2π;D.0。
11016 同一束电力线穿过大小不等的两个平面S 1和S 2,如题图11016所 示,则两平面的E 通量和场强的关系是:A.Φ1>Φ2,E 1=E 2;B.Φ1<Φ2,E 1=E 2;C.Φ1=Φ2 ,E 1>E 2; D .Φ1=Φ2 ,E 1<E 2。
11017 如题图11017所示高斯面S 外一点电荷+q 从P 点移到R 处(OP=OR),O 为S 上一点。
则:题图 110151题图 11016A.通过S 的通量Φe 要变,O 处E 0要变;B.Φe 不变,E 0变;C.Φe 变,E 0不变;D.Φe 不变,E 0不变。
11018 关于静电场下列说法中正确的是: A.电场和试探电荷同时存在同时消失; B.由E=F/q 知道,电场强度与试探电荷成反比;C.电场的存在与试探电荷无关;D.电场是试探电荷和场源电荷共同产生的。
11019 真空中某静电场区域内的电力线是疏密均匀方向相同的平行直线,则在该区域内场强E 和电位U:A.都是常数; B .都不是常数; C.E 是常数U 不是常数; D.E 不是常数U 是常数。
11020 一个充电至电量为q ,面积为S ,板间距离为d 的空气平行板电容器,用力将两极板慢慢拉开,使板间距离增至2d ,则外力F 在拉开平板的过程中做的功为:A.Sd q 022ε-;B. Sd q 022ε;C. Sd q 02ε-;D. Sd q 02ε。
11021 电荷分布区域有限,则空间任意二点P 1、P 2的电位差ΔU: A.由试验电荷q 0(从P 1移到P 2)决定; B.由E P1、E P2的值决定;C.由q 0从P 1→P 2的路径决定;D.由⎰⋅21dl E P P 决定。
11022 在相距为2R 的点电荷+q 和-q 的电场中,把点电荷+Q 从O 点沿OCD 圆孤移到D 点(见题图11022)。
则电场力做功与+Q 电位能的增量分别为: A.R qQ04πε,RqQ04πε-; B. R qQ04πε-,RqQ04πε;C. RqQ 06πε,R qQ 06πε-;D. R qQ 06πε-, RqQ 06πε。
11023 电荷-Q 均匀分布在半径为R ,长为L 的圆孤上,圆弧的两端有一小空隙,空隙长为ΔL 《R(见题图11023),则圆弧中心O 点的电场强度和电位分别为: A i L R L Q 204πε∆-,RQ04πε-;B.i L R L Q 204πε∆,RLQ04πε- ;C. i R Q 204πε-,RLQ04πε;D. i L R L Q 204πε∆-,RLLQ 04πε∆-。
11024 题图11024中A 、B 是真空中的两块相互平行的无限大均匀带电平面, 电荷面密度分别为+σ和-2σ,若A 板选作零电位参考点,则图中a 点的电位是:R题图01017ODR 题图11022题图11023A.23εσd;B. 0εσd-;C. 023εσd-; D.3εσd。
11025 有一半径为R 的圆环形带电导线,其轴线上有两点a 和b ,且R ab oa ==(见题图11025),若取无限远处电位为零,a 、b 两点的电位分别为U 1和U 2,则U 1/U 2为:A.31; B.52; C.21; D.25。
11026 两条电荷密度分别是+η和-η的无限长均匀带电直线,一条位于x 轴 上,另一条与z 轴平行并与y 轴相交于B ,且OB=2a ,A 点为y 轴上的另一点OA=a ,则A 点处的场强为: A.aE 0πεη=,沿y 轴正方向; B. aE 02πεη= ,沿y 轴正方向;C.0=E;D. aE 0πεη=,沿y 轴负方向。
11027 两无限大平行平面均匀带电,电荷面密度均为+σ,则图中三个区域 内场强的大小为: A.0,00=,=ⅢⅡⅠE E E εσ=; B. 000,εσεσ=,=ⅢⅡⅠE E E =;C. 0020,2εσεσ=,=ⅢⅡⅠE E E =;D. 0002,2εσεσεσ=,=ⅢⅡⅠE E E =。
11028 一均匀带电的球形橡皮气球,在气球被吹大的过程中,场强不断变小的点是: A.始终在气球内部的点; B.始终在气球外部的点;C.气球表面上的点;D.找不到这样的点。
11029 一点电荷q 位于一立方体中心,通过立方体每个表面的E 通量是:A.16εq; B.8εq ; C.4εq; D.6εq 。
11030 当一对电偶极子对称地分布在球内一条直径上时; A.球面上场强处处相等; B.球面上场强处处为零;C.球面上总的E 通量为零;D.球面内没有包围电荷。
11031 两个电量都是+q 的点电荷分别位于A 、O 两点处,如题图11031所示。
S 是以O 为心的一个球面,P 是球面上的一点,当A 处的点电荷从A 移向B 时,则:题图11024题图11025A.通过S 面的E 通量将不变,P 点的场强将增大;B.通过S 面的E 通量将增加,P 点的场强将增大;C.通过S 面的E 通量将不变,P 点的场强将不变;D.通过S 面的E 通量将增加,P 点的场强将不变。
11032 在球形高斯面的球心处有一点电荷q 1,那么,要使通过高斯面的 E 通量发生变化,应该: A.使点电荷q 1偏离球心但仍在面内; B.将另一点电荷q 2放在高斯面外;C.使高斯面外的q 2不断远离;D.将q 2由高斯面外移入面内。
11033 电场中一个高斯面S 内有电荷q 1和q 2,S 面外有电荷q 3和q 4,关于高斯高理:iSq dS E ∑=⋅⎰⎰1ε正确的说法是: A.积分号内E 是q 1、q 2共同激发的; B.积分号内E 是q 1、q 2、q 3、q 4共同激发的;C.积分号内E 是q 3、q 4共同激发的;D.以上说法都不对。
11034 如题图11034,在点电荷+q 和-q 的静电场中,作高斯面S 1、S 2、 S 3,那么能够利用高斯定理直接计算出场强的合适的高斯面是: A.S 1; B.S 2; C.S 3; D.在这样的电场中找不到合适的高斯面。
11035 关于点电荷的电场有下列说法,其中正确的是:A.公式204r QE πε=中的Q 也是试探电荷;B.由204r QE πε=知,r →0时E →∞;C.对正点电荷由0204r r Q E πε=知,r 越小电场越强,对负点电荷由0204r rQ E πε=知,r 越小,电场越弱;D.利用点电荷的场强公式与迭加原理, 原则上可求各种带电体的场强。
11036 一均匀带电球面,电荷面密度为σ,面内电场强度处处为零,则球面上带电量为σdS 的面元在球面内产生的场强:A.处处为零; B .不一定处处为零; C.一定处处不为零; D.无法判断。
11037 空间某处附近的正电荷越多,则:+σ+σⅠ Ⅱ Ⅲ 题图11027题图11031题图11034A.位于该处的点电荷所受的力越大;B.该处的场强越大;C.若无限远处为电位零点,则该处的电位越高;D.若无限远处为零电位点,则该处的电位能越大。
