几个经典概率故事的解读
几个经典概率故事的解读

几个经典概率故事的解读摘要伴随着社会科学的迅猛发展,数学在生活中的应用越来越广泛,在我们的身边可以说是“无所不在”的;作为数学的一个重要部分——概率论,同样也具备着十分重要的作用.概率论是数学的一个重要分支,是专门研究讨论和揭示自然界中随机发生的现象及规律的数学学科,在实际生活有广泛的应用,把条件概率的知识运用到生活中,提出并解决问题.关键词:条件概率;贝叶斯公式;诚信;坚持不懈AbstractWith the rapid development of social sciences ,mathematics has widely used in our daily life ,can to say no wherever ,whatever as an important part of mathematics, probability theory,and also play a very important role .Probability theory as an important branch of mathematics, it is a specialized research and reveal the random phenomenon and its regularity in mathematics discipline, has widely application in real life, can only be better reasonable use conditional probability knowledge to practice. Using probability knowledge to explain the case in real life.Keywords:Conditional Probability;Bayes formula;integrity;persistence目录摘要 (I)Abstract........................................................................................................................ I I 目录 . (III)1.引言 (1)2.《范进中举》故事及其概率解读 (1)2.1《范进中举》的故事概述 (1)2.2概率乘法公式解读《范进中举》 (1)2.2.1条件概率 (1)2.2.2 概率乘法公式 (1)2.2.3 用概率乘法公式解读《范进中举》 (2)2.3 用概率思想解释水滴石穿 (2)2.4用概率思想解释的现实问题 (3)2.5《范进中举》引申的社会意义 (3)3.《狼来了》故事及其概率解读 (5)3.1《狼来了》故事概述 (5)3.2 用贝叶斯公式解读《狼来了》 (5)3.2.1贝叶斯公式 (5)3.2.2 用贝叶斯公式解读《狼来了》 (5)3.3用概率思想解释银行贷款问题 (6)3.4用概率思想解释现实问题 (7)3.5《狼来了》引申的社会意义 (9)4.总结 (11)参考文献 (12)谢辞 (13)1.引言条件概率是概率论知识的一个重要部分,它是在解决各种实际问题的实践过程中发展起来的,而利用条件概率知识也可以解释我们熟悉的故事或者身边的实例.本文从概率论的角度出发,用概率乘法公式对熟悉的《范进中举》故事进行概率解读,用贝叶斯公式对《狼来了》故事进行概率解读,并用故事中包含的概率思想解释现实生活中的问题.从故事本身出发引申出社会意义,对读者有一定的启发.2.《范进中举》故事及其概率解读2.1 《范进中举》的故事概述《范进中举》出自《儒林外史》,主人公范进,一生穷困潦倒,但却不愿放弃科考,想要金榜题名,光宗耀祖,可一考就是二十多次,都屡试落第,直至年过半百才迎来他人生中的第一大喜事——中秀才,继而他乘胜追击,参加乡试,获得举人这个士子都梦寐以求的称号.文章中对主人公范进的描写生动形象,大量运用夸张的措辞,深刻揭露了古代仕人渴望官职的丑恶灵魂,同时也批露了世态的炎凉.2.2概率乘法公式解读《范进中举》2.2.1条件概率一般来说,条件概率就是 在“已知某事件B 发生”的条件下,求事件A 发生的概率,这个概率称为在事件B 发生的条件下,事件A 发生的条件概率,表示为()B A P |.定义:设A 与B 是样本空间Ω中的两事件,若0)(>B P ,则称()()()B P AB P B A P =|为“在B 发生下A 的条件概率”,称为条件概率.2.2.2 概率乘法公式对∀的两个事件B A ,,若0)(>B P ,则有()()()B P B A P AB P ⋅=|,推广有,若0)...(121>-n A A A P ,则()()()()()1-n 21n 213121n 21|||A A A A P A A A P A A P A P A A A P ⋅⋅⋅⋅⋅⋅=⋅⋅⋅即为概率乘法公式.2.2.3 用概率乘法公式解读《范进中举》在故事中范进前20多次都未能考中,直到老年,最后一次中的举人,求他中举的可能性为多少,关于这个问题我们可以用概率论的知识来解决,即用乘法公式来解释:假设每一次考试,范进考中的概率为0.3(可能性很小),令j A 表示“第j 次考试并未考中”⋅⋅⋅=3,2,1j 则连续十次他都不中的概率()()()()()0282.03.01||10921101211021≈-=⋅⋅⋅⋅⋅⋅=⋅⋅⋅A A A A P A A P A P A A A P , 即考中的概率为9718.00282.0-1=,即为%18.97,所以他最后一次中举是肯定的.2.3 用概率思想解释水滴石穿以前,每逢下雨,屋檐下就会出现一个一个的小坑.原来,这是雨水击打地面,时间久了就会出现小坑,如果在雨水击打地面的地方放一块石头,一段时间的连阴雨过后,石块上雨水击打的部位就会陷下去,随后即会出现一个小坑.在海边经常会出现一块石块中间部位有一个或两个圆形的小洞.原来啊,这是由于海水击打岸边的碎石,时间久了,石块中间就会被海水击打出小洞,这就是水滴石穿.而在概率论里,我们可以用概率的乘法公式来解释这一现象,为什么“弱小”的水滴可以穿透“强大”的石块?假设水滴每次落下的概率为0.2(非常小),令i A 表示“第i 次水滴落下未打穿”⋅⋅⋅=2,1i ,则它连续十次都未能打穿的可能性用概率乘法公式表示为()()1074.02.01101021≈-=⋅⋅⋅A A A P ,即打穿的可能性为8926.01074.01=-,即为%26.89,所以如果水滴击打石块次数越多,石块被打穿的可能性就越大.所以当水滴击打石块的次数到达一定的时候,石块就会被穿透。
高中数学概率统计小故事

1.分赌本问题A ,B 二人赌博,各出注金a 元,每局每个人获胜的概率都是12,约定:谁先胜S 局,即赢得全部注金a 2元,现进行到A 胜1S 局、B 胜2S 局(1S 与2S 都小于S )时赌博因故停止,问此时注金a 2应如何分配给A 和B 才算公平?此问题文字最早见于1494年帕西奥利的一本著作,是对6=S ,51=S 和22=S 的情况的分析.由于对“公平分配”一词的意义没有一个公认的正确理解,在早期文献中出现过关于此问题的种种不同的解法,如今看来都不正确.例如,帕西奥利本人提出按2:S S 1的比例分配.塔泰格利亚则在1556年怀疑能找到一种数学解法的可能性,他认为这是一个应由法官来解决的问题,但他也提出了如下的解法:若2S S 1>,则A 取回自己下的注a ,并取走B 下的注的S S S 1/)(2-,这等于按)(:)(22S S S S S S 11+--+的比例瓜分注金.法雷斯泰尼在1603年根据某种理由,提出按)12(:)12(22S S S S S S 11+---+-的比例分配.卡丹诺在其1539年的著作中,通过较深的推理提出了一种解法:记1S S r -=1,22S S r -=.把注金按)1(22+r r ︰)1(11+r r 之比分给A 和B.他这个解法如今看来虽然仍不正确,但有一个重要之处,即他注意到起作用的是1S ,2S 与S 的差距,而不在其本身.这个问题的症结在于:它关乎每个人在当时状况下的期望值.从以上这些五花八门的解法中,似乎可以认为,这些作者已多少意识到这一点,但未能明确期望与概率的关系.而与此处有关的是:假定赌博继续进行下去,各人最终取胜的概率.循着这个想法问题很易解决:至多再赌121-+=r r r 局,即能分出胜负.假如A 获胜,他在这r 局中至少须胜1r 局.因此按二项分布,A 取胜的概率为r rr i A i r p -=∑⎪⎪⎭⎫ ⎝⎛=21,而B 取胜的概率为1B A p p =-.注金按B A p p :之比分配给A 和B ,因A ap 2和B ap 2是A ,B 在当时状态下的期望值.这个解是巴斯噶(B.Pascal, 1623~1662)在1654年提出的.他用了两种方法,其一是递推公式法,其二是用“巴斯噶三角”(即杨辉三角).1710年,蒙特姆特在一封信中给出了我们在前面写出的解法,且不必规定二人的获胜概率相同.后来他又把此问题推广到多个赌徒的情形.分赌本问题在概率史上起的作用,在于通过对这个在当时来说较复杂的问题的探索,对数学期望及其与概率的关系有了启示.有的解法,特别是巴斯噶的解法,使用或隐含了若干直到现在还广为使用的计算概率的工具.如组合法、递推公式、条件概率和全概率公式等.可以说,通过对这个问题的研究,概率计算从初期简单计数步入较为精细的阶段.2. 巴斯噶与费尔马的通信巴斯噶与费尔马(P. de Fermat ,1601-1665)的名字,对学习过中学以上数学的人来说,想必不陌生.巴斯噶三角,在我国称杨辉三角,中学教科书中已有提及.至于费尔马,因其“费尔马大定理”(不存在整数,,,≠xyx z y x xyz≠0和整数3≥n ,使n n n z y x =+) 于近年得到证明,名声更远播数学圈子内外.费尔马在数学上的名声主要因其数论方面的成就,其在概率史上占到一席地位,多少有些偶然,由于他与巴斯噶在1654年7~10月间来往的7封信件,其中巴致费的有3封.这几封信全是讨论具体的赌博问题.与前人一样,他们用计算等可能的有利与不利情况数,作为计算“机遇数”即概率的方法(他们没有使用概率这个名称).与前人相比,他们在方法的精细和复杂性方面大大前进了.他们广泛使用组合工具和递推公式,初等概率一些基本规律也都用上了.他们引进了赌博的值(value)的概念,值等于赌注乘以获胜概率.3年后,惠更斯改“值”为“期望” (expectation),这就是概率论的最重要的概念之一——(数学)期望的形成和命名过程.前文已指出:此概念在更早的作者中已酝酿了一段时间.这些通信中讨论的一个重要问题之一是分赌本问题,还讨论了更复杂的输光问题:甲、乙二人各有赌本a 和b 元(a ,b 为正整数),每局输赢1元,要计算各人输光的概率.这个问题拿现在的标准看也有相当的难度.由此也可看出这组通信达到的水平及其在概率论发展史上的重要性.有的学者,如丹麦概率学者哈尔德,认为巴、费2人在1654年的这些信件奠定了概率论的基础.这话相当有道理,但也应指出,这些通信的内容是讨论具体问题,没有明确陈述并提炼出概率运算的原则性内容.例如,他们想当然地使用了概率加法和乘法定理.但未将其作为一般原则凸现出来.促使巴、费2人进行这段通信的,是一个名叫德梅尔的人,他曾向巴斯噶请教几个有关赌博的问题.1564年7月29日巴斯噶首先给费尔马写信,转达了这些问题之一,请费尔马解决.所提问题并不难,但不知为何巴斯噶未亲自回答:将两颗骰子掷24次,至少掷出一个“双6”的机遇小于2/1(其值为.0)36/35(124≈-≈0.491 4).但从另一方面看,掷两颗骰子只有36种等可能结果,而24占了36的3/2,这似乎有矛盾,如何解释.现今学过初等概率论的读者都必能毫无困难地回答这个问题.巴、费通信中涉及的有关分赌本问题的解法,包含了一些在当时看很先进且直到现在仍广为使用的想法和技巧.3. 惠更斯的《机遇的规律》惠更斯是一个有多方面成就的、在当时声名与牛顿相若的大科学家.人们熟知他的贡献之一是单摆周期公式g l T /2π=.他在概率论的早期发展史上也占有重要地位,其主要著作《机遇的规律》出版于1657年,出版后得到学术界的高度重视,在欧洲作为概率论的标准教本长达50年之久.该著作的写作方式不大像一本书,而更像一篇论文.他从关于公平赌博(fair game)的值的一条公理出发,推出关于“期望”(这是他首先引进的术语)的3条定理.基于这些定理并利用递推法等工具,惠更斯解决了当时感兴趣的一些机遇博弈问题.最后,他提出了5个问题,对其中的3个给出了答案但未加证明.3条定理加11个问题,被称为惠更斯的14个命题.前3条如下述:命题1若某人在赌博中以等概率12得a ,b 元,则其期望为2/)(b a +元.命题2若某人在赌博中以等概率13得a ,b 和c 元,则其期望为3/)(c b a ++元.命题3若某人在赌博中以概率p ,)1(=+q p q 得a ,b 元,则其期望为qb pa +元.看了这些命题,现代的读者或许会感到惶惑:为何一个应取为定义的东西,要当作需要证明的定理? 答案在于,这反映了当时对纯科学的一种公认的处理方法,即应从尽可能少的“第一原理”(first principle ,即公理)出发,把其他内容推演出来.惠更斯只从一条公理出发而导出上述命题,其推理颇为别致,此处不细述.这几个命题是期望概念的一般化.此前涉及或隐含这一概念只是相当于命题3中0=b 的特例,即注金乘取胜概率,因而本质上没有超出概率这个概念的范围.惠更斯的命题将其一般化,是这个重要概念定型的决定性的一步.实际上,据惠更斯的命题不难证明:若某人在赌博中分别以概率得k a a ,,1 元,则其期望为11k k p a p a ++.这与现代概率论教科书中关于离散随机变量的期望的定义完全一致.余下的11个命题及最后的5个问题,都是在形形色色的赌博取胜约定下,去计算各方取胜的概率,其中命题4~9是关于2人和多人的分赌本问题.对这些及其他问题,惠更斯都用了现行概率论教科书中初等概率计算方法,通过列出一定的方程求解,大体上与巴斯噶的做法相似.这种方法后来被伯努利称为“惠更斯的分析方法”.最后5个问题较难一些,其解法的技巧性也较强.现举其一为例:A ,B 二人约定按ABBAABBAABB …掷两颗骰子,即A 先掷一次,然后从B 开始轮流各掷两次.若A 掷出和为6点,则A 胜;若B 掷出和为7点,则B 胜.求A ,B 获胜的概率.A 在一次投掷时掷出和为6的概率36/5=A p ,而B 在一次投掷时掷出和为7的概率6/136/6==B p .记B B A A p q p q -=-=1,1,又记i e 为在第1i -次投掷完时A ,B 都未取胜,求在这一条件下A 最终取胜的概率.利用全概率公式,并注意到约定的投掷次序,可以列出方程组:14433221,,,e q p e e q e e q e e q p e A A B B A A +===+=.由此容易得出略小于1/2.故此赌法对A 不利.机遇博弈在概率概念的产生及其运算规则的建立中,起了主导的作用.这一点不应当使人感到奇怪:虽说机遇无时不在,但要精确到数量上去考虑,在几百年前那种科学水平之下,只有在像掷骰子这类很简单的情况下才有可能.但这门学科建立后,既脱离赌博的范围又找到了多方面的应用.这也是一个有趣的例子,表明一种看似无益的活动(如赌博),可以产生对人类文明极有价值的副产物.把概率论由局限于对赌博机遇的讨论拓展出去的转折点和标志,应是1713年伯努利划时代著作《推测术》的出版,是在惠更斯的《机遇的规律》出版后56年.惠更斯这一著作,内容基本上限于掷骰子等赌博中出现各种情况的概率的计算,而伯努利这本著作不仅对以前的成果作了总结和发挥,更提出了“大数定律”这个无论从理论和应用角度看都有着根本重要性的命题,可以说其影响一直到今日而不衰.其对数理统计学的发展也有不可估量的影响,许多统计方法和理论都是建立在大数定律的基础上.有的概率史家认为,这本著作的出版,标志着概率概念漫长的形成过程的终结与数学概率论的开端.假定有一个事件A ,根据某种理论,我们算出其概率为p A P =)(.这理论是否正确呢?一个检验的方法就是通过实际观察,看其结果与此理论的推论——p A P =)(是否符合.或者,一开始我们根本就不知道)(A P 等于多少,而希望通过实际观察去估计其值.这些包含了数理统计学中两类重要问题——检验与估计.这个检验与估计概率p 的问题,是数理统计学中最常见、最基本的两个问题.要构造具体例子,最方便的做法是使用古典概率模型.拿一个缸子,里面装有大小、质地一样的球b a +个,其中白球a 个,黑球b 个.这时,随机从缸中抽出一球(意指各球有同等可能被抽出),则“抽出之球为白球”这事件A 有概率)/(b a a p +=.如果不知道a ,b 的比值,则p 也不知道.但我们可以反复从此缸内抽球(每次抽出记下其颜色后再放回缸中).设抽了N 次,发现白球出现N X 次,则用N X N /去估计p .这个估计含有一定程度不确定的误差,但我们直观上会觉得,抽取次数N 愈大,误差一般会愈小.这一点如伯努利所说:“哪怕最愚笨的人,也会经由他的本能,不需他人的教诲而理解的”.但对这个命题却无人能给出一个严格的理论证明.伯努利决心着手解决这个问题,其结果导致了以他的名字命名的大数定律的发现.这个发现对概率论和数理统计学有极重大的意义.伯努利把这一研究成果写在他的著作《推测术》的第四部分中,是该著作的精华部分.由于该书在概率统计史上的重要意义,在此对伯努利其人及此书的整个面貌先做一点介绍.4. 伯努利的《推测术》伯努利1654年出生于瑞士巴塞尔.在其家族成员中,对数学各方面做出过不同程度贡献的至少有12人,在概率论方面有5人,其中杰出的除他本人外,还有其弟弟约翰与侄儿尼科拉斯.伯努利的父亲为其规划的人生道路是神职人员.但他的爱好却是数学.他对数学的贡献除概率论外,还包括微积分、微分方程和变分法等.后者包括著名的悬链线问题.他和牛顿、莱布尼兹是同时代人,并与后者有密切的通信联系,因而非常了解当时新兴的微积分学的进展,学者们认为他在这方面的贡献,是牛、莱之下的第一人.此外,他对物理学和力学也做出过贡献.他与惠更斯长期保持通信联系,仔细阅读过惠更斯的《机遇的规律》,由此引发了他对概率论的兴趣.从他与莱布尼兹的通信中,可知他写《推测术》这一著作是在他生命的最后两年.在1705年他去世时,此书尚未整理定稿.由于家族内部的问题,整理和出版遗稿的工作,迟迟未能实现.先是其遗孀因对其弟约翰的不信任,不愿把整理和出版的事委托给他,后来又拒绝了欧洲一位富有学者捐资出版的建议.最后在莱布尼兹的敦促下,才决定由其侄儿尼科拉斯来负责这件事情.尼科拉斯也是当时重要的数学家,与欧拉和莱布尼兹保持通信联系.当时尚无科学期刊,学者的通信是学术交流的一种重要方式.《推测术》一书共239页,分四个部分.第一部分(P 2~71)对《机遇的规律》一书作了详细的注解,总量比惠更斯的原书长4倍.第二部分(P 72~137)是关于排列组合的系统的论述.第三部分(P 138~209)利用前面的知识,讨论了一些使用骰子等的赌博问题.第四部分(P 210~239)是关于概率论在社会、道德和经济等领域中的应用,其中包括了该书的精华、奠定了概率史上不朽地位的,以其名字命名的“伯努利大数定律”——大数定律的名称不是出自该书,首见于泊松1837年的一篇著作中.该书若缺了这一部分,则很可能会像某些早期概率论著作那样湮没无闻,或至多作为一本一般著作被人评价.该书最后有一长为35页的附录,用与友人通信的形式讨论网球比赛中计分问题.5. 伯努利大数定律现在我们来介绍伯努利《推测术》中最重要的部分——包含了如今被称之为“伯努利大数定律”的第四部分.回到前面的缸中抽球模型:缸中有大小、质地一样的球b a +个,其中白球a 个,黑球b 个,“抽出之球为白球”的概率为p ,则有)/(b a a p +=.假设有放回地从缸中抽球N 次,记N X 为抽到白球的次数,以N X N /估计p .这种估计法现今仍是数理统计学中最基本的方法之一.此处的条件是,每次抽取时都要保证缸中b a +个球的每一个有同等机会被抽出,但这一点在实践中并不见得容易保证.例如,产生中奖号码时可能要用复杂的装置.在实际工作中,统计学家有时用一种叫做“随机数表”的工具.这是一本很厚的书,各页按行、列排列着数字9,,2,1,0 ,它们是用据说是“充分随机”的方法产生的.在使用时,“随机地”翻到一页并随机地点到一个位置,以此处的数字确定抽出的对象.伯努利企图证明的是:用N X N /估计p 可以达到事实上的确定性——他称为道德确定性.其确切含义是:任意给定两个数0>ε和0>η,总可以取足够大的抽样次数N ,使事件{}ε>-|)/(|p N X N 的概率不超过η.这意思就很显然:ε>-|)/(|p N X N 表明估计误差未达到指定的接近程度ε,但这种情况发生的可能性可以“随心所欲地小”(代价是加大N ).为忠实于伯努利的表达形式,应指出两点:一是伯努利把ε限定于1)(-+b a ,虽然其证明对一般ε也有效.但他做这一模型限定与所用缸子模型的特殊性有关:必要时把缸中的白、黑球分别改为ra 和rb 个,则p 不变,1)(-+b a 改为1)(-+rb ra ,只须取r 足够大,便可使1)(-+rb ra 任意小.二是伯努利欲证明的是:对任给的0>c ,只要抽取次数足够大,就可使⎭⎬⎫⎩⎨⎧>->⎭⎬⎫⎩⎨⎧≤-εεp N X cP p N X P N N . (5)这与前面所说是一回事.因为由上式得.11c p N X P N +<⎭⎬⎫⎩⎨⎧>-ε (6)取c 充分大,可使(6)式右边小于η.另外要指出的是:伯努利使用的这个缸子模型使被估计的p 值只能取有理数,因而有损于结果的普遍性.但其证明对任意的p 成立,故这一细节并不重要.伯努利上述对事实上确定性数学的理解,即(5)式,有一个很值得赞赏的地方,即他在概率论的发展刚刚起步的阶段,就给出了问题的一个适当的提法.因为,既然我们欲证明的是当N 充分大时,N X N /和p 可以任意接近,则一个看来更直截了当的提法是,lim p N X N N =∞→ (7)而这不可能实现.因为原则上不能排除“每次抽到白球”的可能性,这时N X N /总为1,不能收敛到1<p .或者退一步:要求(7)式成立的概率为1,这一结论是对的,但直到1909年才由波莱尔给予证明,证明的难度比伯努利的提法大得多.设想一下,如果当时伯努利就采用该提法,他也许在有生之年不能完成这一工作.由于波莱尔的结论比伯努利的结论强,现今人们又把他们的结论分别称之为强大数定律和弱大数定律.6. 泊松公式、泊松分布与泊松大数定律泊松(Possion )的名字对学概率论与数理统计的人来说,可谓耳熟能详.原因主要在于泊松近似公式,以及更重要的是源于该近似公式的泊松分布,泊松分布的重要性和知名度在离散型分布中仅次于二项分布.泊松的另一个重要工作是把伯努利大数定律推广到每次试验中事件发生的概率可以不同的情况,现称泊松大数定律.继狄莫佛给出二项概率近似计算公式(10)之后,丹尼尔和拉普拉斯也给出了二项概率近似计算公式,但这些公式在现今的教科书上已很少提及,只有泊松近似公式则不然,其形式为,!),,(lim k e k p N b k N λλ-∞→= (11)其中Np N ∞→=lim λ,N k ,,2,1,0 =.公式(11)在教科书上通称为泊松逼近公式、泊松近似公式或泊松公式.它是泊松在1838年于《概率在法律审判的应用》一书中所引进,此公式适用于p 很小,N 很大而Np 又不很大时,这正好填补了狄莫佛公式(10)的不足,因后者只适用于p 不太接近于0和1的时候.不过,从历史上看,狄莫佛早在1712年已做出了这个结果.7. 贝叶斯及其传世之作托马斯•贝叶斯(Thomas Bayes,1701-1761)在18世纪上半叶的欧洲学术界,恐怕不能不算是一个很知名的人物.在他生前,没有发表过任何的科学论著.那时,学者之间的私人通信,是传播和交流科学成果的一种重要方式.许多这类信件得以保存下来并发表传世,而成为科学史上的重要文献,例如,前面提到的费尔马和巴斯噶的通信、伯努利与莱布尼兹的通信等.但对贝叶斯来说,这方面材料也不多.在他生前,除在1755年有一封致约翰•康顿的信(其中讨论了辛普森有关误差理论的工作)外,历史上没有记载他与当时的学术界有何重要的交往.但他曾在1742年当选为英国皇家学会会员(相当于科学院院士),因而可以想到,他必定曾以某种方式表现出其学术造诣而被当时的学术界所承认.如今,我们对这个生性孤僻、哲学气味重于数学气味的学术怪杰的了解,是因他的一篇题为“An essay towards solving a problem in the doctrine of chance(机遇理论中一个问题的解)”的遗作.此文发表后很长一个时期在学术界没有引起什么反响,但到20世纪以来突然受到人们的重视,成为贝叶斯学派的奠基石.1958年,国际权威性的统计杂志《Biometrika》(生物计量)重新刊载了这篇文章.此文也有中译本(见廖文等译《贝叶斯统计学——原理、模型及应用》的附录4,中国统计出版社1992年版).此文是他的两篇遗作之一,首次发表于1764年伦敦皇家学会的刊物《Philosophical Transactions》上.此文在贝叶斯生前已写就,为何当时未交付发表,后来的学者有些猜测,但均不足定论.据文献记载,在他逝世之前4个月,他在一封遗书中将此文及100英镑托付给一个叫普莱斯的学者,而贝叶斯当时对此人在何处也不了然.所幸的是,后来普莱斯在贝叶斯的文件中发现了这篇文章,他于1763年12月23日在皇家学会上宣读了此文,并在次年得以发表.发表时普莱斯为此文写了一个有实质内容的前言和附录.据普莱斯说,贝叶斯自己也准备了一个前言.这使人们无法确切区分:哪些思想属于贝叶斯本人,哪些又是普莱斯所附加的.贝叶斯写作此文的动机,说法也不一.一种表面上看来显然的说法是为了解决伯努利和狄莫佛未能解决的、二项分布概率p的“逆概率”问题,因为当时距这两位学者的工作发表后尚不久,有人认为他是受了辛普森误差工作的触动,想为这种问题的处理提供一种新的思想.还有人主张,贝叶斯写作此文,是为了给“第一推动力”的存在提供一个数学证明.这些说法现在都无从考证.上面提到“逆概率”这个名词.在较早的统计学著作中这个名词用得较多,现在已逐渐淡出.顾名思义,它是指“求概率这个问题的逆问题”:已知事件的概率为p,可由之计算某种观察结果出现的概率如何.反过来,给定了观察结果,问由之可以对概率p做出何种推断.推广到极处可以说,“正概率”是由原因推结果,是概率论;“逆概率”是由结果推原因,是数理统计.8. 拉普拉斯的“不充分推理原则”贝叶斯的遗作发表后很长一段时期,都没有得到学术界的注意,因而他的这种思想未能及早地发展成为一种得到广泛应用的统计推断方法.但是,也有些学者独立地朝这个方向思考,提出类似的思想并付诸实用,其中最重要的当属拉普拉斯.拉普拉斯在1774年的一篇文章中提出了所谓的“不充分推理原则”(principle of insufficient reasoning ).他的思想大致如下:如果一个问题中存在若干个不同的原因(cause) n A A A ,,,21 ,则在没有理由认为其中哪一个特别有优势时,概率应各取n /1,即认为各原因有同等机会出现.在统计问题中,这里所说的不同“cause ”n A A A ,,,21 可看作代表未知参数的不同的可能值.以E 记在这原因下可能产生的事件(例如,在某参数值之下观察到的样本),拉普拉斯提出:)|(/)|(i i A E P E A P 与i 无关. (12)用现今熟知的概率论知识很容易证明(12),但拉普拉斯在其文章中用了一个很复杂的证法.拉普拉斯的原则(12)可用于由)|(i A E P 推)|(E A P i ,这与贝叶斯的原则完全一样,也并未超出贝叶斯思想的范围.因此,现在统计学史上也把拉普拉斯视为贝叶斯统计的一个奠基者.9. 勒让德发明最小二乘法勒让德是法国大数学家,在数学的许多领域,包括椭圆、积分、数论和几何等方面,都有重大的贡献.最小二乘法最先出现在他于1805年发表的一本题为《计算彗星轨道的新方法》著作的附录中,该附录占据了这本长达80页著作的最后9页.勒让德在这本书前面几十页关于彗星轨道计算的讨论中没有使用最小二乘法,可见在他刚开始写作时,这一方法尚未在他头脑中成形.历史资料还表明,勒让德在参加测量巴黎子午线长这项工作很久以后还未发现这个方法.考虑到此书发表于1805年且该法出现在书尾的附录中,可以推测他发现这个方法应当在1805年或之前不久的某个时间.勒让德在该书72~75页描述了最小二乘法的思想、具体做法及方法的优点.他提到:使误差平方和达到最小,在各方程的误差之间建立了一种平衡,从而防止了某一极端误差(对决定参数的估计值)取得支配地位,而这有助于揭示系统的更接近真实的状态.的确,考察勒让德之前一些学者的做法,都是把立足点放在解出一个线性方程组上.这种做法对于误差在各方程之间的分布的影响如何,是不清楚的.在方法的具体操作上,勒让德指出,为实现20111()n i i ki k i x x x θθ=+++=∑最小而对各i θ求偏导数所形成的线性方程组⎪⎪⎩⎪⎪⎨⎧=====+∑∑==.,,1,,,1,0,,,,1,0110k j k r x x s k j s n i ji ri rj kr j r rj θθ (13)只涉及简单的加、乘运算,至于解线性方程组,这是当时已知的其他方法也难免的.现今我们把(13)叫做正则方程组,这是后来高斯引进的称呼.关于最小二乘法的优点,勒让德指出了以下几条:第一,通常的算术平均值是其一特例.第二,如果观察值全部严格符合某一线性方程,则这个方程必是最小二乘法的解.第三,如果在事后打算弃置某些观察值不用或增加新的观察值,对正则方程组的修改易于完成.从现在的观点看,这方法只涉及解线性方程组是其最重要的优点之一(其他的重要优点包括此法在统计推断上的一些优良性质,以及其广泛的适用性).近年发展起来的,从最小二乘法衍生出的其他一些方法,尽管在理论上有其优点,可是由于计算上的困难而影响了其应用.最小二乘法在19世纪初发明后,很快得到了欧洲一些国家的天文和地测学工作者的广泛使用.据不完全统计,自1805年至1864年的60年期间,有关这一方法的研究论文约250篇,一些百科全书,包括1837年出版的《不列颠百科全书》(第7版),都收进了有关这个方法的介绍.在研究论文中,有一些是关于。
有关概率的趣味小故事

《有关概率的趣味小故事》嘿,朋友!今天来给你讲几个有关概率的趣味小故事,可有意思啦。
有这么一个事儿,有个小镇上举办抽奖活动。
一等奖是一辆超级酷炫的汽车。
好多人都去参加,那场面可热闹了。
有个小伙子也去凑凑热闹,他心里想着,说不定自己运气好,能把汽车开回家呢。
抽奖开始了,大家都紧张得不行。
这个小伙子也在心里默默祈祷。
结果呢,他没中一等奖,不过也别灰心嘛。
这抽奖啊,概率可不大,那么多人参加,能中一等奖的那可真是幸运儿。
就像在大海里捞针一样难。
但是呢,大家还是愿意去试试,为啥?因为有那个万一呀,万一自己就是那个幸运的人呢。
还有一个故事。
有个学校要选学生代表去参加一个重要的活动。
从全校学生里选,每个班都有机会。
有个班级的同学们都很期待,大家都觉得自己有可能被选上。
这就像玩游戏,不知道幸运会降临到谁头上。
其实啊,这也是个概率问题。
全校那么多学生,能被选上的毕竟是少数。
但是大家还是充满希望,都在努力表现自己,说不定自己就是那个幸运的代表呢。
最后,虽然不是每个人都能被选上,但是大家在这个过程中也学到了很多,变得更加优秀了。
再讲一个。
有个老爷爷喜欢买彩票,他每周都去买。
他的家人就说他,别浪费钱啦,哪有那么容易中奖。
老爷爷可不这么想,他觉得自己总有一天会中奖的。
虽然中奖的概率很低,但是他享受这个期待的过程。
有一次,老爷爷真的中了个小奖,高兴得像个孩子一样。
这概率啊,有时候就是这么神奇,说不定什么时候就给你一个惊喜。
你看,概率这东西,在我们生活中到处都有。
有时候它让我们充满期待,有时候又让我们有点小失落。
但是不管怎样,这些小故事都让我们感受到了生活的趣味。
博弈论66个经典例子之六
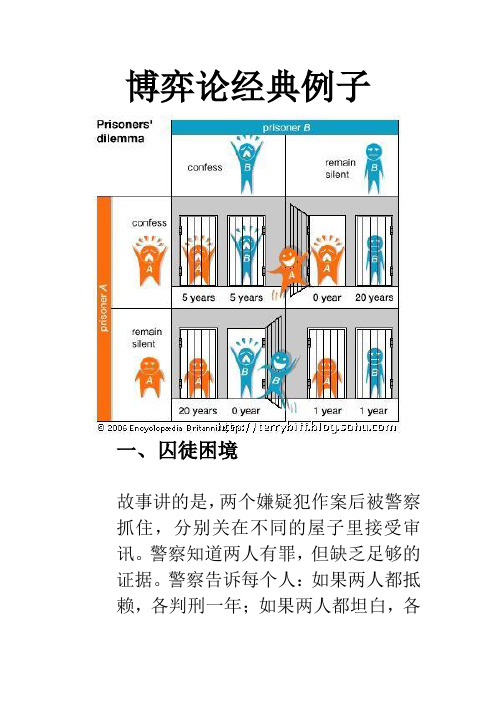
博弈论经典例子一、囚徒困境故事讲的是,两个嫌疑犯作案后被警察抓住,分别关在不同的屋子里接受审讯。
警察知道两人有罪,但缺乏足够的证据。
警察告诉每个人:如果两人都抵赖,各判刑一年;如果两人都坦白,各判八年;如果两人中一个坦白而另一个抵赖,坦白的放出去,抵赖的判十年。
于是,每个囚徒都面临两种选择:坦白或抵赖。
然而,不管同伙选择什么,每个囚徒的最优选择是坦白:如果同伙抵赖、自己坦白的话放出去,不坦白的话判一年,坦白比不坦白好;如果同伙坦白、自己坦白的话判八年,不坦白的话判十年,坦白还是比不坦白好。
结果,两个嫌疑犯都选择坦白,各判刑八年。
如果两人都抵赖,各判一年,显然这个结果好。
但这个帕累托改进办不到,因为它不能满足人类的理性要求。
囚徒困境所反映出的深刻问题是,人类的个人理性有时能导致集体的非理性——聪明的人类会因自己的聪明而作茧自缚。
二、旅行者困境两个旅行者从一个以出产细瓷花瓶著称的地方旅行回来,他们都买了花瓶。
提取行李的时候,发现花瓶被摔坏了,于是他们向航空公司索赔。
航空公司知道花瓶的价格大概在八九十元的价位浮动,但是不知道两位旅客买的时候的确切价格是多少。
于是,航空公司请两位旅客在100元以内自己写下花瓶的价格。
如果两人写的一样,航空公司将认为他们讲真话,就按照他们写的数额赔偿;如果两人写的不一样,航空公司就认定写得低的旅客讲的是真话,并且原则上按这个低的价格赔偿,同时,航空公司对讲真话的旅客奖励2元,对讲假话的旅客罚款2元。
为了获取最大赔偿而言,本来甲乙双方最好的策略,就是都写100元,这样两人都能够获赔100元。
可是不,甲很聪明,他想:如果我少写1元变成99元,而乙会写100元,这样我将得到101元。
何乐而不为?所以他准备写99元。
可是乙更聪明,他算计到甲要算计他写99元,于是他准备写98元。
想不到甲还要更聪明一个层次,估计到乙要写98元来坑他,于是他准备写97元……大家知道,下象棋的时候,不是说要多“看”几步吗,“看”得越远,胜算越大。
用概率知识解读《狼来了》

用概率知识解读《狼来了》李祥学习生活中,不知你有没有看到过这样的公式:O.99"M).O3,1.01叫=37.8。
它讲的是这样的生活道理:积睦步,以至千里;积怠惰,以致无成。
这个公式是概率在生活中的应用,不会随着人的意志而转移。
概率思维是人们正确观察事物所必须具备的品质。
希望大家能够用概率的思维分析并解决现实问题。
《狼来了》选自《伊索寓言》。
从前,在一个僻静遥远而又淳朴的山村里,有一个小孩,他每天都会赶着成群的羊到山间的草丛里吃草。
因为山里经常会有狼出没,所以山民对狼的警惕性很高。
有一天,小孩闲得无聊,想要做点“刺激”的事情,于是在山上喊:“狼来了!狼来了!”Lb下的村民闻声便拿起“武器”冲出去打狼何是到了山上,并没有发现狼的踪迹,村民们奇怪而又无奈地回去了。
第二天小孩故伎重施,又一次欺骗村民,喊:“狼来了!狼来了!”到了第三天,狼果真来了,可此时,无论小孩怎么喊叫,也没有人上±1来救他。
最后,他和羊群被狼“追杀”。
在故事中,设村民对这个小孩的最初的可信度为0.8。
假设小孩说第一次谎,信任度下降20%。
之后的每一次说谎,信任度下降率都是之前的2倍。
则小孩第一次说谎时村民对他的信任度为:P=薛-(;_20%J =0.640这个数据表明,村民对小孩的信任度由原来的0.8下降到0.64c当小孩第二次说谎时,村民对他的信任度为P= 0.64X(1,2x20%)=0.384。
此时的数据说明,村民对小孩的信任度由0.64下降到0.384。
所以小孩第三次喊“狼来了”,村民对他的信任度为P=0384X(「go%)=0.0768o这个数据表明,村民对小孩的信任度由0.64下降到0.0768。
由于前两次小孩对村民的欺骗,所以村民们第三次听到喊声后并没有上山救小孩。
感兴趣的同学也可以去网上搜索并学习用贝叶斯公式来定量分析小孩说谎概率是如何变化的。
随着概率知识的不断学习,你将会发现,先学习概率知识,再学会应用,对我们做出正确的判断和决策有极大作用。
用概率知识解读《狼来了》

龙源期刊网 用概率知识解读《狼来了》作者:李祥来源:《初中生世界·八年级》2018年第04期学习生活中,不知你有没有看到过这样的公式:0.99365≈0.03,1.01365≈37.8.它讲的是这样的生活道理:积跬步,以至千里;积怠惰,以致深渊.这个公式是概率在生活中的应用,不会随着人的意志而转移.概率思维是人们正确观察事物所必须具备的品质.希望大家能够用概率的思维分析并解决现实问题.《狼来了》选自《伊索寓言》.从前,在一个僻静遥远而又淳朴的山村里,有一个小孩,他每天都会赶着成群的羊到山间的草丛里吃草.因为山里经常会有狼出没,所以山民对狼的警惕性很高.有一天,他闲得无聊,想要做点“刺激”的事情,于是在山上喊:“狼来了!狼来了!”山下的村民闻声便拿起“武器”冲出去打狼,可是到了山上,并没有发现狼的踪迹,村民们奇怪而又无奈地回去了.第二天小孩故伎重施,又一次欺骗村民,喊“狼來了,狼来了”.到了第三天,狼果真来了,可此时,无论小孩怎么喊叫,也没有人上山来救他.最后,他和羊群被狼“追杀”.在故事中,设村民对这个小孩的最初的可信度为0.8.假设小孩说第一次谎,信任度下降20%.之后的每一次说谎,信任度都下降之前的2倍.则小孩第一次说谎时村民对他的信任度为:P=0.8×(1-20%)/1=0.64].这个数据表明,村民对小孩的信任度由原来的0.8下降到0.64.当小孩第二次说谎时,村民对他的信任度为P=0.64×(1-2×20%)/1=0.384].此时的数据说明,村民对小孩的信任度由0.64下降到0.384.所以小孩第三次喊“狼来了”,村民对他的信任度为P=[0.384×(1-4×20%)1=0.0768].这个数据表明,村民对小孩的信任度由0.64下降到0.0768.由于前两次小孩对村民的欺骗,所以村民们第三次听到喊声后并没有上山救小孩.随着概率知识的不断学习,你将会发现,先学习概率知识,再学会应用,对我们做出正确的判断和决策有极大作用.(作者单位:江苏省无锡市新安中学)。
著名的概率故事

著名的概率故事
著名的概率故事之一是“蒙提霍尔问题”,也被称为“三门问题”。
这个问题首次由美国数学家蒙提霍尔于1975年提出,并在电视游戏
节目《Let's Make a Deal》中引起了巨大的争议和讨论。
故事背景是:参赛者面对三扇门,其中一扇后面有一辆汽车,另外两扇门后面是山羊。
参赛者首先选择其中一扇门,然后主持人打开另外两扇门中的一扇,露出其中一只山羊。
接着,主持人询问参赛者是否要改变他的选择。
问题是,如果参赛者改变选择,他将有更高的几率选到汽车吗?
这个问题的答案是:是的,参赛者应该改变他的选择。
这个结果令人困惑的原因是,直觉上认为改变选择和不改变选择应该是一样的。
然而,通过概率计算,可以证明改变选择的几率为2/3,而不改变选择的几率仅为1/3。
这个问题的解释可以通过排除法来理解。
在最开始,参赛者选择任意一扇门的概率为1/3。
一旦主持人打开一扇门露出山羊,参赛者改变选择的概率就变成了剩下两扇门中有一扇是汽车的情况,即2/3。
因此,参赛者改变选择可以增加他选到汽车的几率。
蒙提霍尔问题引发了广泛的争议和讨论,许多人难以接受这个结果,甚至有些人坚持认为答案是错误的。
然而,通过数学推理和模拟实验,这个问题的答案已经被充分证明。
蒙提霍尔问题成为了概率学中一个经典的教学案例,也被广泛用于讲解概率和统计的课程中。
它揭示了我们常常受到直觉的影响而做
出错误的概率判断,强调了概率计算的重要性和奇妙性。
数学故事《概率之旅》

数学故事《概率之旅》概率之旅:数学故事引言概率,这个数学领域中的一部分,以其独特的魅力吸引着无数数学家和爱好者。
本故事将带领读者踏上一场概率之旅,从古代的骰子游戏到现代的随机模型,探索概率的起源、发展和应用。
起源:古代骰子游戏概率的起源可以追溯到古代文明。
古埃及、古希腊和古罗马的人们都喜欢玩骰子游戏。
他们通过观察骰子的结果,开始思考并计算事件发生的可能性。
发展:概率论的诞生17世纪,法国数学家布莱士·帕斯卡和皮埃尔·德·费马通过通信讨论了概率问题,奠定了概率论的基础。
他们提出了著名的帕斯卡定理和费马小定理。
1713年,雅各布·伯努利发表了《推测术》,这是第一本关于概率论的专著。
随后,丹尼尔·伯努利和雅各布·伯努利兄弟继续研究概率论,并将其应用于赌博问题。
应用:现代概率论的应用随着概率论的发展,它在各个领域得到了广泛的应用。
在物理学中,概率论为量子力学提供了数学基础。
在经济学中,概率论被用于研究市场的随机性。
在工程学中,概率论帮助工程师评估系统的可靠性。
随机模型:从生日问题到蒙特卡洛方法生日问题是一个经典的概率问题,它探讨了在一定人数中,至少有两个人生日相同的概率。
这个问题引出了许多有趣的数学结论。
蒙特卡洛方法是一种基于随机抽样的数值计算方法。
它通过模拟随机过程,得到问题的近似解。
蒙特卡洛方法在许多领域都有应用,如计算物理、金融衍生品定价等。
结论概率之旅让我们领略了概率论的奇妙世界。
从古代的骰子游戏到现代的随机模型,概率论不断发展,并在各个领域中发挥着重要作用。
这场旅程让我们明白,概率不仅是数学的一部分,也是我们生活中不可或缺的一部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例 某家商店出售某种零件,每箱装有 只,且已知每箱中都混杂有 只不合格零件,商店为了提高人气,采用“假一赔十”的销售方式:即顾客买一箱这种零件,如果随机的取出一只零件发现是不合格品,商店要立刻把 只合格的零件放在箱子里,不合格的那只零件不再放回,如果某一顾客在一个箱中随机地先后取出 只零件进行测试,求他发现的全是合格零件的概率.
设
,
第一次未还清贷款,银行对贷款者的信任度为
,
表明银行在贷款者第一次未还清贷款后,信任度由原来的
下降到 ,下降后 .贷款者第二次未还之前的 下降到 ,此时
.
当贷款者第三次贷款时,银行对他的信任度为
,
所以第三次,银行不再相信贷款者有能力还清贷款,便不会给予贷款者贷款.
关键词:条件概率;贝叶斯公式;诚信;坚持不懈
Abstract
With the rapid development of social sciences ,mathematics has widely used in our daily life ,can to say no wherever ,whatever as an important part of mathematics, probability theory,and also play a very important role .Probability theory as an important branch of mathematics, it is a specialized research and reveal the random phenomenon and its regularity in mathematics discipline, has widely application in real life, can only be better reasonable use conditional probability knowledge to practice. Usingprobabilityknowledge to explain the case in real life.
摘要
伴随着社会科学的迅猛发展,数学在生活中的应用越来越广泛,在我们的身边可以说是“无所不在”的;作为数学的一个重要部分——概率论,同样也具备着十分重要的作用.概率论是数学的一个重要分支,是专门研究讨论和揭示自然界中随机发生的现象及规律的数学学科,在实际生活有广泛的应用,把条件概率的知识运用到生活中,提出并解决问题.
3.3
某人向银行申请贷款,前两次未还清银行贷款,那么银行第三次还会给予他贷款吗?
记事件 为“贷款人未还清贷款”,事件 为“此贷款人可信”,设银行对贷款人的印象为 ,则 (即在未还清贷款的条件下,银行对贷款人的信任度),这里需要 ,前者为可信的贷款者未还清贷款的概率,后者为不可信的贷款者未还清贷款的概率.
米开朗琪罗——意大利伟大的雕塑家、画家和诗人,1508年,他接受了为罗马西斯廷教堂绘屋顶壁画的这一非常艰巨任务.高达20米的屋顶, 的面积, 多个画中人物,这无疑是一个无法完成的任务.可是他没有因为困难而退缩,坚定信念,夜以继日的工作,甚至多次从脚手架上摔下来,摔成重伤也要坚持奋斗在第一线,相信自己,永不放弃,终于经过四年的努力,完成了任务,给自己交了一份满意的答卷.但在此时,他的身体却已了摔成畸形.然而,就是因为他的坚持,他的执着,我们才得以看到这副优秀的,撼动人心的伟大作品.
3
3.1《狼来了》故事概述
《狼来了》选自《伊索寓言》,从前,在一个僻静遥远而又淳朴的山村里,有一个小孩,每天都会赶着成群的羊到山间的草丛里吃草.因为山里经常会有狼出没,所以山民对狼的警惕性很高.有一天,他闲的无聊,想要做点“刺激”的事情,于是在山上喊:“狼来了!狼来了!”,山下的村民闻声便拿起“武器”冲出去打狼,可是到了山上,并没有发现有狼的踪迹,山民奇怪而又无奈的回去了;第二天小孩故伎重施,又一次欺骗山民,喊到“狼来了,狼来了”;到了第三天,狼果真来了,可此时,无论小孩怎么喊叫,也没有人上山来救他,最后羊群被狼所“追杀”.
,
即考中的概率为 ,即为 ,所以他最后一次中举是肯定的.
2.3 用概率思想解释水滴石穿
以前,每逢下雨,屋檐下就会出现一个一个的小坑.原来,这是雨水击打地面,时间久了就会出现小坑,如果在雨水击打地面的地方放一块石头,一段时间的连阴雨过后,石块上雨水击打的部位就会陷下去,随后即会出现一个小坑.在海边经常会出现一块石块中间部位有一个或两个圆形的小洞.原来啊,这是由于海水击打岸边的碎石,时间久了,石块中间就会被海水击打出小洞,这就是水滴石穿.而在概率论里,我们可以用概率的乘法公式来解释这一现象,为什么“弱小”的水滴可以穿透“强大”的石块?
设山民对这个小孩的最初印象为 .用贝叶斯公式来求这个小孩说慌后山民对小孩的可信度 ,(即小孩说谎的条件下,小孩的话可信的可能性),在这个计算过程中需要知道 .前者解释为在小孩说话可信 的条件下孩子说谎 的可能性;后者解释为在小孩说话不可信 的条件下孩子说谎 的概率;
设 ,小孩第一次说谎,山民对他的信任度
欧立希——著名细菌学家,“阿托什尔”的发现者,这种药品治愈了当时流行的“昏睡病”,而有利就有弊,这种药品却导致患者失去光明,尽管如此,他并没有就此放弃,他和他的助手们坚持不懈,不断试验,失败了605次,终于在第606次的时候,研发出了既可以治疗昏睡病,又不会损害患者视力的可以双管齐下的药品,这就是后来的“六零六”.试想如果当时他在刚开始研发失败的时候就放弃了,亦或者在第605次失败时放弃了,那么就不会有“六零六”的问世,就不会有治疗昏睡病的良药.
即为概率乘法公式.
2.2.3 用概率乘法公式解读《范进中举》
在故事中范进前20多次都未能考中,直到老年,最后一次中的举人,求他中举的可能性为多少,关于这个问题我们可以用概率论的知识来解决,即用乘法公式来解释:
假设每一次考试,范进考中的概率为0.3(可能性很小),令 表示“第 次考试并未考中” 则连续十次他都不中的概率
2.2概率乘法公式
2.2.1条件概率
一般来说,条件概率就是 在“已知某事件 发生”的条件下,求事件 发生的概率,这个概率称为在事件 发生的条件下,事件 发生的条件概率,表示为 .
定义:设 与 是样本空间 中的两事件,若 ,则称 为“在 发生下 的条件概率”,称为条件概率.
2.2.2 概率乘法公式
对 的两个事件 ,若 ,则有 ,推广有,若 ,则
3.2 用贝叶斯公式解读《狼来了》
3.2.1贝叶斯公式
设 为一完备事件组,则 事件 有
,
右边的公式为分母,为全概率公式,是 项之和,分子是分母中的某一项.这个就是在概率乘法公式和全概率公式的基础上得出的著名的贝叶斯公式,也叫逆概公式.
3.2.2 用贝叶斯公式解读《狼来了》
在故事中记事件 为“小孩说谎”,记事件 为“小孩的话可信”,
这个数据表明,山民对小孩的信任度由原来的 下降到 ,所以下降后
.
当小孩第二次说谎时,山民对他的信任度
,
此时的数据说明,山民对小孩的信任度由 下降到 ,所以下降后
.
小孩第三次喊“狼来了”,山民对他的信任度
,
这个数据表明,山民对小孩的信任度由 下降到 ,由于前两次小孩对山民的欺骗,所以山民们第三次听到喊声没有上山救小孩.
坚持梦想就是选择了一条艰苦奋斗的道路,成功不仅需要追梦者自身的才华与能力,更需要的是永不言弃和永不言败的执着拼搏精神,愿意将自己的梦想或者想法付诸行动.在追梦路上为什么有人能够到达辉煌的顶峰,而为什么有的人却还是站在原地?原因就在于失败者没有成功者的那份坚持,没有成功者的那份执着,没有成功者那份选择迎难而上,一路披荆斩棘,就算受伤也把它当做一种人生的历练的坚持,只有经历了过程才知其中苦乐与酸甜,而失败者或者选择知难而退,又或者选择一味等待,就如守株待兔一般,等待所谓的适合自己的时机,适合自己的机遇,永远不会向前迈出艰难的一步,因为他们怕失败,怕失败后带来的种种打击,恐惧前方的荆棘,所以坚持的人成功了,他们实现了自己的梦想,逃避的人失败了,他们只一味在乎他们失败后的感受,从来没有考虑如何成功,如何能获得成功.有人说过,“一个人无论做任何事,在采取行动之前,都要谨慎考虑,严谨思路,一旦认定目标就要付出行动,不断前进,而不是迟疑,前怕狼后怕虎,畏首畏尾”.要相信,只有坚持才会让一切不可能变为可能,只有坚持才是硬道理.
3.4
案例一 游乐场经常有打气球的游戏,现在假设有3把枪同时对气球射击,射中气球概率分别为 ,一枪射中气球的的概率为 ,两枪射中气球的概率为 ,3枪均射中气球的概率为 ,求3枪一次射中气球的概率大概为?
设 ={3枪一次射中气球}
={恰有 发击中目标}, =1,2,3……{ }为互斥的完备事件组.
故
所以3枪一次射中气球的概率大概为0.253
2.
2.1
《范进中举》出自《儒林外史》,主人公范进,一生穷困潦倒,但却不愿放弃科考,想要金榜题名,光宗耀祖,可一考就是二十多次,都屡试落第,直至年过半百才迎来他人生中的第一大喜事——中秀才,继而他乘胜追击,参加乡试,获得举人这个士子都梦寐以求的称号.文章中对主人公范进的描写生动形象,大量运用夸张的措辞,深刻揭露了古代仕人渴望官职的丑恶灵魂,同时也批露了世态的炎凉.
假设水滴每次落下的概率为0.2(非常小),令 表示“第 次水滴落下未打穿” ,则它连续十次都未能打穿的可能性用概率乘法公式表示为 ,即打穿的可能性为 ,即为 ,所以如果水滴击打石块次数越多,石块被打穿的可能性就越大.所以当水滴击打石块的次数到达一定的时候,石块就会被穿透。这就是我们所谓的“水滴石穿”的道理.
Keywords:
Conditional Probability;Bayesformula;integrity;persistence
1.
条件概率是概率论知识的一个重要部分,它是在解决各种实际问题的实践过程中发展起来的,而利用条件概率知识也可以解释我们熟悉的故事或者身边的实例.本文从概率论的角度出发,用概率乘法公式对熟悉的《范进中举》故事进行概率解读,用贝叶斯公式对《狼来了》故事进行概率解读,并用故事中包含的概率思想解释现实生活中的问题.从故事本身出发引申出社会意义,对读者有一定的启发.
