二次函数与一元二次方程练习题(家庭作业)
二次函数与一元二次方程练习题(含答案)
二次函数与一元二次方程一、选择题1．如图2－128所示的是二次函数y ＝ax 2＋bx ＋c 的图象，则一次函数y=ax －b 的图象不经过 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．在二次函数y ＝ax 2＋bx ＋c 中，若a 与c 异号，则其图象与x 轴的交点个数为 ( )A ．2个B ．1个C ．0个D ．不能确定 3．根据下列表格的对应值：x 3.23 3.24 3.25 3.26 ax 2＋bx ＋c－0.06－0.020.030.09判断方程 ax 2＋bx ＋c=0(a ≠0，a ，b ，c 为常数)的一个解x 的取值范围是 ( )A ．3＜x ＜3.23B ．3．23＜x ＜3.24C ．3.24＜x ＜3.25D ．3.25＜x ＜3.26 4．函数cbx axy ++=2的图象如图l －2－30，那么关于x 的方程a x 2+b+c-3=0的根的情况是（ ）A ．有两个不相等的实数根B ．有两个异号实数根C ．有两个相等实数根D ．无实数根5．二次函数cbx ax y ++=2的图象如图l －2－31所示，则下列结论成立的是（ ）A ．a ＞0，bc ＞0，△＜0 B.a ＜0，bc ＞0，△＜0 C ．a ＞0，bc ＜0，△＜0 D.a ＜0，bc ＜0，△＞06．函数cbx ax y ++=2的图象如图 l －2－32所示，则下列结论错误的是（ ）A ．a ＞0B ．b 2－4ac ＞0C 、20ax bx c ++=的两根之和为负D 、20ax bx c ++=的两根之积为正7.不论m 为何实数，抛物线y=x 2－mx ＋m －2（ ） A ．在x 轴上方 B ．与x 轴只有一个交点 C ．与x 轴有两个交点 D ．在x 轴下方 二、填空题8．已知二次函数y ＝－x 2＋2x ＋m 的部分图象如图 2－129所示，则关于x 的一元二次方程－x 2＋2x ＋m ＝0的解为 ．9．若抛物线y=kx 2－2x ＋l 与x 轴有两个交点，则k 的取值范围是 ． 10．若二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象与x 轴只有一个交 点，则这个交点的坐标是 .11．已知函数y=kx 2－7x —7的图象和x 轴有交点，则k 的取值范围是 12．直线y=3x —3与抛物线y=x 2 －x+1的交点的个数是 . 三、解答题13.已知二次函数y=-x 2+4x-3,其图象与y 轴交于点B,与x 轴交于A, C 两点. 求△ABC 的周长和面积.14..在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某二次函数图象的一部分(如图),若这个男生出手处A 点的坐标为(0,2),铅球路线的最高处B 点的坐标为B(6,5).(1)求这个二次函数的表达式;(2)该男生把铅球推出去多远?(精确到0.01米).B(6,5)A(0,2)14121086420246xCy15.如图,已知抛物线y=-x 2+bx+c 与x 轴的两个交点分别为A(x 1,0),B(x 2,0) , 且x 1+x 2=4,1213x x .(1)求抛物线的代数表达式; (2)设抛物线与y 轴交于C 点,求直线BC 的表达式; (3)求△ABC 的面积.16．如果一个二次函数的图象经过点A(6，10)，与x 轴交于B ，C 两点，点B ，C 的横坐标分别为x 1，x 2，且x 1＋x 2＝6，x 1x 2＝5，求这个二次函数的解析式．17．已知关于x 的方程x 2＋(2m ＋1)x ＋m 2＋2＝0有两个不相等的实数根，试判断直线y ＝(2m －3)x －4m ＋7能否经过点A(－2，4)，并说明理由．18．二次函数y=ax 2＋bx ＋c(a ≠0)的图象如图2－130所示，根据图象解 答下列问题．(1)写出方程ax 2＋bx ＋c ＝0的两个根； (2)写出不等式ax 2＋bx ＋c ＞0的解集；(3)写出y 随x 的增大而减小的自变量x 的取值范围；BxOCy A(4)若方程ax2＋bx＋c＝k有两个不相等的实数根，求k的取值范围．19．如图2－131所示，已知抛物线P：y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F，G分别在线段BC，AC上，抛物线P上的部分点的横坐标对应的纵坐标如下.x …－3 －2 1 2 …y …－52－4 －520 …(1)求A，B，C三点的坐标；(2)若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系式，并指出m的取值范围；(3)当矩形DEFG的面积S最大时，连接DF并延长至点M，使FM＝k·DF，若点M不在抛物线P上，求k的取值范围；(4)若点D的坐标为(1，0)，求矩形DEFG的面积．参考答案1．B[提示：a ＞0，－2ba＜0，∴b ＞0．] 2．A 3．C 4.C 5.D 6.D 7.C8．x 1＝－l ，x 2＝3[提示：由图象可知，抛物线的对称轴为x=l ，与x 轴的交点是(3，0)，根据对称性可知抛物线与x 轴的另一个交点坐标为(－l ，0)，所以一元二次方程－x 2＋2x ＋m ＝0的解为x 1＝－1，x 2＝3．故填x 1＝－l ，x 2＝3．]9．k ＜1，且k ≠0[提示：若抛物线与x 轴有两个交点，则(－2)2－4k ＞0．] 10．(－2ba，0) 11.略 12.113.令x=0,得y=-3,故B 点坐标为(0,-3). 解方程-x 2+4x-3=0,得x 1=1,x 2=3. 故A 、C 两点的坐标为(1,0),(3,0).所以AC=3-1=2,AB=221310+=,BC=223332+=, OB=│-3│=3. C △ABC =AB+BC+AC=21032++. S △ABC =12AC ·OB=12×2×3=3.14.(1)设y=a(x-6)2+5,则由A(0,2),得2=a(0-6)2+5,得a=112-. 故y=112-(x-6)2+5. (2)由 112-(x-6)2+5=0,得x 1=26215,6215x +=-.结合图象可知:C 点坐标为(6215+ 故OC=6215+13.75(米)即该男生把铅球推出约13.75米15..(1)解方程组1212413x xxx+=⎧⎪⎨=⎪⎩, 得x1=1,x2=3故2210330b cb c⎧-++=⎪⎨-++=⎪⎩,解这个方程组,得b=4,c=-3.所以,该抛物线的代数表达式为y=-x2+4x-3.(2)设直线BC的表达式为y=kx+m.由(1)得,当x=0时,y=-3,故C点坐标为(0,-3).所以330mk m=-⎧⎨+=⎩, 解得13km=⎧⎨=-⎩∴直线BC的代数表达式为y=x-3 (3)由于AB=3-1=2,OC=│-3│=3.故S△ABC =12AB·OC=12×2×3=3.16．解：设函数为y＝ax2＋bx＋c(a≠0)，将A(6，10)代入，得10＝36a＋6b＋c①，当y＝0时，ax2＋bx＋c=0，又x1＋x2＝－ba=6②，x1x2＝ca＝5③，由①②③解得a=2，b＝－12，c＝10．所以解析式为y＝2x2－12x＋10．17．解：该直线不经过点A．理由如下：∵方程x2＋(2m＋1)x＋m2＋2＝0有两个不相等的实数根，∴△=(2m＋1)2－4(m2＋2)=4m－7＞0，∴2m－72＞0，∴2m－3＞0．又由4m－7＞0，得－4m＋7＜0，∴直线y=(2m－3)x－4m＋7经过第一、三、四象限，而A(－2，4)在第二象限，∴该直线不经过点A.18．解：(1)由二次函数y=ax2＋bx＋c(a≠0)的图象可知，抛物线与x轴交于(1，0)，B(3，0)两点，即x＝1或x＝3是方程ax2＋bx＋c＝0的两个根．(2)不等式ax2＋bx＋c＞0的解集，即是求y＞0的解集，由图象可知l＜x ＜3．(3)因为a＜0，故在对称轴的右侧y随x的增大而减小，即当x＞2时，y随x的增大而减小．(4)由图可知，22,242,43,baac baca⎧-=⎪⎪-⎪=⎨⎪⎪=⎪⎩解得2,8,6.abc=-⎧⎪=⎨⎪=-⎩代入方程得－2x2＋8x－6－k＝O．又因为方程有两个不相等的实数根，所以△＞0，即82－4×(－2)×(－6－k)＞0，解得k＜2．19．解法l：(1)任取x，y的三组值代入y=ax2＋bx＋c(a≠0)，求出解析式为y＝12x2＋x－4．令y＝0，得x1＝－4，x2＝2；令x＝0，得y=－4，∴A，B，C三点的坐标分别为A(2，0)，B(－4，0)，C(0，－4)．解法2：(1)由抛物线P过点(1，－52)，(－3，－52)可知，抛物线P的对称轴为x＝－1．又∵抛物线P过(2，0)，(－2，－4)，则由抛物线的对称性可知，点A，B，C的坐标分别为A(2，0)，B(－4，0)，C(0，－4)． (2)由题意，知AD DG AO OC=，而AO=2，OC=4，AD=2－m，故DG=4－2m．又BE EFBO OC=，EF=DG，得BE=4－2m，∴DE＝3m，∴S矩形DEFG ＝DG·DE＝(4－2m)·3m=12m－6m2(0＜m＜2)． (3)∵S矩形DEFG=12m－6m2(0＜m＜2)，∴m=1时，矩形的面积最大，且最大面积是6．当矩形面积最大时，其顶点为D(1，0)，G(1，－2)，F(－2，－2)，E(－2，0)．设直线DF的解析式为y＝kx＋b，易知k＝23，b＝－23.∴y=23x－23.又抛物线P的解析式为y＝12x2＋x－4．令23x－23=12x2＋x－4，解得x161-±.如图2－132所示，设射线DF与抛物线P相交于点N，则N161--．过N作x轴的垂线交x轴于H，得1612561339FN HEDF DE-----+===.∵点M不在抛物线P上，即点M不与N重合，此时k的取值范围是k561-+且k＞0． (4)由(3)知S矩形DEFG＝6．。
九年级数学上册《第二十二章二次函数与一元二次方程》同步练习题及答案(人教版)
九年级数学上册《第二十二章二次函数与一元二次方程》同步练习题及答案（人教版) 班级姓名学号一、单选题1．二次函数y＝ax2＋bx＋c，若ac＜0，则其图象与x轴( )A．有两个交点B．有一个交点C．没有交点D．可能有一个交点2．已知关于x的方程ax−x2+2x−3=0只有一个实数根，则实数a的取值范围是（）A．a＞0 B．a＜0 C．a≠0 D．a为一切实数3．已知二次函数y=x2−2x+m（m为常数）的图象与x轴的一个交点为(3,0)，则关于x的一元二次方程x2−2x+m=0的两个实数根是（）A．x1=−1，x2=3 B．x1=1C．x1=−1，x2=1 D．x1=34．若二次函数y=ax²+1图象经过点（-2，0），则关于x的方程a（x-2）²+1=0实数根为（）A．x1=0，x2=4 B．x1=-2，x2=6C．x1= 32，x2= 52D．x1=-4，x2=05．已知抛物线y＝ax2+bx−2与x轴没有交点，过A(−2,y1)、B(−3,y2)、C(1,y2)、D(√3,y3)四点，则y1,y2,y3的大小关系是( )A．y1>y2>y3B．y2>y1>y3C．y1>y3>y2D．y3>y2>y16．下表示用计算器探索函数y=x2+5x﹣3时所得的数值：x 0 0.25 0.5 0.75 1y ﹣3 ﹣1.69 ﹣0.25 1.31 3则方程x2+5x﹣3=0的一个解x的取值范围为（）A．0＜x＜0.25 B．0.25＜x＜0.5C．0.5＜x＜0.75 D．0.75＜x＜17．如图，抛物线y=ax2+bx+3（a≠0）的对称轴为直线x=1，如果关于x的方程ax2+bx﹣8=0（a≠0）的一个根为4，那么该方程的另一个根为（）A．﹣4 B．﹣2 C．1 D．38．二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①a﹣3b+2c ＞0；②3a﹣2b﹣c＝0；③若方程a（x+5）（x﹣1）＝﹣1有两个根x1和x2，且x1＜x2，则﹣5＜x1＜x2＜1；④若方程|ax2+bx+c|＝1有四个根，则这四个根的和为﹣8.其中正确的结论有（）A．1个B．2个C．3个D．4个二、填空题9．试写出一个二次函数关系式，使它对应的一元二次方程的一个根为0，另一个根在1到2之间：．10．已知抛物线y=ax2+bx+c与x轴有两个交点，那么一元二次方程ax2+bx+c=0 的根的情况是.11．二次函数y=ax2+bx+c(a≠0)的部分图象如图所示，对称轴为直线x=1，则关于x的方程ax2+bx+c=0(a≠0)的解为.12．在平面直角坐标系中，抛物线y=ax2+bx+c（a，b，c是常数，a＞0）的部分图象如图所示，直线x=1是它的对称轴．若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2＜x1＜3，则它的另一个根x2的取值范围是．13．已知二次函数y＝ax2+bx+c（a≠0）自变量x与函数值y之间满足下列数量关系：x ....... ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 ......y ....... 24 15 8 3 0 ﹣1 0 3 8 15 ......观察表中数据，代数式−b+√b2−4ac2a +−b−√b2−4ac2a+（a+b+c）（a﹣b+c）的值是；若s、t是两个不相等的实数，当s≤x≤t时，二次函数y＝ax2+bx+c（a≠0）有最小值0和最大值24，那么s t的值是．三、解答题14．在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-m+2的顶点为D.线段AB的两个端点分别为A(-3,m),B(1,m).（1）求点D的坐标(用含m的代数式表示);（2）若该抛物线经过点B(1,m),求m的值;（3）若线段AB与该抛物线只有一个公共点,结合函数的图象,求m的取值范围.15．某商场出售一种成本为20元的商品，市场调查发现，该商品每天的销售量(千克)与销售价(元/千克)有如下关系：w=-2x+80.设这种商品的销售利润为y (元).(1)求y与x之间的函数关系式；(2)在不亏本的前提下，销售价在什么范围内每天的销售利润随售价增加而增大?最大利润是多少?(3)如果物价部门规定这种产品的销售价不得高于28元/千克，该农户想要每天获得150元的销售利润，销售价应定为多少元?16．设二次函数y1=2x2+bx+c(b，c是常数)的图象与x轴交于A，B两点．（1）若A，B两点的坐标分别为(1，0)，(2，0)，求函数y)的表达式及其图象的对称轴．（2）若函数y1的表达式可以写成心=2(x-h)2-2(h是常数)的形式，求b+c的最小值．（3）设一次函数y2=x-m(m是常数)，若函数y1的表达式还可以写成y1=2(x-m)(x-m-2)的形式，当函数y=y1-y2的图象经过点(x0，0)时，求x0-m的值．17．已知二次函数y＝ax2+bx+c的图象过点(−1，0)，且对任意实数x，都有4x−12≤ax2+bx+c≤2x2+8x+6.二次函数与x轴的正半轴交点为A，与y轴交点为C；点M是中二次函数图象上的动点.在x轴上存在点N，使得以A、C、M、N为顶点的四边形是平行四边形.请求出所有满足条件的点N的坐标.18．某公司生产A种产品，它的成本是6元/件，售价是8元/件，年销售量为5万件．为了获得更好的效益，公司准备拿出一定的资金做广告，根据经验，每年投入的广告费是x万元，产品的年销售量将是原销售量的y倍，且y与x之间满足我们学过的二种函数（即一次函数和二次函数）关系中的一种，它们的关系如下表：x（万元）0 0.5 1 1.5 2 …y 1 1.275 1.5 1.675 1.8 …（1）求y与x的函数关系式（不要求写出自变量的取值范围）（2）如果把利润看作是销售总额减去成本费用和广告费用，试求出年利润W（万元）与广告费用x（万元）的函数关系式，并计算每年投入的广告费是多少万元时所获得的利润最大？（3）如果公司希望年利润W（万元）不低于14万元，请你帮公司确定广告费的范围．19．某菜农搭建了一个横截面为抛物线的大棚，尺寸如图：(1)如图建立平面直角坐标系，使抛物线对称轴为y轴，求该抛物线的解析式；(2)若需要开一个截面为矩形的门（如图所示），已知门的高度为1.60米，那么门的宽度最大是多少米（不考虑材料厚度）?（结果保留根号）参考答案1．A2．C3．A4．A5．A6．C7．B8．C9．y=x2﹣32x10．有两个不相等的实数根11．x1=312．﹣1＜x2＜013．-1；1或2 614．（1）∵y=x2-2mx+m2-m+2=(x-m)2-m+2,∴D点的坐标为(m,-m+2).（2）∵抛物线经过点B(1,m),∴m=1-2m+m2-m+2,解得m=3或m=1.（3）根据题意,∵A点的坐标为(-3,m),B点的坐标为(1,m),∴线段AB为y=m(-3≤x≤1),与y=x2-2mx+m2-m+2联立得x2-2mx+m2-2m+2=0,令y'=x2-2mx+m2-2m+2,若抛物线y=x2-2mx+m2-m+2与线段AB只有1个公共点,即函数y'在-3≤x≤1范围内只有一个零点,当x=-3时,y'=m2+4m+11<0,∵Δ>0,∴此种情况不存在,当x=1时,y'=m2-4m+3≤0,解得1≤m≤3.15．解：（1）y=w（x-20）=（x-20）（-2x+80）=-2x2+120x-1600则y=-2x2+120x-1600．由题意，有{x≥20−2x+80≥0解得20≤x≤40．故y与x的函数关系式为：y=-2x2+120x-1600，自变量x的取值范围是20≤x≤40；（2）∵y=-2x2+120x-1600=-2（x-30）2+200∴当x=30时，y有最大值200．故当销售价定为30元/千克时，每天可获最大销售利润200元； （3）当y=150时，可得方程-2x 2+120x-1600=150 整理，得x 2-60x+875=0 解得x 1=25，x 2=35．∵物价部门规定这种产品的销售价不得高于28元/千克，∴x 2=35不合题意，应舍去． 故当销售价定为25元/千克时，该农户每天可获得销售利润150元． 16．（1）解：由题意，得y 1=2(x-1)(x-2)． 图象的对称轴是直线x= 32（2）解：由题意，得y 1=2x 2-4hx+2h 2-2 ∴b+c=2h 2-4h-2 =2(h-1)2-4∴当h=1时，b+c 的最小值是-4. （3）解：由题意，得y=y 1-y 2 =2(x-m)(x-m-2)-(x-m) =(x-m)[2(x-m)-5]∵函数y 的图象经过点(x 0，0) ∴(x 0-m)[2(x 0-m)-5]=0 ∴x 0-m=0，或x 0-m= 52.17．解：令4x −12=2x 2−8x +6，解得：x 1=x 2=3 当x =3时4x −12=2x 2−8x +6=0 ∴y =ax 2+bx +c 必过(3，0) 又∵y =ax 2+bx +c 过(−1，0){a −b +c =09a +3b +c =0解得：{b =−2ac =−3a ∴y =ax 2−2ax −3a 又∵ax 2−2ax −3a ≥4x −12 ∴ax 2−2ax −3a −4x +12≥0 整理得：ax 2−2ax −4x +12−3a ≥0∴a >0且Δ=0∴(2a +4)2−4a(12−3a)=0 ∴(a −1)2=0∴a =1，b =−2，c =−3∴该二次函数解析式为y =x 2−2x −3令y =x 2−2x −3中y =0，得x =3，则A 点坐标为(3，0) 令x =0，得y =−3，则点C 坐标为(0，−3) 设点M 坐标为(m ，m 2−2m −3) N(n ，0)根据平行四边形对角线性质以及中点坐标公式可得： ①当AC 为对角线时，{x A +x C =x M +xN y A +y C =y M +y N即{3+0=m +n0−3=m 2−2m −3+0 解得：m 1=0（舍去） m 2=2 ∴n =1，即N 1(1，0)；②当AM 为对角线时，{x A +x M =x C +xN y A +y M =y C +y N即{3+m =0+n0+m 2−2m −3=−3+0 解得：m 1=0（舍去） m 2=2 ∴n =5，即N 2(5，0)；③当AN 为对角线时，{x A +x N =x C +xM y A +y N =y C +y M即{3+n =0+m0+0=−3+m 2−2m −3 解得：m 1=1+√7 m 2=1−√7 ∴n =√7−2或−√7−2∴N 3(√7−2，0)，N 4(−√7−2，0)；综上所述，N 点坐标为(1，0)或(5，0)或(√7−2，0)或(−√7−2，0). 18．解：（1）设y 与x 的函数关系式为y=ax 2+bx+c ，由题意，得{1=c1.5=a +b +c 1.8=4a +2b +c解得：{a =−0.1b =0.6c =1∴y=﹣0.1x 2+0.6x+1； （2）由题意，得W=（8﹣6）×5（﹣0.1x 2+0.6x+1）﹣x W=﹣x 2+5x+10W=﹣（x ﹣2.5）2+16.25． ∴a=﹣1＜0∴当x=2.5时，W 最大=16.25．答：年利润W （万元）与广告费用x （万元）的函数关系式为W=﹣x 2+5x+10，每年投入的广告费是2.5万元时所获得的利润最大为16.25万元． （3）当W=14时 ﹣x 2+5x+10=14 解得：x 1=1，x 2=4∴1≤x ≤4时，年利润W （万元）不低于14万元． 19．（1）由图可设抛物线的解析式为：y =ax 2+2由图知抛物线与轴正半轴的交点为（2，0），则a ×22+2=0 ∴a =−12∴抛物线的解析式为：y =−12x 2+2 （2）当y=1.60时，得：x=±2√55所以门的宽度最大为2√55-（-2√55）=4√55米。
二次函数与一元二次方程练习题(含答案)
二次函数与一元二次方程一、选择题1．如图2－128所示的是二次函数y ＝ax 2＋bx ＋c 的图象，则一次函数y=ax －b 的图象不经过 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．在二次函数y ＝ax 2＋bx ＋c 中，若a 与c 异号，则其图象与x 轴的交点个数为 ( )A ．2个B ．1个C ．0个D ．不能确定 3．根据下列表格的对应值：x 3.23 3.24 3.25 3.26 ax 2＋bx ＋c－0.06－0.020.030.09判断方程 ax 2＋bx ＋c=0(a ≠0，a ，b ，c 为常数)的一个解x 的取值范围是 ( )A ．3＜x ＜3.23B ．3．23＜x ＜3.24C ．3.24＜x ＜3.25D ．3.25＜x ＜3.26 4．函数cbx axy ++=2的图象如图l －2－30，那么关于x 的方程a x 2+b+c-3=0的根的情况是（ ）A ．有两个不相等的实数根B ．有两个异号实数根C ．有两个相等实数根D ．无实数根5．二次函数cbx ax y ++=2的图象如图l －2－31所示，则下列结论成立的是（ ）A ．a ＞0，bc ＞0，△＜0 B.a ＜0，bc ＞0，△＜0 C ．a ＞0，bc ＜0，△＜0 D.a ＜0，bc ＜0，△＞06．函数cbx ax y ++=2的图象如图 l －2－32所示，则下列结论错误的是（ ）A ．a ＞0B ．b 2－4ac ＞0C 、20ax bx c ++=的两根之和为负D 、20ax bx c ++=的两根之积为正7.不论m 为何实数，抛物线y=x 2－mx ＋m －2（ ） A ．在x 轴上方 B ．与x 轴只有一个交点 C ．与x 轴有两个交点 D ．在x 轴下方 二、填空题8．已知二次函数y ＝－x 2＋2x ＋m 的部分图象如图 2－129所示，则关于x 的一元二次方程－x 2＋2x ＋m ＝0的解为 ．9．若抛物线y=kx 2－2x ＋l 与x 轴有两个交点，则k 的取值范围是 ． 10．若二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象与x 轴只有一个交 点，则这个交点的坐标是 .11．已知函数y=kx 2－7x —7的图象和x 轴有交点，则k 的取值范围是 12．直线y=3x —3与抛物线y=x 2 －x+1的交点的个数是 . 三、解答题13.已知二次函数y=-x 2+4x-3,其图象与y 轴交于点B,与x 轴交于A, C 两点. 求△ABC 的周长和面积.14..在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某二次函数图象的一部分(如图),若这个男生出手处A 点的坐标为(0,2),铅球路线的最高处B 点的坐标为B(6,5).(1)求这个二次函数的表达式;(2)该男生把铅球推出去多远?(精确到0.01米).B(6,5)A(0,2)14121086420246xCy15.如图,已知抛物线y=-x 2+bx+c 与x 轴的两个交点分别为A(x 1,0),B(x 2,0) , 且x 1+x 2=4,1213x x .(1)求抛物线的代数表达式; (2)设抛物线与y 轴交于C 点,求直线BC 的表达式; (3)求△ABC 的面积.16．如果一个二次函数的图象经过点A(6，10)，与x 轴交于B ，C 两点，点B ，C 的横坐标分别为x 1，x 2，且x 1＋x 2＝6，x 1x 2＝5，求这个二次函数的解析式．17．已知关于x 的方程x 2＋(2m ＋1)x ＋m 2＋2＝0有两个不相等的实数根，试判断直线y ＝(2m －3)x －4m ＋7能否经过点A(－2，4)，并说明理由．18．二次函数y=ax 2＋bx ＋c(a ≠0)的图象如图2－130所示，根据图象解 答下列问题．(1)写出方程ax 2＋bx ＋c ＝0的两个根； (2)写出不等式ax 2＋bx ＋c ＞0的解集；(3)写出y 随x 的增大而减小的自变量x 的取值范围；BxOCy A(4)若方程ax2＋bx＋c＝k有两个不相等的实数根，求k的取值范围．19．如图2－131所示，已知抛物线P：y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F，G分别在线段BC，AC上，抛物线P上的部分点的横坐标对应的纵坐标如下.x …－3 －2 1 2 …y …－52－4 －520 …(1)求A，B，C三点的坐标；(2)若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系式，并指出m的取值范围；(3)当矩形DEFG的面积S最大时，连接DF并延长至点M，使FM＝k·DF，若点M不在抛物线P上，求k的取值范围；(4)若点D的坐标为(1，0)，求矩形DEFG的面积．参考答案1．B[提示：a ＞0，－2ba＜0，∴b ＞0．] 2．A 3．C 4.C 5.D 6.D 7.C8．x 1＝－l ，x 2＝3[提示：由图象可知，抛物线的对称轴为x=l ，与x 轴的交点是(3，0)，根据对称性可知抛物线与x 轴的另一个交点坐标为(－l ，0)，所以一元二次方程－x 2＋2x ＋m ＝0的解为x 1＝－1，x 2＝3．故填x 1＝－l ，x 2＝3．]9．k ＜1，且k ≠0[提示：若抛物线与x 轴有两个交点，则(－2)2－4k ＞0．] 10．(－2ba，0) 11.略 12.113.令x=0,得y=-3,故B 点坐标为(0,-3). 解方程-x 2+4x-3=0,得x 1=1,x 2=3. 故A 、C 两点的坐标为(1,0),(3,0).所以AC=3-1=2,AB=221310+=,BC=223332+=, OB=│-3│=3. C △ABC =AB+BC+AC=21032++. S △ABC =12AC ·OB=12×2×3=3.14.(1)设y=a(x-6)2+5,则由A(0,2),得2=a(0-6)2+5,得a=112-. 故y=112-(x-6)2+5. (2)由 112-(x-6)2+5=0,得x 1=26215,6215x +=-.结合图象可知:C 点坐标为(6215+ 故OC=6215+13.75(米)即该男生把铅球推出约13.75米15..(1)解方程组1212413x xxx+=⎧⎪⎨=⎪⎩, 得x1=1,x2=3故2210330b cb c⎧-++=⎪⎨-++=⎪⎩,解这个方程组,得b=4,c=-3.所以,该抛物线的代数表达式为y=-x2+4x-3.(2)设直线BC的表达式为y=kx+m.由(1)得,当x=0时,y=-3,故C点坐标为(0,-3).所以330mk m=-⎧⎨+=⎩, 解得13km=⎧⎨=-⎩∴直线BC的代数表达式为y=x-3 (3)由于AB=3-1=2,OC=│-3│=3.故S△ABC =12AB·OC=12×2×3=3.16．解：设函数为y＝ax2＋bx＋c(a≠0)，将A(6，10)代入，得10＝36a＋6b＋c①，当y＝0时，ax2＋bx＋c=0，又x1＋x2＝－ba=6②，x1x2＝ca＝5③，由①②③解得a=2，b＝－12，c＝10．所以解析式为y＝2x2－12x＋10．17．解：该直线不经过点A．理由如下：∵方程x2＋(2m＋1)x＋m2＋2＝0有两个不相等的实数根，∴△=(2m＋1)2－4(m2＋2)=4m－7＞0，∴2m－72＞0，∴2m－3＞0．又由4m－7＞0，得－4m＋7＜0，∴直线y=(2m－3)x－4m＋7经过第一、三、四象限，而A(－2，4)在第二象限，∴该直线不经过点A.18．解：(1)由二次函数y=ax2＋bx＋c(a≠0)的图象可知，抛物线与x轴交于(1，0)，B(3，0)两点，即x＝1或x＝3是方程ax2＋bx＋c＝0的两个根．(2)不等式ax2＋bx＋c＞0的解集，即是求y＞0的解集，由图象可知l＜x ＜3．(3)因为a＜0，故在对称轴的右侧y随x的增大而减小，即当x＞2时，y随x的增大而减小．(4)由图可知，22,242,43,baac baca⎧-=⎪⎪-⎪=⎨⎪⎪=⎪⎩解得2,8,6.abc=-⎧⎪=⎨⎪=-⎩代入方程得－2x2＋8x－6－k＝O．又因为方程有两个不相等的实数根，所以△＞0，即82－4×(－2)×(－6－k)＞0，解得k＜2．19．解法l：(1)任取x，y的三组值代入y=ax2＋bx＋c(a≠0)，求出解析式为y＝12x2＋x－4．令y＝0，得x1＝－4，x2＝2；令x＝0，得y=－4，∴A，B，C三点的坐标分别为A(2，0)，B(－4，0)，C(0，－4)．解法2：(1)由抛物线P过点(1，－52)，(－3，－52)可知，抛物线P的对称轴为x＝－1．又∵抛物线P过(2，0)，(－2，－4)，则由抛物线的对称性可知，点A，B，C的坐标分别为A(2，0)，B(－4，0)，C(0，－4)． (2)由题意，知AD DG AO OC=，而AO=2，OC=4，AD=2－m，故DG=4－2m．又BE EFBO OC=，EF=DG，得BE=4－2m，∴DE＝3m，∴S矩形DEFG ＝DG·DE＝(4－2m)·3m=12m－6m2(0＜m＜2)． (3)∵S矩形DEFG=12m－6m2(0＜m＜2)，∴m=1时，矩形的面积最大，且最大面积是6．当矩形面积最大时，其顶点为D(1，0)，G(1，－2)，F(－2，－2)，E(－2，0)．设直线DF的解析式为y＝kx＋b，易知k＝23，b＝－23.∴y=23x－23.又抛物线P的解析式为y＝12x2＋x－4．令23x－23=12x2＋x－4，解得x161-±.如图2－132所示，设射线DF与抛物线P相交于点N，则N161--．过N作x轴的垂线交x轴于H，得1612561339FN HEDF DE-----+===.∵点M不在抛物线P上，即点M不与N重合，此时k的取值范围是k561-+且k＞0． (4)由(3)知S矩形DEFG＝6．。
二次函数与一元二次方程(习题及答案)
二次函数与一元二次方程（习题）例题示范例：若一元二次方程(x -a )(x -b ) = - 3a <b ）的两个实数根分别2为 x 1，x （2 x 1 < x 2），则实数 a ，b ，x 1，x 2 的大小关系为（ ） A ． a < x 1 < b < x 2 C ． x 1 < a < x 2 < b 思路分析B ． a < x 1 < x 2 < b D ． x 1 < a < b < x 2a ，b 可以看做抛物线 y =(x -a )(x -b )与 x 轴交点的横坐标，x 1，x 2可以看做抛物线 y =(x -a )(x -b )与直线 y = - 3的交点的横坐标．2如图所示，-b )a < x 1 < x 2 <b 故选 B ．巩固练习1.二次函数y=x2-2x-3 的图象如图所示，当y < 0 时，自变量x的取值范围是（）A．-1 <x <3 C．x > 3 B．x <-1D．x <-1或x > 3第1 题图第2 题图2.二次函数y =ax2 +bx +c （a≠0）的图象如图所示，若ax2 +bx +c +k = 0（k≠0）有两个不相等的实数根，则k 的取值范围是（）A．k<-3 B．k >-3 C．k< 3 D．k> 33.抛物线y =-x 2 +bx +c 的部分图象如图所示，若y > 0 ，则x的取值范围是（）A．- 4 <x < 1C．x <-4 或x > 1B．- 3 <x < 1D．x <-3 或x > 1第3 题图第4 题图4.函数y =x2 -2x -2 的图象如图所示，根据该图象提供的信息，可求得使y ≥1成立的x 的取值范围是（）A．-1≤x ≤3C．x <-1或x > 3B．- 1 <x < 3D．x ≤-1或x ≥35.如图是二次函数 y = ax 2 + bx + c 的部分图象，由图象可知不等式ax 2 + bx + c < 0 的解集是（ ）A ． -1 < x < 5C ． x < -1且x > 5B ． x > 5D ． x < -1或x > 5第 5 题图第 6 题图6.如图，若抛物线 y =x 2+1与双曲线 y = k的交点 A 的横坐标x为 1，则关于 x 的不等式 k+ x 2 +1 < 0 的解集是（ ）xA ． x > 1B ． x < -1C ．0 < x < 1D ．-1 < x < 0 7.坐标平面上，若平移二次函数 y =2(x -175)(x -176)+6 的图象， 使其与 x 轴交于两点，且此两点的距离为 1 个单位，则平移方式可为下列哪一种（ ）A ．向上平移 3 个单位B ．向下平移 3 个单位C ．向上平移 6 个单位D ．向下平移 6 个单位 8.设一元二次方程(x -1)(x - 3) = k （ k < 0 ）的两根分别为 α，β， 且α < β ，则 α，β，1，3 之间的大小关系为；(x -1)(x - 3) < k 的解集为．9.若二次函数的图象 y = (m - 2)x 2 + x 与直线 y = 2x -1 没有交点，求m 的取值范围．10.已知P(-3，m)和Q(1，m)是抛物线y = 2x2 +bx +1 上的两点．（1）求b 的值；（2）将抛物线y = 2x2 +bx +1 的图象先向上平移2 个单位，再向左平移1 个单位，请判断新抛物线与x 轴的交点情况．11.已知二次函数y =x 2 + 2x +m 的图象C1 与x 轴有且只有一个交点，则C1 的顶点坐标为．12.若关于x 的一元二次方程x2 -x -n = 0 无实数根，则函数y =x 2 -x -n 的图象顶点在第象限．13.抛物线y =ax2 +bx +c 上部分点的横坐标x，纵坐标y 的对应值如下表：①一元二次方程ax2 +bx +c = 0 的根为．②抛物线经过点(-3，)；③在对称轴右侧，y 随x 的增大而．（2）确定抛物线y =ax2 +bx +c 的解析式，并求出该函数的最值．思考小结1. 对于二次函数y =ax2 +bx +c 和一元二次方程ax2 +bx +c = 0的关系，尝试着进行总结：①函数与x 轴交点坐标，与方程的根：．②函数与x 轴交点个数，与方程解的个数：当Δ> 0 时，函数与x 轴有个交点，方程有根；当Δ= 0 时，函数与x 轴有个交点，方程有根；当Δ< 0 时，函数与x 轴交点，方程根．5【参考答案】 巩固练习1. A2. C3. B4. D5. D6. D7. D8.1 < α < β < 3； α < x< β9. m >9410. （1）b =4 （2）无交点 11. (-1，0) 12. 一13. （1）① x 1 = -2，x 2 = 1 ②8 ③增大（2） y = 2x 2 + 2x - 4 ，最小值： -92思考小结1. ①函数与 x 轴交点的横坐标即为方程的根②两，两；一，一；无，无．6。
九年级数学《二次函数与一元二次方程》同步练习题
九年级数学《二次函数与一元二次方程》同步练习题第1题. 抛物线2283y x x =--与x 轴有个交点，因为其判别式24b ac -=0，相应二次方程23280x x -+=的根的情况为 ．答案：0 92-<没有实数根．第2题. 函数22y mx x m =+-（m 是常数）的图像与x 轴的交点个数为（ ）Ａ．0个 Ｂ．1个 Ｃ．2个 Ｄ．1个或2个答案：Ｃ第3题. 关于二次函数2y ax bx c =++的图像有下列命题：①当0c =时，函数的图像经过原点；②当0c >，且函数的图像开口向下时，方程20ax bx c ++=必有两个不相等的实根；③函数图像最高点的纵坐标是244ac b a-；④当0b =时，函数的图像关于y 轴对称． 其中正确命题的个数是（ ）Ａ．1个 Ｂ．2个 Ｃ．3个Ｄ．4个答案：Ｃ第4题. 关于x 的方程25mx mx m ++=有两个相等的实数根，则相应二次函数25y mx mx m =++-与x 轴必然相交于点，此时m =．答案：一 4第5题. 抛物线2(21)6y x m x m =---与x 轴交于两点1(0)x ，和2(0)x ，，若121249x x x x =++，要使抛物线经过原点，应将它向右平移 个单位．答案：4或9第6题. 关于x 的二次函数22(81)8y mx m x m =+++的图像与x 轴有交点，则m 的范围是（ ）Ａ．116m <-Ｂ．116m -≥且0m ≠ Ｃ．116m =-Ｄ．116m >-且0m ≠ 答案：Ｂ第7题. 已知抛物线21()3y x h k =--+的顶点在抛物线2y x =上，且抛物线在x 轴上截得的线段长是h 和k 的值．答案：21()3y x h k =--+，顶点()h k ，在2y x =上，2h k ∴=，22221122()3333y x h h x hx h ∴=--+=-++．又它与x 轴两交点的距离为12x x a∴-==== 求得2h =±，4k =，即2h =，4k =或2h =-，4k =．第8题. 已知函数22y x mx m =-+-．（1）求证：不论m 为何实数，此二次函数的图像与x 轴都有两个不同交点； （2）若函数y 有最小值54-，求函数表达式．答案：（1）222()4(2)48(2)4m m m m m ∆=---=-+=-+，不论m 为何值时，都有0∆>，此时二次函数图像与x 轴有两个不同交点．（2）2244(2)5444ac b m m a ---==- ，2430m m -+=，1m ∴=或3m =，所求函数式为21y x x =--或231y x x =-+．第9题. 下图是二次函数2y ax bx c =++的图像，与x 轴交于B ，C 两点，与y 轴交于A 点． （1）根据图像确定a ，b ，c 的符号，并说明理由；（2）如果A 点的坐标为(03)-，，45ABC ∠=，60ACB ∠=，求这个二次函数的函数表达式．答案：（1）抛物线开口向上，0a >；图像的对称轴在y 轴左侧，02ba-<，又0a >， 0b ∴>；图像与y 轴交点在x 轴下方，0c ∴<．0a ∴>，0b >，0c <．（2）(03)A -，，3OA =，45ABC ∠=，60ACB ∠=，3tan OA OB ABC==∠，tan 60OA OC ==(30)B ∴-，，C．设二次函数式为(3)(y a x x =+， 把(03)-，代入上式，得3a =∴所求函数式为2(3)(1)333y x x x x =+=+-．第10题. 已知抛物线222m y x mx =-+与抛物线2234m y x mx =+-在直角坐标系中的位置如图所示，其中一条与x 轴交于A ，B 两点．（1）试判断哪条抛物线经过A ，B 两点，并说明理由；（2）若A ，B 两点到原点的距离AO ，OB 满足条件1123OB OA -=，求经过A ，B 两点的这条抛物线的函数式．答案：（1）抛物线不过原点，0m ≠，令2202m x m x -+=，2221()402m m m ∆=--⨯=-<，222m y x mx =-+∴与x 轴无交点，∴抛物线2234y x mx m =+-经过A ，B 两点． （2）设1(0)A x ，，2(0)B x ，，1x ，2x 是方程22304x mx m +-=的两根12x x m +=-，21234x x m =-，A 在原点左边，B 在原点右边，则1AO x =-，2OB x =．123OB OA 1-=．211123x x ∴+=，121223x x x x +=，22334m m -=-，得2m =，∴所求函数式为223y x x =+-．第11题. 已知二次函数2224y x mx m =-+．（1）求证：当0m ≠时，二次函数的图像与x 轴有两个不同交点；（2）若这个函数的图像与x 轴交点为A ，B ，顶点为C ，且△ABC的面积为表达式．答案：（1）22222(4)421688m m m m m ∆=--⨯⨯=-=．0m ≠ ，280m ∴>，∴这个抛物线与x 轴有两个不同交点．（2）设1(0)A x ，，212(0)()B x x x >，，则1x ，2x 是方程22240x mx m -+=两根，122x x m +=，2122m x x =，21AB x x =-====， C 点纵坐标22224816442c ac b m m y m a --===-⨯， ∴△ABC 中AB 边上的高22h m m =-=．212ABC S AB h m m === ，2m =，2m =±， 2284y x x ∴=++或2284y x x =-+．第12题.如图所示，函数2(2)(5)y k x k =-+-的图像与x 轴只有一个交点，则交点的横坐标0x =．答案：第13题. 已知抛物线2y ax bx c =++与y 轴交于C 点，与x 轴交于1(0)A x ，，212(0)()B x x x <，两点，顶点M 的纵坐标为4-，若1x ，2x 是方程222(1)70x m x m --+-=的两根，且221210x x +=． （1）求A ，B 两点坐标； （2）求抛物线表达式及点C 坐标；（3）在抛物线上是否存在着点P ，使△PAB 面积等于四边形ACMB 面积的2倍，若存在，求出P 点坐标；若不存在，请说明理由．答案：（1）由122(1)x x m +=-，2127x x m =-，22222121212()24(1)2(7)10x x x x x x m m +=+-=---=，得2m =，11x ∴=-，23x =，(10)A -，，(30)B ，．（2） 抛物线过A ，B 两点，其对称轴为1x =，顶点纵坐标为4-，∴抛物线为2(1)4y a x =--． 把1x =-，0y =代入得1a =，∴抛物线函数式为223y x x =--，其中(03)C -，．（3）存在着P 点．(10)A - ，，(03)C -，，(14)M -，，(30)B ，，∴9ACMB S =四形，18ABP S = ， 即1182P y AB =．4AB = ，9P y ∴=．把9y =代入抛物线方程得11x =，21x =+，(1P ∴-或(1P +．第14题. 二次函数269y x x =-+-的图像与x 轴的交点坐标为 ．答案：（3，0）第15题. 二次函数25106y x x =-+的图像与x 轴有 个交点． 答案：0第16题. 对于二次函数2135y x x =++，当12x =时，y = ． 答案：11320第17题. 如图是二次函数2246y x x =--的图像，那么方程22460x x --=的两根之和 0．答案：>第18题. 求下列函数的图像与x 轴的交点坐标，并作草图验证． （1）25166y x x =-+； （2）2336y x x =+-．答案：（1）（13，0），（12，0），图略 （2）（1，0），（2-，0），图略第19题. 一元二次方程20ax bx c ++=的两根为1x ，2x ，且214x x +=，点(38)A -，在抛物线2y ax bx c =++上，求点A 关于抛物线的对称轴对称的点的坐标．答案：（1，8-）第20题. 若二次函数2y ax c =+，当x 取1x 、2x （12x x ≠）时，函数值相等，则当x 取12x x +时，函数值为（ ）Ａ．a c + Ｂ．a c - Ｃ．c - Ｄ．c 答案：Ｄ第21题. 下列二次函数中有一个函数的图像与x 轴有两个不同的交点，这个函数是（ ） Ａ．2y x =Ｂ．24y x =+ Ｃ．2325y x x =-+Ｄ．2351y x x =+-答案：Ｄ第22题. 二次函数256y x x =-+与x 轴的交点坐标是（ ）Ａ．（2，0）（3，0） Ｂ．（2-，0）（3-，0） Ｃ．（0，2）（0，3） Ｄ．（0，2-）（0，3-） 答案：A第23题. 试说明一元二次方程2441x x -+=的根与二次函数244y x x =-+的图像的关系，并把方程的根在图象上表示出来．答案：一元二次方程2441x x -+=的根是二次函数244y x x =-+与直线1y =的交点的横坐标，图略．第24题. 利用二次函数图象求一元二次方程的近似根．210x x +-=答案：1 1.6x ≈-，20.6x ≈第25题. 利用二次函数图象求一元二次方程的近似根．24834x x --=-答案：1 1.9x ≈，20.1x ≈第26题. 函数2y ax bx c =++的图象如图所示，那么关于x 的一元二次方程230ax bx c ++-=的根的情况是（ ）Ａ．有两个不相等的实数根 Ｂ．有两个异号的实数根 Ｃ．有两个相等的实数根Ｄ．没有实数根答案：Ｃ第27题. 利用二次函数的图象求一元二次方程的近似值．2530x x --=答案：1 5.5x ≈，20.5x ≈-第28题. 抛物线2321y x x =-+-的图象与坐标轴交点的个数是（ ）Ａ．没有交点Ｂ．只有一个交点 Ｃ．有且只有两个交点Ｄ．有且只有三个交点答案：Ａ第29题. 已知二次函数212y x bx c =-++，关于x 的一元二次方程2102x bx c -++=的两个实 根是1-和5-，则这个二次函数的解析式为答案：215322y x x =---第30题. 已知二次函数2(0)y ax bx c a =++≠的顶点坐标(1 3.2)--，及部分图象（如图４所示），由图象可知关于x 的一元二次方程20ax bx c ++=的两个根分别是1 1.3x =和2x = ．答案： 3.3-y。
二次函数与一元二次方程 练习题
二次函数与一元二次方程练习题1.抛物线y=2x-8-3x与x轴有2个交点，因为其判别式b-4ac=25>0.2，相应二次方程3x^2-2x+8=0的根的情况为2个不相等的实根。
3.关于二次函数y=ax^2+bx+c的图像有下列命题：①当c=0时，函数的图像经过原点；②当c>0，且函数的图像开口向下时，方程ax^2+bx+c=0必有两个不相等的实根；③函数图像最高点的纵坐标是-Δ/4a；④当b=0时，函数的图像关于y 轴对称。
其中正确命题的个数是3个。
4.关于x的方程mx^2+mx+5=m有两个相等的实数根，则相应二次函数y=mx^2+mx+5-m与x轴必然相交于点(0,5-m)，此时m=1.5.要使抛物线y=x^2-(2m-1)x-6m与x轴交于两点(x1,0)和(x2,0)，经过原点，应将它向右平移1个单位。
6.关于x的二次函数y=2mx+(8m+1)x+8m的图像与x轴有交点，则m的范围是m≥-11/16且m≠16/27.7.已知抛物线y=-(x-h)^2+k的顶点在抛物线y=x上，且抛物线在x轴上截得的线段长是4/3，求h和k的值。
解得h=±1/3，k=2/3.8.已知函数y=x-mx+m-2.(1) 求证：不论m为何实数，此二次函数的图像与x轴都有两个不同交点；(2) 若函数y有最小值-2，求m的值。
(1) 当y=0时，解得x=1和x=m-2，因此与x轴有两个交点；(2) 当m=1时，函数的最小值为-2，因此m=1.9.下图是二次函数y=ax^2+bx+c的图像，与x轴交于B，C两点，与y轴交于A点。
已知BC=5，∠ABC=45°，∠ACB=60°，(1) 根据图像确定a，并说明理由；(2) 如果A点的坐标为(0,-3)，b，c的符号，求这个二次函数的函数表达式。
(1) 因为∠ABC=45°，∠ACB=60°，所以BC的长度为5，AB的长度为5cos45°=5/√2，AC的长度为5cos30°=5√3/2.因此，函数的开口向下，a<0.又因为函数与y轴交于A点，所以c=0.(2) 由于A点的坐标为(0,-3)，所以c=-3.又因为函数与x轴交于B，C两点，所以b=-a(Bx+Cx)=-a(BC)=5a。
22.2二次函数与一元二次方程课后练「含答案」
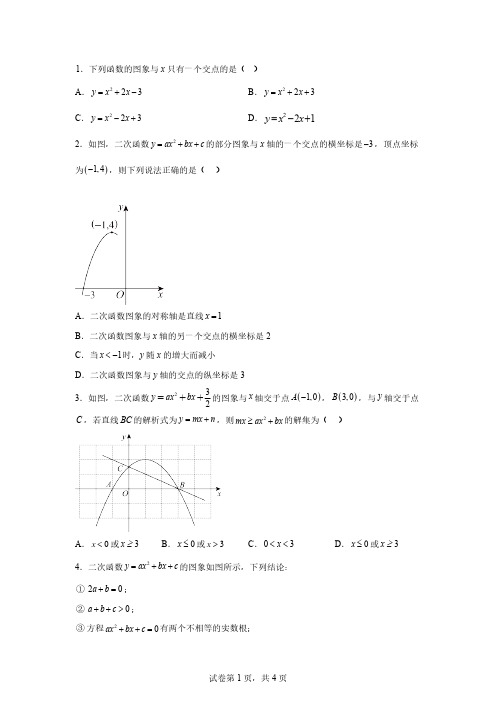
1．下列函数的图象与x 只有一个交点的是（ ）A ．223y x x =+-B ．223y x x =++C ．223y x x =-+D ．221y x x =-+2．如图，二次函数2y ax bx c =++的部分图象与x 轴的一个交点的横坐标是3-，顶点坐标为()1,4-，则下列说法正确的是（ ）A ．二次函数图象的对称轴是直线1x =B ．二次函数图象与x 轴的另一个交点的横坐标是2C ．当1x <-时，y 随x 的增大而减小D ．二次函数图象与y 轴的交点的纵坐标是33．如图，二次函数232y ax bx =++的图象与x 轴交于点()1,0A -，()3,0B ，与y 轴交于点C ，若直线BC 的解析式为y mx n =+，则2mx ax bx ³+的解集为（ ）A ．0x <或3x ³B ．0x £或3x >C ．03x <<D ．0x £或3x ³4．二次函数2y ax bx c =++的图象如图所示，下列结论：①20a b +=；②0a b c ++>；③方程20ax bx c ++=有两个不相等的实数根；④不等式20ax bx c ++<的解集是03x <<．其中所有正确结论的序号是（ ）A ．①③B ．②④C ．①③④D ．①②③④5．已知二次函数()20y ax bx c a =++¹的部分图象如图所示，图象经过点()0,2，其对称轴为直线=1x -．下列结论中正确的有（ ）个．①30a c +>②若点()14,y -，()23,y 均在二次函数图象上，则12y y <③关于x 的一元二次方程21ax bx c ++=-有两个相等的实数根④满足22ax bx c ++>的x 的取值范围为20x <<﹣A ．1B ．2C ．3D ．46．如图，抛物线2y ax bx c =++的顶点坐标是()1,m ，若关于x 的一元二次方程240ax bx c ++-=无实数根，则m 的取值范围是 ．7．已知二次函数2y ax bx c =++的图象如图所示，若方程2ax bx c k ++=有两个不相等的实数根，则k 的取值范围是 ．8．如图，拋物线()240y ax ax c a =-+<与x 轴的一个交点的坐标为()2,0-，则关于x 的方程240ax ax c -+=的解为 ，9．如图，已知抛物线242y x x =-+-和线段MN ，点M 和点N 的坐标分别为()()0,4,5,4，将抛物线向上平移()0k k >个单位长度后与线段MN 仅有一个交点，则k 的取值范围是 ．10．如图，是抛物线21(0)y ax bx c a =++¹图象的一部分，抛物线的顶点坐标是()1,3A ，与x 轴的一个交点()4,0B ，直线2(0)y mx n m =+¹与抛物线交于A ，B 两点 ．①20a b +=；②抛物线与x 轴的另一个交点是()2,0-③方程23ax bx c ++=有两个相等的实数根；④当时14x <<，有21y y <；⑤若221122ax bx ax bx +=+，且12x x ¹；则121x x =+．11．如图，抛物线213442y x x =-++与x 轴交于点A ，B ，与y 轴交于点C ，(1)求A ，B ，C 的坐标；(2)直线4:43l y x =-+上有一点(),4D m -，在图中画出直线l 和点D ，并判断四边形ACBD 的形状，说明理由．12．已知抛物线245(0)y ax ax a a =-->与x 轴交于A B 、两点（点A 在点B 的左侧）．(1)求抛物线的对称轴及点,A B 的坐标；(2)当36x ££时，y 有最大值为14，求抛物线的解析式；(3)已知点()()1,1,6,56E F a -+，若抛物线245(0)y ax ax a a =-->与线段EF 只有一个公共点，求a 的取值范围．【分析】本题考查抛物线与x 轴的交点，二次函数2y ax bx c =++（a ，b ，c 是常数，0a ¹）的交点与一元二次方程20ax bx c ++=根之间的关系，根据各个选项中的函数解析式可以计算出D 的值，然后即可判断与x 轴的交点情况．【详解】选项A 中()2242413160b ac -=-´´-=>，与x 轴有2个交点；选项B 中224241380b ac -=-´´=-<，与x 轴没有交点；选项C 中()224241380b ac -=--´´=-<，与x 轴没有交点；选项D 中()22424110b ac -=--´´=，所以选项D 的函数图象与x 轴只有一个交点，故选：D ．2．D【分析】本题考查了二次函数的性质，待定系数法求二次函数解析式，利用二次函数的性质，对称性，增减性判断选项A 、B 、C ，利用待定系数法求出二次函数的解析式，再求出与y 轴的交点坐标即可判定选项D ．【详解】解∶ ∵二次函数2y ax bx c =++的顶点坐标为()1,4-，∴二次函数图象的对称轴是直线=1x -，故选项A 错误；∵二次函数2y ax bx c =++的图象与x 轴的一个交点的横坐标是3-，对称轴是直线=1x -，∴二次函数图象与x 轴的另一个交点的横坐标是1，故选项B 错误；∵抛物线开口向下， 对称轴是直线=1x -，∴当1x <-时，y 随x 的增大而增大，故选项C 错误；设二次函数解析式为()214y a x =++，把()3,0-代入，得()20314a =-++，解得1a =-，∴()214y x =-++，当0x =时，()20143y =-++=，∴二次函数图象与y 轴的交点的纵坐标是3，故选项D 正确，故选D ．【分析】本题考查了二次函数的图象与性质，一次函数图象与性质，待定系数法求一次函数参数，熟练掌握函数图象与不等式的关系是解题的关键．先由二次函数可求得C 点坐标，代入y mx n =+即可得到32n =，然后由2mx ax bx ³+变形为23322mx ax bx +³++，观察图象即可得到答案．【详解】解：Q 232y ax bx =++与y 轴交于点C ，即0x =时，32y =，30,2C æö\ç÷èø又Q 点C 在直线BC ：y mx n =+上，将30,2C æöç÷èø代入y mx n =+，得32n =\直线BC 的解析式为32y mx =+观察图象可知，当0x <时，直线BC 在抛物线的上面，当03x <<时，直线BC 在抛物线的下面，当3x >时，直线BC 在抛物线的上面，2mx ax bx \³+，即23322mx ax bx +³++观察图象可知，该不等式的解集为：0x £或3x ³．故选：D ．4．A【分析】本题考查了二次函数的图象和性质，根据抛物线与x 轴的交点坐标求出对称轴，即可判断①；当1x =时，0y <，即可判断②；由抛物线与x 轴有两个不同的交点即可判断③；由图象可知，当13x -<<时，0y <，即可判断④；掌握二次函数的图象和性质是解题的关键．【详解】解：由图象可得，抛物线与x 轴的交点坐标为()1,0-和()3,0，∴抛物线的对称轴为直线1312x -+==，即12b a-=，∴20a b +=，故①正确；由图象可得，当1x =时，0y <，∴0a b c ++<，故②错误；∵抛物线与x 轴有两个不同的交点，∴方程20ax bx c ++=有两个不相等的实数根，故③正确；由图象可知，当13x -<<时，0y <，∴不等式20ax bx c ++<的解集是13x -<<，故④错误；∴正确的结论为①③，故选：A ．5．A【分析】本题主要考查了二次函数的图象与系数的关系，二次函数的图象上点的坐标特征，抛物线与x 轴的交点，函数与方程的关系，数形结合是解题的关键．依据题意，由图象可得抛物线的对称轴是直线12b x a =-=-，与y 轴的交点为()0,2，当1x =时，0y <，然后逐个选项判断即可得解．【详解】解：由题意，∵抛物线的对称轴是直线12b x a=-=-，∴2b a =．又由图象，可得当1x =时，0y a b c =++<，∴30a c +<，故①错误．∵抛物线的对称轴是直线=1x -，∴点()14,y -到对称轴的距离小于点()23,y 到对称轴的距离，∵抛物线开口向下，∴12y y >，故②错误．由题意，令1y =-，∴抛物线2y ax bx c =++与直线1y =-有两个不同的交点．∴关于x 的一元二次方程21ax bx c ++=-有两个不相等的实数根，故③错误．∵当0x =时，y ＝2，又∵抛物线的对称轴是直线x ＝﹣1，∴当2x =-时，2y =．又抛物线开口向下，∴满足22ax bx c ++>的x 的取值范围为20x -<<，故④正确．故选：A ．6．4m <【分析】本题考查抛物线与直线的交点问题．解题的关键将一元二次方程根的情况转化为抛物线与直线的交点问题，据此列式解答即可．【详解】解：∵关于x 的一元二次方程240ax bx c ++-=无实数根，∴抛物线2y ax bx c =++与4y =没有交点，∵抛物线2y ax bx c =++的顶点坐标是()1,m ，∴4m <．故答案为：4m <．7．2k >-##2k-<【分析】本题主要考查了抛物线与x 轴的交点问题，以及数形结合法；根据顶点坐标为()12-，，求出248b ac a -=．根据题意可得()()224448442>0b a c k b ac ak a ak a k --=-+=+=+求值即可．【详解】解：由图象可知：二次函数2y ax bx c =++的顶点坐标为()12-，，∴2424ac b a-=-，即248b ac a -=，∵2ax bx c k ++=有两个不相等的实数根，∴()()224448442>0b ac k b ac ak a ak a k --=-+=+=+∵抛物线开口向上∴0a >∴20k +>∴2k >-．故答案为2k >-．8．122,6x x =-=【分析】由拋物线()240y ax ax c a =-+<，可求出对称轴为2,2b x a=-=根据抛物线与x 轴的一个交点的坐标为()2,0-，可求出另外一个交点()6,0,即可得到关于x 的方程240ax ax c -+=的解，【详解】解：∵拋物线()240y ax ax c a =-+<，∴对称轴为：2,2b x a=-=∵与x 轴的一个交点的坐标为()2,0-∴与x 轴的一个交点的坐标为()6,0,∴关于x 的方程240ax ax c -+=的解为：122, 6.x x =-=故答案为：122, 6.x x =-=【点睛】本题主要考查了二次函数和一元二次方程的关系，求出二次函数的对称轴是解此题的关键．9．611k <£或2k =【分析】本题考查二次函数的性质及图象的平移，由题意可知，将抛物线向上平移()0k k >个单位长度后抛物线为()224222y x x x k =-+-=--++，结合图形，找到临界点：当抛物线顶点恰好平移到线段MN 上，当抛物线经过点()5,4N 时，求出对应k 的值，结合图形即可求解．【详解】()224222y x x x =-+-=--+，将抛物线向上平移()0k k >个单位长度后抛物线为()222y x k =--++，当抛物线顶点恰好平移到线段MN 上，此时，24k +=，可得2k =；当抛物线经过点()0,4M 时，此时()20224k --++=，可得6k =，此时()0,4M 关于对称轴2x =对称的点()4,4M ¢，在线段MN 上，不符合题意；当抛物线经过点()5,4N 时，此时()25224k --++=，可得11k =，此时()5,4N 关于对称轴2x =对称的点()1,4N ¢-，不在线段MN 上，符合题意；结合图形可知，平移后的抛物线与线段MN 仅有一个交点时，2k =或611k <£；故答案为：2k =或611k <£．10．①②③④【分析】本题考查了二次函数与不等式的关系，根据二次函数与方程，不等式的关系及函数的图象和性质求解．【详解】解：由题意得：抛物线的对称轴为直线1x =，\12b a-=，20a b \+=，故①正确；由抛物线的对称性得：()1412--=-，抛物线与x 轴的另一个交点是 ()2,0-，故②正确；Q 抛物线的顶点坐标是()1,3A ，\抛物线与直线3y =只有一个交点方程23ax bx c ++=有两个相等的实数根；故③正确；由图象得：当时14x <<，有21y y <；故④正确；Q 221122ax bx ax bx +=+，且12x x ¹；\1212x x +=\122x x +=，故⑤错误，故答案为：①②③④．11．(1)()2,0A -，()8,0B ，()0,4C ；(2)图见详解，四边形ACBD 是平行四边形．【分析】()1分别将0x =和0y =代入213442y x x =-++即可求解；()2求出D 点坐标后画出图形，再分别计算AC 、BC 、BD 、AD 的长度，根据平行四边形的判定定理即可得解．本题考查的知识点是抛物线与x 轴和y 轴的交点、勾股定理、平行四边形的判定定理，解题关键是熟练掌握平行四边形的判定．【详解】（1）解：当0y =时，2134042x x -++=，解得8x =或 2x =-,()2,0A \-，()8,0B ，当0x =时，4y =，()0,4C \．（2）解：由213444423x x x -++=-+可得0x =，\抛物线与直线的交点为()0,4C ，Q 点D 在直线l 上，4443m \-+=-，解得6m =，即()6,4D -，如图所示：AC \==BC ==，BD ==，AD ==AC BD \=，BC AD =，\四边形ACBD 是平行四边形．12．(1)2x =，(1,0)(50)A B -，，(2)抛物线的解析式为22810y x x =--(3)a 的取值范围是3a ³【分析】（1）根据2b x a=-求得抛物线的对称轴为2x =，令2450ax ax a --=即可解得,A B 的坐标；（2）根据抛物线对称轴为2x =可得当36x ££时，y 随x 的增大而增大，可得当6x =时，y 取得最大值14，代入抛物线解析式可得2a =，从而可得22810y x x =--；（3）由（1）可知抛物线与x 轴交于点(1,0)(50)A B -，，，可得点(11)E -，在抛物线内侧，根据线段EF 与抛物线只有一个公共交点，可知点F 在抛物线上或者在抛物线下方，将6x =代入245y ax ax a =--可得362457y a a a a =--=，当点F 的纵坐标小于等于7a 时可满足EF 与抛物线只有一个公共交点，即567a a +£，解得3a ³．【详解】（1）解：Q 422a x a-=-=\对称轴为直线2x =令2450ax ax a --=即()2450a x x --=Q 0a >\11x =-，25x =\(1,0)(5,0)A B -，（2）解：Q 抛物线245y ax ax a =--（0a >）的开口向上，对称轴为直线2x =，当36x ££时，y 随x 的增大而增大\当6x =时，y 取得最大值14\把6x =，14y =代入245y ax ax a =--，得3624514a a a --=\2a =\抛物线的解析式为：22810y x x =--（3）解：由（1）可知抛物线与x 轴交于点(1,0)(50)A B -，，故点(11)E -，在抛物线内侧Q 线段EF 与抛物线只有一个交点\点F 在抛物线上或者在抛物线下方将6x =代入245y ax ax a =--，得：362457y a a a a=--=\当点F 的纵坐标小于等于7a 时，EF 与抛物线只有一个交点，即567a a+£解得：3a ³\a 的取值范围是3a ³【点睛】本题考查求二次函数的对称轴，与x 轴的交点坐标，抛物线上的点的坐标，以及根据图形求所含参数的取值问题，解题的关键是熟练掌握二次函数图象的性质和数形结合思想的运用．。
(精)人教版数学九年级上册《二次函数和一元二次方程》习题及解析
二次函数与一元二次方式练习题 附答案一、选择题（共15 小题）1、已知二次函数 2）y=ax +bx+c 的图象以下列图， 对称轴为直线 x=1，则以下结论正确的选项是（A 、 ac ＞ 0B 、方程 ax 2+bx+c=0 的两根是 x 1=﹣ 1， x 2=3C 、 2a ﹣ b=0D 、当 x ＞ 0 时， y 随 x 的增大而减小 2 、已知二次函数y=ax 2+bx+c 的图象以下列图，那么以下判断不正确的选项是（）A 、 ac ＜ 0B 、 a ﹣b+c ＞ 0C 、 b=﹣ 4aD 、关于 x 的方程 ax 2+bx+c=0 的根是 x 1=﹣ 1， x 2=523、已知抛物线 y=ax +bx+c 中， 4a ﹣ b=0， a ﹣ b+c ＞ 0，抛物线与 x 轴有两个不同样的交点，且 这两个交点之间的距离小于 2，则以下判断错误的选项是（ ）A 、 abc ＜0B 、 c ＞ 0C 、 4a ＞ cD 、 a+b+c ＞ 04、抛物线 y=ax 2+bx+c 在 x 轴的下方，则所要满足的条件是（）A 、 a ＜0， b 2﹣ 4ac ＜ 0B 、 a ＜ 0， b 2﹣ 4ac ＞ 0C 、 a ＞ 0， b 2﹣4ac ＜0D 、 a ＞ 0， b 2﹣ 4ac ＞ 05、以下列图，二次函数 21， 2），且与 x 轴交点的横坐y=ax +bx+c （ a ≠0）的图象经过点（﹣ 标分别为 x 1， x 2，其中﹣ 2＜ x 1＜﹣ 1， 0＜ x 2＜1，以下结论： ① abc ＞ 0；② 4a ﹣ 2b+c ＜0；③ 2a ﹣ b ＜ 0；④b 2+8a ＞ 4ac ． 其中正确的有（）A 、1 个B 、2 个C 、3 个D 、4 个6、已知： a ＞ b ＞ c ，且 a+b+c=0，则二次函数 y=ax 2+bx+c 的图象可能是以下列图象中的 （）1A 、B 、C 、D 、7、已知 y =a x 2+b x+c，y =a x 2+b x+c 且满足．则称抛物线y ， y 互为 “友好抛物线 ”，则1111222212以下关于 “友好抛物线 ”的说法不正确的选项是（）A 、 y 1， y 2 张口方向、张口大小不用然同样B 、由于 y 1， y 2 的对称轴同样C 、若是 y 的最值为 m ，则 y 的最值为 kmD 、若是 y 与 x 轴的两交点间距离为212d ，则 y 1 与 x 轴的两交点间距离为|k|d8、已知二次函数的 y=ax 2+bx+c 图象是由的图象经过平移而获得，若图象与x 轴交于 A 、 C（﹣ 1， 0）两点，与 y 轴交于 D （0，），极点为 B ，则四边形 ABCD 的面积为（ ）A 、 9B 、 10C 、 11D 、 129、依照以下表格的对应值：判断方程 ax 2+bx+c=0（ a ≠0， a ， b ， c 为常数）的一个解 x 的范围是（）A 、 8＜ x ＜ 9B 、 9＜ x ＜ 10C 、 10＜ x ＜ 11D 、 11＜x ＜ 1210、如图，已知二次函数y=ax 2 +bx+c 的部分图象，由图象可知关于 x 的一元二次方程2）ax +bx+c=0 的两个根分别是 x 1=1.6， x 2=（A 、﹣ 1.6B 、 3.2C 、 4.4D 、以上都不对11、如图，抛物线 2与双曲线 y=的交点 A 的横坐标是 1，则关于 2y=x +1 x 的不等式 +x +1＜ 0的解集是（ ）A 、 x ＞ 1C 、 0＜ x ＜ 1B 、 x ＜﹣ 1D 、﹣ 1＜ x ＜ 012、已知二次函数 y=ax 2+bx+c 的图象以下列图， 则关于 x 的不等式bx+a ＞ 0 的解集是 （）A 、 x ＜B 、 x ＜C 、 x ＞D 、 x ＞13、方程 7x 2﹣（ k+13）x+k 2﹣ k ﹣ 2=0（ k 是实数）有两个实根 α、β，且 0＜ α＜ 1，1＜ β＜ 2， 那么 k 的取值范围是（ ）A 、 3＜ k ＜ 4B 、﹣ 2＜ k ＜﹣ 1C 、 3＜ k ＜ 4 或﹣ 2＜ k ＜﹣ 1D 、无解14、关于整式 x 2和 2x+3，请你判断以下说法正确的选项是（）A 、关于任意实数x ，不等式 x 2＞ 2x+3 都成立B 、关于任意实数 x ，不等式 x 2＜ 2x+3都成立C 、 x ＜ 3 时，不等式 x 2＜ 2x+3 成立D 、 x ＞ 3 时，不等式 x 2＞ 2x+3 成立二、解答题（共7 小题）215、已知抛物线 y=x +2px+2p ﹣2 的极点为 M ，（2）设抛物线与 x 轴的交点分别为 A ， B ，求实数 p 的值使 △ABM 面积达到最小．216、已知：二次函数 y=（ 2m ﹣ 1） x ﹣（ 5m+3） x+3m+5（1） m 为何值时，此抛物线必与 x 轴订交于两个不同样的点； （2） m 为何值时，这两个交点在原点的左右两边； （3） m 为何值时，此抛物线的对称轴是y 轴；（4） m 为何值时，这个二次函数有最大值．17、已知下表：（ 1）求 a 、 b 、 c 的值，并在表内空格处填入正确的数；（ 2）请你依照上面的结果判断：① 可否存在实数 x ，使二次三项式 2ax +bx+c 的值为 0？若存在， 求出这个实数值； 若不存在， 请说明原由．② 画出函数 y=ax 2+bx+c 的图象表示图，由图象确定，当 x 取什么实数时， ax 2+bx+c ＞ 0．18 、 请 将 下 表 补 充 完 整 ；（Ⅱ）利用你在填上表时获得的结论，解不等式﹣x 2﹣ 2x+3＜0； （Ⅲ）利用你在填上表时获得的结论，试写出一个解集为全体实数的一元二次不等式；（Ⅳ） 试写出利用你在填上表时获得的结论解一元二次不等式ax 2+bx+c ＞0（a ≠0）时的解题 步骤．219、二次函数 y=ax +bx+c （a ≠0）的图象以下列图，依照图象解答以下问题：（ 1）写出方程 ax 2+bx+c=0 的两个根；（ 2）写出不等式 ax 2+bx+c ＞ 0 的解集；（3）写出 y 随 x 的增大而减小的自变量 x 的取值范围；（4）若方程 ax 2+bx+c=k 有两个不相等的实数根，求 k 的取值范围．20、阅读资料，解答问题．x 2﹣ 2x ﹣ 3＞ 0．例．用图象法解一元二次不等式：解：设 y=x 2﹣2x ﹣ 3，则 y 是 x 的二次函数．∵ a=1＞0，∴抛物线张口向上．22又∵当 y=0 时， x ﹣ 2x ﹣ 3=0，解得 x 1=﹣ 1，x 2=3．∴由此得抛物线y=x ﹣2x ﹣ 3 的大体图象以下列图．观察函数图象可知：当 x ＜﹣ 1或 x ＞ 3 时， y ＞ 0．∴ x 2﹣ 2x ﹣ 3＞0 的解集是： x ＜﹣ 1 或 x ＞ 3．x 2﹣ 2x ﹣ 3＜ 0 的解集是（1）观察图象，直接写出一元二次不等式： _________ ；（2）模拟上例，用图象法解一元二次不等式：x 2﹣5x+6＜ 0．（画出大体图象） ．三、填空题（共 4 小题）21、二次函数 y=ax 2+bx+c （a ≠0）的图象以下列图，依照图象解答以下问题：（1）写出方程 ax 2+bx+c=0 的两个根． x 1= _________ ， x 2= _________ ；（2）写出不等式 ax 2+bx+c ＞ 0 的解集． _________ ； （3）写出 y 随 x 的增大而减小的自变量 x 的取值范围． _________ ；（4）若方程 ax 2+bx+c=k 有两个不相等的实数根，求 k 的取值范围． _________ ．22、如图是抛物线y=ax 2+bx+c 的一部分，其对称轴为直线x=1，若其与 x 轴一交点为 B （3 ，0），则由图象可知，不等式 2．ax +bx+c ＞ 0 的解集是 _________23、二次函数 y=ax 2+bx+c 和一次函数 y=mx+n 的图象以下列图，则 ax 2+bx+c ≤ mx+n 时， x的取值范围是_________ ．24、如图，已知函数 y=ax 2+bx+c 与 y=﹣的图象交于 A （﹣ 4，1）、B （2，﹣ 2）、 C （ 1，﹣ 4）三点，依照图象可求得关于 x 的不等式 ax 2+bx+c ＜﹣的解集为 _________ ．答案与评分标准一、选择题（共 15 小题）21、（ 2011?山西）已知二次函数 y=ax +bx+c 的图象以下列图，对称轴为直线 x=1，则以下结论正确的选项是（ ）A 、 ac ＞ 0B 、方程 ax 2+bx+c=0 的两根是 x 1=﹣ 1， x 2=3C 、 2a ﹣ b=0D 、当 x ＞ 0 时， y 随 x 的增大而减小考点 ：二次函数图象与系数的关系；抛物线与 x 轴的交点。
二次函数与一元二次方程(习题及答案)
二次函数与一元二次方程（习题）1. （1）一元二次方程-x 2-4x +4=2x -3的根为_____________，直线y =2x -3与抛物线y =-x 2-4x +4的交点坐标为___________．（2）若二次函数的图象经过点A (1，0)，B (-4，0)，C (0，4)，则该二次函数的表达式为________________．2. 已知二次函数y =x 2+4x +m 的图象C 1与x 轴有且只有一个交点，则m 的值为______；若y =-x 2+2x +m 的函数值总为负数，则图象顶点在第_____象限，m 的取值范围是_________．3. 在平面直角坐标系中，抛物线y =(x +5)(x -3)经过向右平移____个单位后得到抛物线y =(x +3)(x -5)；平移后的抛物线与x 轴的交点为___________．4. 已知二次函数y =x 2+2x +m 的图象C 1与x 轴有且只有一个交点，则C 1的顶点坐标为__________．5. 若关于x 的一元二次方程x 2-x -n =0无实数根，则函数y =x 2-x -n 的图象顶点在第____象限．6. 二次函数y =x 2-2x -3的图象如图所示，当y ＜0时，自变量x 的取值范围是（ ）A ．-1＜x ＜3B ．x ＜-1C ．x ＞3D ．x ＜-1或x ＞3第6题图 第7题图7. 二次函数y =ax 2+bx +c （a ≠0）的图象如图所示，若ax 2+bx +c +k =0（k ≠0）有两个不相等的实数根，则k 的取值范围是（ ）A ．k ＜-3B ．k ＞-3C ．k ＜3D ．k ＞38. 抛物线y =-x 2+bx +c 的部分图象如图所示，若y ＞0，则x 的取值范围是（ ）A ．-4＜x ＜1B ．-3＜x ＜1C ．x ＜-4或x ＞1D ．x ＜-3或x ＞1第8题图 第9题图 9. 函数y =x 2-2x -2的图象如图所示，根据该图象提供的信息，可求得使y ≥1成立的x的取值范围是（ ） A ．-1≤x ≤3B ．-1＜x ＜3C ．x ＜-1或x ＞3D ．x ≤-1或x ≥3复习巩固10. 如图是二次函数y =ax 2+bx +c 的部分图象，由图象可知不等式ax 2+bx +c ＜0的解集是（ ） A ．-1＜x ＜5B ．x ＞5C ．x ＜-1且x ＞5D ．x ＜-1或x ＞5第10题图 第11题图11. 如图，若抛物线y =x 2+1与双曲线ky x=的交点A 的横坐标为1，则关于x 的不等式210xx k++<的解集是（ ） A ．x ＞1 B ．x ＜-1 C ．0＜x ＜1 D ．-1＜x ＜012. 若二次函数的图象y =(m -2)x 2+x 与直线y =2x -1没有交点，求m 的取值范围．13. 已知P (-3，m )和Q (1，m )是抛物线y =2x 2+bx +1上的两点．（1）求b 的值；（2）将抛物线y =2x 2+bx +1的图象先向上平移2个单位，再向左平移1个单位，请判断新抛物线与x 轴的交点情况．14. 二次函数y =ax 2+bx +c 的图象如图所示，其对称轴为直线x =-1．给出下列结论：①abc ＞0；②2a +b =0；③a +b +c ＞0；④a -b +c ＜0．其中正确的是（ ） A ．②③B ．①③④C ．①②④D ．③④15. 二次函数y =ax 2+bx +c （a ≠0）的图象如图所示，有下列结论：①abc ＞0；②2a +b ＜0；③a +b ＜m (am +b )（m ≠1）；④(a +c )2＜b 2；⑤a ＞1．其中正确的是（ ） A ．①⑤B ．①②⑤C ．②⑤D ．①③④1. 对于二次函数y =ax 2+bx +c 和一元二次方程ax 2+bx +c =0的关系，尝试着进行总结：①函数与x 轴交点坐标，与方程的根：_________________________________________________． ②函数与x 轴交点个数，与方程解的个数：当Δ＞0时，函数与x 轴有____个交点，方程有______根； 当Δ=0时，函数与x 轴有_____个交点，方程有_______根； 当Δ＜0时，函数与x 轴______交点，方程________根．思考小结【参考答案】复习巩固1.（1）x1=1，x2=-7；(1，-1)，(-7，-17)；（2）y=-x2-3x+42.4；四；m＜-13.2；(-3，0)，(5，0)4.(-1，0)5.一6. A7. C8. B9. D10. D11. D12.m的取值范围是94m ．13.（1）b的值为4；（2）新抛物线与x轴无交点．14. D15. A思考小结1.①函数与x轴交点的横坐标即为方程的根；②两；两个不相等的实数；一；两个相等的实数；无；无实数。
二次函数与一元二次方程同步练习题
二次函数与一元二次方程同步练习第1题. 抛物线2283y x x =--与x 轴有个交点，因为其判别式24b ac -=0，相应二次方程23280x x -+=的根的情况为 ．答案：0 92-<没有实数根．第2题. 函数22y mx x m =+-（m 是常数）的图像与x 轴的交点个数为（ ）Ａ．0个 Ｂ．1个 Ｃ．2个 Ｄ．1个或2个答案：Ｃ第3题. 关于二次函数2y ax bx c =++的图像有下列命题：①当0c =时，函数的图像经过原点；②当0c >，且函数的图像开口向下时，方程20ax bx c ++=必有两个不相等的实根；③函数图像最高点的纵坐标是244ac b a-；④当0b =时，函数的图像关于y 轴对称．其中正确命题的个数是（ ）Ａ．1个 Ｂ．2个 Ｃ．3个Ｄ．4个答案：Ｃ第4题. 关于x 的方程25mx mx m ++=有两个相等的实数根，则相应二次函数25y mx mx m =++-与x 轴必然相交于点，此时m =．答案：一 4第5题. 抛物线2(21)6y x m x m =---与x 轴交于两点1(0)x ，和2(0)x ，，若121249x x x x =++，要使抛物线经过原点，应将它向右平移 个单位．答案：4或9第6题. 关于x 的二次函数22(81)8y mx m x m =+++的图像与x 轴有交点，则m 的范围是（ ）Ａ．116m <-Ｂ．116m -≥且0m ≠ Ｃ．116m =-Ｄ．116m >-且0m ≠答案：Ｂ第7题. 已知抛物线21()3y x h k =--+的顶点在抛物线2y x =上，且抛物线在x 轴上截得的线段长是h 和k 的值．答案：21()3y x h k =--+，顶点()h k ，在2y x =上，2h k ∴=，22221122()3333y x h h x hx h ∴=--+=-++．又它与x 轴两交点的距离为12x x a∴-==== 求得2h =±，4k =，即2h =，4k =或2h =-，4k =．第8题. 已知函数22y x mx m =-+-．（1）求证：不论m 为何实数，此二次函数的图像与x 轴都有两个不同交点； （2）若函数y 有最小值54-，求函数表达式．答案：（1）222()4(2)48(2)4m m m m m ∆=---=-+=-+，不论m 为何值时，都有0∆>，此时二次函数图像与x 轴有两个不同交点． （2）2244(2)5444ac b m m a ---==-，2430m m -+=，1m ∴=或3m =， 所求函数式为21y x x =--或231y x x =-+．第9题. 下图是二次函数2y ax bx c =++的图像，与x 轴交于B ，C 两点，与y 轴交于A 点． （1）根据图像确定a ，b ，c 的符号，并说明理由；（2）如果A 点的坐标为(03)-，，45ABC ∠=，60ACB ∠=，求这个二次函数的函数表达式．答案：（1）抛物线开口向上，0a >；图像的对称轴在y 轴左侧，02ba-<，又0a >， 0b ∴>；图像与y 轴交点在x 轴下方，0c ∴<．0a ∴>，0b >，0c <．（2）(03)A -，，3OA =，45ABC ∠=，60ACB ∠=，3tan OAOB ABC ==∠， 3tan 60OAOC==(30)B∴-，，C ．设二次函数式为(3)(ya x x =+-， 把(03)-，代入上式，得3a=，∴所求函数式为2(3)(1)333y x x x x =+=+-．第10题. 已知抛物线222m y x mx =-+与抛物线2234m yx mx =+-在直角坐标系中的位置如图所示，其中一条与x 轴交于A ，B 两点．（1）试判断哪条抛物线经过A ，B 两点，并说明理由； （2）若A ，B 两点到原点的距离AO ，OB 满足条件1123OB OA -=，求经过A ，B 两点的这条抛物线的函数式．答案：（1）抛物线不过原点，0m ≠，令2202m x mx -+=，2221()402m m m ∆=--⨯=-<，222m y x mx =-+∴与x 轴无交点，∴抛物线2234y x mx m =+-经过A ，B 两点．（2）设1(0)A x ，，2(0)B x ，，1x ，2x 是方程22304x mx m +-=的两根12x x m +=-，21234x x m =-，A 在原点左边，B 在原点右边，则1AO x =-，2OB x =．123OB OA 1-=．211123x x ∴+=，121223x x x x +=，22334m m -=-，得2m =，∴所求函数式为223y x x =+-．第11题. 已知二次函数2224y x mx m =-+．（1）求证：当0m ≠时，二次函数的图像与x 轴有两个不同交点；（2）若这个函数的图像与x 轴交点为A ，B，顶点为C ，且△ABC 的面积为，求此二次函数的函数表达式．答案：（1）22222(4)421688m m m m m ∆=--⨯⨯=-=．0m ≠，280m ∴>，∴这个抛物线与x 轴有两个不同交点．（2）设1(0)A x ，，212(0)()B x x x >，，则1x ，2x 是方程22240x mx m -+=两根， 122x x m +=，2122m x x =，21AB x x m =-====，C 点纵坐标22224816442c ac b m m y m a --===-⨯， ∴△ABC 中AB 边上的高22h m m =-=．21124222ABCSAB h m m ===，2m =，2m =±， 2284y x x ∴=++或2284y x x =-+．第12题. 如图所示，函数2(2)(5)y k x k =-+-的图像与x 轴只有一个交点，则交点的横坐标x =．答案：第13题. 已知抛物线2y ax bx c =++与y 轴交于C 点，与x 轴交于1(0)A x ，，212(0)()B x x x <，两点，顶点M 的纵坐标为4-，若1x ，2x 是方程222(1)70x m x m --+-=的两根，且221210x x +=．（1）求A ，B 两点坐标； （2）求抛物线表达式及点C坐标；（3）在抛物线上是否存在着点P ，使△PAB 面积等于四边形ACMB 面积的2倍，若存在，求出P 点坐标；若不存在，请说明理由．答案：（1）由122(1)x x m +=-，2127x x m =-，22222121212()24(1)2(7)10x x x x x x m m +=+-=---=，得2m =，11x ∴=-，23x =，(10)A -，，(30)B ，．（2）抛物线过A ，B 两点，其对称轴为1x =，顶点纵坐标为4-，∴抛物线为2(1)4y a x =--．把1x =-，0y =代入得1a =，∴抛物线函数式为223y x x =--，其中(03)C -，． （3）存在着P 点．(10)A -，，(03)C -，，(14)M -，，(30)B ，，∴9ACMB S =四形，18ABPS =，即1182P y AB =．4AB =，9P y ∴=．把9y =代入抛物线方程得11x =，21x =(1P ∴或(1P +．第14题. 二次函数269y x x =-+-的图像与x 轴的交点坐标为 ．答案：（3，0）第15题. 二次函数25106y x x =-+的图像与x 轴有 个交点．答案：0第16题. 对于二次函数2135y x x =++，当12x =时，y = ．答案：11320第17题. 如图是二次函数2246y x x =--的图像，那么方程22460x x --=的两根之和 0．答案：>第18题. 求下列函数的图像与x 轴的交点坐标，并作草图验证． （1）25166y x x =-+； （2）2336y x x =+-．答案：（1）（13，0），（12，0），图略 （2）（1，0），（2-，0），图略第19题. 一元二次方程20ax bx c ++=的两根为1x ，2x ，且214x x +=，点(38)A -，在抛物线2y ax bx c =++上，求点A 关于抛物线的对称轴对称的点的坐标．答案：（1，8-）第20题. 若二次函数2y ax c =+，当x 取1x 、2x （12x x ≠）时，函数值相等，则当x 取12x x +时，函数值为（ ）Ａ．a c + Ｂ．a c - Ｃ．c - Ｄ．c答案：Ｄ第21题. 下列二次函数中有一个函数的图像与x 轴有两个不同的交点，这个函数是（ ） Ａ．2y x =Ｂ．24y x =+ Ｃ．2325y x x =-+Ｄ．2351y x x =+-答案：Ｄ第22题. 二次函数256y x x =-+与x 轴的交点坐标是（ ）Ａ．（2，0）（3，0） Ｂ．（2-，0）（3-，0） Ｃ．（0，2）（0，3） Ｄ．（0，2-）（0，3-）答案：A第23题. 试说明一元二次方程2441x x -+=的根与二次函数244y x x =-+的图像的关系，并把方程的根在图象上表示出来．答案：一元二次方程2441x x -+=的根是二次函数244y x x =-+与直线1y =的交点的横坐标，图略．第24题. 利用二次函数图象求一元二次方程的近似根．210x x +-=答案：1 1.6x ≈-，20.6x ≈第25题. 利用二次函数图象求一元二次方程的近似根．24834x x --=-答案：1 1.9x ≈，20.1x ≈第26题. 函数2y ax bx c =++的图象如图所示，那么关于x 的一元二次方程230ax bx c ++-=的根的情况是（ ）Ａ．有两个不相等的实数根 Ｂ．有两个异号的实数根 Ｃ．有两个相等的实数根Ｄ．没有实数根答案：Ｃ第27题. 利用二次函数的图象求一元二次方程的近似值．2530x x --=答案：1 5.5x ≈，20.5x ≈-第28题. 抛物线2321y x x =-+-的图象与坐标轴交点的个数是（）Ａ．没有交点Ｂ．只有一个交点 Ｃ．有且只有两个交点Ｄ．有且只有三个交点答案：Ａ第29题. 已知二次函数212y x bx c =-++，关于x 的一元二次方程2102x bx c -++=的两个实根是1-和5-，则这个二次函数的解析式为答案：215322y x x =---第30题. 已知二次函数2(0)y ax bx c a =++≠的顶点坐标(1 3.2)--，及部分图象（如图４所示），由图象可知关于x 的一元二次方程20ax bx c ++=的两个根分别是1 1.3x =和2x = ．答案： 3.3-y。
九年级数学上册《第二十二章 二次函数与一元二次方程》同步练习题及答案(人教版)
九年级数学上册《第二十二章二次函数与一元二次方程》同步练习题及答案(人教版)班级姓名学号一、单选题1．二次函数y＝−x2+（6 −m）x+8，当x＞− 2时，y随x的增大而减小；当x＜− 2时，y随x的增大而增大，则m的值为（）A．10 B．8 C．6 D．42．已知抛物线y=ax2+bx+c经过点(−1，0)，(3，0)则关于x的一元二次方程a(x+1)2−cx=a+2b 的解为（）A．x=−1或x=−4B．x=−1或x=−2C．x=−4或x=−2D．x=−1或x=3,y3)在函数y=x2+2x+m的图象上，则y1，y2，y3的大小关系是3．已知点(−1,y1)，(3,y2)，(12（）A．y1>y2>y3B．y2>y1>y3C．y2>y3>y1D．y3>y1>y24．根据下面表格中的对应值：x 3.23 3.24 3.25 3.26ax2+bx+c ﹣0.06 ﹣0.02 0.03 0.09判断方程ax2+bx+c＝0（a≠0，a，b，c为常数）的一个解x的范围是（）A．3.22＜x＜3.23 B．3.23＜x＜3.24C．3.24＜x＜3.25 D．3.25＜x＜3.265．小兰画了一个函数y=x2+ax+b的图象如图，则关于x的方程x2+ax+b=0的解是（）A．无解B．x=1 C．x=﹣4 D．x=﹣1或x=46．如图，抛物线y=ax2+bx+c（a≠0）的开口向上，与x轴交点的横坐标分别为﹣1、3，则下列说法错误的是（）A．对称轴是直线x=1B．方程ax2+bx+c=0的解是x1=﹣1，x2=3C．当x＜1，y随x的增大而增大D．当﹣1＜x＜3时，y＜07．如图，已知关于x的一元二次方程a(x−k)2−1=0的两根在数轴上对应的点分别在区域①和区域②，区域均含端点，则k的值可能是（）A．-1 B．0 C．1 D．28．已知关于x的一元二次方程(x−2)(x−3)=m有两个不相等的实数根x1，x2有下列结论：①x1=2,x2=3；②m>−1；③三次函数y=(x−x1)(x−x2)+m的图象与x轴交点的横坐标分别为4a和b则a+b=5．其中，正确结论的个数是（）A．0 B．1 C．2 D．3二、填空题9．已知关于x的方程（x+1）（x﹣3）+m＝0（m＜0）的两根为a和b，且a＜b，用“＜”连接﹣1、3、a、b的大小关系为.10．如图，是抛物线y=ax2+bx+c（a≠0）的一部分，已知抛物线的对称轴为x=2，与x轴的一个交点是（-1，0），则方程ax2+bx+c=0（a≠0）的两根是11．下列表格是二次函数y=ax2+bx+c(a≠0)中x，y的部分对应值，则一元二次方程ax2+ bx+c=0(a≠0)的一个近似解是.（精确度0.1）x 6.1 6.2 6.3 6.4y−0.3−0.10.20.412．已知抛物线y=ax2+bx+c(b>a>0)与x轴只有一个交点，以下四个结论：①该抛物线的对⩽称轴在y轴左侧；②关于x的方程ax2+bx+c+2=0有实数根；③a+b+c>0；④b−ac1．其中结论正确的为．13．二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx=m有实数根，则m的最小值为三、解答题14．利用图象法求一元二次方程x2﹣2x﹣2=0的近似根．（精确到0.1）15．已知：二次函数y=x2−mx+m−2，求证：无论m为任何实数，该二次函数的图象与x轴都在两个交点；16．已知二次函数y=﹣x2+2x+m的部分图象如图所示，你能确定关于x的一元二次方程﹣x2+2x+m=0的解？17．如图，抛物线y=ax2+bx−4a(a≠0)经过A(−1，0)，C(0，4)两点，与x轴交于另一点B，连接AC，BC．（1）求抛物线的解析式；（2）平行于x轴的直线y=−14与抛物线分别交于点D，E，求线段DE的长．18．已知二次函数y=x2+x−m的部分图象如图所示（1）求该二次函数图象的对称轴，并利用图象直接写出一元二次方程x2+x−m=0的解. （2）向上平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式。
九年级数学上册《第二十二章 二次函数与一元二次方程》》练习题及答案-人教版
九年级数学上册《第二十二章二次函数与一元二次方程》》练习题及答案-人教版一、选择题1.若y＝ax2＋bx＋c，则由表格中信息可知y与x之间的函数关系式是( )x ﹣1 0 1y＝ax2 1y＝ax2＋bx＋c 8 3A.y＝x2﹣4x＋3B.y＝x2﹣3x＋4C.y＝x2﹣3x＋3D.y＝x2﹣4x＋82.已知二次函数y＝ax2＋bx＋c，当x＝1时，有最大值8，其图象的形状、开口方向与抛物线y＝﹣2x2相同，则这个二次函数的解析式是( )A.y＝﹣2x2﹣x＋3B.y＝﹣2x2＋4C.y＝﹣2x2＋4x＋8D.y＝﹣2x2＋4x＋63.若y＝ax2＋bx＋c，则由表格中信息可知y关于x的二次函数的表达式为( ).A.y＝x2﹣4x＋3B.y＝x2﹣3x＋4C.y＝x2﹣3x＋3D.y＝x2﹣4x＋84.已知二次函数y＝x2－3x＋m(m为常数)的图象与x轴的一个交点为(1，0)，则关于x的一元二次方程x2－3x＋m＝0的两实数根是( )A.x1＝1，x2＝－1 B.x1＝1，x2＝2C.x1＝1，x2＝0 D.x1＝1，x2＝35.函数y＝kx2﹣6x＋3的图象与x轴有交点，则k的取值范围是( )A.k＜3B.k＜3且k≠0C.k≤3D.k≤3且k≠06.如图是二次函数y＝－x2＋2x＋4的图象，使y≤1成立的x的取值范围是( )A.－1≤x≤3B.x≤－1C.x≥1D.x≤－1或x≥37.若二次函数y＝ax2＋bx＋c的x与y的部分对应值如下表：x …﹣10 1 2 3 …y (7)4﹣54﹣94﹣5474…则下列说法错误的是( )A.二次函数图象与x轴交点有两个B.x≥2时y随x的增大而增大C.二次函数图象与x轴交点横坐标一个在﹣1～0之间，另一个在2～3之间D.对称轴为直线x＝1.58.已知抛物线y＝x2﹣x﹣2与x轴的一个交点为(m，0)，则代数式m2﹣m＋2 023的值为( )A.2 023B.2 024C.2 025D.2 0269.如图，一次函数y＝﹣x与二次函数为y＝ax2＋bx＋c的图象相交于点M，N，则关于x的一元二次方程ax2＋(b＋1)x＋c＝0的根的情况是( )A.有两个不相等的实数根B.有两个相等的实数C.没有实数根D.以上结论都正确10.关于二次函数y＝ax2＋bx＋c图象有下列命题：(1)当c＝0时，函数的图象经过原点；(2)当c＞0时，函数的图象开口向下时，方程ax2＋bx＋c＝0必有两个不等实根；(3)当b＝0时，函数图象关于原点对称.其中正确的个数有( )A.0个B.1个C.2个D.3个二、填空题11.若二次函数y＝(k﹣2)x2＋2x＋1的图象与x轴有交点，则k的取值范围是.12.抛物线y＝2x2＋8x＋m与x轴只有一个公共点，则m的值为.13.如图，抛物线y＝ax2与直线y＝bx＋c的两个交点分别为A(－2，4)，B(1，1)，则方程ax2＝bx＋c的解是__________.14.如图，若抛物线y＝ax2＋bx＋c上的P(4，0)，Q两点关于它的对称轴直线x＝1对称，则点Q的坐标为________.15.如果a＜0，关于x的方程ax2＋bx＋c＝0有两个不相等的实数根，那么抛物线y＝ax2＋bx ＋c的顶点在x轴________.(填“上方”或“下方”)16.已知函数y＝|x2﹣2x﹣3|的大致图象如图所示，如果方程|x2﹣2x﹣3|＝m(m为实数)有2个不相等的实数根，则m的取值范围是.三、解答题17.已知二次函数y＝﹣316x2＋bx＋c的图象经过A(0，3)，B(﹣4，﹣92)两点(1)求b、c的值；(2)二次函数y＝﹣316x2＋bx＋c的图象与x轴是否有公共点？若有，求公共点的坐标；若没有，请说明理由.18.在平面直角坐标系中，已知抛物线y＝ax2﹣4ax＋2．(1)抛物线的对称轴为直线，抛物线与y轴的交点坐标为；(2)若当x满足1≤x≤5时，y的最小值为﹣6，求此时y的最大值．19.已知抛物线y＝x2﹣4mx＋4m2﹣1．(1)求此抛物线的顶点的坐标；(2)若直线y＝n与该抛物线交于点A、B，且AB＝4，求n的值；(3)若这条抛物线经过点P(2m＋1，y1)，Q(2m﹣t，y2)，且y1＜y2，求t的取值范围．20.已知二次函数y＝﹣x2＋2x＋3.(1)求函数图象的顶点坐标和图象与x轴交点坐标；(2)当x取何值时，函数值最大？(3)当y＞0时，请你写出x的取值范围.21.已知关于x的方程x2＋mx＋n＋3＝0的一根为2.(1)求n关于m的关系式(2)求证：抛物线y＝x2＋mx＋n与x轴有两个交点.22.已知抛物线y＝ax2＋bx＋c(a，b，c是常数，a≠0)的对称轴为直线x＝﹣2.(1)b＝________；(用含a的代数式表示)(2)当a＝﹣1时，若关于x的方程ax2＋bx＋c＝0在﹣3＜x＜1的范围内有解，求c的取值范围；(3)若抛物线过点(﹣2，﹣2)，当﹣1≤x≤0时，抛物线上的点到x轴距离的最大值为4，求a 的值.参考答案1.A2.D3.A4.B.5.C.6.D.7.D.8.C9.B.10.C.11.答案为：k ≤3且k ≠2.12.答案为：8.13.答案为：x 1＝－2，x 2＝1.14.答案为：(－2，0).15.答案为：上方.16.答案为：m ＝0或m ＞4.17.解： (1)将点A(0，3)，B(﹣4，﹣92 )代入二次函数解析式，得⎩⎨⎧c ＝3，－316×（－4）2－4b ＋c ＝－92， 解得⎩⎨⎧c ＝3b ＝98.(2)由(1)知，二次函数解析式为y ＝﹣316x 2＋98x ＋3令y ＝0，得﹣316x 2＋98x ＋3＝0整理得x 2﹣6x ﹣16＝0，解得x 1＝﹣2，x 2＝8即该二次函数的图象与x 轴有两个不同交点，坐标分别为(﹣2，0)，(8，0). 18.解：(1)∵抛物线y ＝ax 2﹣4ax ＋2的对称轴为直线x ＝2．令x ＝0，则y ＝2．∴抛物线y＝ax2﹣4ax＋2与y轴的交点为(0，2)．故答案为：x＝2；(0，2)．(2)∵抛物线y＝ax2﹣4ax＋2的对称轴为直线x＝2∴顶点在1≤x≤5范围内∵当x满足1≤x≤5时，y的最小值为﹣6∴当a＜0时，抛物线开口向下，x＝5时y有最小值﹣6∴25a﹣20a＋2＝﹣6，解得a＝﹣∴抛物线为y＝﹣x2＋x＋2当x＝2时，y＝﹣×22＋×2＋2＝∴此时y的最大值为．当a＞0，抛物线开口向上，x＝2时y有最小值﹣6∴4a﹣8a＋2＝﹣6，解得a＝2∴抛物线为y＝2x2﹣8x＋2当x＝5时，y＝2×25﹣8×5＋2＝12∴此时y的最大值12．综上，y的最大值为12．19.解：(1)∵y＝x2﹣4mx＋4m2﹣1＝(x﹣2m)2﹣1∴抛物线顶点坐标为(2m，﹣1)．(2)∵点A，B关于抛物线对称轴对称，AB＝4，对称轴为直线x＝2m ∴抛物线经过(2m＋2，n)，(2m﹣2，n)将(2m＋2，n)代入y＝(x﹣2m)2﹣1得n＝22﹣1＝3．(3)点P(2m＋1，y1)关于抛物线对称轴的对称点P'坐标为(2m﹣1，y1)∵抛物线开口向上∴当2m﹣t＞2m＋1或2m﹣t＜2m﹣1时，且y1＜y2解得t＜﹣1或t＞1．20.解：(1)∵y＝﹣x2＋2x＋3＝﹣(x﹣1)2＋4 ∴图象顶点坐标为(1，4)当y＝0时，有﹣x2＋2x＋3＝0解得：x1＝﹣1，x2＝3∴图象与x轴交点坐标为(﹣1，0)，(3，0)；(2)由(1)知，抛物线顶点坐标为(1，4)，且抛物线开口方向向下，当x＝1时，函数值最大；(3)因为图象与x轴交点坐标为(﹣1，0)，(3，0)，且抛物线开口方向向下所以当y＞0时，﹣1＜x＜3.21.解：(1)将x＝2代入方程，得：4＋2m＋n＋3＝0整理可得n＝﹣2m﹣7；(2)∵△＝m2﹣4(n＋3)＝m2﹣4(﹣2m﹣7)＝m2＋8m＋28＝(m＋4)2＋12＞0∴一元二次方程x2＋mx＋n＝0有两个不相等的实根∴抛物线y＝x2＋mx＋n与x轴有两个交点.22.解：(1)4a；(2)当a＝﹣1时，∵关于x的方程﹣x2﹣4x＋c＝0在﹣3＜x＜1的范围内有解，即关于x的方程x2＋4x﹣c＝0在﹣3＜x＜1的范围内有解∴根的判别式＝16＋4c≥0，即c≥﹣4抛物线y＝x2＋4x＝(x＋2)2﹣4与直线y＝c在﹣3＜x＜1的范围内有交点.当x＝﹣2时，y＝﹣4；当x＝1时，y＝5.由图象可知：﹣4≤c＜5.(3)∵抛物线y＝ax2＋4ax＋c过点(﹣2，﹣2)∴c＝4a﹣2∴抛物线对应的函数解析式为：y＝ax2＋4ax＋4a﹣2＝a(x＋2)2﹣2.方法一：①当a＞0时，抛物线开口向上.∵抛物线的对称轴为直线x＝﹣2∴当﹣1≤x≤0时，y随x增大而增大.∵抛物线上的点到x轴距离的最大值为4由图象可知：4a﹣2＝4.∴a＝3 2 .②当a＜0时，抛物线开口向下. ∵抛物线对称轴为直线x＝﹣2∴当﹣1≤x≤0时，y随x增大而减小. ∵抛物线上的点到x轴距离的最大值为4由图象可知：4a﹣2＝﹣4.∴a＝﹣1 2 .综上所述：a＝32或a＝﹣12.。
二次函数与一元二次方程同步练习题
二次函数与一元二次方程同步练习第1题.抛物线y=2 x - 8 - 3 x 2与x轴有个交点，因为其判别式b 2—4 ac =0,相应二次方程3 x 2 — 2 x + 8 = 0的根的情况为.答案：0 -92 < 没有实数根.第2题.函数y=mx2 + x - 2m（m是常数）的图像与x轴的交点个数为（）A.0个B.1个C.2个D.1个或2个答案：C第3题.关于二次函数y=ax2 + bx + c的图像有下列命题：①当c = 0时，函数的图像经过原点；②当c > 0，且函数的图像开口向下时，方程ax2 + bx + c = 0必有两个不相等的实根；③函数图像最高点的纵坐4ac - b2标是「一；④当b = 0时，函数的图像关于y轴对称.4a其中正确命题的个数是（）A.1个B.2个C.3个D.4个答案：C第4题.关于x的方程mx2 + mx + 5 = m有两个相等的实数根，则相应二次函数y=mx2 + mx + 5 - m与x轴必然相交于点，此时m=.答案：一4第5题.抛物线尸x 2-(2m -1)x - 6m 与x 轴交于两点(X i ，0)和(x 『0)，若X i X 2=x i + x 2 + 49，要使答案：B第7题.已知抛物线y = -3(x -h )2 + k 的顶点在抛物线y = x 2上，且抛物线在x 轴上截得的线段长是 4v3，求h 和k 的值.答案：y = -3(x -h )2+ k ，顶点(h ，k )在y = x 2上，1 122 /. y 二 一一 (x-h )2 + h 2 = -—x 2 + — hx + — h 2.3333x -x I = \:'(x -x )2 = ：(x + x )2 -4xx1 2 1 2 1 2 1 2求得 h = ±2, k = 4，即 h = 2 , k = 4 或 h = —2, k = 4.第8题. 已知函数y = x 2 - mx + m - 2 .(1)求证：不论m 为何实数，此二次函数的图像与x 轴都有两个不同交点；5(2)若函数y 有最小值一^,求函数表达式.答案：(1) A = (-m )2 - 4(m - 2) = m 2 - 4m + 8 = (m - 2)2 + 4，不论 m 为何值时，都有 A > 0,- 2 -抛物线经过原点，应将它向右平移 个单位.答案：4或9第6题.关于％的二次函数y = 2mx 2 + (8m +1)x + 8m 的图像与x 轴有交点， 则m 的范围是(1A. m <--16B. m 三——且m 丰1C. m =--16D. m >-—且 m 丰 016又它与x 轴两交点的距离为4<3 , /.|此时二次函数图像与X 轴有两个不同交点.4ac - b 2 4(m - 2) - m 2 5----------- = 二——,m 2 — 4m + 3 = 0 ,「. m — 1 或 m — 3 ,4 a 4 4， '或' 所求函数式为y — X 2 — X — 1或y — X 2 — 3X +1 .第9题.下图是二次函数y ― aX 2+ bX + c 的图像，与X 轴交于B ，C 两点，与y 轴交于A 点. (1)根据图像确定a , b , c 的符号，并说明理由；(2)如果A 点的坐标为(0,— 3), /ABC = 45 , /ACB = 60，求这个二次函数的函数表达式.b答案：(1)抛物线开口向上，a >0 ；图像的对称轴在y 轴左侧，-k <0,又a >0 , 2a••• b > 0 ；图像与y 轴交点在X 轴下方，，c < 0. a > 0, b > 0 , c < 0 .(2) A (0,— 3) , |0A | = 3 , /ABC = 45 , N ACB = 60 , 把(0，— 3)代入上式，得a =(，.二所求函数式为 y — ；(X+ 3)(X — V3) = 3X X 2 + (<3 — 1)X — 3 .m 2 3m 2第10题.已知抛物线y — X 2 — mX + —与抛物线y =X 2 + mx —-二一在直角坐标系中的位置如图所示，其中一条与X 轴交于A , B 两点.(2) ^Cl = 0A|tan 60B (—3,0),C (<3,0).设二次函数式为 y = a (X + 3)(X -6), tan /ABC(1 )试判断哪条抛物线经过A , B两点，并说明理由；112(2)若A , B两点到原点的距离AO , OB满足条件- =-，求经过A , B两点的这条抛物线OB OA 3的函数式．m2答案：(1)抛物线不过原点，m中0 ,令x2 - mx + ——=0 , A = (-m)2 - 4 义m2 3 m2——=-m 2 < 0 2⑵设A(x ,0), B(x ,0),12x，x是方程x 2 + mx一3—m2 = 0的两根x +x 4xx-3m2, A4在原点左边，n …… 1 1 2B在原点右边，则AO =-x , OB = x . 一=-11二. 一 +—=x + x------- ;xx1223,-m--m 24得m = 2 ,二.所求函数式为y = x2 + 2x - 3.第11题. 已知二次函数y = 2 x 2 — 4 mx + m 2 .(1)求证：当m中0时，二次函数的图像与x轴有两个不同交点;(2)若这个函数的图像与x轴交点为A , B，顶点为。
人教版九年级数学上第22章二次函数22.2《二次函数与一元二次方程》同步练习(含答案)
22.2《二次函数与一元二次方程》同步练习一、选择题1．已知抛物线y＝ax2＋bx＋c的图象如图，则一元二次方程ax2＋bx＋c＝0( )A．没有实根B．有两个实根，且一根为正，一根为负C．只有一个实根D．有两个实根，且一根小于1，一根大于22．一次函数y＝2x＋1与二次函数y＝x2－4x＋3的图象交点( )A．只有一个B．恰好有两个C．可以有一个，也可以有两个D．无交点3．函数y＝ax2＋bx＋c的图象如图所示，那么关于x的方程ax2＋bx＋c－3＝0的根的情况是( )A．有两个不相等的实数根B．有两个异号实数根C．有两个相等的实数根D．无实数根4．二次函数y＝ax2＋bx＋c对于x的任何值都恒为负值的条件是( )A．a＞0，＞0 B．a＞0，＜0C．a＜0，＞0 D．a＜0，＜05．直线y＝4x＋1与抛物线y＝x2＋2x＋k有唯一交点，则k是( )A．0 B．1 C．2 D．－16．二次函数y＝ax2＋bx＋c，若ac＜0，则其图象与x轴( )A．有两个交点B．有一个交点C．没有交点D．可能有一个交点7．y＝x2＋kx＋1与y＝x2－x－k的图象相交，若有一个交点在x轴上，则k值为( )1A．0 B．－1 C．2 D．48．已知二次函数y＝ax2＋bx＋c的图象如图所示，那么关于x的方程ax2＋bx＋c＋2＝0的根的情况是( )A ．无实根B ．有两个相等实数根C ．有两个异号实数根D ．有两个同号不等实数根9．已知二次函数的图象与y 轴交点坐标为(0，a )，与x 轴交点坐标为(b ，0)和(－b ，0)，若a ＞0，则函数解析式为( ) A ．a x b ay +=2B ．a x b a y +-=22 C ．a x ba y --=22 D ．a x bay -=2210．若m ，n (m ＜n )是关于x 的方程1－(x －a )(x －b )＝0的两个根，且a ＜b ，则a ，b ，m ，n 的大小关系是( ) A ．m ＜a ＜b ＜n B ．a ＜m ＜n ＜b C ．a ＜m ＜b ＜nD ．m ＜a ＜n ＜b二、填空题11．二次函数y ＝ax 2＋bx ＋c (a ≠0)与x 轴有交点，则b 2－4ac ______0；若一元二次方程ax 2＋bx ＋c ＝0两根为x 1，x 2，则二次函数可表示为y ＝________． 12．若二次函数y ＝x 2－3x ＋m 的图象与x 轴只有一个交点，则m ＝______． 13．若二次函数y ＝mx 2－(2m ＋2)x －1＋m 的图象与x 轴有两个交点，则m 的取值范围是______．14．若二次函数y ＝ax 2＋bx ＋c 的图象经过P (1，0)点，则a ＋b ＋c ＝______． 15．若抛物线y ＝ax 2＋bx ＋c 的系数a ，b ，c 满足a －b ＋c ＝0，则这条抛物线必经过点______．16．关于x 的方程x 2－x －n ＝0没有实数根，则抛物线y ＝x 2－x －n 的顶点在第______象限．1.二次函数y=－x 2+4x －3的图象交x 轴于A 、B 两点，交y 轴于C 点，则△ABC 的面积为（ ）A ．6B ． 4C ．3D ．117．已知直线y ＝5x ＋k 与抛物线y ＝x 2＋3x ＋5交点的横坐标为1，则k ＝______，交点坐标为______．18．当m ＝______时，函数y ＝2x 2＋3mx ＋2m 的最小值为⋅98 三、解答题19．已知抛物线y ＝ax 2＋bx ＋c 与x 轴的两个交点的横坐标是方程x 2＋x －2＝0的两个根，且抛物线过点(2，8)，求二次函数的解析式．20．对称轴平行于y 轴的抛物线过A (2，8)，B (0，－4)，且在x 轴上截得的线段长为3，求此函数的解析式．21．二次函数y ＝ax 2＋bx ＋c (a ≠0，a ，b ，c 是常数)中，自变量x 与函数y 的对应值如下表：(1)判断二次函数图象的开口方向，并写出它的顶点坐标；(2)一元二次方程ax 2＋bx ＋c ＝0(a ≠0，a ，b ，c 是常数)的两个根x 1，x 2的取值范围是下列选项中的哪一个______．①223,02121<<<<-x x ②252,21121<<-<<-x x③252,02121<<<<-x x④223,21121<<-<<-x x22．m 为何值时，抛物线y ＝(m －1)x 2＋2mx ＋m －1与x 轴没有交点?23．当m 取何值时，抛物线y ＝x 2与直线y ＝x ＋m(1)有公共点；(2)没有公共点．24．已知抛物线y ＝－x 2－(m －4)x ＋3(m －1)与x 轴交于A ，B 两点，与y 轴交于C 点．(1)求m 的取值范围．(2)若m ＜0，直线y ＝kx －1经过点A 并与y 轴交于点D ，且25=⋅BD AD ，求抛物线的解析式．参考答案1．D ． 2．B ． 3．C ． 4．D ．5．C ． 6．A ． 7．C ． 8．D ． 9．B ． 0．A ． 11．≥0，y ＝a (x －x 1)(x －x 2)． 12．⋅4913．31->m 且m ≠0． 1 4．0． 15．(－1，0)． 1 6．一．12．45665182-+-=x x y 或y ＝2x 2＋2x －4． 17．4，(1，9)． 18．⋅9819．y ＝2x 2＋2x －4．20.21．(1)开口向下，顶点(1，2)，(2)③． 22．⋅<21m 23．由x 2－x －m ＝0(1)当＝1＋4m ≥0，即41-≥m 时两线有公共点．(2)当＝1＋4m ＜0，即41-<m 时两线无公共点．24．(1)＝(m ＋2)2＞0，∴m ≠－2；(2)m ＝－1，∴y ＝－x 2＋5x －6．。
一元二次方程及二次函数同步训练卷
一元二次方程及二次函数同步训练卷一．选择题（共7小题）1．将二次函数y＝x2的图象向上平移1个单位，则平移后图象的函数表达式为（）A．y＝x2﹣1B．y＝x2+1C．y＝（x﹣1）2D．y＝（x+1）2 2．已知抛物线y＝2x2+8x﹣6，下列说法正确的是（）A．抛物线的开口方向向下B．抛物线的对称轴是直线x＝2C．抛物线与y轴交于点（0，﹣6）D．抛物线与x轴没有交点3．设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y＝3（x+1）2+4m（m为常数）上的三点，则y1，y2，y3的大小关系为（）A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y3＜y2＜y14．二次函数y＝ax2+bx+c的图象如图所示，则一次函数y=(c+3a)x−ba的图象可能是（）A．B．C．D．5．方程2x2﹣x﹣3＝0的根的情况是（）A．有两个不相等的实数根B．没有实数根C．有两个负实数根D．有两个正实数根6．若方程（x﹣1）2＝m有解，则m的取值范围是（）A ．m ≤0B ．m ≥0C ．m ＜0D ．m ＞07．第二十二届世界杯足球赛于2022年11月20日在卡塔尔举办开幕赛，为了迎接世界杯，某市举行了足球邀请赛，规定参赛的每两支球队之间比赛一场，共安排了45场比赛．设比赛组织者邀请了x 个队参赛，则下列方程正确的是（ ）A ．12x(x +1)=45B ．x （x ﹣1）＝45C ．x （x +1）＝45D ．12x(x −1)=45 二．填空题（共4小题）8．如图，甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分．甲在O 点正上方的A 处发出一球，以点O 为原点建立平面直角坐标系，羽毛球飞行的高度y （m ）与水平距离x （m ）之间满足函数解析式y =−15（x ﹣4）2+215，球网BC 离点O 的水平距离为5米，甲运动员发球过网后，乙运动员在球场上N （n ，0）处接球，乙原地起跳可接球的最大高度为2.4米，若乙因接球高度不够而失球，则n 的取值范围是 ．9．抛物线y ＝ax 2+bx +c 上部分点的横坐标与纵坐标的对应值如表：x… ﹣4 ﹣2 0 2 4 … y … m n m 1 0 …由表可知，抛物线与x 轴的一个交点的坐标是（4，0），则抛物线与x 轴的另一个交点的坐标是 ．10．标准大气压下，质量一定的水的体积V （cm 3）与温度t （℃）之间的关系满足二次函数V =18t 2−t +104（t ＞0），则当温度为16℃时，水的体积为 cm 3．11．对于实数a ，b ，定义运算“a *b ={a 2−ab(a ＞b)ab −b 2(a ≤b)，例如4*2，因为4＞2，所以4*2＝42﹣4×2＝8．若x 1，x 2是一元二次方程x 2﹣8x +16＝0的两个根，则x 1*x 2＝ ．三．解答题（共9小题）12．抛物线y ＝﹣2x 2+8x ﹣6．（1）用配方法求顶点坐标，对称轴；（2）x取何值时，y随x的增大而减小？（3）x取何值时，y＝0；x取何值时，y＞0；x取何值时，y＜0．13．在平面直角坐标系中，已知抛物线y＝x2+（k﹣2）x+3．（1）该抛物线经过一个定点：（写出坐标）；（2）点P（m，n）是抛物线上一点，当点P在抛物线上运动时，n存在最小值N．①若N＝3，求k的值；②若﹣1＜k＜3，结合该抛物线，直接写出N的取值范围．14．抛物线y＝ax2+（3a﹣1）x﹣3（a＞0）与x轴交于A、B两点（A左B右），AB＝4，与y轴的交点是C，顶点是D．（1）求抛物线的解析式；（2）E为对称轴上一点，F为平面内一点，A、C、E、F为矩形的四个顶点，求出符合条件的E点坐标；（3）直线PQ与抛物线交于P、Q两点，连接DP，DQ，满足DP⊥DQ，求证；直线恒过定点，并求出定点坐标．15．某水果商场经销一种高档水果，原价每千克50元．（1）连续两次降价后每千克32元，若每次下降的百分率相同．求每次下降的百分率；（2）若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，但商场规定每千克涨价不能超过8元，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，那么每千克应涨价多少元？16．随着疫情防控全面放开，“复工复产”成为主旋律．中航无人机公司统计发现：公司今年2月份生产A型无人机2000架，4月份生产A型无人机达到12500架．（1）求该公司生产A型无人机每月产量的平均增长率；（2）该公司还生产B型无人机，已知生产1架A型无人机的成本200元，生产1架B 型无人机的成本是300元．若生产A、B两种型号无人机共100架，预算投入生产的成本不高于22500元，问最多能生产B型无人机多少架？17．解下列方程：（1）4x2﹣8x+1＝0（2）3（x﹣5）2＝2（5﹣x）18．如图是一张长20cm、宽12cm的矩形纸板，将纸板四个角各剪去一个边长为xcm的正方形，然后将四周突出部分折起，可制成一个无盖纸盒．（1）这个无盖纸盒的长为cm，宽为cm；（用含x的式子表示）（2）若要制成一个底面积是180cm2的无盖长方体纸盒，求x的值．19．列方程解应用题：某化肥厂5月份生产某种化肥600吨，6月份因部分设备检修，产量比5月份减少了10%．从7月份起产量逐月上升，8月份达到653.4吨．该厂7，8两个月产量的平均月增长率是多少？20．“疫情”期间，小颖在家制作一种工艺品，并通过网络进行线上销售．经过一段时间后发现：当售价是40元/件时，每天可售出该商品60件，且售价每降低1元，就会多售出3件．若每件工艺品需要19元成本，设该工艺品的售价为x元/件（19≤x≤40）．（1）请用含x的代数式表示：①销售每件工艺品的利润：元；②每天能售出该工艺品的件数：；（2）为了支持“抗疫”行动，小颖决定每销售一件该工艺品便通过网络平台自动向医疗基金会捐款1元，若每天销售该工艺品的纯利润为900元，求该工艺品的售价．。
二次函数与一元二次方程练习题(家庭作业)
二次函数与一元二次方程 练习题（家庭作业）拟题：黄昌芹一、抛物线2283y x x =--与x 轴有 个交点，因为其判别式24b ac -= 0，相应二次方程23280x x -+=的根的情形为．二、函数22y mx x m =+-（m 是常数）的图像与x 轴的交点个数为（） Ａ、0个 Ｂ、1个Ｃ、2个 Ｄ、1个或2个 3、关于二次函数2y ax bx c =++的图像有以下命题：①当0c =时，函数的图像通过原点；②当0c >，且函数的图像开口向下时，方程20ax bx c ++=必有两个不相等的实根；③函数图像最高点的纵坐标是244ac b a-；④当0b =时，函数的图像关于y 轴对称．其中正确命题的个数是（ ）Ａ、1个Ｂ、2个 Ｃ、3个 Ｄ、4个 4、关于x 的方程25mx mx m ++=有两个相等的实数根，那么相应二次函数25y mx mx m =++-与x 轴必然相交于 点，现在m = ．5、抛物线2(21)6y x m x m =---与x 轴交于两点1(0)x ，和2(0)x ，，假设121249x x x x =++，要使抛物线通过原点，应将它向右平移个单位． 六、关于x 的二次函数22(81)8y mx m x m =+++的图像与x 轴有交点，那么m 的范围是（） Ａ、116m <- Ｂ、116m -≥且0m ≠ Ｃ、116m =- Ｄ、116m >-且0m ≠7、 已知抛物线21()3y x h k =--+的极点在抛物线2y x =上，且抛物线在x 轴上截得的线段长是h 和k 的值．八、已知函数22y x mx m =-+-．（1）求证：不论m 为何实数，此二次函数的图像与x 轴都有两个不同交点；（2）假设函数y 有最小值54-，求函数表达式．9、已知二次函数2224y x mx m =-+．（1）求证：当0m ≠时，二次函数的图像与x 轴有两个不同交点；（2）假设那个函数的图像与x 轴交点为A ，B ，极点为C ，且△ABC的面积为数表达式．10、如下图，函数2(2)(5)y k x k =-+-的图像与x 轴只有一个交点，那么交点的横坐标0x =．11、已知抛物线2y ax bx c =++与y 轴交于C 点，与x 轴交于1(0)A x ，，212(0)()B x x x <，两点，极点M 的纵坐标为4-，假设1x ，2x 是方程222(1)70x m x m --+-=的两根，且221210x x +=．（1）求A ，B 两点坐标；（2）求抛物线表达式及点C 坐标；（3）在抛物线上是不是存在着点P ，使△PAB 面积等于四边形ACMB 面积的2倍，假设存在，求出P 点坐标；假设不存在，请说明理由．1二、二次函数269y x x =-+-的图像与x 轴的交点坐标为 ．13、二次函数25106y x x =-+的图像与x 轴有 个交点．14、假设二次函数2y ax c =+，当x 取1x 、2x （12x x ≠）时，函数值相等，那么当x 取12x x +时，函数值为（ ）Ａ、a c + Ｂ、a c - Ｃ、c - Ｄ、c1五、以下二次函数中有一个函数的图像与x 轴有两个不同的交点，那个函数是（ ）Ａ、2y x = Ｂ、24y x =+ Ｃ、2325y x x =-+Ｄ、2351y x x =+- 1六、二次函数256y x x =-+与x 轴的交点坐标是（ ）Ａ、（2，0）（3，0） Ｂ、（2-，0）（3-，0） Ｃ、（0，2）（0，3） Ｄ、（0，2-）（0，3-）17、函数2y ax bx c =++的图象如下图，那么关于x2） Ａ、有两个不相等的实数根Ｂ、有两个异号的实数根 Ｃ、有两个相等的实数根Ｄ、没有实数根1八、 已知二次函数212y x bx c =-++，关于x 的一元二次方程2102x bx c -++=的两个实根是1-和5-，那么那个二次函数的解析式为。
九年级数学二次函数与一元二次方程同步练习题(供参考)
九年级数学《二次函数与一元二次方程》同步练习题第1题. 抛物线2283y x x =--与x 轴有个交点，因为其判别式24b ac -=0，相应二次方程23280x x -+=的根的情形为．第2题. 函数22y mx x m =+-（m 是常数）的图像与x 轴的交点个数为（ ）Ａ．0个Ｂ．1个Ｃ．2个Ｄ．1个或2个第3题. 关于二次函数2y ax bx c =++的图像有以下命题：①当0c =时，函数的图像通过原点；②当0c >，且函数的图像开口向下时，方程20ax bx c ++=必有两个不相等的实根；③函数图像最高点的纵坐标是244ac b a-；④当0b =时，函数的图像关于y 轴对称． 其中正确命题的个数是（ ）Ａ．1个Ｂ．2个Ｃ．3个Ｄ．4个第4题. 关于x 的方程25mx mx m ++=有两个相等的实数根，那么相应二次函数25y mx mx m =++-与x 轴必然相交于点，现在m =．第5题. 抛物线2(21)6y x m x m =---与x 轴交于两点1(0)x ，和2(0)x ，，假设121249x x x x =++，要使抛物线通过原点，应将它向右平移个单位．第6题. 关于x 的二次函数22(81)8y mx m x m =+++的图像与x 轴有交点，那么m 的范围是（）Ａ．116m <-Ｂ．116m -≥且0m ≠ Ｃ．116m =-Ｄ．116m >-且0m ≠ 第7题. 已知抛物线21()3y x h k =--+的极点在抛物线2y x =上，且抛物线在x轴上截得的线段长是求h 和k 的值．第8题. 已知函数22y x mx m =-+-．（1）求证：不论m 为何实数，此二次函数的图像与x 轴都有两个不同交点； （2）假设函数y 有最小值54-，求函数表达式． 第9题. 以下图是二次函数2y ax bx c =++的图像，与x 轴交于B ，C 两点，与（1）依照图像确信a ，b ，c 的符号，并说明理由；（2）若是A 点的坐标为(03)-，，45ABC ∠=，60ACB ∠=，求那个二次函数的函数表达式．第10题. 已知抛物线222m y x mx =-+与抛物线2234m y x mx =+-在直角坐标系中的位置如下图，其中一条与x 轴交于A ，B 两点．（1）试判定哪条抛物线通过A ，B 两点，并说明理由； （2）假设A ，B 两点到原点的距离AO ，OB 知足条件1123OB OA -=，求通过A ，B 两点的这条抛物线的函数式．第11题. 已知二次函数2224y x mx m =-+．（1）求证：当0m ≠时，二次函数的图像与x 轴有两个不同交点；（2）假设那个函数的图像与x 轴交点为A ，B ，极点为C ，且△ABC的面积为，求此二次函数的函数表达式．第12题.如下图，函数2(2)(5)y k x k =-+-的图像与x 轴只有一个交点，那么交点的横坐标0x =．第13题. 已知抛物线2y ax bx c =++与y 轴交于C 点，与x 轴交于1(0)A x ，，212(0)()B x x x <，两点，极点M 的纵坐标为4-，假设1x ，2x 是方程222(1)70x m x m --+-=的两根，且221210x x +=．（1）求A ，B 两点坐标； （2）求抛物线表达式及点C 坐标；（3）在抛物线上是不是存在着点P ，使△PAB 面积等于四边形ACMB 面积的2倍，假设存在，求出P 点坐标；假设不存在，请说明理由．第14题. 二次函数269y x x =-+-的图像与x 轴的交点坐标为．第15题. 二次函数25106y x x =-+的图像与x 轴有 个交点．第16题. 关于二次函数2135y x x =++，当12x =时，y = ．第17题. 如图是二次函数2246y x x =--的图像，那么方程22460x x --=的两根之和 0．第18题. 求以下函数的图像与x 轴的交点坐标，并作草图验证．（1）25166y x x =-+； （2）2336y x x =+-． 第19题. 一元二次方程20ax bx c ++=的两根为1x ，2x ，且214x x +=，点(38)A -，在抛物线2y ax bx c=++上，求点A 关于抛物线的对称轴对称的点的坐标．第20题. 假设二次函数2y ax c =+，当x 取1x 、2x （12x x ≠）时，函数值相等，那么当x 取12x x +时，函数值为（ ）Ａ．a c + Ｂ．a c - Ｃ．c - Ｄ．c第21题. 以下二次函数中有一个函数的图像与x 轴有两个不同的交点，那个函数是（ ） Ａ．2y x =Ｂ．24y x =+ Ｃ．2325y x x =-+Ｄ．2351y x x =+-第22题. 二次函数256y x x =-+与x 轴的交点坐标是（ ）Ａ．（2，0）（3，0） Ｂ．（2-，0）（3-，0） Ｃ．（0，2）（0，3） Ｄ．（0，2-）（0，3-）第23题. 试说明一元二次方程2441x x -+=的根与二次函数244y x x =-+的图像的关系，并把方程的根在图象上表示出来．第24题. 利用二次函数图象求一元二次方程的近似根．210x x +-=第25题. 利用二次函数图象求一元二次方程的近似根．24834x x --=-第26题. 函数2y ax bx c =++的图象如下图，那么关于x 的一元二次方程230ax bx c ++-=的根的情形是（）Ａ．有两个不相等的实数根 Ｂ．有两个异号的实数根 Ｃ．有两个相等的实数根Ｄ．没有实数根第27题. 利用二次函数的图象求一元二次方程的近似值．2530x x --=第28题. 抛物线2321y x x =-+-的图象与坐标轴交点的个数是（ ）Ａ．没有交点Ｂ．只有一个交点Ｃ．有且只有两个交点 Ｄ．有且只有三个交点第29题. 已知二次函数212y x bx c =-++，关于x 的一元二次方程2102x bx c -++=的两个实根是1-和5-，那么那个二次函数的解析式为第30题. 已知二次函数2(0)y ax bx c a =++≠的极点坐标(1 3.2)--，及部份图象（如图４所示），由图象可知关于x 的一元二次方程20ax bx c ++=的两个根别离是1 1.3x =和2x = ．一、答案：092-<没有实数根． 二、答案：Ｃ 3、答案：Ｃ 4、答案：一 4五、答案：4或9 六、答案：Ｂ7、答案：21()3y x h k =--+，极点()h k ，在2y x =上，2h k ∴=，y22221122()3333y x h h x hx h ∴=--+=-++．又它与x轴两交点的距离为12x x a∴-==== 求得2h =±，4k =，即2h =，4k =或2h =-，4k =．八、答案：（1）222()4(2)48(2)4m m m m m ∆=---=-+=-+，不论m 为何值时，都有0∆>， 现在二次函数图像与x 轴有两个不同交点． （2）2244(2)5444ac b m m a ---==-，2430m m -+=，1m ∴=或3m =， 所求函数式为21y x x =--或231y x x =-+．九、答案：（1）抛物线开口向上，0a >；图像的对称轴在y 轴左侧，02ba-<，又0a >， 0b ∴>；图像与y 轴交点在x 轴下方，0c ∴<．0a ∴>，0b >，0c <．（2）(03)A -，，3OA =，45ABC ∠=，60ACB ∠=，3tan OAOB ABC==∠，3tan 60OAOC ==(30)B ∴-，，C ．设二次函数式为(3)(ya x x =+， 把(03)-，代入上式，得a =∴所求函数式为23)(1)3y x x x x =+=+-． 10、答案：（1）抛物线只是原点，0m ≠，令2202m x mx -+=，2221()402m m m ∆=--⨯=-<，222m y x mx =-+∴与x 轴无交点，∴抛物线2234y x mx m =+-通过A ，B 两点．（2）设1(0)A x ，，2(0)B x ，，1x ，2x 是方程22304x mx m +-=的两根12x x m +=-，21234x x m =-，A 在原点左侧，B 在原点右边，那么1AO x =-，2OB x =．123OB OA 1-=．211123x x ∴+=，121223x x x x +=，22334m m -=-，得2m =，∴所求函数式为223y x x =+-．1一、答案：（1）22222(4)421688m m m m m ∆=--⨯⨯=-=．0m ≠，280m ∴>，∴那个抛物线与x 轴有两个不同交点．（2）设1(0)A x ，，212(0)()B x x x >，，那么1x ，2x 是方程22240x mx m -+=两根，122x x m +=，2122m x x =，21AB x x =-====，C 点纵坐标22224816442c ac b m m y m a --===-⨯， ∴△ABC 中AB 边上的高22h m m =-=．21124222ABCSAB h m m ===，2m =，2m =±， 2284y x x ∴=++或2284y x x =-+．1二、答案：13、答案：（1）由122(1)x x m +=-，2127x x m =-，22222121212()24(1)2(7)10x x x x x x m m +=+-=---=，得2m =，11x ∴=-，23x =，(10)A -，，(30)B ，．（2）抛物线过A ，B 两点，其对称轴为1x =，极点纵坐标为4-，∴抛物线为2(1)4y a x =--．把1x =-，0y =代入得1a =，∴抛物线函数式为223y x x =--，其中(03)C -，． （3）存在着P 点．(10)A -，，(03)C -，，(14)M -，，(30)B ，，∴9ACMB S =四形，18ABPS =，即1182P y AB =．4AB =，9P y ∴=．把9y =代入抛物线方程得11x =，21x =，(1P ∴-或(1P +．14、答案：（3，0） 1五、答案：0 1六、答案：1132017、答案：> 1八、答案：（1）（13，0），（12，0），图略 （2）（1，0），（2-，0），图略 1九、答案：（1，8-） 20、答案：Ｄ 2一、答案：Ｄ 2二、答案：A23、答案：一元二次方程2441x x -+=的根是二次函数244y x x =-+与直线1y =的交点的横坐标，图略．24、答案：1 1.6x ≈-，20.6x ≈ 2五、答案：1 1.9x ≈，20.1x ≈ 2六、答案：Ｃ 27、答案：1 5.5x ≈，20.5x ≈- 2八、答案：Ａ 2九、答案：215322y x x =--- 30、答案： 3.3-。
二次函数与一元二次方程练习(精)
二次函数与一元二次方程关系练习一、选择题1、已知二次函数y=x 2-3x+m(m 为常数)的图象与x 轴的一个交点为（1,0），则关于x 的一元二次方程x 2-3x+m=0的两实数根是（ ）A 、x 1=1，x 2=﹣1B 、x 1=1，x 2=2C 、x 1=1，x 2=0D 、x 1=1，x 2=32、若一元二次方程ax 2+bx+c=0的两个根为﹣3和1，则二次函数y=ax 2+bx+c 的对称轴是（ ）A 、x=﹣2B 、x=2C 、x=﹣3D 、 x=﹣13、 若x 1，x 2（x 1＜x 2）是方程（x-a ）（x-b ）=1（a ＜b ）的两个根，实数x 1，x 2，a ，b 的大小关系为（ ）A 、x 1＜x 2＜a ＜bB 、x 1＜a ＜x 2＜bC 、x 1＜a ＜b ＜x 2D 、a ＜x 1＜b ＜x 24、 若关于x 的一元二次方程（x-2）（x-3）=m 有实数根x 1、x 2，且x 1≠x 2，有下列结论： ①x 1=2，x 2=3；②m ＞-41；③二次函数y=（x-x 1）（x-x 2）+m 的图象与x 轴交点的坐标为（2，0）（3，0）．其中，正确结论的个数是（ ）A 、 0B 、 1C 、 2D 、 35、已知一元二次方程ax 2+bx+c=0（a ＞0）的两个实数根x 1，x 2满足x 1+x 2=4和x 1 x 2=3，那么二次函数y=ax 2+bx+c （a ＞0）的图象有可能是（ ）AB CD6、关于x 的一元二次方程x 2-x-n=0无实数根，则 抛物线y=x 2-x-n 的顶点在（ ）A ．第一象限 B.第二象限 C. 第三象限 D.第四象限二、填空题1、如果抛物线y=x 2-2(m+1)x+m 2与x 轴有交点，则m2、若二次函数y=﹣x 2+2x+k 的部分图象如图（2）所示，则关于x 的一元二次方程﹣x 2+2x+k=0的一个解x 1=3，另一个解x 2= ；3、已知二次函数y=﹣x 2+2x+m 的部分图象如图（3y=﹣x 2+2x+m=0的解为 。
二次函数与一元二次方程_练习题
二次函数与一元二次方程 练习题附参考答案1、抛物线2283y x x =--与x 轴有个交点，因为其判别式24b ac -=0，相应二次方程23280x x -+=的根的情况为． 答案：0 92-< 没有实数根．2、函数22y mx x m =+-（m 是常数）的图像与x 轴的交点个数为（）Ａ、0个Ｂ、1个Ｃ、2个Ｄ、1个或2个 答案：Ｃ3、关于二次函数2y ax bx c =++的图像有下列命题：①当0c =时，函数的图像经过原点；②当0c >，且函数的图像开口向下时，方程20ax bx c ++=必有两个不相等的实根；③函数图像最高点的纵坐标是244ac b a-；④当0b =时，函数的图像关于y 轴对称．其中正确命题的个数是（ ）Ａ、1个Ｂ、2个Ｃ、3个Ｄ、4个 答案：Ｃ4、关于x 的方程25mx mx m ++=有两个相等的实数根，则相应二次函数25y mx mx m =++-与x 轴必然相交于点，此时m =． 答案：一 45、抛物线2(21)6y x m x m =---与x 轴交于两点1(0)x ，和2(0)x ，，若121249x x x x =++，要使抛物线经过原点，应将它向右平移 个单位． 答案：4或96、关于x 的二次函数22(81)8y mx m x m =+++的图像与x 轴有交点，则m 的范围是（ ）Ａ、116m <-Ｂ、116m -≥且0m ≠ Ｃ、116m =-Ｄ、116m >-且0m ≠ 答案：Ｂ7、 已知抛物线21()3y x h k =--+的顶点在抛物线2y x =上，且抛物线在x 轴上截得的线段长是43，求h 和k 的值．答案：21()3y x h k =--+，顶点()h k ，在2y x =上，2h k ∴=，22221122()3333y x h h x hx h ∴=--+=-++．22∆求得2h =±，4k =，即2h =，4k =或2h =-，4k =．8、已知函数22y x mx m =-+-．（1）求证：不论m 为何实数，此二次函数的图像与x 轴都有两个不同交点； （2）若函数y 有最小值54-，求函数表达式．答案：（1）222()4(2)48(2)4m m m m m ∆=---=-+=-+，不论m 为何值时，都有0∆>， 此时二次函数图像与x 轴有两个不同交点．（2）2244(2)5444ac b m m a ---==-，2430m m -+=，1m ∴=或3m =， 所求函数式为21y x x =--或231y x x =-+．9、下图是二次函数2y ax bx c =++的图像，与x 轴交于B ，C 两点，与y 轴交于A 点．（1）根据图像确定a ，b ，c 的符号，并说明理由；（2）如果A 点的坐标为(03)-，，45ABC ∠= ，60ACB ∠=，求这个二次函数的函数表达式．答案：（1）抛物线开口向上，0a >；图像的对称轴在y 轴左侧，02ba-<，又0a >， 0b ∴>；图像与y 轴交点在x 轴下方，0c ∴<．0a ∴>，0b >，0c <．（2）(03)A -，，3OA =，45ABC ∠= ，60ACB ∠=，3tan OAOB ABC==∠，3tan 60OAOC ==，(30)B ∴-，，(30)C ，．设二次函数式为(3)(3)y a x x =+-，ＡＣＯ Ｂ xy把(03)-，代入上式，得33a =， ∴所求函数式为233(3)(3)(31)333y x x x x =+-=+--． 10、已知抛物线222m y x mx =-+与抛物线2234m y x mx =+-在直角坐标系中的位置如图所示，其中一条与x 轴交于A ，B 两点．（1）试判断哪条抛物线经过A ，B 两点，并说明理由； （2）若A ，B 两点到原点的距离AO ，OB 满足条件1123OB OA -=，求经过A ，B 两点的这条抛物线的函数式．答案：（1）抛物线不过原点，0m ≠，令2202m x m x -+=，2221()402m m m ∆=--⨯=-<，222m y x mx =-+∴与x 轴无交点，∴抛物线2234y x mx m =+-经过A ，B 两点．（2）设1(0)A x ，，2(0)B x ，，1x ，2x 是方程22304x mx m +-=的两根12x x m +=-，21234x x m =-，A 在原点左边，B 在原点右边，则1AO x =-，2OB x =．123OB OA 1-= ．211123x x ∴+=，121223x x x x +=，22334m m -=-，得2m =，∴所求函数式为223y x x =+-．11、已知二次函数2224y x mx m =-+．（1）求证：当0m ≠时，二次函数的图像与x 轴有两个不同交点； Ａ ＢＯ xy数表达式．答案：（1）22222(4)421688m m m m m ∆=--⨯⨯=-=．0m ≠ ，280m ∴>，∴这个抛物线与x 轴有两个不同交点．（2）设1(0)A x ，，212(0)()B x x x >，，则1x ，2x 是方程22240x mx m -+=两根，122x x m +=，2122m x x =，222221212112()()4422AB x x x x x x x x m m m =-=-=+-=-=， C 点纵坐标22224816442c ac b m m y m a --===-⨯，∴△ABC 中AB 边上的高22h m m =-=．21124222ABC S AB h m m === ，2m =，2m =±， 2284y x x ∴=++或2284y x x =-+．12、如图所示，函数2(2)7(5)y k x x k =--+-的图像与x 轴只有一个交点，则交点的横坐标0x =． 答案：7-13、已知抛物线2y ax bx c =++与y 轴交于C 点，与x 轴交于1(0)A x ，，212(0)()B x x x <，两点，顶点M的纵坐标为4-，若1x ，2x 是方程222(1)70x m x m --+-=的两根，且221210x x +=．（1）求A ，B 两点坐标；（2）求抛物线表达式及点C 坐标；（3）在抛物线上是否存在着点P ，使△PAB 面积等于四边形ACMB 面积的2倍，若存在，求出P 点坐标；若不存在，请说明理由． Ｏy x答案：（1）由122(1)x x m +=-，2127x x m =-，22222121212()24(1)2(7)10x x x x x x m m +=+-=---=，得2m =，11x ∴=-，23x =，(10)A -，，(30)B ，． （2） 抛物线过A ，B 两点，其对称轴为1x =，顶点纵坐标为4-，∴抛物线为2(1)4y a x =--．把1x =-，0y =代入得1a =，∴抛物线函数式为223y x x =--，其中(03)C -，． （3）存在着P 点．(10)A - ，，(03)C -，，(14)M -，，(30)B ，，∴9ACMB S =四形，18ABP S = ， 即1182P y AB =．4AB = ，9P y ∴=．把9y =代入抛物线方程得1113x =-，2113x =+，(1139)P ∴-，或(1139)P +，．14、二次函数269y x x =-+-的图像与x 轴的交点坐标为 ． 答案：（3，0） 15、二次函数25106y x x =-+的图像与x 轴有 个交点． 答案：0 16、对于二次函数2135y x x =++，当12x =时，y = ． 答案：1132017、如图是二次函数2246y x x =--的图像，那么方程22460x x --=的两根之和 0．答案：>18、求下列函数的图像与x 轴的交点坐标，并作草图验证． （1）25166y x x =-+； （2）2336y x x =+-．答案：（1）（13，0），（12，0），图略 （2）（1，0），（2-，0），图略19、一元二次方程20ax bx c ++=的两根为1x ，2x ，且214x x +=，点(38)A -，在抛物线2y ax bx c =++上，求点A 关于抛物线的对称轴对称的点的坐标． 答案：（1，8-） ＣＢＯ Ａ xy20、若二次函数2y ax c =+，当x 取1x 、2x （12x x ≠）时，函数值相等，则当x 取12x x +时，函数值为（ ）Ａ、a c + Ｂ、a c - Ｃ、c - Ｄ、c 答案：Ｄ21、下列二次函数中有一个函数的图像与x 轴有两个不同的交点，这个函数是（ ） 答案：Ｄ Ａ、2y x =Ｂ、24y x =+ Ｃ、2325y x x =-+Ｄ、2351y x x =+-22、二次函数256y x x =-+与x 轴的交点坐标是（ ） 答案：AＡ、（2，0）（3，0） Ｂ、（2-，0）（3-，0） Ｃ、（0，2）（0，3） Ｄ、（0，2-）（0，3-） 23、试说明一元二次方程2441x x -+=的根与二次函数244y x x =-+的图像的关系，并把方程的根在图象上表示出来．答案：一元二次方程2441x x -+=的根是二次函数244y x x =-+与直线1y =的交点的横坐标，图略．24、利用二次函数图象求一元二次方程的近似根．210x x +-=答案：1 1.6x ≈-，20.6x ≈25、利用二次函数图象求一元二次方程的近似根．24834x x --=-答案：1 1.9x ≈，20.1x ≈26、函数2y ax bx c =++的图象如图所示，那么关于x 的一元二次方程230ax bx c ++-=的根的情况是（）Ａ、有两个不相等的实数根 Ｂ、有两个异号的实数根 Ｃ、有两个相等的实数根 Ｄ、没有实数根答案：Ｃ27、利用二次函数的图象求一元二次方程的近似值．2530x x --=3Ｏxy28、抛物线2321y x x =-+-的图象与坐标轴交点的个数是（） 答案：Ａ Ａ、没有交点 Ｂ、只有一个交点 Ｃ、有且只有两个交点 Ｄ、有且只有三个交点29、 已知二次函数212y x bx c =-++，关于x 的一元二次方程2102x bx c -++=的两个实根是1-和5-，则这个二次函数的解析式为 答案：215322y x x =---30、已知二次函数2(0)y ax bx c a =++≠的顶点坐标(1 3.2)--，及部分图象（如图４所示），由图象可知关于x 的一元二次方程20ax bx c ++=的两个根分别是1 1.3x =和2x = ．答案： 3.3-1-2-3- 4- 12y。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
11 二次函数与一元二次方程 练习题（家庭作业）
拟题：黄昌芹
1、抛物线2283y x x =--与x 轴有 个交点，因为其判别式24b ac -= 0，相应二次方程23280x x -+=的根的情况为
．
2、函数22y mx x m =+-（m 是常数）的图像与x 轴的交点个数为（
） Ａ、0个 Ｂ、1个
Ｃ、2个 Ｄ、1个或2个 3、关于二次函数2y ax bx c =++的图像有下列命题：①当0c =时，函数的图像经过原点；②当0c >，
且函数的图像开口向下时，方程20ax bx c ++=必有两个不相等的实根；③函数图像最高点的纵坐标是2
44ac b a
-；④当0b =时，函数的图像关于y 轴对称．其中正确命题的个数是（ ）
Ａ、1个
Ｂ、2个 Ｃ、3个 Ｄ、4个 4、关于x 的方程25mx mx m ++=有两个相等的实数根，则相应二次函数2
5y mx mx m =++-与x 轴必然相交于 点，此时m = ．
5、抛物线2(21)6y x m x m =---与x 轴交于两点1(0)x ，
和2(0)x ，，若121249x x x x =++，要使抛物线经过原点，应将它向右平移
个单位． 6、关于x 的二次函数22(81)8y mx m x m =+++的图像与x 轴有交点，则m 的范围是（
） Ａ、116m <- Ｂ、116m -≥且0m ≠ Ｃ、116m =- Ｄ、116
m >-且0m ≠ 7、 已知抛物线21
()3
y x h k =--+的顶点在抛物线2y x =上，且抛物线在x 轴上截得的线段长是3求h 和k 的值．
22 8、已知函数22y x mx m =-+-．
（1）求证：不论m 为何实数，此二次函数的图像与x 轴都有两个不同交点；
（2）若函数y 有最小值54-
，求函数表达式．
9、已知二次函数2224y x mx m =-+．（1）求证：当0m ≠时，二次函数的图像与x 轴有两个不同交点；
（2）若这个函数的图像与x 轴交点为A ，B ，顶点为C ，且△ABC 的面积为42数表达式．
10、如图所示，函数2(2)7(5)y k x x k =--+-的图像与x 轴只有一个交点，则交点的横坐标0x =
．
11、已知抛物线2y ax bx c =++与y 轴交于C 点，与x 轴交于1(0)A x ，
，212(0)()B x x x <，两点，顶点M 的纵坐标为4-，若1x ，2x 是方程222(1)70x m x m --+-=的两根，且221210x x +=．
（1）求A ，B 两点坐标；（2）求抛物线表达式及点C 坐标；
（3）在抛物线上是否存在着点P ，使△PAB 面积等于四边形ACMB 面积的2倍，若存在，求出P 点坐标；若不存在，请说明理由．
12、二次函数2
69y x x =-+-的图像与x 轴的交点坐标为 ．
Ｏ y x
33 13、二次函数2
5106y x x =-+的图像与x 轴有 个交点．
14、若二次函数2y ax c =+，当x 取1x 、2x （12x x ≠）时，函数值相等，则当x 取12x x +时，函数值为（ ）
Ａ、a c + Ｂ、a c - Ｃ、c - Ｄ、c
15、下列二次函数中有一个函数的图像与x 轴有两个不同的交点，这个函数是（ ）
Ａ、2y x = Ｂ、24y x =+ Ｃ、2325y x x =-+
Ｄ、2351y x x =+- 16、二次函数256y x x =-+与x 轴的交点坐标是（ ）
Ａ、（2，0）（3，0） Ｂ、（2-，0）（3-，0） Ｃ、（0，2）（0，3） Ｄ、（0，2-）（0，3-）
17、函数2
y ax bx c =++的图象如图所示，那么关于x 的一元二次方程230ax bx c ++-=的根的情况是（
） Ａ、有两个不相等的实数根
Ｂ、有两个异号的实数根 Ｃ、有两个相等的实数根
Ｄ、没有实数根
18、 已知二次函数212y x bx c =-++，关于x 的一元二次方程2102
x bx c -++=的两个实根是1-和5-，则这个二次函数的解析式为
3 Ｏ x y。