实验 二叉树遍历算法及应用
二叉树的遍历方法

二叉树的遍历方法1. 前序遍历:先访问根节点,再遍历左子树,最后遍历右子树。
详细描述:从根节点开始,首先访问根节点并打印它的值。
接着,递归地遍历左子树,然后递归地遍历右子树。
2. 中序遍历:先遍历左子树,再访问根节点,最后遍历右子树。
详细描述:从根节点开始,首先递归地遍历左子树。
然后,访问根节点并打印它的值。
递归地遍历右子树。
3. 后序遍历:先遍历左子树,再遍历右子树,最后访问根节点。
详细描述:从根节点开始,首先递归地遍历左子树。
然后,递归地遍历右子树。
访问根节点并打印它的值。
4. 层序遍历:按照层级顺序从上往下逐层遍历二叉树。
详细描述:从根节点开始,将其放入队列中。
然后,循环执行以下步骤直到队列为空:取出队列头部的节点,访问该节点并打印它的值,将其左子节点和右子节点(如果存在)依次放入队列尾部。
5. 深度优先遍历(DFS):按照深度优先的顺序遍历二叉树。
详细描述:深度优先遍历可以使用递归或者栈来实现。
从根节点开始,首先访问根节点并打印它的值。
接着,递归地遍历左子树,并递归地遍历右子树。
6. 广度优先遍历(BFS):按照广度优先的顺序遍历二叉树。
详细描述:广度优先遍历使用队列来实现。
从根节点开始,首先将根节点放入队列中。
然后,开始循环,直到队列为空:取出队列头部的节点,访问该节点并打印它的值,将其左子节点和右子节点(如果存在)依次放入队列尾部。
7. 反序前序遍历:先访问右子树,再访问左子树,最后访问根节点。
详细描述:从根节点开始,首先递归遍历右子树。
然后,递归遍历左子树。
访问根节点并打印它的值。
8. 反序中序遍历:先遍历右子树,再访问根节点,最后遍历左子树。
详细描述:从根节点开始,首先递归遍历右子树。
然后,访问根节点并打印它的值。
递归遍历左子树。
9. 反序后序遍历:先访问根节点,再遍历右子树,最后遍历左子树。
详细描述:从根节点开始,首先访问根节点并打印它的值。
接着,递归地遍历右子树。
递归地遍历左子树。
二叉树遍历操作的基本应用(复制、求深度、求叶子数、求节点数等)

二叉树遍历操作的基本应用(复制、求深度、求叶子数、求节点数等)1. 引言1.1 概述二叉树是计算机科学领域中常用的数据结构之一,具有广泛的应用场景。
在二叉树的操作中,遍历是其中最基本和常见的操作之一。
通过遍历,我们可以按照特定规则依次访问二叉树中的所有节点。
本文将探讨二叉树遍历操作的基本应用,包括复制、求深度、求叶子数、求节点数等。
这些操作不仅在实际开发中有重要意义,而且对于理解和掌握二叉树数据结构及其相关算法也具有重要作用。
1.2 文章结构本文将分为五个部分进行论述。
首先,在引言部分(第1节)我们将概述文章的主题和目标。
紧接着,在第2节中,我们将介绍二叉树遍历的基本应用,包括复制、求深度、求叶子数和求节点数等。
在第3节中,我们将详细解析这些基本应用,并给出相应算法和实例分析。
接下来,在第4节中,我们将通过实际案例应用来验证并讨论这些基本应用的性能与适用范围。
最后,在第5节中总结全文内容,并对未来研究方向进行展望。
1.3 目的本文的目的是通过对二叉树遍历操作的基本应用进行详细剖析,帮助读者深入理解和掌握二叉树数据结构及其相关算法。
同时,我们希望通过实际案例应用与讨论,探讨如何优化算法性能、提高效率以及适应大规模二叉树遍历问题。
通过本文的阅读,读者将能够全面了解并应用二叉树遍历操作的基本方法,在实际开发中解决相关问题,并为进一步研究和探索提供思路与参考。
该部分主要介绍了文章的概述、结构和目的,引导读者了解全文并明确阅读目标。
2. 二叉树遍历的基本应用:二叉树是一种常见的数据结构,其遍历操作可以应用于多种实际问题中。
本节将介绍四个基本的二叉树遍历应用:复制二叉树、求二叉树的深度、求二叉树的叶子数和求二叉树的节点数。
2.1 复制二叉树:复制一个二叉树意味着创建一个与原始二叉树结构完全相同的新二叉树。
该应用场景在涉及对原始数据进行修改或者对数据进行独立操作时非常有用。
复制操作可以以递归方式实现,通过先复制左子树,再复制右子树,最后创建一个与当前节点值相等的新节点来完成。
二叉树实验报告

二叉树实验报告二叉树实验报告引言:二叉树作为一种常用的数据结构,在计算机科学领域中具有广泛的应用。
本实验旨在通过实际操作和观察,深入理解二叉树的特性和运用。
一、二叉树的基本概念1.1 二叉树的定义二叉树是一种特殊的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
树的最顶层节点称为根节点。
1.2 二叉树的特点二叉树具有以下特点:- 每个节点最多有两个子节点,分别称为左子节点和右子节点;- 左子节点的值小于等于父节点的值,右子节点的值大于等于父节点的值;- 二叉树的左子树和右子树也是二叉树。
二、二叉树的遍历方式2.1 先序遍历先序遍历是指先访问根节点,然后按照先序遍历的方式依次访问左子树和右子树。
2.2 中序遍历中序遍历是指按照中序遍历的方式依次访问左子树,根节点和右子树。
2.3 后序遍历后序遍历是指按照后序遍历的方式依次访问左子树,右子树和根节点。
三、二叉树的实验操作3.1 二叉树的创建为了便于实验操作,我们选择使用Python编程语言来实现二叉树的创建和操作。
首先,我们需要定义一个二叉树节点的类,包含节点的值、左子节点和右子节点。
3.2 二叉树的插入在已有的二叉树中插入一个新的节点,需要遵循二叉树的规则。
如果插入的节点值小于当前节点的值,则将节点插入到当前节点的左子树;如果插入的节点值大于当前节点的值,则将节点插入到当前节点的右子树。
3.3 二叉树的查找在二叉树中查找一个特定的节点,需要遍历整个二叉树。
从根节点开始,如果要查找的节点值小于当前节点的值,则继续在左子树中查找;如果要查找的节点值大于当前节点的值,则继续在右子树中查找;如果要查找的节点值等于当前节点的值,则找到了目标节点。
3.4 二叉树的删除在二叉树中删除一个节点,需要考虑多种情况。
如果要删除的节点没有子节点,直接将其删除即可;如果要删除的节点只有一个子节点,将子节点替换为要删除的节点;如果要删除的节点有两个子节点,需要找到其右子树中的最小节点,将其值替换到要删除的节点,然后删除最小节点。
二叉树的遍历实验报告_数据结构

实验报告||实验名称二叉树的遍历课程名称算法与数据结构试验||专业班级:信息管理信息系统学号:实验日期:姓名:慕鑫鑫一、实验名称:二叉树的遍历二、实验目的综合应用所学的知识分析问题、解决问题,学会用建立二叉树并对其进行遍历,提高实际编程能力及程序调试能力。
三、实验要求建立一个二叉树并对其进行遍历(先序,中序,后序)四、实验内容1、问题描述:建立一个二叉树,并分别用前序、中序、后序遍历该二叉树。
2、说明:输入数据:1,2,3,0,0,4,5,0,0,6,7,0,0,0,8,9,0,0,10,11,12,0,0,13,0,0,14,0,0其中“0”表示空子树。
输出数据:先序:1,2,3,4,5,6,7,8,9,10,11,12,13,14。
中序:3,2,5,4,7,6,1,9,8,12,11,13,10,14。
后序:3,5,7,6,4,2,9,12,13,11,14,10,8,1。
五、实验仪器与设备计算机,JDK,记事本六、实验原理建立一个二叉树,利用递归的方法实现对该二叉树的前序,中序,后序的遍历,并输出遍历结果。
七、实验程序及结果#include<iostream>#include<>#include<>using namespace std;typedef struct btnode{int data;btnode *Lchild,*Rchild;}*Btnode;void Creat(Btnode & t){int ch;cin>>ch;if(ch==0)t=NULL;else{btnode *p=new btnode;p->data=ch;t=p;Creat(t->Lchild);Creat(t->Rchild);}}void Preorder(Btnode & p) {if(p!=NULL){cout<<p->data<<",";Preorder(p->Lchild);Preorder(p->Rchild);}}void Midorder(Btnode & p) {if(p!=NULL){Midorder(p->Lchild);cout<<p->data<<",";Midorder(p->Rchild);}}void Folorder(Btnode & p) {if(p!=NULL){Folorder(p->Lchild);Folorder(p->Rchild);cout<<p->data<<",";}}void main(){btnode *head=new btnode;cout<<"请输入数据:";Creat(head);cout<<"前序遍历:";Preorder(head);cout<<endl;cout<<"中序遍历:";Midorder(head);cout<<endl;cout<<"后序遍历:";Folorder(head);getch();}八、实验体会通过本次试验,让我更深刻的理解了二叉树的性质,在上机的操作过场中,发现了自己平时疏忽的细节,以后再学习过程中会注意。
实验四 二叉树运算与遍历实验报告

实验四二叉树运算与遍历实验报告学号-姓名实验时间 2010 年05月24日诚信声明本实验及实验报告所写内容为本人所做,没有抄袭。
实验题目与实验目的题目一:二叉树的遍历运算。
基本要求:在二叉树的二叉链表存储结构基础上,实现二叉树的以下运算:(1)创建二叉树的二叉树链表表示;(2)实现二叉树的先序遍历运算,输出先序遍历运算序列;(3)实现二叉树的中序遍历运算,输出中序遍历运算序列;(4)实现二叉树的后续遍历运算,输出后续遍历运算序列。
实验过程中遇到的主要问题1.根结点忘记申请内存;2.没有添加if(ch=='.')T=NULL;这个作为条件来创造一棵二叉树;3.遍历时没有弄清楚顺序,搞混了先序和中序的顺序。
实验小结1.对结构体的进一步的掌握;2.对递归算法的进一步认识与运用;3.对二叉树的理解由思想到代码实现;4.代码实现思想就是我们应该把问题循环化。
数据结构(自定义数据类型)typedef struct BiTnode{int date;struct BiTnode *lchild, *rchild;}BiTnode,*Bitree; //二叉树链式存储定义主要算法(或算法说明)int createbitree(Bitree &T){char ch;scanf("%c",&ch);if(ch=='.')T=NULL; //条件的判定else{ if(!(T=(Bitree)malloc(sizeof(BiTnode)))) return -1;T->date=ch;createbitree(T->lchild);createbitree(T->rchild);}return 0;} //建立一棵二叉树int preordertraverse(Bitree T){if(T==NULL)return -1;printf("%c",T->date);preordertraverse(T->lchild);preordertraverse(T->rchild);} //先序遍历。
二叉树的遍历算法实验报告

二叉树实验报告09信管石旭琳 20091004418一、实验目的:1、理解二叉树的遍历算法及应用2、理解哈夫曼树及其应用。
3、掌握哈夫曼编码思想。
二、实验内容:1、建立二叉树二叉链表2、实现二叉树递归遍历算法(中序、前序、后序)3、求二叉树高度4、求二叉树结点个数5、求二叉树叶子个数6、将序号为偶数的值赋给左子树三、主要程序:#include<stdio.h>#include<stdlib.h>typedef int ElemType;struct BiTNode{ElemType data;struct BiTNode *lch,*rch;}BiTNode,*BiTree;struct BiTNode *creat_bt1();struct BiTNode *creat_bt2();void preorder (struct BiTNode *t);void inorder (struct BiTNode *t);void postorder (struct BiTNode *t);void numbt (struct BiTNode *t);int n,n0,n1,n2;void main(){int k;printf("\n\n\n");printf("\n\n 1.建立二叉树方法1(借助一维数组建立)"); printf("\n\n 2.建立二叉树方法2(先序递归遍历建立)"); printf("\n\n 3.先序递归遍历二叉树");printf("\n\n 4.中序递归遍历二叉树");printf("\n\n 5.后序递归遍历二叉树");printf("\n\n 6.计算二叉树结点个数");printf("\n\n 7.结束程序运行");printf("\n==================================="); do{printf("\n请输入你要执行的操作(1,2,3,4,5,6,7)");scanf("%d",&k);printf("\n");switch(k){case 1:{printf("你选择的是操作1,现用方法1进行建立二叉树\n");BiTree=creat_bt1(); /* 调用性质5建立二叉树算法*/break;}case 2:{printf("你选择的是操作2,现用方法2进行建立二叉树\n");BiTree=creat_bt2(); /* 调用递归建立二叉树算法*/break;}case 3:{printf("你选择的是操作3,现进行先序递归遍历二叉树\n结果为:");preorder(BiTree);break;}case 4:{printf("你选择的是操作4,现进行中序递归遍历二叉树\n结果为:");inorder(BiTree);break;}case 5:{printf("你选择的是操作5,现进行后序递归遍历二叉树\n结果为:");postorder(BiTree);break;}case 6:{ n=0,n0=0,n1=0,n2=0; /*全局变量置0 */printf("你选择的是操作6,现进行计算二叉树结点个数\n结果为:");numbt(BiTree);printf("\n 二叉树结点总数是:%d",n);printf("\n 二叉树叶子结点数是:%d",n0);printf("\n 度为1的结点数是:%d",n1);printf("\n 度为2的结点数是:%d",n2);break;}case 7:{printf("你选择的是操作8,将结束本程序运行,谢谢你的使用,再见!\n");break;}}}while(k>=1&&k<7);}struct BiTNode *creat_bt1(){struct BiTNode *v[50],*p,*t;int i,j;ElemType e; /*输入结点的序号i、结点的数据e */printf("\n i,data=");scanf("%d,%d",&i,&e);while(i!=0&&e!=0){p=(struct BiTNode *)malloc(sizeof(struct BiTNode));p->data=e;p->lch=NULL;p->rch=NULL;v[i]=p;if (i==1) /*序号为1的结点是根*/t=p;else{j=(i+1)/2;if(i%2==0) /*序号为偶数,做左孩子*/v[j]->lch=p;elsev[j]->rch=p;}printf("\n i,data=");scanf("%d,%d",&i,&e);}return t;}struct BiTNode *creat_bt2(){struct BiTNode *t;int e;printf("\n data=");scanf("%d",&e);if(e==0) t=NULL; /*对于0值,不分配新结点*/else{t=(struct BiTNode *)malloc(sizeof(struct BiTNode));t->data=e;t->lch=creat_bt2(); /*左孩子获得新指针值*/t->rch=creat_bt2();}return (t);}void preorder (struct BiTNode *t){if(t){printf("%d ",t->data);preorder(t->lch);preorder(t->rch);}}void inorder (struct BiTNode *t){if(t){inorder(t->lch);printf("%d ",t->data);inorder(t->rch);}}void postorder(struct BiTNode *t){if(t){postorder(t->lch);postorder(t->rch);printf("%d ",t->data);}}void numbt(struct BiTNode *t){if(t){numbt(t->lch);{n++;if(t->lch==NULL&&t->rch==NULL)n0++;if((t->lch==NULL&&t->rch!=NULL)||(t->lch!=NULL&&t->rch==NUL L))n1++;if(t->lch!=NULL&&t->rch!=NULL)n2++;}numbt(t->rch);}}四、测试结果:五、小结:实操后还是会搞不清楚数据域及指针域的定义类型的不同。
二叉树应用实验

二叉树应用实验实验目的(1)掌握二叉树的动态链表存储结构及表示。
(2)掌握二叉树的三种遍历算法(递归和非递归两类)。
(3)运用二叉树三种遍历的方法求解有关问题。
实验运行环境Visual C++实验任务为使实验程序简洁直观,下面的部分实验程序中的一些功能实现仍以调用库函数程序"btrechar.h"中的函数的形式给出,并假设该库函数中定义了二叉树指针和结点类型分别为bitre和bnode,以及部分常用运算,例如构建二叉树、以某种方式显示二叉树等。
各运算的名称较为直观,因而易于理解。
为便于数据的描述,将测试数据结构列出,并以一个文件名的形式给出标注,例如测试数据名为full41.cbt的二叉树,其具体结构形式参见二叉树列表中的标有full41.cbt 的二叉树。
实验内容第一题:求二叉树的高度。
实验测试数据基本要求:第一组数据: full41.cbt第二组数据: cbitre.cbt实验准备:第一步:将指针指向根结点,判断根结点是否为空,如果是则返回0,否则进入第二步。
第二步:判断当前结点是否有子树,如果没有,当前结点的高度为1,否则进入第三步。
第三步:求当前结点左右子树的高度,并将两者中较大的加1作为该结点的高度。
进入下一个结点,返回第二步。
第二题:设计算法按中序次序输出二叉树中各结点的值及其所对应的层次数。
实验测试数据基本要求:第一组数据: full41.cbt第二组数据: cbitre.cbt实验准备:第一步:将根节点的层次赋值为1。
第二步:判断当前结点是否为先序遍历的最后一个结点,是则输出二叉树中各结点的值及其所对应的层次数,并结束;否则,将当前结点的值以及层次输出,并将它的层次加1赋值给左右子树的层次。
移向下一个结点继续进行。
第三题:将按顺序方式存储在数组中的二叉树转换为二叉链表形式。
实验测试数据基本要求:第一组数据: full41.cbt第二组数据: letter.cbt实验准备:第一步:根据数组中的信息判断当前结点是否有左右子树,如果有并且已经建立了连接,就返回上一层,如果有但没建立连接就建立它与子树的连接。
二叉树的遍历
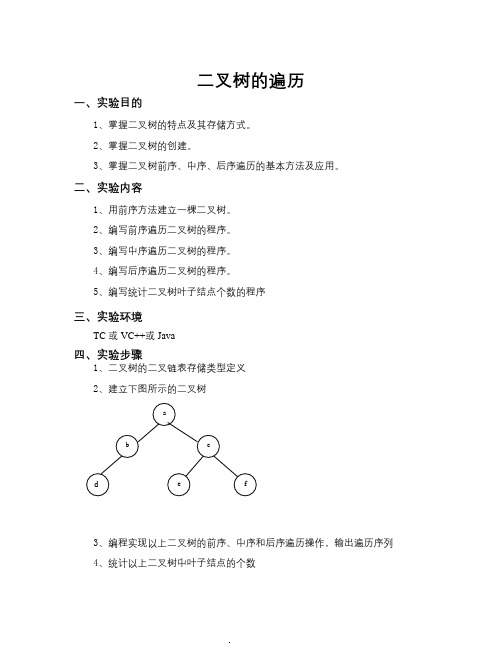
二叉树的遍历一、实验目的1、掌握二叉树的特点及其存储方式。
2、掌握二叉树的创建。
3、掌握二叉树前序、中序、后序遍历的基本方法及应用。
二、实验内容1、用前序方法建立一棵二叉树。
2、编写前序遍历二叉树的程序。
3、编写中序遍历二叉树的程序。
4、编写后序遍历二叉树的程序。
5、编写统计二叉树叶子结点个数的程序三、实验环境TC 或VC++或Java四、实验步骤1、二叉树的二叉链表存储类型定义2、建立下图所示的二叉树3、编程实现以上二叉树的前序、中序和后序遍历操作,输出遍历序列4、统计以上二叉树中叶子结点的个数五、问题讨论 c abe fd1、先序、中序、后序遍历二叉树的区别?2、在先序、中序非递归算法中为什么使用栈?能不能借助其它数据结构来实现?六、实验报告内容1、实验目的2、实验内容和具体要求3、完成情况和实验记录,实验记录为实验过程中遇到的问题及解决方法4、程序清单5、所输入的数据及相应的运行结果6、问题回答7、实验心得实验代码:#include<stdio.h>#include<stdlib.h>typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;BiTree CreateBiTree(){BiTree T;char ch;scanf("%c",&ch);if(ch==' ')T = NULL;else{T = (BiTree)malloc(sizeof(BiTNode));if(!T)exit(0);T->data = ch;T->lchild = CreateBiTree();T->rchild = CreateBiTree(); }return T;}void previsit(BiTree T){if(T){printf("%c,",T->data);previsit(T->lchild);previsit(T->rchild);}}void inorder(BiTree T){if(T){inorder(T->lchild);printf("%c,",T->data);inorder(T->rchild);}}void postorder(BiTree T){if(T){postorder(T->lchild);postorder(T->rchild);printf("%c,",T->data);}}int preorder(BiTree T){int m,n;if(!T)return 0;if((!T->lchild)&&(!T->rchild))return 1;m = preorder(T->lchild);n = preorder(T->rchild);return m+n;}menu(){printf("************目录***********\n"); printf(" 先序遍历二叉树 1\n"); printf(" 中序遍历二叉树 2\n"); printf(" 后续遍历二叉树 3\n"); printf("统计二叉树的叶子节点数 4\n"); printf(" 结束程序 0\n"); printf("***************************\n"); }void main(){int m,n;BiTree T;printf("按照先序方法依次输入元素:");T = CreateBiTree();do{printf("\n");menu();printf("输入你的选择:");scanf("%d",&m);switch(m){case 1:previsit(T);printf("\n");break;case 2:inorder(T);printf("\n");break;case 3:postorder(T);printf("\n");break;case 4:n = preorder(T);printf("二叉树的叶子节点为%d\n",n); break;case 0:printf("程序已结束!!!\n");break;default:printf("输入错误!!!\n");}}while(m!=0);}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二叉树遍历算法及应用
实验报告二叉树的遍历应用算法测试实验日期:______________ 学生姓
名:______________ 班级:_______________ 一、实习目的:
1、深入了解二叉树的存储结构及二叉树的遍历方法;
2、掌握二叉树的遍历算法及应用。
二、实习内容及要求
----------------------------------------------------------------------------------------------------------------------------------------- 应用遍历思想,建立一棵如下图所示的二叉树,并能够完成如下操作:
1. 输出该二叉树的先序、中序、后序遍历序列;
2. 拷贝该树,生成一棵新树;
3. 将原树拆分成左右2棵树,并分别输出该二叉树左子树的遍历序列和右子树的遍历序列;
4. 利用遍历算法输出复制生成的树中结点总数、叶子总数、二叉树高度,并能够输出此二叉树中的叶子
结点。
----------------------------------------------------------------------------------------------------------------------------------------- 附加:应用二叉树的顺序存储结构,实现建树。
并设计一个算法,实现能够输入一棵树中的双亲结点,输出该双亲结点的所有孩子结点的算法。
三、数据结构设计
(请将数据结构设计填写在此部分。
)
四、测试
分别给出以下三棵树的测试结果
(此部分要求给出此二叉树建树及遍历应用算法的测试截屏。
)
六、请给出本实验建立的二叉树的先序遍历算法递归调用的过程。
(参照如下示例写明调用过程)。
