数字信号处理习题课---2012.10.31
数字信号处理教程课后习题及答案

分析:已知边界条件,如果没有限定序列类型(例如因果序列、反因果序列等), 则递推求解必须向两个方向进行(n ≥ 0 及 n < 0)。
解 : (1) y1 (0) = 0 时, (a) 设 x1 (n) = δ (n) ,
按 y1 (n) = ay1 (n − 1) + x1 (n) i) 向 n > 0 处递推,
10
T [ax1(n)+ bx2 (n)] =
n
∑
[ax1
(n
)
+
bx2
(n
)]
m = −∞
T[ax1(n) + bx2(n)] = ay1(n) + by2(n)
∴ 系统是线性系统
解:(2) y(n) =
[x(n )] 2
y1(n)
= T [x1(n)] = [x1(n)] 2
y2 (n) = T [x2 (n)] = [x2 (n)] 2
β α
n +1
β α β =
n +1− N −n0
N−
N
α −β
y(n) = Nα n−n0 ,
(α = β )
, (α ≠ β )
如此题所示,因而要分段求解。
2 .已知线性移不变系统的输入为 x( n ) ,系统的单位抽样响应
为 h( n ) ,试求系统的输出 y( n ) ,并画图。
(1)x(n) = δ (n)
当n ≤ −1时 当n > −1时
∑ y(n) = n a −m = a −n
m=−∞
1− a
∑ y(n) =
−1
a−m =
数字信号处理习题及答案

数字信号处理习题及答案数字信号处理作业(1)1、画出离散信号的波形(1))2(3)3(2)(1++-=n n n x δδ(2))2()(2+-=n u n x(3))5()()(3--=n u n u n x(4))()()(214n u n x n ?= (5))()25.0sin(3)(5n u n n x ??=π2、设x (n )、y (n )分别为系统的输⼊、输出变量,根据定义确定系统是否为:(1)线性,(2)稳定,(2)因果① )()]([ )(2n ax n x T n y == ② b n x n x T n y +==)()]([ )( ③ )0( )()]([ )(00>-==n n n x n x T n y④ ∑+-=>=0)0( )( )(0n n n n m n m x n y3、已知:描述系统的差分⽅程为)()1(5- )(n x n y n y =-且初始条件为: 0)1(=-y 求:系统的单位冲激响应h (n )4、已知:线性时不变系统的单位脉冲响应为10 , )( )(<求:该系统的单位阶跃响应。
数字信号处理作业(1)解答1、画出离散信号的波形(1))2(3)3(2)(1++-=n n n x δδ(2))2()(2+-=n u n x(3))5()()(3--=n u n u n x(4))()()(214n u n x n ?= (5))()25.0sin(3)(5n u n n x ??=π2、设x (n )、y (n )分别为系统的输⼊、输出变量,根据定义确定系统是否为:(1)线性,(2)稳定,(3)因果因果:输出只取决于当前和之前的输⼊。
线性移不变系统的因果的充要条件:h (n )=0 , n < 0稳定系统:有界输⼊产⽣有界输出。
线性移不变系统稳定的充要条件:∞<=∑∞-∞=n n n x n x T n y (线性,稳定,因果)④ )0( )( )(0>=∑+-=n m x n y n n n n m (线性,稳定,⾮因果)注意:⾮线性系统的稳定、因果只能按定义判断,不能按线性、移不变系统的h (n )特点判断。
数字信号处理习题集(附答案解析)

第一章数字信号处理概述简答题:1.在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器,它们分别起什么作用?答:在A/D变化之前为了限制信号的最高频率,使其满足当采样频率一定时,采样频率应大于等于信号最高频率2倍的条件。
此滤波器亦称为“抗混叠”滤波器。
在D/A变换之后为了滤除高频延拓谱,以便把抽样保持的阶梯形输出波平滑化,故又称之为“平滑”滤波器。
判断说明题:2.模拟信号也可以与数字信号一样在计算机上进行数字信号处理,自己要增加一道采样的工序就可以了。
()答:错。
需要增加采样和量化两道工序。
3.一个模拟信号处理系统总可以转换成功能相同的数字系统,然后基于数字信号处理理论,对信号进行等效的数字处理。
()答:受采样频率、有限字长效应的约束,与模拟信号处理系统完全等效的数字系统未必一定能找到。
因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析,再考虑幅度量化及实现过程中有限字长所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础。
第二章 离散时间信号与系统分析基础一、连续时间信号取样与取样定理 计算题:1.过滤限带的模拟数据时,常采用数字滤波器,如图所示,图中T 表示采样周期(假设T 足够小,足以防止混叠效应),把从)()(t y t x 到的整个系统等效为一个模拟滤波器。
(a ) 如果kHz rad n h 101,8)(=π截止于,求整个系统的截止频率。
(b ) 对于kHz T 201=,重复(a )的计算。
解 (a )因为当0)(8=≥ωπωj e H rad 时,在数 — 模变换中)(1)(1)(Tj X Tj X Te Y a a j ωω=Ω=所以)(n h 得截止频率8πω=c 对应于模拟信号的角频率c Ω为8π=ΩT c因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ,因此对T8π没有影响,故整个系统的截止频率由)(ωj e H 决定,是625Hz 。
(完整word版)《数字信号处理》复习习题

《数字信号处理》复习思考题、习题(一)一、选择题1.信号通常是时间的函数,数字信号的主要特征是:信号幅度取 ;时间取 。
A.离散值;连续值B.离散值;离散值C.连续值;离散值D.连续值;连续值2.一个理想采样系统,采样频率Ωs =10π,采样后经低通G(j Ω)还原,⎪⎩⎪⎨⎧≥Ω<Ω=Ωππ5 05 51)(j G ;设输入信号:t t x π6cos )(=,则它的输出信号y(t)为: 。
A .t t y π6cos )(=; B. t t y π4cos )(=;C .t t t y ππ4cos 6cos )(+=; D. 无法确定。
3.一个理想采样系统,采样频率Ωs =8π,采样后经低通G(j Ω)还原,G j ()ΩΩΩ=<≥⎧⎨⎩14404 ππ;现有两输入信号:x t t 12()cos =π,x t t 27()cos =π,则它们相应的输出信号y 1(t)和y 2(t): 。
A .y 1(t)和y 2(t)都有失真; B. y 1(t)有失真,y 2(t)无失真;C .y 1(t)和y 2(t)都无失真; D. y 1(t)无失真,y 2(t)有失真。
4.凡是满足叠加原理的系统称为线性系统,亦即: 。
A. 系统的输出信号是输入信号的线性叠加B. 若输入信号可以分解为若干子信号的线性叠加,则系统的输出信号是这些子信号的系统输出信号的线性叠加。
C. 若输入信号是若干子信号的复合,则系统的输出信号是这些子信号的系统输出信号的复合。
D. 系统可以分解成若干个子系统,则系统的输出信号是这些子系统的输出信号的线性叠加。
5.时不变系统的运算关系T[·]在整个运算过程中不随时间变化,亦即 。
A. 无论输入信号如何,系统的输出信号不随时间变化B. 无论信号何时输入,系统的输出信号都是完全一样的C. 若输入信号延时一段时间输入,系统的输出信号除了有相应一段时间延时外完全相同。
数字信号处理习题及答案

==============================绪论==============================1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1.①写出图示序列的表达式答:3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2))81(j e )(π-=n n x 解: (1) 因为ω=73π, 所以314π2=ω, 这是有理数, 因此是周期序列, 周期T =14。
(2) 因为ω=81, 所以ωπ2=16π, 这是无理数, 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法乘法序列{2,3,2,1}与序列{2,3,5,2,1}相加为__{4,6,7,3,1}__,相乘为___{4,9,10,2} 。
移位翻转:①已知x(n)波形,画出x(-n)的波形图。
②尺度变换:已知x(n)波形,画出x(2n)及x(n/2)波形图。
卷积和:①h(n)*求x(n),其他02n 0n 3,h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=}23,4,7,4,23{0,h(n)*答案:x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5},则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3),求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案:x(n)=4. 如果输入信号为,求下述系统的输出信号。
数字信号处理_习题与解答

[ax (k ) bx (k )]
1 2 2 1 2
x1( k ) b
n n0
k n n0
x (k ) aT[ x (n)] bT[ x (n)]
系统是线性系统 9
( 4)T [ x( n )] x( n n0) ( a )若 | x( n ) | M ,则: | T [ x( n )] || x( n n0 ) | M 系统是稳定系统 (b ) y( n ) x( n n0 ), (i )n0 0, n n0 n, y( n )与n时刻之后的输入无关 系统是因果系统 (ii )n0 0, n n0 n, y( n )与n时刻之后的输入有关 系统不是因果系统 (c ) T [ax1( n ) bx2 ( n )] ax1( n n0 ) bx2 ( n n0 ) aT[ x1( n )] bT[ x2 ( n )] 系统是稳定系统
15
1 2 j n x( n ) X ( j )e d 2 0 1 2 j 2 n x ( 2n ) X ( j )e d 2 0 1 4 j ' n X ( j '/ 2)e d ' ( ' 2) 4 0 1 2 j n 1 4 j n X ( j )e d X ( j )e d 4 0 2 4 2 2 1 2 j n 1 2 2 j n X ( j )e d X( j )e d 2 0 2 4 0 2 2 1 2 1 j n [ X ( j ) X [ j ( )]e d G ( j )e j d 0 0 2 2 2 2 16
数字信号处理》课后作业参考答案
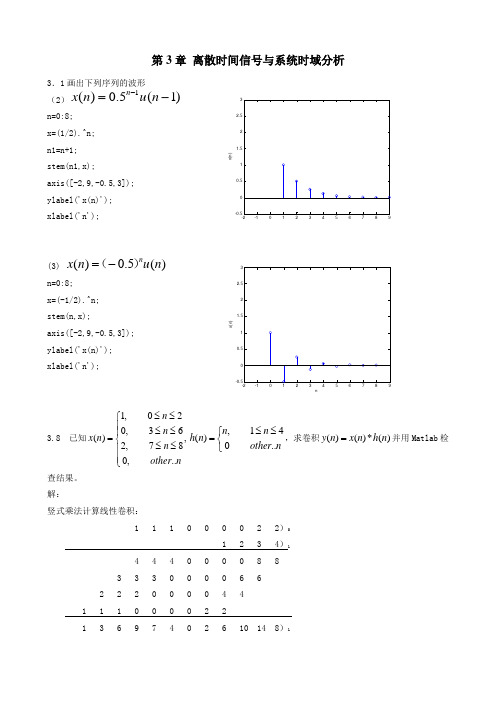
第3章 离散时间信号与系统时域分析3.1画出下列序列的波形(2)1()0.5(1)n x n u n -=- n=0:8; x=(1/2).^n;n1=n+1; stem(n1,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');(3) ()0.5()nx n u n =-()n=0:8; x=(-1/2).^n;stem(n,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');3.8 已知1,020,36(),2,780,..n n x n n other n≤≤⎧⎪≤≤⎪=⎨≤≤⎪⎪⎩,14()0..n n h n other n≤≤⎧=⎨⎩,求卷积()()*()y n x n h n =并用Matlab 检查结果。
解:竖式乘法计算线性卷积: 1 1 1 0 0 0 0 2 2)01 2 3 4)14 4 4 0 0 0 0 8 83 3 3 0 0 0 0 6 62 2 2 0 0 0 0 4 41 1 1 0 0 0 02 21 3 6 9 7 4 02 6 10 14 8)1x (n )nx (n )nMatlab 程序:x1=[1 1 1 0 0 0 0 2 2]; n1=0:8; x2=[1 2 3 4]; n2=1:4; n0=n1(1)+n2(1);N=length(n1)+length(n2)-1; n=n0:n0+N-1; x=conv(x1,x2); stem(n,x);ylabel('x(n)=x1(n)*x2(n)');xlabel('n'); 结果:x = 1 3 6 9 7 4 0 2 6 10 14 83.12 (1) 37πx (n )=5sin(n) 解:2214337w πππ==,所以N=14 (2) 326n ππ-x (n )=sin()-sin(n)解:22211213322212,2122612T N w T N w N ππππππ=========,所以(6) 3228n π-x (n )=5sin()-cos(n) 解:22161116313822222()T N w T w x n ππππππ=======,为无理数,所以不是周期序列所以不是周期序列3.20 已知差分方程2()3(1)(2)2()y n y n y n x n --+-=,()4()nx n u n -=,(1)4y -=,(2)10,y -=用Mtalab 编程求系统的完全响应和零状态响应,并画出图形。
数字信号处理课后习题答案(全)1-7章

最后结果为 0
n<0或n>7
y(n)= n+1 0≤n≤3 8-n 4≤n≤7
y(n)的波形如题8解图(一)所示。 (2) y(n) =2R4(n)*[δ(n)-δ(n-2)]=2R4(n)-2R4(n-2)
=2[δ(n)+δ(n-1)-δ(n+4)-δ(n+5) y(n)的波形如题8解图(二)所示
因此系统是非线性系统。
第 1 章 时域离散信号和时域离散系统
(6) y(n)=x(n2)
令输入为
输出为
x(n-n0)
y′(n)=x((n-n0)2) y(n-n0)=x((n-n0)2)=y′(n) 故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n2)+bx2(n2) =aT[x1(n)]+bT[x2(n)]
因此系统是非时变系统。
第 1 章 时域离散信号和时域离散系统
(5) y(n)=x2(n)
令输入为
输出为
x(n-n0)
y′(n)=x2(n-n0) y(n-n0)=x2(n-n0)=y′(n) 故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=[ax1(n)+bx2(n)]2 ≠aT[x1(n)]+bT[x2(n) =ax21(n)+bx22(n)
第 1 章 时域离散信号和时域离散系统
题4解图(一)
第 1 章 时域离散信号和时域离散系统
题4解图(二)
第 1 章 时域离散信号和时域离散系统
题4解图(三)
第 1 章 时域离散信号和时域离散系统
(4) 很容易证明: x(n)=x1(n)=xe(n)+xo(n)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
滤波器的模拟截止角频率为
C C / T m / 3
所以,恢复出来的信号频谱 Ya j 为
m / 3, m / 3
2012/10/30
武汉大学 电子信息学院
18
• 7.
2012/10/30
武汉大学 电子信息学院
19
知识回顾:圆周卷积与线性卷积的关系
• 长度为L的序列X[n]与长度为M的序列Y[n],其线性卷积 为L[n],长度为L+M-1。
j R
1 e
j R
1 e j R e j R 2 2 2 cos R 1 H e j 2 2 cos R 1
0 ,当 cos R 1 时,取峰值为 1 ,此时
幅度响应在 0 2 范围内的峰点和谷点出现的个数和
位置,并作出 R 6 时的幅度响应和相位响应。
2012/10/30
武汉大学 电子信息学院
11
• 5.解答: 频率响应 H e 幅度
H e
j
j
2
1e
j
j R
j
H e
H e 1 e
解答: a X 1 z
n
b x2 n a nu n
an z n
n2
x n z
1
n
a 2 z 2 ,z a 1 1 az
b X 2 z
n
x2 n z n
n
nM
n j n
n 1 n M
a e
n j n
a n e j n
k n n0 j
nM
a n e j n
1 a M 1e 1 ae j
j M 1
ae
1 ae
j M
1 ae j
• CTFT DTFT ,时域抽样离散化,频域周期化(连续)
• DTFT DFT ,频域抽样离散化(K点),时域周期化 (离散),时域、频域各取主值区间(K点) • 时域圆周卷积,频域DFT相乘
2012/10/30
武汉大学 电子信息学院
21
• 7.解答: a) 线性卷积,长度为6, yL n 4,10, 6,8, 7, 3 b) 圆周卷积,长度为4,列表法,yC n 3, 7, 6,8 c) DFT结果,与4点圆周卷积结果相同,yC n 3,7, 6,8 d) 6点圆周卷积,6=3+4-1,故圆周卷积与线性卷积的结果 相同,同a)
则这个系统是线性的吗?是时不变吗?是因果吗?
2012/10/30
武汉大学 电子信息学院
7
• 2.解答:
y n x 2 n x n 1 x n 1
线性:含有平方项,为非线性系统 移不变性:输入 x n n0 ,输出为
y n x 2 n n0 x n n0 1 x n n0 1 y n n0
2 T 2 fT 进行周期延拓。 T
模拟角频率 与数字角频率 之间的关系:
T / fT
2012/10/30
武汉大学 电子信息学院
17
• 6.解答: 奈奎斯特抽样定理:T 2 max 则抽样周期为 T / m 采样后的频谱是对 X a j 以周期 T 2 m 进行延拓。
0
等比数列求和q<1 时极限存在; z的收敛域不能包含 “=”号,否则序列 将不会收敛
所以为移不变系统
因果性:由于系统非线性,所以不能用冲激响应判断因果 性,只有当 x n 1 0 时,才能保证系统是因果系统, 否则该系统为非因果。
2012/10/30
武汉大学 电子信息学院
8
• 3.求下列序列的DTFT
• 解答:(1) X e
j
a e
n 0 k M k 1
• 双边无限长序列
– n1= - ∞,n2=∞,收敛域为两个同心圆之间的环
2012/10/30
武汉大学 电子信息学院
23
2012/10/30
武汉大学 电子信息学院
24
• 特别注意: 因果序列 非因果序列
1 , z a 1 1 az 1 Z n a u n 1 , z a 1 az 1
对 xa t 抽样,得到:x n xa nT , n
1 Ga j X a j k T T n
xa t e jt dt
即对 X a j 以周期
x n 的DTFT为: G e j Ga j | / T
2012/10/30
武汉大学 电子信息学院
13
=1 时 的 幅 值 响 应 和 相 位 响 应
2
Magnitude
1.5 1 0.5 0
0
0.5
1 /
1.5
2
2 1
Phase
0 -1 -2
0
0.5
1 /
1.5
2
2012/10/30
武汉大学 电子信息学院
14
• 6.
2012/10/30
h n 0
S h n
2012/10/30
武汉大学 电子信息学院
6
• 2.离散时间系统描述如下:
y n x 2 n x n 1 x n 1 其中 x n 和 y n 分别表示离散时间系统的输入和输出,
R 2 k ,
得
0 k R 1,共 R 个。
2k 1 0, 2 , k Z R
2012/10/30
武汉大学 电子信息学院
12
• 当 cos R 1 时,取谷值为 1 ,此时
R 2 k ,
得
0 k R 1,共 R 个。
• 长度为L的序列X[n]与长度为M的序列Y[n] L M ,其
T T L 点圆周卷积为C[n],长度为T。 • 当 T L M 1 时,T点圆周卷积与线性卷积结果相同。
2012/10/30
武汉大学 电子信息学院
20
知识回顾:CTFT、DTFT、DFT的关系
• 周期连续信号的傅立叶谱离散 • 非周期连续信号的傅立叶谱连续 • 非周期离散信号的傅立叶谱周期 • 周期离散信号的傅立叶谱周期离散
2012/10/30
2
10 , 0 3 2 2 50 , 0 7
r 3, N 10 r 7, N 50 r 9, N 40 r 11, N 40 r 13, N 40
40 , 0 9 40 , 0 11 2 40 , 0 13 2
而当 2 / 0 为无理数时,基本周期 N 不存在。
2012/10/30
武汉大学 电子信息学院
3
• 1.解答:
a 0 0.6 , b 0 0.28 , c 0 0.45 , d 0 0.55 , e 0 0.65 ,
武汉大学 电子信息学院
4
知识回顾:LTI离散时间系统的分类(P59)
• 线性系统:
– 若输入为 x1 n 和 x2 n ,系统输出分别为 y1 n 和 y2 n ,则当输 入为 x n x1 n x2 n 时,输出为 y n y1 n y2 n , 则系统为线性系统。
武汉大学 电子信息学院
Hale Waihona Puke 5知识回顾:LTI离散时间系统的分类
• 稳定系统
– 当且仅当系统对于有界输入产生有界输出时,称为稳定系统,即 对所有 n 值, x n Bx ,有 y n By ,BIBO稳定性。
• 用冲激响应描述LTI系统
– 输入输出关系: y n h n x n , h n 为冲激响应 – 因果性: 当 n 0 时,有 – 稳定性:
数字信号处理 习题课
授 课 教 师:徐 新 教 授 助 教:石 博
• 1.当角频率 0 取下列值时,求正弦序列 x n A sin 0 n 的 基本周期:
a 0.6 ; b 0.28 ; c 0.45 ; d 0.55 ; e 0.65
2k 0, 2 , k Z R
matlab 代码:
x = 0:2*pi/255:2*pi; y = 1-1*exp(-1i*x*6); subplot(2,1,1) plot(x/pi,abs(y)); title(‘\alpha=1 时的幅度响应和 相位响应'); set(gca,'xtick',0:0.5:2) xlabel('\omega/\pi'); ylabel('Magnitude'); grid on; subplot(2,1,2) plot(x/pi,angle(y)); set(gca,'xtick',0:0.5:2) xlabel('\omega/\pi'); ylabel('Phase'); grid on;
武汉大学 电子信息学院
15
知识回顾:抽样过程
• 抽样过程:
x n x t | t nT
n与抽样时刻t的关系:
则有
0
20 0T 0 / FT T
武汉大学 电子信息学院
