朱慈勉结构力学-静定结构-三铰拱-桁架
(完整版)完整的结构力学答案-同济大学朱慈勉
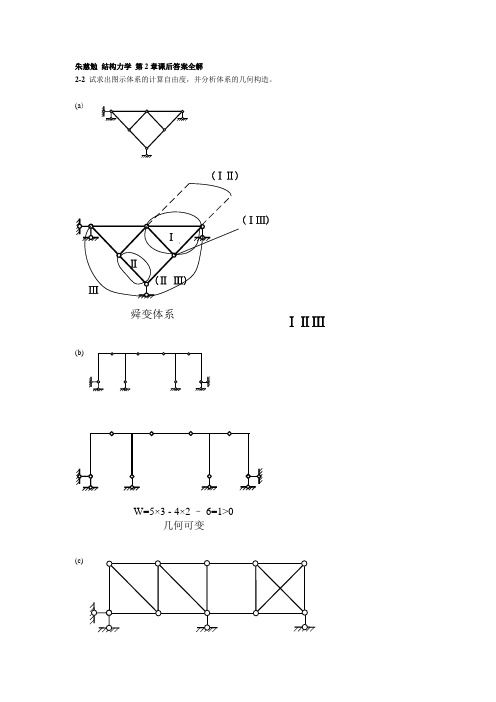
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学朱慈勉版上课件7

h E2 A2
s3 2h2E3 A3
三、超静定排架的计算
1、排架有那几部分组成,是工程中哪一类结构的 简化?
2、排架的受力特点是什么?
3、如何用力法计算排架,一般将排架的哪一部分 作为多余约束对待?
第7章
7.5 两铰拱及系杆拱的计算 一、两铰拱的特点:
二、计算方法:
1、不带拉杆两铰拱的计算:
P1
基本结构(2)
解:力法方程:
11x1
12x2
1P
x1 k
21x1
22x2
1P
x2 k
第7章
A
8m A
x2
B
C
k
8m
8m
原结构
B
C
k
x1
基本结构(3)
p
D k
2m
p
D k
解:力法方程:
1211xx111222xx2211PP
0 0
第7章
二、超静定刚架的计算
例题7-3 用力法计算图示超静定刚架,作内力图。各杆EI相同。
δ11x1 δ21x1
δ12x2 δ22x2
Δ Δ12P P00
δ11E 1I2 1442 3436E 4I
64 3EI
x1
24 EI
x2
640 EI
结构力学
STRUCTURE MECHANICS
天津城市建设学院力学教研室
第7章
第7章 力法 7.1超静定结构的概念和超静定次数的确定 一、超静定结构的概念
1、超静定结构的定义 具有几何不变性、而又有多余约束的结构。其反力和内
力只凭静力平衡方程不能确定或不能完全确定。 2、超静定结构的特点 (1)结构的反力和内力只凭静力平衡方程不能确定或不能
结构力学三铰拱ppt课件

第一节 三铰拱的组成和类型
2. 三铰拱的构成
拱顶
矢高:起拱线至拱顶的
竖直距离。
矢高f
拱趾
起拱线
精选课件 跨度L
拱轴 拱趾
第一节 三铰拱的组成和类型
2. 三铰拱的构成
精选课件
带拉杆的拱:在 屋架中,为消除 水平推力对墙或 柱的影响,在两 支座间增加一拉 杆,由拉杆来承 担水平推力,桥 梁中应用也非常 广泛。
精选课件
第三节 竖向荷载作用下三铰拱的内力特点
三铰拱在竖向荷载作用下的弯矩由两部分组成,水平反力 产生负弯矩,可以抵消一部分正弯矩,与简支梁相比拱的弯 矩、剪力较小,轴力较大(压力),应力沿截面高度分布较均 匀。
拱结构的优点:选用耐压性能好而抗拉性能差的砖石、混凝 土材料,节省用料,重量轻,可用于大跨、大空间结构。
• 集中力偶作用处,弯矩图将发生突变;
• 上述公式仅适合于平拱,且承受竖向荷载情况;
• 拱的内力仍然有FQ=dM/ds
精选课件
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算 2 竖向荷载作用下指定截面内力计算 3 拱的内力图
由于拱轴线是弯曲的,所以内力图都是曲 线形的,内力图要通过逐点描图的方法绘制, 总的规律仍符合荷载和内力的微分关系。
第一节 三铰拱的组成和类型
2. 三铰拱的构成
铁路拱桥:在桥梁中为了降低桥面高 度,可将桥面吊在拱上。
精选课件
第一节 三铰拱的组成和类型
3. 三铰拱的分类
三铰拱 拉杆拱1
两铰拱 无铰拱
拉杆拱2 精选课件
斜拱
第一节 三铰拱的组成和类型
4. 三铰拱的受力特点
FP
曲梁
朱慈勉结构力学 静定结构-三铰拱-桁架

②求截面6的内力:
dy tan 6 dx
6 2634 x6 12m 4f y6 2 x 6 ( l x 6 ) 3 m l
x x6
4f 2 (l 2 x6 ) 0.5 l
0 M6 M6 FH y6 8kN m L FQ 6 ( FP FyB )cos 6 FH sin 6 7.15kN R FQ 6 FyB cos 6 FH sin 6 7.15kN L FN 6 ( FP FyB )sin 6 FH cos 6 23.24kN R FN 6 FyB sin6 FH cos 6 30.40kN
结点2、6符合情况(c), 所以:
(a ) (b)
(d )
(c )
FN 1 FN 2 0
FN 1 FN 2 FN 3 0
FN 1 FN 2 FN 3 FN 4
FN 1 FN 2
结点9符合情况(a), 所以:
FN 97 0, FN 98 0
结点5符合情况(b), 所以:
例3-7
设三铰拱承受沿水平方向均匀分布的竖向荷载,求其合理轴线。
q y C q B l/2 B x A
A
l/2
f
M x [解] 由式 y x H
ql 2
x
ql 2
先列出简支梁的弯矩方程
q M x x l x 2
拱的推力为:
MC ql 2 H f 8f
K
压力线的概念在砖石和混凝土拱的设计中有重要意义。由于 这些材料的抗拉强度较抗压强度低得多,通常要求截面上不出现 拉应力。因此,压力线不应超出截面的核心区。若拱的截面为矩 形,由材料力学算得核心区高度为截面高度的1/3, 故压力线不应 超出截面三等分的中段范围。 借助于压力线的概念,可以用图解的方法求出拱任一截面上 kN )
结构力学课后习题答案(朱慈勉)

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kNm3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kNmABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
朱慈勉结构力学静定结构的影响线

的D以右部分为隔离体:
FyA影响线
MD
d
3d
1
FyB影响线
2 2
F NAE
F yB
MD 0:
M DFyB4d22FNAEd
MD影响线 精选ppt
4d
7 8
x
FNAC
2x 288d
例4-3 作图示桁架a、b、c 三杆轴力的影响线。
解:先作支座反力影响线。
⑴ 作FNa影响线(下承):
(作截面Ⅰ-Ⅰ)
精选ppt
ab l
MC影响线
14
4. 内力影响线与内力图的比较
x FP 1
A
C
a
b
l
B
x
A
FP 1
C
B
a
b
l
ab
l MC影响线
M图
ab
l
弯矩影响线与弯矩图的比较
荷载位置 截面位置 横坐标
影响线 变
不变
单位移动 荷载位置
竖坐标yD
单位移动荷载移到D点时, 产生的C截面的弯矩
弯矩图 不变
变
截面位置
F RA
1
l
l2
FRA影响线 F R B
l2
l
FRB影响线 1
1 l2
l
②作FRB 影响线。
由∑MA=0,得:
FRBx l, (l1xll2)
精选ppt
16
例 作FRA、FRB、FQC、FQD
的影响线。 解:⑵作剪力FQC的影响线:
E
A x FP 1
C
a
b
BF D
d
当FP = 1 在C 截面以左时,
6
在移动荷载作用下的结构内力分析,要 考虑任意指定截面上的最大或最小内力 值,用以做截面设计或验算;还要考虑 结构所有截面中的最大或最小内力及它 们所在的截面,用以确定结构设计中的 最危险控制截面。
同济大学 朱慈勉版 结构力学 课后答案(下)
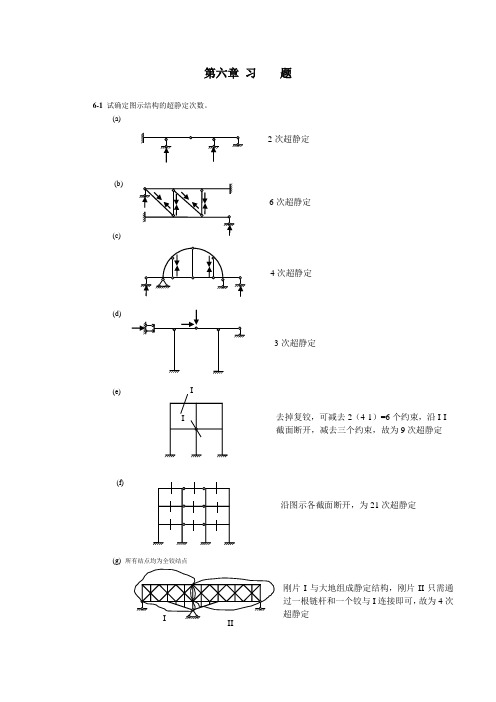
第六章 习 题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I 截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4次超静定(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误,为可变体系。
+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解:基本结构为:l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)l2l 2 l2l l 2Q 图12解:基本结构为:1Mp M01111=∆+p X δ p M X M M +=11(b)解:基本结构为:4a 2a4a4a3m6m 6m810810计算1M,由对称性知,可考虑半结构。
同济大学-朱慈勉版-结构力学-课后答案(上)

2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)【W=5×3 - 4×2 – 6=1>0几何可变(c)】有一个多余约束的几何不变体系(d)|2-3 试分析图示体系的几何构造。
(a)/W=3×3 - 2×2 – 4=1>0可变体系(ⅡⅢ) (b);Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变-(b)~(ⅠⅢ)(ⅡⅢ)几何不变~W=4×3 -3×2 -5=1>0几何可变体系(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体@(e)(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系…(f)?(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(g):(h)|二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)%(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)!Ⅲ(ⅡⅢ)(ⅠⅢ)`3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)%aa *a a2P F a 2P F a4P F Q34P F 2P F(b)"2020Q10/326/310(c){2m6m`4m2m3m2m2m3m3m4m18060(d)]7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)3m2m2m2m2m2m 2m2m4kNm%6m1k N /m2kNCB{242018616MQ18(b),30303011010QM 2106m10kN>3m3m40kNmAB CD:45MQ(d)…444444/32MQN3m3m6m)2m2m(e))4481``(f)#222220M…4m2m3m4m/3-4试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)—(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f 8f
*合理轴线对应的是 一组固 定荷载(M0与荷载有关);
所以拱的合理轴线方程为:
*合理轴线是一组具有不同高
yx
q 2
xl
x
8f ql 2
4f l2
xl x
跨比的抛物线(拱高 f 未定)。
纯受压状态的合力拱轴是一种理想状态,这一 状态只可能对应一种确定不变化的荷载(恒载 或静力荷载)才做得到。实际设计中,合理拱 轴是针对主要荷载,并使在各类荷载的不利组 合下拱的弯矩最小。
3-3-1 三铰拱的内力计算
Fx 0, FxA FxB FH
FyA Fy0A FyB Fy0B
MC 0,
M
0 C
FH
f
0
FH
M
0 C
f
(推力计算公式 )
相当梁
⑴在给定荷载作用下,三铰拱的支座反力仅与三个铰的位置有 关,而与拱轴的形状无关。
⑵在竖向荷载作用下,三铰平拱的支座竖向反力与相应简支梁
借助于压力线的概念,可以用图解的方法求出拱任一截面上 的内力。
从结构优化设计观点出发,寻找合理轴线即拱结构的优化选型。
对三铰拱而言,在竖向荷载作用下,任意截面上弯矩计算式为: M M Hy
它是由两项组成,第一项是简支梁的弯矩,而后一项 与拱轴形状有关。令 M M Hy 0
yx M x
y
4f l2
x(l x)
解:求支座反力。
FyA Fy0A 28kN,
FyB Fy0B 20kN
M
0 C
20kN
8m
16kN
4m
96kN m
FH
M
0 C
f
96 4
24kN
①求截面2的内力:
x2 4m 2 2634
y2
4f l2
x2(l x2 ) 3m
tan2
dy dx
x x2
反力相同,而水平推力与拱高成反比。拱的高跨比(矢跨比)
愈大则推力愈小;反之,则推力愈大。
FH
M
0 C
f
三铰拱的内力计算:
MK
M
0 K
FH
yK
相当梁
注:作拱结构的内力图时,为方便起见,可以取拱的水平投影 线为基线进行绘制。
MK
M
0 K
FH
yK
FH
M
0 C
f
例3-6 绘制图示三铰拱的内力图。
拱轴线方程:
第4章
3-3 三铰拱
第4章
3-3 三铰拱 一、定义:
通常杆轴线为曲线,在竖向荷载作用下,支座产生水 平反力的结构,拱式结构也常称为推力结构。
二、特点: (1)弯矩比相应简支梁小,水平推力存在的原因。 (2)用料省、自重轻、跨度大。 (3)可用抗压性能强的砖石材料。 (4)构造复杂,施工费用高。
第4章
3-3-2 三铰拱的压力线
1、压力线 在荷载作用下,三铰拱的任意截面一般有三个内力分量MK、FQK、
FNK。这三个内力分量可用它的合力FR代替。将三铰拱每一截面上合力 作用点用折线或曲线连接起来,这些折线或曲线成为三铰拱的压力线。
3-3-2 三铰拱的压力线
K
压力线的概念在砖石和混凝土拱的设计中有重要意义。由于 这些材料的抗拉强度较抗压强度低得多,通常要求截面上不出现 拉应力。因此,压力线不应超出截面的核心区。若拱的截面为矩 形,由材料力学算得核心区高度为截面高度的1/3, 故压力线不应 超出截面三等分的中段范围。
拱轴线方程:
y
4f l2
x(l x)
解:求支座反力。
FyA Fy0A 28kN,
FyB Fy0B 20kN
M
0 C
20kN
8m
16kN
4m
96kN m
FH
M
0 C
f
96 4
24kN
②求截面6的内力:
x6 12m 6 2634
y6
4f l2
x6(l x6 ) 3m
tan6
例3-8 求图示三铰拱的合理拱轴线。
填土的容重为:γ。
竖向分布荷载:q( x) qC y
解:
d2M0 dx 2
q
d2y dx 2
1 FH
d2M dx 2
0
q( x) FH
本例y轴向下,所以:
d2y dx 2
q( x ) FH
d2y dx 2
1 FH
qC
y
即:
d2y dx 2
FH
y qC FH
H 在竖向荷载作用下,三铰拱的合理轴线的纵标值与简支梁 的弯矩纵标值成比例。
例3-7 设三铰拱承受沿水平方向均匀分布的竖向荷载,求其合理轴线。
q
y
C
q
A l/2
f
Bx
A
ql x
l/2
2
[解] 由式 yx M x
H
先列出简支梁的弯矩方程
M x q xl x
2
注意
B
ql 2
拱的推力为:
H
M
C
ql 2
例3-6 绘制图示三铰拱的内力图。
拱轴线方程:
y
4f l2
x(l x)
解:求支座反力。
FyA Fy0A 28kN,
FyB Fy0B 20kN
M
0 C
20kN
8m
16kN
4m
96kN m
M图(kN m)
FH
M
0 C
f
96 4
24kN
绘制内力图: FQ图(kN )
FN图(kN )
解得: y Acosh
x B sinh
FH
FH
x
qC
确定常数:
当x 0时, y
0, 得:
最后得合理拱轴线:
A
qC
y
qC
cosh
当x
0时,
dy dx
0,得:
B0
FH
x
1
y M0 FH
例3-9 试证圆弧线是三铰拱拱轴线法线 方拱的情况。作用 于圆弧上的径向均布荷载q 可以用两 个垂直方向上等值的均布荷载等效替 代。
三、拱的种类:
三铰拱
带拉杆的三铰拱
四、拱各部分的名称:
两铰拱
无铰拱
吊杆
拉杆
花篮螺丝
带吊杆的三铰拱
第4章
五、拱与曲梁的区别
3-3-1三铰拱的内力计算
一、拱的内力计算原理仍然是截面法。 二、拱通常受压力,所以计算拱时,规定轴力以受压为正。 三、实际计算时常将拱与相应简支梁对比,通过公式完成 计算。这些公式为绘制拱的影响线提供了方便。
dy dx
x x6
4f l2
(l
2x6 )
0.5
M6
M
0 6
FH
y6
8kN
m
FQL6 (FP FyB )cos6 FH sin6 7.15kN
FQR6 FyB cos6 FH sin6 7.15kN
FNL6 (FP FyB )sin6 FH cos6 23.24kN
FNR6 FyB sin6 FH cos6 30.40kN
4f l2
(l
2x2 )
0.5
M2 80kN m 24kN 3m 8kN m
FQ2 (FyA qx2 )cos2 FH sin2 0kN
FN 2 (FyA qx2 ) sin2 FH cos2
26.8kN
MK
M
0 K
FH
yK
FH
M
0 C
f
例3-6 绘制图示三铰拱的内力图。
