(完整word版)概率论与数理统计公式集锦
概率论及数理统计公式整理完整精华版

第1章随机事件及其様率第二章II机变量及其分布x>0x<0x>0x<0o若X 〜N 出■氓的分布函数为F(x) =「一 f eJ2/ZEToo指数分布fM =0.正态分布r2°-XPg <X <x 2) = ^F(x)= 记住Rftaa :[x n e^x dx = n\分布函数为1 * £ =—卜2力。
/⑴具有如下性质:其中久>°,则称随机变量X服从参数为乂的指数分布。
X的分布因数为(6)分位数下分位表:P(X < jLi a )= a ;上分位表:P{X>p a)=a0(7)函數分布离散型已SIX的分布列为X X2,…,劝,・・P(X =〉y = g(x)Y仃)/儿/?2,…,m…’的分布列(” =g(旺)互不«|等)如下:g(R), g(Q),…,g(X”),•…P(u 若有杲些g9(屏馆等,他应将廿/ft p' ttl加作为g3)的闵率。
连续型先利用X的欄率密度fx(x)耳出Y的分布函数Fr(y) = P(g(X)wy), 再利用变上下限枳分的求导公直求岀fY(y)。
第三章二维葩机变量员其分布如果二维师机向量纟(X, Y )的所有可能取値力至务可列个有序对(x,y),则称纟力离股型葩机量。
设<=(X, Y)的所有可能职值为3,儿)(心=1,2,…), 且事件{§ = (旺,兀)}的闵率为必,称P{(X, Y)=(兀,儿)}=卩沁J = 1,2,…)为疔=(X, Y )的分布偉或林为X和Y的曲合分布律。
联合分离歆里分布若XM …)UXmwXnia 互独立,h,g 为连续函数,M : h (Xi, &…Xm)ff 0 ()Ul,…Xn)相互独立。
特例:若X 与丫詼立,M : h (X )和g (Y )独立。
MA :若X 与丫独立,剧:3X+1和5Y-2决立。
其他其中SoHESD 的面SL 则称(X, Y)服JAD 上的均匀分布,记为(X, Y) ~ u (D)o(8)二维 均匀分布 设IS HI 向量(X, Y)的分布密度因数为 S D(兀)0 e Dc图 3.3砸HI 变量的 函数o,可以证明因数T 亠y/Y7nn+l— (―oo<r < -HX >).我们称HJI 变量T 服从自由度为n 的t 分布,记为T~t (n )。
概率论与数理统计公式整理(超全免费版)

「 ef(x) w0,其中 0,则称随机变量X 服从参数为X 的分布函数为1xe, xF(x)'0,x<0。
记住积分公式:x ne xdx n!指数分布的指数分布如果二维随机向量(X, Y)的所有可能取值为至多可列个有序对(x,y),则称为离散型随机(1)联合分离散型布设=(X,Y)的所有可能取值为(X i,y j)(i,j 1,2,),且事件{ =(X i,y j)}的概率为P ij,,称P{(X,Y) (X i,y j)} P j(i,j 1,2,)为=(X,Y)的分布律或称为X和Y的联合分布律。
联合分布有时也用下面的概率分布表来表示:这里P ij具有下面两个性质(1)P ij>0 (i,j=1,2,…);(2)P j 1.i j(1)大数定律X 切比雪夫大数定律设随机变量冶,X2,…相互独立,均具有有限方差,且被同一常数C所界:D (X i) <C(i=1,2,…),则对于任意的正数£,有limnPLx,丄n i 1 n° E(X i)i 11特殊情形: 若X1,X2,…具有相同的数学期望 E (X)=「则上式成为lim Pn1n X i大数定辛钦大数定律1.设卩是n次独立试验中事件A发生的次数,p是事件A在每次试验中发生的概率,则对于任意的正数£,有limn伯努利大数定律说明,当试验次数小,即limn这就以严格的数学形式描述了频率的稳定性。
很大时,事件1.A发生的频率与概率有较大判别的可能性很0.设X1, X2,…,Xi,…是相互独立同分布的随机变量序列,且 E ( X n) =g,则对于任意的正数£有lim Pn1 nX in i 11.(2)中心极限定理2X N(,)n 格定理设随机变量X1,X2,…相互独立,服从同一分布,且具有相同的数学期望和方差:E(X k) ,D(X k) 0(k 1,2, ),则随机变量的分布函数F n(x)对任意的实数X,Y nnX k nk 1X k nlim F n(x) limn n此定理也称为独立同分布的中心极限定理。
概率论与数理统计公式汇总【范本模板】
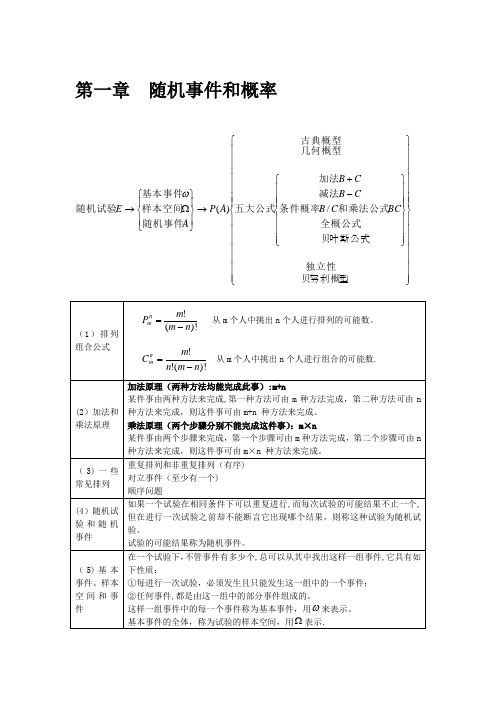
第一章 随机事件和概率⎪⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧-+→⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧Ω→贝努利概型贝叶斯公式/)(独立性全概公式和乘法公式条件概率减法加法五大公式几何概型古典概型随机事件样本空间基本事件随机试验BC C B C B C B A P A E ω第二章 随机变量及其分布⎭⎬⎫⎩⎨⎧-→⎭⎬⎫⎩⎨⎧≤<→⎭⎬⎫⎩⎨⎧)()()()(a F b F A P b X a A X 随机事件随机变量基本事件ωω第三章 二维随机变量及其分布⎪⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=+=⎭⎬⎫⎩⎨⎧→⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧→分布分布分布三大统计分布函数分布正态分布均匀分布常见二维分布独立性条件分布边缘分布连续型分布密度离散型分布律联合分布F t X X X Z Y X Z Y X n 221),,min(max,),(χξ第四章 随机变量的数字特征⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧→切比雪夫不等式矩方差期望一维随机变量⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧→协方差矩阵相关系数协方差方差期望二维随机变量第五章 大数定律和中心极限定理⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧→辛钦大数定律伯努利大数定律切比雪夫大数定律大数定律⎭⎬⎫⎩⎨⎧→棣莫弗-拉普拉斯定理列维-林德伯格定理中心极限定理二项定理 泊松定理第六章 数理统计的基本概念正态总体下的四大分布统计量样本函数样本个体总体数理统计的基本概念→⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧第七章 参数估计{}⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧→⎭⎬⎫⎩⎨⎧单正态总体的区间估计区间估计一致性有效性无偏性估计量的评选标准极大似然估计矩估计点估计从样本推断总体第八章 假设检验单正态总体的假设检验两类错误基本步骤基本思想假设检验的基本概念→⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧。
概率论与数理统计公式汇总

1 n
n i 1
X
k i
,
k
1,2
(5)样本 k
阶中心距: Bk
Mk
1 n
n
(Xi
i 1
X )k ,k
2,3
3、三大抽样分布
(1) 2 分布:设随机变量 X1, X 2 X n 相互独立,且都服从标准正态分布 N (0,1) ,
则随机变量
2
X
2 1
X
2 2
k
(
x1
,
x2
,
,
xn
)
4.估计量的评价标准
无偏性 设 (x1, x2,L , xn) 为未知参数 的估计量。若 E( )= ,
估
则称 为 的无偏估计量。
计
量
设 1 1(x1, x,2 ,L , xn) 和 2 2 (x1, x,2 ,L , xn) 是 未 知 参
7、协方差和相关系数的性质
(1) Cov( X , X ) D( X ) Cov( X ,Y ) Cov(Y , X )
(2) Cov( X1 X 2 ,Y ) Cov( X1,Y ) Cov( X 2 ,Y )
Cov(aX c,bY d ) abCov( X ,Y )
P(A∪B)=P(A)+P(B)-P(AB) 当 P(AB)=0 时,P(A∪B)=P(A)+P(B) P(A-B)=P(A)-P(AB), B A 时 P(A-B)=P(A)-P(B)
条件概率公式 P(B A) P( AB) P( A)
概率论与数理统计公式整理超全版

函数 F(x) 表示随机变量落入区间(– ∞,x]内的概率。
分布函数具有如下性质:
1° 0 F(x) 1, x ;
2° F(x) 是单调不减的函数,即 x1 x2 时,有 F(x1) F (x2) ;
3° F() lim F(x) 0, F() lim F(x) 1;
a≤x≤b 其他,
则称随机变量 X 在[a,b]上服从均匀分布,记为 X~U(a,b)。
分布函数为
x
F (x) f (x)dx
0,
xa, ba
1,
x<a, a≤x≤b x>b。
当 a≤x1<x2≤b 时,X 落在区间( x1 , x2 )内的概率为
x
F (x) f (x)dx
,
则称 X 为连续型随机变量。 f (x) 称为 X 的概率密度函数或密度函数,简称概
率密度。 密度函数具有下面 4 个性质:
1° f (x) 0 。 f 源自x)dx 12° 。
P(X x) P(x X x dx) f (x)dx
x
x
4° F(x 0) F(x) ,即 F(x) 是右连续的;
5° P(X x) F(x) F(x 0) 。
对于离散型随机变量, F(x) pk ; xk x
x
对于连续型随机变量, F (x) f (x)dx 。
(5)八大 0-1 分布 分布
二项分布
P(X=1)=p, P(X=0)=q
在 n 重贝努里试验中,设事件 A 发生的概率为 p 。事件 A 发生
的次数是随机变量,设为 X ,则 X 可能取值为 0,1,2,, n 。
(完整版)大学概率论与数理统计公式全集

大学概率论与数理统计公式全集一、随机事件和概率1、随机事件及其概率2、概率的定义及其计算二、随机变量及其分布1、分布函数性质FbF(aba<≤=P-X)(b()()bFX()P=≤)2、离散型随机变量3、连续型随机变量三、多维随机变量及其分布1、离散型二维随机变量边缘分布∑∑======⋅jjijjii i py Y x X P x X P p ),()(∑∑======⋅iiijjij j py Y x X P y Y P p ),()(2、离散型二维随机变量条件分布2,1,)(),()(=========⋅i P p y Y P y Y x X P y Y x X P p jij j j i j i j i2,1,)(),()(=========⋅j P p x X P y Y x X P x X y Y P p i ij i j i i j i j3、连续型二维随机变量( X ,Y )的联合分布函数⎰⎰∞-∞-=xydvdu v u f y x F ),(),( 4、连续型二维随机变量边缘分布函数与边缘密度函数边缘分布函数:⎰⎰∞-+∞∞-=xX dvdu v u f x F ),()( 边缘密度函数:⎰+∞∞-=dv v x f x f X ),()( ⎰⎰∞-+∞∞-=y Y dudv v u f y F ),()( ⎰+∞∞-=du y u f y f Y ),()(5、二维随机变量的条件分布+∞<<-∞=y x f y x f x y f X X Y ,)(),()( +∞<<-∞=x y f y x f y x f Y Y X ,)(),()(四、随机变量的数字特征1、数学期望离散型随机变量:∑+∞==1)(k k k p x X E 连续型随机变量:⎰+∞∞-=dx x xf X E )()(2、数学期望的性质(1)为常数C ,)(C C E = )()]([X E X E E = )()(X CE CX E =(2))()()(Y E X E Y X E ±=± b X aE b aX E ±=±)()( )()()(1111n n n n X E C X E C X C X C E +=+ (3)若XY 相互独立则:)()()(Y E X E XY E = (4))()()]([222Y E X E XY E ≤ 3、方差:)()()(22X E X E X D -= 4、方差的性质(1)0)(=C D 0)]([=X D D )()(2X D a b aX D =± 2)()(C X E X D -<(2)),(2)()()(Y X Cov Y D X D Y X D ±+=± 若XY 相互独立则:)()()(Y D X D Y X D +=± 5、协方差:)()(),(),(Y E X E Y X E Y X Cov -= 若XY 相互独立则:0),(=Y X Cov 6、相关系数:)()(),(),(Y D X D Y X Cov Y X XY==ρρ 若XY 相互独立则:0=XYρ即XY 不相关7、协方差和相关系数的性质 (1))(),(X D X X Cov = ),(),(X Y Cov Y X Cov =(2)),(),(),(2121Y X Cov Y X Cov Y X X Cov +=+ ),(),(Y X abCov d bY c aX Cov =++8、常见数学分布的期望和方差五、大数定律和中心极限定理1、切比雪夫不等式若,)(,)(2σμ==X D X E 对于任意0>ξ有2)(})({ξξX D X E X P ≤≥-或2)(1})({ξξX D X E X P -≥<- 2、大数定律:若n X X 1相互独立且∞→n 时,∑∑==−→−ni iDni i X E nX n 11)(11(1)若n X X 1相互独立,2)(,)(i i i i X D X E σμ==且M i ≤2σ则:∑∑==∞→−→−ni iPni i n X E nX n11)(),(11(2)若n X X 1相互独立同分布,且i i X E μ=)(则当∞→n 时:μ−→−∑=Pn i i X n 11 3、中心极限定理(1)独立同分布的中心极限定理:均值为μ,方差为02>σ的独立同分布时,当n 充分大时有:)1,0(~1N n n XY nk kn −→−-=∑=σμ(2)拉普拉斯定理:随机变量),(~)2,1(p n B n n =η则对任意x 有:⎰∞--+∞→Φ==≤--xt n x x dtex p np np P )(21})1({lim 22πη(3)近似计算:)()()()(11σμσμσμσμσμn n a n n b n n b n n Xn n a P b X a P nk knk k -Φ--Φ≈-≤-≤-=≤≤∑∑==1、总体和样本总体X 的分布函数)(x F 样本),(21n X X X 的联合分布为)(),(121k nk n x F x x x F =∏=2、统计量(1)样本平均值:∑==ni i X n X 11(2)样本方差:∑∑==--=--=ni i ni i X n X n X X n S 122122)(11)(11(3)样本标准差:∑=--=ni i X X n S 12)(11(4)样本k 阶原点距: 2,1,11==∑=kXn A ni ki k(5)样本k 阶中心距:∑==-==ni k ik k k X XnM B 13,2,)(1(6)次序统计量:设样本),(21n X X X 的观察值),(21n x x x ,将n x x x 21,按照由小到大的次序重新排列,得到)()2()1(n x x x ≤≤≤ ,记取值为)(i x 的样本分量为)(i X ,则称)()2()1(n X X X ≤≤≤ 为样本),(21n X X X 的次序统计量。
概率论与数理统计公式整理(完整精华版)

2° 。
(3)离散与连续型随机变量的关系
积分元 在连续型随机变量理论中所起的作用与 在离散型随机变量理论中所起的作用相类似。
(4)分布函数
设 为随机变量, 是任意实数,则函数
称为随机变量X的分布函数,本质上是一个累积函数。
可以得到X落入区间 的概率。分布函数 表示随机变量落入区间(–∞,x]内的概率。
,其中 ,
则称随机变量 服从参数为 , 的二项分布。记为 。
当 时, , ,这就是(0-1)分布,所以(0-1)分布是二项分布的特例。
泊松分布
设随机变量 的分布律为
, , ,
则称随机变量 服从参数为 的泊松分布,记为 或者P( )。
泊松分布为二项分布的极限分布(np=λ,n→∞)。
超几何分布
随机变量X服从参数为n,N,M的超几何分布,记为H(n,N,M)。
①可分离变量
②正概率密度区间为矩形
二维正态分布
=0
随机变量的函数
若X1,X2,…Xm,Xm+1,…Xn相互独立,h,g为连续函数,则:
h(X1,X2,…Xm)和g(Xm+1,…Xn)相互独立。
特例:若X与Y独立,则:h(X)和g(Y)独立。
例如:若X与Y独立,则:3X+1和5Y-2独立。
(8)二维均匀分布
设 =(X,Y)的所有可能取值为 ,且事件{ = }的概率为pij,,称
为 =(X,Y)的分布律或称为X和Y的联合分布律。联合分布有时也用下面的概率分布表来表示:
Y
X
y1
y2
…
yj
…
x1
p11
p12
…
p1j
…
x2
p21
概率论与数理统计公式整理(超全免费版)
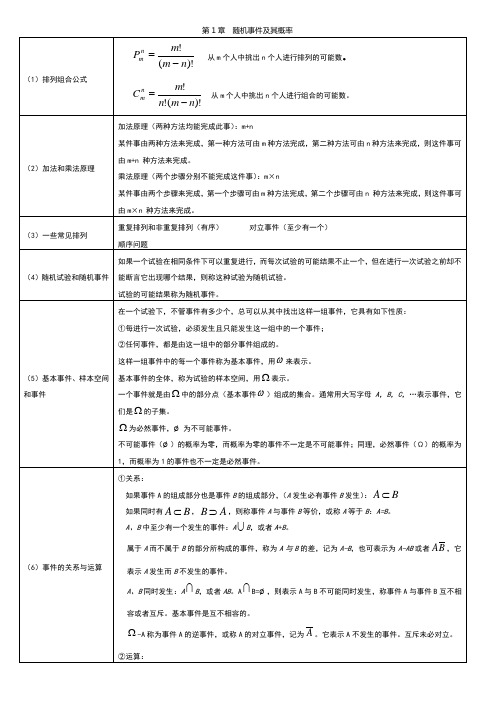
(9)几何概型 (10)加法公式 (11)减法公式
(12)条件概率
(13)乘法公式 (14)独立性
若随机试验的结果为无限不可数并且每个结果出现的可能性均匀,同时样本空间中的每一个基本事件可以 使用一个有界区域来描述,则称此随机试验为几何概型。对任一事件 A,
P( A) L( A) 。其中 L 为几何度量(长度、面积、体积)。 L()
对于离散型随机变量, F (x)
pk ;
xk x
(5)八大分 0-1 分布
P(X=1)=p, P(X=0)=q
x
对于连续型随机变量, F (x) f (x)dx 。
布
二项分布
在 n 重贝努里试验中,设事件 A 发生的概率为 p 。事件 A 发生的次数是随机变量,设为 X ,则
泊松分布
X 可能取值为 0,1,2,, n 。
Ai Ai
德摩根率: i1
i 1
AB AB,AB AB
设 为样本空间, A 为事件,对每一个事件 A 都有一个实数 P(A),若满足下列三个条件:
1° 0≤P(A)≤1,
2° P(Ω) =1
3° 对于两两互不相容的事件 A1, A2 ,…有
P Ai P(Ai) i1 i1
常称为可列(完全)可加性。
则称 P(A)为事件 A 的概率。
1° 1, 2 n ,
2°
P(1 )
P( 2件 A ,它是由1 , 2 m 组成的,则有
P(A)= (1 ) (2 ) (m ) = P(1 ) P( 2 ) P(m )
m n
A所包含的基本事件数 基本事件总数
x1 a
。
指数分布
f (x)
e x ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
估计
参数
枢轴量
枢轴量
分布
置信水平为 的置信区间
已知
未知
已知
未知
八、假设检验
1.假设检验的基本概念
基本思想
假设检验的统计思想是小概率原理。
这里所说的小概率事件就是事件 ,其概率就是显著性水平α,通常我们取α=0.05,有时也取0.01或0.10。
基本步骤
1.提出原假设H0;2.选择统计量K;3.对于α查表找分位数λ;
第二类错误
当H1为真时,而样本值却落入了接受域,按照我们规定的检验法则,应当接受H0。这时,我们把客观上H0不成立判为H0成立(即接受了不真实的假设),称这种错误为“取伪错误”或第二类错误,记 为犯此类错误的概率,即:
P{接受H0|H1为真}= 。
两类错误的关系
人们当然希望犯两类错误的概率同时都很小。但是,当容量n一定时, 变小,则 变大;相反地, 变小,则 变大。取定 要想使 变小,则必须增加样本容量。
2.单正态总体均值和方差的假设检验
条件
原假设
检验统计量
统计量
分布
拒绝域
已知
未知
未知
或
已知Leabharlann (少见)或条件概率公式
乘法公式
全概率公式
贝叶斯公式
(逆概率公式)
两件事件
相互独立
; ;
二、随机变量及其分布
1、分布函数性质
2、离散型随机变量及其分布
分布名称
分布律
0–1分布X~
二项分布X~
泊松分布X~
3、连续型随机变量及其分布
分布名称
密度函数
分布函数
均匀分布
X~
指数分布
X~
正态分布
X~
标准正态
分布
X~
4、随机变量函数Y=g(X)的分布
离散型: ,
连续型:①分布函数法,②公式法
三、多维随机变量及其分布
1、离散型二维随机变量及其分布
分布律: 分布函数
边缘分布律:
条件分布律: ,
2、连续型二维随机变量及其分布
①分布函数及性质
分布函数:
性质:
②边缘分布函数与边缘密度函数
分布函数: 密度函数:
③条件概率密度
,
3、随机变量的独立性
随机变量X、Y相互独立 ,
概率论与数理统计公式集锦
一、随机事件与概率
公式名称
公式表达式
德摩根公式
,
古典概型
几何概型
,其中μ为几何度量(长度、面积、体积)
求逆公式
加法公式
P(A∪B)=P(A)+P(B)-P(AB)
当P(AB)=0时,P(A∪B)=P(A)+P(B)
减法公式
P(A-B)=P(A)-P(AB), 时P(A-B)=P(A)-P(B)
③解方程: ,解得:
4.估计量的评价标准
估计量的评价标准
无偏性
设 为未知参数 的估计量。若E( )= ,则称 为 的无偏估计量。
有效性
设 和 是未知参数 的两个无偏估计量。若 ,则称 有效。
一致性
设 是 的一串估计量,如果对于任意的正数 ,都有
则称 为 的一致估计量(或相合估计量)。
5. 单正态总体参数的置信区间
样本均值: 或
求法步骤:设总体X的分布中包含有未知参数 ,它的前k阶原点矩 中包含了未知参数 ,即 。又设 为总体X的n个样本值,用样本矩 代替 ,在所建立的方程组中解出的k个未知参数即为参数 的矩估计量
3.点估计中的极大似然估计
极大似然估计法: 取自 的样本,设 或 ,
求法步骤:
①似然函数:
②取对数: 或
4.由样本值 计算统计量之值K;将 进行比较,作出判断:当 时拒绝H0,否则认为接受H0。
两类错误
第一类错误
当H0为真时,而样本值却落入了拒绝域,应当否定H0。这时,我们把客观上H0成立判为H0为不成立(即否定了真实的假设),称这种错误为“弃真错误”或第一类错误,记 为犯此类错误的概率,即:P{拒绝H0|H0为真}= ;
③辛钦大数定律:若 独立同分布,且 ,则
3、中心极限定理
①独立同分布的中心极限定理:均值为 ,方差为 的独立同分布时,
当n充分大时有:
②拉普拉斯定理:随机变量 则对任意x有:
③近似计算:
六、数理统计的基本概念
1、总体和样本
总体 的分布函数 样本 的联合分布为
2、统计量
(1)样本均值: (2)样本方差:
性质:① ②
(3) 分布:设随机变量 ,且 与 独立,则随机变量 所服从的分布称为自由度 的 分布,
记为 ,性质:设 ,则
七、参数估计
1.参数估计
(1)定义:用 估计总体参数 ,称 为 的估计量,相应的 为总体 的估计值。
(2)当总体是正态分布时,未知参数的矩估计值=未知参数的极大似然估计值
2.点估计中的矩估计法:(总体矩=样本矩)
(3)样本标准差: (4)样本 阶距:
(5)样本 阶中心距:
3、三大抽样分布
(1) 分布:设随机变量 相互独立,且都服从标准正态分布 ,则随机变量 所服从的分布称为自由度为 的 分布,记为
性质:① ②设 且相互独立,则
(2) 分布:设随机变量 ,且X与Y独立,则随机变量: 所服从的分布称为自由度的 的 分布,记为
③协方差和相关系数的性质: ,
4、随机变量分布的期望和方差
分布
数学期望
方差
0-1分布
p
p(1-p)
二项分布
np
np(1-p)
泊松分布
均匀分布
正态分布
指数分布
五、大数定律与中心极限定理
1、切比雪夫不等式
若 对于任意 有
2、大数定律:①切比雪夫大数定律:若 相互独立,
且 ,则:
②伯努利大数定律:设nA是n次独立试验中事件A发生的次数,p是事件A在每次试验中发生的概率,则 ,有:
离散型: ,连续型:
4、二维随机变量和函数的分布
离散型:
连续型:
四、随机变量的数字特征
1、数学期望
①定义:离散型 ,连续型
②性质: , ,
,当X、Y相互独立时:
2、方差
①定义:
②性质: , ,
当X、Y相互独立时:
3、协方差与相关系数
①协方差: ,当X、Y相互独立时:
②相关系数: ,当X、Y相互独立时: (X,Y不相关)
