3第三章 能控性和能观测性
第三章 线性系统的能控性与能观测性

。 显见第二、三行元素相同。 rank Qk 2 3 故不能控。
例6 桥式电路图中,若取电感L的电流 i及电容 L C的电压 v 为状态变量,取 为输出变量,则系 iL c 统方程为:
R R 1 R R iL ( 1 2 3 4 ) d L R1 R2 R3 R4 1 dt ( R2 R4 ) vC C R1 R2 R3 R4 1 R3 1 R1 ( ) iL L R1 R2 R3 R4 L u 1 1 1 ( ) vC 0 C R1 R2 R3 R4
1 0 ~ 2 A n 0 中,输入矩阵
~ b11 ~ ~ b21 , B ~ bn1
~ b12 ~ b21 ~ bn 2
~ b1r ~ b2r ~ bnr
(3.4)
.
表明: 状态变量 , x1 都可通过选择输入u而 x2 由始点 终点完全能控。 输出y只能反映状态变量 ,所以 不能观测。 x x
2
1
完全能控,不完全能观系统!
例3: 桥式电路如图所示, 选取电感L的电流为 为 状态变量, i (t ) x(t )
u (t ) 为电桥输 入,输出
量为 y (t ) 。 解: 从电路可以直观看出,如果 x(t 0 ) 0 u (t ,则不论 如何 ) 选取,对于所有 ,有 t 0 ,即ut(t)不能控制x(t)的变化, x( ) 0 t 故系统状态为不能控。 若u(t)=0,则不论电感L上的 x(t 0 ) 初始电流 取为多少, 对所有时刻 t 都恒有y(t)=0,即状态x(t)不能由输出y(t)反映,故 t0 系统是状态不能观测的。 该电路为状态既不能控,也不能观测系统。
第三章 线性系统的能控性

的变换矩阵将原系统方程变换成不同的规范形。
1 搜索线性无关的列(行)的两种方案
以从Qc中找寻线性无关的列或行为例。
系统完全能控,rank Qc=n.Qc中有且最多仅有n个线性无关的列。 如何找出它们?用格栅图表示。 方案 I 列搜索
第三章 线性系统的能控性和能观测性
3.1 能控性和能观测性的定义
• 能控性
– 状态点的能控性 对t0,x0, 存在t1>t0 和容许控制u(t), t属于[t0,t1], 使系统状态从x0→x(t1)=0 称此x0在t0时刻能控。
– 系统的能控性 状态空间中的所有x0 ,在t0时刻都能控,则称系统在t0时刻完全 能控。
该搜索方法的特点是, Ai bi 是其左边的向量的线性组合。
方案II 行搜索
先找[b1,b2, ,b p ]中的线性无关列; 再找[Ab1, Ab2, , Ab p ]中的线性无关列;
直到找够n个线性无关列。 找够后, 再排列成如下形式
{b1,
Ab1, , A11b1;
b
,
2
Ab2, ,
A2 1b2; ;
e11 e12 e1v1 ; ; el1 el2 elvl
的表达。 而B的第1列b1就是e1v1 , 所以其表达为
0 0 1; ; 0 0 0T
余类推。 所以,Bc的形式如前所示。
3 龙伯格规范形
3.8 线性系统的结构分解
• 能控性和能观测性在线性非奇异变换下保持不变。 • 线性定常系统按能控性的结构分解
Q
np
B p
AB p
A 1B p
p
现代控制理论第三章

方法二:
转化为约旦标准形 ( Aˆ, Bˆ ) ,再根据 Bˆ 判断
方法三: 传递函数
3.2 线性连续系统的能控性
方法一:线性定常连续系统(A,B), 其状态完全能控的 充要条件是其能控性矩阵的秩为n,即:
rankQc = n Qc = [ B AB A2B … An 1B ]
0 0 2
3
4 1 0
4 2
(2)
x (t)
0
4
0 x(t) 0 0u(t)
0 0 2
3 0
3.2 线性连续系统的能控性 方法三:
3.2 线性连续系统的能控性 例:从输入和状态矢量间的传递函数确定其能控性?
3.2 线性连续系统的能控性 例:判断线性连续系统能控性?
解:
3.2 线性连续系统的能控性
3.3 线性系统的能观测性
例:判断能观测性?
x (t)
2 1
1 3
x(t
)
1
1
u(t)
y(t
)
1 1
0 0 x(t)
解:
C Q0 CA
10 1 0
2 1 2 1
rankQo = 2 = n
系统能观测
3.3 线性系统的能观测性
例: 若系统的状态空间表达式为
x (t)
a d
5
x(t
)
1
7
(2)
x (t)
5
x(t)
1
y(t) 0 4 5x(t)
3 2 0 y(t) 0 3 1 x(t)
(3)
3 1 0
0 3 1
x (t) 0 0 3
x(t)
2
现代控制理论第三章线性系统的能控性和能观测性

1 x1 u x 2 2 x2 u x y x x 1 2
1 x
u
1 s 1 s
2
x1
y
x2
2 x
由于状态变量x1、x2都受控于输入u,所以系统 是能控的;输出y能反映状态变量x1,又能反映状 态变量x2的变化,所以系统是可观测的。 即状态变量x1能控、可观测;状态变量x2能控、 可观测。
任意初态 x(t0 ) x 零终态 x(t f ) 0
状态完全能控
Байду номын сангаас
第 三章 线性控制系统式的能控性和能观测性
②把系统的初始状态规定为状态空间的原点, 即 x(t 0 ) 0,终端状态规定为任意非零有限点, 则可达定义表述如下: 对于给定的线性定常系统
Ax Bu ,如果 x
存在一个分段连续的输入 u (t ),能在 [t 0 , t f ] 有限时间间隔内,将系统由零初始状态 x(t 0 ) 转移 到任一指定的非零终端状态 x(t f ) ,则称此系统 是状态完全可达的,简称系统是可达的(能达的)。 任意初态 x(t0 ) 0 零终态 x(t f ) x 状态完全可达
第 三章 线性控制系统式的能控性和能观测性
1. 直接由A,B矩阵的结构判断系统的能控性 定理: 系统
( A, B )
即
A(t )x B(t )u x y C (t )x D(t )u
状态完全能控的充分必要条件是其能控性矩阵
Qk [ B AB A2 B An1 B]
一、线性定常连续系统状态能控性的定义 定义3.1(状态能控性定义):
Ax Bu,如果存在一个 对于线性定常系统 x 分段连续的输入u(t),能在有限时间间隔[t0,tf]内, 使得系统从某一初始状态x(t0)转移到指定的任一 终端状态x(tf) ,则称此状态是能控的。若系统的 所有状态都是能控的,则称此系统是状态完全能 控的,简称系统是能控的。
能控性和能观测性

0 0
0 0
−1 0
0 2
0 1
0 0
0⎥⎥ 0⎥
x
+
⎢⎢0 ⎢0
0 0
04⎥⎥⎥u
⎢
⎥⎢
⎥
⎢ 0 0 0 0 0 2 0 0⎥ ⎢1 2 0⎥
⎢ ⎢
0
0
0
0 0 0 2 0⎥⎥
⎢⎢0 3 3⎥⎥
⎢⎣ 0 0 0 0 0 0 0 5⎥⎦ ⎣⎢3 0 0⎥⎦
解:此为8阶系统,n=8
19
S=
⎡0 0 0 1 0 0 −2 0 0 3 0 0 −4 0 0 5 0 0 −6 0 0 7 0 0 ⎤
再证必要性,即已知系统能控,证明rankS=n。
同样采用反证法假设rankS<n,表明S的各行线性相关,那么一
定存在一个非零的向量α使
α T [B AB L An−1B] = 0,
α T Ai B = 0,i = 1,2,Ln −1
12
α T Ai B = 0, i = 1,2,Ln −1
根据凯莱-哈密尔顿定理 α T Ai B = 0, i = n, n +1,L
α T e−At B = α T [I − At + 1 A2t 2 − 1 A3t3 + L]B
2!
3!
= α T B −α T ABt + 1 α T A2Bt 2 − 1 α T A3Bt 3 + L = 0
2!
3!
∫t1 [α T e−Aτ B][α T e−Aτ B]T dτ = 0
0
∫ ∫ t1 α T e−Aτ BBT e−ATταdτ = α T t1 e−Aτ BBT e−ATτ dτα
(整理)控制系统的能控性和能观测性
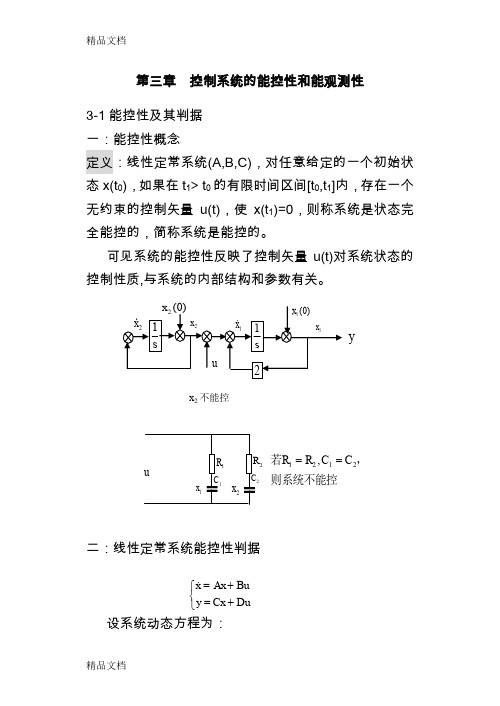
第三章 控制系统的能控性和能观测性3-1能控性及其判据 一:能控性概念定义:线性定常系统(A,B,C),对任意给定的一个初始状态x(t 0),如果在t 1> t 0的有限时间区间[t 0,t 1]内,存在一个无约束的控制矢量u(t),使x(t 1)=0,则称系统是状态完全能控的,简称系统是能控的。
可见系统的能控性反映了控制矢量u(t)对系统状态的控制性质,与系统的内部结构和参数有关。
二:线性定常系统能控性判据设系统动态方程为:x 2不能控y2则系统不能控,若2121,C C R R ==⎩⎨⎧+=+=DuCx y Bu Ax x设初始时刻为t 0=0,对于任意的初始状态x(t 0),有: 根据系统能控性定义,令x(t f )=0,得:即:由凯莱-哈密尔顿定理:令 上式变为:对于任意x(0),上式有解的充分必要条件是Q C 满秩。
判据1:线性定常系统状态完全能控的充分必要条件是:⎰-+=ft f f f d Bu t x t t x 0)()()0()()(τττφφ⎰⎰---=--=-ff t f f t f f d Bu t t d Bu t t x 01)()()()()()()0(τττφφτττφφ⎰--=f t d Bu x 0)()()0(τττφ∑-=-==-1)()(n k kk A A eτατφτ∑⎰⎰∑-=-=-=-=101)()()()()0(n k t k k t n k k k ff d u B A d Bu A x ττταττταkt k u d u f=⎰)()(ττταUQ u u u u B A B A AB B Bu A x c k n n k kk -=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=-=--=∑ 321121],,,[)0(能控性矩阵Q C =[B ,AB ,A 2B ,…A n-1B]满秩。
对于单输入系统,Q C =[b ,Ab ,A 2b ,…A n-1b] 如果系统是完全能控的,称(A 、B )或(A 、b )为能控对。
第3章 能控性和能观性

t 0, t 1
0
W (0, t1 ) 奇异,
与已知条件矛盾
rank W n
说明:1.
在应用格拉姆矩阵判据时计算矩阵指数
函数以及积分的计算量非常大,所以这一判据主要 用在理论分析中。 2. 矩阵W可以利用Matlab函数ctrb(A,B)来计算, 不过其计算在数值上容易导致病态,所以建议使用
1.2 可观性
[例]电路 ((信息)观测的可能性)
如果 u 0,不管电容储存了多少电荷, 由于 y 0 无法知道状态(信息) 图 假定输入恒为0
u
R
R C R
y
R
(信息)观测的可能性
y ce At x0 (未知量
有输入时
At t
(u 0) x0 )
y y ce
0
y ce x0 ce A(t )bu( )d
, T An1B 0
B AB
T
系统不可控。
n1 T A B W 0 rank W n
充分性:证明过程与上相反。
所以输入维数增加 那么特征值 i 不可控。 约当标准形判据 线性定常系统可控的充分必要条件是 系统可控的可能性增加。
T i T i
t 0 A( t )
bu ( )d 可将它看做输出
已知
可观性的直观意义和定义
所谓系统可观是指通过观测系统的外部变量即输 入输出变量就能正确地知道系统的内部状态。 定义 如果基于有限长的输入输出数据:
u(t ), y(t ),
0 t T
能唯一地确定系统的初始状态 x0 ,则称点 x0 可观 测。进一步,如果状态空间中任意的初始状态 x0 都可观测,则称系统可观测。
能控性及能观测性

第三章:控制系统的能控性及能观测性(第五讲)内容介绍:能控性和能观测性定义、判据、对偶关系、标准型、结构分解。
能控性和能观测性是现代控制理论中最基本概念,是回答:“输入能否控制状态的变化”及“状态的变化能否由输出反映出来”这样两个问题。
换句话说,能控性是“能否找到一向量u(t)有效控制x(t)变化”。
能观测性问题是:“能否通过输出y(t)观测到状态的变化。
”一、能控性定义及判据 给出一个多变量系统(多输入、多输出)若系统G(s)在适当的控制u(t)作用下,每个状态都受影响,亦在有限的时间内能使系统G 由任意初始状态转移到零状态,或者说在有限的时间内能使系统由零状态转移到任意指定状态。
这说明:输入对状态的控制能力强,反之若G 的某一状态根本不受影响,那么在有限时间内就无法利用控制使这个状态变量发生变化。
说明输入对状态控制能力差。
可见:反映输入对状态控制能力的概念是能控性概念。
1. 定义:若对系统,在时刻的任意状态x()都存在一个有限的时间区间(ξt t ,0)(0t t 〉ξ)和定义在[]ξt ,t 0上适当的控制u(t),使在u(t)作用下x()=0。
则称系统在时刻是状态能控的。
如果系统在有定义的时间区域上的每一时刻都能控,称系统为完全能控。
()x u x 01011012=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-=考查能控性?状态变量图(信号流图):y2由于u 的作用只影响不影响,故()t x 2为不能控。
某一状态不能控,则称系统不能控。
2.判据:u 1 : y1:对线性定常系统=Ax+Bu ,若对某一时刻能控,则称系统完全能控。
设: p输出 n n A *、p n B *、n m C *给出一定理:由=Ax+Bu 所描述的系统是状态完全能控的必要且充分条件为下列n ×np 阵的秩等于n 。
=BAB ……B A n 1-称为能控性阵。
换言之:系统的状态完全能控的必要且充分的条件是能控性阵的秩为n 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1.2 线性系统能控性的判据
x&(t) = Ax(t) + Bu(t)
1、线性定常连续系统可控性的格拉姆矩阵判据
线性定常连续系统{A,B} 状态完全可控的充要条件是:存在时
刻t1>0,使如下定义的可控性格拉姆(Gram)矩阵为非奇异。
∫Δ
Wc (0, t1) =
t1 e− Aτ BB T e− ATτ dτ
,τ
)dτ
10
2、线性定常连续系统能控性的秩判据
线性定常连续系统{A,B} 状态完全能控的充要条件是:
能控性判别阵S行满秩,其中
为能控性判别阵。S = [BM ABM A2BMLM An−1B]
证明:充分性:已知S满秩,证系统能控。
用反证法,假设rankS=n,而系统不能控,那么根据格拉姆矩
阵判据可知
第三章 线性系统的 能控性和能观测性
1
3.1 线性连续系统的能控性 线性连续系统的能控性概念 线性连续系统的能控性判据 线性连续系统的能控性指数
2
3.1.1 线性连续系统能控性的概念
1、状态能控
x&(t) = A(t)x(t) + B(t)u(t)
对于系统{A(t),B(t)} 及某一个特定的初始状态xi(t0)。若 对每一个tf>t0,总有定义在时间域[t0,tf]上的控制函数u(·),能 把系统{A(t),B(t)}从初始状态xi (t0),转移到状态xi (tf)=0,则 称该系统的这一特定状态xi (t0)在t0时刻是能控的。 若xi (t0)对所有初始时刻都是能控的,则称xi (t)为一致能控的。
3
2、系统状态完全能控 如果系统的每一个状态xi (t0)(i=1~n)都能控,则称该系
统为状态完全可控,简称状态能控。 物理意义是: 不论初始状态在何处,通过控制函数u(t),可以将初始状态 转移到原点位置。 相关概念——能达性:初始状态在原点位置,可以通过控制 函数u(t),可以将初始状态转移到状态空间中任意指定位置。
∫Δ
Wc (0, t1) =
t1 e− Aτ BB T e− ATτ dτ
0
为奇异,即存在一个非零n维向量α使
∫ α TWc (0, t1)α =
t1 α T e− Aτ BB T e− ATταdτ
0
∫= t1 [α T e−Aτ B][α T e−Aτ B]T dτ = 0 0
α T e− Aτ B = 0, ∀t ∈[0, t1]
采用反证法,假设系统能控,而Wc(0,t1)是奇异,那么一定存在
一个非零的向量 x0 使下式成立
x0TWc (0, t1)x0 = 0
∫t1
0
x0T e− Aτ BBT e− ATτ
⋅ x0dτ
=
0
∫t1 [BT e−ATτ
0
⋅ x0 ]T BT e−ATτ
⋅ x0dτ
=
0
∫t1
0
BT e− ATτ
线性定常连续系统{A,B} 状态完全能控的充要条件是:存在时
刻t1>0,使如下定义的格拉姆(Gram)矩阵为非奇异。对于
∫Δ
Wc (0, t1) =
t1 e− Aτ BB T e− ATτ dτ
0
对于初始时刻不为零的情况,格拉姆(Gram)矩阵为
∫ τ Δ
Wc (t0 , t1) =
e BB e d t1 − A(τ −t0 )
4
3、线性连续系统的输出能控性
x&(t) = A(t)x(t) + B(t)u(t) y(t) = C(t)x(t) + D(t)u(t)
系统{A(t),B(t),C(t),D(t)})及某一个特定的初始输出y(t0)。 若对每一个tf>t0,总存在定义在时间域[t0,tf]上的控制函数 u(·),能把系统{A(t),B(t),C(t),D(t)}从初始输出y(t0),转 移到任意输出y(tf),则称该系统{A(t),B(t),C(t),D(t)}为输 出完全能控的。 物理意义是: 不论初始输出在何处,通过控制函数u(t),可以将初始输出 转移到指定位置。 这个问题实际上是系统设计的基本问题。
0
=0
∫ ∫ x0
= −e− At1
t1 e A(t1−τ ) Bu (τ )dτ
0
= − t1 e−Aτ Bu(τ )dτ 0
∫ x0
2
=
x0T x0
= [−
t1 0
e−
Aτ
Bu
(τ
)dτ
]T
x0
∫ =
−
t1 0
u
T
Hale Waihona Puke (τ)BT
e
−
ATτ
x0
dτ
=0
向量 x0 为零,与假设矛盾,必要性得证。
9
1、线性定常连续系统可控性的格拉姆矩阵判据
⋅ x0
2
dτ
=0
BT e− ATt ⋅ x0 = 0, ∀t ∈[0, t1]
8
BT e− ATt ⋅ x0 = 0, ∀t ∈[0, t1]
其中 x0 ≠ 0,
而因为系统完全能控,对于这样一个非零向量 x0 找到一个控制
量u,使得
∫ x(t1) = eAt1 x0 +
t1 e A(t1−τ ) Bu (τ )dτ
T − AT (τ −t0 )
t0
实际上,对于线性时变系统也存在类似的能控性判据
线性时变连续系统{A(t),B (t)} 状态完全能控的充要条件是:存
在时刻t1> t0 ,使如下定义的格拉姆(Gram)矩阵为非奇异。
∫Δ
Wc (t0 , t1) =
t1 t0
Φ(t0
,τ
)
B(t
)
BT
(t
)Φ
T
(t
0
⋅Wc−1(0, t1)x0
= 0 = e At1 x0 − e At1 ⋅Wc (0, t1) ⋅Wc−1(0, t1)x0
结果表明,对于任一x0≠0,存在有限时间t1>0和控制量u(t), 使状态由x0转移到t1时刻x(t1 ) =0。充分性得证。
7
再证必要性:即系统能控那么Wc(0,t1)一定非奇异。
t1
)
x0
,
t ∈[0, t1]
∫ x(t1) = e At1 x0 +
t1 e A(t1−τ ) Bu (τ )dτ
0
∫ = e At1 x0 − e At1
t1 0
e
−
Aτ
BB
T
e
−
ATτ
Wc−1
(0,
t1
)
x0
dτ
∫ = e At1 x0 − e At1
t1 0
e− Aτ
BB T
e− ATτ
dτ
0
证明:充分性,已知Wc(0,t1)非奇异,证明系统完全能控。 因为Wc(0,t1)非奇异,那么Wc-1存在,因此对任意非零初始状态 x0,可构造控制u(t)为
u (t )
=
−BT
e−
AT
W t −1 c
(0,
t1 ) x0
,
t ∈[0, t1]
6
u (t )
=
−BT
e−
AT
W t −1 c
(0,
