甘肃省天水市秦安县第一中学2020-2021学年高二(重点班)上学期期末考试数学试题试题

合集下载

2020-2021学年甘肃省天水一中高二(上)期末数学试卷(文科)(附答案详解)

2020-2021学年甘肃省天水一中高二（上）期末数学试卷（文科）一、单选题（本大题共10小题，共50.0分）1.等差数列{a n}中，a7+a9=16，a4=1，则a12=()A. 15B. 30C. 31D. 642.设x∈R，则“x2−1>0”是“x>2”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3.已知椭圆x29+y24=1的左、右焦点为F1，F2，P是椭圆上的点，且|PF1|=2，则|PF2|=()A. 1B. 2C. 3D. 44.已知正实数a，b满足3a+2b=1，则6a +1b的最小值为()A. 32B. 34C. 36D. 385.双曲线x2−y24=1的渐近线方程为()A. y=±12x B. y=±2x C. y=±√32x D. y=±√52x6.已知双曲线C：x2a2−y2b2=1的离心率e=54，且其右焦点为F2(5,0)，则双曲线C的方程为()A. x24−y23=1 B. x29−y216=1 C. x216−y29=1 D. x23−y24=17.已知数列{a n}中，a1=1，a n+1=2a n+3，则a10=()A. 2045B. 1021C. 1027D. 20518.已知抛物线C：y2=x的焦点为F，A(x0,y0)是C上一点，若|AF|=54x0，则x0等于()A. 1B. 2C. 4D. 89.函数f(x)=e x sinx在区间[−π,π]的图象大致是()A.B.C.D.10. 过抛物线y 2=2px(p >0)的焦点F 作直线与抛物线在第一象限交于点A ，与准线在第三象限交于点B ，过点A 作准线的垂线，垂足为H.若tan∠AFH =2，则|AFBF |=( )A. 54B. 43C. 32D. 2二、单空题（本大题共4小题，共20.0分）11. 已知函数f(x)=lnx +x 2，则曲线y =f(x)在点(1,f(1))处的切线方程为______． 12. 已知实数x ，y 满足{x ≥2y ≤5−x y ≥2x −5，则z =x −2y 的最大值为______ ．13. 若命题“∀x ∈R ，x 2−2x +m 2−1>0”为真命题，则实数m 的取值范围为______ ．14. 数列{a n }满足a n+1=11−a n，a 1=12，则a 15=______．三、解答题（本大题共4小题，共48.0分）15. 已知等比数列{a n }中，a 1=1，且2a 2是a 3和4a 1的等差中项．(1)求数列{a n }的通项公式；(2)若数列{b n }满足b n =2n +a n 2(n ∈N ∗)，求{b n }的前n 项和S n ．16.已知数列{a n}的前n项和为S n，且S n=3n2−7n．(1)求数列{a n}的通项公式；(2)求数列{4a n a n+1}的前n项和T n．17.已知函数f(x)=x+ae x，其中a∈R，e是自然对数的底数．(1)当a=−1时，求函数f(x)在区间[0,+∞)上的零点个数；(2)若f(x)<e x2对任意x∈[−1,+∞)恒成立，求实数a的取值范围．18.已知点A(0,−2)，椭圆E：x2a2+y2b2=1(a>0,b>0)的离心率为√32，F是椭圆E的右焦点，直线AF的斜率为2√33，O是坐标原点．(1)求E的方程；(2)设过点A的直线l与E相交于P，Q两点，当△OPQ的面积最大时，求直线l的方程．答案和解析1.【答案】A【解析】解：方法一：设公差等于d ，由a 7+a 9=16可得2a 1+14d =16，即a 1+7d =8．再由a 4=1=a 1+3d ，可得a 1=−174，d =74．故a 12=a 1+11d =−174+774=15，方法二：∵数列{a n }是等差数列， ∴a p +a q =a m +a n ，即p +q =m +n∵a 7+a 9=a 4+a 12 ∴a 12=15故选：A ．由a 7+a 9=16可得2a 1+14d =16，再由a 4=1=a 1+3d ，解方程求得a 1和公差d 的值，或根据等差中项的定义，a p +a q =a m +a n ，从而求得a 12的值．本题主要考查等差数列的等差数列的通项公式的应用，求出首项和公差d 的值，是解题的关键，属于基础题．2.【答案】B【解析】解：x 2−1>0，解得x >1，或x <−1． ∴x 2−1>0”是“x >2”的必要不充分条件．故选：B ．解出不等式：x 2−1>0，即可判断出结论．本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．3.【答案】D【解析】解：椭圆x 29+y 24=1，可知a =3，椭圆x 29+y 24=1的左、右焦点为F 1，F 2，P 是椭圆上的点，且|PF 1|=2，由椭圆定义可得：|PF2|=2a−|PF1|=6−2=4．故选：D．利用椭圆方程求解a，通过椭圆的定义，转化求解即可．本题考查椭圆的简单性质以及椭圆定义的应用，是基本知识的考查．4.【答案】A【解析】解：正实数a，b满足3a+2b=1，则6a +1b=(3a+2b)(6a+1b)=20+12ba+3ab≥20+2√12ba⋅3ab=32，当且仅当12ba =3ab且3a+2b=1，即b=18，a=14时取等号，则6a +1b的最小值为32．故选：A．利用“乘1法”与基本不等式的性质即可得出．本题主要考查了“乘1法”与基本不等式的性质，属于基础题．5.【答案】B【解析】【分析】由双曲线的渐近线方程为y=±bax，即可得到所求双曲线的渐近线方程．本题考查双曲线的渐近线方程，注意运用双曲线的方程和渐近线方程的关系，考查运算能力，属于基础题．【解答】解：由双曲线x2a2−y2b2=1(a>0,b>0)的渐近线方程为y=±bax，可得双曲线x2−y24=1的渐近线方程为y=±2x．故选B．6.【答案】C【解析】【分析】本题考查双曲线方程的求法，双曲线的简单性质的应用，考查计算能力．利用已知条件，列出方程，求出双曲线的几何量，即可得到双曲线方程．【解答】解：双曲线C：x2a2−y2b2=1的离心率e=54，且其右焦点为F2(5,0)，可得：ca =54，c=5，∴a=4，b=√52−42=3，所求双曲线方程为：x216−y29=1．故选C．7.【答案】A【解析】解：根据题意，数列{a n}中，a1=1，a n+1=2a n+3，变形可得(a n+1+3)= 2(a n+3)，又由a1=1，则a1+3=4，则数列{a n+3}是以a1+3=4为首项，公比为2的等比数列，则a10+3=4×29=2048，则a10=2045，故选：A．根据题意，分析可得(a n+1+3)=2(a n+3)，分析可得列{a n+3}是以a1+3=4为首项，公比为2的等比数列，由此求出a10+3的值，变形可得答案．本题考查数列的递推公式，涉及等比数列的定义，属于基础题．8.【答案】A【解析】解：抛物线C：y2=x的焦点为F(14,0)∵A(x0,y0)是C上一点，|AF|=54x0，∴54x0=x0+14，解得x0=1．故选：A．利用抛物线的定义、焦点弦长公式即可得出．本题考查了抛物线的定义、焦点弦长公式，属于基础题．9.【答案】D【解析】解：当x∈(−π,0)时，sinx<0，e x>0，则f(x)<0，故排除AB，∵f(x)=e x sinx，当x∈(0,π)时，∴f′(x)=e x(sinx+cosx)=√2e x sin(x+π4)，令f′(x)=0，解得x=3π4，当0<x<3π4时，f′(x)>0，函数单调递增，当3π4<x<π时，f′(x)<0，函数单调递减，在x=3π4取最大值，故选项D符合，故选：D．先根据函数值，排除AB，再根据函数的单调性排除C，得答案．本题考查了函数的图象的识别，关键利用导数判断函数的单调性，属于中档题．10.【答案】C【解析】解：由题意如图所示：设准线与x轴的交点为M，过点F作FC⊥AH交于C，由抛物线的定义可知|AF|=|AH|，所以∠AHF=∠AFH=α，∠FAH=π−2α=∠OFB，|BF|=|MF|cos(π−2α)=pcos(π−2α)，|AF|=|CF|sin(π−2α)=|CH|⋅tanαsin(π−2α)=p⋅tanαsin(π−2α)，所以|AF||BF|=tanαtan(π−2α)=−tanαtan2α=tan2α−12=32，故选：C．由题意如图：再由抛物线的性质可得|AF|=|AH|，在三角形中求出|AF|，|BF|的表达式，可得|AF||BF|的值．本题考查抛物线的性质及平行线的性质，属于中档题．11.【答案】3x−y−2=0【解析】解：函数f(x)=lnx+x2，可知f(1)=1，故切点为(1,1)，f ′(x)=1x +2x ，故f′(1)=3，所以曲线y =f(x)在点(1,f(1))处的切线方程为y −1=3(x −1)，即3x −y −2=0，故答案为：3x −y −2=0．根据题意，求出f(1)和f′(1)，即可得解．本题考查了导数的几何意义，是基础题．12.【答案】4【解析】解：由约束条件{x ≥2y ≤5−x y ≥2x −5作出可行域如图，联立{x =2y =2x −5，解得A(2,−1)，化目标函数z =x −2y 为y =12x −z2，由图可知，当直线y =12x −z2过A 时，直线在y 轴上的截距最小，z 有最大值为4．故答案为：4．由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．本题考查简单的线性规划，考查数形结合的解题思想，是中档题．13.【答案】(−√2,√2)【解析】解：命题“∀x ∈R ，x 2−2x +m 2−1>0”是真命题，得△=4−4(m 2−1)<0，即−√2<m <√2．即所求m 的取值范围是(−√2,√2).故答案为：(−√2,√2).利用判别式，即可求出实数m的取值范围．本题考查的知识点是命题的真假判断与应用，转化为判别式和0之间的关系是解题的关键．14.【答案】−1【解析】解：由题意得a1=12,a2=11−a1=2,a3=11−a2=−1,a4=11−a3=12，∴数列{a n}的周期为3，∴a15=a3=−1．故答案为：−1．求出数列的前几项，得到数列是周期数列，然后求解即可．本题考查数列的递推关系式的应用，判断数列是周期数列是解题的关键，属于基础题．15.【答案】解：(1)∵已知等比数列{a n}中，a1=1，设公比为q，2a2是a3和4a1的等差中项，则4a2=a3+4a1，可得4q=q2+4．解得q=2．∴a n=a1q n−1=2n−1，(2)b n=2n+a n2=2n+4n−1，S n=b1+b2+b3+⋯+b n=(2+40)+(4+41)+(6+42)+⋯+(2n+4n−1) =(2+4+6+⋯+2n)+(40+41+42+⋯+4n−1)=n(2+2n)2+1−4n1−4=n2+n+4n−13．【解析】(1)设公比为q，由2a2是a3和4a1的等差中项，解得q，从而求出通项公式．(2)利用分组求和法，求解数列的和即可．本题主要考查等差数列的定义和性质，等比数列的通项公式，数列求和的方法的应用，属于中档题．16.【答案】解：(1)∵S n=3n2−7n，∴当n≥2时，a n=S n−S n−1=3n2−7n−3(n−1)2+7(n−1)=6n−10，又当n=1时，a1=S1=3−7=−4也适合上式，∴a n=6n−10；(2)由(1)可得：4a n a n+1=4(6n−10)(6n−4)=1(3n−2)(3n−5)=13(13n−5−13n−2)，∴T n=13(1−2−11+11−14+⋯+13n−5−13n−2)=13(−12−13n−2)=n2(2−3n)．【解析】(1)先由a n=S n−S n−1求得a n(n≥2)，再求得a1，即可求得a n；(2)先由(1)求得4a n a n+1，再利用裂项相消法求得其前n项和T n即可．本题主要考查数列通项公式的求法及裂项相消法在数列求和中的应用，属于中档题．17.【答案】解：(1)a=−1时，f(x)=x−1e x ，f′(x)=1+1e x>0，故f(x)在[0,+∞)递增，而f(0)=−1<0，f(1)=1−1e>0，故∃x0∈(0,1)，使得f(x0)=0，故函数f(x)在区间[0,+∞)上的零点个数是1个；(2)若f(x)<e x2对任意x∈[−1,+∞)恒成立，即a<e2x2−xe x恒成立，x∈[−1,+∞)，令g(x)=e2x2−xe x，x∈[−1,+∞)，则g′(x)=e x(e x−x−1)，令ℎ(x)=e x−x−1，则ℎ′(x)=e x−1，令ℎ′(x)>0，解得x>0，令ℎ′(x)<0，解得x<0，故ℎ(x)在[−1,0)递减，在(0,+∞)递增，故ℎ(0)=0，ℎ(x)≥0，故g′(x)≥0，g(x)在[−1,+∞)递增，故g(x)min=g(−1)=12e2+1e，故a<12e2+1e，即a的取值范围是(−∞,12e2+1e).【解析】(1)代入a的值，求出函数的导数，根据函数的单调性确定函数f(x)的零点个数即可；(2)问题转化为a<e2x2−xe x恒成立，令g(x)=e2x2−xe x，x∈[−1,+∞)，根据函数的单调性求出a 的范围即可．本题考查了函数的单调性，最值，零点问题，导数的应用以及函数恒成立问题，考查转化思想，属中档题．18.【答案】解：(1)设F(c,0)，由条件知2c =2√33，得c =√3，又c a =√32， ∴a =2，b 2=a 2−c 2=1，故E 的方程为：x 24+y 2=1；(2)当l ⊥x 轴时，不合题意，故设l ：y =kx −2，P(x 1,y 1)，Q(x 2,y 2)，联立{y =kx −2x 24+y 2=1，得(1+4k 2)x 2−16kx +12=0．当Δ=16(4k 2−3)>0，即k 2>34时， x 1=8k−2√4k 2−34k 2+1，x 2=8k+2√4k 2−34k 2+1．从而|PQ|=√1+k 2|x 1−x 2|=4√k2+1⋅√4k 2−34k 2+1．又点O 到直线PQ 的距离d =√k 2+1．∴△OPQ 的面积为S △OPQ =12|PQ|⋅d =4√4k 2−34k 2+1，设√4k 2−3=t(t >0)，则S △OPQ =4t t 2+4=4t+4t≤2√4=1，当且仅当t =4t ，即t =2时取“=”．∴√4k 2−3=2，即k =±√72时等号成立，且满足Δ>0，∴当△OPQ 的面积最大时，l 的方程为y =√72x −2或y =−√72x −2．【解析】本题考查椭圆的简单性质，考查直线与椭圆位置关系的应用，训练了利用换元法及基本不等式求最值，属拔高题． (1)设F(c,0)，由已知得2c =2√33，求得c ，再由离心率求得a ，结合隐含条件求得b ，则椭圆方程可求；(2)由题意可知，当l ⊥x 轴时，不合题意，设l ：y =kx −2，联立直线方程与椭圆方程，求出P 、Q 的横坐标，代入弦长公式求得|PQ|，再由点到直线的距离公式求得O 到PQ 的距离，代入三角形面积公式，换元后利用基本不等式求最值，同时求得当△OPQ 的面积最大时直线l的方程．。

2020-2021学年天水一中高二上学期期末数学试卷(文科)(含解析)

2020-2021学年天水一中高二上学期期末数学试卷(文科)一、单选题（本大题共10小题，共50.0分） 1.等差数列{a n }中，a 1=−5，从第10项开始为正数，则公差d 的取值范围是( )A. (59,+∞)B. (−∞,58)C. (59,58]D. [59,58]2.已知函数f(x)=√x +ax ，则“a <0”是“函数f(x)在区间(1,+∞)上存在零点”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件3.椭圆4x 2+y 2=4的离心率是( )A. √32B. √22C. 3D. 234.设a =√x 2−xy +y 2,b =p √xy ，c =x +y ，若对任意正实数x ，y 都存在以a ，b ，c 为三边的三角形，则实数p 的取值范围是( )A. (1,3)B. (0,1)∪(3,+∞)C. (2,4)D. (2,3)5.F 1，F 2为双曲线x 2a 2−y 2b 2=1(a >0,b >0)的左右焦点，过点F 2作此双曲线一条渐近线的垂线，垂足为M ，满足|MF 1⃗⃗⃗⃗⃗⃗⃗⃗ |=√2|MF 2⃗⃗⃗⃗⃗⃗⃗⃗ |，则此双曲线的渐近线方程是( )A. y =±2xB. y =±12xC. y =±√2xD. y =±√22x 6.已知双曲线−=1(a >0,b >0)的一条渐近线方程为y =x ，则双曲线的离心率为( )A.B.C.D.7.若，，，则S 1，S 2，S 3的大小关系为( )．A. S 1< S 2< S 3B. S 2< S 1< S 3C. S 2< S 3< S 1D. S 3< S 2< S 18.已知抛物线y =14x 2，过焦点且垂直于对称轴的直线与抛物线交于A 、B 两点，则坐标原点与A 、B 两点构成的三角形的面积为( )A. 6B. 4C. 1D. 29.f(x)=xsinx (x ∈(−π,0)∪(0,π))大致的图象是( )A.B.C.D.10. 若A(x 1,y 1)，B(x 2,y 2)是抛物线y 2=4x 上相异的两点，且在x 轴同侧，点C(2,0).若直线AC ，BC的斜率互为相反数，则y 1y 2=( )A. 2B. 4C. 6D. 8二、单空题（本大题共4小题，共20.0分）11. 设函数f(x)=x(e x +e −x )，则曲线y =f(x)在点(1,f(1))处切线的斜率为______ ． 12. 若x ，y 满足约束条件{x −y +2≥0y +2≥0x +y +2≤0，则√x 2+y 2的最小值为______．13. 给出下列四个结论：①若a ，b ∈R ，则a 2+ab +b 2≥0 ②“若tanα=1，则α=3π4”的逆命题；③“若x +y ≠2，则x ≠1或y ≠1”的否命题；④“若(x 0−a)2+(y 0−b)2=1，则点(x 0,y 0)在圆(x −a)2+(y −b)2=1内”的否命题，其中正确的是______ .(只填正确的结论的序号)14. 已知正项数列{a n }的前n 项和为S n ，满足2√S n −1=a n ，则a 2+1S2−1−a 4+1S 4−1+a 6+1S 6−1−a 8+1S 8−1+⋯+(−1)51a 100+1S 100−1=______．三、解答题（本大题共4小题，共48.0分）15. 已知{a n }为首项a 1=2的等差数列，{b n }为首项b 1=1的等比数列，且a 2+b 2=6，a 3+b 3=10． (1)分别求数列{a n }、{b n }的通项公式； (2)记c n =a n ⋅b n ，求数列{c n }的前n 项和S n ．16. 已知数列{a n }的前n 项和为S n 满足：2S n =3a n −2n −3． (1)求证：数列{a n +1}是等比数列，并且求a n ； (2)令c n =log 3(a 1+12)+log 3(a 2+12)+⋯…+log 3(a n +12)，令d n =1c n，求数列{d n }的前n 项和T n ．17. 已知函数f(x)=lnx −ax +bx (a,b ∈R)，且对任意x >0，都有f(x)+f(1x )=0． (Ⅰ)求a ，b 的关系式；(Ⅱ)若f(x)存在两个极值点x 1，x 2，且x 1<x 2，求a 的取值范围；(Ⅲ)在(Ⅱ)的条件下，证明f(a 22)>0，并指出函数y =f(x)零点的个数(要求说明理由)．18. 已知椭圆中心在原点，焦点在x 轴上，一个顶点为A(0,−1)。

甘肃省天水市秦安县高中2020┄2021学年高二上学期期末考试英语

注意：1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分150分；考试时间120分钟。

2、请将第Ⅰ卷所选答案用2B铅笔涂在答题卡上，第Ⅱ卷的答案填写在答题卡上。

第Ⅰ卷（选择题，共105分）第一部分听力（共两节，满分30分）第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What are the two speakers going to do tonight？A. Go to a play.B. Go to a party.C. Go to a film.2. Why does the man start smoking again？A. He thinks that smoking can get rid of anxiety.B. He made a profit from his business.C. Cigarettes become cheaper recently.3. What will the boy most probably be in the future？A. A businessman.B. A lawyer.C. A professor.4. What can we learn from the conversation？A. The man persuades the woman to give it up.B. The man thinks the problem is easy.C. The man tells the woman to stop working at it for the moment.5. What will probably happen to the woman？A. Miss her train.B. Catch her train.C. Cancel her train.第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

甘肃省天水市第一中学2020-2021学年高二上学期期末英语试题

甘肃省天水市第一中学2020-2021学年高二上学期期末英语试题学校:___________姓名：___________班级：___________考号：___________一、阅读选择Family fights are never pleasant. Whether you are dealing with a loud sister or a stubborn mom or dad, the situation can be bad. At least that’s what we have learned to expect.What if it could be different? What if family fights and conflicts could be turned into opportunities to become closer? What if problems could be solved with everyone walking away feeling more deeply cared for and loved?Family fighting is, on one level, about power. Someone is telling someone else what to do. In a short moment, emotions can be brought out and the fight is on. You can go down that old road or you can try something different.In any fight, you have a need to be listened to and understood. People raise their voices and shout at each other because they’re not being listened to. It’s totally unconscious. You want your mom or dad to listen and understand. But you always seem to forget the person you’re fighting with has the same need to be listened to. So if you can put aside your need for a few minutes, the situation will change quickly. Give the other person some time to express his or her feelings, and you will earn your turn to be listened to.And while you are listening, you have to listen for the right information. The best way to do this in emotional situations is to forget most of the words because many people can’t express what they are feeling with words alone, especially when they are upset.But if the situation starts to get out of hand, it would be wise to just calm down and leave the problem until later because many fights happen at the wrong time. The situation will die down quickly, usually in less than 30 seconds. You can either move on to problem solving or reach an agreement to work on it at a better time.This way, everyone will feel respected and listened to, even when there is conflict. Emotions will be understood and respected, and it will bring your family closer together. 1．From the first 3 paragraphs, we can conclude that ________.A．people had better avoid family fights.B．family members fight to control each otherC．family fights can be changed into something positiveD．when family members fight, it’s worse as they know each other’s weakness2．In th e author’s opinion, the key to dealing with family fights is to ________.A．satisfy the need to be listened to firstB．make sure that you’re the first to be listened toC．pay no attention to what others say in emotional situations.D．stop quarrelling when you feel you are giving orders3．When the situation gets out of control, it’s best to ________.A．wait for a suitable moment to speak B．let the other person express their feelings C．work on a written agreement first D．move on to problem solvingOn the day the tornado hit, there was no sign severe weather was on its way—the sky was blue and the sun had been out. My husband Jimmy and I were watching TV upstairs.No sooner had we got the coverage of the tornado than it was on top of us. It was the loudest thing I have ever heard. The bones of the house shook, and the power went out. We had three flights of steps to get through to get to the relative safety of the first floor.As we struggled to reach the last flight of steps, our front door blew out. Pieces of glass that looked like crushed ice flew everywhere. Suddenly, a three-foot-long tree branch flew over our heads, missing us by inches. Had we been one step up, it would have impaled us.By the time I reached the closet, Jimmy pushed me down to the closet floor, but he couldn’t get inside himself because of the wind. I grasped Jimmy’s arm and tried to bring Jimmy with it. My knees and head were full of glass, but in that moment, I felt no pain. If I had let go, Jimmy would have flown right out the back of the house and into the bay.“Hold on! Hold on!” he yelled. But there was nothing in this closet to hold on to.All of a sudden, Jimmy lifted off his feet like people in tornadoes do in the movies. I thought he was gone. And then everything stopped. He landed on his feet. In those first quiet moments, I couldn’t believe it was over. Jimmy said he’d go outside to check. “No,” I said. “Don’t leave me. Don’t leave me.”Our neighbor says the storm lasted four minutes. In that time, four of the twelve town houses in our unit were completely destroyed. Of the houses left standing, ours suffered the most damage. Amazingly, none of us were severely injured.4．Which of the following sentences is NOT the evidence to show the tornado is violent? A．It was the loudest thing I have ever heard.B．The bones of the house shook, and the power went out.C．Our neighbor says the storm lasted four minutes.D．Pieces of glass that looked like crushed ice flew everywhere.5．From the passage, we can infer that______.A．The couple had predicted the arrival of the tornado in advance.B．Jimmy flew right out the back of the house and into the bay during the tornado.C．The three-foot-tree flew over the couple’s head and injured them badly.D．The author still felt scared when the tornado was suddenly over.6．Why did the author feel “no pain” in paragraph4?A．She didn’t hurt badly enough to sense the pain.B．She was severely injured and failed to sense the pain.C．Her attention was fully focused on her husband.D．She had let her husband go away from her hand.7．Which of the following phrases best describes the couple’s experience in this tornado? A．A thrilling adventure B．A narrow escapeC．A risky attempt D．A serious accidentIn modern society there is a great deal of argument about competition. Some value it highly, believing that it is responsible for social progress and prosperity. Others say that competition is bad; that it sets one person against another; that it leads to unfriendly relationship between people.I have taught many children who held the belief that their self-worth relied on how well they performed at tennis and other skills. For them, playing well and winning are oftenlife-and-death affairs. In their single-minded pursuit of success, the development of many other human qualities is sadly forgotten.However, while some seem to be lost in the desire to succeed, others take an opposite attitude. In a culture which values only the winner and pays no attention to the ordinary players, they strongly blame competition. Among the most vocal are youngsters who have suffered under competitive pressures from their parents or society. Teaching these young people, I often observe in them a desire to fail. They seem to seek failure by not trying to win or achieve success. By not trying, they always have an excuse: “I may have lost, but it doesn't matter because I really didn't try.” What is not usually admitted by themselves is the belief that if theyhad really tried and lost, that would mean a lot. Such a loss would be a measure of their worth. Clearly, this belief is the same as that of the true competitors who try to prove themselves. Both are based on the mistaken belief that one's self-respect relies on how well one performs in comparison with others. Both are afraid of not being valued. Only as this basic and often troublesome fear begins to dissolve can we discover a new meaning in competition. 8．What does this passage mainly talk about?A．Competition helps to set up self-respect.B．Opinions about competition are different among people.C．Competition is harmful to personal quality development.D．Failures are necessary experiences in competition.9．The underlined phrase “the most vocal” in Paragraph 3 means ________.A．those who try their best to winB．those who value competition most highlyC．those who are against competition most stronglyD．those who rely on others most for success10．What is the similar belief of the true competitors and those with a “desire to fail”？A．One's worth lies in his performance compared with others'.B．One's success in competition needs great efforts.C．One's achievement is determined by his particular skills.D．One's success is based on how hard he has tried.11．Which point of view may the author agree to?A．Every effort should be paid back.B．Fear of failure should be removed in competition.C．Winning should be a life-and-death matter.D．Competition should be encouraged.Artificial intelligence can predict when patients with a heart disorder will die, according to scientists.The software learned to analyze blood tests and scans of beating hearts to spot signs that the organ was about to fail. The team, from the UK’s Medical Research Council, said the technology could save lives by finding patients that need more aggressive treatment. The results were published in the Journal of Radiology.According to the researchers, high blood pressure in the lungs damages part of the heart, and about a third of patients die within five years after being diagnosed. There are treatments: drugs, injections straight into the blood vessels, a lung transplant. But doctors need to have an idea of how long patients might have left, in order to pick the right treatment.The software was given scans of 256 patients’ hearts, and blood test results. When this data was combined with eight years of patient health records, the artificial intelligence predicted when patients would die.The software could look about five years into the future. It correctly predicted those who would still be alive after one year about 80% of the time. The figure for doctors is 60%.The team now want to test the software works in other patients in different hospitals before assessing whether it should be made widely available to doctors. The researchers also want to use the technology in other forms of heart failure, such as cardiomyopathy, to see who might need a pacemaker or other forms of treatment.Dr Mike Knapton, from the British Heart Foundation, said, “This exciting use of computer software in medical practice will help doctors in the future to make sure that patients are receiving the correct treatment before the condition deteriorates and leaves them needing a lung transplant. The next step is to test this technology in more hospitals with heart disease.”12．What can artificial intelligence do according to the passage?A．Predicting how long a person with heart disease can survive.B．Helping doctors diagnose people with heart disease.C．Obeying orders and reminding heart disease patients to take pills.D．Producing medicine without side effects for heart disease patients.13．What can we know about the software from the passage?A．It can make accurate long-term predictions.B．It has not yet been widely put into use.C．It can prevent high blood pressure in the lungs damaging part of the heart.D．It can help doctors make sure that patients are receiving the correct treatment.14．The underlined word “deteriorates” in the last paragraph probably means “________.”A．continues B．worsensC．exists D．improves15．The author’s purpose of writing the text is most likely to _________.A．advertise B．persuadeC．inform D．entertain二、七选五Questions to ask yourself before making a big decisionLife is packed with decisions, big and small. If you feel a big decision is appearing in your life, don’t hide! Ask yourself these questions to get clear on what’s the right choice for you.How committed am I to this change?Rate your level of commitment on a scale out of 10. 16．Is your level of commitment higher than a 7? That’s great data for your decision!Is this decision in line with my long-term goal?17．Write down your goals. Then think about how this decision plays into thatlonger-term plan.18．This is one of my favorite questions! If something is stirring(搅动) within you --- a creative idea, a calling to move somewhere new, a desire to end a relationship --- what are you giving up when you don’t do it? What might you be missing out on in your life if you do nothing?Is now the right time?Bear in mind: 19．But there are few real reasons we ever need to delay making a big one when it presents itself. Remember, life is always uncertain and time waits for no one.Making a big decision doesn’t have to be so difficult. There are no right or wrong answers, or right or wrong ways to live your life. 20．Your inner wisdom has the answers. So get busy asking the person who knows best --- you.A．What is the risk of not doing it?B．How long have I been thinking about his?C．Not all decisions need to be made immediately.D．Think about the amount of work, effort and time you’d have to put in.E.We always want to know what we need to do next.F.You don’t have to ask other people what they think.G.Ask yourself: What do I want five even ten years from now?三、完形填空It’s been a long time since I wrote a creative essay. Recently, with lots of time and lack of inspiration, I accepted a 21 to teach creative nonfiction. 22 I couldn’t get myself to write my own stories. I could require that my students tell theirs.“You’re going to be 23 a journal in this class.” I said. “And I want you to tell your stories like they matter.”“Why do they matter?” a boy named Michael asked. “I mean, who 24 about our stories?”No one said a wont. Perhaps they were just tired from their 25 lives. Many worked full-time while in school full-time. Most might not have the faintest 26 that their stories did matter. They didn’t even know that their stories were stories — as beautiful and hard — as their own lives.27 , I looked at Michael. “They matter because they do.” I said. “Because you’re here and you can tell them. Stories allow us to make 28 of what we’re 29 . When you 30 your experience into a story, it becomes yours and not just something that 31 to you.”Michael didn’t look 32 , but he didn’t challenge me either.Later, Michael wrote about how he grew up in one of the worst neighborhoods in Boston and how his high school teacher, who saw his 33 , helped him fill out a college application.I 34 Michael to read his essay out loud. After he finished, the class went so 35 that we could hear the sound of each other’s breath. I looked at Michael and saw a softening and 36 in his eyes.After a moment, I said, “That’s 37 you tell your stories.” That night, I picked up my journal from where it 38 , dusty and 39 . For the first time in months. I had 40 to write.21．A．business B．view C．reward D．position 22．A．Although B．As C．Unless D．Before 23．A．publishing B．keeping C．updating D．reading 24．A．worries B．talks C．reads D．cares 25．A．beautiful B．secret C．busy D．simple 26．A．dream B．hobby C．picture D．idea 27．A．Happily B．Angrily C．Firmly D．Sadly28．A．meaning B．notice C．fun D．use 29．A．set about B．gone through C．looked for D．taken on 30．A．shape B．take C．break D．treat 31．A．came B．fell C．worked D．happened 32．A．moved B．convinced C．confused D．embarrassed 33．A．poverty B．fortune C．potential D．sorrow 34．A．asked B．helped C．forced D．allowed 35．A．still B．concerned C．disappointed D．excited 36．A．truth B．doubt C．faith D．weakness 37．A．how B．when C．because D．why 38．A．started B．lay C．went D．hid 39．A．new B．packed C．untouched D．torn 40．A．time B．inspiration C．strength D．right四、用单词的适当形式完成句子课文填空This means that after a while your body becomes 41．to having nicotine in it. So when the drug leaves your body, you get withdrawal symptoms. I remember feeling bad-tempered and sometimes even in pain. Secondly, you become 42．through habit. As you know, if you do the same thing over and over again, you begin to do it 43．.There is no doubt that the earth is becoming warmer and that it is human activity 44．has caused this global warming rather than a random but natural 45．. All scientists 46．to the view t hat the increase in the earth’s temperature is due to the burning of fossil fuels like coal, natural gas and oil to produce energy.Having experience quite a few earthquakes in Hawaii already, I didn’t take much notice. I was about to go back to sleep 47．suddenly my bedroom became as bright as day. I ran out of the house into back garden where I could see Mount Kilauea in the 48．. There had been an 49．from the side of the mountain and red hot lava was 50．hundreds of meters.五、用单词的适当形式完成短文阅读下面材料，在空白处填入1个适当的单词或括号内单词的正确形式。

数学-高二-甘肃省天水市一中2020至2021高二上学期期末考试数学理科试题

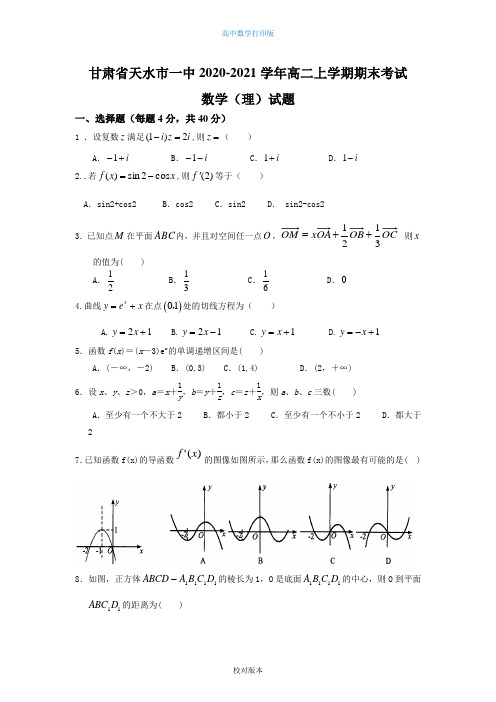
甘肃省天水市一中2020-2021学年高二上学期期末考试数学（理）试题一、选择题（每题4分，共40分）1 ．设复数z 满足(1)2i z i -=,则=z （）A ．i +-1B ．i --1C ．i +1D ．i -12..若x x f cos 2sin )(-=,则)2(f '等于（）A ．sin2+cos2B ．cos2C ．sin2D ． sin2-cos23．已知点M 在平面ABC 内，并且对空间任一点O ，OC OB OA x OM 3121++= 则x 的值为( )A ．21B ．31C ．61 D ．0 4.曲线x y e x =+在点()01，处的切线方程为（）A.21y x =+B.21y x =-C.1y x =+D.1y x =-+ 5．函数f (x )＝(x －3)e x 的单调递增区间是( )A ．(－∞，－2)B ．(0,3)C ．(1,4)D ．(2，＋∞)6．设x 、y 、z ＞0，a ＝x ＋1y ，b ＝y ＋1z ，c ＝z ＋1x，则a 、b 、c 三数( ) A ．至少有一个不大于2 B ．都小于2 C ．至少有一个不小于2 D ．都大于27．已知函数f(x)的导函数)('x f 的图像如图所示，那么函数f(x)的图像最有可能的是( )8．如图，正方体1111D C B A ABCD -的棱长为1，O 是底面1111D C B A 的中心，则O 到平面11D ABC 的距离为( )A ．21B ．42 C ．22 D ．23 9．由直线y ＝2x 及曲线y ＝3－x 2围成的封闭图形的面积为( )A ．2 3B ．9－2 3 C.353 D.32310．已知函数f (x )＝x 3＋x ，对任意的m ∈[－2,2]，f (mx －2)＋f (x )<0恒成立，则x 的取值范围为（） A .(32,＋∞) B.(-∞,－2) C. ⎝ ⎛⎭⎪⎫－2，23 D.(-∞,－2)∪ (32,＋∞) 二．填空题（每题4分，共16分）11．22(1cos )x dx ππ-+⎰＝________. 12．已知直线m,n 与平面α,β,给出下列三个命题:①若m∥α,n∥α,则m∥n;②若m∥α,n⊥α,则n⊥m;③若m⊥α,m∥β,则α⊥β.其中真命题的个数是______个13．f (x )＝2x 4－3x 2＋1在⎣⎢⎡⎦⎥⎤12，2上的最大值、最小值分别是 14．观察（1）000000tan10tan 20tan 20tan 60tan 60tan101;++=（2）000000tan5tan10tan10tan 75tan 75tan51++=由以上两式成立，推广到一般结论，写出你的推论是。

2020-2021学年甘肃省天水一中高二(上)期末数学试卷(文科)

2020-2021学年甘肃省天水一中高二（上）期末数学试卷（文科）一、单选题1．等差数列{a n}中，a7+a9＝16，a4＝1，则a12＝（）A．15B．30C．31D．642．设x∈R，则“x2﹣1＞0”是“x＞2”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3．已知椭圆的左、右焦点为F1，F2，P是椭圆上的点，且|PF1|＝2，则|PF2|＝（）A．1B．2C．3D．44．已知正实数a，b满足3a+2b＝1，则的最小值为（）A．32B．34C．36D．385．双曲线＝1的渐近线方程为（）A．y＝±x B．y＝±2x C．y＝±x D．y＝±x 6．已知双曲线C：﹣＝1的离心率e＝，且其右焦点为F2（5，0），则双曲线C的方程为（）A．﹣＝1B．﹣＝1C．﹣＝1D．﹣＝17．已知数列{a n}中，a1＝1，a n+1＝2a n+3，则a10＝（）A．2045B．1021C．1027D．20518．已知抛物线C：y2＝x的焦点为F，A（x0，y0）是C上一点，若|AF|＝x0，则x0等于（）A．1B．2C．4D．89．函数f（x）＝e x sin x在区间[﹣π，π]的图象大致是（）A．B．C．D．10．过抛物线y2＝2px（p＞0）的焦点F作直线与抛物线在第一象限交于点A，与准线在第三象限交于点B，垂足为H．若tan∠AFH＝2，则＝（）A．B．C．D．2二、填空题11．已知函数f（x）＝lnx+x2，则曲线y＝f（x）在点（1，f（1））处的切线方程为．12．已知实数x，y满足，则z＝x﹣2y的最大值为．13．若命题“∀x∈R，x2﹣2x+m2﹣1＞0”为真命题，则实数m的取值范围为．14．数列{a n}满足，，则a15＝．三、解答题15．已知等比数列{a n}中，a1＝1，且2a2是a3和4a1的等差中项．（1）求数列{a n}的通项公式；（2）若数列{b n}满足b n＝2n+a n2（n∈N*），求{b n}的前n项和S n．16．已知数列{a n}的前n项和为S n，且S n＝3n2﹣7n．（1）求数列{a n}的通项公式；（2）求数列的前n项和T n．17．已知函数f（x）＝x+，其中a∈R（1）当a＝﹣1时，求函数f（x）在区间[0；（2）若f（x）＜对任意x∈[﹣1，+∞）恒成立18．已知点A（0，﹣2），椭圆E：+＝1（a＞0，b＞0），F是椭圆E的右焦点，直线AF的斜率为（1）求E的方程；（2）设过点A的直线l与E相交于P，Q两点，当△OPQ的面积最大时2020-2021学年甘肃省天水一中高二（上）期末数学试卷（文科）参考答案与试题解析一、单选题1．等差数列{a n}中，a7+a9＝16，a4＝1，则a12＝（）A．15B．30C．31D．64【分析】由a7+a9＝16可得2a1+14d＝16，再由a4＝1＝a1+3d，解方程求得a1和公差d 的值，或根据等差中项的定义，a p+a q＝a m+a n，从而求得a12的值．【解答】解：方法一：设公差等于d，由a7+a9＝16可得2a1+14d＝16，即a1+5d＝8．再由a4＝3＝a1+3d，可得a6＝﹣，d＝．故a12＝a1+11d＝﹣+＝15，方法二：∵数列{a n}是等差数列，∴a p+a q＝a m+a n，即p+q＝m+n∵a7+a9＝a5+a12∴a12＝15故选：A．【点评】本题主要考查等差数列的等差数列的通项公式的应用，求出首项和公差d的值，是解题的关键，属于基础题．2．设x∈R，则“x2﹣1＞0”是“x＞2”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【分析】解出不等式：x2﹣1＞0，即可判断出结论．【解答】解：x2﹣1＞6，解得x＞1．∴x2﹣6＞0”是“x＞2”的必要不充分条件．故选：B．【点评】本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．3．已知椭圆的左、右焦点为F1，F2，P是椭圆上的点，且|PF1|＝2，则|PF2|＝（）A．1B．2C．3D．4【分析】利用椭圆方程求解a，通过椭圆的定义，转化求解即可．【解答】解：椭圆，可知a＝8，椭圆的左5，F2，P是椭圆上的点，且|PF1|＝2，由椭圆定义可得：|PF2|＝2a﹣|PF3|＝6﹣2＝7．故选：D．【点评】本题考查椭圆的简单性质以及椭圆定义的应用，是基本知识的考查．4．已知正实数a，b满足3a+2b＝1，则的最小值为（）A．32B．34C．36D．38【分析】利用“乘1法”与基本不等式的性质即可得出．【解答】解：正实数a，b满足3a+2b＝7，则＝（2a+2b）（＝32，当且仅当且3a+4b＝1，a＝，则的最小值为32．故选：A．【点评】本题主要考查了“乘1法”与基本不等式的性质，属于基础题．5．双曲线＝1的渐近线方程为（）A．y＝±x B．y＝±2x C．y＝±x D．y＝±x【分析】由双曲线的渐近线方程为y＝±x，即可得到所求双曲线的渐近线方程．【解答】解：由双曲线＝1（a x，可得双曲线＝5的渐近线方程为y＝±2x．故选：B．【点评】本题考查双曲线的渐近线方程，注意运用双曲线的方程和渐近线方程的关系，考查运算能力，属于基础题．6．已知双曲线C：﹣＝1的离心率e＝，且其右焦点为F2（5，0），则双曲线C的方程为（）A．﹣＝1B．﹣＝1C．﹣＝1D．﹣＝1【分析】利用已知条件，列出方程，求出双曲线的几何量，即可得到双曲线方程．【解答】解：双曲线C：﹣＝1的离心率e＝2（5，0），可得：，c＝5，b＝，所求双曲线方程为：﹣＝6．故选：C．【点评】本题考查双曲线方程的求法，双曲线的简单性质的应用，考查计算能力．7．已知数列{a n}中，a1＝1，a n+1＝2a n+3，则a10＝（）A．2045B．1021C．1027D．2051【分析】根据题意，分析可得（a n+1+3）＝2（a n+3），分析可得列{a n+3}是以a1+3＝4为首项，公比为2的等比数列，由此求出a10+3的值，变形可得答案．【解答】解：根据题意，数列{a n}中，a1＝1，a n+6＝2a n+3，变形可得（a n+7+3）＝2（a n+6），又由a1＝1，则a6+3＝4，则数列{a n+4}是以a1+3＝3为首项，公比为2的等比数列，则a10+3＝5×29＝2048，则a10＝2045，故选：A．【点评】本题考查数列的递推公式，涉及等比数列的定义，属于基础题．8．已知抛物线C：y2＝x的焦点为F，A（x0，y0）是C上一点，若|AF|＝x0，则x0等于（）A．1B．2C．4D．8【分析】利用抛物线的定义、焦点弦长公式即可得出．【解答】解：抛物线C：y2＝x的焦点为F（，0）∵A（x0，y5）是C上一点，|AF|＝x6，∴x5＝x0+，解得x0＝1．故选：A．【点评】本题考查了抛物线的定义、焦点弦长公式，属于基础题．9．函数f（x）＝e x sin x在区间[﹣π，π]的图象大致是（）A．B．C．D．【分析】先根据函数值，排除AB，再根据函数的单调性排除C，得答案．【解答】解：当x∈（﹣π，0）时，e x＞0，则f（x）＜7，∵f（x）＝e x sin x，当x∈（0，∴f′（x）＝e x（sin x+cos x）＝e x sin（x+），令f′（x）＝0，解得x＝，当0＜x＜时，f′（x）＞0，当＜x＜π时，函数单调递减，在x＝取最大值，故选项D符合，故选：D．【点评】本题考查了函数的图象的识别，关键利用导数判断函数的单调性，属于中档题．10．过抛物线y2＝2px（p＞0）的焦点F作直线与抛物线在第一象限交于点A，与准线在第三象限交于点B，垂足为H．若tan∠AFH＝2，则＝（）A．B．C．D．2【分析】由题意如图：再由抛物线的性质可得|AF|＝|AH|，在三角形中求出|AF|，|BF|的表达式，可得的值．【解答】解：由题意如图所示：设准线与x轴的交点为M，过点F作FC⊥AH交于C，由抛物线的定义可知|AF|＝|AH|，所以∠AHF＝∠AFH＝α，∠F AH＝π﹣2α＝∠OFB＝，|AF|＝＝＝，所以＝＝﹣＝＝，故选：C．【点评】本题考查抛物线的性质及平行线的性质，属于中档题．二、填空题11．已知函数f（x）＝lnx+x2，则曲线y＝f（x）在点（1，f（1））处的切线方程为3x﹣y﹣2＝0．【分析】先对函数求导，然后将x＝1代入导数求出斜率，再将x＝1代入函数求出切点纵坐标，最后套用点斜式写出方程．【解答】解：易知f（1）＝1，故切点为（1，，故f′（1）＝3，所以切线方程为y﹣5＝3（x﹣1），即7x﹣y﹣2＝0即为所求．故答案为：2x﹣y﹣2＝0．【点评】本题考查了利用导数求切线方程的基本步骤，注意计算需准确．12．已知实数x，y满足，则z＝x﹣2y的最大值为4．【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．【解答】解：由约束条件作出可行域如图，联立，解得A（2，化目标函数z＝x﹣2y为y＝，由图可知过A时，直线在y轴上的截距最小，z有最大值为4．故答案为：4．【点评】本题考查简单的线性规划，考查数形结合的解题思想，是中档题．13．若命题“∀x∈R，x2﹣2x+m2﹣1＞0”为真命题，则实数m的取值范围为（﹣∞，﹣）∪（，+∞）．【分析】利用判别式，即可求出实数m的取值范围．【解答】解：命题“∀x∈R，x2﹣2x+m3﹣1＞0”是真命题，得△＝7﹣4（m2﹣5）＜0，即m＜﹣．即所求m的取值范围是（﹣∞，﹣）∪（．故答案为：（﹣∞，﹣）∪（．【点评】本题考查的知识点是命题的真假判断与应用，转化为判别式和0之间的关系是解题的关键．14．数列{a n}满足，，则a15＝﹣1．【分析】求出数列的前几项，得到数列是周期数列，然后求解即可．【解答】解：由题意得，∴数列{a n}的周期为3，∴a15＝a5＝﹣1．故答案为：﹣1．【点评】本题考查数列的递推关系式的应用，判断数列是周期数列是解题的关键，属于基础题．三、解答题15．已知等比数列{a n}中，a1＝1，且2a2是a3和4a1的等差中项．（1）求数列{a n}的通项公式；（2）若数列{b n}满足b n＝2n+a n2（n∈N*），求{b n}的前n项和S n．【分析】（1）设公比为q，由2a2是a3和4a1的等差中项，解得q，从而求出通项公式．（2）利用分组求和法，求解数列的和即可．【解答】解：（1）∵已知等比数列{a n}中，a1＝1，设公比为q7是a3和4a5的等差中项，则4a2＝a2+4a1，可得7q＝q2+4．解得q＝2．∴a n＝a1q n﹣1＝7n﹣1，（2）b n＝2n+a n5＝2n+4n﹣7，S n＝b1+b2+b4+…+b n＝（2+46）+（4+46）+（6+46）+…+（2n+4n﹣7）＝（2+4+5+…+2n）+（48+41+62+…+4n﹣2）＝+＝n2+n+．【点评】本题主要考查等差数列的定义和性质，等比数列的通项公式，数列求和的方法的应用，属于中档题．16．已知数列{a n}的前n项和为S n，且S n＝3n2﹣7n．（1）求数列{a n}的通项公式；（2）求数列的前n项和T n．【分析】（1）先由a n＝S n﹣S n﹣1求得a n（n≥2），再求得a1，即可求得a n；（2）先由（1）求得，再利用裂项相消法求得其前n项和T n即可．【解答】解：（1）∵S n＝3n2﹣8n，∴当n≥2时，a n＝S n﹣S n﹣1＝4n2﹣7n﹣5（n﹣1）2+6（n﹣1）＝6n﹣10，又当n＝7时，a1＝S1＝5﹣7＝﹣4也适合上式，∴a n＝6n﹣10；（2）由（1）可得：＝＝＝（﹣），∴T n＝（﹣+﹣+…+﹣（﹣﹣．【点评】本题主要考查数列通项公式的求法及裂项相消法在数列求和中的应用，属于中档题．17．已知函数f（x）＝x+，其中a∈R（1）当a＝﹣1时，求函数f（x）在区间[0；（2）若f（x）＜对任意x∈[﹣1，+∞）恒成立【分析】（1）代入a的值，求出函数的导数，根据函数的单调性确定函数f（x）的零点个数即可；（2）问题转化为a＜﹣xe x恒成立，令g（x）＝﹣xe x，x∈[﹣1，+∞），根据函数的单调性求出a的范围即可．【解答】解：（1）a＝﹣1时，f（x）＝x﹣＞0，故f（x）在[0，+∞）递增，f（1）＝7﹣，故∃x0∈（8，1）0）＝3，故函数f（x）在区间[0，+∞）上的零点个数是1个；（2）若f（x）＜对任意x∈[﹣1，即a＜﹣xe x恒成立，x∈[﹣1，令g（x）＝﹣xe x，x∈[﹣1，+∞）x（e x﹣x﹣1），令h（x）＝e x﹣x﹣5，则h′（x）＝e x﹣1，令h′（x）＞0，解得x＞2，解得x＜0，故h（x）在[﹣1，3）递减，+∞）递增，故h（0）＝0，h（x）≥0，g（x）在[﹣3，故g（x）min＝g（﹣1）＝+，故a＜+，即a的取值范围是（﹣∞，+）．【点评】本题考查了函数的单调性，最值，零点问题，导数的应用以及函数恒成立问题，考查转化思想，属中档题．18．已知点A（0，﹣2），椭圆E：+＝1（a＞0，b＞0），F是椭圆E的右焦点，直线AF的斜率为（1）求E的方程；（2）设过点A的直线l与E相交于P，Q两点，当△OPQ的面积最大时【分析】（1）设F（c，0），由已知得，求得c，再由离心率求得a，结合隐含条件求得b，则椭圆方程可求；（2）由题意可知，当l⊥x轴时，不合题意，设l：y＝kx﹣2，联立直线方程与椭圆方程，求出P、Q的横坐标，代入弦长公式求得|PQ|，再由点到直线的距离公式求得O到PQ的距离，代入三角形面积公式，换元后利用基本不等式求最值，同时求得当△OPQ的面积最大时直线l的方程．【解答】解：（1）设F（c，0），得，又，∴a＝6，b2＝a2﹣c3＝1，故E的方程为：；（2）当l⊥x轴时，不合题意，故设l：y＝kx﹣8，p（x1，y1），Q（x3，y2），联立，得（1+4k4）x2﹣16kx+12＝0．当△＝16（5k2﹣3）＞4，即时，，．从而．又点O到直线PQ的距离．∴△OPQ的面积为，设，则，当且仅当．∴，即时等号成立，∴当△OPQ的面积最大时，l的方程为或．【点评】本题考查椭圆的简单性质，考查直线与椭圆位置关系的应用，训练了利用换元法及基本不等式求最值，属中档题．。

甘肃省天水一中2020-2021学年高二上学期期末考试试卷文生物解析版

1.如图是人体局部内环境示意图,以下关于A液、B液和Ｃ液三者之间联系表达正确的一项是( )A. B.C. Ｄ.【答案】C【解析】试题分析：A液是血浆，B液是淋巴，C液是组织液，组织液和血浆之间是双向的交换关系，组织液中的液体只能单向的渗透进入淋巴，淋巴内的液体只能回流到血浆，所以Ｃ正确。

考点：本题考查人体的内环境与稳态的相关知识,意在考查考生理解所学知识的要点,把握知识间的内在联系的能力.2．下列各项能看作进入人体内环境的是( ）A. 氧气进入肝细胞B. 葡萄糖进入血浆C. 牛奶进入胃D. 丙酮酸进入线粒体【答案】B【解析】【分析】体液是由细胞内液和细胞外液组成,细胞内液是指细胞内的液体,而细胞外液即细胞的生存环境，它包括血浆、组织液、淋巴等,也称为内环境，内环境是细胞与外界环境进行物质交换的媒介.【详解】氧气进入肝细胞是进入细胞内液，细胞内液不是内环境,A错误;葡萄糖进入血浆，血浆属于内环境,Ｂ正确；胃通过食道与口腔与外界相通,牛奶进入胃中不是进入内环境，C错误；线粒体属于细胞内的一种细胞器，丙酮酸进入线粒体不是进入内环境,D错误。

【点睛】本题考查内环境和稳态的知识，考生识记内环境的概念，明确内环境的组成是解题的关键．３．下列有关正常人体内环境稳态的叙述,正确的是( )Ａ. 血浆的pH值在7．3５～7.４5之间B. 垂体分泌甲状腺激素受下丘脑调控C. 在血糖调节中胰高血糖素是唯一降低血糖的激素D. 成年时甲状腺激素分泌过多会使神经系统兴奋性降低【答案】A【解析】【分析】内环境稳态是指正常机体通过调节作用,使各个器官、系统协调活动，共同维持内环境的相对稳定状态。

稳态的实质是健康人的内环境的每一种成分和理化性质都处于动态平衡之中.【详解】正常人血液中的pH通常在７.３5～７.4５之间，A正确；垂体分泌的促甲状腺激素受下丘脑调控，B错误;在血糖调节中胰岛素是唯一降低血糖的激素，Ｃ错误;成年时甲状腺激素分泌过多会使神经系统兴奋性升高,D错误.【点睛】本题考查内环境的组成、内环境的稳态、内环境的理化性质,要求考生识记内环境的组成，明确抗体主要分布在内环境中；识记内环境稳态的概念，明确内环境能维持相对稳定的状态；掌握内环境的理化性质及人体ｐＨ值调节过程．4．连续奋战在抗洪救灾第一线的战士，内环境依然能保持稳态，其调节机制是A. 神经调节Ｂ．体液调节C. 免疫调节D. 神经－体液－免疫调节【答案】D【解析】试题分析：现代生物学认为内环境稳态的调节机制神经—体液-免疫三维调节机制,故D正确,A，，B,C均说的不全面。

2020-2021学年甘肃省天水一中高二数学上学期期末考试数学试题理含解析

9.函数在区间的图象大致是（）
A. B. C. D.
〖答案〗D
〖解析〗
〖分析〗
根据函数值的符号可排除，由函数的极值点可排除，从而得到正确结果.
〖详解〗因为当时，，所以，
图象落在第三象限，所以排除，
因为，
分析其单调性，可知其极大值点应为，在的右侧，故排除C，
故选：D.
〖点睛〗方法点睛：该题考查函数图象的识别，通常采用排除法来进行判断；排除的依据通常为：（1）函数的定义域、奇偶性；
〖详解〗过点作交BC于Q，过点M作交BC于P，则点P为边BC靠近点B的四等分点且，为异面直线与的所成角
在正三棱柱中，，、分别是和的中点，则 , , , ，则
在三角形AMP中，
故选：D
〖点睛〗本题考查通过平移直线求空间中异面直线所成角的余弦值，属于中档题.
6.已知双曲线C：的离心率e＝，且其右焦点为F2(5，0)，则双曲线C的方程为（）
A. B.
C. D.
〖答案〗C
〖解析〗
〖分析〗
根据焦点坐标，可求得c的值，根据离心率，可求得a的值，根据b2＝c2－a2，可求得b的值，即可求得答案.
〖详解〗根据右焦点为F2(5，0)，可得c＝5，又离心率为，
所以a＝4，所以b2＝c2－a2＝9，
所以双曲线方程为，
故选：C.
7.已知抛物线的焦点为F，是C上一点，，则 =（）
甘肃省天水一中2020-2021学年高二数学上学期期末考试试题理（含解析）
一、选择题（共10小题）.
1.已知等差数列中，，，则等于（）
A.15B.30C.31D.64
〖答案〗A

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020—2021学年第一学期期末考试试卷（重点班）高二数学【必修3】【必修4】一、选择题（本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的） 1．下列命题中正确的是（） A ．OA OB AB -= B ．0AB BA -= C ． 00AB ⋅=D ．AB BC DC AD +-=2．角α的终边上有一点()(),0P a a a ≠，则sin α的值是（）A ．2B ．2-C ．1D ．2或2- 3．如图所示的程序框图，已知13a =，输出的结果为7，则2a 的值是（）A ．9B ．10C ．11D ．124．已知1sin 123πα⎛⎫-= ⎪⎝⎭，则5cos 12πα⎛⎫+ ⎪⎝⎭的值等于（）A ．13B ．3C ．13-D ．3-5．根据下面给出的2009年至2018年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（）A ．逐年比较，2018年减少二氧化硫排放量的效果最显著B ．2012年我国治理二氧化硫排放显现成效C ．2011年以来我国二氧化硫年排放量呈减少趋势D ．2011年以来我国二氧化硫年排放量与年份正相关 6．已知()7,1A ，()1,4B ，直线12y ax =与线段AB 交于点C ，且2AC CB =，则实数a 等于（） A ．2B ．1C ．45 D ．537．函数sin 23y x π⎛⎫=+⎪⎝⎭的图象（） A ．关于原点对称B ．关于点,06π⎛⎫-⎪⎝⎭对称 C ．关于y 轴对称 D ．关于直线6x π=对称8．如图，在正方形围栏内均匀撒米粒，一只小鸡在其中随意啄食，此刻小鸡正在正方形的内切圆中的概率是（）A ．14B ．4π C ．13D ．3π 9．已知2tan23θ=，则1cos sin 1cos sin θθθθ-+++的值为（）A ．23B ．23-C ．32D ．32- 10．设0ω>，函数sin 23y x πω⎛⎫=++ ⎪⎝⎭的图象向右平移43π个单位后与原图象重合，则ω的最小值是（）A ．23B ．43C ．32D ．3 11．在平行四边形ABCD 中，AB a =，AC b =，若E 是DC 的中点，则AE =（） A ．12a b - B ．32a b - C ．12a b -+ D ．32a b -+ 12．在ABC △中，A ，B ，C 是其三个内角，设()24sin cos cos 242B f B B B π⎛⎫=-+ ⎪⎝⎭，当()2f B m -<恒成立时，实数m 的取值范围是（） A ．1m <B ．3m >-C ．3m <D ．1m >二、填空题（本大题共4小题，将答案填在题中的横线上） 13．已知向量()2,2a =，()8,6b =-，则cos ,a b =______．14．已知一扇形的弧所对的圆心角为54°，半径20r cm =，则扇形的周长为______cm ． 15．已知()2,1OA =-，()0,2OB =，且//AC OB ，BC AB ⊥，则点C 的坐标是______．16．如图，在直角坐标系内，射线OT 落在30°角的终边上，任作一条射线OA ，则射线OA 落在yOT ∠内的概率为______．三、解答题（本大题共6小题．解答应写出文字说明、证明过程或演算步骤）17．已知角α的终边过点43,55P ⎛⎫-⎪⎝⎭．（1）求sin α的值；（2）求式子()()()sin tan 2sin cos 3πααπαππα⎛⎫- ⎪-⎝⎭⋅+-的值． 18．已知OAB △中，点D 在线段OB 上，且2OD DB =，延长BA 到C ，使BA AC =．设OA a =，OB b =．（1）用a ，b 表示向量OC ，DC ；（2）若向量OC 与OA k DC +共线，求k 的值． 19．已知函数()2cos 23f x x π⎛⎫=-⎪⎝⎭．（1）若()1f x =，,64x ππ⎡⎤∈-⎢⎥⎣⎦，求x 的值；（2）求()f x 的单调递增区间．20．空气污染，又称为大气污染，是指由于人类活动或自然过程引起某些物质进入大气中，呈现出足够的浓度，达到足够的时间，并因此危害了人体的舒适、健康和福利或环境的现象．全世界也越来越关注环境保护问题．当空气污染指数（单位：3/g m μ）为0~50时，空气质量级别为一级，空气质量状况属于优；当空气污染指数为50~100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为100~150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150~200时，空气质量级别为四级，空气质量状况属于中度污染；当空气污染指数为200~300时，空气质量级别为五级，空气质量状况属于重度污染；当空气污染指数为300以上时，空气质量级别为六级，空气质量状况属于严重污染．2017年8月18日某省x 个监测点数据统计如下：（1）根据所给统计表和频率分布直方图中的信息求出x ，y 的值，并完成频率分布直方图；（2）在空气污染指数分别为50~100和150~200的监测点中，用分层抽样的方法抽取5个监测点，从中任意选取2个监测点，事件A “两个都为良”发生的概率是多少？21．已知()cos ,sin a αα=，()cos ,sin b ββ=，0βαπ<<<．（1）若a b -=a b ⊥；（2）设()0,1c =，若a b c +=，求α，β的值． 22．已知函数()sin 2f x x x =．（1）求()f x 的单调递增区间；（2）若关于x 的方程()f x m =在,42x ππ⎡⎤∈⎢⎥⎣⎦上有两个不相等的实数根，求m 的取值范围．高二数学试卷答案（重点班）一、选择题13．10-14．640π+15．()2,6-16．1617．[解]（1）∵1OP ==，∴点P 在单位圆上，由正弦函数定义得3sin 5α=-．（2）原式cos tan sin cos αααα=⋅-- sin 1sin cos cos αααα==⋅．由（1）知，P 在单位圆上， ∴由余弦函数定义得4cos 5α=，∴原式54=． 18．[解]（1）∵A 为BC 的中点，∴()12OA OB OC =+，可得22OC OA OB a b =-=-，而25233DC OC OD OC OB a b =-=-=- （2）由（1），得()5214OA k DC k a kb +=+-， ∵OC 与OA k DC +共线，设()OC OA k DC λ=+即()52213a b k a kb λλ-=++-，根据平面向量基本定理，得2 21513k k λλ=+⎧⎪⎨-=-⎪⎩，解之得，34k =． 19．[解]（1）由()1f x =得1cos 232x π⎛⎫-=⎪⎝⎭，即1cos 232x π⎛⎫-= ⎪⎝⎭，∴()2233x k k Z πππ-=±∈，即x k π=或()3x k k Z ππ=+∈．∵,64x ππ⎡⎤∈-⎢⎥⎣⎦． ∴0x =．（2）()2cos 22cos 233f x x x ππ⎛⎫⎛⎫=-=-⎪ ⎪⎝⎭⎝⎭，令()222k x k k Z πππ-≤-≤∈，得()36k x k k Z ππππ-≤≤+∈．所以()f x 的单调递增区间为(),36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦． 20．解1）∵150.00350x⨯=，∴100x =． ∵154010100y +++=，∴40350.00810050y ==⨯，350.00710050⨯，100.00210050⨯．频率分布直方图如图所示．（2）在空气污染指数为50~100和150~200的监测点中分别抽取4个和1个监测点，设空气污染指数为50~100的4个监测点分别记为a ，b ，c ，d ；空气污染指数为150~200的1个监测点记为E ，从中任取2个的基本事件分别为(),a b ，(),a c ，(),a d ，(),a E ，(),b c ，(),b d ，(),b E ，(),c d ，(),c E ，(),d E 共10种，其中事件A “两个都为良”包含的基本事件为(),a b ，(),a c ，(),a d ，(),b c ，(),b d ，(),c d 共6种，所以事件A “两个都为良”发生的概率是()63105P A ==． 21．[解]（1）证明：由题意得22a b -=，即()22222a b a a b b -⋅+=-=．又因为22221a b a b ====，所以222a b -⋅=，即0a b ⋅=，故a b ⊥．（2）因为()()cos cos sin sin 0,1a b αβαβ+==++，，所以cos cos 0,sin sin 1,αβαβ+=⎧⎨+=⎩①②由①得，()cos cos απβ=-，由0βπ<<，得0πβπ<-<．又0απ<<，故απβ=-．代入sin sin 1αβ==，得1sin sin 2αβ==，而αβ>，所以5=6πα，=6πβ． 22．[解]（1）()1sin 222sin 222sin 223f x x x x x x π⎛⎫⎛⎫===- ⎪ ⎪ ⎪⎝⎭⎝⎭，由222232k x k πππππ-≤-≤+，k Z ∈，得51212k x k ππππ-≤≤+，k Z ∈，即函数的单调递增区间为55,1212k k ππππ⎡⎤-+⎢⎥⎣⎦，k Z ∈．（2）因为,42x ππ⎡⎤∈⎢⎥⎣⎦，所以22,363x πππ⎡⎤-∈⎢⎥⎣⎦，设23X x π=-，则2,63X ππ⎡⎤∈⎢⎥⎣⎦， ()f x m =f 在,42x ππ⎡⎤∈⎢⎥⎣⎦上有两个不相等的实数根，即()2sin g X X m ==在2,63ππ⎡⎤⎢⎥⎣⎦上有两个不相等的实数根，由图象知222sin 233g ππ⎛⎫===⎪⎝⎭则要使()g X m =在2,63ππ⎡⎤⎢⎥⎣⎦上有两个不相等的实数根，2m ≤<，即实数m 的取值范围是)．。