数学测试题1综合
高一数学必修一综合测试题(含答案)

高一数学必修一综合测试题(含答案)一、选择题(每题5分,共50分)1、已知集合M={0,1,2},N={xx=2a,a∈M},则集合MN=A、{ }B、{0,1}C、{1,2}D、{0,2}答案:B解析:将M中的元素代入N中得到:N={2,4,8},与M 的交集为{0,1},故MN={0,1}。
2、若f(lgx)=x,则f(3)=()A、lg3B、3C、10D、310答案:C解析:将x=3代入f(lgx)=x中得到f(lg3)=3,又因为lg3=0.477,所以f(0.477)=3,即f(3)=10^0.477=3.03.3、函数f(x)=x−1x−2的定义域为()A、[1,2)∪(2,+∞)B、(1,+∞)C、[1,2)D、[1,+∞)答案:A解析:由于分母不能为0,所以x-2≠0,即x≠2.又因为对于x<1,分母小于分子,所以x-1<0,即x<1.所以定义域为[1,2)∪(2,+∞)。
4、设a=log13,b=23,则().A、a<b<cB、c<b<aC、c<a<bD、b<a<c答案:A解析:a=log13=log33-log32=1/2-log32,b=23=8,c=2^3=8,所以a<b=c。
5、若102x=25,则10−x等于()A、−15B、51C、150D、0.2答案:B解析:由102x=25可得x=log10(25)/log10(102)=1.3979,所以10^-x=1/10^1.3979=0.1995≈0.2.6、要使g(x)=3x+1+t的图象不经过第二象限,则t的取值范围为A.t≤−1B.t<−1C.t≤−3D.t≥−3答案:B解析:当x=0时,y=1+t,要使图像不经过第二象限,则1+t>0,即t>-1.又因为g(x)的斜率为正数,所以对于任意的x,g(x)的值都大于1+t,所以t< -1.7、函数y=2x,x≥1x,x<1的图像为()答案:见下图。
人教版四年级上册数学第一单元综合测试题(含答案)

第1单元综合测试一、填空题。
1.太平洋是世界第一大洋,面积约为一亿八千一百三十四万平方千米,南北最宽一万五千五百千米。
一亿八千一百三十四万写作________;一万五千五百写作________。
2.用4、8、5、2、0、0、0七个数字,按要求写出七位数。
(只写一个即可)(1)一个0也不读的数有________(2)只读一个0的数有________(3)只读两个0的数有________(4)三个0都读的数有________(5)最大的七位数是________,省略万位后面的尾数约________万,最小的七位数是________。
3.你能读出下面横线上的数吗?读作:________4.写出下面的数.(1)十五万写作:________(2)八千万八千写作:________5.根据题意填空:(1)一亿三千五百万三千五百,写作________(2)四亿零四万四千,写作________.6.填上>、=或<.(1)27000________27万(2)1500000________150万7.你能写出横线上的数吗?写作:________8.读出下面各数.(按题中数的顺序填写)409600 576006 283600200468 5070820 1637001402860 36000 4060600506070其中:(1)读一个0的有:________(2)读两个0的有:________(3)一个0都不读的有:________9.读出下面的数,然后省略万位后面的尾数求出近似数.507096000读作:________507096000≈________万10.九亿八千万,写作________,省略亿位后面的尾数约是________。
二、选择题。
1.八十六万写作( )A. 86000000B. 860000C. 86000D. 86000002.五万三千零二写作( )A. 53020B. 500302C. 50302D. 530023.3080070读出这个数,下面的哪种读法正确?( )A.三百零八万零零七十B. 三千零八万零七十B.C. 三百零八万七十 D. 三百零八万零七十4.下面各数中一个零也不读出来的数是( )A. 640700B. 604700C. 640070D. 6400075.把“3”写在万位上比把“3”写在百位上多( )A. 9700B. 29700C. 19700D. 279006.“782600 783400”,比较大小,在里应填的符号是()A. >B. <C. =D. ÷7.一个鸡蛋约重60克.照这样推算,100个这样的鸡蛋大约重6千克,10万个这样的鸡蛋大约重6吨,1亿个这样的鸡蛋大约重多少吨?在你认为合适的答案是()A. 60吨B. 600吨C. 6000吨8.个、十、百、千、万、这些都是()A. 数B. 数位C. 计数单位D. 位数三、应用题。
人教新课标四年级上册数学第一单元综合测试题(含答案)

人教版小学数学四年级上第一单元综合测试卷(含答案)一、单选题(共10题;共20分)1.我国的陆地国土面积约为960万平方千米,横线上的数是( )A. 是精确数B. 是近似数2.新华小学四年级同学向希望小学共捐图书1875册横线上的数是( )A. 是精确数B. 是近似数3.下面的键中,()是乘法运算键.A. ×B. +C. ﹣4.100个一百万是()A. 100万B. 1亿C. 1000万5.个位、万位、亿位是几个不同的()A. 数位B. 数级C. 计数单位6.三百二十亿零八十,写这个数时一共要写()个0。
A. 7B. 8C. 97.下面说法正确的是()A. 个位、十位、百位、千位…是计数单位B. 493600省略万后面的尾数约是49C. 604000是由6个十万和4个千组成的8.一个数用四舍五入法省略万后面的尾数约是45万,这个数最大的可能是()A. 454999B. 445999C. 4599999.1枚1元的硬币大约重6克.照这样计算,1000枚1元的硬币大约重6千克,100万枚1元的硬币大约重6吨,1亿枚1元的硬币大约重多少吨?合适的答案是()A. 6吨B. 60吨C. 600吨10.100张纸大约厚1厘米.照这样推算,10000张这样的纸大约厚1米,10亿张这样的纸大约厚多少米?在你认为合适的答案是()A. 100米B. 1000米C. 100000米二、填空题(共8题;共21分)11.写出下面各数.九百六十万________ 一百四十亿________12.我国香港特别行政区的总面积是十亿九千二百万平方米,写作________平方米,改写成用“万”作单位的数是________平方米,省略“亿”后面的尾数写作________平方米。
13.最大的八位数是________,比它大1的数是________。
14.把下面的数四舍五入到万位或亿位.960000≈________34999≈________15.一个数的百万位上是6,万位上是5,个位上是8,其余各位上都是0,这个数是________,省略万位后面的尾数约是________。
北师大版初中数学七上第一章综合测试试题试卷含答案1
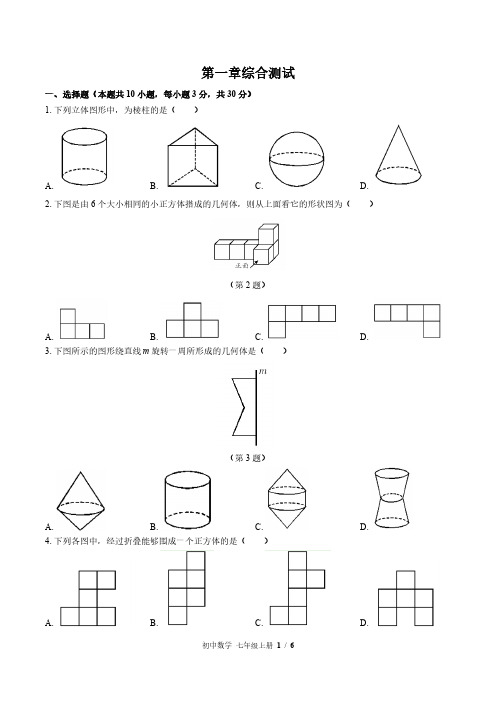
第一章综合测试一、选择题(本题共10小题,每小题3分,共30分)1.下列立体图形中,为棱柱的是()A.B.C.D.2.下图是由6个大小相同的小正方体搭成的几何体,则从上面看它的形状图为()(第2题)A.B.C.D.3.下图所示的图形绕直线m旋转一周所形成的几何体是()(第3题)A.B.C.D.4.下列各图中,经过折叠能够围成一个正方体的是()A.B.C.D.5.如图,用一个平面去截圆柱体,截面形状不可能是()(第5题)A.B.C.D.6.下图是一个长方体的表面展开图,六个面上分别标有数字1,2,3,4,5,6(数字都在表面),与标有数字6的面相对面上的数字是()A.3B.5C.2D.1(第6题)7.下图所示的正方体盒子的外表面上画有三条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是()(第7题)A.B.C.D.8.下图是由六个相同的小立方块搭成的几何体,则下列说法正确的是()(第8题)A.从正面看到的形状图面积最大B.从上面看到的形状图面积最大C.从左面看到的形状图面积最大D.从三个方向看到的形状图面积一样大9.一个几何体由一些小正方体摆成,从正面看与从左面看这个几何体得到的形状图如图所示,从上面看这个几何体得到的形状图不可能是()(第9题)A.B.C.D.10.下图是某一几何体从三个方向看的形状图,则组成这个几何体的小立方块有()(第10题)A.5个B.6个C.7个D.8个二、填空题(本题共8小题,每小题4分,共32分)11.七棱柱有________个面.12.笔尖在纸上快速滑动写出字母C,这说明了________.13.图是一个几何体的表面展开图,这个几何体是________.(第13题)14.下图是由4个大小相同的棱长为1 cm的小正方体搭成的几何体,则从左面看它的形状图的面积为cm.________2(第14题)+=________.15.下图是一个正方体的表面展开图,若正方体标注的相对面上的数字相同,则x y(第15题)16.下图是棱长为2 cm的正方体,过相邻三条棱挖取一个棱长为1 cm的小正方体,则剩下部分的表面积为cm.________2(第16题)17.下图是5个边长相等的小正方形拼成的一个平面图形,小丽手中还有一个同样的小正方形,她想将它与该图中的平面图形拼接在一起,从而可以构成一个正方体的表面展开图,则小丽共有________种拼接方法.(第17题)18.下图是由一些小立方块所搭的几何体从三个方向看得到的形状图,若在所搭的几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.三、解答题(本题共5小题,共58分)19.(本题10分)将如图所示的几何体与它的名称用线连接起来.(第19题)20.(本题10分)如图,将图形沿着虚线进行折叠.(1)写出所能折叠成的几何体的名称:________(2)在所折叠成的几何体中:①有多少条棱?哪些棱的长度相等?②有多少个面?它们分别是什么图形?哪些面的形状、大小完全相同?(第20题)21.(本题12分)如图,正方体被竖直截取了一部分.(1)这个正方体的截面形状是________;(2)被截去的那一部分的几何体的名称是________,求该几何体的体积.(友情提示:棱柱的体积=底面积 高)(第21题)22.(本题12分)如图是从正面和从上面看由若干个小立方块所搭成的几何体得到的形状图,这样搭建的几何体最少、最多各需要多少个小立方块?(第22题)23.(本题14分)在平整的地面上,有若干个完全相同的立方块堆成的一个几何体,如图所示.(1)请分别画出从三个方向看这个几何体得到的形状图.(2)如果在这个几何体露出地面的部分喷上黄色的漆,则在所有的小立方块中,有________个立方块只有一个面是黄色,有________个立方块只有两个面是黄色,有________个立方块只有三个面是黄色.(3)若现在你手头还有一些相同的立方块,如果保持从上面和从左面看到的形状图不变,最多可以再添加几个立方块?(第23题)附加题(15分,不计入总分)24.有一个小立方块,在它的各个面上分别标有数字1,2,3,4,5,6,建制、中原和永清三位同学从三个不同角度去观察这个小立方块,观察的结果如图①.(1)请你画出这个小立方块的三种表面展开图,并说明理由(要求把数字标注在表面展开图中).(2)聪明的建制用与图①大小相同的小立方块若干块搭成一个几何体,他从上面观察这个几何体,看到的形状图如图②,小正方形内的数字表示在该位置上小立方块的个数,请画出这个几何体从正面、左面看到的形状图.第一章综合测试答案一、 1.【答案】B 2.【答案】D 3.【答案】D 4.【答案】C 5.【答案】B 6.【答案】C 7.【答案】D 8.【答案】B 9.【答案】C 10.【答案】A 二、 11.【答案】9 12.【答案】点动成线 13.【答案】圆锥 14.【答案】2 15.【答案】18 16.【答案】24 17.【答案】4 18.【答案】22 三、19.【答案】如下图所示:20.【答案】(1)直六棱柱.(2)①该六棱柱有18条棱,底面棱的长度相等,侧面棱的长度相等;②该六棱柱有8个面,底面是形状、大小完全相同的六边形,侧面是形状、大小完全相同的长方形. 21.【答案】(1)长方形 (2)直三棱柱因为这个直三棱柱的底面是一个直角三角形,直角三角形的两条直角边长分别为()541cm -=(cm ),()532cm -=,所以这个直三棱柱的底面积为21221cm ⨯÷=(),所以这个直三棱柱的体积为3155cm ⨯=(). 22.【答案】搭这样的几何体最少需要54211++=(个)小立方块,最多需要96217++=(个)小立方块. 23.【答案】如图所示:(2)2 3 2(3)最多可以再添加7个小立方块.24.【答案】解:(1)由3个小立方块上的数字可知,与写有数字1的相邻面上的数字是2,3,4,6,所以数字1相对面上的数字为5;与写有数字3的相邻面上的数字是1,2,4,5,所以数字3相对面上的数字为6;故数字4相对面上的数字为2,画图如图1(画法不唯一).图1(2)从正面、左面看到的形状图如图2.图2。
高中数学选修一综合测试题重点易错题(带答案)

高中数学选修一综合测试题重点易错题单选题1、已知双曲线C:x2a2−y2b2=1(a>0,b>0)的左焦点为F,点F到双曲线C的一条渐近线的距离为12a,则双曲线C的渐近线方程为()A.y=±12x B.y=±2xC.y=±4x D.y=±14x 答案:A分析:首先根据题意得到d=√b2+a2=b=12a,从而得到ba=12,即可得到答案.由题知:设F(−c,0),一条渐近线方程为y=bax,即bx−ay=0.因为d=√b2+a2=b=12a,所以ba=12,故渐近线方程为y=±12x.故选:A2、已知正方体ABCD−A1B1C1D1的棱长为a,则平面AB1D1与平面BDC1的距离为()A.√2a B.√3a C.√23a D.√33a答案:D分析:建立空间直角坐标系,用空间向量求解由正方体的性质,AB1∥DC1,D1B1∥DB,AB1∩D1B1=B1,DC1∩DB=D,易得平面AB1D1∥平面BDC1,则两平面间的距离可转化为点B到平面AB1D1的距离.以D为坐标原点,DA,DC,DD1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,则A (a,0,0),B (a,a,0),A 1(a,0,a ),C (0,a,0),B 1(a,a,a ),D 1(0,0,a ) 所以CA 1⃑⃑⃑⃑⃑⃑⃑ =(a,−a,a ),BA ⃑⃑⃑⃑⃑ =(0,−a,0),AB 1⃑⃑⃑⃑⃑⃑⃑ =(0,a,a ),B 1D 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =(−a,−a,0).连接A 1C ,由CA 1⃑⃑⃑⃑⃑⃑⃑ ⋅AB 1⃑⃑⃑⃑⃑⃑⃑ =(a,−a,a )⋅(0,a,a )=0,CA 1⃑⃑⃑⃑⃑⃑⃑ ⋅B 1D 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =(a,−a,a )⋅(−a,−a,0)=0,且AB 1∩B 1D 1=B 1,可知A 1C ⊥平面AB 1D 1,得平面AB 1D 1的一个法向量为n ⃑ =(1,−1,1), 则两平面间的距离d =|BA ⃑⃑⃑⃑⃑ ⋅n⃑ |n ⃑ ||=√3=√33a . 故选:D3、已知两圆分别为圆C 1:x 2+y 2=49和圆C 2:x 2+y 2−6x −8y +9=0,这两圆的位置关系是( ) A .相离B .相交C .内切D .外切 答案:B分析:先求出两圆圆心和半径,再由两圆圆心之间的距离和两圆半径和及半径差比较大小即可求解. 由题意得,圆C 1圆心(0,0),半径为7;圆C 2:(x −3)2+(y −4)2=16,圆心(3,4),半径为4, 两圆心之间的距离为√32+42=5,因为7−4<5<7+4,故这两圆的位置关系是相交. 故选:B.4、已知直线斜率为k ,且−1≤k ≤√3,那么倾斜角α的取值范围是( ) A .[0,π3]∪[π2,3π4)B .[0,π3]∪[3π4,π)C.[0,π6]∪[π2,3π4)D.[0,π6]∪[3π4,π)答案:B分析:根据直线斜率的取值范围,以及斜率和倾斜角的对应关系,求得倾斜角α的取值范围. 解:直线l的斜率为k,且−1≤k≤√3,∴−1≤tanα≤√3,α∈[0,π).∴α∈[0,π3]∪[3π4,π).故选:B.5、过点P(√3,−2√3)且倾斜角为135∘的直线方程为()A.3x−y−4√3=0B.x−y−√3=0C.x+y−√3=0D.x+y+√3=0答案:D分析:由倾斜角为135∘求出直线的斜率,再利用点斜式可求出直线方程解:因为直线的倾斜角为135∘,所以直线的斜率为k=tan135°=−1,所以直线方程为y+2√3=−(x−√3),即x+y+√3=0,故选:D6、如图,下列各正方体中,O为下底面的中心,M,N为顶点,P为所在棱的中点,则满足MN∥OP的是()A.B.C.D.答案:A分析:根据给定条件,建立空间直角坐标系,再对每一个选项逐一分析,利用空间位置关系的向量证明推理作答.在正方体中,对各选项建立相应的空间直角坐标系,令正方体棱长为2,点O (1,1,0), 对于A ,M (0,0,2),N (2,0,0),P (2,0,1),MN ⃑⃑⃑⃑⃑⃑⃑ =(2,0,-2),OP ⃑⃑⃑⃑⃑ =(1,-1,1),MN ⃑⃑⃑⃑⃑⃑⃑ ∥OP ⃑⃑⃑⃑⃑ =0,MN ∥OP ,A 是;对于B ,M (2,0,2),N (0,2,2),P (0,2,1),MN ⃑⃑⃑⃑⃑⃑⃑ =(-2,2,0),OP ⃑⃑⃑⃑⃑ =(-1,1,1),MN ⃑⃑⃑⃑⃑⃑⃑ ∥OP ⃑⃑⃑⃑⃑ =4≠0,MN 与OP 不垂直,B 不是;对于C ,M (0,2,2),N (0,0,0),P (2,1,2),MN →=(0,-2,-2),OP →=(1,0,2),MN ⃑⃑⃑⃑⃑⃑⃑ ∥OP ⃑⃑⃑⃑⃑ =-4≠0,MN 与OP 不垂直,C 不是;对于D ,M (2,2,2),N (0,2,0),P (0,0,1),MN⃑⃑⃑⃑⃑⃑⃑ =(-2,0,-2),OP ⃑⃑⃑⃑⃑ =(1,0,1),MN ⃑⃑⃑⃑⃑⃑⃑ ∥OP ⃑⃑⃑⃑⃑ =-4≠0,MN 与OP 不垂直,D 不是.故选:A7、已知直线l 经过点P(1,3),且l 与圆x 2+y 2=10相切,则l 的方程为( ) A .x +3y −10=0B .x −3y +8=0C .3x +y −6=0D .2x +3y −11=0 答案:A分析:直线l 经过点P(1,3),且l 与圆x 2+y 2=10相切可知k l =−1k op,再使用点斜式即可.直线l 经过点P(1,3),且l 与圆x 2+y 2=10相切,则k l =−1k op=−13−01−0=−13,故直线l 的方程为y −3=−13(x −1),即x +3y −10=0. 故选:A.8、已知边长为2的等边三角形ABC ,D 是平面ABC 内一点,且满足DB:DC =2:1,则三角形ABD 面积的最小值是( )A .43(√3−1)B .43(√3+1)C .4√33D .√33答案:A分析:建立直角坐标系,设D(x,y),写出A,B,C 的坐标,利用DB:DC =2:1列式得关于x,y 的等式,可得点D 的轨迹为以(53,0)为圆心,以43为半径的圆,写出直线AB 的方程,计算|AB |和点D 距离直线AB 的最小距离d −r ,代入三角形面积公式计算.以BC 的中点O 为原点,建立如图所示的直角坐标系,则A(0,√3),B (−1,0),C (1,0), 设D (x,y ),因为DB:DC =2:1,所以(x +1)2+y 2=4(x −1)2+4y 2,得(x −53)2+y 2=169,所以点D 的轨迹为以(53,0)为圆心,以43为半径的圆,当点D 距离直线AB 距离最大时,△ABD 面积最大,已知直线AB 的方程为:√3x −y +√3=0,|AB |=2,点D 距离直线AB 的最小距离为:d −r =|5√33+√3|2−43=4√33−43,所以△ABD 面积的最小值为S △ABD =12×2×(4√33−43)=43(√3−1).故选:A多选题9、对抛物线y =4x 2,下列描述正确的是( ) A .开口向上,准线方程为y =-116B .开口向上,焦点为(0,116) C .开口向右,焦点为(1,0) D .开口向右,准线方程为y =-1 答案:AB分析:根据抛物线方程写出焦点、准线方程,并判断开口方向即可. 由题设,抛物线可化为x 2=y4,∴开口向上,焦点为(0,116),准线方程为y =−116. 故选:AB10、已知直线l 1:x −y −1=0,动直线l 2:(k +1)x +ky +k =0 (k ∈R ),则下列结论正确的是( ) A .存在k ,使得l 2的倾斜角为90∘B .对任意的k ,l 1与l 2都有公共点C.对任意的k,l1与l2都不重合D.对任意的k,l1与l2都不垂直答案:ABD分析:当k=0时可判断A;直线l1与l2均过点(0,−1)可判断B;当k=−12时可判断C,由两直线垂直斜率乘积等于−1可判断D,进而可得正确选项.对于A:当k=0时,直线l2:x=0,此时直线l2的倾斜角为90∘,故选项A正确;对于B,直线l1与l2均过点(0,−1),所以对任意的k,l1与l2都有公共点,故选项B正确;对于C,当k=−12时,直线l2为12x−12y−12=0,即x−y−1=0与l1重合,故选项C错误;对于D,直线l1的斜率为1,若l2的斜率存在,则斜率为−k+1k≠−1,所以l1与l2不可能垂直,所以对任意的k,l1与l2都不垂直,故选项D不正确;故选:ABD.11、已知F为椭圆C:x24+y22=1的左焦点,直线l:y=kx(k≠0)与椭圆C交于A,B两点,AE⊥x轴,垂足为E,BE与椭圆C的另一个交点为P,则()A.1|AF|+4|BF|的最小值为2B.△ABE面积的最大值为√2C.直线BE的斜率为12k D.∠PAB为钝角答案:BC分析:A项,先由椭圆与过原点直线的对称性知,|AF|+|BF|=4,再利用1的代换利用基本不等式可得最小值94,A项错误;B项,由直线与椭圆方程联立,解得交点坐标,得出面积关于k的函数关系式,再求函数最值;C项,由对称性,可设A(x0,y0),则B(−x0,−y0),E(x0,0),则可得直线BE的斜率与k的关系;D项,先由A、B对称且与点P均在椭圆上,可得k PA⋅k PB=−b2a2=−12,又由C项可知k PB=k BE=12k,得k PA⋅k AB=−1,即∠PAB=90°,排除D项.对于A,设椭圆C的右焦点为F′,连接AF′,BF′,则四边形AF′BF为平行四边形,∴|AF|+|BF|=|AF|+|AF′|=2a=4,∴1|AF|+4|BF|=14(|AF|+|BF|)(1|AF|+4|BF|)=14(5+|BF||AF|+4|AF||BF|)≥94,当且仅当|BF|=2|AF|时等号成立,A 错误;对于B ,由{x 24+y 22=1y =kx 得x =√1+2k 2,∴|y A −y B |√1+2k 2,∴△ABE 的面积S =12|x A ||y A −y B |=4|k|1+2k 2=41|k|+2|k|≤√2,当且仅当k =±√22时等号成立,B 正确;对于C ,设A(x 0,y 0),则B(−x 0,−y 0),E(x 0,0), 故直线BE 的斜率k BE =0+y 0x 0+x 0=12⋅y 0x 0=12k ,C 正确;对于D ,设P(m,n),直线PA 的斜率额为k PA ,直线PB 的斜率为k PB , 则k PA ⋅k PB = n−y 0m−x 0⋅n+y 0m+x 0=n 2−y 02m 2−x 02,又点P 和点A 在椭圆C 上,∴m 24+n 22=1①,x 024+y 022=1②,①−②得n 2−y 02m 2−x 02=−12,易知k PB =k BE =12k ,则k PA ⋅12k =−12,得k PA =−1k ,∴k PA ⋅k AB =(−1k )⋅k =−1,∴∠PAB =90°,D 错误. 故选:BC.小提示:椭圆常用结论:已知椭圆x 2a 2+y 2b 2=1(a >b >0),AB 为椭圆经过原点的一条弦,P 是椭圆上异于A 、B 的任意一点,若k PA ,k PB 都存在,则k PA ⋅k PB =−b 2a 2. 填空题12、设a∈R,若直线l经过点A(a,2)、B(a+1,3),则直线l的斜率是___________.答案:1分析:利用直线的斜率公式求解.解:因为直线l经过点A(a,2)、B(a+1,3),=1,所以直线l的斜率是k=3−2a+1−a所以答案是:113、已知圆x2+y2+2x−4y−5=0与x2+y2+2x−1=0相交于A、B两点,则公共弦AB的长是___________.答案:2分析:两圆方程相减可得公共弦所在直线方程,利用垂径定理即可得解.解:由题意AB所在的直线方程为:(x2+y2+2x−4y−5)−(x2+y2+2x−1)=0,即y=−1,因为圆x2+y2+2x−1=0的圆心O(−1,0),半径为r=√2,所以,圆心O(−1,0)到直线y=−1的距离为1,所以|AB|=2√2−12=2.所以答案是:214、直线y=kx+2(k>0)被圆x2+y2=4截得的弦长为2√3,则直线的倾斜角为________.答案:60∘分析:由已知求得圆心到直线的距离,再由点到直线的距离公式列式求得k,然后利用斜率等于倾斜角的正切值求解.∵直线y=kx+2(k>0)被圆x2+y2=4截得的弦长为2√3,所以,圆心O(0,0)到直线kx−y+2=0的距离d=√22−(√3)2=1,=1,解得k=√3(k>0).即√k2+1设直线的倾斜角为θ(0∘≤θ<180∘),则tanθ=√3,则θ=60∘.因此,直线y=kx+2(k>0)的倾斜角为60∘.所以答案是:60∘.解答题15、设直线l 的方程为(a +1)x +y −3+a =0(a ∈R ). (1)若l 在两坐标轴上的截距相等,求a 的值; (2)若l 不经过第三象限,求a 的取值范围. 答案:(1)0或3 (2)[−1,3]分析:(1)通过讨论−3+a 是否为0,求出a 的值即可; (2)根据一次函数的性质判断a 的范围即可.(1)当直线l 过原点时,该直线l 在x 轴和y 轴上的截距为零, ∴a =3,方程即为4x +y =0; 若a ≠3,则3−a a+1=3−a ,即a +1=1,∴a =0,方程即为x +y −3=0, ∴a 的值为0或3.(2)若l 不经过第三象限,直线l 的方程化为y =−(a +1)x +3−a , 则{−(a +1)≤03−a ≥0 ,解得−1≤a ≤3,∴a 的取值范围是[−1,3].。
初一数学综合试题及答案

初一数学综合试题及答案一、选择题(每题3分,共30分)1. 下列各数中,最小的数是()A. -3B. 0C. 2D. 52. 计算下列式子的结果,正确的是()A. \( 3^2 = 6 \)B. \( (-2)^3 = -8 \)C. \( 2^3 = 8 \)D. \( (-3)^2 = -9 \)3. 如果 \( a \) 和 \( b \) 是两个非零数,且 \( a \div b = 3 \),那么\( a \) 和 \( b \) 的比值是()A. 1:3B. 3:1C. 1:1D. 3:44. 一个数的相反数是它本身,这个数是()A. 0B. 1C. -1D. 25. 一个角的补角是它的余角的两倍,这个角的度数是()A. 30°B. 45°C. 60°D. 90°6. 下列哪个选项是正确的不等式()A. \( 3x > 2x + 1 \)B. \( 2x - 1 < 2x \)C. \( 5x \leq 5 \)D. \( 4x = 4x + 1 \)7. 一个数的绝对值是5,这个数可能是()A. 5B. -5C. 5 或 -5D. 08. 下列哪个图形是轴对称图形()A. 等边三角形B. 圆C. 正方形D. 所有选项都是9. 一个数的平方是16,这个数是()A. 4B. -4C. 4 或 -4D. 010. 一个数的立方是-8,这个数是()A. 2B. -2C. 8D. -8二、填空题(每题4分,共20分)11. 计算 \( 2^4 \) 的结果是 _______。
12. 如果 \( x = 3 \),那么 \( 2x + 1 \) 的值是 _______。
13. 一个角的补角是 \( 180° - \) 这个角的度数,如果这个角是\( 60° \),那么它的补角是 _______。
14. 如果 \( a \) 和 \( b \) 是两个数,且 \( a + b = 10 \) 且 \( a - b = 2 \),那么 \( a \) 和 \( b \) 的值分别是 _______ 和 _______。
人教版四年级上册数学《第一单元综合测试题》含答案
人教版数学四年级上学期第一单元达标测试卷一、填空题。
1、五百零四万零九百是()位数,其中“5”、“4”、“9”分别在()位、()位和()位,这个数写作(),省略万后面的尾数是()。
2、一个九位数,最高位是5,百万位是8,个位是l,其余各位都是0,这个数写作( ),四舍五入到亿位约是( )。
3、三个千万,三个十万,三个千和八个一组成的数是(),约是()万。
4、比99999多1的数是(),比1000少1的数是()。
5、在5和3之间添( )个0,就成为五十亿零三。
6、最小的自然数是( ),与最小的六位数相邻的自然数是( )和( )。
7、把9999、10001、10000和10100按从小到大的顺序排列是:()<()<()<()。
8、比最大的四位数多1的数是(),比最小的五位数少1的数是(),它们的差是(),和是()。
二.判断。
(对的在括号里打“√”,错的打“×”)1.一个一万、一个一千和一个十组成的数是10000100010。
…………()2. 2001103 〉 20万。
………………………………………………()3.五千八百万零九十写作5800095。
…………………………()4.与“十万”相邻的两个计数单位分别是百万位和万位。
………()5. 9080000千克改写成用“万”作单位的数是908千克。
………()6.读404000时,一个零也不读。
……………………………………()三、在里填上“>”“<”或“=”。
6012006000120 5010000克501千克402万402000 500千米500000米四. 选择。
1、九万零四写作:()A、90004B、90040C、 9000402、下面各数中,一个零也不读的数是:A、 340570B、4078000C、2050003、用2个2和3个0可以组成()个不同的五位数。
A、 3B、4C、54、由8个亿,80个万和800个一组成的数是()A、880800B、 80800800C、 8008008005、个、十、百、千、万……是()A、计数法B、数位名称C、计数单位6、在49□438≈50万的括号里填上合适的数。
人教新课标四年级上册数学第一单元综合能力测试卷(含答案)
第一单元综合能力测试卷一、填空题1.一个八位数,它的最高位是( )位,这一位的计数单位是( )。
最小的八位数是( ),最大的八位数是( )。
2.在数位顺序表中,右起第4位是( )位,第7位是( )位,第10位是( )位。
3. 1206840000是( )位数,最高位是( )位,这个数读作( ),将它改写成用“万”作单位的数是( ),省略亿位后面的尾数求近似数约是( )。
4. 10个十万是( ),10个( )是1亿,比1亿少二百万的数是( ),读作( )。
5.一个数百万位和千位上的数都是5,其他各位上的数字为0,这个数是( ),省略万位后面的尾数求近似数约是( )。
6.把425变成四亿二千五百万,5后面添( )个0。
7. 99998后面连续的四个数是( ),( ),( ),( )。
8.在5505500,5550500,5050505,5055005,5050550中,一个0也不读的是( ),只读一个0的是( ),读两个0的是( ),读三个0的是( )。
9.省略万位后面的尾数后是19万,这个数最大是( ),最小是( )。
10. 一个九位数,千万位上是8,这个九位数的近似数最小是( )亿,最大是( )亿。
二、判断题1. 428690省略万位后面的尾数,428690=43万。
( )2.个级包括个位,十位,百位,千位。
( )3.一千亿是最大的自然数。
( )4.两个计数单位之间的进率是10。
( )5.在读数时,从高位到低位读。
( ) 6. 42000100,这个数只读一个0。
( )7.读0最多的最小八位数是10101010。
( )8. 540000,这个数的计数单位是万。
( )9.读两级数时,中间的“0”都不读。
( )10.在数字1和2之间添5个0,就组成一百万零二。
( )三、选择题1.一个六位数,最高位与千位上都是6,其余各位上都是0,把它四舍五入到万位后是( )。
A.60万 B.61万 C.70万 D.71万2.由3个百万、4个万组成的数是( )。
人教版数学四年级上册第一单元综合测试题(含答案)
人教版数学四年级上学期第一单元测试考试时间:90分钟;满分:100分一.填空题(共10小题,每空1分,共23分)1.(2019春•新田县期中)数位表上(整数部分)从右往左数第七位是,它的计数单位是,与它左边相邻的数位是位,计数单位是.2.(2019春•东台市校级期中)与万相邻的两个计数单位是和.3.(2019•防城港模拟)10个十万是,10个一百万是,一百万包含个万.4.(2019春•明光市期末)由7个十亿,5个千万4个百和9个一组成的数写作,最高位的计数单位是.5.(2019•长沙)由一个亿,二十七个万,四个百,十八个一组成的数是6.(2019•保定模拟)先把下面各数改写成用“万”作单位的数,再精确到十分位.49600=万万7.(2019•保定模拟)把下面的数字改写成用“亿”做单位的数,再省略亿后面的尾数.102839000=亿亿8.(2019春•东台市校级期中)在横线里填上“”“”或“”.345万354000010000万1亿606100⨯19999000020000000⨯106609.(2019春•嘉定区校级月考)有3个连续的自然数的和是36,那么其中最大的自然数是.10.(2019•衡阳模拟)键CE是键,它的功能是.二.判断题(共6小题,每小题1分,共6分)11.(2019春•新田县期中)自然数有无限个,最小的自然数是1.( ) 12.(2018秋•蕲春县期中)个位、十位、百位、千位、万位、十万位都是计数单位.( ) 13.(2019春•新田县期中)个、十、百、千⋯⋯都是计数单位,它们之间的进率都是10.( ) 14.(2019春•柯桥区校级月考)5005005000读作:五十亿五百万五千.( ) 15.(2019春•东兴市期中)一个数四舍五入到万位约为15万,这个数最大是149999.( ) 16.(2018秋•番禺区期末)所有的六位数都比1000000小,所有的七位数都比999999大.( )三.选择题(共8小题,每小题2分,共16分)17.(2014秋•赣州期中)下面说法错误的是A.最大的自然数是999999999999B.最小的自然数是0C.所有的自然数都是整数D.自然数的个数是无限的18.(2016秋•临川区校级月考)下面是计数单位的是A.千位B.千亿C.千万位19.(2019春•镇江期末)下面的数中,读的“零”最多.A..506060B.5060606C.500660620.(2019春•东台市校级期中)四十万零四,两个“4”之间有个零.A.3B.4C.521.(2018秋•成华区期末)据统计,2015年末,我国大陆总人口约为十三亿七千四百六十二万人,横线上的数是几位数A.十二B.十C.九22.(2019•郴州模拟)下列各数中,四舍五入后近似数是3亿的数是A.3300万B.30001230C.29600798523.(2019春•兴仁县期中)以下三个数最大的是A.它是一个8位数B.它的最高位是百万位C.它读作九十九万五千D.它们一样大24.(2018秋•单县期末)100个一百万是A.100万B.1亿C.1000万四.解答题(共10小题,满分55分)25.(2019春•江苏校级期末)读出下面各数.(共4分)28800600读作:80120070读作:906705008 读作:30050007000 读作:.26.(2019春•洛阳月考)写出下面各数.(共4分)九十万零七百写作:;二亿三千五百万九千三百二十写作:;八千二百四十万一千零三写作:;五亿零二千写作:.27.(2019春•洛阳月考)将下面各数按照从小到大的顺序排列.(共3分)3500760 11302400 4002190 980998 3500670.28.(2019春•洛阳月考)用“万”或“亿”作单位表示数.(共6分)4007000000=27600000000=153610000=29.(2019•大田县)将下列数由小到大排列.(共6分)(1)54万539000 54000 540200(2)200000200 202000000 2000001000 2010000000(3)7053300米、705千米、70533千米、7050000米.30.(2019春•洛阳月考)用3、7、9和4个0组成一个七位数.(共6分)(1)一个零都不读的数是;(2)只读一个零的数是;(3)读两个零的数是.31.(2019秋•黄梅县月考)用0、0、0、2、3、4、5这七个数字按要求组成七位数.(只写出一个符合要求的数)(共8分)(1)所有的0都不读:(2)只读一个(3)只读两个(4)读三个.32.先根据计算器前三道算式结果找出规律,再直接写出后面各题的答案.(共6分)129⨯=108⨯=11071239⨯=1110612349123459⨯=⨯=123456912345679⨯=33.按要求写出下面的数.(共8分)(1)一个数省略万位后面的尾数约是20万,这个数最大是多少?最小是多少?(2)一个数省略亿位后面的尾数约是123亿,这个数最大是多少?最小是多少?34.一个九位数,各个数位上的数字和为15,其中万位上的数字是亿位上的2倍,这个数最大是多少?最小是多少?(共4分)答案与解析一.填空题(共10小题,每空1分,共23分)1.(2019春•新田县期中)数位表上(整数部分)从右往左数第七位是百万位,它的计数单位是,与它左边相邻的数位是位,计数单位是.【分析】小数点左面依次为:个位,十位,百位,千位;计数单位是:个(1),十,百,千;据此解答.【解答】解:数位表上(整数部分)从右往左数第七位是百万位,它的计数单位是百万,与它左边相邻的数位是千万位,计数单位是千万;故答案为:百万位,百万,千万位,千万.【点评】考查了数位顺序表和计数单位,是需要识记的知识,是基础题型.2.(2019春•东台市校级期中)与万相邻的两个计数单位是千和.【分析】根据整数的数位顺序可知,万位和十万位、千位相邻,十万位的计数单位是十万,千位的计数单位是千,所以十万和千是和万位相邻的两个计数单位,据此解答.【解答】解:与万位相邻的两个计数单位是千和十万;故答案为:千,十万.【点评】本题主要考查整数的计数单位,注意计数单位和数位的区别.3.(2019•防城港模拟)10个十万是一百万,10个一百万是,一百万包含个万.【分析】根据相邻的两个计数单位间的进率是“十”,十万和百万,百万和千万,千万和亿都是两个相邻的计数单位,它们的进率都是“十”,据此解答即可.【解答】解:10个十万是一百万,10个一百万是一千万,一百万包含100个万.故答案为:一百万,一千万,100.【点评】此题考查十进制计数法,每相邻的两个计数单位间的进率是“十”.4.(2019春•明光市期末)由7个十亿,5个千万4个百和9个一组成的数写作7050000409,最高位的计数单位是.【分析】根据整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,据此写出;根据整数的数位顺序表可知:这个数是十位数,它的最高位是十亿位,据此解答.【解答】解:由7个十亿,5个千万4个百和9个一组成的数写作:7050000409,最高位的计数单位是十亿位.故答案为:7050000409,十亿位.【点评】本题主要考查整数的写法和整数的认识.5.(2019•长沙)由一个亿,二十七个万,四个百,十八个一组成的数是100270418【分析】这是一个九位数,最高位亿位上是1,十万位上是2,万位上是7,百位上是4,十位上是1,个位上是8,写这个数时,从高位到低位,一级一级地写,哪一个数位上一个计数单位也没有,就在那个数位上写0;据此写出.【解答】解:由一个亿,二十七个万,四个百,十八个一组成的数是100270418.故答案为:100270418.【点评】本题是考查整数的读、写,记住数位顺序是读写数的关键.6.(2019•保定模拟)先把下面各数改写成用“万”作单位的数,再精确到十分位.49600= 4.96万万【分析】改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,在数的后面带上“万”字;再把改写成的用“万”作单位的数的小数部分百分数位上的数进行四舍五入,解答即可.【解答】解:49600 4.96≈万=万 5.0故答案为:4.96,5.0.【点评】本题主要考查整数的改写和求近似数,改写和求近似数时要带计数单位.7.(2019•保定模拟)把下面的数字改写成用“亿”做单位的数,再省略亿后面的尾数.102839000= 1.02839亿亿【分析】改成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“亿”字;省略“亿”后面的尾数就是四舍五入到亿位,把亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字.【解答】解:102839000 1.02839=亿亿故答案为:1.02839,1.【点评】本题主要考查整数的改写和求近似数,注意改写和求近似数时要带计数单位.8.(2019春•东台市校级期中)在横线里填上“”“”或“”.345万354000010000万1亿⨯⨯1066060610019999000020000000【分析】(1)(2)(4)根据整数大小比较的方法判断即可.(3)先求出算式的结果,再根据整数大小比较的方法判断即可.【解答】解:(1)345万3540000<(2)10000万亿(3)60610010660⨯>⨯(4)19999000020000000>故答案为:;;;.【点评】此题主要考查了整数比较大小的方法的应用,以及积不变的规律,要熟练掌握.9.(2019春•嘉定区校级月考)有3个连续的自然数的和是36,那么其中最大的自然数是13.【分析】根据“相邻的两个自然数相差1”,先求出这三个连续自然数的平均数,最大的一个比平均数多1,据此解答.【解答】解:3631÷+=+121=13答:这3个数中最大的一个数是13.故答案为:13.【点评】此题考查的目的是理解自然数的意义,掌握自然数的排列规律,应明确相邻的两个自然数相差1.10.(2019•衡阳模拟)键CE是清除键,它的功能是.【分析】CE键是清除键,就是清除刚刚输入的数据.【解答】解:键CE是清除键,它的功能是清除数据.故答案为:清除.清除数据.【点评】熟记一些计算器按键的功能,如:ON,是开机键,OFF是关机键,CE是清除键,是存储键.二.判断题(共6小题,每小题1分,共6分)11.(2019春•新田县期中)自然数有无限个,最小的自然数是1..(判断对错)【分析】根据自然数的意义:表示物体个数的1、2、3、4、5、6、7、8、9、10、11,都是自然数,一个物体也没有用0表示.0也是自然数,最小的自然数是0,自然数的个数是无限的.【解答】解:由分析得出:自然数有无限个,最小的自然数是0.所以题干说法错误.故答案为:.【点评】本题主要考查自然数的意义,注意最小的自然数是0,没有最大的自然数,自然数的个数是无限的.12.(2018秋•蕲春县期中)个位、十位、百位、千位、万位、十万位都是计数单位..(判断对错)【分析】计数单位与数位形式上的区别是:数位后面带个“位”字,而计数单位后面没有“位”字.【解答】解:个位、十位、百位、千位、万位、十万位,后面都带有“位”字,是数位,不是计数单位.故答案为:.【点评】本题考查了数位和计数单位的区别:数位表示数字所占的位置,而计数单位表示数字的单位是什么.13.(2019春•新田县期中)个、十、百、千⋯⋯都是计数单位,它们之间的进率都是10.(判断对错)【分析】每相邻的两个计数单位之间的进率都为十的计数法则,就叫做“十进制计数法”,由此求解.【解答】解:个、十、百、千⋯⋯都是计数单位,这是正确的;它们之间的进率都是10,没有说“相邻两个计数单位之间的进率”,所以不能说进率都是10,这部分说法是错误的;故答案为:.【点评】本题考查了计数单位的含义,以及每相邻的两个计数单位之间的进率都为10,注意关键词“相邻”.14.(2019春•柯桥区校级月考)5005005000读作:五十亿五百万五千.(判断对错)【分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零,读出此数再作判断.【解答】解:5005005000读作:五十亿零五百万五千.原题说法错误.故答案为:.【点评】本题是考查整数的读法,分级读或借助数位顺序表读能较好的避免读错数中“0”的情况.15.(2019春•东兴市期中)一个数四舍五入到万位约为15万,这个数最大是149999.(判断对错)【分析】根据省略“万”后面的尾数求它的近似数,要把万位的下一位千位上的数进行四舍五入,再在数的后面带上“万”字,这个数的万位是5,千位上是4,百位、十位、个位上都是9时最大.【解答】解:一个数四舍五入到万位约为15万,这个数最大是154999.原题说法错误.故答案为:.【点评】此题主要是考查用“四舍五入”法求近似数的方法,一个数省略万后面的尾数时,千位上是最大是4,百位、十位、个位上都是最大的一位数时,这个数最大.16.(2018秋•番禺区期末)所有的六位数都比1000000小,所有的七位数都比999999大.(判断对错)【分析】比较整数的大小,位数多的那个数就大;如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,哪一位上的数大,那个数就大.【解答】解:1000000是七位数,所以,所有的所有的六位数都比1000000小;999999是六位数,所以,所有的七位数都比999999大;原题说法正确.故答案为:.【点评】此题考查了整数大小比较方法的运用.三.选择题(共8小题,每小题2分,共16分)17.(2019秋•赣州期中)下面说法错误的是A.最大的自然数是999999999999B.最小的自然数是0C.所有的自然数都是整数D.自然数的个数是无限的【分析】根据题意,对各选项进行依次分析、进而得出结论.【解答】解:错误,因为在自然数中没有最大的自然数.正确,在自然数中,0是最小的自然数.正确,因为整数包括自然数.正确,因为自然数的个数是无限的.故选:.【点评】本题考查了自然数的意义和整数的分类,本题是选择错误的说法.18.(2019秋•临川区校级月考)下面是计数单位的是A.千位B.千亿C.千万位【分析】计数单位与数位形式上的区别是:数位后面带个“位”字,而计数单位后面没有“位”字;个级包括四个数位:个位、十位、百位、千位;万级包括四个数位:万位、十万位、百万位、千万位;亿级包括四个数位:亿位、十亿位、百亿位、千亿位;据此解答.【解答】解:千亿位的计数单位是千亿,千亿是计数单位;千位、千万位都是数位,不是计数单位.故选:.【点评】本题考查了数位和计数单位的区别:数位表示数字所占的位置,而计数单位表示数字的单位是什么.19.(2019春•镇江期末)下面的数中,读的“零”最多.A..506060B.5060606C.5006606【分析】根据整数中0的读法,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零.读出各数再判断.【解答】解:506060读作:五十万六千零六十;5060606读作:五百零六万零六百零六;5006606读作:五百万六千六百零六;故选:.【点评】本题是考查整数的读法,注意分级读可以避免读错0.20.(2019春•东台市校级期中)四十万零四,两个“4”之间有个零.A.3B.4C.5【分析】这是一个六位数,最高位十万位和个位上都是4,写这个数时,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0.写出该数即可确定两个“4”之间有多少个零.【解答】解:四十万零四写作:400004,两个“4”之间有4个零.故选:.【点评】用数位表写数能较好的避免漏写0或写错位的情况,是常用的方法,要熟练掌握.21.(2018秋•成华区期末)据统计,2015年末,我国大陆总人口约为十三亿七千四百六十二万人,横线上的数是几位数A.十二B.十C.九【分析】从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,由此写出这个数,再判断这个数的位数.【解答】解:十三亿七四百六十二万写作:1374620000.横线上的数是十位数.故选:.【点评】解决本题也可以根据数位顺序表,各位数位是从右往左数的第几位进行判断,十三亿七四百六十二万最高位是亿位,也就是第十位.22.(2019•郴州模拟)下列各数中,四舍五入后近似数是3亿的数是A.3300万B.30001230C.296007985【分析】根据“四舍五入法”省略亿位后面的尾数求近似数的方法,根据千万位上四则的大小确定用“四舍”还是用“五入”,据此解答即可.【解答】解:、3300万,最高位千万上是3,不符合题意、30001230,最高位千万位上是3,不符合题意、296007985,千万位上是9大于5,所以用“五入”法,即296079853亿故选:.【点评】此题考查的目的是理解掌握利用“四舍五入法”省略亿位后面的尾数求近似数的方法及应用.23.(2019春•兴仁县期中)以下三个数最大的是A.它是一个8位数B.它的最高位是百万位C.它读作九十九万五千D.它们一样大【分析】首先判断出所给的3个数的位数的多少;然后根据:数位不同,那么数位多的数就大,如果数位相同,从最高位开始,相同数位上的数大的那个数就大,判断出哪个数最大即可.【解答】解::它是一个8位数,:它的最高位是百万位,则它是一个7位数,:它读作九十九万五千,则它是一个6位数,因为876>>,所以所给的三个数中8位数最大.故选:.【点评】此题主要考查了整数比较大小的方法的应用,要熟练掌握.24.(2018秋•单县期末)100个一百万是A.100万B.1亿C.1000万【分析】根据相邻两个计数单位之间的进率都是10进行求解:百万位后面是千万位,千万位后面是亿位,所以100个一百万是一亿.【解答】解:100个一百万是一亿,故选:.【点评】此题考查了乘法的意义,明确求个相同加数的和是多少用乘法解答.四.解答题(共10小题,满分55分)25.(2019春•江苏校级期末)读出下面各数.(共4分)28800600读作:二千八百八十万零六百80120070读作:906705008 读作:30050007000 读作:.【分析】读多位数的方法是先把这个多位数分级,从高位到低位一级一级地往下读,读万级时,按个级的读法去读,只要在后面再加上级的单位“万”,每级开头或中间有一个0,或者连续有几个0的,都只读一个零,级的末尾所有0都不读出来.【解答】解:2880 0600读作:二千八百八十万零六百,8012 0070读作:八千零一十二万零七十,9 0670 5008 读作:九亿零六百七十万五千零八,300 50007000 读作:三百亿五千万七千,故答案为:二千八百八十万零六百,八千零一十二万零七十,九亿零六百七十万五千零八,三百亿五千万七千【点评】考查了整数的读法和写法.解答本题要知道整数的数位顺序表,整数的读法关键是要分好级,熟练掌握多位数的读写法则,准确理解“亿”级、“万”级“、个”级的计数单位.26.(2019春•洛阳月考)写出下面各数.(共4分)九十万零七百写作:90 0700;二亿三千五百万九千三百二十写作:;八千二百四十万一千零三写作:;五亿零二千写作:.【分析】根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,即可写出各数.【解答】解:九十万零七百写作:90 0700;二亿三千五百万九千三百二十写作:2 3500 9320;八千二百四十万一千零三写作:8240 1003;五亿零二千写作:5 0000 2000.故答案为:90 0700,2 3500 9320,8240 1003,5 0000 2000.【点评】本题是考查整数的写法,分级写即可快速、正确地写出此数.27.(2019春•洛阳月考)将下面各数按照从小到大的顺序排列.(共3分)3500760 11302400 4002190 980998 3500670980998.【分析】整数比较大小的方法:比较两个整数的大小,首先要看他们的数位,如果数位不同,那么数位多的数就大,如果数位相同,从最高位开始,相同数位上的数大的那个数就大,据此判断即可.【解答】解:根据整数比较大小的方法,可得<<<<.98099835006703500760400219011302400故答案为:980998、3500670、3500760、4002190、11302400.【点评】此题主要考查了整数比较大小的方法的应用.28.(2019春•洛阳月考)用“万”或“亿”作单位表示数.(共6分)4007000000=27600000000=153610000=【分析】(1)改成用“万”作单位的数,是把万位后面的4个“0”去掉,或者在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字,据此改写;(2)改写成用“亿”作单位的数,是把亿位后面的8个“0”去掉,或者在亿位数的右下角点上小数点,然后把小数末尾的0去掉,在数的后面带上“亿”字,据此写出.【解答】解:400700000040.07=亿;27600000000276=亿;=万.15361000015361【点评】本题主要考查整数的改写,注意带计数单位.29.(2019•大田县)将下列数由小到大排列.(共6分)(1)54万539000 54000 540200(2)200000200 202000000 2000001000 2010000000(3)7053300米、705千米、70533千米、7050000米.【分析】整数比较大小的方法:比较两个整数的大小,首先要看他们的数位,如果数位不同,那么数位多的数就大,如果数位相同,从最高位开始,相同数位上的数大的那个数就大,据此判断即可.【解答】解:(1)54万540000=,<;<<万5402005400053900054(2)20000020020200000020000010002010000000<<<;(3)因为7050000米7050=千米,7053300米7053.3=千米,所以705千米7050000<米70533<千米.<米7053300【点评】此题主要考查了整数比较大小的方法的运用.30.(2019春•洛阳月考)用3、7、9和4个0组成一个七位数.(共6分)(1)一个零都不读的数是3790000(答案不唯一);(2)只读一个零的数是;(3)读俩个零的数是.【分析】根据整数中“零”的读法,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零.要想一个“零”也不读,就要把所有的0都写在每级的末尾;要想只读一个“零”,就要有一个0或连续几个0不能写在每级的末尾;要想读出两个“零”,就要把这4个0分两组0不能写在每级的末尾,且不能相邻.【解答】解:用3、7、9和4个0组成一个七位数.(1)一个零都不读的数是3790000(答案不唯一);(2)只读一个零的数是3700009(答案不唯一);(3)读俩个零的数是3000709(答案不唯一).故答案为:3790000(答案不唯一),3700009(答案不唯一),3000709(答案不唯一).【点评】本题是考查整数的读法,分级读或借助数位顺序表读能较好的避免读错数中“0”的情况.31.(2019秋•黄梅县月考)用0、0、0、2、3、4、5这七个数字按要求组成七位数.(只写出一个符合要求的数)(共8分)(1)所有的0都不读:5432000(2)只读一个(3)只读两个(4)读三个.【分析】根据整数中“零”的读法,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零.要想一个“零”也不读,就要把所有的0都写在每级的末尾;要想只读一个“零”,就要有一个0或连续几个0不能写在每级的末尾;要想读出两个“零”,就要有两个或两组0不能写在每级的末尾,且不能相邻;要想读出三个“零”,就要有三个或三组0不能写在每级的末尾,且不能相邻.【解答】解:(1)所有的0都不读:5432000;(2)只读一个0:5430200(3)只读两个0:5043020(4)读三个0:5040302.故答案为:5432000,5430200,5043020,5040302.【点评】本题是考查整数的读法,分级读即可快速、正确地读出此数,是常用的方法,要掌握.32.先用计算器前三道算式找出规律,再直接写出后面各题的答案.(共6分)⨯=108129⨯=11071239⨯=1110612349⨯=123459⨯=123456912345679⨯=【分析】计算129108⨯=,可以看出第一个因数是从1开始几个连续自然数组⨯=,12391107⨯=,1234911106成的,第二个因数都是9,从计算结果可以看出从左向右的数字是1,1的个数等于组成第一个因数的最后一个自然数减去1,再后面有一个0,最后的数字是9减去前面所有数字1的和,由此规律计算即可.【解答】解:129108⨯=⨯=12391107⨯=1234911106123459111105⨯=⨯=123456911111041234567911111103⨯=.【点评】从简单开始,通过计算进一步发现算式规律,进一步利用规律解决问题.33.按要求写出下面的数.(共8分)(1)一个数省略万位后面的尾数约是20万,这个数最大是多少?最小是多少?(2)一个数省略亿位后面的尾数约是123亿,这个数最大是多少?最小是多少?【分析】(1)一个整数省略“万”后的尾数约是20万,要求这个数最大是多少,就要考虑是用“四舍”法求得的近似值,也就是千位上是4,其它各位上是9;最大是204999.要求这个数最小是多少,就要考虑是用“五入”法求得的近似值,也就是千位上是5,其它各位上都是0,即最小是195000.(2)一个数省略亿位后面的尾数是123亿,最大是千万位上的数舍去得到的,舍去的数中4是最大的,其它数位上都是最大的一位数9即可;最小是千万位上的数进一得到的,进一的数中5是最小的,其它数位上都是最的小自然数0即可.【解答】解:(1)根据“四舍五入”法知:当千位上小于5时,直接舍去,所以千位上4,所以最大的数是:204999,根据“四舍五入”法知:当千位上大于5时,要向前一位进一,所以千位上是5,最小的数是:195000.答:最大数是204999,最小数是195000.(2)一个数省略亿位后面尾数是123亿,那么这个数最大是12349999999,最小是12250000000.答:最大数是12349999999,最小数是12250000000.【点评】此题主要考查利用“四舍五入法”,省略万位后面的尾数求近似数.明确:用“四舍”法求出的近似数比准确数小;用“五入”法求出的近似数比准确数大.34.一个九位数,各个数位上的数字和为15,其中万位上的数字是亿位上的2倍,这个数最大是多少?最小是多少?(共4分)【分析】因为已知万位上的数字是亿位上的2倍,所以先找出在0、1、2、3、4、5、6、7、8、9中,有哪两个数是2倍关系,从中再选择哪两数个最大,哪两个数最小,确定亿位与万位上的数字分别是几;因为各个数位上的数字和为15,所以据此就可以确定其它数位的上数字分别是几;再根据整数大小比较的方法,分别找出最大的数是几,最小的数是几.【解答】解:212÷=,632÷=,422÷=÷=,842因为8412-=+=,15123最大需亿位最大为4,则万位是8,千万位则是3,其余为0所以这个数最大是430080000,因为要使整个数最小,位数越高数字越小,则亿位最小为1,则万位是2,个位则是9,十位为3,其余为0所以这个数最小是100020039.答:这个数最在是430080000,最小是100020039.【点评】解答本题的关键是:首先要明确最高位上的数字不能为0,找出哪几个一位数之间存在2倍关系,并且能够熟练掌握整数大小的比较方法,即比较整数的大小,位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,下一位上的数大那个数就大.。
人教版五年级上册数学第一单元综合测试题(带答案)
最新人教版五年级数学上册精编单元试卷第一单元检测卷考试时间:90分钟满分:100分附加题10分一.填空题(共11小题,每题1分,第6,7,10题每空1分,共20分)1.(2019•怀化模拟)计算小数乘法时,一般先将其转化为整数乘法来计算,那么4.0653.8⨯可以转化为⨯.2.(2017秋•卢龙县期末)0.60.60.60.60.6(++++=⨯)=.3.(2019•防城港模拟)3.64 1.7⨯的积是位小数,得数保留整数约是,保留两位小数约是.4.(2018春•台安县期末)西瓜毎千克0.95元,买一个5.6千克的西瓜要花元.5.(2011秋•横峰县期末)小马虎在计算一个两位小数乘一个整数时,把积的小数点忘了,结果比正确的积多4950.正确的积是.6.(2014秋•宁远县校级月考)在横线里填上“>”、“<”或“=”⨯⨯ 1.83 6.51 6.53950.26⨯395 1.83 1.6⨯0.9 0.210.910.21⨯⨯32.6 5.80.910 3.267.(2014秋•正定县期末)比较大小.⨯0.1500.51038000平方米4公顷5公顷49000平方米.0.210.21⨯0.021 2.18.(2018秋•石林县期末)计算0.560.04⨯时,先算⨯的积,再从积的边起数出位点上小数点.9.(2016秋•华容区期中)2.155⨯运算时先把2.15看作,因数就扩大为原来的倍,运算结果也必须缩小为原来的,才能得到2.155⨯的积.10.(2019•江苏模拟)计算 2.556.4⨯=⨯= 4.0620.511.(2018秋•西山区期末)3个4.5是多少?用加法计算列式为:;用乘法计算列式为:;80的12.5倍是;二.判断题(共5小题,每小题1分,共5分)12.一个数(0除外)乘大于1的数,积比原数大.( ) 13.(2016秋•昭阳区月考) 1.25a⨯.( )a⨯一定大于0.9514.一个数乘以小数后得到的积可能还和它原来相等.( ) 15.430.75⨯,0.437.5⨯这三道题中,积最大的是第二道题( )⨯,4.37516.(2018春•平桂区期末)在进行小数计算时,要把小数的末位对齐.( )三.选择题(共5小题,每小题1分,共5分)17.(2014秋•黔东南州期末)下面的算式结果小于0.28的是()A.0.280.14⨯⨯B.0.280.14÷C.0.28118.下面观点错误的是( )A .一位小数乘两位小数,积可能是两位小数B .一个大于0的数乘0.8的积,一定小于这个数C .3.5小时,就是3小时50分钟D .一个两位小数,把它保留一位小数后是2.8,那么这个小数最大是2.84,最小是2.75 19.通过估算,( )的得数肯定不超过3.6. A .4.080.92⨯B .4.080.89⨯C .3.980.98⨯D .3.980.89⨯20.(2019春•浦城县期中)如果甲0.42⨯=乙 1.75⨯(甲、乙都不等于0),那么( ) A .甲<乙B .甲=乙C .甲>乙D .无法确定21.(2014秋•金华期末)两个因数相乘,所得的积( )其中一个因数. A .一定大于 B .一定小于 C .可能大于、小于或等于四.计算题(共33分)22.(2018春•山西月考)直接写出得数.(共8小题,每小题1分,共8分) 0.60.8⨯= 30.9⨯= 2.50.4⨯= 3.60.4⨯= 12.58⨯= 500.04⨯= 800.3⨯= 1.19⨯=23.(2018秋•祁东县月考)列竖式计算.(共3小题,每小题3分,共9分)5.68 2.3⨯= 4.76 2.8⨯≈ (保留两位小数) 18.750.4⨯=24.(2015秋•道真县校级期末)简便计算.(共4小题,每小题3分,共12分)1010.85⨯ 412.50.250.8⨯⨯⨯ 8(20 1.25)⨯- 50 1.919⨯-.25.列式计算.(共2小题,每小题2分,共4分)(1)1.25的8倍是多少? (2)5.7乘3.2与6.8的和,积是多少?五.解答题(共8小题,满分37分)26.(5分)(2017秋•重庆期中)某地打固定电话每次前3分钟内收费0.22元,超过3分钟每分钟收费0.11元(不足1分钟按1分钟计算),爸爸一次通话时间为8分26秒,他这次通话的费用是多少?27.(6分)(2019春•梁河县期中)妈妈带100元去超市购物,她买了2袋大米,每袋33.5元;还买了0.8千克的肉,每千克24元.(1)剩下的钱够买1桶12元的油吗?(2)剩下的钱够买2桶7.5元一桶的油吗?28.(5分)(2018秋•荔湾区期末)五(1)班42名师生照相合影.每人一张照片,一共需要付多少钱?加印一张:2.8元29.(5分)在一个汽车停车场停车至少要交费5元,如果停车超过3小时每多停1小时(不足1小时按1小时计算)要多交1.2元.一辆汽车在停车场停了9小时36秒,这辆汽车的司机应交多少元停车费?30.(5分)星期六,小明和爸爸一起去离家80千米的外婆家去为外婆祝寿.出发时,发现油箱中只剩下3升汽油了,爸爸问小明:“每升汽油可行驶8.5千米,我们往返一趟加15升汽油够吗?”请你帮小明回答这个问题.(要通过计算来判断)31.(5分)移动公司有两种手机卡,采用的收费标准如下表,王叔叔的一个月通信量是200分钟左右,你帮他选一种合适他的手机卡.32.(6分)(2010秋•沾化区校级期末)快乐比较(1)一幢大楼有21层,每层高2.8米,这幢大楼约高多少米?(得数保留整数)(2)一幢大楼有21层,乘电梯每上升一层需3.3秒,从底层到最高层需要多少时间?六.附加题(10分)33.为了鼓励节约用电,某市实行“阶梯电价”,收费标准如下表:(2)小张家这个月用电189千瓦时,电费是多少元?(3)小丽家这个月用电245千瓦时,电费是多少元?答案与解析一.填空题(共11小题,每题1分,第6,7,10题每空1分,共20分)1.计算小数乘法时,一般先将其转化为整数乘法来计算,那么4.0653.8⨯可以转化为406⨯.【分析】根据小数乘法的计算法则进行分析解答.【解答】解:计算小数乘法时,一般先将其转化为整数乘法来计算,那么计算4.0653.8⨯;先把4.06扩大100倍,变为4.06100406⨯=;再把53.8扩大10倍变为53.8210538⨯=;根据积的变化规律,此时的积扩大了100101000⨯=倍,则两个整数乘得的积缩小到原来的11000即可.故答案为:406,538.【点评】此题考查的目的是理解掌握小数乘法的计算法则.2.0.60.60.60.60.6(++++=0.6⨯)=.【分析】0.60.60.60.60.6++++,是5个0.6相加,根据小数乘整数的意义,用0.65⨯,然后再进一步解答.【解答】解:0.60.60.60.60.6++++0.65=⨯3=故答案为:0.6,5,3.【点评】小数乘整数的意义,与整数乘法的意义相同,都表示求几个相同加数的和是多少.3.3.64 1.7⨯的积是3位小数,得数保留整数约是,保留两位小数约是.【分析】根据小数乘法的计算法则,积的小数位数等于两个因数小数位数的和,再利用“四舍五入法”分别求此它的近似数即可.【解答】解:3.64 1.7 6.188⨯=保留整数:6.1886≈保留两位小数:6.188 6.19≈故答案为:3;6;6.19.【点评】本题考查的目的是掌握小数乘法的计算法则、及利用“四舍五入法”求小数的近似数的方法.4.西瓜毎千克0.95元,买一个5.6千克的西瓜要花 5.32元.【分析】根据乘法的意义,用西瓜单价乘所买数量,即得需要花多少钱.【解答】解:0.95 5.6 5.32⨯=(元)答:买一个5.6千克的西瓜要花5.32元. 故答案为:5.32.【点评】本题体现了价格问题的基本关系式:单价⨯数量=总价.5.小马虎在计算一个两位小数乘一个整数时,把积的小数点忘了,结果比正确的积多4950.正确的积是 50 .【分析】因为一个两位小数乘一个整数,积可能是两位小数,因为把小数点忘了,所以把积扩大了100倍,所以现在的积-正确的积4950=,据此解答即可.【解答】解:设两个因数分别是a 、b ,则正确的积是ab ,则: 1004950ab ab -=,994950ab =, 495099ab =÷, 50ab =. 所以正确的积是50. 故答案为:50.【点评】解决本题的关键是得出:把小数点忘了,所以把积扩大了100倍,所以现在的积-正确的积4950=. 6.在横线里填上“>”、“ <”或“=”3950.26⨯ < 395 1.83 1.6⨯ 1.83 6.5 1 6.5⨯ 10 3.26⨯ 32.65.80.9⨯ 0.90.21 0.910.21⨯【分析】一个数(0除外)乘一个小于1的数和除以大于1的数,得到的结果小于它本身;一个数(0除外)除以一个小于1的数和乘大于1的数,得到的结果大于它本身;依此比较即可;其中一个非0数乘1等于它本身;一个小数乘10,只要把这个小数的小数点向右移动一位即可. 【解答】解:3950.26395⨯< 1.83 1.6 1.83⨯> 6.51 6.5=⨯ 10 3.2632.6⨯=5.80.90.9⨯>0.210.910.21>⨯故答案为:<,>,=,=,>,>.【点评】不用计算,根据一个数乘或者除以的数比1大还是比1小进行比较. 7.比较大小.0.210.21⨯ = 0.021 2.1⨯0.150 0.51038000平方米4公顷5公顷49000平方米.【分析】(1)根据积的变化规律解答.(2)根据小数的大小比较方法进行比较.(3)根据1公顷10000=平方米,把4公顷化为40000平方米,再进行比较.(4)根据1公顷10000=平方米,把5公顷化为50000平方米,再进行比较.【解答】解:(1)0.210.210.021 2.1⨯=⨯0.1500.510<4公顷40000=平方米38000平方米40000<平方米38000平方米4<公顷5公顷50000=平方米49000平方米50000<平方米5公顷49000>平方米故答案为:=;<;<;>.【点评】高级单位化低级单位乘以进率,低级单位化高级单位除以进率.8.计算0.560.04⨯时,先算56⨯的积,再从积的边起数出位点上小数点.【分析】根据小数乘法的计算法则,计算小数乘法,先按照整数乘法的计算法则算出积,再看两个因数一个有几位小数,就从积的右边起数出几位点上小数点.据此解答即可.【解答】解:计算0.560.04⨯时,先算564⨯的积,即564224⨯=,因为两个因数一共有四位小数,所以再从积的右边起数出四位点上小数点.故答案为:56、4、右、四.【点评】此题考查的目的是理解掌握小数乘法的计算法则及应用.9.2.155⨯运算时先把2.15看作215,因数就扩大为原来的倍,运算结果也必须缩小为原来的,才能得到2.155⨯的积.【分析】根据积的变化规律,一个因数不变,另一个因数扩大或缩小几倍(0除外),积也扩大或缩小相同的倍数;由此解答.【解答】解:2.155⨯运算时先把2.15看作215,第一个因数就扩大了100倍,运算结果必须缩小为原来的1 100,才能得到2.1515⨯的积.故答案为:215,100,1 100.【点评】此题考查了小数乘法运算法则的掌握.10.计算: 2.556.4⨯=141 4.0620.5⨯=83.23【分析】根据小数乘除法运算的计算法则计算即可求解.【解答】解:2.556.4141⨯=⨯=4.0620.583.23故答案为:141;83.23.【点评】考查了小数乘除法运算,关键是熟练掌握计算法则正确进行计算.11.3个4.5是多少?用加法计算列式为: 4.5 4.5 4.5++;用乘法计算列式为:;80的12.5倍是;【分析】(1)求3个4.5连加的和的加法算式,把3个4.5连加即可;乘法算式,用453⨯即可.(2)根据求一个数的几倍是多少用乘法计算,据此解答即可.【解答】解:(1)根据题意可得:4.5 4.5 4.513.5++=⨯=4.5313.5(2)8012.51000⨯=故答案为:4.5 4.5 4.5⨯;1000.++;4.53【点评】(1)求几个相同加数和的简便计算,用乘法进行计算即可;然后再进一步解答即可.(2)已知一个数求它的几倍是多少用乘法计算,据此解答即可.二.判断题(共5小题,每小题1分,共5分)12.一个数(0除外)乘大于1的数,积比原数大.√(判断对错)【分析】一个数(0除外)乘一个大于1的数,积比原来的数大.据此解答.【解答】解:一个数(0除外)乘大于1的数,积比原来的数大.如5210⨯=,10大于5,⨯=,1大于0.2.0.251故答案为:√.【点评】本题主要考查了学生对一个数(0除外)乘一个大于1的数,积比原来的数大,这一积的变化规律的掌握情况.13. 1.25a⨯.⨯.(判断对错)a⨯一定大于0.95【分析】这道题是错误的,因为当a是0的时候,这两个式子相等,所以错误.【解答】解:当0a=时, 1.250a⨯=,这两个式子相等.a⨯=,0.950所以原题说法错误.故答案为:⨯.【点评】解答本题的关键是知道当a是0的时候,这两个式子相等.14.一个数乘以小数后得到的积可能还和它原来相等.√.(判断对错)【分析】一个数乘以小数后得到的积可能还和它原来相等的有两种情况:第一种情况,这个数是0,因为0乘任何数都得0,所以乘积仍是0;第二种情况,这个数乘上的小数化简后是1,任何数乘上1都得都得原数,所以这个数乘上小数后还与它原来相等.【解答】解:0乘上一个小数或者这个数乘上1.0,得到的积仍是原数,如:⨯=0 3.250⨯=4.3 1.0 4.3所以原题说法正确.故答案为:√.【点评】解决本题运用找特例的方法,找出符合题意的算式,从而进行判断.15.430.75⨯这三道题中,积最大的是第二道题√.(判断对错)⨯,0.437.5⨯,4.375【分析】分别求出这三道题的得数,然后根据小数大小比较的方法进行比较即可.【解答】解:430.7532.25⨯=,⨯=,4.375322.5⨯=,0.437.5 3.225因为322.532.25 3.225>>,所以积最大的是第二道题;故答案为:√.【点评】此题也可以把其中的一个因数进行转化,根据两个非0的因数相乘,一个因数相同,另一个因数大的积就大.16.在进行小数计算时,要把小数的末位对齐.⨯(判断对错)【分析】由计算法则可知,列竖式计算小数加减法时,都要把相同数位对齐,不一定要把小数的末位对齐;由此判断.【解答】解:列竖式计算小数加减法时,都要把相同数位对齐,不一定要把小数的末位对齐;所以在进行小数计算时,要把小数的末位对齐说法是错误的.故答案为:⨯.【点评】解决本题要注意列竖式计算小数加减法时,都要把相同数位对齐,不一定要把小数的末位对齐.三.选择题(共5小题,每小题1分,共5分)17.下面的算式结果小于0.28的是()A.0.280.14⨯÷C.0.281⨯B.0.280.14【分析】乘法算式中,一个数(0除外)乘以小于1的数得到的积的小于原数,一个数(0除外)除以一个小于1的数,得到的商大于原数,一个数(0除外)乘以1得到的积等于原数,据此解答.【解答】解:由分析可知:.0.280.140.28A⨯<B÷>.0.280.140.28C⨯=.0.2810.28故选:A.【点评】本题主要考查小数乘法中积的变化规律,注意积的小数位数.18.下面观点错误的是()A.一位小数乘两位小数,积可能是两位小数B.一个大于0的数乘0.8的积,一定小于这个数C.3.5小时,就是3小时50分钟D.一个两位小数,把它保留一位小数后是2.8,那么这个小数最大是2.84,最小是2.75【分析】A:当两个小数的末尾数字的乘积的个位上是0时,积可能是两位小数,据此判断即可.B:一个非零数乘以一个小于1的数(不为0),积小于原来的数;一个非零数乘以一个大于1的数,积大于原来的数,据此判断即可.=分,可得3.5小时,就是3小时30分钟,据此判断即可.C:根据1小时60D:应用四舍五入法判断即可.【解答】解:因为一位小数乘两位小数,积可能是两位小数,例如:1.5 1.06 1.59⨯=,积是一个两位小数,所以选项A正确.因为一个大于0的数乘0.8的积,一定小于这个数,所以选项B正确.因为1小时60=分,所以3.5小时,就是3小时30分钟,所以选项C错误.因为一个两位小数,把它保留一位小数后是2.8,所以这个小数最大是2.84,最小是2.75;所以选项D正确.故选:C.【点评】(1)此题主要考查了小数乘法的运算方法,要熟练掌握,解答此题的关键是要明确:一个非零数乘以一个小于1的数(不为0),积小于原来的数;一个非零数乘以一个大于1的数,积大于原来的数.(2)此题还考查了四舍五入法求近似值问题的应用,以及时分秒之间的单位换算,注意高级单位的名数化成低级单位的名数,乘以单位间的进率,反之,则除以单位间的进率.19.通过估算,()的得数肯定不超过3.6.A.4.080.92⨯⨯D.3.980.89⨯C.3.980.98⨯B.4.080.89【分析】根据40.9 3.6⨯=,如果两个因数分别大于4和0.9,得数就大于3.6,如果两个因数分别小于4和0.9,乘积就小于3.6,据此判断.【解答】解:选项A:因为4.084>,所以4.080.92 3.6⨯>,>,0.920.9选项B:因为4.084⨯>,≈,所以4.080.89 3.6>,0.890.9选项C:因为3.984⨯>,≈,0.980.9>,所以3.980.98 3.6选项D:因为3.984⨯<.<,0.890.9<,所以3.980.89 3.6故选:D.【点评】本题考查估算,解决的关键是知道4936⨯=,然后把算式中的两个数和4、9比较,估算出结果进行判断.20.如果甲0.42⨯(甲、乙都不等于0),那么()⨯=乙 1.75A.甲<乙B.甲=乙C.甲>乙D.无法确定【分析】首先比较出0.42、1.75的大小关系,然后根据积一定时,其中的一个因数越小,则另一个因数越大,判断出甲、乙的关系即可.【解答】解:因为甲0.42<,⨯(甲、乙都不等于0),0.42 1.75⨯=乙 1.75所以甲>乙.故选:C.【点评】此题主要考查了小数乘法的运算方法,要熟练掌握,解答此题的关键是要明确:积一定时,其中的一个因数越小,则另一个因数越大.21.两个因数相乘,所得的积()其中一个因数.A.一定大于B.一定小于C.可能大于、小于或等于【分析】两个因数相乘有三种情况:(1)当一个因数等于1时,所得的积就等于另一因数;(1)当一个因数大于1时,所得的积就大于另一因数;(3)当一个因数小于1时,所得的积就小于另一因数,据此解答.【解答】解:两个因数相乘,所得的积可能大于、小于或等于其中一个因数;故选:C.【点评】本题主要考查小数乘法中因数与积的关系.四.计算题(共33分)22.直接写出得数.(共8小题,每小题1分,共8分)⨯= 3.60.4⨯=⨯=30.9⨯= 2.50.40.60.8⨯= 1.19⨯=800.3⨯=12.58⨯=500.04【分析】根据小数乘法的计算方法直接求解即可.【解答】解:⨯=⨯= 3.60.4 1.44⨯=30.9 2.7⨯= 2.50.410.60.80.48⨯=800.324⨯=⨯= 1.199.9⨯=500.04212.58100【点评】本题考查了小数乘法的计算方法,注意小数的位数.23.列竖式计算.(共3小题,每小题3分,共9分)5.68 2.3⨯=⨯(得数保留两位小数)≈4.76 2.8⨯=18.750.4【分析】根据小数乘法竖式的计算方法解答,注意对计算结果的要求.【解答】解:(1)5.68 2.313.064⨯=(2)4.76 2.8≈⨯(得数保留两位小数)13.33(3)18.750.47.5⨯=【点评】本题主要考查了小数乘法的笔算,根据其计算方法解答,注意对计算结果的要求.24.简便计算.(共4小题,每小题3分,共12分)⨯1010.85⨯⨯⨯412.50.250.8⨯-8(20 1.25)⨯-.50 1.919【分析】(1)把101分解成1001+,然后根据乘法分配律进行简算;(2)根据乘法交换律和结合律进行简算;(3)根据乘法分配律进行简算;(4)把19变成10 1.9⨯,然后根据根据乘法分配律进行简算.【解答】解:(1)1010.85⨯(1001)0.85=+⨯=⨯+⨯1000.8510.85=+850.8585.85=(2)412.50.250.8⨯⨯⨯(40.25)(12.50.8)=⨯⨯⨯=⨯11010=(3)8(20 1.25)⨯-8208 1.25=⨯-⨯=-16010=150(4)50 1.919⨯-50 1.910 1.9=⨯-⨯=-⨯(5010) 1.940 1.9=⨯=76【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.25.列式计算.(共2小题,每小题2分,共4分)(1)1.25的8倍是多少?(2)5.7乘3.2与6.8的和,积是多少?【分析】(1)根据小数乘法的意义列出算式1.258⨯,再根据小数乘法的计算法则计算即可求解;(2)先求出3.2与6.8的和,再用5.7乘它们的和即可求解.【解答】解:(1)1.25810⨯=答:1.25的8倍是10.(2)5.7(3.2 6.8)⨯+5.710=⨯=57答:积是57.【点评】此题考查列式计算.弄题里的关系,确定先列什么,再列什么,列出算式计算.五.解答题(共8小题,满分37分)26.(5分)某地打固定电话每次前3分钟内收费0.22元,超过3分钟每分钟收费0.11元(不足1分钟按1分钟计算),爸爸一次通话时间为8分26秒,他这次通话的费用是多少?【分析】爸爸通话时间8分26秒,应看成9分钟进行计算;把9分钟分成两部分,第一部分是前3分钟,收费0.22元,剩下的6分钟按照分钟0.11元收费;先用0.11乘6求出后6分钟收费的钱数,再加上前3分钟收费的钱数即可求解.【解答】解:8分26秒,应看成9分钟进行计算;-⨯+(93)0.110.22=⨯+60.110.22=+0.660.22=(元)0.88答:他这次通话的费用是0.88元.【点评】解答此题需要分情况探讨,明确题目中所给数量属于哪一种情况,由此选择正确的解题方法.27(6分)妈妈带100元去超市购物,她买了2袋大米,每袋33.5元;还买了0.8千克的肉,每千克24元.(1)剩下的钱够买1桶12元的油吗?(2)剩下的钱够买2桶7.5元一桶的油吗?【分析】(1)首先根据:总价=单价⨯数量,分别求出买大米和肉花了多少钱;然后用妈妈带的钱减去一共花的钱,求出剩下的钱数是多少;然后把它和买1桶12元的油花的钱比较大小即可.(2)首先根据:总价=单价⨯数量,用一桶油的价格乘2,求出买2桶7.5元一桶的油需要多少钱;然后把它和剩下的钱比较大小即可.【解答】解:(1)100(33.52240.8)-⨯+⨯=-+100(6719.2)=-10086.213.8=(元)因为13.812>所以剩下的钱够买1桶12元的油.答:剩下的钱够买1桶12元的油.(2)7.5215⨯=(元)因为1513.8>所以剩下的钱不够买2桶7.5元一桶的油.答:剩下的钱不够买2桶7.5元一桶的油.【点评】此题主要考查了乘法、加法的意义和应用,要熟练掌握,解答此题的关键是要明确单价、总价和数量的关系.28.五(1)班42名师生照相合影.每人一张照片,一共需要付多少钱? 加印一张:2.8元【分析】根据图意,五(1)班42名师生照相合影,共需42张照片,合影定价40元含8张照片,即还需加印42834-=张,每张2.8元,即可求出总价,进而解决问题.【解答】解:4034 2.8+⨯ 4095.2=+ 135.2=(元)答:一共需要付135.2元.【点评】解决此题的关键是读懂图意,根据总价=单价⨯数量,解决问题即可.29.在一个汽车停车场停车至少要交费5元,如果停车超过3小时每多停1小时(不足1小时按1小时计算)要多交1.2元.一辆汽车在停车场停了9小时36秒,这辆汽车的司机应交多少元停车费?【分析】首先用这辆车的停车时间减去3,求出超过3小时是多少时间,再乘每多停1小时车要多交的钱数,求出超过3小时部分需要交多少元,然后再加上5即可求出应交多少元. 【解答】解:9小时36秒3-小时6=小时36秒7≈(小时) 1.275⨯+ 8.45=+ 13.4=(元).答:这辆汽车的司机应交13.4元停车费.【点评】此题主要考查了乘法的意义,解答此题的关键是求出超过3小时部分需要交多少元.30.星期六,小明和爸爸一起去离家80千米的外婆家去为外婆祝寿.出发时,发现油箱中只剩下3升汽油了,爸爸问小明:“每升汽油可行驶8.5千米,我们往返一趟加15升汽油够吗?”请你帮小明回答这个问题.(要通过计算来判断)【分析】首先根据乘法的意义,用每升汽油可行驶的路程乘18(15318)+=,求出18升汽油可以行驶多少千米;然后把它和往返的路程比较大小即可. 【解答】解:8.5(153)⨯+=⨯8.518=(千米)153⨯=(千米)802160因为153160<,所以往返一趟加15升汽油不够.答:往返一趟加15升汽油不够.【点评】此题主要考查了乘法、加法的意义的应用,要熟练掌握,解答此题的关键是求出18升汽油可以行驶多少千米.31.移动公司有两种手机卡,采用的收费标准如下表,王叔叔的一个月通信量是200分钟左右,你帮他选一种合适他的手机卡.【分析】分别求出王叔叔,用两种卡各花的钱数,再进行比较,然后选择需要的是哪种卡,据此解答.【解答】解:王叔叔用A卡每月用的钱是:+⨯300.3200=+3060=(元),90王叔叔用B卡每月用的钱是:⨯=(元),0.6200120因90120<,用A卡花的钱少,所以王叔叔可用A卡.答:王叔叔用A卡合算,这样省钱.【点评】本题的关键是求出分别用两种卡每月花的钱数,再进行选择需的种类.32.(5分)快乐比较(1)一幢大楼有21层,每层高2.8米,这幢大楼约高多少米?(得数保留整数)(2)一幢大楼有21层,乘电梯每上升一层需3.3秒,从底层到最高层需要多少时间?【分析】(1)根据题意,可直接用21乘2.8进行计算即可;(2)从1楼到21楼一共有21120-=个间隔,每个间隔需要3秒,用乘法即可解答.【解答】解:(1)21 2.858.859⨯=≈(米),答:这幢大楼约高59米;(2)(211) 3.366-⨯=(秒),答:从底层到最高层需要66秒时间.【点评】此题主要考查的是乘法的意义和“四舍五入”法的应用;注意,爬楼的间隔数=层数1-.六.附加题(10分)33.(6分)为了鼓励节约用电,某市实行“阶梯电价”,收费标准如下表:(1)小华家这个月用电175千瓦时,电费是多少元?(2)小张家这个月用电189千瓦时,电费是多少元?(3)小丽家这个月用电245千瓦时,电费是多少元?【分析】(1)175千瓦时在0~180之间,单价是0.52元,用175度乘0.52即可计算出总价;(2)189比180度超出了1891809-=度,这9度按照0.57的单价收费,前180度按照单价0.52元收费,根据单价⨯数量=总价分别计算出两个部分的收费,再相加即可;(3)分为3部分:①180度以下部分:1800.52-⨯,③240以上部分⨯,②180~240之间部分:(240180)0.57 -⨯,三部分相加即可.(245240)0.87【解答】解:(1)1750.5291⨯=(元)答:电费是91元.(2)1800.52(189180)0.57⨯+-⨯=+93.6 5.13=(元)98.73答:电费是98.73元.(3)1800.52(240180)0.57(245240)0.87⨯+-⨯+-⨯93.634.2 4.35=++=(元)132.15答:电费是132.15元.【点评】解答此题需要分情况探讨,明确题目中所给数量属于哪一种情况,由此选择正确的解题方法.。
