2017年初中大同杯数学竞赛-答案
2017年全国初中数学联合竞赛(初二年级)试题参考答案及

在 Rt △ EAD 中,有 422 (98 x)2 x2 ,解得 x 58 .
2017 年全国初中数学联合竞赛试题(初二年级)参考答案及评分标准 第 2 页(共 5 页)
二、填空题:(本题满分 28 分,每小题 7 分)
1.使得等式 1 1 a 3 a 成立的实数 a 的值为_______. 【答】 8 . 由所给等式可得 (1 1 a)3 a2 .令 x 1 a ,则 x 0 ,且 a x2 1,于是有 (1 x)3 (x2 1)2 ,
4.已知正整数 a,b, c 满足 a2 6b 3c 9 0 , 6a b2 c 0 ,则 a2 b2 c2 = ( )
A. 424. 【答】C.
B. 430.
C. 441.
D. 460.
由已知等式消去 c 整理得 (a 9)2 3(b 1)2 75 ,所以 3(b 1)2 75 ,又 b 为正整数,解得1 b 6 .
2
2
Байду номын сангаас
3
A
D
F
所以梯形的面积为 1 (1 4) 4 2 10 2 .
2
3
3
E
6.如图,梯形 ABCD 中, AD // BC , A 90 ,点 E 在 AB 上,若 AE 42 ,
BE 28, BC 70 , DCE 45 ,则 DE =
()
B
C
A. 56.
B. 58.
C.60.
D. 62.
为 A. 4. 【答】B.
B.3.
C.2.
D.1.
()
若 (a,b, c) 为好数组,则 abc 2(a b c) 6c ,所以 ab 6 .显然, a 只能为 1 或 2.
2017年数学竞赛初中初赛答案

伊
1 006 1 007
伊…伊
2 004 2 005
伊
2 005 2 006
……………………………… 2 分
= 2 伊(1 + 2 + 3 + … + 2 005 + 2 006)
4分
= 2 006 伊 2 007
5分
= 4 026 042.
6分
14.(员)设爸爸追上乐乐用了 x 分钟援由题意列方程,得
5分
所以甲说的“801 班得第四”是对的;则丙说“803 班得第三”的对的;乙说“802 班得冠军”是对的.所以 804 班
是亚军.
9分
四、一鼓作气(本大题共 2 道小题,17 题 12 分,18 题 12 分,总计 24 分)
17. 当 a > 1 时,a >
1 a
;
1分
当 a = 1 时,a =
1 a
;当 a = 0 时,1a
不存在,没法比较;当 0 < a
< 1 或 a < -1 时,a <
1 a
.
12 分
18.(1)设年降水量为 x 万 m3,每人年平均用水量为 y m3.
1分
嗓 由题意,得
12 12
000 000
+ +
20x 15x
= 16 伊 20y, =(16 + 4)伊 15y.
9分
所以 a + b + c + d = 45,俞
11 分
将俞代入虞,愚,舆,余得
a = 3,b = 9,c = 12,d = 21,
13 分
所以 d - a = 21 - 3 = 18.
2017年全国初中数学联赛(初三组)初赛试卷参考答案及评分细则详解

2017年全国初中数学联赛(初三组)初赛试卷试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准.选择题和填空题只设7分和0分两档;解答题,请严格按照本评分标准规定的评分档次给分,不要再增加其他中间档次.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.一、选择题(本题满分42分,每小题7分)1、设实数a 、b 满足1-=-b a ,则ab b a 333+-的值为( B ) A 、3-B 、1-C 、1D 、3解析:()()()13332222233-=--=+---=+++-=+-b a ab b ab a ab b ab a b a ab b a 2、若实数a 为常数,关于x 的不等式组⎩⎨⎧-≤+722 x aa x 的整数解只有8个,则a 的值为(C )A 、1-B 、0C 、1D 、2解析:()10122127722222=⇒≤-⇒+-≤⇒+--⇒⎩⎨⎧-≤+a a a a a a x x a a x 3、在菱形ABCD 中,4=AB ,︒=∠60A ,E 为AB 的中点,若在线段BD 上取一点P ,则PE PA +的最小值是( D )A 、32B 、4C 、52D 、72解析:如图,连结AC ,EC 交BD 于点P ,则点P 是所求的 菱形ABCD 中,4=AB ,︒=∠60A ,E 为AB 的中点 32=⇒DE281612222=+=+=⇒DC DE CE72=⇒CE4、对于任意实数a ,b ,c ,用{}c b a M ,,表示三个数的平均数,用{}c b a ,,min 表示这三个数中最小的数,若{}=-+++y x y x y x M 2222,,{}y x y x y x -+++2222min ,,,则=+y x (A )A 、4-B 、2-C 、2D 、4解析:不妨设a 最小,则()()033=-+-⇒=++⇒=++⇒a c ab ac b a a cb a 00≥-≥-⇒ac a b , c a b ==⇒故4132222-=+⇒-=-=⇒-=+=++y x y x y x y x y x ,5、如图,ABC Rt ∆的斜边AB 与⊙O 相切于点P ,直角顶点C 在⊙O 上,若22=AC ,4=BC ,BEACDP则⊙O 的半径是( B )A 、3B 、32C 、4D 、62解析:如图,由射影定理得: DC AC BC ⋅=⇒2 24=⇒CD48222=+=⇒BC CD BD34=⇒BD 32=⇒BO6、不超过()615+的最大整数是( D )A 、1142B 、1145C 、1148D 、1151解析:()()3652615+=+a =+⇒526,b =-5261612==+⇒ab b a ,b a ,⇒是016122=+-x x 的两根016122=+-⇒a a ,016122=+-b b a a a 161223-=⇒, b b b 161223-=()()()[]()115216212161222233=+--+=+-+=+⇒b a ab b a b a b a b a由10103 b b ⇒ 3a ⇒的最大整数不超过1151二、填空题(本大题满分28分,每小题7分)7、若012=-+x x ,则()()11124---+x x x x 的值为 .答案:3解析:()()11124---+x x x x ()()()()()3221111122322=++=++=--+-++⇒x x xxx x x x x x x x 8、在正方形ABCD 中,点E 、F 分别在线段BC 、CD 上,且︒=∠20BAE ,︒=∠25DAF ,则CEF ∠等于 .答案:︒40解析: 如图所示,ABG ADF ∆≅∆AE AE AD AG DAF GAB ==︒=∠=∠⇒,,25 AFE AGE ∆≅∆⇒ ︒=∠=∠⇒70AEB AEF︒=∠⇒40CEF9、小丽与小明一起用A 、B 两个骰子玩游戏,以小丽掷的A 骰子朝上的数字为x ,小明掷的BBEAFGBDC骰子朝上的数字为y ,来确定点(x ,y ),那么,他们各掷一次所确定的点P (x ,y )落在已知抛物线542+-=x x y 的概率为 .答案:91解析:两个立方体都有6个数字,那么共有36种可能,可在抛物线上的有(1,2)、(2,1)、(3,2)、(4,5)共4种情况,故概率为9110、如图,设点P 在函数x y 6=的图像上,x PC ⊥轴于点C ,交函数xy 2=的图像于点A ,y PD ⊥轴于点D ,交函数xy 2=的图像于点B ,则四边形P AOB 的面积为 .答案:4 解析:四边形P AOB 的面积=矩形ODPC AOC DBO S S ∆∆--=426=- 三、(本大题满分20分)11、已知关于x 的一元二次方程052=+-kx x 与052=-+k x x 只有一个公共的实根,求关于x 的方程k kx x =+2所有的实根之和。
2017年第31届大同中学杯详解
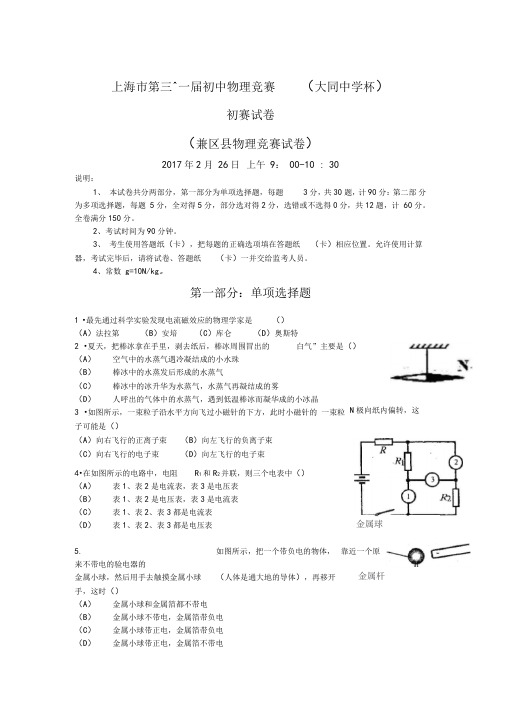
N 极向纸内偏转,这金属球金属杆上海市第三^一届初中物理竞赛(大同中学杯)初赛试卷(兼区县物理竞赛试卷)2017年2月 26日 上午 9: 00-10 : 30说明:1、 本试卷共分两部分,第一部分为单项选择题,每题3分,共30题,计90分:第二部 分为多项选择题,每题 5分,全对得5分,部分选对得2分,选错或不选得0分,共12题,计 60分。
全卷满分150分。
2、 考试时间为90分钟。
3、 考生使用答题纸(卡),把每题的正确选项填在答题纸 (卡)相应位置。
允许使用计算器,考试完毕后,请将试卷、答题纸(卡)一并交给监考人员。
4、 常数 g=10N/kg 。
第一部分:单项选择题1 •最先通过科学实验发现电流磁效应的物理学家是 ()(A )法拉第 (B )安培(C )库仑(D )奥斯特2 •夏天,把棒冰拿在手里,剥去纸后,棒冰周围冒出的白气”主要是()(A ) 空气中的水蒸气遇冷凝结成的小水珠 (B ) 棒冰中的水蒸发后形成的水蒸气(C ) 棒冰中的冰升华为水蒸气,水蒸气再凝结成的雾(D )人呼出的气体中的水蒸气,遇到低温棒冰而凝华成的小冰晶3 •如图所示,一束粒子沿水平方向飞过小磁针的下方,此时小磁针的 一束粒子可能是()(A )向右飞行的正离子束 (B )向左飞行的负离子束 (C )向右飞行的电子束(D )向左飞行的电子束4•在如图所示的电路中,电阻 R 1和R 2并联,则三个电表中()(A ) 表1、表2是电流表,表3是电压表 (B ) 表1、表2是电压表,表3是电流表 (C ) 表1、表2、表3都是电流表 (D ) 表1、表2、表3都是电压表5.如图所示,把一个带负电的物体, 靠近一个原来不带电的验电器的金属小球,然后用手去触摸金属小球 (人体是通大地的导体),再移开手,这时()(A ) 金属小球和金属箔都不带电 (B ) 金属小球不带电,金属箔带负电 (C ) 金属小球带正电,金属箔带负电 (D )金属小球带正电,金属箔不带电6•木块静止在水平桌面上,关于桌面对木块的弹力跟木块受到的重力之间关系的说法中,(B) 一对平衡力(D)作用在同一物体上的力(A) 7 (B)12 (C)16 (D)17错误的是()(A)—对作用力和反作用力(C) 一对大小相等、方向相反的力7•如图所示,底面积不同的柱状容器甲、乙分别盛有两种液体,液体对容器底部的压强P甲<P乙•若要使两容器中的液体对容器底部的压强相等,一定可行的方法是在()(A)甲中抽取、乙中倒入相同高度的原有液体(B)乙中抽取、甲中倒入相同高度的原有液体(C)甲、乙中同时抽取相同高度的原有液体(D)甲、乙中同时倒入相同高度的原有液体8.列车匀速进站,机车发出频率为f i的汽笛声,一站在站台上的旅客听到的汽笛声频率为f2, 则下列判断中正确的是()(A) f i < f2 (B) f i = f2 (C) f i > f2 (D)无法判断9.电阻R i=1 Q, R2=1 Q, R3=3 Q,禾U用这三个电阻可能获得的不同阻值的个数最多为()10.如图所示,在柱状容器内放入一块长方体实心铜块,然后缓慢注入水,并且使铜块与容器底紧贴(使水不进入铜块与容器底部之间接触处),此时容器底部所承受的压力大小为F i,若略微抬起铜块,使水进入接触处,待铜块稳定后,容器底部所承受的压力大小为F2,则()(A)F i >F2 (B)F i <F2 (C)F i =F2 (D)无法判断ii .形状一样、质量相等的A , B两个契形物块放置在水平桌面上。
2017年大同杯初赛试卷及答案

上海市第三十一届初中物理竞赛(大同中学杯)初赛试卷(兼区县物理竞赛试卷)2017年2月26日上午9:00-10:30说明:1、本试卷共分两部分,第一部分为单项选择题,每题3分,共30题,计90分:第二部分为多项选择题,每题5分,全对得5分,部分选对得2分,选错或不选得0分,共12题,计60分。
全卷满分150分。
2、考试时间为90分钟。
3、考生使用答题纸(卡),把每题的正确选项填在答题纸(卡)相应位置。
允许使用计算器,考试完毕后,请将试卷、答题纸(卡)一并交给监考人员。
4、常数g=10N/kg。
第一部分:单项选择题1.最先通过科学实验发现电流磁效应的物理学家是( )(A)法拉第(B)安培(C)库仑(D)奥斯特2.夏天,把棒冰拿在手里,剥去纸后,棒冰周围冒出的“白气”主要是( )(A)空气中的水蒸气遇冷凝结成的小水珠(B)棒冰中的水蒸发后形成的水蒸气(C)棒冰中的冰升华为水蒸气,水蒸气再凝结成的雾(D)人呼出的气体中的水蒸气,遇到低温棒冰而凝华成的小冰晶3.如图所示,一束粒子沿水平方向飞过小磁针的卞方,此时小磁针的N极向纸内偏转,这一束粒子可能是( )(A)向右飞行的正离子束(B)向左飞行的负离子束(C)向右飞行的电子束(D)向左飞行的电子束4.在如图所示的电路中,电阻R1和R2并联,则三个电表中( )(A)表1、表2是电流表,表3是电压表(B)表1、表2是电压表,表3是电流表(C)表1、表2、表3都是电流表(D)表1、表2、表3都是电压表5.如图所示,把一个带负电的物体,靠近一个原来不带电的验电器的金属小球,然后用手去触摸金属小球(人体是通大地的导体),再移开手,这时( )(A)金属小球和金属箔都不带电(B)金属小球不带电,金属箔带负电(C)金属小球带正电,金属箔带负电(D)金属小球带正电,金属箔不带电6.木块静止在水平桌面上,关于桌面对木块的弹力跟木块受到的重力之间关系的说法中,错误的是( )(A)一对作用力和反作用力(B)一对平衡力(C)一对大小相等、方向相反的力(D)作用在同一物体上的力7.如图所示,底面积不同的柱状容器甲、乙分别盛有两种液体,液体对容器底部的压强P 甲<P乙.若要使两容器中的液体对容器底部的压强相等,一定可行的方法是在( )(A)甲中抽取、乙中倒入相同高度的原有液体(B)乙中抽取、甲中倒入相同高度的原有液体(C)甲、乙中同时抽取相同高度的原有液体(D)甲、乙中同时倒入相同高度的原有液体8.列车匀速进站,机车发出频率为f1的汽笛声,一站在站台上的旅客听到的汽笛声频率为f2,则下列判断中正确的是( )(A) f1 < f2 (B) f1 = f2(C) f1 > f2(D)无法判断9.电阻R1=1Ω,R2=1Ω,R3=3Ω,利用这三个电阻可能获得的不同阻值的个数最多为( ) (A)7 (B)12 (C)16 (D)1710.如图所示,在柱状容器内放入一块长方体实心铜块,然后缓慢注入水,并且使铜块与容器底紧贴(使水不进入铜块与容器底部之间接触处),此时容器底部所承受的压力大小为F1,若略微抬起铜块,使水进入接触处,待铜块稳定后,容器底部所承受的压力大小为F2,则( ) (A)F1 >F2 (B)F1 <F2(C)F1 =F2(D)无法判断11.形状一样、质量相等的A,B两个契形物块放置在水平桌面上。
2017年全国初中数学联合竞赛试题及详细解答(含一试二试)

2. 设 O是 锐 角 三 角 形 ABC的 外 心 , D,E分 别 为 线 段 BC,OA的 中 点 ,
,
,则
_________.
3.题目与(A)卷第 3题相同. 4.题目与(A)卷第 4题相同
第二试 (A)
一、(本题满分 20分)已知实数 x,y满足 x+y=3,
,求
的值.
二、(本题满分25分)如图,△ABC中,AB AC, BAC 45,E是 BAC的 外角平分线与△ABC 的外接圆的交点,点F在AB 上且EF AB.已知AF 1,BF
1.已知二次函数 y ax2 bx c(c 0)的图象与x轴有唯一交点,则二次函
数
y a3x2 b3x c3 的图象与x轴的交点个数为 ( )
A.0
B.1
C.2
D.不确定.
2.题目与(A)卷第1 题相同.
3.题目与(A)卷第3 题相同.
4.已知正整数a,b,c满足 a2 6b 3c 9 0, 6a b2 c 0,则a2 b2 c2
CB的延长线上, 满足
.已知BC=15,BF=6,BD=3,则AE= ( )
A.
B.
C.
D.
6.对于正整数 n,设 an是最接近 的整数,则
A.191/7
B.192/7
C.193/7
() D.194/7
二、填空题(本题满分 28分,每小题 7分) (本题共有 4个小题,要求直接将答案写在横线上.)
1.使得等式
2017 年全国初中数学联合竞赛试题
2017年3月26日(星期日)上午8:30-11:30
第一试(A)
一、选择题(本题满分 42分,每小题 7分) (本题共有 6个小题,每题均给出了代号为 A,B,C,D的四个答案,其中有且仅
2017年全国初中数学联合竞赛试题参考答案和评分标准(1)

2017年全国初中数学联合竞赛试题参考答案和评分标准(1)2017年全国初中数学联合竞赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试(A)一、选择题:(本题满分42分,每小题7分)1.已知实数,,abc满足213390abc,3972abc,则32bcab??=()A.2.B.1.C.0.D.1?.【答】B.已知等式可变形为2(2)3(3)90abbc,3(2)(3)72abbc,解得218ab??,318bc??,所以32bcab1.2.已知△ABC的三边长分别是,,abc,有以下三个结论:(1)以,,abc为边长的三角形一定存在;(2)以222,,abc为边长的三角形一定存在;(3)以||1,||1,||1abbcca为边长的三角形一定存在.其中正确结论的个数为()A.0.B.1.C.2.D.3.【答】C.不妨设abc??,则有bca??.(1)因为bca??,所以2bcbca,即22()bca??(),即bca??,故以,,abc为边长的三角形一定存在;(2)以2,3,4abc为边长可以构成三角形,但以2224,9,16abc为边长的三角形不存在;(3)因为abc??,所以||11,||11,||11ababbcbccaac,故三条边中||1ca??大于或等于其余两边,而||1||111abbcabbc()()()()111||1acacca=,故以||1ab??,||1bc??,||1ca??为边长的三角形一定存在.3.若正整数,,abc满足abc??且2()abcabc,则称(,,)abc为好数组.那么,好数组的个数为()A.1.B.2.C.3.D.4.【答】C.若(,,)abc为好数组,则2()6abcabcc,所以6ab?.显然,a只能为1或2.若a=2,由6ab?可得2b?或3,2b?时可得4c?,3b?时可得52c?(不是整数);若a=1,则2(1)bcbc,于是可得(2)(2)6bc,可求得(,,)abc =(1,3,8)或(1,4,2017年全国初中数学联合竞赛试题参考答案及评分标准第1页(共7页)5).综合可知:共有3个好数组,分别为(2,2,4),(1,3,8)和(1,4,5).4.设O是四边形ABCD的对角线AC、BD的交点,若180BADACB,且3BC?,4AD?,5AC?,6AB?,则DOOB=()A.109.B.87.C.65.D.43.【答】A.过B作//BEAD,交AC的延长线于点E,则180ABEBAD ACB??,所以△ABC∽△AEB,所以ACBCABEB?,所以631855ABBCEBAC.再由//BEAD,得4101895DOADOBBE.5.设A是以BC为直径的圆上的一点,ADBC?于点D,点E在线段DC上,点F在CB的延长线上,满足BAFCAE.已知15BC?,6BF?,3BD?,则AE=()A.43.B.213.C.214.D.215.【答】B.如图,因为BAFCAE,所以BAFBAECAEBAE,即90FAEBAC.又因为ADBC?,故2ADDEDFDBDC.而639DFBFBD,15312DCBCBD,所以29312ADDE,所以6AD?,4DE?.从而222264213AEADDE.6.对于正整数n,设na是最接近n的整数,则1232001111aaaa()A.1917.B.1927.C.1937.D.1947.【答】A.对于任意自然数k,2211()24kkk不是整数,所以,对于正整数n,12n?一定不是整数.设m是最接近n的整数,则1||2mn??,1m?.易知:当1m?时,1||2mn2211()()mnm??221144mmnmm.于是可知:对确定的正整数m,当正整数n满足221mmnmm时,m是最接近n的整数,即nam?.所以,使得na=m的正整数n的个数为2m.注意到2213131822001414210,因此,12200,,,aaa?中,有:2个1,4个2,6个3,2017年全国初中数学联合竞赛试题参考答案及评分标准第2页(共7页)EOCBADCBFDE8个4,……,26个13,18个14.所以123200111111111191246261812313147aaaa.二、填空题:(本题满分28分,每小题7分)1.使得等式311aa成立的实数a的值为_______.【答】8.由所给等式可得32(11)aa.令1xa??,则0x?,且21ax??,于是有322(1)(1)xx,整理后因式分解得2(3)(1)0xxx,解得10x?,23x?,31x??(舍去),所以1a??或8a?.验证可知:1a??是原方程的增根,8a?是原方程的根.所以,8a?.2.如图,平行四边形ABCD中,72ABC,AFBC?于点F,AF交BD于点E,若2DEAB?,则AED?=_______.【答】66?.取DE的中点M,在Rt△ADE中,有12AMEMDEAB.设AED,则1802AME,18ABM.又ABMAMB,所以180218,解得66.3.设,mn是正整数,且mn?.若9m与9n的末两位数字相同,则mn?的最小值为.【答】10.由题意知,999(91)mnnmn是100的倍数,所以91mn??是100的倍数,所以9mn?的末两位数字是01,显然,mn?是偶数,设2mnt??(t是正整数),则29981mntt.计算可知:281的末两位数字是61,381的末两位数字是41,481的末两位数字是21,581的末两位数字是01.所以t的最小值为5,从而可得mn?的最小值为10.4.若实数,xy满足3331xyxy,则22xy?的最小值为.【答】12.因为333322031()(1)333xyxyxyxyxyxy22(1)[()()(1)(1)]3(1)xyxyxyxyxy2017年全国初中数学联合竞赛试题参考答案及评分标准第3页(共7页)MEFCBDA22(1)(1)xyxyxyxy2221(1)[()(1)(1)]2xyxyxy,所以1xy或1xy??.若1xy,则22xy?=2.若1xy??,则22222111[()()][1()]222xyxyxyxy,当且仅当12xy??时等号成立.所以,22xy?的最小值为12.第一试(B)一、选择题:(本题满分42分,每小题7分)1.已知二次函数2(0)yaxbxcc的图象与x轴有唯一交点,则二次函数3233yaxbxc的图象与x轴的交点个数为()A.0.B.1.C.2.D.不确定.【答】C.因为二次函数2yaxbxc的图象与x轴有唯一交点,所以2140bac,所以240bac??.故二次函数3233yaxbxc的判别式323363623211()4(4)()1616bacbacbb61516b?0?,所以,二次函数3233yaxbxc的图象与x轴有两个交点.2.题目和解答与(A)卷第1题相同.3.题目和解答与(A)卷第3题相同.4.已知正整数,,abc满足26390abc,260abc,则222abc??=()A.424.B.430.C.441.D.460.【答】C.由已知等式消去c整理得22(9)3(1)75ab,所以23(1)75b??,又b为正整数,所以16b??.若b=1,则2(9)75a??,无正整数解;若b=2,则2(9)72a??,无正整数解;若b=3,则2(9)63a??,无正整数解;若b=4,则2(9)48a??,无正整数解;若b=5,则2(9)27a??,无正整数解;若b=6,则2(9)0a??,解得9a?,此时18c?.2017年全国初中数学联合竞赛试题参考答案及评分标准第4页(共7页)因此,9a?,b=6,18c?,故222abc=441.5.设O是四边形ABCD的对角线AC、BD的交点,若180BADACB,且3BC?,4AD?,5AC?,6AB?,则DOOB=()A.43.B.65.C.87.D.109.【答】D.解答过程与(A)卷第4题相同.6.题目和解答与(A)卷第5题相同.二、填空题:(本题满分28分,每小题7分)1.题目和解答与(A)卷第1题相同.2.设O是锐角三角形ABC的外心,,DE分别为线段,BCOA的中点,7ACBOED,5ABCOED,则OED?=_________.【答】10?.如图,设OEDx??,则5ABCx??,7ACBx??,DOC??18012BACx,10AOCx??,所以1802AODx,180(1802)ODExxx,所以1122ODOEOAOC,所以60DOC,从而可得10x??.3.题目和解答与(A)卷第3题相同.4.题目和解答与(A)卷第4题相同.第二试(A)一、(本题满分20分)已知实数,xy满足3xy??,221112xyxy,求55xy?的值.解由221112xyxy可得2233222()xyxyxyxyxy.设xyt?,则222()292xyxyxyt,332()[()3]3(93)xyxyxyxyt,代入上式可得22(392)3(93)tttt,解得1t?或3t?.……………………10分当3t?时,3xy?,又3xy??,故,xy是一元二次方程2330mm的两实数根,但易知此方程没有实数根,不合题意.……………………15分当1t?时,1xy?,又3xy??,故,xy是一元二次方程2310mm的两实数根,符合题意.此时552233222()()()(92)[3(93)]3123xyxyxyxyxyttt.……………………20分2017年全国初中数学联合竞赛试题参考答案及评分标准第5页(共7页)DEOBAC二、(本题满分25分)如图,△ABC中,ABAC?,45BAC,E 是BAC?的外角平分线与△ABC的外接圆的交点,点F在AB上且EFAB?.已知1AF?,5BF?,求△ABC的面积.解在FB上取点D,使FD=AF,连接ED并延长,交△ABC的外接圆于点G.由EF⊥AD,AF=FD知△AED是等腰三角形,所以∠AED=1802??∠EAD=∠BAC,……………………10分所以??AGBC?,所以??ACBG?,所以AC=BG (15)分又∠BGE=∠BAE=∠ADE=∠BDG,所以BG=BD,所以AC=BD =5-1=4,……………………20分△ABC的AB边上的高sin4522hAC.所以,△ABC的面积116226222SABh (25)分三、(本题满分25分)求所有的正整数数对(,)ab,使得34938ba.解显然,4938b??为奇数,所以a为奇数.又因为33493849385ba,所以5a?.……………………5分由34938ba可得38493ba,即22(2)(24)73baaa.……………………10分设2(2,24)aaad,则d为奇数.注意到224(2)(4)12aaaa,所以|12d,所以d=1或3.……………………15分若d=1,则有22 27, 243,b aaa或22 23, 247, ba aa均无正整数解.……………………20分若d=3,则有221237,243,baaa?或12223,2437,baaa解得11a?,3b?.所以,满足条件的正整数对只有一个,为(11,3).……………………25分第二试(B)一、(本题满分20分)已知实数,,abc满足abc??,16abc,22211284abcabc,求c的值.解设abx??,aby?,依题意有2212(16)(16)1284xyxyx,整理得21(8)(8)8xyx,所以8x?或8(8)yx??.……………………10分2017年全国初中数学联合竞赛试题参考答案及评分标准第6页(共7页)FEABCD(1)若8x?,则8ab??,此时c=8.(2)若8(8)yx??,即8(8)abab,则(8)(8)0ab,所以8a?或8b?.当8a?时,结合abc??可得24abc,与16abc矛盾.当8b?时,结合abc??及16abc可得0a?,8c?.综合可知:8c?.……………………20分二、(本题满分25分)求所有的正整数m,使得21221mm 是完全平方数.解当m=1时,212211mm是完全平方数.……………………5分当1m?时,设212221mmn(n为正整数).注意到2112112122212(2)221(21)(2)mmmmmm,故可得12122(21)(2)mmn,……………………10分所以22212112(21)(21)(21)mmmmnnn.……………………15分设121mxn,121myn,则xy?,222mxy??,所以,xy均为2的方幂.……………………20分又22myx被4除余数为2,所以,只可能2x?,2my?,故22222mm,解得3m?.综上可知:满足条件的正整数m有两个,分别为1和3.……………………25分三、(本题满分25分)如图,O为四边形ABCD内一点,OADOCB,OAOD?,OBOC?.求证:2222ABCDADBC.证明由题设条件可知90AODBOC,又OADOCB,所以△AOD∽△COB,……………………5分所以ODAOOBCO?,从而OCAOOBOD?.……………………10分又AOCAOBBOCAOBAODDOB,所以△AOC∽△DOB,所以OACODB.……………………15分设AC和BD交于点P,则90APDAOD,所以ACDB?,……………………20分所以222222222222()()()()ABCDAPPBPDPCAPPDPBPCADBC .……………………25分2017年全国初中数学联合竞赛试题参考答案及评分标准第7页(共7页)PDAO CB。
2017年全国初中数学联赛(初三组)初赛试卷参考答案及评分细则详解

2017年全国初中数学联赛(初三组)初赛试卷参考答案及评分细则详解2017年全国初中数学联赛(初三组)初赛试卷试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准。
选择题和填空题只设7分和分两档;解答题,请严格按照本评分标准规定的评分档次给分,不要再增加其他中间档次。
如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数。
一、选择题(本题满分42分,每小题7分)1、设实数a、b满足a-b=-1,则a³-b³+3ab的值为(B)A、-3B、-1C、1D、3解析:a³-b³+3ab=(a-b)(a²+ab+b²)+3ab=-(a-b)=-12、若实数a为常数,关于x的不等式组{x+a²≤2a x≤-7}的整数解只有8个,则a的值为(C)A、-1B、0C、1D、2解析:{x+a²≤2a x≤-7}⇒-7≤x≤-a²+2a⇒1≤-a²+2a⇒(a-1)≤0⇒a≤1因为a是常数,所以a=13、在菱形ABCD中,AB=4,E为AB的中点,若在线段BD上取一点P,则PA+PE∠A=60°,的最小值是(D)A、23B、4C、25D、27解析:如图,连结AC,EC交BD于点P,则点P是所求的菱形ABCD中,AB=4,∠A=60°,E为AB的中点DE=√3×AB/2=2√3CE=DE+DC=2√3+4AE=√(CE²+AC²)=√(28²+16)=4√10PA+PE∠A=AE×sin(∠APE)=4√10×sin(60°+∠BPD)令∠BPD=θ,则∠APE=60°+θPA+PE∠A=4√10×(cosθ+√3sinθ)=4√10×(sinθ+√3cosθ+2)/24√10×(sin(θ-60°)+2)/2=2√10×(√3cosθ+sinθ+1)≥2√10所以最小值为2√10,即274、对于任意实数a,b,c,用M{a,b,c}表示三个数的平均数,用min{a,b,c}表示这三个数中最小的数,若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},则x+y=(A)A、-4B、-2C、2D、4解析:不妨设a最小,则M{a,b,c}=aa+b+c=3ab-a)+(c-a)=ab-a≥0,c-a≥0b=a,c=a2x+y+2=x+2y=2x-yx=-3,y=-1x+y=-45、如图,RtΔABC的斜边AB与⊙O相切于点P,直角顶点C在⊙O上,若AC=22,BC=4,则⊙O的半径是(B)A、3B、23C、4D、26解析:如图,由射影定理得:BC²=AC×DCCD=4²/22BD²=CD²+BC²=48BO=BD/2=√48/2=2√3OP=OB-√AB²-AP²=2√3-√22²-4²=2√3-2r=OP=2√3-2=2(√3-1)=2∙236、不超过1142无明显问题的段落,不需修改)即有:x2kx5x 2x25x k x 2将两式相减,得:10x52x化XXX:2x210x50由于方程只有一个公共实根,所以判别式为0,即:24250解得:2或 5又因为x2kx k的实根为0或k,所以:当2时,实根为0,k,所以实根之和为k;当5时,实根为0,k,所以实根之和为k;综上所述,关于x的方程x2kx k所有的实根之和为k k0.题目一:已知方程组 $\begin{cases}\alpha^2-k\alpha+5=0 \\\alpha^2+5\alpha-k=0\end{cases}$,求所有实数根的和。
