信号与系统课件第八章(电子)
合集下载
信号与系统ppt课件

2.对于(at+b)形式的冲激信号,要先利用冲激信 号的展缩特性将其化为(t+b/a) /|a|形式后,
方可利用冲激信号的抽样特性与筛选特性。
完整版ppt课件
25
二、奇异信号
3. 斜坡信号
定义:
r(t)
t 0
t 0 t 0
或 r(t)tu(t)
r (t )
1
0
1
t
完整版ppt课件
26
二、奇异信号
x(t)(t t0)x(t0)(t t0)
完整版ppt课件
x(t ) (1)
t t0 x(t) (t t0 )
( x(t0 ) ) t
t0
19
二、奇异信号
2. 冲激信号
(6) 冲激信号的性质
② 抽样特性
x(t)(tt0)dtx(t0)
证明:
x(t)(t t0)dt
利用筛
选特性
x(t0)(t t0)dt x(t0) (t t0)dt x(t0)
(7)e4t (22t) (8)e2tu(t)(t1)
完整版ppt课件
23
解:
(1 ) sit)n ((tπ 4)d t siπ 4 n )(2/2
(2 ) 2 3 e 5 t (t 1 )d t e 5 1 1 /e 5
(3) 4 6e2t (t8)dt0
(4 ) e t(2 2 t)d t e t1 2( t 1 )d t 2 1 e
(2) x ( t) u ( t 1 ) 2 r ( t) 2 r ( t 1 )
完整版ppt课件
28
二、奇异信号
4. 冲激偶信号 定义: '(t) d(t)
dt
方可利用冲激信号的抽样特性与筛选特性。
完整版ppt课件
25
二、奇异信号
3. 斜坡信号
定义:
r(t)
t 0
t 0 t 0
或 r(t)tu(t)
r (t )
1
0
1
t
完整版ppt课件
26
二、奇异信号
x(t)(t t0)x(t0)(t t0)
完整版ppt课件
x(t ) (1)
t t0 x(t) (t t0 )
( x(t0 ) ) t
t0
19
二、奇异信号
2. 冲激信号
(6) 冲激信号的性质
② 抽样特性
x(t)(tt0)dtx(t0)
证明:
x(t)(t t0)dt
利用筛
选特性
x(t0)(t t0)dt x(t0) (t t0)dt x(t0)
(7)e4t (22t) (8)e2tu(t)(t1)
完整版ppt课件
23
解:
(1 ) sit)n ((tπ 4)d t siπ 4 n )(2/2
(2 ) 2 3 e 5 t (t 1 )d t e 5 1 1 /e 5
(3) 4 6e2t (t8)dt0
(4 ) e t(2 2 t)d t e t1 2( t 1 )d t 2 1 e
(2) x ( t) u ( t 1 ) 2 r ( t) 2 r ( t 1 )
完整版ppt课件
28
二、奇异信号
4. 冲激偶信号 定义: '(t) d(t)
dt
通信原理(第八章新型数字带通调制技术)PPT课件

实例分析
QPSK(四相相移键控调制)
在PSK的基础上,将相位划分为四个不同的状态,每个状态表示两个 比特的信息,提高了频谱利用率和传输速率。
16-QAM(十六进制正交幅度调制)
在QAM的基础上,将幅度划分为16个不同的状态,每个状态表示4个 比特的信息,进一步提高了频谱利用率和传输速率。
OFDM(正交频分复用调制)
20世纪70年代,随着数字信号处理技 术的发展,多种新型数字带通调制技 术如QPSK、QAM等开始出现。
02
数字带通调制技术的基本原理
数字信号的调制过程
调制概念
调制是将低频信号(如声音、图像等)转换成高频信号的过程, 以便传输。
数字信号的调制方式
数字信号的调制方式主要有振幅键控(ASK)、频率键控(FSK) 和相位键控(PSK)等。
通信原理(第八章新型数字带 通调制技术)ppt课件
• 引言 • 数字带通调制技术的基本原理 • 新型数字带通调制技术介绍 • 新型数字带通调制技术的应用场景
• 新型数字带通调制技术的优势与挑 战
• 新型数字带通调制技术的实现方法 与实例分析
01
引言
新型数字带通调制技术的定义与重要性
定义
新型数字带通调制技术是指利用数字 信号调制载波的幅度、频率或相位, 以实现信号传输的技术。
光纤通信系统
在光纤通信系统中,新型数字带通调制技术如偏振复用正交频分复用(PD-OFDM) 被用于实现高速、大容量的数据传输,满足不断增长的网络流量需求。
卫星通信系统
广播卫星
在广播卫星中,新型数字带通调制技术如正交频分复用(OFDM)被用于发送多路电视信号和其他多媒 体内容,提供高质量的广播服务。
将高速数据流分割成多个低速数据流,在多个子载波上进行调制,提 高了频谱利用率和抗多径干扰能力。
信号与系统3-8波特图课件
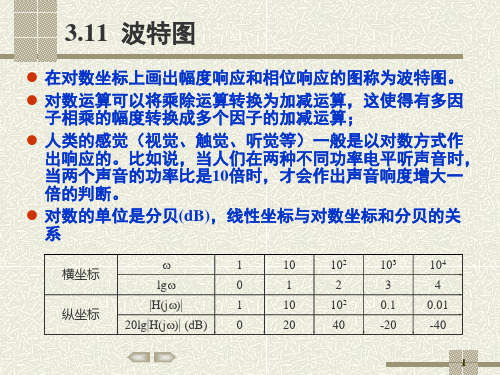
当=0.1时,G1= -20dB; =1时,G1=0dB; =10时,G1= 20dB。
G2(dB) 20dB/ dec
20
1()
90
0 0.1
1
10
20
0
(a) 幅度的波特图
(b) 相位的波特图
4
一阶极点因子
一阶极点因子为
H1 (s)
s
a
a
1 1 s/
a
H1 ( j)
1
1
j
/a
G1 20 lg | 1 j / a |
11
二阶极点因子
幅度波特图
= a 称为转折频率,最大误差
G1( a ) 20 lg(b a / a)dB
二阶极点因子的相位
1
()
arc
tan( 1
b
/
2
a /
a
)
在低频段,当<< a 时
1() 0
在高频段,当>> a 时
1() 180
当= a 时
1 () 90
转折频率也称截止频率
G1(dB)
a
0
20
40
10 a
40dB/ dec
1()
0.1 a 0 90 180
a
10 a
90/ dec
12
二阶零点因子
二阶零点因子
H 2 (s)
s2
bs a
a
1
bs /
a
s2
/
a
画法与二阶极点的画法相同,仅仅有一个正负号 的变化。
G2 (dB)
40 20
0
a
40dB/ dec
10 a
G2(dB) 20dB/ dec
20
1()
90
0 0.1
1
10
20
0
(a) 幅度的波特图
(b) 相位的波特图
4
一阶极点因子
一阶极点因子为
H1 (s)
s
a
a
1 1 s/
a
H1 ( j)
1
1
j
/a
G1 20 lg | 1 j / a |
11
二阶极点因子
幅度波特图
= a 称为转折频率,最大误差
G1( a ) 20 lg(b a / a)dB
二阶极点因子的相位
1
()
arc
tan( 1
b
/
2
a /
a
)
在低频段,当<< a 时
1() 0
在高频段,当>> a 时
1() 180
当= a 时
1 () 90
转折频率也称截止频率
G1(dB)
a
0
20
40
10 a
40dB/ dec
1()
0.1 a 0 90 180
a
10 a
90/ dec
12
二阶零点因子
二阶零点因子
H 2 (s)
s2
bs a
a
1
bs /
a
s2
/
a
画法与二阶极点的画法相同,仅仅有一个正负号 的变化。
G2 (dB)
40 20
0
a
40dB/ dec
10 a
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第8章 z变换、离散时间系统的z域分

(7)
X
z
1 2
n
u
n
u
n
10
z
n
9 n0
1 2
n
z
n
9 n0
1 2z
n
1
1 2z
1 1
10
z 0
2z
X(z)的零、极点分布图如图 8-2-1(g)所示。
(8)
8 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平
X
z
n台
1 2
圣才电子书
十万种考研考证电子书、题库视频学习平
台
第 8 章 z 变换、离散时间系统的 z 域分析
8.1 复习笔记
从本章开始陆续讨论 Z 变换的定义、性质以及它与拉氏变换、傅氏变换的联系。在此 基础上研究离散时间系统的 z 域分析,给出离散系统的系统函数与频率响应的概念。通过 本章,读者应掌握对于离散时间信号与系统的研究,是先介绍 z 变换,然后引出序列的傅 里叶变换以及离散傅里叶变换(第九章)。
4 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平
台
于实轴的直线映射到 z 平面是负实轴;
(3)在 s 平面上沿虚轴移动对应于 z 平面上沿单位圆周期性旋转,每平移 ωs,则沿
单位圆转一圈。
2.z 变换与拉氏变换表达式
Z
x nT X z zesT X s Z
n
u
n
1 3
n
u
n
z
n
n
(3)
X
z
n
1 3
n
u
n
z
n
n0
信号与系统(第3版)课件8.5

BX
(
z)
H(z)
整理得
Q(z) (zI A)1 zq[0] (zI A)1 BX (z)
Y
(
z)
C
(
zI
A)1
zq[0]
[C
(
zI
A)1
B
D]X
(
z)
Yzi (z)
Yzs (z)
然后再对Q(z)和Y(z)进行z反变换即可得到q[k]和y[k]。
离散系统的状态方程和输出方程的z域求解
[例] 已知描述某离散系统的状态方程和输出方程为
便于计算机迭代求解
0
1
6
1 5 6
19
1613 36
0 1
1
113
36
667
216
0
A
1
6
1
5
6
B
0
1
q[0]
2 3
x[k] u[k]
离散系统的状态方程和输出方程的时域求解
求解输出方程: y[k] Cq[k] Dx[k]
k=0代入得:
y[0] Cq[0] Dx[0]
x[k] u[k]
离散系统的状态方程和输出方程的时域求解
离散系统的状态方程为:
q[k +1] Aq[k] Bx[k]
在给定系统的初始状态q[k0]后,可直接用迭代法进行求解。
q[k0 1] Aq[k0 ] Bx[k0 ] q[k0 2] Aq[k0 1] Bx[k0 1]
A2q[k0 ] ABx[k0 ] Bx[k0 1]
求解状态方程: q[k +1] Aq[k] Bx[k]
k=0代入得:
q[1] Aq[0] Bx[0]
信号与系统-吴大正PPT课件

■ 第 17 页
§1.2 信号的描述和分类
信号的描述 信号的分类 几种典型确定性信号
■ 第 18 页
一、信号的描述
信号是信息的一种物理体现。它一般是随时间或 位置变化的物理量。
信号按物理属性分:电信号和非电信号。它们 可以相互转换。
电信号容易产生,便于控制,易于处理。本课 程讨论电信号——简称“信号”。
▲
■
第1页
信号与系统
是电子技术、信息工程、通信工程 等专业重要的学科基础课
课程介绍
Signals and Systems
电子技术、 信息工程、 通信工程 等专业的 考研课程
■
第3页
课程位置
先修课
后续课程
《高等数学》 《通信原理》
《线性代数》 《数字信号处理》
《复变函数》 《自动控制原理》
《电路分析基础》 《数字图像处理》
▲
■
第7页
参考书目
(1)郑君里等. 信号与系统(第二版) . 北京:高等教育出 版社, 2000 (2) 管致中等 . 信号与线性系统 (第四版) . 北京:高等 教育出版 社, 2004 (3)A.V.OPPENHEIM. 信号与系统 (第二版) .北京 :电 子工业出版 社, 2002 (4)王松林、张永瑞、郭宝龙、李小平.信号与线性系统 分析 (第4版) 教学指导书. 北京:高等教育出版 社, 2006
▲
■
第8页
信号与系统
第一章 信号与系统
第二章 连续系统的时域分析
第三章 离散系统的时域分析
第四章 傅里叶变换和系统的频域分析
第五章 连续系统的s域分析
第六章 离散系统的z域分析
第七章 系统函数
第八章 系统的状态变量分析
§1.2 信号的描述和分类
信号的描述 信号的分类 几种典型确定性信号
■ 第 18 页
一、信号的描述
信号是信息的一种物理体现。它一般是随时间或 位置变化的物理量。
信号按物理属性分:电信号和非电信号。它们 可以相互转换。
电信号容易产生,便于控制,易于处理。本课 程讨论电信号——简称“信号”。
▲
■
第1页
信号与系统
是电子技术、信息工程、通信工程 等专业重要的学科基础课
课程介绍
Signals and Systems
电子技术、 信息工程、 通信工程 等专业的 考研课程
■
第3页
课程位置
先修课
后续课程
《高等数学》 《通信原理》
《线性代数》 《数字信号处理》
《复变函数》 《自动控制原理》
《电路分析基础》 《数字图像处理》
▲
■
第7页
参考书目
(1)郑君里等. 信号与系统(第二版) . 北京:高等教育出 版社, 2000 (2) 管致中等 . 信号与线性系统 (第四版) . 北京:高等 教育出版 社, 2004 (3)A.V.OPPENHEIM. 信号与系统 (第二版) .北京 :电 子工业出版 社, 2002 (4)王松林、张永瑞、郭宝龙、李小平.信号与线性系统 分析 (第4版) 教学指导书. 北京:高等教育出版 社, 2006
▲
■
第8页
信号与系统
第一章 信号与系统
第二章 连续系统的时域分析
第三章 离散系统的时域分析
第四章 傅里叶变换和系统的频域分析
第五章 连续系统的s域分析
第六章 离散系统的z域分析
第七章 系统函数
第八章 系统的状态变量分析
信号与系统教案第8章参考幻灯片

状态变量是通过求解由状态变量构成的一阶微分方 程组来得到,该一阶微分方程组称为状态方程。
状态方程描述了状态变量的一阶导数与状态变量和 激励之间的关系 。而描述输出与状态变量和激励之 间关系的一组代数方程称为输出方程 。
通常将状态方程和输出方程总称为动态方程或系统方程。
第8-6页
■
©西安电子科技大学电路与系统教研中6 心
信号与系统 电子教案
第八章 系统状态变量分析03.10.2020
8.1 状态变量与状态方程
一、状态变量与状态方程 二、动态方程的一般形式
8.2 状态方程的建立
一、电路状态方程的列写
二、由输入-输出方程建立状态方程
8.3 离散系统状态方程的建立 8.4 连续系统状态方程的解 8.5 离散系统状态方程的解
点击目录
第8-1页
,进入相关章节
■
©西安电子科技大学电路与系统教研中1 心
信号与系统 电子教案
03.10.2020
第八章 系统状态变量分析
前面的分析方法称为外部法,它强调用系统的输 入、输出之间的关系来描述系统的特性。其特点: (1)只适用于单输入单输出系统,对于多输入多输出 系统,将增加复杂性; (2)只研究系统输出与输入的外部特性,而对系统的 内部情况一无所知,也无法控制。
三个内部变量和激励求
u(t)R2iL2(t)uS2(t)
iC(t)iL1(t)iL2(t)
出:
一组代数方程
第8-4页
■
©西安电子科技大学电路与系统教研中4 心
信号与系统 电子教案 状态与状态变量的定义
8.1 状态变量与状态方程 03.10.2020
系统在某一时刻t0的状态是指表示该系统所必需最 少的一组数值,已知这组数值和t≥t0时系统的激励, 就能完全确定t≥t0时系统的全部工作情况。
状态方程描述了状态变量的一阶导数与状态变量和 激励之间的关系 。而描述输出与状态变量和激励之 间关系的一组代数方程称为输出方程 。
通常将状态方程和输出方程总称为动态方程或系统方程。
第8-6页
■
©西安电子科技大学电路与系统教研中6 心
信号与系统 电子教案
第八章 系统状态变量分析03.10.2020
8.1 状态变量与状态方程
一、状态变量与状态方程 二、动态方程的一般形式
8.2 状态方程的建立
一、电路状态方程的列写
二、由输入-输出方程建立状态方程
8.3 离散系统状态方程的建立 8.4 连续系统状态方程的解 8.5 离散系统状态方程的解
点击目录
第8-1页
,进入相关章节
■
©西安电子科技大学电路与系统教研中1 心
信号与系统 电子教案
03.10.2020
第八章 系统状态变量分析
前面的分析方法称为外部法,它强调用系统的输 入、输出之间的关系来描述系统的特性。其特点: (1)只适用于单输入单输出系统,对于多输入多输出 系统,将增加复杂性; (2)只研究系统输出与输入的外部特性,而对系统的 内部情况一无所知,也无法控制。
三个内部变量和激励求
u(t)R2iL2(t)uS2(t)
iC(t)iL1(t)iL2(t)
出:
一组代数方程
第8-4页
■
©西安电子科技大学电路与系统教研中4 心
信号与系统 电子教案 状态与状态变量的定义
8.1 状态变量与状态方程 03.10.2020
系统在某一时刻t0的状态是指表示该系统所必需最 少的一组数值,已知这组数值和t≥t0时系统的激励, 就能完全确定t≥t0时系统的全部工作情况。
信号与系统课件8.3

它们构成了近代线性系统时域分析的理论基础的内涵。
1. 零状态响应与单位冲激响应
①. 已知系统构成求零状态响应
当系统的构成已知,可列出反映系统输入与输出关系 的线性微分积分方程,通过拉氏变换进而求出系统在零状态下的响应。
dx1(t) 8y(t) 2x(t) dt
dy(t) dt 6y(t) 2x1(t)
C
dvo (t) dt
1 R1
vi
(t )
或
vo (t) vo (0 )
式中
t 0
1 R1C
vi
(
)d
t0
vo (0 )
0
1 R1C
vi
(
)d
表示 t 0 电容器的初始储能,取决于 t 0
的历史状态是一个常量。
图8.15(b)
【例8-16】一个电系统由RLC元件串联而成,如图8.16所示,已知输入 x(t) vi (t) 输出 y(t) vc (t),求该系统的数学模型。
8.3 连续系统的时域 分析
目的
通过在时间域对系统的分析从而找出表征连续系统 时间特性的特征量——冲激响应h(t)并以h(t)为核心 进而分析在不同信号作用下系统的响应。 系统分析过程 完全响应 零状态响应 零输入响应 系统函数 瞬态响应 稳态响应 自由响应 强制响应
系统分析过程
建立系统的数学模型,即写出联系系统输入和 输出信号之间的数学表达式;
i1(t) i2 (t) 0
vi (t) R1
vo (t) R2
C
dvo (t) dt
0
C
dvo (t) dt
vo (t) R2
1 R1
vi
(t)
(8.20)
1. 零状态响应与单位冲激响应
①. 已知系统构成求零状态响应
当系统的构成已知,可列出反映系统输入与输出关系 的线性微分积分方程,通过拉氏变换进而求出系统在零状态下的响应。
dx1(t) 8y(t) 2x(t) dt
dy(t) dt 6y(t) 2x1(t)
C
dvo (t) dt
1 R1
vi
(t )
或
vo (t) vo (0 )
式中
t 0
1 R1C
vi
(
)d
t0
vo (0 )
0
1 R1C
vi
(
)d
表示 t 0 电容器的初始储能,取决于 t 0
的历史状态是一个常量。
图8.15(b)
【例8-16】一个电系统由RLC元件串联而成,如图8.16所示,已知输入 x(t) vi (t) 输出 y(t) vc (t),求该系统的数学模型。
8.3 连续系统的时域 分析
目的
通过在时间域对系统的分析从而找出表征连续系统 时间特性的特征量——冲激响应h(t)并以h(t)为核心 进而分析在不同信号作用下系统的响应。 系统分析过程 完全响应 零状态响应 零输入响应 系统函数 瞬态响应 稳态响应 自由响应 强制响应
系统分析过程
建立系统的数学模型,即写出联系系统输入和 输出信号之间的数学表达式;
i1(t) i2 (t) 0
vi (t) R1
vo (t) R2
C
dvo (t) dt
0
C
dvo (t) dt
vo (t) R2
1 R1
vi
(t)
(8.20)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x1 a11 x1 a12 x2 a1n xn b11 f1 b12 f2 b1 p f p
x 2
a21 x1
a22 x2
a2n xn
b21
f1
b22
f2
b2 p
fp
x n an1 x1 an2 x2 ann xn bn1 f1 bn2 f2 bnp f p
时刻 t0 的值 uC t0 、iL1t0 和 iL2t0 已知,则根据 t t0 时 的给定的激励 uS1t 和 uS2t 就可唯一地确定该微分方程组 在 t t0 时的解 uC t、 iL1t 和 iL2t 。这样系统的输出为:
ut R2iL2t uS2t iC t iL1t iL2t
状态:一个动态系统在某一时刻的状态是表示该 系统所必需的最少的一组数值,已知这组数值及 t t0 时 的激励,就能完全确定 t t0 时系统的全部工作情况。
状态变量:描述系统内部状态所需用的最少的物理量。 通过这些物理量在 t0 时刻的值(状态)以及 t t0 时的激 励,可以计算出系统内部其它物理量在 t t0 时的值。
其它的输出均可由这三个内部变量和激励线性表示。
通过上面的分析可见,三个内部变量的初始值提供了 确定系统全部情况的必不可少的信息。
这里把 uC t0 、iL1t0 和 iL2t0 称为系统在 t t0 时刻 的状态;而把描述该状态随时间变化的物理量 uC t 、iL1t 和 iL2t 称为状态变量。
ann
b11 b12 b1 p
B
b21
b22
b2
p
bn1
bn2bnpFra bibliotek对于LTI系统,它们都是常数矩阵。 A称为系统矩阵(n×n) ,B称为控制矩阵(n×p )。
类似地,如果系统有q个输出,那么,它们中的 每一个都是用状态变量和激励表示的代数方程,其 矩阵形式可写为:
式中
x(t) [ x1(t)
x(t) [ x1(t) f (t) [ f1(t)
x2 (t ) xn (t )]T 状态矢量
x 2 (t ) x n (t )]T 状态矢量的一阶导数 f2(t) f p (t)]T 激励矢量
a11 a12 a1n
A
a21
a22
a2n
an1
an2
步是根据系统的初始状态和
t t0时或的k激励k0求 出状
态变量(求解状态方程);第二步是用这些状态变量
来确定初始时刻以后的系统的输出(求解输出方程)。
通常把状态方程和输出方程总称为动态方程或系 统方程。
下面我们看一下动态方程的一般形式。
状态方程和输出方程的一般形式: 设有一个n阶多输入-多输出系统如图所示。
f1 (t ) f2 (t )
{x(t0)}
y1(t) y2(t)
f p(t)
yq(t)
它有p个输入
f1(t ), f2 (t ),, f p (t )
它有q个输出
y1(t ), y2 (t ),, yq (t )
将系统的n个状态变量记为 x1(t), x2(t),, xn(t)
那么,状态方程的一般形式为:
dt
uC
t
uS1t
0
L2
diL2 t
dt
R2iL2 t
uS2 t
uC
t
0
整理得:
duC t
dt
1 C
iL1t
1 C
iL2 t
diL1t
dt
1 L1
uC
t
R1 L
iL1t
1 L
uS1t
diL2 t
dt
1 L2
uC t
R2 L2
iL2 t
1 L2
uS2 t
x1(t ) a11 a12 a1n x1(t ) b11 b12 b1 p f1(t )
x 2 (t
)
a21
a22
a2n
x2(t
)
b21
b22
b2
p
f2
(t
)
x n
(t
)
an1
an2
ann
xn
(t
)
bn1
bn2
bnp
f
p
(t
)
上式就简记为 x(t ) Ax(t ) Bf (t )
指定 ut 和 iC t 为输出。
思路:对于多输入多输出的系统,如果我们先求出 uC t 、 iL1t 和 iL2t ,那么,任何输出都可用它们和激励来线性 组合来描述。
为此,首先找出这三个内部变量与激励的关系。
根据电路理论可得:
C
duC t
dt
iL2
t
iL1
t
0
R1iL1 t
L1
diL1t
状态方程:描述状态变量变化规律的一组一阶微分方 程组,其中每个等式左端为状态变量的一阶导数,右 边是只包含系统参数、状态变量和激励的一般函数表 达式,其中没有变量的微分和积分运算。
输出方程:描述系统的输出与状态变量及输入之间关 系的代数方程组,其中每个等式左端为输出变量,右 边是只包含系统参数、状态变量和激励的一般函数表 达式,其中没有变量的微分和积分运算。
第八章 系统的状态变量分析
要对一个系统进行分析,首先要用数学模型描述系统。 描述系统的方法有:输入输出法和状态变量法。
输入输出法----适合分析单输入单输出系统; 状态变量法----适合分析多输入多输出系统;
便于研究系统内部情况; 便于计算机求解; 容易推广应用于时变系统或非线性系统。
状态变量法:状态方程和输出方程。
duC t
dt
1 C
iL1 t
1 C
iL2 t
diL1 t
dt
1 L1
uC t
R1 L
iL1 t
1 L
uS1 t
diL2 t
dt
1 L2
uC t
R2 L2
iL2 t
1 L2
uS 2 t
这是描述三个内部变量与激励之间关系的一阶微分 方程组。由微分方程理论可知:如果这三个变量在初始
一阶微分方程组 代数方程组
§8.1 状态变量与状态方程 §8.2 连续系统状态方程的建立 § 8.3 离散系统状态方程的建立
§8.1 状态变量与状态方程
一、状态与状态变量的概念
R1 iL1 L1
a
L2 iL2 R2
uS1
iC
uC
u uS 2
图 8.1-1 三阶电路系统
图示一个三阶系统,电压源 uS1 和 uS2 是系统的激励,
状态变量通常用 x1(t), x2 t ,, xn t 来表示。
需要指出,状态变量的选择并不是唯一的,对 于同一个系统,选择不同的状态变量可得出不同的 状态方程。
以上论述也适用于离散系统。
二、状态方程和输出方程
在给定系统和激励信号并选定状态变量的情况下,
用状态变量法来分析系统时,一般分两步进行:第一
