定积分的几何意义
定积分的概念 课件

a
f(x)dx等于由直线x=a,x=b,y=0与
曲线y=f(x)围成曲边梯形的面积,这是定积分的几何意义.
b
(2)计算
a
f(x)dx时,先明确积分区间[a,b],从而确定曲
边梯形的三条直边x=a,x=b,y=0,再明确被积函数f(x),
从而确定曲边梯形的曲边,这样就可以通过求曲边梯形的面积
S而得到定积分的值:
c
f(x)dx
(其中a<c<b).
[点睛] 性质(1)的等式左边是一个定积分,等式右边是常数与 一个定积分的乘积. 性质(2)对于有限个函数(两个以上)也成立. 性质(3)对于把区间[a,b]分成有限个(两个以上)区间也 成立.
利用定义求定积分
3
[典例] 利用定义求定积分0x2dx. [解] 令f(x)=x2,
n
(3)求和:
i=1Leabharlann f(ξi)·b-n a;
b
(4)取极限:a
n
f(x)=lim n i=1
b-a f(ξi)· n .
用定积分的性质求定积分
[典例]
(1)f(x)=x2+ x2,1,1≤0≤x≤x<21.,
2
则
f(x)dx=(
0
)
2
A. (x+1)dx 0
2
B. 2x2dx 0
1
2
C. (x+1)dx+ 2x2dx
(1)如果被积函数是几个简单函数的和的形式,利用定 积分的线性性质进行计算,可以简化计算.
(2)如果被积函数含有绝对值或被积函数为分段函数, 一般利用积分区间的连续可加性计算.
用定积分的几何意义求定积分
[典例] 根据定积分的几何意义,求下列定积分的值.
定积分的几何意义是什么

定积分的几何意义是什么定积分的几何意义是被积函数与坐标轴围成的面积,x轴之上局部为正,x轴之下局部为负,根据cosx在[0,2π]区间的图像可知,正负面积相等,因此其代数和等于0。
定积分的几何意义是被积函数与坐标轴围成的面积,x轴之上局部为正,x轴之下局部为负,根据cosx 在[0,2π]区间的图像可知,正负面积相等,因此其代数和等于0。
定积分的几何意义
定积分定积分是积分的一种,是函数f(x)在区间[a,b]上积分和的极限。
定积分就是求函数f(X)在区间[a,b]中的图像包围的面积。
即由y=0,x=a,x=b,y=f(X)所围成图形的面积。
这个图形称为曲边梯形,特例是曲边三角形。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。
一个连续函数,一定存在定积分和不定积分;假设只有有限个连续点,那么定积分存在;假设有跳跃连续点,那么原函数一定不存在,即不定积分一定不存在。
定积分几何意义
图形的面积。
y
解 如图所示,阴影部分面积
1
2
S 0 xdx 1 (x 2)dx
1
1
xdx
2
(x 2)dx
60
1
y x 2 yx
y x
1 1 1 11 622
7 6
0
1
2x
(3)用定积分的几何意义求定积分的值的方法 步骤: ①画图形; ②求交点定区间; ③由图像查找“一边恒在一边上”:i全 部就直接作差ii部分就分段。
n(n
1)(2n
1)
1 31
1 0
(2 6
x2dx lim n
n n2
Sn
lim
n
)
1 6
(2
3 n
1 n2
)
0
1x
1(以直代曲、逼近)
3
二、探究新知
探究1:你能通过观察图形得到定积分的 几何意义吗?
y
y f (x)
oa
bx
定积分的几何意义:
当
f(x)0
时,积分
b
f
(x)dx
a
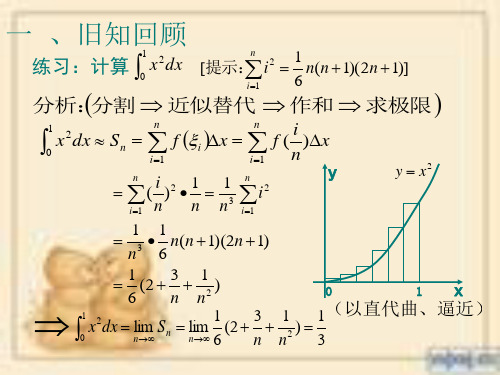
一 、旧知回顾
练习:计算 1 x2dx
n
[提示:
i2
1 n(n 1)(2n 1)]
0
i 1
6
分析:分割 近似替代 作和 求极限
1 0
x2dx
Sn
n i 1
f
i
x
n i 1
f ( i )x n
y
n ( i )2 • 1 i1 n n
1 n3
n
i2
i 1
y x2
1 n3
•
1 6
计算定积分
定积分几何意义公式

定积分几何意义公式定积分是微积分中的一个重要概念,在数学和物理学等科学领域有着广泛的应用。
它不仅可以用于求解函数在一段区间内的面积、体积等几何问题,还可以用于描述变化率、累积效应等动态的物理过程。
在本文中,我们将介绍定积分的几何意义和相关公式,并举例说明其应用。
首先,我们来理解定积分的几何意义。
定积分可以用于计算曲线下的面积,这是因为定积分可以看作是对一个函数在给定区间内的“加和”。
具体而言,如果我们有一个连续函数f(x)在区间[a, b]上的图像,那么用定积分来求解f(x)在该区间内的面积就是将该区间分成无数个无穷小的矩形,并将这些矩形的面积相加得到。
对于一个函数f(x)在区间[a, b]上的连续图像,我们可以将区间[a, b]等分成n个小区间,每个小区间的长度为Δx = (b-a)/n。
然后,我们在每个小区间上找到一个样本点ξi,并计算函数f(ξi)在该小区间内矩形的面积(即f(ξi) * Δx)。
最后,我们将所有小区间的面积相加得到近似面积Sn = f(ξ1) * Δx + f(ξ2) * Δx + ... +f(ξn) * Δx。
当我们将n趋向于无穷大时,也就是将每个小区间的长度无限缩小,那么每个小区间的面积也会无限接近于曲线下的面积。
此时,我们可以得到定积分的几何意义公式如下:∫[a,b] f(x) dx = lim(n→∞) Sn = lim(n→∞) [f(ξ1) *Δx + f(ξ2) * Δx + ... + f(ξn) * Δx]其中,∫[a,b]表示从a到b的定积分,f(x)表示被积函数,dx表示无穷小的区间长度。
除了用于计算曲线下的面积,定积分还可以用于求解其他几何问题。
例如,我们可以通过定积分来计算某个形状的物体的体积。
如果我们有一个截面积为A(x)、从a到b的连续函数在坐标轴上的图像,那么这个形状的体积可以通过定积分来计算:V = ∫[a,b] A(x) dx这个公式的几何解释是,我们可以将这个形状分成无数个无穷小的薄片,每个薄片的厚度为dx,然后将每个薄片的体积(即A(x) * dx)相加得到整个形状的体积。
1.5定积分的几何意义

1、求曲边梯形面积 、 分割-----近似代替 近似代替-----求和 求和-----取极限 分割 近似代替 求和 取极限 2、定积分定义 、 3、定积分几何意义 、 4、定积分计算性质 、
1.求由连续曲线 =f(x)对应的曲边梯形面积的方法 求由连续曲线y= 求由连续曲线 对应的
n
O
a
b
x
积分
式
3、定积分的几何意义: 定积分的几何意义:
b ∫a
f ( x) d x
的实质
b (1)当f(x)在区间[a,b]上大于0时,a 在区间[ 大于0 ∫
f ( x) d x 表示
直线x ),y 和曲线y 由 直线x=a,x=b(a≠b),y=0和曲线y=f(x)所围成的曲 边梯形的面积 ,这也是定积分的几何意义. 这也是定积分的几何意义. (2)当f(x)在区间[a,b]上小于0时,b f ( x ) d x 表示 在区间[ 小于0 ∫ a 由直线x ),y 和曲线y 由直线x=a,x=b (a≠b),y=0和曲线y=f(x)所围成的 曲边梯形的面积的相反数.
特别地,当 a=b 时,有 ∫ f (x)dx=0。
a
定积分的几何意义: 定积分的几何意义: 当f(x)≤0时,由y=f (x)、x=a、x=b 与 x 轴所围成的 ≤ 时 = 、 = 、 = 轴的下方, 曲边梯形位于 x 轴的下方,
积分 ∫ f (x)dx 在几何上表示
a b
y y=−f (x)
O
a
c
b
x
1.∫ f ( x)dx =
b a
S
f ( x) ≥ 0
-S f ( x ) < 0 表示以y=f(x)为曲边的曲边梯形面积 S表示以 为曲边的曲边梯形面积 y
定积分的几何意义公式

定积分的几何意义公式定积分是微积分中的重要概念之一,它在几何学中有着重要的应用。
定积分的几何意义公式可以帮助我们理解定积分的几何意义以及它在图形面积、曲线长度等方面的应用。
定积分的几何意义公式如下:若函数f(x)在区间[a, b]上连续且非负,那么f(x)在区间[a, b]上的定积分∫[a, b]f(x)dx表示曲线y=f(x)与x轴所围成的平面图形的面积。
这个公式告诉我们,通过计算函数f(x)在区间[a, b]上的定积分,我们可以得到曲线y=f(x)与x轴所围成的图形的面积。
这个定积分的几何意义公式是我们理解定积分的几何意义的基础。
举个例子来说明这个公式的应用。
假设有一个函数f(x)=x^2在区间[0, 2]上,我们可以通过计算定积分∫[0, 2]x^2dx来求得曲线y=x^2与x轴所围成的图形的面积。
根据定积分的计算方法,我们可以将区间[0, 2]划分成许多小的区间,然后计算每个小区间上的面积并求和。
这样,我们就可以得到整个区间[0, 2]上的曲线与x轴所围成的图形的面积。
通过这个例子,我们可以看到定积分的几何意义公式在计算图形的面积方面的应用。
同时,这个公式也可以推广到计算曲线长度、体积等方面。
除了图形的面积,定积分的几何意义公式还可以帮助我们计算曲线的长度。
如果我们有一个函数f(x)在区间[a, b]上,那么它的曲线长度可以通过计算定积分∫[a, b]√(1+(f'(x))^2)dx来得到。
这个公式告诉我们,通过计算函数f(x)在区间[a, b]上的定积分,我们可以得到曲线的长度。
这个定积分的几何意义公式在计算曲线的长度方面有着重要的应用。
通过定积分的几何意义公式,我们可以看到定积分在几何学中的重要作用。
它不仅可以帮助我们计算图形的面积、曲线的长度,还可以应用于计算体积、质心等方面。
总结起来,定积分的几何意义公式是微积分中的重要概念,它可以帮助我们理解定积分的几何意义以及它在图形面积、曲线长度等方面的应用。
1.5.3定积分的几何意义3.14

a
b
f (x)dx =Sf (x)dx
a
c
ba (2)定积分的几何意义: f ( x)dx lim f (i ) a n n i 1
b n
当f(x)0时,由yf (x)、xa、xb 与y=0所围成的曲 边梯形位于 x 轴的下方,
y yf (x)
积分 f (x)dx 在几何上表示
a a
例1、
利用定积分的几何意义 说明等式 成立。
2
2
sin xdx 0
y
解: 在右图中,被积函数 ( x) sin x f
在[
, ]上连续,且在 ,]上 [ 0 2 2 2
2
f(x)=sinx 1
sin x 0, 在[0, ]上sin x 0,并有 2 A1 A2 , 所以
S
y f (x)
x
f ( x) 0,
b
a
f ( x)dx S
曲边梯形的面积的负值
一般地, f(x)在[a, b]上的定积分表示介于y=0、曲线 y=f(x)及直线x=a、x=b之间的各部分面积的代数和.
y
y=f(x)
A1 a
A3
A5
A2
A4
b x
b a
f ( x)d x A1 A2 A3 A4 A5
A1
-1
A2
2
x
2
2
f ( x)dx A2 A1 0
例2、用定积分表示图中四个阴影部分面积
y
f(x)=x2
y
f(x)=x2
定积分的意义及其在几何中的应用

定西师范高等专科学校本科毕业论文(设计)题目:定积分的意义及其在几何中的应用学院兰州大学数学与统计学院专业数学应用班级 09数学教育二班学号 **********姓名蔡兴盛指导教师王宾国兰州大学教务处制二O一二年三月定积分的意义及其在几何中应用定积分在大学数学中起着非常重要的作用,是大学数学的基础,在我们的生活中也起着很重要的作用!内容摘要: 一直以来定积分问题就是大学数学学习的重点,也是本科及研究生入学考试重点考察的内容之一,所以本文对定积分的起源、发展以及它在数学、几何学的应用做了重点研究。
幷利用一些例题对这些问题做除了详细解析。
关键词: 定积分 柯西 微分 方程 几何一、定积分的概念 1.1定积分的定义一般地,设函数()f x 在区间[,]a b 上连续,用分点0121i i n a x x x x x x b -=<<<<<<<=将区间[,]a b 等分成n 个小区间,每个小区间长度为x ∆(b ax n-∆=),在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=,作和式:11()()n nn i i i i b aS f x f nξξ==-=∆=∑∑如果x ∆无限接近于0(亦即n →+∞)时,上述和式n S 无限趋近于常数S ,那么称该常数S 为函数()f x 在区间[,]a b 上的定积分.记为:()baS f x dx =⎰其中()f x 成为被积函数,x 叫做积分变量,[,]a b 为积分区间,b 积分上限,a 积分下限.说明:(1)定积分()ba f x dx ⎰是一个常数,即n S 无限趋近的常数S (n →+∞时)称为()baf x dx ⎰,而不是n S .(2)用定义求定积分的一般方法是: ①分割:n 等分区间[],a b ; ②近似代替:取点[]1,i i i x x ξ-∈; ③求和:1()ni i b af nξ=-∑; ④取极限:()1()lim nbi an i b af x dx f nξ→∞=-=∑⎰(3)曲边图形面积:()baS f x dx =⎰;变速运动路程21()t t S v t dt =⎰;变力做功 ()baW F r dr =⎰1.2定积分的几何意义如果在区间[,]a b 上函数连续且恒有()0f x ≥,那么定积分()baf x dx ⎰表示由直线,x a x b ==(a b ≠),0y =和曲线()y f x =所围成的曲边梯形的面积.说明:一般情况下,定积分()ba f x dx ⎰的几何意义是介于x 轴、函数()f x 的图形以及直线,x a x b ==之间各部分面积的代数和,在x 轴上方的面积取正号,在x 轴下方的面积去负号.分析:一般的,设被积函数()y f x =,若()y f x =在[,]a b 上可取负值. 考察和式()()()12()i n f x x f x x f x x f x x ∆+∆++∆++∆不妨设1(),(),,()0i i n f x f x f x +<于是和式即为()()()121(){[()][]}i i n f x x f x x f x x f x x f x x -∆+∆++∆--∆++-∆()b af x dx ∴=⎰阴影A 的面积—阴影B 的面积(即x 轴上方面积减x 轴下方的面积)1.3定积分的性质性质1 a b dx ba -=⎰1性质2 ⎰⎰=bab adx x f k dx x kf )()( (其中k 是不为0的常数) (定积分的线性性质)性质3 1212[()()]()()b b baaaf x f x dx f x dx f x dx ±=±⎰⎰⎰ (定积分的线性性质)性质4 ()()()b c baacf x dx f x dx f x dx =+⎰⎰⎰ (其中a<c<b )1.4用定积分求解简单的问题 1.4.1 求立体图形的体积用类似求图形面积的思想我们也可以求一个立体图形的体积,常见的已知几何体的截面积求几何体的体积,另一种是求旋转体的体积,解此类题常用的方法是我们将此物体划分成许多基本的小块,每块的厚度为)(x σ,假设每一个基本的小块横截面积为A (x ),则此小块的体积是A(x))(x σ,将所有的小块加起来,另0)(→x σ,我们可以得到其体积v=lim ∑==bx a x x x A )()(σ其中 a 和 b 分别为计算体积的起始值和终了值. 下面来看几个例题例1 求椭圆面1222222=++cz b y a x 所围立体的体积解:以平面0x x =a x ≤0()截椭球面,得椭圆在YOZ 平面上的正投影1)1()1(22222222=-+-ax c z ax b y所以截面面积函数为)1()(22a x bc x A -=π []a a x ,-∈于是求得椭球体积abc dx ax bc v aa ππ34)1(22=-=⎰-显然当c b a ===r 时,就等于球的体积334r π1.4.2定积分在初等数学里的应用近些年来,定积分还越来越多的被广泛应用到初等数学中的一些问题上来,下面来讨论一下定积分在证明不等式,等式和一些数列的极限的方面的应用一、证明不等式运用积分来证明不等式,一般要利用到积分的如下性质:设)(x f 与)(x g 都在[]b a 上可积且)()(x g x f ≤;则⎰⎰≤babax g dx x f )()(特别的当0)(≡x f 时,有0)(≥⎰badx x g例2 证明贝努利不等式 已知1->x 且N n x ∈≠0且2≥n求证:nx x n +≥+1)1(证明:若01<<-x 或110<+<x 且2≥n 时,1)1(1<+-n x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A = ∫ [( x − 1) − 1]dx − ∫ [( x − 1) − 1]dx
0 −1 2 2 0 2
例2:
利用定积分的几何意义说明等式∫
π
2 −
π
2
sin xdx = 0
y f(x)=sinx
成立。
解: 在右图中,被积函数 f ( x ) = sin x
在[ −
π π
, ]上连续,且在 [ − ,]上 0 2 2 2
π
−
π
2
1
A2
A1 -1
π
2
sin x ≤ 0, 在[ 0, ]上 sin x ≥ 0,并有 2 π A1 = A2 , 所以
π
x
∫
2
−
π
2
f ( x)dx = A2 − A1 = 0
练习: பைடு நூலகம்.利用定积分的几何意义,判断下列定积分 (A)
值的正、负号。
1).∫ sin xdx
2 0
π
2). ∫−1
∫
0
y
f(x)=x2
y
f(x)=x2
y
f(x)=1
y
f(x)=(x-1)2-1
0
a
x
-1 0
2
x
a
0
b x
-1 0
2 x
①
②
③
2
④
( 2 解: 2)在图②中,被积函数f ( x) = x 在[−1,] 上连续,且f ( x) ≥ 0, 根据定积分的几何意 义,可得阴影部分的面积为 A = 2 x 2 dx
2
x 2 dx
(B) 2.利用定积分的几何意义,说明下列各式。 1). sin xdx = 0 ∫
0 2π
成立:
2).
∫
π
0
sin xdx = 2∫ 2 sin xdx
0
π
(B) 3.试用定积分表示下列各图中影阴部分的面积。 y y=x2 y y=f(x)
0 1 2
x
0 a
y=g(x) b x
f ( x)dx = A1 − A2 + A3
3.结论: f ( x)dx的值都可用区边梯形面积 ∫
的代数和表示
几何意义
4.应用
例1.用定积分表示图中四个阴影部分面积
y
f(x)=x2
y
f(x)=x2
y
f(x)=1
y
f(x)=(x-1)2-1
0
a
x
-1 0
2
x
a
0
b x
2
-1 0
2 x
①
②
③
④
( 解: 1)在图①中,被积函数f ( x) = x 在[0,a] 上连续,且f ( x) ≥ 0, 根据定积分的几何意 义,可得阴影部分的面积为 A = a x 2 dx
y
f(x)=x2
y
f(x)=x2
y
f(x)=1
y
f(x)=(x-1)2-1
0
a
x
-1 0
2
x
a
0
b x
-1 0
2 x
①
②
③
④
解:4)在图④中,被积函数f ( x) = ( x − 1) 2 − 1在[−1,] ( 2
[ , 2 上连续,且在 −1 0]上f ( x) ≥ 0, 在[0,]上f ( x) ≤ 0, 根据定积分的几何意义可得阴影部分的面积为
∫
−1
y
f(x)=x2
y
f(x)=x2
y
f(x)=1
y
f(x)=(x-1)2-1
0
a
x
-1 0
2
x
a
0
b x
-1 0
2 x
①
②
③
④
( 解: 3)在图③中,被积函数f ( x) = 1在[a,b] 上连续,且f ( x) > 0, 根据定积分的几何意 b 义,可得阴影部分的面积为
A = ∫ a dx
A
f ( x) ≥ 0
f ( x) < 0
1.∫ f ( x)dx =
b a
-A
A表示以y=f(X)为曲边的曲边梯形面积
y=f(x)>0 A 0 a b x 0
y
y a A y=f(x)<0 b x
2.如果f(x)在[a,b]上时正,时负,如下图
y y=f(x) a
A1
0
A3
A2
b
x
则
∫
b a
b a
