第7章答案
第7章参数估计答案

·61·第7章 参数(点)估计系 班姓名 学号一、填空题1、设总体X 服从二项分布),(p N B ,10<<P ,n X X X 21,是其一个样本,那么矩估计量=N ˆ )X /B 1/(X 2- ,=p ˆ XB 12- .2、设总体X 服从指数分布 )0(00)(>⎩⎨⎧≤>=-λλϕλx x e x x n X X X ,,21是来自X的样本,则未知参数λ的矩估计量是 X /1 ,极大似然估计量是 X /1 .3. 设 总 体)p ,1(B ~X , 其 中 未 知 参 数 01<<p , X X X n 12,, 是 X的 子样, 则 p 的 矩 估 计 为_∑=n 1i i X n 1_, 子 样 的 似 然 函 数 为_ii X 1n 1i X )p 1(p -=-∏__。
(x x)p 1(p)p ;x (f -= 为 X 的 概 率 密 度 函 数 ).4、 总 体 X 服 从 密 度 函 数 为f x x x (;)[()],()θπθ=+--∞<<+∞112 的 哥 西分 布。
),,(1n X X 为 从 X 抽 得 的 样 本, 则 当 n =1时 θ有 极 大 似 然 估 计 为θ=_1X。
5. 设 X X X n 12,, 是 来 自 总 体),(N ~X 2σμ的 样 本, 则 有 关 于 μ及 σ2的似 然 函 数L X X X n (,,£;,)12 μσ=_2i )X (21n1i e21μ-σ-=∏σπ__。
二、选择题1、设n X X X ,,21是取自总体),0(2σN 的样本,则可以作为2σ的无偏估计量是( A ).A 、∑=n i i X n 121B 、∑=-n i i X n 1211C 、∑=ni i X n 11D 、∑=-ni i X n 1112、设罐子里装有黑球和白球,有放回地抽取一个容量为n 的样本,其中k 个白球,则罐子里黑球数与白球数之比R 的最大似然估计量为( B ).·62·A 、nk B 、1-knC 、1D 、kn三、计算和证明题1、设总体X 具有分布密度10,)1(),(<<+=x x x P ααα,其中1->α是未知参数,n X X X ,,21为一个样本,试求参数α的矩估计和极大似然估计.解:因⎰⎰++=+=1011α1α1αdx x dx x x X E a)()()(2α1α2α1α102++=++=+|a x 令2α1α++==ˆˆ)(X X EXX --=∴112αˆ为α的矩估计 因似然函数221211αα),()(),,(n n n X X X X X X L +=∑=++=∴ni i X n L 1α1αln )ln(ln ,由∑==++=∂∂ni i X nL 101ααln ln 得,α的极大似量估计量为)ln (ˆ∑=+-=ni iXn11α2、设总体X 服从二项分布),(p k b ,k 是正整数,10<<p ,两者都是未知参数,n X X X 21,是一个样本,试求k 和p 的矩估计.解:由于)(~1P k b Xkp X =∈∴)( )1()(p kp X D -=于是令⎪⎩⎪⎨⎧--==∑=ni i X X n X D XX E 1)(11)()( 解之得XX X n X p ni i ∑=---=12)(11ˆ])(11[ˆ122∑=---=ni i X X n X Xk3、设n X X X ,,21为从一总体中抽出的一组样本,总体均值μ已知,用∑=--ni i X n 12)(11μ去估计总体方差2σ,它是否是2σ的无偏估计,应如何修改,才能成为无偏估计.·63·解:因∑∑==--=--n i n i ii X E n X n E 1122)(11])(11[μμ221σσ≠-=n n ∑=--∴ni i X n 12)(11μ不是2σ的无偏估计 但∑=-n i i X n 12)(1μ是2σ的无偏估计4、设一批产品中含有废品,从中随机抽取75件,其中有废品10件,试估计这批产品的废品率.解:设这批产品的废品率为p ,⎩⎨⎧=次抽到合格品第次抽到废品第i i X i 01于是p X P i ==)1(p X P i -==1)0(即ii x xi i ij p p x X P p x f --===1)1()()(72,11,0 ==i x i故极大似然函数∑-∑=-===--=751751751751)1()1(i ii iii x x x x i p pp p L π∑∑==--+=751751)1ln()75(ln ln i i i i p x p x p L令∑∑===---=7517510)75(111ln i i i i x p x p dp L d解之得p 的极大似然估计值 ∑====7511527510751ˆi i x p。
第7章 习题参考答案

习题七一、用适当内容填空1. ①数据处理,②文件,③表之间的联系,④安全控制规则,⑤二维,⑥描述实体,⑦实体联系。
2. ①人工管理,②文件系统,③数据库系统,④分布式数据库系统,⑤人工管理,⑥分布式数据库系统,⑦人工管理,⑧数据库系统。
3. ①DBS,②人员,③数据库,④计算机软件,⑤数据库,⑥数据库,⑦数据库管理系统。
4. ①数据定义,②数据操纵,③数据查询。
5. ①操作,②不一致性,③共享型锁,④排他型锁。
6. ①信息,②概念模型,③实体,④实体属性,⑤数据模型,⑥一行数据或记录,⑦数据项、列或字段。
7. ①并发控制,②数据安全性控制,③数据备份与恢复。
8. ①实体间的联系②一对一,③一对多,④多对多,⑤属性名,⑥属性值。
9. ①层次数据模型,②网状数据模型,③关系数据模型,④面向对象数据模型,⑤两个,⑥数据模型,⑦网状,⑧层次,⑨实体型或实体之间的联系,⑩一个实体或实体之间的联系,○11属性值,○12具有相同含义的属性。
10. ①矩形,②椭圆,③菱形。
11. ①包含对象数据的变量,②描述对象行为特性的方法,③对象所响应的消息,④调用说明,⑤程序代码,⑥属性,⑦方法,⑧类。
12. ①二维表,②一个元组,③实体,④属性值域,⑤n元关系或n目关系。
13. ①结构,②数据类型,③取值范围。
14. ①数据结构,②数据操作,③完整性约束。
15. ①查询数据,②插入数据,③删除数据,④数据项投影,⑤数据记录选择,⑥两个表连接,⑦数据插入,⑧数据删除。
16. ①域完整性约束,②实体完整性约束,③参照完整性约束,④用户定义完整性约束。
17. ①投影操作,②选择操作,③连接操作,④Where 性别=’1’,⑤*,⑥ 1。
18. ①数据定义语言,②数据操纵语言,③数据查询语言,④数据控制语言,⑤数据查询语言,⑥数据定义语言,⑦数据操纵语言。
二、从参考答案中选择一个最佳答案1. A2. D3. B4. C5. A6. B7.B8. C9. C10. C11. B12. C13. D14. C15. D16. D17.C18. C19. D20. D21. C22. B23. A24. B25. A26. D27. C28. C29. D30. B31. D32. C33. B34. B35. C36. C三、从参考答案中选择全部正确答案1. CD2. BD3. CE4. BC5. BCE6. AC7. CDF8. ACD9. ACE10. BD11. BCE12. ADE13. ABE14. BD15. AEF16. CDE17. ABEF18. BE19. BE20. BC21. BF。
第7章习题及参考答案
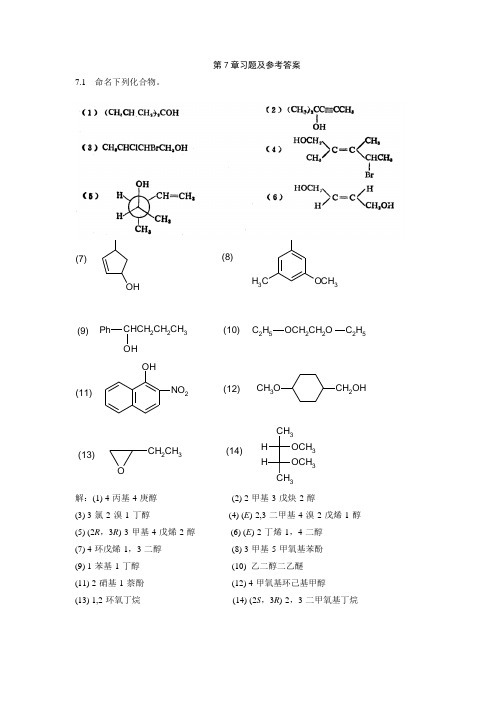
第7章习题及参考答案7.1 命名下列化合物。
OH OHOHO CH 3CH 3PhCHCH 2CH 2CH 3OHC 2H 5OCH 2CH 2O C 2H 5(7)(8)(9)(10)CH 3OHNO 2OCH 2OHCH 3OCH 2CH 3CH 3CH 3H O HO CH 3(11)(12)(13)(14)解:(1) 4-丙基-4-庚醇 (2) 2-甲基-3-戊炔-2-醇(3) 3-氯-2-溴-1-丁醇 (4) (E )-2,3-二甲基-4-溴-2-戊烯-1-醇 (5) (2R ,3R )-3-甲基-4-戊烯-2-醇 (6) (E )-2-丁烯-1,4-二醇 (7) 4-环戊烯-1,3-二醇 (8) 3-甲基-5-甲氧基苯酚 (9) 1-苯基-1-丁醇 (10) 乙二醇二乙醚 (11) 2-硝基-1-萘酚 (12) 4-甲氧基环己基甲醇 (13) 1,2-环氧丁烷 (14) (2S ,3R )-2,3-二甲氧基丁烷7.2 写出下列化合物的结构式。
(1) 3,3-二甲基环戊醇 (2) 肉桂醇(3) 环戊基叔丁基醚 (4) 3-环己烯基异丙基醚 (5) 顺-1,2-环己二醇 (6) 2,3-二巯基-1-丙醇 (7) 4-丁基-1,3-苯二酚 (8) 二苯并-18-冠-6 解:CH CHCH 2OHOHC H 3CH 3(1)(2)OOC(CH 3)3CH(CH 3)2(3)(4)SHSHOH OHCH 2CH CHOH(5)(6)OHOHC(CH 3)3O OOOO O (7)(8)7.3 将下列化合物按沸点降低的顺序排列成序。
(1)丙三醇,乙二醇二甲醚,乙二醇,乙二醇单甲醚 (2)3-己醇,正己醇,正辛醇,2-甲基-2-戊醇解:(1)丙三醇>乙二醇>乙二醇单甲醚>乙二醇二甲醚 (2)正辛醇>正己醇>3-己醇>2-甲基-2-戊醇7.4 将下列各组化合物按与卢卡斯试剂作用的速率快慢排列成序。
教材课后题答案-第7章

习题7一 单选题1.设有如下定义,则表达式sizeof(y)的值是【 】。
struct data {long *ln; char c;struct data *last,*next; }y; A.7 B.9 C.13 D.17 【答案】C【解析】指针变量在内存中占用4个字节,所以sizeof(y)的值是4+1+4+4=13 2.设有以下程序段,则表达式的值不为100的是【 】。
struct st{int a;int *b;}; void main(){int m1[]={10,100},m2[]={100,200}; struct st *p,x[]={99,m1,100,m2}; p=x; ... }A.*(++p->b)B.(++p)->aC.++p->aD.(++p)->b 【答案】D【解析】根据题意,p 指向x 数组,x[0]的b 成员指向m1数组,x[1]的b 成员指向m2数组,如图7-1所示。
选项A 中p->b 指向m1[0],通过“++”运算p->b 指向m1[1],所以选项A 的表达式的值为100。
选项B 中++p 使p 指向x[1],x[1]的a 成员的值是100。
选项C 中p 指向x[0],x[0]的a 成员做“++”运算,结果为100。
选项D 中++p 使p 指向x[1],x[1]的b 成员的值是指针,所以选择选项D 。
m1m2p图7-13.设有以下定义,且如图7-2所示,指针head 和p 指向链表的第一个结点,指针q 指向新的结点,则不能把新结点插入在第一个结点之前的语句是【 】。
headpq图7-2struct node{int a;struct node *next;}*head,*p,*q;A.head=q,q->next=p;B.head=q,q->next=head;C.q->next=head,head=q;D.head=q,head->next=p;【答案】B4.设有如下结构体说明和变量定义,且如图7-3所示,指针p指向变量one,指针q指向变量two,则不能将结点two接到结点one之后的语句是【】。
第七章 习题答案
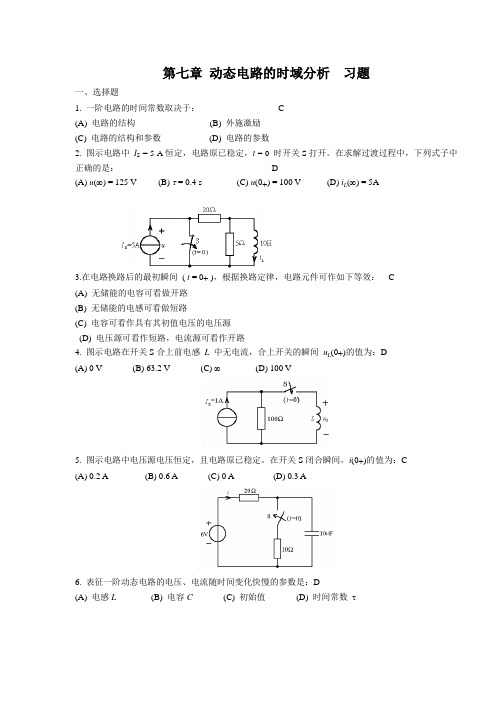
第七章动态电路的时域分析习题一、选择题1. 一阶电路的时间常数取决于: C(A) 电路的结构(B) 外施激励(C) 电路的结构和参数(D) 电路的参数2. 图示电路中I S = 5 A恒定,电路原已稳定,t = 0时开关S打开。
在求解过渡过程中,下列式子中正确的是: D(A) u(∞) = 125 V (B) τ = 0.4 s (C) u(0+) = 100 V (D) i(∞) = 5AL3.在电路换路后的最初瞬间( t = 0+ ),根据换路定律,电路元件可作如下等效: C(A) 无储能的电容可看做开路(B) 无储能的电感可看做短路(C) 电容可看作具有其初值电压的电压源(D) 电压源可看作短路,电流源可看作开路(0+)的值为:D4. 图示电路在开关S合上前电感L中无电流,合上开关的瞬间uL(A) 0 V (B) 63.2 V (C) ∞(D) 100 V5. 图示电路中电压源电压恒定,且电路原已稳定。
在开关S闭合瞬间,i(0+)的值为:C(A) 0.2 A (B) 0.6 A (C) 0 A (D) 0.3 A6. 表征一阶动态电路的电压、电流随时间变化快慢的参数是:D(A) 电感L(B) 电容C(C) 初始值(D) 时间常数τ7. 图示正弦脉冲信号的数学表达式为:B (A) sin ω t ⋅ ε (t ) + sin ω ( t - T ) ⋅ ε ( t - T ) (B) sin ω t ⋅ ε (t ) - sin ω t ⋅ ε ( t - T ) (C) sin ω t ⋅ ε (t ) - sin ω ( t - T ) ⋅ ε ( t - T ) (D) sin ω t ⋅ ε (t ) + sin ω t ⋅ ε ( t - T )8. 图示电路中,原已达稳态, t = 0开关 S 打开,电路的时间常数为:D (A)s 41 (B) s 61(C) s 4 (D)s 69. 示电路中,t = 0 时开关打开,则 u (0+)为:C(A) 0V (B) 3.75V (C) – 6V (D) 6V10.图示电路中,开关打开已久,在 t = 0 时开关闭合,i (0+) 为:D(A) 0A (B) 0.8A(C) 2A (D)1A11.R 、C 串联电路,已知全响应()()10C 83V,0t u t e t -=-≥,其零状态响应为:(A )(A) 1088V te-- (B) 1083V t e -- (C) 103V t e -- (D) 105V t e -12. .一阶电路的全响应()()10C 106V,0tu t et -=-≥若初始状态不变而输入增加一倍,则全响应u C (t)为 ( D ) (A) 20-12e -10t ; (B) 20-6e -10t ; (C) 10-12e -10t ; (D) 20-16 e -10t 。
大学物理第7章静电场中的导体和电介质课后习题及答案

大学物理第7章静电场中的导体和电介质课后习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第7章 静电场中的导体和电介质 习题及答案1. 半径分别为R 和r 的两个导体球,相距甚远。
用细导线连接两球并使它带电,电荷面密度分别为1σ和2σ。
忽略两个导体球的静电相互作用和细导线上电荷对导体球上电荷分布的影响。
试证明:Rr=21σσ 。
证明:因为两球相距甚远,半径为R 的导体球在半径为r 的导体球上产生的电势忽略不计,半径为r 的导体球在半径为R 的导体球上产生的电势忽略不计,所以半径为R 的导体球的电势为R R V 0211π4επσ=14εσR= 半径为r 的导体球的电势为r r V 0222π4επσ=24εσr= 用细导线连接两球,有21V V =,所以R r =21σσ 2. 证明:对于两个无限大的平行平面带电导体板来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同。
证明: 如图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ(1)取与平面垂直且底面分别在A 、B 内部的闭合圆柱面为高斯面,由高斯定理得S S d E S ∆+==⋅⎰)(10320σσε 故 +2σ03=σ上式说明相向两面上电荷面密度大小相等、符号相反。
(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ 又 +2σ03=σ 故 1σ4σ=3. 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量。
解:如图所示,设金属球表面感应电荷为q ',金属球接地时电势0=V由电势叠加原理,球心电势为=O V R qdq R 3π4π4100εε+⎰03π4π400=+'=Rq R q εε故 -='q 3q 4.半径为1R 的导体球,带有电量q ,球外有内外半径分别为2R 、3R 的同心导体球壳,球壳带有电量Q 。
大学物理 第7章 真空中的静电场 答案
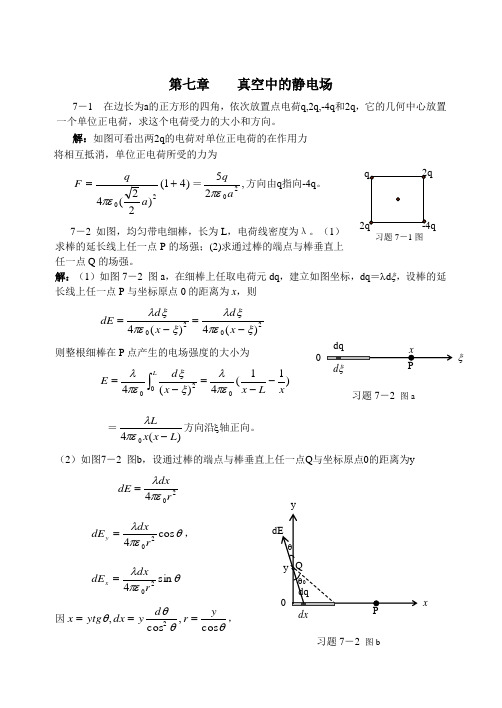
第七章 真空中的静电场7-1 在边长为a 的正方形的四角,依次放置点电荷q,2q,-4q 和2q ,它的几何中心放置一个单位正电荷,求这个电荷受力的大小和方向。
解:如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消,单位正电荷所受的力为)41()22(420+=a q F πε=,2520aqπε方向由q 指向-4q 。
7-2 如图,均匀带电细棒,长为L ,电荷线密度为λ。
(1)求棒的延长线上任一点P 的场强;(2)求通过棒的端点与棒垂直上任一点Q 的场强。
解:(1)如图7-2 图a ,在细棒上任取电荷元dq ,建立如图坐标,dq =λd ξ,设棒的延长线上任一点P 与坐标原点0的距离为x ,则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(40020xL x x d E L--=-=⎰πελξξπελ=)(40L x x L-πελ方向沿ξ轴正向。
(2)如图7-2 图b ,设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y204rdxdE πελ=θπελcos 420r dxdE y =,θπελsin 420rdxdE x = 因θθθθcos ,cos ,2yr d y dx ytg x ===,习题7-1图dq ξd ξ习题7-2 图axxdx习题7-2 图by代入上式,则)cos 1(400θπελ--=y =)11(4220Ly y +--πελ,方向沿x 轴负向。
θθπελθd y dE E y y ⎰⎰==00cos 400sin 4θπελy ==2204Ly y L+πελ 7-3 一细棒弯成半径为R 的半圆形,均匀分布有电荷q ,求半圆中心O 处的场强。
解:如图,在半环上任取d l =Rd θ的线元,其上所带的电荷为dq=λRd θ。
对称分析E y =0。
θπεθλsin 420R Rd dE x =⎰⎰==πθπελ00sin 4RdE E x R02πελ=2022Rq επ=,如图,方向沿x 轴正向。
有机化学课后习题答案7第七章答案
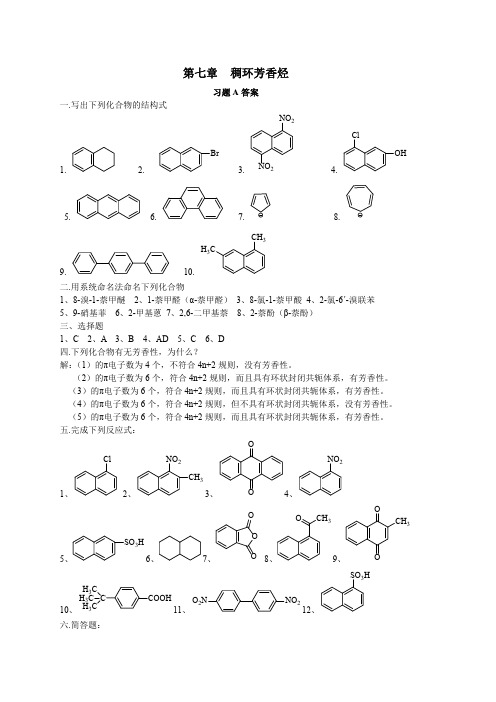
4.
V2O5, O2
一. 命名或写出结构式
1.
2. C2H5
NO2
Br2 Fe
NO2 Br
O
O
O
O
浓H2SO4
AlCl3 O
COOH
O
习题 B 答案
CH3 3.
OH 4.
SO3H
H3C
5.
6.
7. 2-乙基-9,10-蒽醌 8. 2-环丙基萘
9. 1,4-二甲基萘 10. 邻苯二甲酸酐
二.用休克尔规则判断下列化合物是否有芳香性
CHO
CHO
CH3 NBS
O2, V2O5 400-500℃
CH2MgBr 无水乙醚
CH2Br Mg 无水乙醚
CH2MgBr
O
O AlCl3
O
O Zn-Hg HCl
HOOC
H2SO4 HOOC
H3O+
H2/Ni HO CH2
H2SO4 HO CH2
O CH2
5.
O
O
Zn-Hg
浓H2SO4
O AlCl3
第七章 稠环芳香烃
一.写出下列化合物的结构式
习题 A 答案
NO2
Cl
Br
OH
1.
2.
3. NO2
4.
5.
6.
7.
8.
CH3 H3C
9.
10.
二.用系统命名法命名下列化合物 1、8-溴-1-萘甲醚 2、1-萘甲醛(α-萘甲醛) 3、8-氯-1-萘甲酸 4、2-氯-6ˊ-溴联苯 5、9-硝基菲 6、2-甲基蒽 7、2,6-二甲基萘 8、2-萘酚(β-萘酚) 三、选择题 1、C 2、A 3、B 4、AD 5、C 6、D 四.下列化合物有无芳香性,为什么? 解:(1)的π电子数为 4 个,不符合 4n+2 规则,没有芳香性。
