圆心角与圆周角能力提升训练(含答案)
九年级上册数学弧、弦、圆心角和圆周角练习及答案
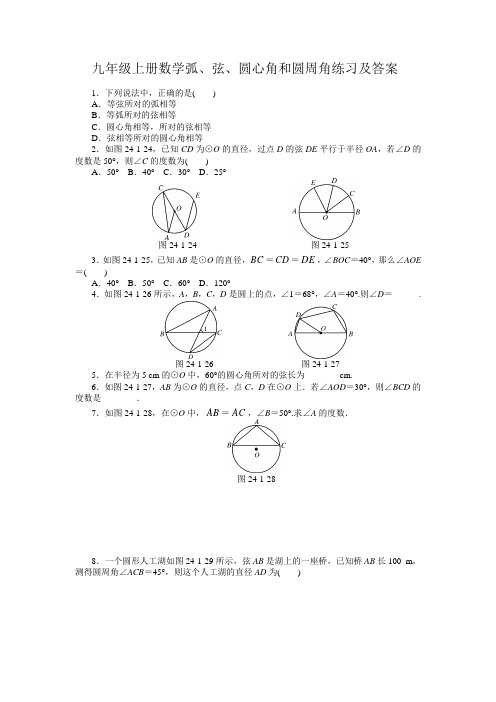
九年级上册数学弧、弦、圆心角和圆周角练习及答案1.下列说法中,正确的是()A.等弦所对的弧相等B.等弧所对的弦相等C.圆心角相等,所对的弦相等D.弦相等所对的圆心角相等2.如图24-1-24,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数为()A.50°B.40°C.30°D.25°图24-1-24 图24-1-253.如图24-1-25,已知AB是⊙O的直径,BC=CD=DE,∠BOC=40°,那么∠AOE =()A.40°B.50°C.60°D.120°4.如图24-1-26所示,A,B,C,D是圆上的点,∠1=68°,∠A=40°.则∠D=______.图24-1-26 图24-1-275.在半径为5 cm的⊙O中,60°的圆心角所对的弦长为________cm.6.如图24-1-27,AB为⊙O的直径,点C,D在⊙O上.若∠AOD=30°,则∠BCD的度数是________.7.如图24-1-28,在⊙O中,AB=AC,∠B=50°.求∠A的度数.图24-1-288.一个圆形人工湖如图24-1-29所示,弦AB是湖上的一座桥,已知桥AB长100 m,测得圆周角∠ACB=45°,则这个人工湖的直径AD为()图24-1-29 A .50 2 m B .100 2 m C .150 2 m D .200 2 m9.如图24-1-30,已知AB 是⊙O 的直径,AC 是弦,过点O 作OD ⊥AC 于点D ,连接BC .(1)求证:OD =12BC ; (2)若∠BAC =40°,求∠AOC 的度数.图24-1-3010.如图24-1-31,AB 是⊙O 的直径,点C 是BD 的中点,CE ⊥AB 于点E ,BD 交CE 于点F .(1)求证:CF =BF ;(2)若CD =6, AC =8,求⊙O 的半径及CE 的长.图24-1-31答案:1.B 2.D 3.C4.28° 5.5 6.105°7.解:∵AB =CD ,∴AB =AC .∴∠B =∠C .又∵∠B =50°,∴∠C =50°.∵∠A +∠B +∠C =180°,∴∠A =180°-(∠B +∠C )=80°.8.B9.(1)证明:∵OD ⊥AC ,∴AD =CD .∵AB 是⊙O 的直径,∴OA =OB .∴OD 是△ABC 的中位线.∴OD =12BC . (2)解:连接OC ,∵OA =OC ,∠BAC =40°,∴∠OCA =40°.∴∠AOC =180°-(40°+40°)=100°.10.(1)证明:如图D32,∵AB 是⊙O 的直径,图D32∴∠ACB =90°.又∵CE ⊥AB ,∴∠CEB =90°.∴∠A +∠B =90°,∠2+∠B =90°.∴∠A =∠2.又∵C 是弧BD 的中点,∴∠1=∠A .∴∠1=∠2. ∴ CF =BF . (2)解:由(1)可知:CD =BC ,∴CD =BC =6.又∵在Rt △ACB 中,AC =8,∴AB =10,即⊙O 的半径为5.S △ACB =AC ·BC 2=CE ·AB 2,∴CE =245.。
(完整版)圆心角和圆周角的专题练习

圆周角和圆心角的练习题、选择题1.圆周角是24°,则它所对的弧是 ___________ A .12°; B. 24°; C. 36°; D. 482•在O O中,/ AOB84°,则弦AB所对的圆周角是___________A. 42°;B. 138°;C. 84°;D. 42。
或138 ° .3.如图,圆内接四边形ABCD勺对角线AC, BD把四边形的四个角分成八个角,这八个角中相等的角的对数至少有___________________ .()A. 1 对;B. 2 对;C. 3 对;D. 4 对.4.如图,AC是O O的直径,AB CD是O O的两条弦,且AB// CD.如果/ BAC32°,贝U[]A . 16°; B. 32°; C. 48°; D. 64、计算题6.如图,AD>^ ABC外接圆的直径,AD=6cm,Z DA(=Z AB C求AC的长.7.已知:△ DBC和等边△ ABC都内接于O O BC=a,Z BCD75°(如图).求BD的长.10 .已知:如图, AD 平分/ BAC DE AC 且AB=a .求DE 的长.11.如图,在O O 中,F , G 是直径AB 上的两点,C, D,E 是半圆上的三点,如果弧 AC 的度数为60°,弧BE 的度数为20 °,/ CF/=Z DFB / DGAZ EG3.求/ FDG 勺大小.12•如图,OO 的内接正方形 ABCD 边长为1, P 为圆周上与 A, B, C, D 不重合的任意点.求 PA + PB + PC + PD 的值.13.如图,在梯形 ABCDh A D / BC , / BAD 135° ,以A 为圆心,AB 为半径作O A 交ADBC 于 E , F 两::,-1 ■- -1^ - . 泊亠X14.如图,O O 的半径为R ,弦AB=a ,弦BC/ OA 求AC 的长.15.如图,在△ ABC 中,/ BAC / ABC / BCA 的平分线交厶 ABC 的外接圆于 D, E 和F ,1 16. 如图,在O O 中,BC DF 为直径,A, E 为O O 上的点,AB=AC EF =- DF.求/ ABD 2/ CBE 的值.17. 如图,等腰三角形 ABC 的顶角为50°, ABAC 以9•如图,圆内接厶 ABC 的外角/ MAB 勺平分线交圆于 E , EC=8cm 求 BE 的长.如果 DE ,p 。
圆心角与圆周角能力提升训练2019.9.26

《圆周角》训练题命题人:刘笑天一、选择题1、如图,内接于,若,则的大小为()A.B. C.D.(第1题)(第2题)(第3题)(第4题)2、如图,AB是的直径,点C、D在上,,则()A.70° B.60° C.50° D.40°3、如图,是的外接圆,已知,则的大小为()A.40° B.30° C.45° D.50°4、如图,四边形ABCD内接于⊙O,BC是直径,AD=DC,∠ADB=20º,则∠ACB,∠DBC分别为()A.15º与30º B.20º与35º C.20º与40º D.30º与35º5、. 如右图,A、B、C、D为⊙O的四等分点,若动点P从点C出发,沿C→D→O→C路线作匀速运动,设运动时间为t,∠APB的度数为y,则y与t之间函数关系的大致图象是A B C D6.如图,在⊙O中,弦AD=弦DC,则图中相等的圆周角的对数是()A.5对 B.6对 C.7对 D.8对7.如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是()8.如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正9.将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是().D二、填空题10、如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63 º,那么∠B= º.(第10题)(第11题)(第12题)(第13题)11、如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB = 20°,则∠OCD = _____________.12、如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交BC于点D,连接DC,则∠DCB= 。
圆的定义圆心角圆周角训练题(含答案)

圆的定义圆心角圆周角训练题一、单选题(共17题;共34分)1.(2020九上·江苏月考)下列说法错误的是()A. 长度相等的两条弧是等弧B. 直径是圆中最长的弦C. 面积相等的两个圆是等圆D. 半径相等的两个半圆是等弧2.(2019九上·台安期中)下列说法中,不正确的个数是()①优弧一定比劣弧长;②面积相等的两个圆是等圆;③长度相等的弧是等弧;④经过圆心的一个定点可以作无数条弦;⑤经过圆内一定点可以作无数条直径.A. 1个B. 2个C. 3个D. 4个3.(2019九上·沭阳月考)下列命题:①直径相等的两个圆是等圆;②等弧是长度相等的弧;③圆中最长的弦是通过圆心的弦;④一条弦把圆分为两条弧,这两条弧不可能是等弧.其中真命题是( )A. ①③B. ①③④C. ①②③D. ②④4.(2019九上·贾汪月考)下列说法中,错误的是()A. 半圆是弧B. 半径相等的圆是等圆C. 过圆心的线段是直径D. 直径是弦5.(2018九上·下城期末)下列命题中是真命题的为()A. 弦是直径B. 直径相等的两个圆是等圆C. 平面内的任意一点不在圆上就在圆内D. 一个圆有且只有一条直径6.(2020九上·浙江期中)如图,是的直径,,,则的度数是().A. 52°B. 57°C. 66°D. 78°7.(2019九上·柳江月考)如图,AB是⊙O的直径,,∠COD=34°,则∠AOE的度数是( )A. 51°B. 56°C. 68°D. 78°8.(2019九上·邯郸月考)如图,AB是O的直径, ,∠BOC=40°,则∠AOE的度数为()A. 30°B. 40°C. 50°D. 60°9.(2019九上·余杭期中)如图,在△ABC中,∠C=90°,的度数为α,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则∠A的度数为()A. 45º-αB. αC. 45º+αD. 25º+α10.(2020九下·南召月考)如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A. AB=ADB. BC=CDC.D. ∠BCA=∠DCA11.(2020九上·无锡月考)在半径为的圆中,长度等于的弦所对的弧的度数为()A. B. C. 或 D. 或12.(2020·西湖模拟)如图,已知点A,B,C,D,E是⊙O的五等分点,则∠BAD的度数是()A. 36°B. 48°C. 72°D. 96°13.(2020·衢州模拟)如图,在⊙O中,=,∠A=40°,则∠B的度数是()A. 60°B. 40°C. 50°D. 70°14.(2020·乾县模拟)如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB 的度数是()A. 70°B. 80°C. 82°D. 85°15.(2019九上·龙湖期末)如图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=( )A. 40°B. 45°C. 50°D. 60°16.(2019九上·道外期末)如图,,是的直径,,若,则的度数是()A. 32°B. 60°C. 68°D. 64°17.(2019九上·光明期中)如图,已知AB是⊙O的直径,∠CBA=25°,则∠D的度数为()A. B. C. D.参考答案一、单选题1.【答案】A【解析】【解答】解:A、等弧就是指能完全重合的两段弧,所以长度相等的弧的度数不一定是等弧,故错误;B、直径是圆中最长的弦,正确;C、面积相等的两个圆是等圆,正确;D、半径相等的两个半圆是等弧,正确.故答案为:A.2.【答案】C【解析】【解答】在同圆或等圆中,优弧一定比劣弧长,所以①错误;面积相等的两个圆半径相等,则它们是等圆,所以②正确;能完全重合的弧是等弧,所以③错误;经过圆内一个定点可以作无数条弦,所以④正确;经过圆内一定点可以作无数条直径或一条直径,所以⑤错误.故答案为:C.3.【答案】A【解析】【解答】解:①直径相等的两个圆能重合,所以是等圆,①是真命题;②长度相等的弧不一定能重合,所以不一定是等弧,②是假命题;③圆中最长的弦是直径,通过圆心的弦是直径,③是真命题;④一条弦把圆分成两条弧,这两条弧可以是半圆,所以可能是等弧,④是假命题.故答案为:A.4.【答案】C【解析】【解答】解:A、半圆是弧,所以A选项的说法正确;B、半径相等的圆是等圆,所以B选项的说法正确;C、过圆心的弦为直径,所以C选项的说法错误;D、直径是弦,所以D选项的说法正确.故答案为:C.5.【答案】B【解析】【解答】解:弦不一定是直径,A是假命题;直径相等的两个圆是等圆,B是真命题;平面内的任意一点在圆上、圆内或圆外,C是假命题;一个圆有无数条直径,D是假命题;故选:B.6.【答案】C【解析】【解答】解:∵AB是⊙O的直径,,∠COD=38°,∴∠BOC=∠COD=∠DOE=38°.∴∠BOE=114°,∴∠AOE=180°-114°=66°.故答案为:C.7.【答案】D【解析】【解答】解:∵,∠COD=34°,∴∠BOC=∠COD=∠DOE=34°,∴∠AOE=180°-∠BOC-∠COD-∠DOE=180°-34°-34°-34°= 78° .故答案为:D.8.【答案】D【解析】【解答】解:∵,∠BOC=40°∴∠BOC=∠COD=∠EOD=40°∴∠BOE=120°∴∠AOE=180°-∠BOE=60°.9.【答案】A【解析】【解答】解:如图,连接CD,∵的度数为,∴∠DCE= ,∵BC=CD,∴∠CBD=∠BDC= ,∵∠C=90°,∴∠CBD+∠A=90°,∴,∴;故选择:A.10.【答案】B【解析】【解答】解:A.∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;B.∵AC平分∠BAD,∴∠BAC=∠DAC,∴BC=CD,故本选项正确;C.∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;D.∠BCA与∠DCA的大小关系不确定,故本选项错误。
圆周角 同步提升训练(附答案) 2021-2022学年苏科版九年级数学上册

2021-2022学年苏科版九年级数学上册《2.4圆周角》同步能力提升训练(附答案)1.如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为()A.45°B.50°C.60°D.75°2.如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为()A.80°B.100°C.110°D.130°3.如图,⊙O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是()A.25°B.27.5°C.30°D.35°4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为()A.50°B.60°C.70°D.80°5.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°6.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为()A.15°B.28°C.29°D.34°7.如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为()A.5cm B.5cm C.5cm D.6cm8.如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P、Q分别是、上一点(不与端点重合),如果∠MNP=∠MNQ,下面结论:①∠1=∠2;②∠P+∠Q =180°;③∠Q=∠PMN;④PM=QM;⑤MN2=PN•QN.其中正确的是()A.①②③B.①③⑤C.④⑤D.①②⑤9.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为.10.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=°.11.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=.12.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为.13.如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2,弦BM平分∠ABC 交AC于点D,连接MA,MC.(1)求⊙O半径的长;(2)求证:AB+BC=BM.14.如图,在△ABC中,CA=CB,E是边BC上一点,以AE为直径的⊙O经过点C,并交AB于点D,连接ED.(1)判断△BDE的形状并证明.(2)连接CO并延长交AB于点F,若BE=CE=3,求AF的长.15.如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.(1)求⊙O的半径;(2)求证:CE=BE.16.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.(1)求证:∠BCO=∠D;(2)若CD=,AE=2,求⊙O的半径.17.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG与DC的延长线交于点F.(1)如CD=8,BE=2,求⊙O的半径长;(2)求证:∠FGC=∠AGD.18.已知△ABC中,AB=AC,以AB为直径的圆O交BC于D,交AC于E,(1)如图①,若AB=6,CD=2,求CE的长;(2)如图②,当∠A为锐角时,使判断∠BAC与∠CBE的关系,并证明你的结论;(3)若②中的边AB不动,边AC绕点A按逆时针旋转,当∠BAC为钝角时,如图③,CA的延长线与圆O相交于E.请问:∠BAC与∠CBE的关系是否与(2)中你得出的关系相同?若相同,请加以证明,若不同,请说明理由.19.已知⊙O的直径为10,点A、点B、点C在⊙O上,∠CAB的平分线交⊙O于点D.(1)如图①,若BC为⊙O的直径,AB=6,求AC、BD、CD的长;(2)如图②,若∠CAB=60°,求BD的长.20.如图,AB是⊙O的直径,C、D为⊙O上的点,且AD平分∠CAB,作DE⊥AB于点E.(1)求证:AC∥OD;(2)若OE=4,求AC的长.参考答案1.解:设∠ADC的度数=α,∠ABC的度数=β;∵四边形ABCO是平行四边形,∴∠ABC=∠AOC;∵∠ADC=β,∠ADC=α;而α+β=180°,∴,解得:β=120°,α=60°,∠ADC=60°,故选:C.2.解:连接OC,如图所示,∵OB=OC,∴∠OCB=∠OBC=40°,∴∠BOC=100°,∵∠1+∠BOC=360°,∴∠1=260°,∵∠A=∠1,∴∠A=130°.故选:D.3.解:∵∠A=60°,∠ADC=85°,∴∠B=85°﹣60°=25°,∠CDO=95°,∴∠AOC=2∠B=50°,∴∠C=180°﹣95°﹣50°=35°故选:D.4.解:∵∠BOD=100°,∴∠A=∠BOD=50°,∵∠B=60°,∴∠C=180°﹣∠A﹣∠B=70°.故选:C.5.解:连接BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,而∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故选:C.6.解:根据圆周角定理可知:圆周角的度数等于它所对的弧的度数的一半,根据量角器的读数方法可得:(86°﹣30°)÷2=28°.故选:B.7.解:连接EC,由圆周角定理得,∠E=∠B,∠ACE=90°,∵∠B=∠EAC,∴∠E=∠EAC,∴CE=CA,∴AC=AE=5(cm),故选:B.8.解:延长MN交圆于点W,延长QN交圆于点E,延长PN交圆于点F,连接PE,QF ∵∠PNM=∠QNM,MN⊥AB,∴∠1=∠2(故①正确),∵∠2与∠ANE是对顶角,∴∠1=∠ANE,∵AB是直径,∴可得PN=EN,同理NQ=NF,∵点N是MW的中点,MN•NW=MN2=PN•NF=EN•NQ=PN•QN(故⑤正确),∴MN:NQ=PN:MN,∵∠PNM=∠QNM,∴△NPM∽△NMQ,∴∠Q=∠PMN(故③正确).故选:B.9.解:当GH为⊙O的直径时,GE+FH有最大值.当GH为直径时,E点与O点重合,∴AC也是直径,AC=14.∵∠ABC是直径上的圆周角,∴∠ABC=90°,∵∠C=30°,∴AB=AC=7.∵点E、F分别为AC、BC的中点,∴EF=AB=3.5,∴GE+FH=GH﹣EF=14﹣3.5=10.5.故答案为:10.5.10.解:如图,连接CE,∵五边形ABCDE是圆内接五边形,∴四边形ABCE是圆内接四边形,∴∠B+∠AEC=180°,∵∠CED=∠CAD=35°,∴∠B+∠E=180°+35°=215°.故答案为:215.11.解:∵∠A=55°,∠E=30°,∴∠EBF=∠A+∠E=85°,∵∠A+∠BCD=180°,∴∠BCD=180°﹣55°=125°,∵∠BCD=∠F+∠CBF,∴∠F=125°﹣85°=40°.故答案为40°.12.解:∵∠CBE=50°,∴∠ABC=180°﹣∠CBE=180°﹣50°=130°,∵四边形ABCD为⊙O的内接四边形,∴∠D=180°﹣∠ABC=180°﹣130°=50°,∵DA=DC,∴∠DAC==65°,故答案为:65°13.解:(1)连接OA、OC,过O作OH⊥AC于点H,如图1,∵∠ABC=120°,∴∠AMC=180°﹣∠ABC=60°,∴∠AOC=2∠AMC=120°,∴∠AOH=∠AOC=60°,∵AH=AC=,∴OA=2,故⊙O的半径为2.(2)证明:在BM上截取BE=BC,连接CE,如图2,∵∠ABC=120°,BM平分∠ABC,∴∠ABM=∠CBM=60°,∵BE=BC,∴△EBC是等边三角形,∴CE=CB=BE,∠BCE=60°,∴∠BCD+∠DCE=60°,∵∠ACM=60°,∴∠ECM+∠DCE=60°,∴∠ECM=∠BCD,∵∠CAM=∠CBM=60°,∠ACM=∠ABM=60°,∴△ACM是等边三角形,∴AC=CM,∴△ACB≌△MCE,∴AB=ME,∵ME+EB=BM,∴AB+BC=BM.14.(1)证明:△BDE是等腰直角三角形.∵AE是⊙O的直径∴∠ACB=∠ADE=90°,∴∠BDE=180°﹣90°=90°.∵CA=CB,∴∠B=45°,∴△BDE是等腰直角三角形.(2)过点F作FG⊥AC于点G,则△AFG是等腰直角三角形,且AG=FG.∵OA=OC,∴∠EAC=∠FCG.∵BE=CE=3,∴AC=BC=2CE=6,∴tan∠FCG=tan∠EAC=.∴CG=2FG=2AG.∴FG=AG=2,∴AF=2.15.(1)解:∵OC为⊙O的半径,OC⊥BD,∴;∵DB=8,∴MB=4设⊙O的半径为r,∵CM=2,∴OM=r﹣2,在Rt△OMB中,根据勾股定理得(r﹣2)2+42=r2,解得r=5;(2)证明:方法一:连接AC、CB,∵AB是直径,∴∠ACB=90°.∴∠ACF+∠FCB=90°.又∵CF⊥AB,∴∠CAF+∠ACF=90°∴∠FCB=∠CAF(3分)∵OC为⊙O的半径,OC⊥BD,∴C是的中点,∴∠CAF=∠CBD.∴∠FCB=∠DBC.∴CE=BE;方法二:如图,连接BC,补全⊙O,延长CF交⊙O于点G;又∵CF⊥AB,AB为直径,∴=.∴OC为⊙O的半径,OC⊥BD.∴C是的中点,∴=.∴=.∴∠FCB=∠DBC.∴CE=BE.16.(1)证明:如图.∵OC=OB,∴∠BCO=∠B.∵∠B=∠D,∴∠BCO=∠D;(2)∵AB是⊙O的直径,且CD⊥AB于点E,∴CE=CD=×4=2,在Rt△OCE中,OC2=CE2+OE2,设⊙O的半径为r,则OC=r,OE=OA﹣AE=r﹣2,∴r2=(2)2+(r﹣2)2,解得:r=3,∴⊙O的半径为3.17.(1)解:连接OC.设⊙O的半径为R.∵CD⊥AB,∴DE=EC=4,在Rt△OEC中,∵OC2=OE2+EC2,∴R2=(R﹣2)2+42,解得R=5.(2)证明:连接AD,∵弦CD⊥AB∴=,∴∠ADC=∠AGD,∵四边形ADCG是圆内接四边形,∴∠ADC=∠FGC,∴∠FGC=∠AGD.18.解:(1)连接AD.∵AB为直径,∴AD⊥BC.又∵AB=AC,∴BD=CD.又CD=2,∴BD=2.∴CE=.(2)∠BAC与∠CBE的关系是:∠BAC=2∠CBE.理由如下:由(1),得AD⊥BC.又AB=AC,∴∠1=∠2.又∠2=∠CBE,∴∠BAC=2∠CBE.(3)相同.理由如下:连接AD.∵AB为直径,∴AD⊥BC,又AB=AC,∴∠1=∠2,∵∠CAD是圆内接四边形AEBD的外角,∴∠2=∠CBE,∴∠CAB=2∠CBE.19.解:(1)如图①,∵BC是⊙O的直径,∴∠CAB=∠BDC=90°.∵在直角△CAB中,BC=10,AB=6,∴由勾股定理得到:AC===8.∵AD平分∠CAB,∴=,∴CD=BD.在直角△BDC中,BC=10,CD2+BD2=BC2,∴易求BD=CD=5;(2)如图②,连接OB,OD,∵AD平分∠CAB,且∠CAB=60°,∴∠DAB=∠CAB=30°,∴∠DOB=2∠DAB=60°.又∵OB=OD,∴△OBD是等边三角形,∴BD=OB=OD.∵⊙O的直径为10,则OB=5,∴BD=5.20.(1)证明:∵AD平分∠CAB,∴∠OAC=2∠OAD.∵∠BOD=2∠BAD,∴∠BOD=∠OAC,∴AC∥OD.(2)解:作OF⊥AC于点F,如图所示:则AF=AC,∵AC∥OD,∴∠DOE=∠OAF.在△DOE和△OAF中,,∴△DOE≌△OAF(AAS),∴OE=AF=AC,∴AC=2OE=8.。
北师大九年级下《3.4圆周角与圆心角的关系》强化训练含答案

《3.4圆心角与圆周角的关系》强化训练一、选择题1.如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是()第1小题图第2小题图第3小题图第4小题图A.150°B.140°C.130°D.120°2.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是()A.75°B.60°C.45°D.30°3.如图,BD是⊙O的直径,点A、C在⊙O上,AB BC,∠AOB=60°,则∠BDC的度数=是()A.60°B.45°C.35°D.30°4.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为()A.140°B.70°C.60°D.40°5.如图,A、D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=()第5小题图第6小题图第7小题图第8小题图A .64°B .58°C .72°D .55° 6.如图,点A ,B ,C 在⊙O 上,∠A=36°,∠C=28°,则∠B=( ) A .100° B .72° C .64°D .36°7.如图,线段AB 是⊙O 的直径,弦CD ⊥AB ,∠CAB=40°,则∠ABD 与∠AOD 分别等于( ) A .40°,80°B .50°,100°C .50°,80°D .40°,100°8.如图,已知AB 是⊙O 的直径,∠D=40°,则∠CAB 的度数为( ) A .20° B .40°C .50°D .70°9.如图,把直角三角板的直角顶点O 放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M 、N ,量得OM=8cm ,ON=6cm ,则该圆玻璃镜的半径是( )第9小题图 第10小题图 第11小题图 第12小题图A B .5cm C .6cm D .10cm10.如图,半径为3的⊙A 经过原点O 和点C (0,2),B 是y 轴左侧⊙A 优弧上一点,则tan ∠OBC 为( )A .13B .CD 11.如图,点A 、B 、C 是圆O 上的三点,且四边形ABCO 是平行四边形,OF ⊥OC 交圆O 于点F ,则∠BAF 等于( ) A .12.5°B .15°C .20°D .22.5°12.如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则()A.DE=EB B C D.DE=OB二、填空题13.如图,AB为⊙O的直径,C,D为⊙O上的两点,若AB=6,BC=3,则∠BDC=度.第13小题图第14小题图第15小题图第16小题图14.如图,在⊙O中,AB是弦,C是 AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC 的大小为度.15.如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=度.16.如图,⊙O是△ABC的外接圆,∠AOB=70°,AB=AC,则∠ABC=.17.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD=°.第17小题图第18小题图第19小题图第20小题图18.如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=.19.如图,A,B,C,D是⊙O上的四个点,∠C=110°,则∠BOD=140度.20.如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O 的直径,AB=BC=CD.连接PA、PB、PC,若PA=a,则点A到PB和PC的距离之和AE+AF=.三、解答题21.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;(2)求证:∠1=∠2.22.如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.(1)求证:∠1=∠F.(2)若EF=2CD的长.23.已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形(1)求证:△DFB是等腰三角形;(2)若,求证:CF⊥AB.24.在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP ⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度;(2)如图2,当点P在BC上移动时,求PQ长的最大值.25.如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且.DE BE(1)试判断△ABC的形状,并说明理由.(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.26.已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.(1)求证:AB=AC;(2)若AB=4,CD的长.参考答案1.A2.D3.D4.B5.B6.C7.B8.C9.B 10.C 11.B 12.D13.30 14.30 15.35 16.35°17.62°18.65 19.140 20.21.(1)∵BC=DC,∴∠CBD=∠CDB=39°,∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,∴∠BAD=∠BAC+∠CAD=39°+39°=78°;(2)∵EC=BC,∴∠CEB=∠CBE,而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,∴∠2+∠BAE=∠1+∠CBD,∵∠BAE=∠BDC=∠CBD,∴∠1=∠2.22.(1)证明:连接DE,∵BD是⊙O的直径,∴∠DEB=90°,∵E是AB的中点,∴DA=DB,∴∠1=∠B,∵∠B=∠F,∴∠1=∠F;(2)∵∠1=∠F,∴AE=EF=2,∴AB=2AE=4,在Rt△ABC中,AC=AB•sinB=4,∴BC==8,设CD=x,则AD=BD=8﹣x,∵AC2+CD2=AD2,即42+x2=(8﹣x)2,∴x=3,即CD=3.23.(1)∵AB是⊙O直径,∴∠ACB=90°,∵△AEF为等边三角形,∴∠CAB=∠EFA=60°,∴∠B=30°,∵∠EFA=∠B+∠FDB,∴∠B=∠FDB=30°,∴△DFB是等腰三角形;(2)过点A作AM⊥DF于点M,设AF=2a,∵△AEF是等边三角形,∴FM=EM=a,,在Rt△DAM中,,,∴DM=5a,∴DF=BF=6a,∴AB=AF+BF=8a,在Rt△ABC中,∠B=30°,∠ACB=90°,∴AC=4a,∵AE=EF=AF=2a,∴CE=AC﹣AE=2a,∵∠AEF=∠ECF +∠EFC=60°,∴∠CFE=30°, ∴∠AFC=∠AFE +∠EFC=60°+30°=90°, ∴CF ⊥AB .24. (1)连结OQ ,如图1,∵PQ ∥AB ,OP ⊥PQ , ∴OP ⊥AB ,在Rt △OBP 中,∵tan ∠B=OPOB,∴OP=3tan30°在Rt △OPQ 中,∵OQ=3,∴= (2)连结OQ ,如图2,在Rt △OPQ 中,=, 当OP 的长最小时,PQ 的长最大, 此时OP ⊥BC ,则OP=12OB=32,∴PQ 2=.25. (1)△ABC 为等腰三角形.理由如下:连结AE ,如图,∵ DEBE =, ∴∠DAE=∠BAE ,即AE 平分∠BAC , ∵AB 为直径,∴AE⊥BC,∴△ABC为等腰三角形;(2)∵△ABC为等腰三角形,AE⊥BC,∴BE=CE=12BC=12×12=6,在Rt△ABE中,∵AB=10,BE=6,∴AE=,∵AB为直径,∴∠ADB=90°,∴12AE•BC=12BD•AC,∴BD=81248 105⨯=,在Rt△ABD中,∵AB=10,BD=485,∴145 =,∴sin∠ABD=14751025 ADAB==.26.(1)证明:∵ED=EC,∴∠EDC=∠C,∵∠EDC=∠B,∴∠B=∠C,∴AB=AC;(2)连接AE,∵AB为直径,∴AE⊥BC,由(1)知AB=AC,∴BE=CE=12BC=,∵△CDE∽△CBA,∴CD CE CB AC=,∴CE•CB=CD•CA,AC=AB=4,,∴CD=32第11 页/ 共11 页。
圆周角—巩固练习(提高)含答案

C圆周角—巩固练习(提高)【巩固练习】一、选择题1.如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有()A、2个B、3个C、4个D、5个2.已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°。
给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC。
其中正确的有()个A.5B.4C.3D.2第1题图第2题图第3题图3.如图,在⊙O中,弦AB的长是半径OA的3倍,为AB中点,AB、OC交于点P,则四边形OACB是() A.平行四边形B.矩形C.菱形D.正方形4.如图,设⊙O的半径为r,弦的长为a,弦与圆心的距离为d,弦的中点到所对劣弧中点的距离为h,下面说法或等式:①r=d+h②4r2=4d2+a2正确结论的序号是()③已知r、a、d、h中任意两个,可求其它两个。
其中A.仅①B.②③C.①②③D.①③5.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为()A.68°B.88°C.90°D.112°6.(2016黔南州)如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为()A.cm B.3cm C.3cm D.6cm二、填空题7.如图所示,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD、CB的延长线相交于P,则∠P=________°.(第7题)(第9题)8.(2016青岛)如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD=°.9.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,BE=1,C D42,则∠AED=°.10.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.11.如图所示,在半径为3的⊙O中,点B是劣弧AC的中点,连接AB并延长到D,使BD=AB,连接AC、BC、CD,如果AB=2,那么CD=________.ABM O P N(第10题图)(第11题图)(第12题图)︵12.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,点B为AN中点,P直径MN上的一个动点,则PA+PB的最小值是.13.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=.三、解答题14.如图,在⊙O中,AB=BC=CD,OB,OC分别交AC,BD于E、F,求证O E=OF15.如图,等腰△ABC中,AC=BC,⊙O为△ABC的外接圆,D为上一点,CE⊥AD于E,求证:AE=BD+DE.16.如图所示,AB是⊙O的直径,C为AE的中点,CD⊥AB于D,交AE于F,连接AC,求证:AF=CF.17.如图所示,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.【答案与解析】一、选择题1.【答案】D.【解析】与∠BCE相等的角有5个,∠DAE=∠AED=∠ABD,∠BAD=∠BAE+∠DAE=∠BAE+∠ABD=∠BCE,同理∠ADO=∠ODE=∠OED=∠BCE,且∠ACD=∠BCE.2.【答案】C.【解析】①②④正确.3.【答案】C.【解析】由弦AB的长是半径OA的3倍,C为AB中点,得∠AOC=60°,△AOC为等边三角形,所以AO=AC,进而得到OA=OB=BC=AC,故则四边形OACB是菱形.4.【答案】C.【解析】根据垂径定理及勾股定理可得①②③都是正确的.5.【答案】B.【解析】如图,∵AB=AC=AD,∴点B、C、D在以点A为圆心,以AB的长为半径的圆上;∵∠CBD=2∠BDC,∠CAD=2∠CBD,∠BAC=2∠BDC,∴∠CAD=2∠BAC,而∠BAC=44°,∴∠CAD=88°,故选B.6.【答案】A.【解析】连接CB.∵AB是⊙O的直径,弦CD⊥AB于点E,∴圆心O到弦CD的距离为OE;∵∠COB=2∠CDB(同弧所对的圆周角是所对的圆心角的一半),∠CDB=30°,=∴∠COB=60°;在 △Rt OCE 中,OC=5cm ,∴OE= cm . 故选 A .二、填空题 7.【答案】40°;【解析】∵ ∠AOC =130°,∴ ∠ADC =∠ABC =65°, 又 AB ⊥CD ,∴ ∠PCD =90°-65°=25°,∴ ∠P =∠ADC -∠PCD =65°-25°=40°.8.【答案】62.【解析】∵AB 是⊙O 的直径,∴∠ACB=90°,∵∠BCD=28°,∴∠ACD=62°,由圆周角定理得,∠ABD=∠ACD=62°,故答案为:62.9.【答案】30°; 10.【答案】3;11.【答案】43;【解析】连结 OA 、OB ,交 AC 于 E ,因为点 B 是劣弧 AC 的中点,所以OB ⊥AC ,设 BE=x,则 OE=3-x ,由 AB 2-BE 2=OA 2-OE 2 得22-x 2=32-(3-x )2,解得 x = 2 4, CD = 2BE = .3 3AB CD 2 CD 4或连接 OA 、△O B , OAB ∽△BCD , , = , CD = . OA BC 3 2 312.【答案】;【解析】作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.(如图)此时PA+PB最小,且等于AC的长.连接OA,OC,根据题意得弧AN的度数是60°,则弧BN的度数是30°,根据垂径定理得弧CN的度数是30°,则∠AOC=90°,又OA=OC=1,则AC=.13.【答案】40°;【解析】∵∠A=55°,∠E=30°,∴∠EBF=∠A+∠E=85°,∵∠A+∠BCD=180°,∴∠BCD=180°﹣55°=125°,∵∠BCD=∠F+∠CBF,∴∠F=125°﹣85°=40°.三、解答题14.【答案与解析】如图,∵AB=BC=CD,∴AC=BD,∴AC=BD,∵B,C是AC,BD的中点,∴BF=CE=1AC,O B⊥AC,O C⊥BD, 2∴Rt OBF≌Rt OCE,∴OE=OF15.【答案与解析】证明:如图,在AE上截取AF=BD,连接CF,CD;在△ACF和△BCD中∴△ACF≌△BCD,∴CF=CD,∵CE⊥AD于E,∴EF=DE,∴AE=AF+EF=BD+DE.16.【答案与解析】证法一:连接BC,如图所示.∵AB是直径,∴∠ACB=90°,即∠ACF+∠BCD=90°.又∵CD⊥AB,∴∠B+∠BCD=90°,∴∠ACF=∠B.∵点C是AE的中点,∴AC=CE,∴∠B=∠CAE,∴∠ACF=∠CAE,∴AF=CF.证法二:如图所示,连接BC,并延长CD交⊙O于点H.∵AB是直径,CD⊥AB,∴AC=AH.∴点C是AE的中点,∴AC=CE,∴AH=CE.∵∠ACF=∠CAF,∴AF=CF.四边形ADBC =S17.【答案与解析】∵AB是直径,∴∠ACB=∠ADB=∠90°.在△R t ABC中,AB=6,AC=2,∴BC=AB2-AC2=62-22=42.∵∠ACB的平分线交⊙O于点D,∴∠DCA=∠BCD.∴AD=DB,∴AD=BD.∴在△R t ABD中,AD2+BD2=AB2=62,∴AD=BD=32.∴S∆ABC +S∆ABD=11A C BC+AD BD22=11⨯2⨯42+⨯(32)2=9+42.22。
北师大版九年级下册数学 3.4圆周角和圆心角之间的关系 同步练习(含解析)

3.4圆周角和圆心角之间的关系同步练习一.选择题1.如图,AB是⊙O的直径,AC是弦,若∠ACO=30°,则sin∠COB的等于()A.B.C.D.2.⊙O中,∠AOB=100°,若C是上一点,则∠ACB等于()A.80°B.100°C.120°D.130°3.如图,==,AD为⊙O的弦,∠BAD=50°,则∠AED等于()A.50°B.60°C.70°D.75°4.如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP =∠CAP=10°,若的度数是40°,则的度数是()A.10°B.15°C.20°D.25°5.AB为半圆O的直径,弦AD,BC相交于点P,若CD=3,AB=4,则tan∠BPD等于()A.B.C.D.6.如图所示,AB是直径,点E是弧AB中点,弦CD∥AB且平分OE,连AD,∠BAD度数为()A.45°B.30°C.15°D.107.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则()A.α=βB.α+2β=90°C.2α+β=90°D.α+β=45°8.如图,已知A、B、C、D、E是⊙O上的五个点,圆心O在AD上,∠BCD=110°,则∠AEB的度数为()A.70°B.35°C.40°D.20°9.如图,⊙O中,若OA⊥BC、∠AOB=66°,则∠ADC的度数为()A.33°B.56°C.57°D.66°10.如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为弧AC的中点,过点D作DE ∥AC,交BC的延长线于点E.若⊙O的半径为5,AB=8,则CE的长为()A.4B.C.D.二.填空题11.如图所示,⊙O的直径CD过弦EF的中点G,∠GEO=46°,则∠DCF=.12.如图,AD是⊙O的直径,若∠B=40°,则∠DAC的度数为.13.如图,⊙O的半径为2.弦AB=2,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是.14.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=70°,则∠BAE=°.15.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM 的最小值为.三.解答题16.如图,以△ABC的一边为直径的半圆与其它两边AC、BC分别交于点D、E,=.(1)求证;AC=AB;(2)若BC=8,BA=6,求CD的长.17.如图,在⊙O中.(1)若=,∠ACB=80°,求∠BOC的度数;(2)若⊙O的半径为13,且BC=10,求点O到BC的距离.18.如图,⊙O的直径AB=12,半径OC⊥AB,D为弧BC上一动点(不包括B、C两点),DE⊥OC,DF⊥AB,垂足分别为E.F.(1)求EF的长.(2)若点E为OC的中点,①求弧CD的度数.②若点P为直径AB上一动点,直接写出PC+PD的最小值.参考答案一.选择题1.解:∵OA=OC,∠ACO=30°,∴∠OAC=∠ACO=30°,∵∠COB是△AOC的外角,∴∠COB=∠ACO+∠OAC=60°,∴sin∠COB=sin60°=.故选:C.2.解:如图:在优弧上取点D,连接AD,BD,∵⊙O中,∠AOB=100°,∴∠ADB=∠AOB=50°,∵四边形ACBD是⊙O的内接四边形,∴∠ACB=180°﹣∠ADB=130°.故选:D.3.解:连接OA,OB,OC,OD,∵∠BAD=50°,==,∴∠BOD=2∠BAD=100°,∵==,∴AOB=∠BOC=∠COD=∠BOD=50°,∴∠AOD=∠AOB+∠BOC+∠COD=150°,∴∠AED=∠AOD=75°.故选:D.4.解:∵的度数是40°,∴∠ACM=40°∵∠CBP=∠CAP=10°,∴A、C、P、B四点共圆,∴∠ACM=∠ABP=40°,∵∠CPB=10°,∴∠ABC=40°﹣10°=30°,∵AC=BC,∴∠CAB=∠ABC=30°,∴∠ACB=120°,∴∠BCN=180°﹣∠ACM﹣∠ACB=20°,∴的度数是20°.故选:C.5.解:连接BD.则∠CDA=∠ABC.(同圆中同弧AC所对的圆周角相等)同理∠DCB=∠DAB,所以△PCD∽△P AB,==.∵AB直径,∴∠ADB=90°.∴∠PDB=∠ADB=90°,在Rt△PDB中,cos∠DPB==,∴sin∠DPB=.(sin2∠DPB+cos2∠DPB=1)tan∠BPD==.故选:A.6.解:设CD与OE交于P,则连接OC,∵CD∥AB且平分OE,∴OP=•OC,∴sin∠PCO=,∴∠PCO=30°,又∵CD∥AB,∴∠COA=∠PCO=30°,∴∠BAD=∠BOD=15°.故选:C.7.解:如图,设AC与DO交点为E,如图,∵OD=OB,∴∠OBD=∠BDO=α,∴∠DOA=2∠OBD=2α,又∵D为中点,AB为⊙O直径,∴OD⊥AC,∴∠EAO+∠EOA=90°,即2α+β=90°.故选:C.8.解:如图,连接DE,数学∵四边形BCDE是⊙O的内接四边形,∴∠BCD+∠BED=180°,∵∠BCD=110°,∴∠BED=70°,∵AD是⊙O的直径,∴∠AED=90°,∴∠AEB=∠AED﹣∠BED=90°﹣70°=20°,故选:D.9.解:如图,连接OC,OB.∵OA⊥BC,∴=,∴∠AOC=∠AOB=66°,∴∠ADC=∠AOC=33°,数学故选:A.10.解:∵⊙O的半径为5,∴AC=10,∴AD=CD=5,∵AC为⊙O的直径,∴∠ABC=90°,∵AB=8,∴BC=6,∵∠BAD=∠DCE,∵∠ABD=∠CDE=45°,∴△ABD∽△CDE,∴,∴,∴CE=,故选:B.二.填空题11.解:∵CD是直径,EG=GF,∴CD⊥EF,∴=,∴∠CDF=∠EOD,∵∠OGE=90°,∠GEO=46°,∴∠EOD=44°,∴∠DCF=22°.故答案为:22°.12.解:连接CD.∵AD是直径,∴∠ACD=90°,∵∠D=∠B=40°,∴∠DAC=90°﹣40°=50°.故答案为50°.13.解:连结OA、OB,作△ABC的外接圆D,如图1,∵OA=OB=2,AB=2,∴△OAB为等边三角形,∴∠AOB=60°,∴∠APB=∠AOB=30°,∵AC⊥AP,∴∠C=60°,∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,∵∠ACB=60°,点C在⊙D上,∴∠ADB=120°,如图2,当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2=,∴△ABC的最大面积为.故答案为:.14.解:∵四边形ABCD是平行四边形,∠D=70°,∴∠DCB=(180°﹣∠D)=110°,∵四边形AECD是圆内接四边形,∴∠AEB=∠D=70°,∠B=180°﹣∠BCD=70°∴∠BAE=180°﹣70°﹣70°=40°,故答案为:4015.解:如图,连接OM,CM,过点A作AT⊥CM交CM的延长线于T.∵=,∴OM⊥PD,∴∠MOD=90°,∴∠MCD=∠MOD=45°,∵∠ACB=90°,∴∠ACT=45°,∵AT⊥CT,∴∠ATC=90°,∵AC=10,∴AT=AC•sin45°=5,∵AM≥AT,∴AM≥5,∴AM的最小值为5,故答案为5.三.解答题16.(1)证明:∵=,∴∠CAE=∠BAE,∵AB为直径,∴∠AEB=90°,∵∠ABE+∠BAE=90°,∠C+∠CAE=90°,∴∠ABC=∠C,∴AC=AB;(2)解:∵∠CAE=∠CBD,∠ACE=∠BCD,∴△CAE∽△CBD,∴=,即=,∴CD=.17.解:(1)∵=,∴∠ABC=∠ACB=80°,∴∠A=180°﹣80°﹣80°=20°,∴∠BOC=2∠A=40°;(2)作OH⊥BC于H,如图,则BH=CH=BC=5,在Rt△OBH中,OH===12,即点O到BC的距离为12.18.解:(1)连接OD,∵⊙O的直径AB=12,∴圆的半径为12÷2=6,∵OC⊥AB,DE⊥OC,DF⊥AB,∴四边形OFDE是矩形,∴EF=OD=6;(2)①∵点E为OC的中点,∴OE=OC=OD,∴∠EDO=30°,∴∠DOE=60°,∴弧CD的度数为60°;②延长CO交⊙O于G,l连接DG交AB于P,则PC+PD的最小值=DG,∵∠G=∠COD=30°,∵EG=9,数学∴DG===6,∴PC+PD的最小值为6.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
松滋市实验中学九年级培优辅差《圆周角》训练题
命题人:胡海洋
题号一、选择题二、填空题三、简答题总分
得分
一、选择题
1、如图,内接于,若,则的大小为()
A.B. C.D.
(第1题)(第2题)(第3题)(第4题)(第5题)
2、如图,AB是的直径,点C、D在上,,则()
A.70° B.60° C.50° D.40°
3、如图,是的外接圆,已知,则的大小为()
A.40° B.30° C.45°
D.50°
4、如图,已知A、B、C、D、E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C= ( )
A.180°B.90°C.45°D.30°
5、如图,四边形ABCD内接于⊙O,BC是直径,AD=DC,∠ADB=20º,则∠ACB,∠DBC分别为()
A.15º与30º B.20º与35º C.20º与40º D.30º与35º
6、. 如右图,A、B、C、D为⊙O的四等分点,若动点P从点C出发,沿C→D→O→C路线作匀速运动,设运动时间为t,∠APB的度数为y,则y与t之间函数关系的大致图象是
A B C
D
二、填空题
7、如图,在⊙O中,∠AOB=46º,则∠ACB=º.
8、如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63 º,那么∠B= º.
(第7题)(第8题)(第9题)(第10题)(第11题)
9、如图,AB是⊙0的直径,弦AC长为4a,弦BC长为5a,∠ACB的平分线交⊙0于点D,则CD的长为 .
10、如图, ⊙P过O、、,半径PB⊥PA,双曲线恰好经过B点,则k的值是
____________.
11、如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB = 20°,则∠OCD = _____________.
12、如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交BC于点D,连接DC,则∠
DCB= 。
(第12题)(第13题)(第14题)
13、如图,为的直径,点为其半圆上任意一点(不含、),点为另一半圆上一定点,若
为度,为度.则与的函数关系是.
14、如图,是半圆的直径,为圆心,是半圆上一点,且,是延长线上一点,与半圆相交于点,如果,则,,.
三、简答题
15、AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连BC.若,求的度数.
16、已知AB、AC为⊙O的两条弦
(1)用直尺(没有刻度)和圆规作出弧BC的中点D;
(2)连接OD,则OD∥AC吗?若成立,请证明;若不成立,请添加一个适当的条
件,使之成立,再证明.
17、如图,AB为半圆直径,O 为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D,若AC=8cm,DE=2cm,求OD的长。
,BF和AD交于E,18、.如图20-12,BC为⊙O的直径,AD⊥BC,垂足为D,AB AF
求证:AE=BE.
19、在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.
20、如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;
(2)已知AD=6求圆心O到BD的距离.
21、如图,⊙ 0是ABC的外接圆,AD是⊙0的直径,DE⊥ BC于E,AF⊥BC于F
(1)求证BE=CF;
(2)作OG ⊥BC于G,若DE=BF=3,OG=1,求弦AC的长.
22、如右图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=10,求弦AC的长.
23、.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD。
(1)P是优弧CAD上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论。
24、如图,⊙O为四边形的外接圆,圆心在上,∥。
(1)求证:AC平分;
(2)若AC = 8,AC:CD=2:1试求⊙C的半径;
(3)
参考答案
一、选择题
1、D
2、D
3、A
4、B
5、B
6、C
二、填空题
7、【考点】圆周角定理.
【分析】由⊙O中,∠AOB=46°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠ACB的度数.
【解答】解:∵⊙O中,∠AOB=46°,
∴∠ACB=1 2 ∠AOB=1 2 ×46°=23°.
故答案为:23.
【点评】此题考查了圆周角定理.此题比较简单,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用,注意数形结合思想的应用.
8、21°
9、
10、-4
11、65°
12、30度
13、
14、
三、简答题
15、证明:切⊙O于是⊙O的直径,
∴.
,∴.
∴.
16、解:(1)作图略……………………………………… 3分
(2) 不成立,添加:AB是直径…………… 2分
证明略……………………………… 3分
17、3
18、证明:连结AB,AC,
∠BAD=∠ABF AE=BE.
19、解:连接BD
∵AB⊙O是直径
∴BD⊥AD
又∵CF⊥AD
∴BD∥CF
∴∠BDC=∠C…………………………3分
又∵∠BDC=∠BOC
∴∠C=∠BOC
∵AB⊥CD
∴∠C=30°
∴∠ADC=60°…………………………………………………………………6分20、考点:圆周角定理;三角形内角和定理;垂径定理。
解答:解:(1)∵∠APD=∠C+∠CAB,
∴∠C=65°﹣40°=25°,
∴∠B=∠C=25°;
(2)作OE⊥BD于E,
则DE=BE,
又∵AO=BO,
∴,
圆心O到BD的距离为3.
21、(1)证明:延长DE交⊙0于B,
连接AH、BH.则四边形AHEF为矩形,
∴AF=EH,AH//EF,∴∠HAB=∠ABC,
∴BH =AC,∴ Rt△BEH≌ Rt△CFA,.∴ BE=CF;
(2)解:连接CD,连接FO并延长交DE于P点.
则AFO≌△DPO,∴ AF=DP,OF=OP,
∴OG= PE,∴PE=2,∴AF=DP=1
∵DE=BF=CE,∴∠BCD=45°
又∠ACD=90°,:. ∠ACB=45°.
∴AC=
湖北松滋实验中学
22、解:∵BD为⊙O的直径,∴∠BAD=90°
,
23、(1)证明:连接OD,∵AB是直径,AB⊥CD,∴∠COB=∠DOB=。
又∵∠CPD=,∴∠CPD=∠COB。
(2)∠CP′D与∠COB的数量关系是:∠CP′D+∠COB=180°。
证明:∵∠CPD+∠CP′D=180°,∠CPD=∠COB,∴∠CP′D+∠COB=180°。
24、解:(1)∵OC//AB,∴∠BAC=∠ACO,
∵ OC=OA∴∠ACO =∠CAO
∴∠CAO=∠BAC即:AC平分∠DAB
(2)AC=8,弧AC 与CD之比为2:1,
∴∠CAD=30°∵AD是直径,∴∠ACD=90°,
∴ AD=∴圆O的半径为
(3)∵点B为弧AC的中点∴∠BAC=∠BCA,
∴∠BAC=∠BCA=∠=OAC=∠OCA∴OA//BC
∴四边形ABCO是平行四边形∵ AO=CO ∴四边形ABCO为菱形
命题人:胡海洋。
