工程力学-位移法计算超静定结构
高等工程力学1 超静定结构内力计算

M i 、Qi、N i ——任取的基本体系在单位力作用下的内力图,而单位力是加在 要求位移的截面上的;
—RK—基本体系支座k在单位力作用下的反力;
cK——k支座的实际位移。 公式(1-7)的前三项表示基本体系在荷载和多余未知力的作用下的位移,后
三项表示基本体系在温度变化和支座移动情况下引起的位移。
1 超静定结构内力计算
⑵ 有结点线位移的情况 计算这类结构时;原利用公式(1-11)考虑各结点的弯矩平衡外,还需考虑 相应杆端剪力的平衡。取适当的截面截出结构的一部分,通常是截断各柱的柱顶 端。取出横梁。考虑剪力平衡,建立剪力平衡方程,即
Qx 0
(1-12)
补充了剪力平衡方程后,方程式的数目仍然与未知数的数目相等,方程式总是 可以求解的。
1 超静定结构内力计算
§1.1.1力法的基本原理(续4)
由力法方程解出未知力X1、X2、…Xn后,超静定结构的内力可根据叠加原理 用下式计算:
M M1X1 M2X2 MnXn MP Q Q1 X 1 Q2 X 2 Qn X n QP N N1X1 N2 X 2 Nn X n NP
§1.2.4利用典型方程求解结构的位移和内力(续1)
同理附加链杆处的反力也为零,即
R2 R21 R22 R2P 0
或写成
r11Z1 r12Z2 R1P 0 r21Z1 r22Z2 R2P 0
对于有n个基本未知数的结构,位移法典型方程式为:
r11Z1 r12 Z2 r1n Zn R1P 0 r21Z1 r22 Z2 r2n Zn R2P 0
§1.2.1等截面直杆的转角位移方程式(续1)
AB杆产生位移后,杆端的总弯矩为
M AB
M
/ AB
M
结构力学_11超静定结构-位移法

§11.3 位移法的基本未知量和基本体系
1、结点角位移数:
结构上可动刚结点数即为位移法计算的结点角位移数。
2、结构独立线位移:
每个结点有两个线位移,为了减少未知量,引入与实际相符的两个假设:
(1)忽略轴向力产生的轴向变形 (2)变形后的曲杆长度与其弦等长。
C
C
D
D
A
B
线位移数也可以用几何方法确定。 将结构中所有刚结点和固定支座,代之以铰结点和铰支座,分析新体系的
基本方法 (手算)
机算
力法
位移法
矩阵 力法
力矩分配法
矩阵 位移法
力法几次9超次静定?
位移法几1次次超静定?
§11.1
P C θA
θA
位移法的基本概念
B
A
附加
刚臂 C
P B
附加刚臂限制结
点位移,荷载作
A 用下附加刚臂上
产生附加力矩
C θA
B
θA
施加力偶使结点产 生的角位移,以实
A 现结点位移状态的
一致性。
D
2
C
F22
A
D
A
D
Fk1111
2i B
1 =1
i
A
C
kF2211
Fk122
B
i
D
A
建立基本方程
F11+F12+F1P=0………………(1a) F21+F22+F2P=0………………(2a)
k111 + k122 +F1P =0………..(1) k211 + k222 +F2P =0………..(2)
结构力学位移法题与答案解析
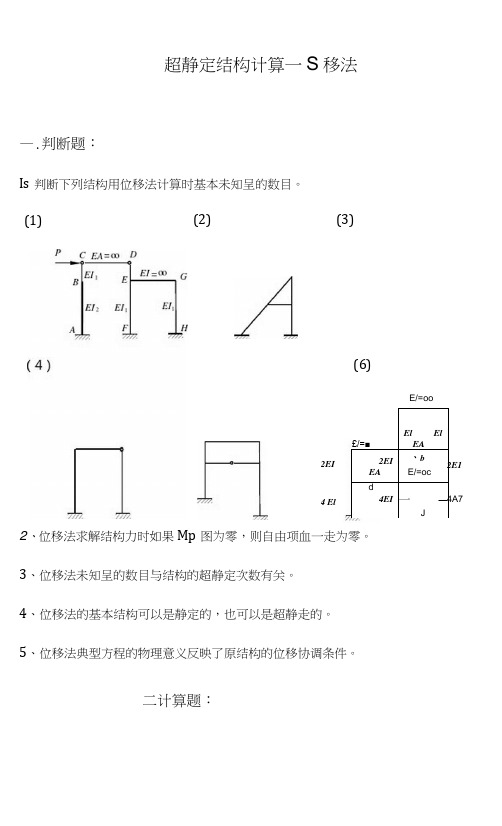
超静定结构计算一S移法—.判断题:Is判断下列结构用位移法计算时基本未知呈的数目。
2、位移法求解结构力时如果Mp图为零,则自由项血一走为零。
3、位移法未知呈的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静走的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
二计算题:(2) (3)(1)(6)£/=■El ElEA2EI、bEA E/=ocd4EI一—JE/=oo2E14A72EI4 El12.用位移法计算图示结构并作〃图,横梁刚度EA -8 ,两柱线刚度/相同。
13、用位移法计算图示结构并作〃图。
F/二常数。
14、求对应的荷载集度g。
图示结构横梁刚度无限大。
已知柱顶的水平位移为512/(3 曰)(T)。
15、用位移法计算图示结构州乍M图。
曰=常数。
16、用位移法计算图示结构r求出未知呈,各杆曰相同。
4m4m19、用位移法计算图示结构并作〃图。
-2/ 2fq 二i i20、用位移法计算图示结构并作〃图。
各杆日=営数r q = 20kN/m o6m4 ------- B6m 6mR --- k ----- 123、用位移法计算图示结构州乍M图。
曰=常数。
7T7F24、用位移法计算图示结构州乍M图。
曰=常数。
°^=ZJ週AV 酔辭圍闕¥觀⑨由、充。
回申Z7阴甘县欲 遍如士星與莎竺园蔑44辛觀⑨由、6乙IcnnM M I Z M fc/i in38、用位移法计算图示结构并作〃图。
曰=常数。
42、用位移法计算图示结构州乍〃图。
43、用位移法计算图示结构州乍〃图。
曰=常数。
48、已知0点的位移0,求几51.用位移法计算图示结构并作M 图。
qP M H 1 1 1El---------JIIk —— ------ H超静定结构计算一^移法(参考答案)(617.14、q = 3kN/m1. (11 4 ; (21 4; (31 9; ⑷ 5;(51 7;2、( X )3、( X )< (0)5. (X)12、x qh 2/40 )("/)M图20、24、3236M图(Xql2 n )(X2(//2/33)42912 El----25 I34&。
国开电大工程力学(本)形成性作业3参考答案

窗体底端
对
错
【答案】:错
题目18.3.位移法典型方程中的主系数恒为正值,副系数可正可负。
对
错
【答案】:对
题目19.4.位移法可用来计算超静定结构也可用来计算静定结构。
对
错
【答案】:对
题目20.5.位移法只能用于超静定结构。
对
错
【答案】:错
题目21.6.在力矩分配法中,结点各杆端分配系数之和恒等于1。
【答案】:第i个附加约束中的约束反力
题目8.8.图示超静定结构结点角位移的个数是()
窗体顶端
窗体底端
A. 2
B. 3
C. 4
D. 5
【答案】:3
题目9.9.用位移法求解图示结构时,基本未知量个数是()
窗体顶端
窗体底端
A. 1
B. 2
C. 3
D. 4
【答案】:3
题目10.10.用位移法计算超静定结构时,其基本未知量为()
B. B
【答案】:A
题目28.k11 =()(3分)
A. 5i
B. 3i
【答案】:5i
题目29.
A. A
B. B
【答案】:A
题目30.(5)解方程,根据叠加原理求杆端弯矩,作出M图如()(3分)
窗体顶端
窗体底端
A. A
B. B
【答案】:A
题目31.作M1图如()(3分)
窗体顶端
窗体底端
A. A
B. B
【答案】:第i个附加约束中的约束反力
题目6.6.图6所示结构的位移法基本未知量数目为()
窗体顶端
窗体底端
A. 2
B. 3
C. 4
电大《土木工程力学》(本)历届试题及答案解析
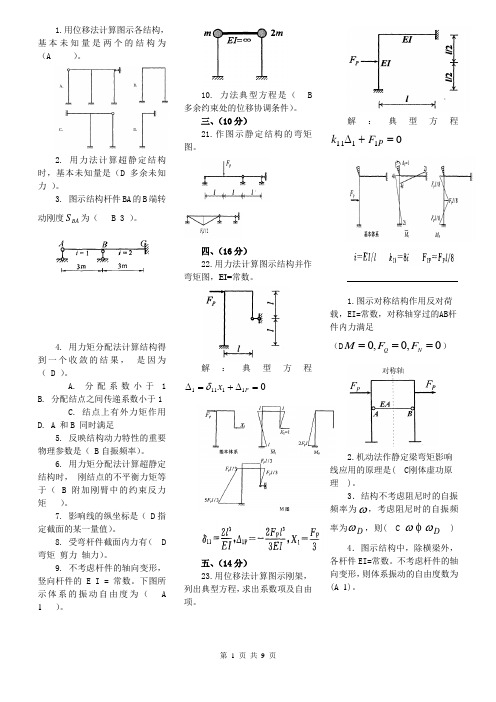
1.用位移法计算图示各结构,基本未知量是两个的结构为(A )。
2. 用力法计算超静定结构时,基本未知量是(D 多余未知力 )。
3. 图示结构杆件BA 的B 端转动刚度BA S 为( B 3 )。
4. 用力矩分配法计算结构得到一个收敛的结果, 是因为( D )。
A. 分配系数小于 1B. 分配结点之间传递系数小于1C. 结点上有外力矩作用D. A 和B 同时满足5. 反映结构动力特性的重要物理参数是( B 自振频率)。
6. 用力矩分配法计算超静定结构时, 刚结点的不平衡力矩等于( B 附加刚臂中的约束反力矩 )。
7. 影响线的纵坐标是( D 指定截面的某一量值)。
8. 受弯杆件截面内力有( D 弯矩 剪力 轴力)。
9. 不考虑杆件的轴向变形,竖向杆件的 E I = 常数。
下图所示体系的振动自由度为( A1 )。
10. 力法典型方程是( B 多余约束处的位移协调条件)。
三、(10分)21.作图示静定结构的弯矩图。
四、(16分)22.用力法计算图示结构并作弯矩图,EI=常数。
解:典型方程011111=∆+=∆P x δ五、(14分)23.用位移法计算图示刚架,列出典型方程,求出系数项及自由项。
解:典型方程01111=+∆P F k1.图示对称结构作用反对荷载,EI=常数,对称轴穿过的AB 杆件内力满足(D 0,0,0===N Q F F M)2.机动法作静定梁弯矩影响线应用的原理是( C 刚体虚功原理 )。
3.结构不考虑阻尼时的自振频率为ω,考虑阻尼时的自振频率为D ω,则( C D ωω ) 4.图示结构中,除横梁外,各杆件EI=常数。
不考虑杆件的轴向变形,则体系振动的自由度数为(A 1)。
5.位移法典型方程是根据( D 附加约束的平衡条件 )列出的。
6.图示a 、b 两体系的自振频率aω与bω的关系为( Bb a ωω )。
7.图示对称结构作用反对称荷载,杆件EI 为常量,利用对称性简化后的一半结构为( A )。
土木工程力学网上形考专业04全部选择题和判断计算
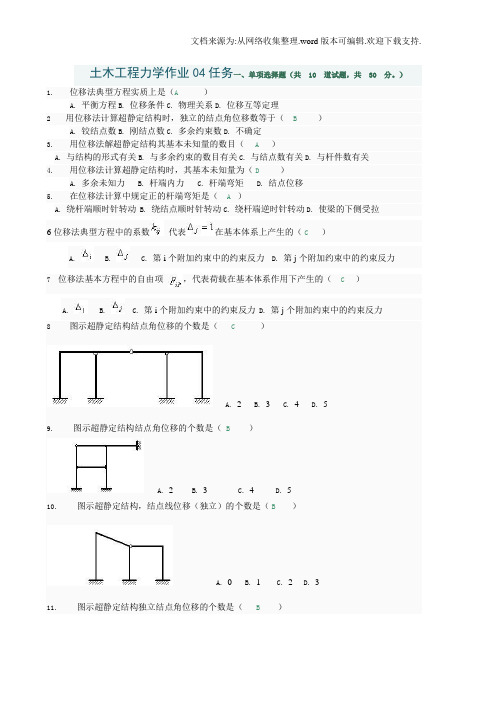
土木工程力学作业04任务一、单项选择题(共10 道试题,共30 分。
)1. 位移法典型方程实质上是(A )A. 平衡方程B. 位移条件C. 物理关系D. 位移互等定理2 用位移法计算超静定结构时,独立的结点角位移数等于( B )A. 铰结点数B. 刚结点数C. 多余约束数D. 不确定3. 用位移法解超静定结构其基本未知量的数目( A )A. 与结构的形式有关B. 与多余约束的数目有关C. 与结点数有关D. 与杆件数有关4. 用位移法计算超静定结构时,其基本未知量为(D )A. 多余未知力B. 杆端内力C. 杆端弯矩D. 结点位移5. 在位移法计算中规定正的杆端弯矩是(A)A. 绕杆端顺时针转动B. 绕结点顺时针转动C. 绕杆端逆时针转动D. 使梁的下侧受拉6位移法典型方程中的系数代表在基本体系上产生的(C)A. B. C. 第i个附加约束中的约束反力 D. 第j个附加约束中的约束反力7 位移法基本方程中的自由项,代表荷载在基本体系作用下产生的(C)A. B. C. 第i个附加约束中的约束反力 D. 第j个附加约束中的约束反力8 图示超静定结构结点角位移的个数是( C )A. 2B. 3C. 4D. 59. 图示超静定结构结点角位移的个数是( B )A. 2B. 3C. 4D. 510. 图示超静定结构,结点线位移(独立)的个数是(B )A. 0B. 1C. 2D. 311. 图示超静定结构独立结点角位移的个数是(B)A. 2B. 3C. 4D. 512. 用位移法求解图示结构时,基本未知量的个数是(B)A. 8B. 10C. 11D. 1213. 用位移法求解图示结构时,基本未知量个数是(B)A. 1B. 2C. 3D. 414. 图示结构位移法方程中的系数=(D )A. 11B. 5C. 9D. 815 图示结构位移法方程中的系数=(C)A. 3B. 8C. 15D. 1316. 图示结构位移法方程中的自由项=( B )A. 2B. -2C. 12D. -26217. 图示刚架在节点集中力偶作用下,弯矩图分布是(D)A 各杆都不产生弯矩B各杆都产生弯矩C 仅AB杆产生弯矩D仅AB、BE杆产生弯矩18 图示单跨超静定梁的固端弯矩=( A )A. B. C. D.19 下图所示三根梁的EI、杆长相同,它们的固定端的弯矩之间的关系是( C )A. 三者的固定端弯矩不同B. (1)、(2)的固定端弯矩相同C. (2)、(3)的固定端弯矩相同D. 三者的固定端弯矩相同20. 下图所示连续梁,欲使A端发生单位转动,需在A端施加的力矩(D)A. B. C. D.21. 图示结构杆件BC的B端转动刚度为( D )。
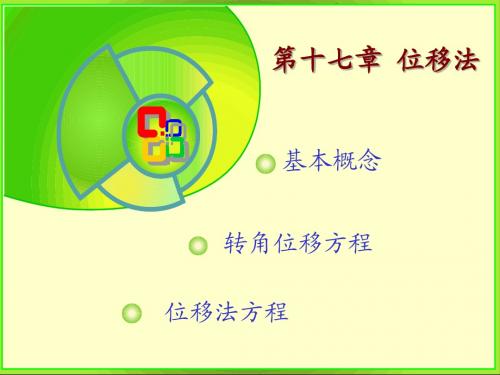
17.位移法
φA MAB
P
q t1˚C βAB EI t2˚C B B' MBA l
A φA QAB
M AB M BA FQAB F QBA
f i A M AB f i A M BA F FQAB
0
位移法的思路
将结构的结点角位移和结点线位移作为基本未知量,固端弯矩、 ø B A C ø B B (al l 固端弯矩、固端剪力,从而将超静定结构转化为静定结构。 Z1= ø B
B 1.15
(4)计算杆端弯矩
A
40
B
62.5
D
C
9.8
M BA 43.5kN .m; M BC 46.9kN .m; M CB 24.5kN .m; M CD 14.7kN
E
3.4
9kN.m; M CB 24.5kN.m; M CD 14.7kN.m;
M BE 3.4kN .m; M EB 1.7kN .m;
φA P q MAB A φA βAB QAB t1˚C βAB EI t2˚C φB B' MBA QBA l B ΔAB
EI EI EI f M 4 2 6 Δ M AB A B AB l l l2 M 2 EI 4 EI 6 EI Δ M f A b BA BA l l l2 Q 6EI 6EI 12EI Δ Q f a b AB AB l2 l2 l3 6EI 6EI 12EI f Q AB 2 a 2 b 3 Δ QBA l l l
B
B C B
C
C
A
D
二、基本假设
1、小变形假设。 2、不考虑轴力和弯曲内力、弯曲变形之间相互影响。 (采用上述假设后,图示刚架有3个基本未知量。)
位移法求解超静定结构

位移法求解超静定结构一、引言超静定结构是指在静力学条件下,其内力和位移无法通过平衡方程和变形方程求解的结构。
由于超静定结构的内力和位移无法直接求解,因此需要采用特殊的方法进行计算。
其中,位移法是一种经典的求解超静定结构的方法。
二、位移法基本原理位移法是一种基于能量原理的方法,其基本思想是将结构中各个部分的变形看作独立自由度,然后通过能量平衡原理得到各个自由度之间的关系,最终求解出整个结构的内力和位移。
具体来说,位移法包括以下几个步骤:1. 将超静定结构中每一个部分看作一个独立自由度,并为每个自由度引入一个未知位移;2. 根据平衡条件列出各部分之间相互制约的方程组;3. 根据能量平衡原理列出总势能和总应变能之间的关系式,并将其转化为未知位移之间的关系式;4. 将各个方程组联立起来,得到未知位移之间的关系式;5. 利用已知边界条件解出未知位移,并进而求解出整个结构的内力和位移。
三、位移法的应用范围位移法适用于各种类型的超静定结构,包括梁、柱、框架等。
此外,位移法还可以用于求解复杂的结构体系,如悬索桥、拱桥等。
四、位移法的优点和缺点1. 优点:(1)能够求解各种类型的超静定结构;(2)计算精度高,适用于复杂结构;(3)计算过程简单明了,易于理解和掌握。
2. 缺点:(1)只能求解超静定结构,不能求解不静定和半静定结构;(2)需要将每个部分看作独立自由度,因此对于复杂结构需要引入大量自由度,计算量较大;(3)需要具备一定的数学基础和结构力学知识。
五、位移法的实例以一根简支梁为例进行说明。
假设梁长为L,截面为矩形截面,宽度为b,高度为h。
在中间加一集中荷载F,则该梁为超静定结构。
采用位移法进行求解:1. 将梁分成两段,并引入两个未知位移u1和u2;2. 根据平衡条件,得到以下方程组:(1)在x=0处:F = R1 + R2(2)在x=L处:R1u1 + R2u2 = FL/43. 根据能量平衡原理,得到以下关系式:(1)总势能:V = (R1u1 + R2u2)hL/2(2)总应变能:T = F^2L^3/48EI4. 将以上方程组和关系式联立起来,得到:(1)F = (3EI/h^3L^3)(u1 - u2)(2)R1 = F/2 - EI/h^3L^3(u1 + u2)(3)R2 = F/2 + EI/h^3L^3(u1 + u2)5. 利用已知边界条件,即梁两端的位移为0,解出未知位移:(1)u1 = FL^3/(48EIh);(2)u2 = -FL^3/(48EIh);6. 最终求解出内力和位移:(1)R1 = F/4;(2)R2 = F/4;(3)Mmax = FL/8;(4)umax = FL^3/(48EIh)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
位移法的基本未知量是独立的结点位移;基本体系是 将基本未知量完全锁住后,得到的超静定梁的组合体。
1、基本未知量的确定: 结点角位移的数目=刚结点的数目
为了减小结点线
位移数目,假定: Δ
①忽略轴向变形,
P P
②结点转角和弦转
θC
角都很微小。
Δ θD P
Δ
P
Δ
Δ
θC
2、基本体系的确定:
即:受弯直杆变形前后,两端之间的距离保持不变。
2i M
3
Δ
由单位杆端位移引起的杆端力称为形常数(表11-1)。
单跨超静定梁简图
θ=1
A
B
A
θ=1
A A
θ=1
A
B1
B
B
1
B
MAB
4i
6i l
3i
3i l
i
MBA
2i
6i l
0 0
-i
QAB= QBA
6i l
12i l2
3i l 3i
l2
0
5
3、载常数:由跨中荷载引 起的固端力
Δ1=δ11X1 + Δ1P=0
11
28 30 16
15kN/m
↓↓↓↓↓↓↓↓
30 i
M图
Δ1 30
2i
48kN
i
4m
15kN/m
↓↓↓↓↓↓↓↓
F1
Δ1
48kN
当F1=0
基本体系
(kN.m) 4m
2m 2m
20 15kFN1/mP 36
↓↓↓↓↓↓↓↓
48kN
4i k11 Δ1=1 i
+ F1P=-16 20
MP
2i k11 =8i
θB
转角位移方程
QBA MBA
5、已知杆端弯矩求剪力:取杆 件为分离体建立矩平衡方程:
QAB
M
AB
l
M
BA
QA0B
注:1、MAB,MBA绕杆端顺时 针转向为正。
2、
Q0 AB
是简支梁的剪力。
MAB QAB
MAB
Q’‘ AB
Q0 AB
P
MBA
+
P
QBA MBA
Q’‘ BA
Q0 B7A
§11-3 位移法的基本未知量和基本体系
基本方程—— 平衡条件
1
l
↓↓↓↓↓↓↓↓↓↓
A βA EI=常数
B l
ql2/24 ↓↓↓↓↓↓↓↓↓↓
A
B
ql2/48
F1P
q ql2/12
q
F1
q
ql2/12 ↓↓↓↓↓↓↓↓↓↓
↓↓↓↓↓↓↓↓↓↓
A
C
C
F1=0
A A
A
C
θA
A A F1 0
A A F1 0
F1P B
F1P
用时,附加约束1、2中产生的约束力矩和约束力;
•F12、F22(k12、k22) ── 基本体系在Δ2(=1)单独作用
时,附加约束1、2中产生的约束力矩和约束力;
•F1P、F2P── 基本体系在荷载单独作用时,附加约
束1、位2中移产法生方的程约的束力含矩义和:约基束本力;体系在结点位
移和荷载共同作用下,产生的附加约束中的 总约束力(矩)等于零。实质上是平衡条件。
• 付系数 kij= kji── 基本体系在Δj=1单独作用时,在第 i个 附 加约束中产生的约束力矩和约束力,可正、可负、可为零;
• 自由项 FiP── 基本体系在荷载单独作用时,在第 i个 附加约 束中产生的约束力矩和约束力,可正、可负、可为零;
•由形常数作Mi (Di 1引起的弯矩图),由载常数作M P (荷载引起 的弯矩图);再由结点矩平衡求附加刚臂中的约束力矩,由截 面投影平衡求附加支杆中的约束力。
3i M1
20 36
d 11
1 EI
l2 2
2l 3
l3 3EI
D 1P
1 EI
1 3
ql 2 2
l
3l 4
ql 4 8EI
X1=-Δ1P / δ11 =3ql/8
各种单跨超静定梁在各 种荷载作用下的杆端力均可 按力法计算出来,这就制成 了载常数表11-2(P241)
q
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓B
mAB
l,EI
ql 2 12
ql2/12
B
q 5ql2/48 C
4EI l
Байду номын сангаас
A
θA
4
E l
I
A
F11
2
E l
I
A
A
C
θA
4EI l
A
F11
4EI A l
4EI A l
F1 F11 F1P 0
8E l
I
A
ql 2 12
0
A
ql3 96 EI
2
E l
I
A
B
2
E l
I
A
4E l
I
θA
A
4i
2
E l
I
A
2
§11-2 等截面直杆的杆端力(形常数、载常数)
M1
l
ql2/2 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
X1=1
MP
ql2/8
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
M图
ql 2
m
AB
8
m 0 BA 6
4、转角位移方程:杆端弯矩的一般公式:
M 4i 2i 6i D
AB
A
B
l
+mAB
M 2i 4i 6i D
BA
A
B
l
+mBA
↓↓↓↓↓↓↓↓
Δ
MAB QAB
β θA
F1P F2P
k11
Δ1 Δ1=1
k21
× Δ1
k12
× Δ2
Δ2=1
k22
10
n个结点位移的位移法典型方程 k11D1 k12D2 k1nDn F1P 0 k21D1 k22D2 k2nDn F2P 0
kn1D1 kn2D2 knnDn FnP 0
• 主系数 kii── 基本体系在Δi=1单独作用时,在第 i个附加约 束中产生的约束力矩和约束力,恒为正;
§11-1 位移法的基本概念
1、超静定结构计算的总原则: 欲求超静定结构先取一个基本体系,然
后让基本体系在受力方面和变形方面与原 结构完全一样。
力法的特点: 基本未知量——多余未知力; 基本体系——静定结构; 基本方程——位移条件
(变形协调条件)。
位移法的特点:
基本未知量—— 独立结点位移
基本体系——一组?单跨超静定梁
1、杆端力和杆端位移的正负规定 MAB
①杆端转角θA、θB ,弦转角
β=Δ/l都以顺时针为正。
QAB
②杆端弯矩对杆端以顺时针为正
β θA
对结点或支座以逆时针为正。 2、形常数:
MAB>0
由单位杆端位移引起的杆端力
用力法求解 i=EI/l
1
M AB 4i, M BA 2i
4i
θB
QBA MBA
MBA<0
结论:原结构独立结点线位移的数目=相应铰结体系的自由度。
=刚架的层数(横梁竖柱的矩形框架)8 。
位移法基本未知量
结点转角数目=刚3结点的数目 独立结点线位移数目=铰结体系的自由度
2 =矩形框架的层数 在确定基本未知量时就考虑了变形协调条件。
1
结点转角的数目:7个
相应的铰接体系的自由度=3 独立结点线位移的数目:3个
也等于层数 3
结点转角的 数目:3个
独立结点线位移的数目:2个 不等于层数 1
9
§11-4 位移法典型方程
Δ2
F1 Δ2
Δ1
Δ1
F1=0 F2=0
Δ1
Δ1
F2
位移法
基本体系
F1=0
k11D1 k12D2 F1P 0
F2=0
k21D1 k22D2 F2P 0
•F11、F21(k11、k21) ── 基本体系在Δ1(=1)单独作
