(计算机图形学)多边形区域扫描线填充或种子填充
基于扫描种子线算法的多边形区域填充实现

基于扫描种⼦线算法的多边形区域填充实现 本学期算法课上我们学习了计算⼏何的基础内容,在课后的深⼊了解学习中我发现,计算⼏何仅仅是算法世界⼀个重要分⽀——计算机图形学的基础部分之⼀,计算机图形学还有很多其他⾮常有趣的算法,例如直线⽣成、圆⽣成、椭圆⽣成。
⽽在本学期进⾏java项⽬实践的过程中,我也遇到了⼀个和计算机图形学息息相关的问题,那就是如何实现windows⾃带画图软件中的⼯具油漆桶?⽹上的开源画图代码基本上均只实现了其他简单的绘制⼯具。
为此,在查阅⼤量相关资料后,我学习到,种⼦填充算法可以很好地实现多边形区域填充,并⽤其中效果最好的基于栈的扫描线种⼦填充算法实现了画板中的油漆桶⼯具。
找到特定的算法,搞懂原理并写出算法的程序代码,在这个过程中,我深刻地认识到了算法的⽆处不在,也深切地感受到算法的乐趣,感受到⽤算法解决问题后的成就感。
简要介绍下算法的原理,实现⾮⽮量图形区域填充常⽤的种⼦填充算法根据对图像区域边界定义⽅式以及对点的颜⾊修改⽅式不同可分为注⼊填充算法(Flood Fill Algorithm)和边界填充算法(Boundary Fill Algorithm)。
两者的核⼼都是递归加搜索,即从指定的种⼦点开始,向上、下、左、右、左上、左下、右上和右下全部⼋个⽅向上搜索,逐个像素进⾏处理,直到遇到边界。
两者的区别仅在于Flood Fill Algorithm不强调区域的边界,它只是从指定位置开始,将所有联通区域内某种指定颜⾊的点都替换成另⼀种颜⾊,即实现颜⾊替换的功能;⽽边界填充算法与注⼊填充算法递归的结束条件不⼀样,Boundary Fill Algorithm强调边界的存在,只要是边界内的点,⽆论是什么颜⾊,都替换成指定的颜⾊。
但是在实际项⽬中,使⽤递归算法效率太低,为了消除递归,有⼀种更为常⽤的改进算法,即扫描线种⼦填充算法。
它通过沿竖直扫描线填充像素段,⼀段⼀段地来处理8-联通的相邻点,这样算法处理过程中就只需要将每个竖直像素段的起始点位置压⼊⼀个特殊的栈,⽽不需要像递归算法那样将当前位置周围尚未处理的所有相邻点都压⼊堆栈,从⽽节省了堆栈空间,本实例采⽤的就是结合泛洪填充算法(或者说注⼊填充算法)的扫描线种⼦填充算法。
实验2:多边形区域扫描线填充或种子填充

实验2:多边形区域扫描线填充或种子填充计科102 蓝广森 1007300441一、实验目的通过实验,进一步理解和掌握几种常用多边形填充算法的基本原理掌握多边形区域填充算法的基本过程掌握在C/C++环境下用多边形填充算法编程实现指定多边形的填充。
二、实验内容及要求实现多边形区域扫描线填充的有序边表算法,并将实现的算法应用于任意多边形的填充,要求多边形的顶点由键盘输入或鼠标拾取,填充要准确,不能多填也不能少填。
要求掌握边形区域扫描线填充的有序边表算法的基本原理和算法设计,画出算法实现的程序流程图,使用C或者VC++实现算法,并演示。
三、实验原理种子填充算法又称为边界填充算法。
其基本思想是:从多边形区域的一个内点开始,由内向外用给定的颜色画点直到边界为止。
如果边界是以一种颜色指定的,则种子填充算法可逐个像素地处理直到遇到边界颜色为止。
种子填充算法常用四连通域和八连通域技术进行填充操作。
四向连通填充算法:a)种子像素压入栈中;b)如果栈为空,则转e);否则转c);c)弹出一个像素,并将该像素置成填充色;并判断该像素相邻的四连通像素是否为边界色或已经置成多边形的填充色,若不是,则将该像素压入栈;d)转b);e)结束。
扫描线填充算法的基本过程如下:当给定种子点(x,y)时,首先填充种子点所在扫描线上的位于给定区域的一个区段,然后确定与这一区段相连通的上、下两条扫描线上位于给定区域内的区段,并依次保存下来。
反复这个过程,直到填充结束。
区域填充的扫描线算法可由下列四个步骤实现:(1)初始化:堆栈置空。
将种子点(x,y)入栈。
(2)出栈:若栈空则结束。
否则取栈顶元素(x,y),以y作为当前扫描线。
(3)填充并确定种子点所在区段:从种子点(x,y)出发,沿当前扫描线向左、右两个方向填充,直到边界。
分别标记区段的左、右端点坐标为xl和xr。
(4)并确定新的种子点:在区间[xl,xr]中检查与当前扫描线y上、下相邻的两条扫描线上的象素。
多边形的扫描转换与区域填充

区域填充
区域填充要求区域是连通的 连通性:4连通、8连通
4 4p4
4
888 8p8 888
(a)p的4-邻接点 (b)p的8-邻接点
邻接点的定义
4连通:
8连通
区域填充
4连通与8连通区域的区别
连通性: 4连通可看作8连通区域,但对边界有 要求
(a)以边界表示的4-连通区域 (b)以内点表示的4-连通区域
x:=x+Δx。 5)将当前的扫描线的纵坐标值y累加1,即y:=y+1。
扫描线算法
特点:算法效率较高。 缺点:对各种表的维持和排序开销太大,适
合软件实现而不适合硬件实现。
扫描线算法
问题:
如何处理多边形的水平边? 如何修改扫描线算法,使它能处理边自交的多
边形?
3.4.1.3 边填充法
{ if(象素 x 被打上边标志)
inside = ! (inside);
if(inside!= FALSE)
drawpixel (x, y, color);
else drawpixel (x, y, background);
}
}
边界标志算法
用软件实现时,扫描线算法与边界标志算法 的执行速度几乎相同,
种子填充算法
适合于内点表示区域的填充算法 设G为一内点表示的区域,(x,y)为区域内一点,old_color为G的
原色。现取(x,y)为种子点对区域G进行填充:即先置像素 (x,y)的颜色为new_color,然后逐步将整个区域G都置为同样 的颜色。 步骤如下: 种子象素入栈,当栈非空时,执行如下三步操作: (1)栈顶象素出栈; (2)将出栈象素置成多边形色; (3)按上、下、左、右的顺序检查与出栈象素相邻的四个象素 ,若其中某个象素不在边界上且未置成多边形色,则把该象素 入栈。
计算机图形学扫描线种子填充算法

2.1 深度递归的种子填充算法
2.2 扫描线种子填充算法
2.1 深度递归的种子填充算法
种子填色又称边界填色(Boundary Filling)。 它的功能是,给出多边形光栅化后的边界位置及边 界色代码oundary_color,以及多边形内的一点(x, y)位置,要求将颜色fill_color填满多边形。
动画演示
扫描线种子填充算法特点
1. 该算法考虑了扫描线上象素的相关性,种子象 素不再代表一个孤立的象素,而是代表一个尚 未填充的区段。 2. 进栈时,只将每个区段选一个象素进栈(每个 区段最右边或最左边的象素),这样解决了堆 栈溢出的问题。 3. 种子出栈时,则填充整个区段。 4. 这样有机的结合:一边对尚未填充象素的登记 (象素进栈),一边进行填充(象素出栈), 既可以节省堆栈空间,又可以实施快速填充。
3. 已知有一个5边形如下。建立新边表 NET,并写出每一条扫描线经过时活性边 表AET中的数据状态。
X ΔX Ymax
第1项存当前扫描线与边的交点坐标x值; 第2项存从当前扫描线到下一条扫描线间x的增量Dx; 第3项存该边所交的最高扫描线号ymax; 第4项存指向下一条边的指针。
假定当前扫描线与多边形某一条边的交点的x 坐标为x,则下一条扫描线与该边的交点不要重计 算,只要加一个增量△x。(连贯性) 设该边的直线方程为:ax+by+c=0; 若y=yi,x=x i;则当y = y i+1时, x i+1=xi-b/a 其中ΔX= -b/a为常数, 另外使用增量法计算时,我们需要知道一条边 何时不再与下一条扫描线相交,以便及时把它从 活性边表中删除出去。
建立或调整AET(ActiveEdgeList);
基本图形处理技术-区域填充1扫描线种子填充

• int CSampleseedfillView::stackpop() • { • int val; • val=stack[stack_top]; • stack_top=stack_top-1; • return val; • }
步骤5:编写扫描线填充算法
• void CSampleseedfillView::floodfill4(int x, int y, COLORREF oldcolor, COLORREF newcolor) { CDC * pDC=GetDC(); int xl,xr,x0,xnextspan,yu,yd; bool spanNeedFill; //将栈清空 setstackempty(); //种子入栈 stackpush(x); stackpush(y);
• • • • • • •
int CSampleseedfillView::isstackempty() { if (stack_top>0) return 1; else return 0; }
• void CSampleseedfillView::stackpush(int p_xy) • { • stack_top+=1; • stack[stack_top]=p_xy; • }
• 步骤3:在构造函数中,对变量和栈初始化; CSampleseedfillView::CSampleseedfillView() { // TODO: add construction code here stack_top=0; FillColor=RGB(0,0,0); }
• 步骤4:编写成员函数程序 void CSampleseedfillView::setstackempty() { int i; for(i=0;i<=stack_top;i++) stack[i]=0; stack_top=0; }
多边形填充算法

多边形填充算法
多边形填充算法是一种计算机图形学中的算法,用于将一个封闭的多边形区域(如矩形、三角形、梯形等)填充成指定的颜色。
在计算机图形学中,多边形是由一系列线段(边)连接成的封闭区域。
填充算法的目的是在多边形的内部填充指定的颜色。
这种算法通常用于计算机辅助设计、计算机游戏开发、计算机动画、计算机视觉等领域。
填充算法有多种实现方法,包括扫描线填充、种子填充、边界填充、区域分割等。
其中,扫描线填充是最常见的一种算法,它的基本思想是从多边形的最上面一行开始,逐行向下扫描,同时记录扫描线和多边形之间的交点。
当扫描线与多边形的边相交时,根据交点的奇偶性来判断该点是否在多边形内部。
如果是奇数个交点,则该点在多边形内部,需要进行填充;如果是偶数个交点,则该点在多边形外部,不需要填充。
种子填充是另一种常见的填充算法,它的基本思想是从多边形内部的一个点(种子)开始,向外扩散填充。
在扩散过程中,同时记录已经填充过的像素点,避免重复填充。
这种算法的优点是填充速度较快,但容易出现填充区域不封闭、填充效果不理想等问题。
边界填充和区域分割是另外两种填充算法,它们的实现方式比较复杂,但可以处
理比较复杂的填充情况,例如多个子多边形共同填充、奇异多边形填充等。
总的来说,多边形填充算法在计算机图形学中具有重要的应用价值和研究意义,不同的填充算法各有优缺点,需要根据具体的需求和应用场景来选择合适的算法。
图形学扫描线填充算法的定义,以及具体的实现过程,具体的操作步骤以及计算步骤。
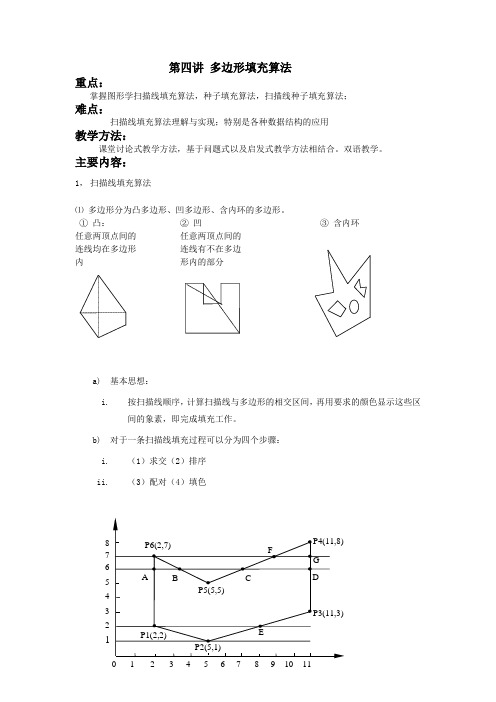
第四讲 多边形填充算法重点:掌握图形学扫描线填充算法,种子填充算法,扫描线种子填充算法;难点:扫描线填充算法理解与实现;特别是各种数据结构的应用教学方法:课堂讨论式教学方法,基于问题式以及启发式教学方法相结合。
双语教学。
主要内容:1, 扫描线填充算法⑴ 多边形分为凸多边形、凹多边形、含内环的多边形。
① 凸: ② 凹③ 含内环 任意两顶点间的 任意两顶点间的连线均在多边形 连线有不在多边内 形内的部分a) 基本思想:i. 按扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的象素,即完成填充工作。
b) 对于一条扫描线填充过程可以分为四个步骤:i.(1)求交(2)排序 ii.(3)配对(4)填色12345678② 步骤· 求交:计算扫描线与多边形各边的交点;· 排序:把所有交点按x 值递增顺序排序;· 配对:12,34,…,交点两两配对;· 填色:把交点对的象素置成多边形颜色,把交点对以外的象素置成背景色。
③ 活性边表算法:处理每一条扫描线时,仅计算和它相交的多边形的边· 活性边:当前扫描线与多边形相交的边;· 活性边表:存放扫描线与活性边交点(按X 递增顺序)的一张链表;8节点:第1项存当前扫描线与边的交点坐标x 值;第2项存从当前扫描线到下一条扫描线间x 的增量∆x ;第3项存边所交的扫描线的y max④ 算法· 增量法:令当前扫描线与多边形某一条边的交点的x 坐标为x ,则下一条扫描线与该边的交点不要重计算,只要加一个增量。
该边的直线方程为:ax+by+c=0;若y =y i ,x=x i ;则当y = y i+1时,x a b y c x b ai i i i ++=-⋅-=-111(); 其中∆x b a=- 为常数, · 算法过程polyfill (polygon, color)int color;多边形定义 polygondef ;{ for (各条扫描线i ){ 初始化新边表头指针NET [i];把y min = i 的边放进边表NET [i]; }y = 最低扫描线号;初始化活性边表AET 为空;for (各条扫描线i ){ 把新边表NET [i] 中的边结点用插入排序法插入AET表,使之按x坐标递增顺序排列;遍历AET表,把配对交点区间(左闭右开)上的象素(x, y),用drawpixel (x, y, color) 改写象素颜色值;遍历AET表,把y max= i 的结点从AET表中删除,并把y max > i 结点的x值递增 x;若允许多边形的边自相交,则用冒泡排序法对AET表重新排序;}} /* polyfill */⑤问题及其求解问题1:扫描线与多边形顶点相交,交点的取舍。
计算机图形学5多边形扫描转换和区域填充

可编辑ppt
1
一、多边形的扫描转换
前面讲的画直线是一维图形的光栅化,就是如何在计算机 屏幕上即在一个离散的像素集上表示一个连续的图形。而多 边形的扫描转换和区域填充这个问题是怎么样在离散的像素 集上表示一个连续的二维图形。
多边形有两种重要的表示方法:顶点表示和点阵表示。
P2
当扫描线与多边形顶点相 交时,会出现异常情况。
解决方案: (1)、若共享顶点的两条 边分别落在扫描线的两边, 交点只算一个;
y
12 11 10
9 8 7 6 5 4 3 2 1
1 2 3 4 5 6 7 8 9 10 11 12 x
与多边形顶点相交的交点的处理
(2)若共享顶点的两条边在扫描线的同一边,这 时交点作为零个或两个。
凸多边形 凹多边形 含内环的多边形
有关概念
1) 区域:一组相邻而且又相连的像素,而且具有 相同属性的封闭区域。 2)种类:①单域 ②复合域
3) 区域填充:以某种属性对整个区域进行设置的过
程。
可编辑ppt
6
逐点判断填充算法
区域填充的基本(初级)方法:逐点判断填充算法
逐点判断绘图窗口内的每一个像素; 若在区域的内部:用指定的属性设置该点; 否则不予处理;
光栅图形的一个基本问题是把多边形的顶点表示转换为点阵 表示。这种转换称为多边形的扫描转换。
为什么叫扫描转换?因为光栅显示器是逐行扫描!
区域填充:指先将区域的一点赋予指定的颜色,然后将该颜 色扩展到整个区域的过程。
可编辑ppt
4
多边形分为凸多边形、凹多边形、含内环的多边 形等: (1)凸多边形 任意两顶点间的连线均在多边形内。 (2)凹多边形 任意两顶点间的连线有不在多边形内的部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
while(p) { q=p->next; insertEdge(active,p); p=q; } } void fillScan(int scan,Edge *active) { Edge *p1,*p2; int i; p1=active->next; while(p1) { p2=p1->next; for(i=p1->xIntersect;i<p2->xIntersect;i++) fill((int)i,scan,3); p1=p2->next; } } void deleteAfter(Edge *q) { Edge *p=q->next; q->next=p->next; free(p); } void updateActiveList(int scan,Edge *active) { Edge *q=active, *p=active->next; while(p) if(scan>=p->yUpper) { p=p->next; deleteAfter(q); } else {
glClearColor(1.0f,1.0f,1.0f,1.0f); glColor3f(1.0f,0.0f,0.0f); } 实验结果:
} } void ChangeSize(GLsizei w,GLsizei h) { GLfloat nRange=400.0f; if(h==0) h=1; glViewport(0,0,w,h); glMatrixMode(GL_PROJECTION); glLoadIdentity(); if(w<=h) glOrtho(-nRange,nRange,-nRange*h/w,nRange*h/w,-nRange,nRange); else glOrtho(-nRange*h/w,nRange*h/w,-nRange,nRange,-nRange,nRange); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); } void Display(void) { glClear(GL_COLOR_BUFFER_BIT); glLineWidth(5.0); int n,x,y,i; cout<<"请输入多边形顶点数:"<<endl; cin>>n; dePt *t=new dePt[n]; for(i=0;i<n;i++){ cout<<"请输入第"<<i+1<<"个顶点坐标"<<endl; cin>>x>>y; t[i].x=x; t[i].y=y; glVertex2i(t[i].x,t[i].y); } glEnd(); glFlush(); scanFill(n,t); glFlush(); } void SetupRC() {
glVertex3f(x1,y1,0.0f); glEnd(); } typedef struct Edge{ int yUpper; float xIntersect, dxPerScan; struct Edge *next; }Edge; void insertEdge(Edge *list, Edge *edge) { Edge *p,*q=list; p=q->next; while(p!=NULL) { if(edge->xIntersect<p->xIntersect) p=NULL; else{ q=p; p=p->next; } } edge->next=q->next; q->next=edge; } int yNext(int k, int cnt, dePt*pts) { int j; if((k+1)>(cnt-1)) j=0; else j=k+1; while(pts[k].y==pts[j].y) if((j+1)>(cnt-1)) j=0; else j++; return (pts[j].y);
实验Байду номын сангаас:多边形区域扫描线填充或种子填充
实验类型:验证、设计 所需时间:3学时 主要实验内容及要求: 实现多边形区域扫描线填充的有序边表算法,并将实现的算法应用 于任意多边形的填充,要求多边形的顶点由键盘输入或鼠标拾取,填充 要准确,不能多填也不能少填。 要求掌握边形区域扫描线填充的有序边表算法的基本原理和算法设计, 画出算法实现的程序流程图,使用C或者VC++实现算法,并演示。 参考试验步骤: 1) 分析多边形区域扫描线填充算法的原理,确定算法流程 1 初始化:构造边表,AET表置空 2 将第一个不空的ET表中的边插入AET表 3 由AET表取出交点进行配对(奇偶)获得填充区间,依次对这 些填充区间着色 4 y=yi+1时,根据x=xi+1/k修改AET表所有结点中交点的x坐标。 同时如果相应的ET表不空,则将其中的结点插入AET表,形成 新的AET表 5 AET表不空,则转(3),否则结束。 2) 编程实现 1 首先确定多边形顶点和ET/AET表中结点的结构 2 编写链表相关操作(如链表结点插入、删除和排序等) 3 根据1)中的算法结合上述已有的链表操作函数实现多边形区 域扫描线填充的主体功能 4 编写主函数,测试该算法 源代码: #include<gl/glut.h> #include<iostream> using namespace std; typedef struct dePt{ int x; int y; }dePt; void fill(GLint x1,GLint y1,GLint z1) { glBegin(GL_POINTS);
} void makeEdgeRec(dePt lower, dePt upper,int yComp,Edge *edge,Edge *edges[]) { edge->dxPerScan=(float)(upper.x-lower.x)/(upper.y-lower.y); edge->xIntersect=lower.x; if(upper.y<yComp) edge->yUpper=upper.y-1; else edge->yUpper=upper.y; insertEdge(edges[lower.y],edge); } void buildEdgeList(int cnt,dePt *pts,Edge *edges[]) { Edge *edge; dePt v1,v2; int i,yPrev=pts[cnt-2].y; v1.x=pts[cnt-1].x;v1.y=pts[cnt-1].y; for(i=0;i<cnt;i++) { v2=pts[i]; if(v1.y!=v2.y) { edge=(Edge *)malloc(sizeof(Edge)); if(v1.y<v2.y) makeEdgeRec(v1,v2,yNext(i,cnt,pts),edge,edges); else makeEdgeRec(v2,v1,yPrev,edge,edges); } yPrev=v1.y; v1=v2; } } void buildActiveList(int scan,Edge *active,Edge *edges[]) { Edge *p,*q; p=edges[scan]->next;
p->xIntersect=p->xIntersect+p->dxPerScan; q=p; p=p->next; } } void resortActiveList(Edge *active) { Edge *q,*p=active->next; active->next=NULL; while(p) { q=p->next; insertEdge(active,p); p=q; } } void scanFill(int cnt,dePt *pts) { Edge *edges[1024],*active; int i,scan; for(i=0;i<1024;i++) { edges[i]=(Edge *)malloc(sizeof(Edge)); edges[i]->next=NULL; } buildEdgeList(cnt,pts,edges); active=(Edge *)malloc(sizeof(Edge)); active->next=NULL; for(scan=0;scan<1024;scan++) { buildActiveList(scan,active,edges); if(active->next) { fillScan(scan,active); updateActiveList(scan,active); resortActiveList(active); }
