数学分析教材和参考书
《数学分析》说课

举例说明如何利用幂级数展开函数,如泰勒级数展开等。
04
教学资源
教材与参考书
教材
《数学分析教程》
参考书
《数学分析习题集》
辅助教材
《数学分析学习指导》
网络资源
01
02
03
MOOC平台
提供数学分析相关课程, 如网易云课堂、中国大学 MOOC等。
学术网站
如知网、万方等,提供数 学分析领域的学术论文和 研究成果。
念和解决问题。
02
学生对课堂互动的评价
学生对课堂互动的满意度,是否认为课堂互动有助于提高学习效果。
03
学生对作业和考试的反馈
学生对作业和考试的难易程度、批改反馈等方面的评价。
教学质量评估
教师教学设计的评估
教师对教学内容的设计是否合理,是否能够有效地引导学生理解 和掌握数学概念。
教师教学能力的评估
教师是否具备良好的教学能力,能够有效地传授知识和解决问题 。
建立合作机制
鼓励教师之间开展合作,共同研究教学问题,提高教学质量。
引进优秀人才
积极引进具有丰富教学经验和学术背景的优秀教师,提升教学团队的 整体实力。
THANKS
06
教学展望
教学内容更新
引入现代数学概念
将最新的数学概念和研究成果融 入教学中,使学生能够紧跟数学
发展的步伐。
强化数学应用
注重数学在实际问题中的应用,提 高学生的数学应用意识和能力。
注重数学思维培养
强调数学思维的训练,引导学生通 过数学分析培养逻辑推理和解决问 题的能力。
教学方法改进
采用案例教学
在互动教学中,教师需要注重培养学 生的合作精神和沟通能力,引导学生 积极参与课堂讨论和小组合作。
数学分析参考书

数学分析参考书1.《微积分学教程》菲赫金哥尔茨人民教育出版社推荐理由:经典的数学分析的百科全书, 论述严谨, 内容全面, 例题丰富, 对希望全面掌握数学分析理论的学生是一本较好的参考书。
2.《数学分析》华东师大数学系高等教育出版社推荐理由:本书是教育部推荐的优秀教材,内容安排自然合理,读者容易接受,选学内容加了“*”适合多层次的需求;读者可以通过附录1和附录2了解微积分的发展线索记实数理论。
3.《数学分析》北大数学系方企勤、沈燮昌、廖可人等高等教育出版社推荐理由:本书阐述细致,引进概念注意讲清实际背景,定理证明、公式推演作了必要的分析,并提出一些值得思考的问题;通过大量不同类型例题,介绍解题基本方法和特殊技巧。
全书还配有习题集一册,其中有不少难度较大的题目。
适合要求进一步提高数学分析素养的同学。
4. 《数学分析》李成章黄玉民科学出版社推荐理由:总体内容与华东师大教材相仿. 书中有大量的习题可作为补充练习题.5. 《数学分析》陈纪修等高等教育出版社推荐理由:书中对三角级数阐述的较为详细,可供参考.6. 《数学分析习题精解》吴良森等高等教育出版社推荐理由:书中题型丰富,可供较为优秀的学生选7. 《数学分析习题课讲义》谢惠民等高等教育出版社推荐理由:李大潜院士是这样评价此书的“它的着眼点,不像现在充斥市面的各种各样的习题解答那样,消极地为读者提供一些习题的解答,而是引导学生理解课程内容,启发学生深入思考,扩大学生知识视野,力求使学生达到举一反三,由小见大,由表及里的境界,较快的高等数学的思想方法,迈进高等数学的广阔天地。
对于学生,这是一本富有启发性且颇有新意的辅导读物。
”8. 《数学分析中的典型问题与方法》裴礼文高等教育出版社推荐理由:本书收录了大量的研究生数学分析入学试题,前苏联高校竞赛题。
选题具有很强的典型性,灵活性,启发性,趣味性和综合性,对培养学生的能力极为有益。
8. 《Calculus(微积分)》Howard Anton, Irl Bivens, Stephen Davis郭镜明改编高等教育出版社推荐理由:本书为高等教育出版社“世界优秀教材中国版”系列教材之一。
数学分析》教学大纲

《数学分析》教学大纲一、课程性质、地位和作用《数学分析》是数学与应用数学专业、信息与计算科学专业的最重要的专业基础课和核心必修课。
本课程理论严谨、系统性强。
通过本课程的学习,要使学生掌握数学分析的基本概念、基本理论和基本方法,为学习后继的所有专业课程奠定必要的数学基础。
要通过各个教学环节逐步培养学生严格的逻辑思维能力与推理论证能力,具备熟练的运算能力和技巧,提高建立数学模型,并应用微积分学这一工具解决实际应用问题的能力,为今后从事基础数学和应用数学方面的研究打下扎实的理论基础。
二、课程教学对象、目的和要求本课程适用于数学与应用数学、信息与计算科学等本科专业。
课程教学目的、要求:了解微积分学的基础理论;充分理解微积分学的历史背景及数学思想.掌握微积分学的基本理论, 方法和技巧,并具备一定的分析论证能力和较强的运算能力。
能较熟练地应用微积分学的思想方法解决实际问题。
1、重视微积分学理论的产生离不开物理学,天文学,几何学等学科的发展。
在教学实践中应强化微积分学与相邻学科的联系,强调应用背景。
2、重视相关知识的整合,将一元函数与多元函数的极限,连续及求导(微分)整合,将不定积分与定积分的计算方法整合,将重积分和线面积分整合,将反常级数与反常积分的收敛性整合, 将函数列, 函数项级数和含参量反常积分的一致收敛性整合。
3、除体现本课程严格的逻辑体系外, 要反映现代数学的发展趋势,吸收和采用现代数学的思想观点与先进的处理方法。
4、为了提高学生的数学修养,应重视基本定理的论证。
用ε-δ的思想贯穿于极限的存在性,定积分的存在性,(一致)收敛性及(一致)连续性等理论的论证中。
5、以课堂教学为主, 重视习题课对学生理解掌握所学知识的作用.6、重视实数理论体系对学习微积分学理论和建立现代数学观点的不可或缺的作用。
三、相关课程及关系本课程在大学本科第一、二、三学期开设,是数学与应用数学、信息与计算科学等本科专业的最重要的专业基础课,是所有后继专业课程(如:微分方程、概率论与数理统计、复变函数、实变函数、泛函分析、计算方法、微分方程数值解等等)的基础。
数学强基书单

数学强基书单数学是一门重要的学科,它是自然科学的基础,也是现代科技的支柱。
而要建立数学的强大基础,一个好的书单是必不可少的。
以下是一些内容生动、全面且有指导意义的数学强基书单,供大家参考。
1.《数学分析教程》(通用):这本经典教材涵盖了数学分析的基本概念和理论,包括极限、导数、积分等重要内容。
它的全面性和深入性会帮助读者建立起扎实的数学基础。
2.《高等代数教程》(通用):代数是数学的一个重要分支,它研究的是数和符号的关系。
这本教程覆盖了线性代数、矩阵理论以及群论等内容,对于培养读者的抽象思维能力非常有帮助。
3.《概率论与数理统计教程》(通用):概率论和数理统计是应用数学的重要组成部分。
这本教程详细介绍了基本概率论的概念、性质和应用,以及统计学中的抽样理论、参数估计和假设检验等内容,为读者打下了坚实的数理统计基础。
4.《微分几何与偏微分方程》(通用):微分几何是研究曲线、曲面及其高维推广的几何学分支,而偏微分方程是通过数学建模来描述自然界中的各种现象。
这本教程系统介绍了微分几何和偏微分方程的基本理论和方法,对于培养读者的几何直观和物理感觉非常有帮助。
5.《实变函数与泛函分析》(通用):实变函数和泛函分析是数学分析的两个重要分支。
这本教程讲解了实数、实变函数、泛函分析的基本概念、性质和方法,对于理解数学分析的深层结构有很大帮助。
6.《代数拓扑学》(通用):代数拓扑学是代数学和拓扑学的交叉学科,它研究的是代数结构与空间的关系。
这本教程详细介绍了拓扑空间、群、环以及拓扑群等内容,对于培养读者的几何直观和抽象思维能力非常有帮助。
7.《数论导引》(通用):数论是研究整数性质的数学分支,它在密码学、编码理论等许多领域有着广泛应用。
这本教材系统地介绍了数论的基本知识和方法,包括素数、同余、数论函数等,对于培养读者的数学逻辑和推理能力非常有帮助。
综上所述,这些书籍涵盖了数学的各个领域,从基础的数学分析、代数到高级的微分几何、泛函分析,再到应用性的概率论、数理统计和数论,每本书都具有较高的权威性和可读性。
高等教育数学分析高等代数参考书书单

数学分析高等代数参考书书单1.前言由于目前网络上数学分析与高等代数的参考书籍鱼龙混杂,特别制作一份书单,帮助学习数学分析与高等代数的学友清除认知障碍.事先声明,由于精力有限,笔者未能将书单中所有书籍细读过,只对笔者精读过的或者主流书籍做详细评价,其中部分评价是来源于网络与网友,若有不同的见解或者认为笔者的理解有误,恳请指出或补充。
2.数学分析板块以下分四个梯队介绍国内主流的数学分析读物(包含教材和习题集),最后还整理了一份硬核书单,建议读者量力而行。
梯队顺序是结合难度、应试、流畅性、流行度等等综合考虑的,并不是排在后面的一定质量不行。
同一梯队中一般不以质量设先后排名。
2.1第一梯队1.谢惠民.恽自求.易法槐.钱定边《数学分析习题课讲义》真正的数学分析习题集,数学分析的巅峰,打穿数学分析的必经之路。
正文介绍了许多在其他书中看不到的内容(如Dirichlet判别法的充要性,Gibbs现象),作者搜集了许多美国数学月刊上的问题。
思考题一针见血,正中靶心,完美诠释了初学者对一些问题的疑问;练习题多为中档题(考研难度,大量题目是考研真题),但也有些难题参杂其中;参考题整体难度偏高,许多题材来自于美国数学月刊,第二组参考题会涉及后续课程(实变泛函拓扑组合概率等等)的内容。
北大历年大一习题课教材,如果能全部独立做完足以和清北大佬谈笑风生。
唯一感觉不足的是小部分习题的选取煞风景,例如多元部分摘取了大量吉米多维奇上的繁琐计算题,又有些参考题难度的习题放在练习题,练习题难度的习题放在参考题。
当然,都是少数,瑕不掩瑜。
谢惠民也有一份讲稿,但不成气候,不作推荐。
2.徐森林.薛春华《数学分析》《数学分析精选习题全解》难度不逊于谢惠民,曾经的CMC数学类题库。
多元部分较为精彩(有较多篇幅介绍流形),高度与深度齐备,内容齐全厚实,许多题目给了多种解法。
题材上与谢惠民史济怀有大量重复,尤其是史济怀的问题基本上可以在徐森林上找到,谢惠民的一些参考难题也可以找到。
数学分析I,II,III
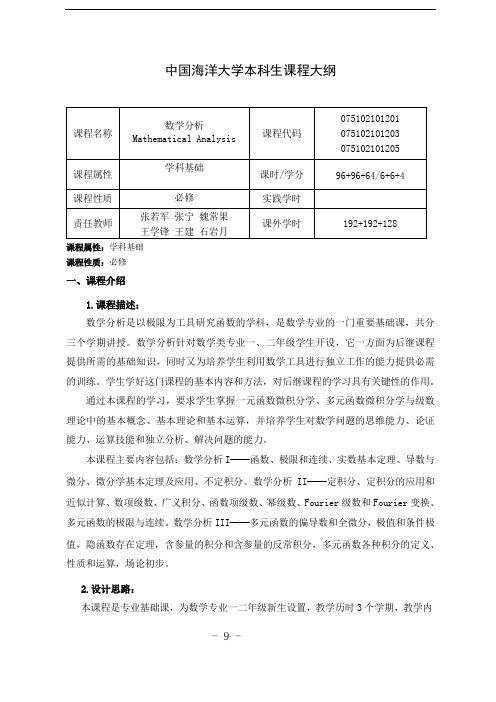
中国海洋大学本科生课程大纲课程属性:学科基础课程性质:必修一、课程介绍1.课程描述:数学分析是以极限为工具研究函数的学科,是数学专业的一门重要基础课,共分三个学期讲授。
数学分析针对数学类专业一、二年级学生开设,它一方面为后继课程提供所需的基础知识,同时又为培养学生利用数学工具进行独立工作的能力提供必需的训练。
学生学好这门课程的基本内容和方法,对后继课程的学习具有关键性的作用。
通过本课程的学习,要求学生掌握一元函数微积分学、多元函数微积分学与级数理论中的基本概念、基本理论和基本运算,并培养学生对数学问题的思维能力、论证能力、运算技能和独立分析、解决问题的能力。
本课程主要内容包括:数学分析I——函数、极限和连续、实数基本定理、导数与微分、微分学基本定理及应用、不定积分。
数学分析II——定积分、定积分的应用和近似计算、数项级数、广义积分、函数项级数、幂级数、Fourier级数和Fourier变换、多元函数的极限与连续。
数学分析III——多元函数的偏导数和全微分,极值和条件极值,隐函数存在定理,含参量的积分和含参量的反常积分,多元函数各种积分的定义、性质和运算,场论初步。
2.设计思路:本课程是专业基础课,为数学专业一二年级新生设置,教学历时3个学期,教学内- 9 -容为学生专业发展的后继学习奠定必要的理论基础。
课程内容的选取基于该课程作为分析类课程的基础性地位。
课程内容主要包括三大模块:单变量微积分学、多变量微积分学、级数理论;三大模块相互联系,体现了数学分析研究的基本内容和方法。
单变量微积分学是数学分析中最基础的部分,内容是研究函数的微分、积分及其应用,重用极限与连续的工具。
主要包括函数、极限和连续、实数基本定理、导数与微分、微分学基本定理及应用、不定积分、定积分、定积分的应用和近似计算、广义积分。
多变量微积分学是在单变量微积分学的基础上,将研究的一元函数推广为更为广泛的多元函数上去。
内容包括多元函数的极限与连续、多元函数的偏导数和全微分、极值和条件极值、隐函数存在定理、含参量的积分和含参量的反常积分、多元函数各种积分的定义、性质和运算、场论初步。
333统考参考书目

333统考参考书目333统考是指全国研究生入学考试,也是硕士研究生招生考试的一种形式。
参加333统考是许多想要攻读硕士学位的学生的选择,而选择适合的参考书目是备考的关键。
本文将为大家介绍一些适合333统考备考的参考书目。
一、数学类1. 《数学分析》(上、下册)- 毛沪石这本书是研究生数学分析的经典教材,全面介绍了数学分析的基本理论和方法,内容深入浅出。
通过学习这本书,可以提高数学分析的实际应用能力。
2. 《高等代数》(上、下册)- 杜萃生这本书主要介绍了线性代数和抽象代数的基本知识,内容系统全面。
通过学习这本书,可以帮助学生更好地掌握代数学的核心概念和方法。
3. 《概率论与数理统计》- 吴喜之这本书是概率论与数理统计的经典教材,全面介绍了概率论和数理统计的基本理论和方法。
通过学习这本书,可以提高概率与统计的应用能力。
二、外语类1. 《新托福听力长难句突破》- 张剑这本书主要针对托福考试的听力部分,介绍了一些长难句的解析和技巧,帮助学生更好地理解听力材料。
通过学习这本书,可以提高英语听力的能力。
2. 《考研英语真题解析》- 钟道隆这本书主要针对考研英语的真题,提供了详细的解析和答题技巧。
通过学习这本书,可以更好地应对考研英语的考试。
3. 《大学英语四六级考试必备词汇》这本书主要是单词的积累,内容涵盖了四级和六级考试的核心词汇。
通过学习这本书,可以提高英语词汇量,更好地理解英语文章。
三、政治经济类1. 《思想道德修养与法律基础》- 李长春这本书主要介绍了思想道德修养和法律基础的相关知识。
通过学习这本书,可以提高对于社会和法律问题的理解和分析能力。
2. 《中国社会主义市场经济理论与实践研究》- 陆铭这本书主要介绍了中国社会主义市场经济的理论和实践,通过学习这本书,可以更好地了解中国的经济体制和发展道路。
3. 《西方经济学导论》- 刘斌这本书主要介绍了西方经济学的基本原理和理论,通过学习这本书,可以扩展经济学的知识广度,拓宽思维视野。
数学系本科生课程设置与简介

数学系本科生课程设置与简介01101011 数学分析(1) mathematical analysis课程性质:专业基础课课内学时:112 学分:7简介:“数学分析”是数学专业最重要的一门专业课。
第一学期主要内容是分析基础。
第一章函数、第二章极限、第三章连续函数、第四章实数的连续性、第五章导数与微分、第六章微分基本定理及其应用、第七章不定积分、第八章定积分。
先修课要求:无教材及参考书:《数学分析讲义》刘玉琏傅沛仁编高等教育出版社适用专业:数学与应用数学开课学期:秋01101021 数学分析(2) mathematical analysis课程性质:专业基础课课内学时:144 学分:8简介:本学期将在此基础上继续学习级数和多元函数微分学。
级数是数学分析的重要组成部分,它分为数值级数和函数级数。
数值级数是函数级数的特殊情况,也是函数级数的基础;函数级数是表示非初等函数的一个重要的数学工具,它在自然科学、工程技术和数学本身都有广泛的应用。
多元函数微分学是一元函数微分学的推广,隐函数、反常积分与含参变量的积分、重积分和曲线积分与曲面积分。
并且对某些概念和定理作了进一步的发展。
先修课要求:数学分析(1)教材及参考书:《数学分析讲义》刘玉琏傅沛仁编高等教育出版社适用专业:数学与应用数学开课学期:春01101031 数学分析(3) mathematical analysis课程性质:专业基础课课内学时:40 学分:2简介:本学期将在此基础上继续学习级数和多元函数积分学。
多元函数积分学是一元函数积分学的推广,隐函数、反常积分与含参变量的积分、重积分和曲线积分与曲面积分。
并且对某些概念和定理作了进一步的发展。
先修课要求:数学分析(1) 、数学分析(2)教材及参考书:《数学分析讲义》刘玉琏傅沛仁编高等教育出版社适用专业:数学与应用数学开课学期:秋01101041 数学分析选讲 Selected Topics of Analysis课程性质:专业选修课课内学时:48 学分:2简介:数学分析教材自身科学规律概述、数学分析的思想方法与表达方式浅析、数学分析解题方法概述、关于数学分析中何种类型习题宜于用反证法证明的问题、形式逻辑与辩证逻辑方面易出现的错误及其分析、函数、数列极限、函数极限、函数的连续性、导数、中值定理与导数的应用、实数的基本定理、不定积分、定积分、数项级数、函数列与函数项级数、含参量正常积分、黎曼积分概念与性质,重积分的计算、曲线积分、曲面积分、各类积分间的联系、非正常积分、含参量非正常积分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教材和参考书
教材:
《数学分析》(第二版),陈纪修,於崇华,金路编
高等教育出版社, 上册:2004年6月,下册:2004年10月
参考书:
(1)《数学分析习题全解指南》,陈纪修,徐惠平,周渊,金路,邱维元高等教育出版社, 上册:2005年7月,下册:2005年11月
(2)《高等数学引论》(第一卷),华罗庚著
科学出版社(1964)
(3)《微积分学教程》,菲赫金哥尔兹编,北京大学高等数学教研室译,人民教育出版社(1954)
(4)《数学分析习题集》,吉米多维奇编,李荣译
高等教育出版社(1958)
(5)《数学分析原理》,卢丁著,赵慈庚,蒋铎译
高等教育出版社(1979)
(6)《数学分析》,陈传璋等编
高等教育出版社(1978)
(7)《数学分析》(上、下册),欧阳光中,朱学炎,秦曾复编,
上海科学技术出版社(1983)
(8)《数学分析》(第一、二、三卷),秦曾复,朱学炎编,
高等教育出版社(1991)
(9)《数学分析新讲》(第一、二、三册),张竹生编,
北京大学出版社(1990)
(10)《数学分析简明教程》(上、下册),邓东皋等编
高等教育出版社(1999)
(11)《数学分析》(第三版,上、下册),华东师范大学数学系,
高等教育出版社(2002)
(12)《数学分析教程》常庚哲,史济怀编,
江苏教育出版社(1998)
(13)《数学分析解题指南》林源渠,方企勤编,
北京大学出版社(2003)
(14)《数学分析中的典型问题与方法》裴礼文编,
高等教育出版社(1993)
复旦大学数学分析全套视频教程全程录像,ASF播放格式,国家级精品课程,三学期视频全程
教师简介:
陈纪修-基本信息
博士生导师教授
姓名:陈纪修
任教专业:理学-数学类
在职情况:在
性别:男
所在院系:数学科学学院
陈纪修-本人简介
姓名:陈纪修
性别:男
学位:博士
职称:教授(博士生导师)
高校教龄22年,曾获2001年上海市教学成果一等奖、获2001年国家级教学成果二等奖、获2002年全国普通高等学校优秀教材一等奖、2002年获政府特殊津贴;获宝钢教育奖(优秀教师奖);被评为“九五”国家基础科学人才培养基金实施和基地建设先进工作者。
代表性著作:“面向21世纪课程教材”、《数学分析》(上,下册)
代表性论文:对《数学分析》教材改革的一些思考、从一个演示课件看“多元函数微分学”的多媒体教学
所教课程:数学分析
研究方向:复变函数
使用教材:
教材:
《数学分析》(上、下册,第二版)
陈纪修,於崇华,金路编著,高等教育出版社出版
数学分析视频录象内容目录如下:
第一章集合与映射
第一章第一节集合(1)(2)(3)
第一章第二节映射与函数(1)(2)(3)
第二章数列极限
第二章第一节实数系的连续性(1)(2)
第二章第二节数列极限(1)(2)(3)(4)
第二章第三节无穷大量(1)(2)
第二章第四节收敛准则(1)(2)(3)(4)(5)(6)(7)
第三章函数极限与连续函数
第三章第一节函数极限(1)(2)(3)(4)(5)(6)
第三章第二节连续函数(1)(2)(3)(4)(5)
第三章第三节无穷小量与无穷大量的阶(1)(2)(3)
第三章第四节闭区间上的连续函数(1)(2)(3)
第四章微分
第四章第一节微分和导数(1)
第四章第二节导数的意义和性质(1)(2)
第四章第三节导数四则运算和反函数求导法则(1)(2)
第四章第四节复合函数求导法则及其应用(1)(2)(3)
第四章第五节高阶导数和高阶微分(1)(2)(3)
第五章微分中值定理及其应用
第五章第一节微分中值定理(1)(2)(3)(4)
第五章第二节L’Hospital法则(1)(2)
第五章第三节Taylor 公式和插值多项式(1)(2)(3)
第五章第四节函数的Taylor 公式及其应用(1)(2)(3)
第五章第五节应用举例(1)(2)(3)
第五章第六节方程的近似求解(1)
第六章不定积分
第六章第一节不定积分的概念和运算法则(1)
第六章第二节换元积分法和分部积分法(1)(2)(3)(4)
第六章第三节有理函数的不定积分及其应用(1)(2)(3)(4)
第七章定积分
第七章第一节定积分的概念和可积条件(1)(2)(3)(4)(5)第七章第二节定积分的基本性质(1)(2)
第七章第三节微积分基本定理(1)(2)(3)(4)
第七章第四节定积分在几何计算中的应用(1)(2)(3)(4)(5)第七章第五节微积分实际应用举例(1)(2)
第七章第六节定积分的数值计算(1)
第八章反常积分
第八章第一节反常积分的概念和计算(1)(2)
第八章第二节反常积分的收敛判别法(1)(2)(3)
第九章数项级数
第九章第一节数项级数的收敛性(1)(2)
第九章第二节上极限与下极限(1)(2)
第九章第三节正项级数(1)(2)(3)
第九章第四节任意项级数(1)(2)(3)(4)
第九章第五节无穷乘积(1)(2)
第十章函数项级数
第十章第一节函数项级数的一致收敛性(1)(2)(3)(4)
第十章第二节一致收敛级数的判别与性质(1)(2)(3)(4)(5)第十章第三节幂级数(1)(2)
第十章第四节函数的幂级数展开(1)(2)(3)(4)
第十章第五节用多项式逼近连续函数(1)
第十一章Euclid空间上的极限与连续
第十一章第一节Euclid空间上的极限和连续(1)(2)(3)(4)
第十一章第二节多元连续函数(1)(2)(3)
第十一章第三节连续函数的性质(1)(2)
第十二章多元函数的微分学
第十二章第一节偏导数与全微分(1)(2)(3)(4)(5)(6)
第十二章第二节多元复合函数的求导法则(1)(2)
第十二章第三节中值定理与Taylor公式(1)(2)
第十二章第四节隐函数(1)(2)(3)(4)
第十二章第五节偏导数在几何中的应用(1)(2)(3)
第十二章第六节无条件极值(1)(2)(3)
第十二章第七节条件极值问题与Lagrange乘数法(1)(2)(3)
第十三章重积分
第十三章第一节有界闭区域上的重积分(1)(2)(3)
第十三章第二节重积分的性质与计算(1)(2)(3)(4)
第十三章第三节重积分的变量代换(1)(2)(3)(4)(5)(6)第十三章第四节反常重积分(1)(2)(3)
第十三章第五节微分形式(1)(2)
第十四章曲线积分、曲面积分与场论
第十四章第一节第一类曲线积分与第一类曲面积分(1)(2)(3)(4)第十四章第二节第二类曲线积分与第二类曲面积分(1)(2)(3)(4)第十四章第三节Green公式、Gauss公式和Stokes公式(1)(2)(3)(4)(5)
第十四章第四节微分形式的外微分(1)(2)
第十四章第五节场论初步(1)(2)(3)(4)
第十五章含参变量积分
第十五章第一节含参变量的常义积分(1)(2)
第十五章第二节含参变量的反常积分(1)(2)(3)(4)(5)
第十五章第三节Euler积分(1)(2)(3)
第十六章Fourier 级数
第十六章第一节函数的Fourier级数展开(1)(2)
第十六章第二节Fourier级数的收敛判别法(1)(2)(3)
第十六章第三节Fourier级数的性质(1)(2)(3)
视频播放截图:。
