第4章 时变电磁场 1PPT课件
合集下载
工程电磁场导论时变电磁场

有限差分法的优点在于简单直观,易于编程实现,适用于处理规则的几 何形状和网格划分。
边界元法
01
边界元法是一种将偏微分方程的求解域离散化为边界离散点的 方法,通过在边界上应用离散化的方程来求解问题。
02
在时变电磁场中,边界元法可以用来求解电磁波散射和辐射等
问题。
边界元法的优点在于精度高,适用于处理复杂的几何形状和边
介电常数
描述电场中物质电容特性的物理量,单位 为法拉/米(F/m)。介电常数的大小与物 质的极化程度有关。
VS
磁导率
如前所述,描述材料对磁场响应能力的物 理量。在时变电磁场中,磁导率是复数, 其实部表示物质的磁性,虚部表示物质的 损耗。
铁电材料与铁磁材料
铁电材料
具有自发极化且在一定温度范围内铁电体从 顺电相转变为铁电相的材料。其特点是具有 较高的介电常数和较弱的磁导率。
包括四个基本方程,其中三个描述了电场和磁场的变化,一个描述了电荷 与电流的关系。
适用于所有频率和波长的电磁波,包括无线电波、可见光、X射线等。
波动方程
是描述波动现象的基 本方程,包括声波、 光波、电磁波等。
波动方程是偏微分方 程,需要求解以获得 电场和磁场的分布和 变化。
在时变电磁场中,波 动方程描述了电场和 磁场在空间中的传播 和变化。
铁磁材料
具有显著磁性的材料,其特点是具有较高的 磁导率和较弱的介电常数。在时变电磁场中, 铁磁材料的磁导率可能表现出强烈的非线性。
06
时变电磁场中的数值计算 方法
有限元法
01
有限元法是一种将连续的求解 域离散化为有限个小的、相互 连接但不重叠的单元,然后对 每个单元进行求解的方法。
02
在时变电磁场中,有限元法可 以用来求解复杂的电磁问题, 如电磁波传播、电磁散射和辐 射等。
边界元法
01
边界元法是一种将偏微分方程的求解域离散化为边界离散点的 方法,通过在边界上应用离散化的方程来求解问题。
02
在时变电磁场中,边界元法可以用来求解电磁波散射和辐射等
问题。
边界元法的优点在于精度高,适用于处理复杂的几何形状和边
介电常数
描述电场中物质电容特性的物理量,单位 为法拉/米(F/m)。介电常数的大小与物 质的极化程度有关。
VS
磁导率
如前所述,描述材料对磁场响应能力的物 理量。在时变电磁场中,磁导率是复数, 其实部表示物质的磁性,虚部表示物质的 损耗。
铁电材料与铁磁材料
铁电材料
具有自发极化且在一定温度范围内铁电体从 顺电相转变为铁电相的材料。其特点是具有 较高的介电常数和较弱的磁导率。
包括四个基本方程,其中三个描述了电场和磁场的变化,一个描述了电荷 与电流的关系。
适用于所有频率和波长的电磁波,包括无线电波、可见光、X射线等。
波动方程
是描述波动现象的基 本方程,包括声波、 光波、电磁波等。
波动方程是偏微分方 程,需要求解以获得 电场和磁场的分布和 变化。
在时变电磁场中,波 动方程描述了电场和 磁场在空间中的传播 和变化。
铁磁材料
具有显著磁性的材料,其特点是具有较高的 磁导率和较弱的介电常数。在时变电磁场中, 铁磁材料的磁导率可能表现出强烈的非线性。
06
时变电磁场中的数值计算 方法
有限元法
01
有限元法是一种将连续的求解 域离散化为有限个小的、相互 连接但不重叠的单元,然后对 每个单元进行求解的方法。
02
在时变电磁场中,有限元法可 以用来求解复杂的电磁问题, 如电磁波传播、电磁散射和辐 射等。
电磁场与电磁波第四章时变电磁场

电磁场与电磁波
第 4 章 时变电磁场
电磁场与电磁波第四章时变电磁 场..
电磁场与电磁波
第 4 章 时变电磁场
2
4.1 电磁场波动方程
麦克斯韦方程 —— 一阶矢量微分方程组,描述电场与磁场 间的相互作用关系。
波动方程 —— 二阶矢量微分方程,揭示电磁场的波动性。
麦克斯韦方程组
波动方程。
无源区域中电磁场波动方程
时变电磁场唯一性定理
在以闭曲面S为边界的有界区域V 中,
V
如果给定t=0 时刻的电场强度和磁场强度 S
的初始值,并且当t 0 时,给定边界面S
上的电场强度或者磁场强度的切向分量已知,那么,在 t > 0 的
任何时刻,区域V 中的电磁场都由麦克斯韦方程组唯一确定。
唯一性定理指出了获得唯一解所必须给定的边界条件。
第 4 章 时变电磁场
17
4.5.1 简谐电磁场的复数表示
简谐场量的复数表示形式
设 A(r,t)是一个以角频率 随时间t 作余弦变化的场量,它
可以是电场或磁场的任意一个分量,也可以是电荷或电流等变量,
它与时间的变化关系可以表示为:
A ( r ,t) A 0 c o s [t ( r ) ]
实数表示法 或称瞬时表示法
只要把微分算子 用 j 代替,就可把麦克斯韦方程转换为
t
简谐电磁场复矢量之间的关系,而得到简谐场的麦克斯韦方程。
H
J D t
E
B t
B 0
D
Hm
Jm
j D m
Em
j B m
Bm 0
D m m
H J j D
E j B
D
式中A0代表振幅、 ( r )为与坐标有关的相位因子。
第 4 章 时变电磁场
电磁场与电磁波第四章时变电磁 场..
电磁场与电磁波
第 4 章 时变电磁场
2
4.1 电磁场波动方程
麦克斯韦方程 —— 一阶矢量微分方程组,描述电场与磁场 间的相互作用关系。
波动方程 —— 二阶矢量微分方程,揭示电磁场的波动性。
麦克斯韦方程组
波动方程。
无源区域中电磁场波动方程
时变电磁场唯一性定理
在以闭曲面S为边界的有界区域V 中,
V
如果给定t=0 时刻的电场强度和磁场强度 S
的初始值,并且当t 0 时,给定边界面S
上的电场强度或者磁场强度的切向分量已知,那么,在 t > 0 的
任何时刻,区域V 中的电磁场都由麦克斯韦方程组唯一确定。
唯一性定理指出了获得唯一解所必须给定的边界条件。
第 4 章 时变电磁场
17
4.5.1 简谐电磁场的复数表示
简谐场量的复数表示形式
设 A(r,t)是一个以角频率 随时间t 作余弦变化的场量,它
可以是电场或磁场的任意一个分量,也可以是电荷或电流等变量,
它与时间的变化关系可以表示为:
A ( r ,t) A 0 c o s [t ( r ) ]
实数表示法 或称瞬时表示法
只要把微分算子 用 j 代替,就可把麦克斯韦方程转换为
t
简谐电磁场复矢量之间的关系,而得到简谐场的麦克斯韦方程。
H
J D t
E
B t
B 0
D
Hm
Jm
j D m
Em
j B m
Bm 0
D m m
H J j D
E j B
D
式中A0代表振幅、 ( r )为与坐标有关的相位因子。
第4章 时变电磁场

(2)
对方程(2)两边取旋度有 E H t 2 2 E H E E ( E ) E
E t
2
对于各向同性的介质,得
2 E 2 E 2 0 t (5)
E 0 t
t
同理可得
2 H 2 H 2 0 t (6)
第四章 时 变 电 磁 场
从上方程可以看出:时变电磁场的电场场量和磁场场量在 空间中是以波动形式变化的,因此称时变电磁场为电磁波。 上两式为关于场量 E、H 的矢量波动方程,表示时变电磁场 以波的形式在空间存在和传播,其波速为
A E ex Am cos(t kz ) t
第四章 时 变 电 磁 场
§4.3 电磁能量守恒定律
能量守恒定律是一切物质运动过程遵守的普遍规律,作为特殊形态的物 质,电磁场及其运动过程也遵守这一规律。 下面讨论电磁场的能量和能量守恒定律,引入重要的坡印廷矢量和坡印廷 定理,分析讨论电磁场能量、电荷电流运动及电磁场做功之间的相互联系。
其中Am、k是常数,求电场强度、磁场强度。
解:
Ax B A ey ey kAm cos(t kz ) z k H ey Am cos(t kz )
A 0 t
C
如果假设过去某一时刻,场还没有建立,则C=0。
量位只决定于ρ,这对求解方程特别有利。只需解出A,无需
解出 就可得到待求的电场和磁场。 电磁位函数只是简化时变电磁场分析求解的一种辅助函数,应 用不同的规范条件,矢量位A和标量位 的解也不相同,但最终 得到的电磁场矢量是相同的。
电磁场与电磁波(电磁场理论)第四章ppt课件
其中kz和Exm为实常数。写出电场强度的瞬时矢量
解 E r(z,t)Re[erxjExmcos(kzz)ejt] Re[erxExmcos(kzz)ej(tπ 2)]
erxExmcos(kzz)cos(tπ 2)
e r x E x m c o s ( k z z ) s in (t)
例题:已知正弦电磁场的电场瞬时值为 E ( z ,t) E 1 ( z ,t) E 2 ( z ,t)
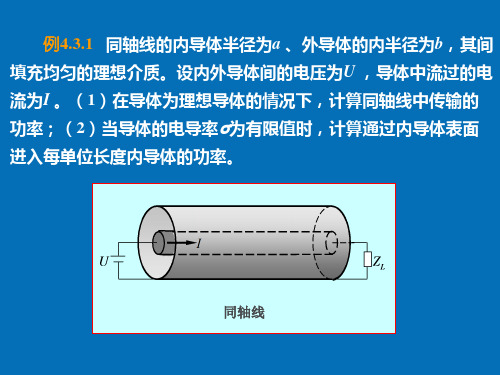
电磁能量在内外导体之间的介质中沿轴方向流动,即由电源流向 负载,如图所示。
同轴线中的电场、磁场和坡印廷矢量 (理想导体情况)
穿过任意横截面的功率为
P SS re rzd Sa b2 π 2 U ln I(ba )2 π d U I
(2)当导体的电导率σ为有限值时,导体内部存在沿电流方
向的电场
r
所以 E r & m ( z ) e r x E x m e j ( k z x ) e r y E y m e j ( k z y π /2 )
(e rxE x m e jx e ryjE y m e jy)e jk z
(2)因为 c o s (k zt) c o s (t k z )
E r ( z ,t ) e r x E x m c o s (t k z x ) e r y E y m c o s (t k z y π 2 ) R e [ e r x E x m e j ( t k z x ) e r y E y m e j ( t k z y π /2 ) ]
erx0.03cos(108πtkzπ2)erx0.04cos(108πtkzπ/3)
Re[erx0.03ej(108πtkzπ/2)]Re[erx0.04ej(108πtkzπ/3)]
解 E r(z,t)Re[erxjExmcos(kzz)ejt] Re[erxExmcos(kzz)ej(tπ 2)]
erxExmcos(kzz)cos(tπ 2)
e r x E x m c o s ( k z z ) s in (t)
例题:已知正弦电磁场的电场瞬时值为 E ( z ,t) E 1 ( z ,t) E 2 ( z ,t)
电磁能量在内外导体之间的介质中沿轴方向流动,即由电源流向 负载,如图所示。
同轴线中的电场、磁场和坡印廷矢量 (理想导体情况)
穿过任意横截面的功率为
P SS re rzd Sa b2 π 2 U ln I(ba )2 π d U I
(2)当导体的电导率σ为有限值时,导体内部存在沿电流方
向的电场
r
所以 E r & m ( z ) e r x E x m e j ( k z x ) e r y E y m e j ( k z y π /2 )
(e rxE x m e jx e ryjE y m e jy)e jk z
(2)因为 c o s (k zt) c o s (t k z )
E r ( z ,t ) e r x E x m c o s (t k z x ) e r y E y m c o s (t k z y π 2 ) R e [ e r x E x m e j ( t k z x ) e r y E y m e j ( t k z y π /2 ) ]
erx0.03cos(108πtkzπ2)erx0.04cos(108πtkzπ/3)
Re[erx0.03ej(108πtkzπ/2)]Re[erx0.04ej(108πtkzπ/3)]
时变电磁场

y, y,
z, z,
t) t)
Exm E ym
(x, (x,
y, y,
z) z)
cos[t cos[t
x (x, y (x,
y, y,
z)] z)]
Ez
(x,
y,
z,
t)
Ezm
(x,
y,
z)
cos[t
z
(
x,
y,
z)]
式中:Exm , Eym , Ezm 为电场在x,y,z方向分量的幅度
x, y,z 为电场x,y,z分量的初始相位
电磁场与电磁波
第4章 时变电磁场
第四章 时变电磁场
时变情况下,电场和磁场相互关联,构成统一的电磁场 时变电场和磁场能量在空间中不断相互转换,并以电磁波动的 形式从一个地方传递到另外一个地方
本章主要内容: ➢ 时变电场和磁场满足的方程——波动方程 ➢ 时变电磁场的辅助函数——标量电位和矢量磁位 ➢ 时变电磁场的能量守恒定律 ➢ 正弦规律变化的时变场——时谐电磁场
对于时变场来说,动态位函数常用的规范条件为洛伦兹规范条件
A
t
洛伦兹规范条件
思考:库仑规范条件和洛伦兹规范条件有何联系?
15:54
电磁场与电磁波
第4章 时变电磁场
4.2.2 达朗贝尔方程
E (
H H
J
1
E
t A
A) 2
t
t
1 A J E
t
(
A)
Σ
J EdV
V
15:54
E, H
V
电磁场与电磁波
第4章 时变电磁场
坡印廷定理物理意义:单位时间内流入体积V内的电磁能量等于 体积V内增加的电磁能量与体积V内损耗的电磁能量之和。
时变电磁场ppt

也是一种电磁波。
当场源不随时间变化时, A, 蜕变为恒定
场中的位函数。
返回 上页 下页
第四章
时变电磁场
4.4 坡印廷定理和坡印廷矢量
Poynting Theorem and Poynting Vector
电磁能量符合自然界物质运动过程中能量守恒
和转化定律——坡印廷定理;
坡印廷矢量是描述电磁场能量流动的物理量。 4.4.1 坡印廷定理(Poynting Theorem)
D
s D dS q
高斯定律
返回 上页 下页
第四章
时变电磁场
构成方程 J E D E B H
电磁场基本方程组全面总结了电磁场的规律,是 宏观电磁场理论的基础。 电磁场基本方程组加上构成方程理论上可以解决 所有的宏观电磁场问题。 静态场和恒定场是时变场的两种特殊形式。
返回 上页 下页
第四章
分界面上衔接条件
达朗贝尔方程
电磁辐射、传输线及波导
返回 上页 下页
第四章
本章要求
时变电磁场
深刻理解电磁场基本方程组的物理意义,其中 包括位移电流的概念;
掌握动态位与场量的关系以及波动方程,理解 电磁场的滞后效应及波动性;
掌握电磁波的产生和传播特性。
返回 上页 下页
第四章
时变电磁场
4.1 电磁感应定律和全电流定律
时变电磁场
4.2.2 分界面上的衔接条件 ( Boundary Conditions )
时变电磁场中媒质分界面上的衔接条件的推导
方式与前三章类似,归纳如下:
磁场: B1n B2n
H2t H1t K
折射定律
电场: D2n D1n
E2t E1t
tan 1 1 tan 2 2 tan 1 1 tan 2 2
当场源不随时间变化时, A, 蜕变为恒定
场中的位函数。
返回 上页 下页
第四章
时变电磁场
4.4 坡印廷定理和坡印廷矢量
Poynting Theorem and Poynting Vector
电磁能量符合自然界物质运动过程中能量守恒
和转化定律——坡印廷定理;
坡印廷矢量是描述电磁场能量流动的物理量。 4.4.1 坡印廷定理(Poynting Theorem)
D
s D dS q
高斯定律
返回 上页 下页
第四章
时变电磁场
构成方程 J E D E B H
电磁场基本方程组全面总结了电磁场的规律,是 宏观电磁场理论的基础。 电磁场基本方程组加上构成方程理论上可以解决 所有的宏观电磁场问题。 静态场和恒定场是时变场的两种特殊形式。
返回 上页 下页
第四章
分界面上衔接条件
达朗贝尔方程
电磁辐射、传输线及波导
返回 上页 下页
第四章
本章要求
时变电磁场
深刻理解电磁场基本方程组的物理意义,其中 包括位移电流的概念;
掌握动态位与场量的关系以及波动方程,理解 电磁场的滞后效应及波动性;
掌握电磁波的产生和传播特性。
返回 上页 下页
第四章
时变电磁场
4.1 电磁感应定律和全电流定律
时变电磁场
4.2.2 分界面上的衔接条件 ( Boundary Conditions )
时变电磁场中媒质分界面上的衔接条件的推导
方式与前三章类似,归纳如下:
磁场: B1n B2n
H2t H1t K
折射定律
电场: D2n D1n
E2t E1t
tan 1 1 tan 2 2 tan 1 1 tan 2 2
第4章 时变电磁场1

2、坡印亭矢量
− ∫
S
v v v 表流入闭合面S的电磁功率, ( E × H )dS 表流入闭合面S的电磁功率,因此
v v 为一与通过单位面积的功率相关的矢量。 与通过单位面积的功率相关的矢量 E × H 为一与通过单位面积的功率相关的矢量。
v 定义:坡印廷矢量( 表示)- 定义:坡印廷矢量(用符号 S 表示)-能流密度矢量
v v 讨论:1 :1、 为与时间相关的函数(瞬时形式), ),则 讨论:1、若 E , H 为与时间相关的函数(瞬时形式),则 v v v S (t ) = E (t ) × H (t )
称为坡印廷矢量的瞬时形式。 称为坡印廷矢量的瞬时形式。 瞬时形式
v v 对某些时变场, 2、对某些时变场, , H 呈周期性变化。则将瞬 E 呈周期性变化。
v v v d v v ⇒ − ( E × H )dS = (We + Wm ) + ∫ E JdV ∫S V dt
坡印廷定理积分形式 说明: 说明:
− ∫
S
坡印廷定理物理意义: 坡印廷定理物理意义: 物理意义 流入体积V 流入体积V内的电磁功率 等于体积V 等于体积V内电磁能量的 增加率与体积V 增加率与体积V内损耗的 电磁功率之和。 电磁功率之和。
坡印廷定理描述了空间中电磁能量守恒关系。 坡印廷定理描述了空间中电磁能量守恒关系。
第4章 时变电磁场
13
1、坡印亭定理
在时变场中, 在时变场中,电、磁能量 相互依存, 相互依存,总能量密度为
1r r 1r r w = we + wm = D ⋅ E + B ⋅ H 2 2 W = ∫V 1 r r r r w dV = ∫V (D ⋅ E + B ⋅ H) V d 2
第4章 时变电磁场

引入洛伦兹规范条件, 引入洛伦兹规范条件,则方程简化为
2 2 ∂ϕ ρ ∇ ϕ − µε 2 = − ε ∂t v 2 v v 2 ∇ A − µε ∂ A = − µ J 2 ∂t
达朗贝尔方程
从达朗贝尔方程可以看出: 从达朗贝尔方程可以看出:
v v v v v v ϕ (r , t )的源是ρ (r , t ),A(r , t )的源是J (r , t )
建立波动方程的意义:通过解波动方程, 建立波动方程的意义 : 通过解波动方程 , 可以求出 空间中电场场量和磁场场量的分布情况。 空间中电场场量和磁场场量的分布情况 。 但需要注 意的是: 意的是 : 只有少数特殊情况可以通过直接求解波动 方程求解。 方程求解。
4.2 电磁场的位函数
4.2.1 矢量位和标量位
v v v (2) S (t ) = E (t ) × H (t ) v v kE0 = −ey E0 cos(ω t − kz ) × ex cos (ω t − kz )
kE0 2 v = ez cos 2 (ω t − kz )
ωµ 0
ωµ 0
v v 1 Tv 1 T v S av = ∫ S (t )dt = ∫ E (t ) × H (t )dt T 0 T 0 v 时间t无关。 注: S av 与时间t无关。
三、例题 已知无源的自由空间中, 例1:已知无源的自由空间中,时变电磁场的电场强度 v v 为 E = e E cos(ω t − kz ) (V / m)
一、坡印廷定理 坡印廷定理描述了空间中电磁能量守恒关系 电磁能量守恒关系。 坡印廷定理描述了空间中电磁能量守恒关系。
v v v v v ∂D ∇ (E × H ) ∇× H = J + v v v v ∂t ⇒ H ∇ × E − E ∇ × H v v v v ∂B v ∂B v v v ∂D ∇× E = − = − H ∂t − E J − E ∂t ∂t v v v v v ∂B v ∂D v v ⇒ ∇ (E × H ) = −H −E −E J ∂t ∂t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电的磁磁场H 感都应J能定产律D 生:t 电麦场克lH 。斯d 韦l第二S(方J 程,D t)表d明S电全荷电和流定变律化
磁通连E续性原B理:表E明d磁l 场是无B 源场dS, 磁电力磁线感总应是定律闭
合曲线。 t
l
S t
:旋表的明形B 电式 荷 产0以 生发 电散 场的)。方SB式d产S生电0场 (变磁化通的连磁续场性以原涡理
2 t A
(2)
定义A 的散度 A 洛仑兹条件
t
返回 上页 下页
第四章
2 A
2A t 2
J
2
2
t 2
时变电磁场
达朗贝尔方程 (Dalangbaier Equation)
说明 确定了 A的值,与 BA共同确定 A;
简化了动态位与场源之间的关系;
若场量不随时间变化,波动方程蜕变为泊松方程
2AJ
2/
洛仑兹条件是电流连续性原理的体现。
返回 上页 下页
第四章
时变电磁场
若激励源是时变电流源时
A(x,y,z,t)
J(x,y,z,tr) vdV (无反射)
4πV
r
达朗贝尔方程解的形式表明:t 时刻的响应取
决于 (tr/v) 时刻的激励源。又称 A, 为滞后
位(Retarded Potential)。
电磁波是以有限速度 v 1 传播的, 光
也是一种电磁波。
当场源不随时间变化时, A, 蜕变为恒定
场中的位函数(拉普拉斯方程或泊松方程)。
返回 上页 下页
第四章
时变电磁场
4.4 坡印廷定理和坡印廷矢量
Poynting Theorem and Poynting Vector
电磁能量符合自然界物质运动过程中能量守恒
和转化定律——坡印廷定理;
坡印廷矢量是描述电磁场能量流动的物理量。
第四章
时变电磁场
微波是一种波长极短的电磁波,波长在1mm到1m之间,其相 应频率在300GHz至300MHz之间。为了防止微波对无线电通 信、广播和雷达的干扰,国际上规定用于微波加热和微波干燥 的频率有四段,分别为:L段,频率为890~940MHz,中心波 长0.330m;S段,频率为2400~2500MHz,中心波长为 0.122m;C段,频率为5725~5875MHz,中心波长为 0.052m;K段,频率为22000~22250MHz,中心波长为 0.008m。家用微波炉中仅用L段和S段。
第四章
时变电磁场
4.2 电磁场基本方程组·分界面上的衔接条件
Maxwill Eguations and Boundary Conditions
4.2.1 电磁场基本方程组 (Maxwell Equations) 全电流定律:麦克斯韦第一方程,表明传导电流和变化 的综电上场所都述能,产电生磁磁场场基。本方程组
时变电磁场
E2t E1t 0
D2nD1n
H2t H1t K
B2nB1n0
分界面介质侧的场量
Et 0
Dn
Ht K Bn 0
导体表面有感应的面电荷和面电流。
返回 上页 下页
第四章
微波炉里为什么不能放入金属?
时变电磁场
这是因为微波碰上金属制品将发生“短路”和反射现象。 如果把食物盛在金属容器里加热,即使烧上一个小时, 容器中的食物温度也不会升高,这是因为微波遇到金属 容器后立即全部反射回去,食物得不到热源加热。更危 险的事还在后头,因为高频微波全部反射回去,就形成 了电子技术上的“高频短路”,这会导致发射微波的电 子管阳极产生q
返回
下页
第四章
构成方程
时变电磁场
J E DE BH
麦克斯韦第一、二方程是独立方程,后面两个方 程可以从中推得。
lH dlS(J D t)dS
B
lEdlStdS
SBdS0
SDdSq
静态场和恒定场是时变场的两种特殊形式。
返回 上页 下页
第四章
时变电磁场
4.2.2 分界面上的衔接条件 ( Boundary Conditions )
分析:在理想导体中
J E 为有限值,当 ,
E 0。
由EB0, 得BC(常)数 0,
图4.2.1 媒质分界面
t
若 C0, B由 0C的建立过程 B0中 , 必 t
即 E 0 ,则 J E , 所 ,只 以 B有 0。
结论: 在理想导体内部无电磁场,电磁波发生全反射。
返回 上页 下页
第四章
根据衔接条件
B0
BA
E B (A) A
t
t
t
(EA)0 t
E A
t
无旋场存在标量位函数。
A, 称为动态位,是时间和空间坐标的函数。
返回 上页 下页
第四章
时变电磁场
由
HJD t
1 A J t( A t )
由 D 矢量恒等式
(A )
t A (A)2A
经整理后,得
2A 2 tA 2 J ( A ) t (1)
第四章
时变电磁场
微波是在电真空器件或半导体器件上通以直流电或50Hz的交 流电,利用电子在磁场中作特殊运动来获得的。家用微波炉中 应用的是磁控管,通过磁控管把电能转换为微波能。磁控管有 脉冲磁控管和连续磁控管两种。微波炉中应用的是连续波磁控 管。微波的传播速度接近光速,它在传播过程中能够发生反射 和折射它有三个与加热相关的重要特性。微波遇到金属物体, 如银、铜、铝等会像镜子反射可见光一样被反射。因此,常用 金属隔离微波。微波炉中常用金属制作箱体和波导,用金属网 外加钢化玻璃制作炉门观察窗。微波遇到绝缘材料,例如玻璃、 塑料、陶瓷、云母等,会像光透过玻璃一样顺利通过。因此, 常用绝缘材料制作盘碟,而不影响加热效果。微波遇到含水或 含脂肪的食品,能够被大量吸收,并转化为热能。微波炉就是 利用这个特性来加热食品的。
时变电磁场中媒质分界面上的衔接条件的推导
方式与前三章类似,归纳如下:
磁场:
B1n B2n
H2tH1tK
电场:
折射定律
D2nD1n
E2t E1t
tan1 1 tan2 2
tan1 1 tan2 2
返回 上页 下页
第四章
时变电磁场
例 4.2.1 试推导时变场中理想导体与理想介质分界面
上的衔接条件。
第四章
时变电磁场
4.3 动态位及其积分解
Kinetic Potentials and Integral Solutions
4.3.1 动态位及其微分方程
(Kinetic Potentials and It’s Differential Equations)
从Maxwell方程组出发, 无源场存在矢量位函数。
