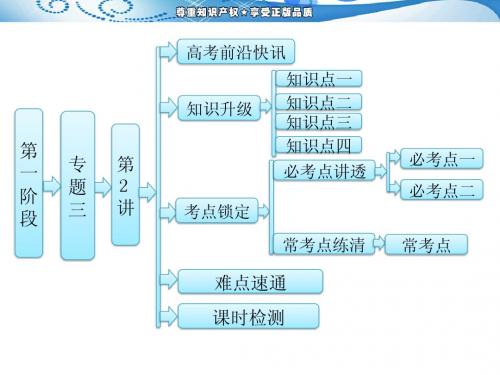
专题三第2讲

《创新设计》图书第2讲三个二次”关系与恒成立问题、存在性问题高考定位 高考对本内容的考查主要有：（1）一元二次不等式是 C 级要求，要求 在初中所学二次函数的基础上，掌握二次函数、二次不等式、二次方程之间的联 系和区别，可以单独考查，也可以与函数、方程等构成综合题; 立问题、存在性问题通常以不等式为载体，体现了转化与化归思想真题感悟1.（2017江苏卷）记函数f （x ）"6+ X — X 2的定义域为D.在区间［—4, 5］上随机取一个数X ,则x € D 的概率是解析 由 6 + x — x 2>0 得一2< x <3,贝U D 为[—2, 3].故所求概率p =3一（一2） = 9.5—（— 4） 92.（2015江苏卷）不等式2x2—x <4的解集为解析 由2x2—x <4,知x 2—x<2,解得一1<x<2，所以原不等式的解集为（一1, 2）.答案 （一1, 2） 3.（2014江苏卷）已知函数f （x ） = x 2 + mx — 1,若对于任意的x € ［m , m +1］,都有 f （x ）vO 成立，则实数m 的取值范围是解析 因为二次函数开口向上，在区间［m , m + 1］上始终满足f （x ）vO ,f (m ) <0,所以只需即可，f (m + 1) <0m 2+ m 2— 1<0,由2(m + 1) + m ( m + 1)— 1<0,⑵含参的恒成—专vm<〒，解得3—2<m<0，故实数m的取值范围为答案—乎,0普,0.考点整合1.三个二次”的关系解一元二次不等式一般要先判断二次项系数的正负也即考虑对应的二次函数图象的开口方向，再考虑方程根的个数也即求出其判别式的符号, 有时还需要考虑其对称轴的位置，根据条件列出方程组或结合对应的函数图象求解2.解含有参数的一元二次不等式，要注意对参数的取值进行讨论：(1)对二次项系数与0的大小进行讨论；(2)在转化为标准形式的一元二次不等式后，对判别式与0的大小进行讨论；⑶当判别式大于0,但两根的大小不确定时，对两根的大小进行讨论；(4)讨论根与定义域的关系3.四个常用结论(1)ax2+ bx+ c> 0(a工0恒成立的条件是a> 0, A< 0.(2)ax2+ bx+ CV 0(aM 0恒成立的条件是av 0, A< 0.(3)a>f (x)恒成立？ a>f (x) max，a< f(X)恒成立？ a< f (x)min. ⑷存在 f (x)<a 成立？ a>f(x)min，存在 f (x)>a 成立？热点一含参一元二次不等式的解法【例1】解关于x的不等式(X- 2)(ax—2)>0.《创新设计》图书解 当a = 0时，原不等式可化为x - 2<0,所以x<2.2当aM0寸，原不等式化为a(x - 2) x -- >0，a2 2 2① 当a>1时，a<2，原不等式化为(x - 2) x -a >0，所以x<2或x>2.a a a 2② 当a = 1时，- = 2,原不等式化为(x -2)2>0，a所以x € R 且xM 2.2 2③ 当0<a<1时，->2，原不等式化为(x - 2) x --a a2 2 J④ 当a<0时，a<2，原不等式化为(x - 2) x -- <0，所以-<x<2.a a a综上所述，当a = 0时，原不等式的解集为{x|x<2};2当a<0时，原不等式的解集为x a <x<2.a探究提高 含有参数的不等式的求解，往往需要比较(相应方程)根的大小，对参 数进行分类讨论:(1) 若二次项系数为常数，可先考虑分解因式，再对参数进行讨论；若不易分解因式，则可对判别式进行分类讨论;(2) 若二次项系数为参数，则应先考虑二次项是否为零，然后再讨论二次项系数不为零的情形，以便确定解集的形式;(3) 其次对相应方程的根进行讨论，比较大小，以便写出解集【训练1】(2017 上海十四校联考改编)已知a € R ，函数f(x) = x 2+ (2 a +1)x,g(x)=ax.解关于x 的不等式：f(X)W g(x). 解 由 f (x) < g(x)得 x 2+ (2a + 1)x < ax ， 即x 2+(a + 1)x < 0.2>0,则 x <2 或 x >a.2当a>1时，原不等式的解集为x x<a或x>2 ;当a= 1时，原不等式的解集为{x|x€ R且xM2}当0vav1时，原不等式的解集为x x<2或x>2;aT-.《创新设计》图书当av— 1 时，解得0Wx<- a—1;当a= —1时，解得x= 0；当a>— 1 时，解得一a— 1 <x<0.所以，当av—1时，不等式f (x)wg(x)的解集为［0，—a—1］; 当a= —1时，不等式f (x)wg(x)的解集为{0};当a>—1时，不等式f(x) < g(x)的解集为［—a—1, 0］.热点二三个二次”之间的关系【例2】(2017苏州调研测试)已知函数f (x) = x|x—a|, a€ R, g(x) = x3 4— 1.(1)当a= 1时，解不等式f (x)>g(x)；⑵记函数f(X)在区间［0，2］上的最大值为F(a)，求F(a)的表达式.解(1)由 f (x)> g(x)，当a= 1 时，即解不等式x|x—1|>x2— 1.3综上，不等式f(X)>g(x)的解集为一2, 1 .⑵因为x€ ［0, 2］,当a<0时，f (x) = x2—ax，则f (x)在区间［0 , 2］上是增函数,所以F(a) = f ⑵二4 —2a.—X2+ ax, 0=«a, a当0vav2时，f(X)= 2 则f(X)在区间0,9上是增函数，在区x — ax, a=<<2 2间a, a上是减函数，在区间［a, 2］上是增函数，所以F(a)= max f | , f (2), a a2a而 f 2 = a，f ⑵=4—2a,令 f 2 vf ⑵，即》v4 —2a,解得—4 —W lvav—4+ M,所以当0vav4迈一4 时，F(a) = 4 —2a；令 f 2 >f (2),即亍>4 —2a,由x> 1时，不等式为x2—x>x2—1，解得x< 1,所以x= 1;当xv1时，不等式为x —x2>x2—1，1 1解得—2=x< 1，所以—2< xv1.4,tz 《创新设计》图书解得 a < — 4— 4慣或 a > — 4+ 4/2,a5 6 所以当4农—4<a<2时，F(a)=—.当 a >2 时，f (x) = — x 2 + ax ,aaa当1 <2<2,即2<a<4时，f （X ）在区间0, 2上是增函数，在2，2上是减函数, a a 2 则 F （a ）= f a = N ；当!>2,即a >4时，f (x)在区间［0, 2］上是增函数, 则 F(a) = f (2) = 2a — 4;4 — 2a , av4迄—4, a 2综上，F(a 戸 a , 404它<4,2a — 4, a >4.三个二次”的关系是解一元二次不等式的理论基础，一般可把a<0的(2017苏北四市一调)已知函数f (x) = 2x — 6+ a , g(x) = bf (1 — x)，其中a ,b € R.若关于x 的不等式f （X ）>g （x ）的解的最小值为2,则实数a 的取值范围 是__________ .解析 因为 g(x)= b(2—x + a),所以 f (x)>g(x),b即 2x — 1 + a >b + ab ,即(2x )2 — 2a(b — 1)2x — 2b >0.由二次不等式与二次方程的根的关系知， 关于2x 的方程（2x ）2 — 2a （b — 1）2x — 2b = 0的2x的值分别为4, —2.因为2x取正值，要想2x最小为4,所以一2<0,即b >0.又因为 4— 2= 2a(b — 1),所以 b = 7(*+ 2)>0,解得 a < — 2 或 a> — f24a +14(1) 若对于任意的x € R , f (x)>0恒成立，求实数a 的取值范围;(2) 若对于任意的x € [ — 1，1]，f (x)>0恒成立，求实数a 的取值范围；答案（—X,— 2] U — 4，+X热点三 恒成立问题与存在性问题6【例3】 已知函数f (x) = x 2 + 2ax — a + 2.探究提高情况转化为 a>0时的情形. 【训练2】I匕凄《创新设计》图书(3)若对于任意的a€ [ —1，1]，X2+ 2ax—a+ 2>0恒成立，求实数x的取值范围.解(1)若对于任意的x€ R，f (x) >0恒成立，需满足△= 4a2—4(— a + 2)<0,解得—2<a< 1.故实数a的取值范围是[—2, 1].(2)由题知对称轴方程为x= —a,当一a<—1,即a>1 时，f (x)min = f (—1) = 3 —3a> 0, 解得a< 1, 与已知矛盾，舍去；当一a>1，即a<— 1 时 f (x)min = f (1)= 3+ a> 0，解得—3< a<—1;当一1W aw 1 时，f(x)min = f (一a) = 一a2—a+ 2》0，解得—K a< 1.综上，实数a的取值范围是[—3，1].(3)对于任意的a€ [ —1，1]，X2+ 2ax— a + 2>0 恒成立，等价于g(a)= (2x—1)a+ X2+ 2>0，所以g(1)>0，g (—1) >0,即：+ 2x—1 + 2>0，x2—2x+1 + 2>0,解得XI 1，所以x的取值范围是{xx^ 1}.探究提高(1)对于一元二次不等式恒成立问题，恒大于0就是相应的二次函数的图象在给定的区间上全部在x轴上方，恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴下方.另外常转化为求二次函数的最值或用分离参数法求最值.(2)解决恒成立问题一定要搞清谁是主元，谁是参数.一般地，知道谁的范围，谁就是主元，求谁的范围，谁就是参数.《创新设计》图书【训练3】（1）（2017江苏冲刺卷）若命题 存在x € R , ax 2 + 4x + a <0”为假命题, 则实数a 的取值范围是 ⑵（2017盐城期中）若不等式x 2-2x + 5>a 2-3a 对任意实数x 恒成立，则实数a 的取值范围是 解析（1）由命题 存在x € R , ax 2+4x + a < 0”为假命题，得 任意x € R , ax 2+ 4x a>0, + a>0”为真命题则 2 解得a>2, △= 16-4a 2<0, 故实数a 的取值范围是（2，+ X ）. ⑵由于x 2-2x + 5= （x - 1）2+ 4的最小值为4, 所以x 2- 2x + 5>a 2-3a 对任意实数x 恒成立, 只需 a — 3aW 4,解得—1W aW 4. 答案(1)(2,+x) (2)[ - 1, 4] 总结思维fl华1.在解一元二次不等式时，通常先将二次项的系数化为正数，然后利用 次”的关系进行求解；在求解含参数的不等式时，则要注意对二次项系数及根的 三个二 大小关系分类讨论,2.（1）在解决不等式 项系数含有字母时, 分别写出解集. ax 2+bx + c >0（或》0）对于一切x € R 恒成立问题时，当二次 需要对二次项系数 a 进行讨论，并研究当a = 0时是否满足 题意. （2）含参数的一元二次不等式在某区间内恒成立问题，常有两种处理方法：一是 利用二次函数在区间上的最值来处理； 二是先分离出参数，再去求函数的最值来 处理，一般后者比较简单. 、填空题I 匚'・《创新设计》图书1.(2017苏中四校联考)若 ?x € R , x 2 + 2x + a < 0”是假命题，贝U 实数a 的取值范围是 解析 由命题？x € R , X 2 + 2X +a < 0”是假命题，可得其否定 ？x € R , 2x 2 + 2x +a>0”是真命题，则 △= 4-4a<0,解得a>1. 答案 (1,+ X) 2.若对任意实数x € [ — 1,1],不等式X 2+ ax — 3a<0恒成立，则实数a 围是 __________ . 的取值范解析 设f (x)= x 2 + ax - 3a.因为对任意实数x € [ —1,1]，不等式 2x + ax — 3a<0恒成立, f 所以 f 答案 (—1)= 1 — a — 3a<0, 1 解得a>1.(1)= 1 + a — 3a<0, 21 2，+x2 3.(2017南师附中调研)若当x> — 3时，不等式a < x +x ^^恒成立, 则实数a 的取值范围是 2 2 解析 设f (x) = x +亠 =(x + 3) +亠 —3,因为x>— 3,所以 x + 3 x + 3 X + 3>0,故 f(x)>2、(x + 3) Z — 3 = 2^/2 — 3,当且仅当x=V 2 — 3时等号成立，所以a V x + 3 的取值范围是(—X, 2迈—3]. 答案 (—X, 2迈—3] 4.(2017镇江模拟)已知函数f(x)是定义在R 上的奇函数，当x>0时，f (x) = x 24x ,则不等式f (x)>x 的解集为 解析 因为函数f(X)是定义在R 上的奇函数，当x>0时，f (x) = x 2 — 4x ,所以当x>0, x <0 时，f (x)= — f (—x)= — x 2—4x,不等式 f (x)>x? 2 xO,或 2解x 2—4x>x— x 2—4x>x,T A《创新设计》图书得x>5或—5<x<0，则不等式f （x）>x的解集为（—5, 0）U （5,+^ ）.答案（—5, 0）U （5,+^）5.当x€ （—^,—1］时，不等式（m2—m） 4x—2x<0恒成立，则实数m的取值范围是________ .1 x 1 x解析原不等式变形为m2—m< 2 ,因为函数y= 2在（—V —1］上是减函数,所以2 X》2 12.当x€ (—V,— 1］时，m2— m<2 x恒成立等价于m2— m<2,解得—1<m<2.答案（—1, 2） 6.（2017苏、锡、常、镇调研）已知f （x）= x2+ 2x+ aln x,若f （x）在区间（0,1］上恒为单调函数，则实数a的取值范围为+：+ a，因为f（X）在区间（0,1］上恒为解析由题意知f 2x+2 + 2x单调函数，所以f X（在区间（0,1］上恒大于等于0或恒小于等于0,所以2x2+ 2x+ a>0 或2x +2x+ a< 0在区间(0, 1］上恒成立，即a> —(2x2+ 2x)或a< —(2x2 + 2x）,而函数y= —2x2—2x在区间（0,1］上的值域为［—4, 0）,所以a>0或a< —4.答案（一V,— 4］ U ［0，+V）7.若对任意实数x>1 , y>1，不等式pw 2y—1 +xE恒成立，则实数P的最大值解析令a=2y—1,b = x—1,则丄+呈=十+十，问题转2y— 1 x— 1 a b(b+1) 2(a+1) 2(b+1) 2(a+1) 2化为求---- a ---- +---- b --- (a>0，b>0)的最小值.又------- a --- + ----- b ---答案(1, 5]二、解答题9. (2017 南京、盐城调研)设函数 f (x) = ax 2+ (b — 2)x + 3(a ^ 0). ⑴若不等式f (x)>0的解集为(—1, 3),求a , b 的值;1 4⑵若f (1) = 2, a>0, b>0,求a +b 的最小值.解(1)由题意得1—1)",即a —b +5 = 0'f (3)= 0,9a + 3b — 3= 0, 解得*— 1,b = 4.⑵因为f (1) = 2,所以a + b = 1,所以 1 + 4=(a + b )1+4 = 5+ a +警 9, 1《创新设计》图书(a +1)( b +1) ab +(a +b ) + 1 1 a + b>2 --------- -------- = 2 X ------ 亡 ------ =2 V OL + 為+丙 >2X(2 + 2) T ab Vab=8,当且仅当a = b = 1,即x = 2, y = 1时取等号.答案 88.(2017徐州、宿迁、连云港模拟)已知对于任意的x € (— V 1) U (5,+^)都 有x 2— 2(a — 2)x + a>0,则实数a 的取值范围是解析 令 f (x) = x 2— 2(a — 2)x + a ,则当△= 4(a — 2)2—4a<0,即 1<a<4 时，f (x)>0 在R 上恒成立，符合题意；当 A>0,即a < 1或a >4时，函数f (x)的两个零点aW 或a 绍,都在［1 , 5］上，则 1<a — 2^5,解得4W a < 5.综上，故实数f (1)= 1— 2 (a — 2)+ a%.f (5)= 25 — 10 (a — 2)+ a%.a 的取值范围是(1, 5].当且仅当b=2a = 2■时取等号.10.已知函数f(X)= ax2+ 2x+ c(a, c€ N*)满足①f (1)= 5;②6<f ⑵<11.(1)求函数f(X)的表达式；(2)若对任意的x€ [1 , 2],都有f (x)—2mx> 0恒成立，求实数m的取值范围. 解(1)由题知5= a+c+ 2,即卩c= 3 — a.1 4又6<4a + c+ 4<11，所以—3<a<3.又a€ N*，所以a= 1, c= 2所以 f (x) = / + 2%+ 2.2⑵由已知得2(m—1)<X + x在x€ [1 , 2]上恒成立.入2因为当x€ [1 , 2]时，X+ x € [2羽，3],入所以2(m—1)<2^/2,所以实数m的取值范围为(一X,迄+ 1].11.(2015浙江卷)设函数 f (x) = x2+ax+ b(a, b€ R).a2(1)当b= 4 + 1时，求函数f (x)在区间[—1, 1]上的最小值g(a)的表达式；⑵已知函数f (x)在区间[—1, 1]上存在零点，且0W b —2a< 1,求实数b的取值范围.2 a 2a解⑴当b= 4+ 1时，函数f (x)= x+2 + 1故其图象的对称轴为直线x= — 2.2a当a< — 2 时，g(a) = f (1) = ^ + a + 2；当一2<a< 2 时，g(a) = f —| = 1;当a>2 时，g(a)= f (—1)=亍—a+ 2.a24 +a+ 2,aJ2,综上，g(a)= 1,—2<a<2詡《创新设计》图书2a4 — a + 2, a>2.⑵设s, t为方程f (x)= 0的解，且一 1 < t< 1 ,s+1= —a, 则st= b.因为OW b —2a< 1,所以一h sw ( —1W tw 1).一2t2t 一2t2当OW tw 1 时，忌w stw y2 —2t^ 1 t—2t2厂由于—3Ww 0和—3W£ w 9—4伍2所以—3= bw 9 —4/5.t一2t2一2t2当一1W t<0 时，^+2W stw w，由于-2w—fvo 和—3w t—22<O,所以一3w b<0.故b的取值范围是［—3, 9—4侗.。