实验一用递推公式计算定积分
定积分运算法则

• 通过定积分求解经济学中的边际产量、边际消费等边际问题
求解经济学中的总量问题
• 通过定积分求解经济学中的总产量、总消费等总量问题
求解经济学中的平均问题
• 通过定积分求解经济学中的平均产量、平均消费等平均问题
谢谢观看.
Thank you for watching.
Docs
⌛️
06
定积分的数值计算方法
数值积分的基本原理与方法
数值积分的定义
数值积分的方法
• 通过数值方法近似求解定积分的值
• 辛普森法
• 龙贝格法
• 高斯积分法
数值积分的误差分析与控制
误差分析
误差控制
• 分析数值积分方法的误差来源
• 选择合适的数值积分方法
• 估计数值积分方法的误差范围
• 控制积分区间的长度
求解物体的速度
• 通过定积分求解物体在变力作用下的速度
求解物体的加速度
• 通过定积分求解物体在变力作用下的加速度
定积分在工程学中的应用
求解工程问题的面积
求解工程问题的体积
求解工程问题的质心位置
• 通过定积分求解曲线围成的面积
• 通过定积分求解曲面围成的体积
• 通过定积分求解物体的质心位置
定积分在经济学中的应用
积分问题
换元积分法的原理
• 利用换元公式将原积分变量变换为新变量,从而简化积分过程
换元积分法的常见类型与方法
01
幂函数换元法
• 将复杂的幂函数积分问题转化为简单的指数函数积分问
题
02
三角函数换元法
• 将复杂的三角函数积分问题转化为简单的指数函数积分
问题
03
《数学实验》实验报告——定积分的近似求解
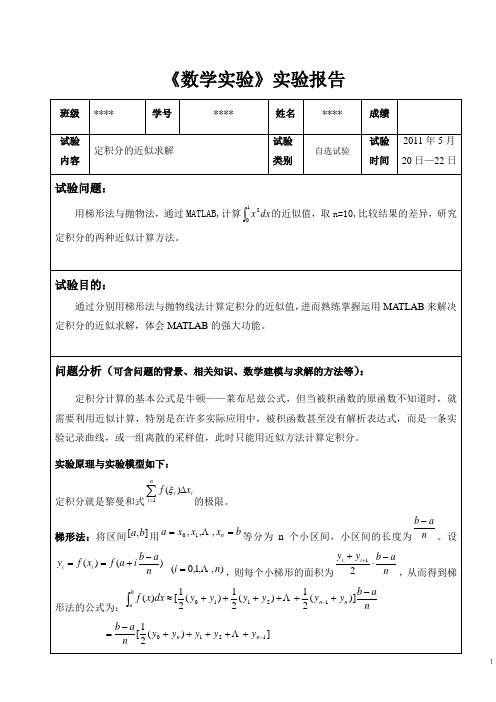
3
2 梯形法程序如下: f=input('请输入被积函数 f(x)='); qujian=input('请输入积分区间[a,b]='); n=input('请输入子区间个数 n='); s=0; for i=1:n-1 x=qujian(1)+(qujian(2)-qujian(1))/n*i; y=eval(f); s=s+y; end x=qujian(1); y=eval(f); s=s+y/2; x=qujian(2); y=eval(f); s=s+y/2; disp('定积分的近似值是:'); s=s*(qujian(2)-qujian(1))/n
《数学实验》实验报告
班级 试验 内容 **** 学号 **** 姓名 试验 类别
自选试验
****
成绩 试验 时间 2011 年 5 月 20 日—22 日
定积分的近似求解
试验问题:
用梯形法与抛物法,通过 MATLAB,计算 x 2 dx 的近似值,取 n=10,比较结果的差异,研究
0 1
定积分的两种近似计算方法。
1 1 1 2 ph 3 6rh h(2 ph 2 6r ) h( y 0 4 y1 y 2 ) 3 3 3 。 ba n ,则上面所求的 S 等于区间 [ x0 , x2 ] 上以抛物线为曲边的曲边梯形的面积。同理可
取
以得到区间 [ xi 1 , xi 1 ] 上以抛物线为曲边的曲边梯形的面积:
试验目的:
通过分别用梯形法与抛物线法计算定积分的近似值, 进而熟练掌握运用 MATLAB 来解决 定积分的近似求解,体会 MATLAB 的强大功能。
数学实验报告定积分计算(3篇)

第1篇一、实验目的1. 理解定积分的概念和意义。
2. 掌握定积分的计算方法。
3. 通过实验,加深对定积分理论知识的理解和应用。
二、实验原理定积分是微积分学中的一个基本概念,它表示某一曲线与x轴及两条垂直于x轴的直线所围成的平面图形的面积。
定积分的计算方法主要有直接积分法、分部积分法、换元积分法等。
三、实验仪器与材料1. 计算机2. 计算软件(如MATLAB、Mathematica等)3. 数学教材和参考书籍四、实验内容1. 理论学习(1)复习定积分的定义、性质和计算方法。
(2)了解定积分在物理学、工程学、经济学等领域的应用。
2. 实验操作(1)计算以下定积分:∫(0到1)x^2 dx(2)使用MATLAB软件进行定积分计算,并比较与手工计算的结果。
3. 结果分析(1)分析手工计算与MATLAB计算的结果差异,找出原因。
(2)总结定积分计算方法在实际应用中的优缺点。
五、实验步骤1. 理论学习(1)阅读数学教材,了解定积分的定义、性质和计算方法。
(2)查阅相关资料,了解定积分在各个领域的应用。
2. 实验操作(1)使用计算器或手工计算定积分∫(0到1)x^2 dx,得到结果。
(2)打开MATLAB软件,编写以下代码进行定积分计算:```matlabsyms x;I = int(x^2, 0, 1);```运行代码,得到结果。
3. 结果分析(1)比较手工计算和MATLAB计算的结果,发现两者基本一致。
(2)分析定积分计算方法在实际应用中的优缺点,总结如下:优点:- 定积分计算方法可以处理各种复杂函数,具有广泛的适用性。
- 定积分在物理学、工程学、经济学等领域的应用非常广泛。
缺点:- 对于某些复杂函数,计算过程较为繁琐,需要花费较多时间。
- 在实际应用中,可能需要根据具体情况选择合适的计算方法。
六、实验总结通过本次实验,我们了解了定积分的概念、性质和计算方法,并掌握了使用MATLAB软件进行定积分计算的方法。
积分计算超强总结(循环递推法)

【解】
.
【注】本例中没有出现循环递推的形式,所以放在这里是为了提醒大家当出现 减 的时候,不能将它们完全抵消,而要留下一个任意常数.
上述问题也可以改作为用循环递推法计算定积分的例子,这意义就不大了.下面举几个原函数不是初等函数的定积分计算例子,注意到定积分值与积分变量名称无关,可以考虑使用换元法.为了与原积分 可以做比较,必须保持积分区间 不变,翻折变换 可以达到此目的.所谓翻折变换是以区间 的中点为不动点的翻折.
【例5】求 .
【解】在翻折变换 下,有
,
所以,有 .
【例6】求 .
【解】在翻折变换 下,有
,
所以,有 .
利用循环递推法计算不定积分时,因为不定积分的计算结果与积分变量的名称有关,所以比较适合用分部积分法,而这时换元积分法恐怕是没有用的.
【例1】求 .
【解】
.
所以 ,即 .
【例2】求 .
【解】
,
所以 .
【例3】求 .
【解】
.
所以,有 .
【注】本题用换元 的方法,一样可以得到结果,但还要用到三角倍角公式和回代的过程,略显麻烦.
循环递推法
循环递推法是积分计算的一种重要的辅助方法.对于某些积分问题,在通过换元积分法或分部积了原积分的表达式
.
这样,实际上也就得到了需要的结果了,这种方法称为循环递推法.
这里需要注意的是:若 表示的是不定积分,等式另一边的 虽然表示的是同一个函数的不定积分,但是应该有一个常数的差别.所以在移项合并时,必须留下一个常数.
定积分的计算

则 有 a f ( x )dx f [ ( t )] ( t )dt .
b
证
设F ( x ) 是 f ( x ) 的一个原函数,
a f ( x )dx F (b) F (a ),
b
( t ) F [( t )],
dF dx f ( x ) ( t ) f [( t )]( t ), ( t ) dx dt
第四节 定积分的计算
一、直接利用牛顿-莱布尼兹公式 二、换元积分法 定理 假设 (1)f ( x ) 在[a , b] 上连续;
(2)函数 x (t ) 在[ , ] 上是单值的且有连续 导数; (3)当t 在区间[ , ] 上变化时, x (t ) 的值
在[a , b]上变化,且 ( ) a 、 ( ) b ,
1 1 4 4 x tan x 0 tan xdx 2 0 2 1 ln 2 4 ln sec x 0 . 8 2 8 4 4
例3 解
计算
1
0
ln(1 x ) dx . 2 (2 x )
0
1
1 ln(1 x ) 1 dx 0 ln(1 x )d 2 (2 x ) 2 x
1 2
xdx 1 x2
练习:
xdx 0 1 cos 2 x .
4
1
0
ln(1 x ) dx . 2 (2 x )
xdx . 例2 计算 0 1 cos 2 x
解
4
1 cos 2 x 2 cos x ,
2
xdx xdx 4 4 x d tan x 2 0 1 cos 2 x 0 2 cos x 0 2
-例谈定积分的计算方法和技巧
-----------------------------------Docin Choose -----------------------------------豆 丁 推 荐↓精 品 文 档The Best Literature----------------------------------The Best Literature例谈定积分的计算方法和技巧韦兰英(南宁师范高等专科学校数学与计算机科学系,广西龙州532400)摘要:文章通过举例,主要从五个方面探讨了简化定积分计算所采用的方法和技巧,这些方法和技巧既可减少计算量,提高效率,又可以开拓解题思路,提高学生定积分的计算能力。
关键词:定积分;计算;方法;技巧中图分类号:O13文献标识码:A文章编号:1008-696X(2008)04-0112-03On Methods and Techniques of Calculation on Definite IntegralWei Lanying(Dept.of Maths and Computer Science,Nanning Teachers College,Longzhou,Guangxi532400,China) Abstract:The methods and techniques on simplified calculation on definite integral are discussed with examples from five aspects,which helps reduce the amount of calculation and improve the efficency and performance in students'exercises.Key words:definite integral;calculation;method;technique定积分是积分学的一个基本问题,是高等数学的重要概念之一。
计算方法与计算 实验一误差分析

% 输出的量--每次迭代次数k和迭代值xk,
%
--每次迭代的绝对误差juecha和相对误差xiangcha,
误差分析
误差问题是数值分析的基础,又是数值分析中一个困难的课题。在实际计算 中,如果选用了不同的算法,由于舍入误差的影响,将会得到截然不同的结果。 因此,选取算法时注重分析舍入误差的影响,在实际计算中是十分重要的。同时, 由于在数值求解过程中用有限的过程代替无限的过程会产生截断误差,因此算法 的好坏会影响到数值结果的精度。 一、实验目的
因为运行后输出结果为: y 1.370 762 168 154 49, yˆ =1.370 744 664 189
38, R 1.750 396 510 491 47e-005, WU= 1.782 679 830 970 664e-005 104 . 所
以, yˆ 的绝对误差为 10 4 ,故 y
③ 运行后输出计算结果列入表 1–1 和表 1-2 中。
④ 将算法 2 的 MATLAB 调用函数程序的函数分别用 y1=15-2*x^2 和
y1=x-(2*x^2+x-15)/(4*x+1)代替,得到算法 1 和算法 3 的调用函数程序,将其保
存,运行后将三种算法的前 8 个迭代值 x1, x2 ,, x8 列在一起(见表 1-1),进行
的精确解 x* 2.5 比较,观察误差的传播.
算法 1 将已知方程化为同解方程 x 15 2x2 .取初值 x0 2 ,按迭代公式
xk1 15 2xk2
定积分基本计算公式

令 xa
a
F ( a ) ( a ) C ,
(a ) a f ( t )dt 0 F (a ) C ,
F ( x ) a f ( t )dt C ,
x
a
x
f ( t )dt F ( x ) F (a ),
令x b
a f ( x )dx F (b) F (a ).
0
b( x )
证:
F ( x)
0
a( x )
f (t )dt
a( x ) 0
0
b( x )
f ( t )dt
f ( t )dt ,
F ( x ) f b( x )b( x ) f a( x )a( x )
例1
e 求 lim cos x
x 0
例3
设 f ( x ) 在[0,1]上连续,且 f ( x ) 1.证明
2 x 0 f ( t )dt 1在[0,1]上只有一个解.
证 令 F ( x ) 2 x f ( t )dt 1,
0 x
x
f ( x ) 1,
F ( x ) 2 f ( x ) 0,
y
x
f ( t )dt ,
由积分中值定理得
( x )
f ( )x,
f ( ), x
在x与x x之间.
lim lim f ( ) x 0 x x 0
( x ) f ( x ).
o
a
x x x b x
x 0, x
F ( x ) 在[0,1]上为单调增加函数. F (0) 1 0,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 用递推公式计算定积分
09信息 符文飞 07
1、实验目的:
由于一个算法是否稳定,十分重要。
如果算法不稳定,则数值计算的结果就会严重背离数学模型的真实结果,因此,在选择数值计算公式来进行近似计算时,我们应特别注意选用那些在数值计算过程中不会导致误差迅速增长的公式。
体会稳定性在选择算法中的地位.误差扩张的算法是不稳定的,是我们所不期望的;误差衰竭的算法是稳定的.是我们努力寻求的,这是贯穿本课程的目标.通过上机计算,了解舍入误差所引起的数值不稳定性。
2、实验题目:
对n =0,1,2,…,20,计算定积分dx x x y n n ⎰+=10
5
3、实验原理
由于y(n)= = –
在计算时有两种迭代方法,如下:
方法一: y(n)= – 5*y(n-1),n=1,2,3, (20)
取y(0)= = ln6-ln5 ≈ 0.182322
方法二:
利用递推公式:y(n-1)=-*y(n),n=20,19, (1)
而且,由 = * ≤≤* =
可取:y(20)≈*()≈0.008730.
4、实验内容:
算法1的程序:
y0=log(6.0)-log(5.0);
y1=0;
n=1;
while n<=30
y1=1/n-5*y0;
fprintf('y[%d]=%-20f',n,y1);
y0=y1;
n=n+1;
if mod(n,1)==0;
fprintf('\n')
end
end
算法2的程序:
y0=(1/105+1/126)/2;
y1=0;
n=1;
while n<=30
y1=1/(5*n)-y0/5;
fprintf('y[%d]=%-20f',n,y1)
y0=y1;
n=n+1;
if mod(n,1)==0
fprintf('\n')
end
end
5、实验结果
对于算法1:
y[1]=0.088392
y[2]=0.058039
y[3]=0.043139
y[4]=0.034306
y[5]=0.028468
y[6]=0.024325
y[7]=0.021233
y[8]=0.018837
y[9]=0.016926。
