圆锥曲线焦点三角形(good)
圆锥曲线中焦点三角形的应用

浅谈圆锥曲线中焦点三角形两个性质的应用无锡市北高级中学 计 巍 214044在近几年的教学以及高考试题中,发现圆锥曲线中焦点三角形的应用比较多,于是对焦点三角形的一些特征进行一点探究和归纳。
圆锥曲线上一点P 和两个焦点1F ,2F 构成的21PF F ∆称为“焦点三角形”。
1、 关于焦点三角形的两个性质性质⑴:焦点三角形的面积公式若1F 、2F 是椭圆)0(12222>>=+b a by a x 的两个焦点,P 是椭圆上一点,且θ=∠21PF F ,则2tan 221θb S PF F =∆。
解:设m PF =1,n PF =2,由余弦定理得2221224cos 2c F F mn n m ==-+θ①由椭圆定义得 a n m 2=+② 由①得:θθcos 12cos 1)(2222+=+-=b c a mn ∴2tan cos 1sin sin 212221θθθθb b mn S PF F =+==∆(Ⅰ)由此类比双曲线还可得到:已知1F 、2F 是双曲线)0,0(12222>>=-b a by a x 的两个焦点,P 是双曲线上一点,且θ=∠21PF F ,则2c ot 221θb S PF F =∆。
(Ⅱ) 以上两个公式对于焦点在y 轴上的椭圆和双曲线同样成立。
性质⑵:焦点三角形中的最大顶角已知1F 、2F 是椭圆)0(12222>>=+b a by a x 的两个焦点,P 是椭圆上一点,且θ=∠21PF F ,则当点P 为短轴端点B 时角θ最大。
解:设m PF =1,n PF =2由余弦定理得2221224cos 2c F F mn n m ==-+θ①由椭圆定义得 a n m 2=+②12242)(cos 222-=--+=∴mnb mnc mn n m θ 而n m a +=2≥mn 2,mn ∴≤21aθcos ∴≥1222-ab (Ⅲ),由余弦函数在()π,0上单调递减 当且仅当n m =)(21PF PF =,θcos 取值最小,即点P 为段轴端点时角θ最大。
圆锥曲线中的焦点三角形.doc

证明:由正弦定理得:由等比定理得:而"司=2csin(a + (3) sin(a + /?)PF 】+ Pg _ 2ci sin a + sin/3sin a + sin /?sin a +sin点P 在椭圆上,且焦点三角形焦点三角形问题是重要考点,考到的内容有:椭圆或双曲线定义和正余弦定理以及面积公式 等。
常与曲线的离心率相结合,注意平面几何知识的应用。
一:椭圆的焦点三角形椭圆的焦点三角形是指以椭圆的两个焦点K ,%与椭圆上任意一点p 为顶点组成的三角形。
22—+ yr = 1(。
〉人〉0) a~ b~(1) \PF ]\ + \PF 2\=2a(2) 4c 2 H I 2 +1 I 2 -2| PF } II PF 2\COS ZF }PF 2(3) 椭圆上的点与两焦点连线的夹角以椭圆短轴顶点与两焦点连线的夹角最大.2 2证明:设P 是椭圆二+ 4 = 1 (。
>人>0,C 为半焦距)上的一点,O 为原点,E 、F 是 erb~椭圆的两焦点,|庭| =所,\PF\ = nm ,Ln — + -4c 2 4/?2-2mn 2b 1,、2〃 , 土人「〜皿而打顼 则cos ZEPF = -------------- = --------- = ------ ,由余弦函数图象性质知2mn 2mn mn aZEPF 有最大值,当且仅当P 在短轴端点时取到该最大值。
(4) 设P 为椭圆上的任意一点,角ZF i F 2P = a, 压叩=0, AF 2PF X =6,则有离心七 sin(a + /?) c ,9 sin 。
盘. ° 率° =——-—— ,S'PFF =b- =b~tan-sin a + sin /?1 21 + cos 0 2sin(l 8(T-a-/?) sin a sin /?入川二|PFj + |P%| sin(a + 0) sin a + sin . c _ sin(a + /7) . . g = — ■ a例题: 2 2圆乌+ 2 = 1(。
圆锥曲线焦点三角形问题解题技巧梳理

圆锥曲线焦点三角形问题解题技巧梳理一.技巧内容 二.技巧推导过程 1.12椭圆中的PF PF222121212212121221212221222122cos =()22cos =()2(1cos ) 442(1cos )422(1cos )1cos =+-+--+-+=-+∴==++F F PF PF PF PF PF PF PF PF PF PF PF PF PF PF c a PF PF b b PF PF θθθθθθ2.椭圆中焦点三角形的面积公式1222212211212=sin sin 2sin cos tan 221cos 222212cos 12∆===++-PF F b b S PF PF b θθθθθθθ12PF F S ∆离心率12PF3. 椭圆中的离心率12122sin sin()(1)2sin sin sin sin +=====+++F F c c e a a PF PF θαβαβαβ222121212212121221212221212212212(2)2cos =()22cos =()2(1cos ) ()2()(1cos )21=()[1(1cos )]21=()(=+-+--+-++≥+-++-++F F PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF θθθθθ12222222cos )==2111144(cos )cos (12sin )sin 222222sin2-∴≥-≥-=--=∴≥(当且仅当取,即在短轴端点处)即PF PF P c c a a e θθθθθθ4.12双曲线中的PF PF222121212212121221212221222122cos =(-)+22cos =(-)+2(1-cos ) 44+2(1-cos )422(1-cos )1-cos =+--=∴==F F PF PF PF PF PF PF PF PF PF PF PF PF PF PF c a PF PF b b PF PF θθθθθθ5.双曲线中焦点三角形的面积公式1222212211212=sin sin 2sin cos 221-cos 2221-1-2sin )tan 22∆===(PF F b b b S PF PF θθθθθθθ6.双曲线中的离心率12122sin sin()2sin sin sin sin +=====---F F c c e a a PF PF θαβαβαβ技巧1 焦点三角形的周长【例1】已知点12,F F 分别是椭圆221259x y +=的左、右焦点,点P 在此椭圆上,则12PF F ∆的周长等于( )A .20B .16C .18D .14【举一反三】1.若椭圆22221x y a b+=(其中a >b >0)的离心率为35,两焦点分别为F 1,F 2,M 为椭圆上一点,且△F 1F 2M的周长为16,则椭圆C 的方程为( )A .2211625x y +=B .221259x y +=C .221925x y +=D .2212516x y +=2.定义:椭圆上一点与两焦点构成的三角形为椭圆的焦点三角形,已知椭圆2222:1(0)x y C a b a b+=>>的焦距为12,则椭圆C 的方程是__________. 技巧2 焦点三角形的面积【例2-1】已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F 、2F ,P 为椭圆上一点,且12PF PF ⊥,若12PF F △的面积为9,则b =__________.【例2-2】已知1F 、2F 为双曲线22:13x C y -=的左、右焦点,点P 在C 上,1260F PF ︒∠=,则12PF F △的面积为 【举一反三】1.已知1F 、2F 为双曲线C :221x y -=的左、右焦点,点P 在C 上,∠1F P 2F =060,则12·PF PF =( )A .2B .4C .6D .82若椭圆2213616x y +=上一点P 与椭圆的两个焦点1F 、2F 的连线互相垂直,则12PF F 的面积为( )A .36B .16C .20D .243.设P 为双曲线2221x y a-=(0a >)的上一点,1223F PF π∠=,(12F F 、为左、右焦点),则12F PF ∆的面积等于( )A 2B .23C .3D .3技巧3 焦点三角形的离心率【例3-1】设椭圆2222:1x y C a b+=(0)a b >>的左、右焦点分别为12,F F ,P 是C 上的点,212PF F F ⊥,1230PF F ∠=,则C 的离心率为 ( )B.13C.12【例3-2】已知12,F F 分别是椭圆22221(0)x y a b a b +=>>的左、右焦点,若椭圆上存在点P ,使1290F PF ∠=,则椭圆的离心率e 的取值范围为( )A .B .C .D . 【举一反三】1.已知点P 在以12,F F 为左,右焦点的椭圆()2222:102x y C b b b +=>上,在12PF F △中,若12PF F α∠=,21PF F β∠=,则()sin sin sin αβαβ+=+( )A .12B .2C D2.记1F ,2F 为椭圆22:1x C y m+=的两个焦点,若C 上存在点M 满足120MF MF ⋅=,则实数m 取值范围是( )A .10,[2,)2⎛⎤⋃+∞ ⎥⎝⎦ B .1,1[2,)2⎡⎫⋃+∞⎪⎢⎣⎭ C .10,(1,2]2⎛⎤⋃ ⎥⎝⎦ D .1,1(1,2]2⎡⎫⋃⎪⎢⎣⎭巩固练习1.已知F 1,F 2是椭圆216x +29y =1的两焦点,过点F 2的直线交椭圆于A ,B 两点.在△AF 1B 中,若有两边之和是10,则第三边的长度为 ( )A .6B .5C .4D .32.设椭圆C :22221x y a b +=(a >0,b >0)的左、右焦点分别为1F ,2F P 是C 上一点,且1F P ⊥2F P .若12PF F △的面积为4,则a =( )A .1B .2C .4D .83.椭圆()222210x y a b a b+=>>的左、右焦点分别为1F ,2F ,椭圆上的点M 满足:1260F MF ∠=︒,且122MF MF ⋅=,则b =( )A .1BC .2. 4.已知对任意正实数m ,n ,p ,q ,有如下结论成立:若m p n q=,则有m p m pn q n q +==+成立,现已知椭圆22221x y a b+=上存在一点P ,1F ,2F 为其焦点,在12PF F △中,1215PF F ∠=︒,2175PF F ∠=︒,则椭圆的离心率为( )A .12B .2C .3D .25.已知椭圆22:14924x y C +=的左,右焦点分别为12,F F ,若C 上的点A 到2F 的距离为6,则△12AF F 的面积为( ) A .48B .25C .24D .126.已知1F ,2F 分别是椭圆22221(0)x y a b a b+=>>的左、右焦点,若椭圆上存在点P ,使得120PF PF ⋅=,则该椭圆的离心率的取值范围是( )A .B .(0,]2C .12⎡⎢⎣⎦D .22⎣⎦7.设椭圆22221x y a b+=()0a b >>的两焦点为1F ,2F ,若椭圆上存在点P ,使12120F PF ∠=︒,则椭圆的离心率e 的最小值为( )A .12B .2C D 8.已知点F 1,F 2分别是椭圆C 1和双曲线C 2的公共焦点,e 1,e 2分别是C 1和C 2的离心率,点P 为C 1和C 2的一个公共点,且1223F PF π∠=,若(22e ∈,则e 1的取值范围是( )A .⎝⎭B .⎝⎭C .⎝⎭D .⎝⎭9.设12,F F 是双曲线22124y x -=的两个焦点,P 是双曲线上的一点,且1234PF PF =,则12PF F △的面积等于( )A ...24 D .4810.设1F 、2F 分别为双曲线()222210,0x y a b a b -=>>的左、右焦点,双曲线上存在一点P 使得123PF PF b +=,1294PF PF ab ⋅=,则该双曲线的离心率为( )A .43B .53C .94D .311.已知点P 是双曲线22184x y -=上一点,1F ,2F 分别为双曲线的左、右焦点,若12F PF △的外接圆半径为4,且12F PF ∠为锐角,则12PF PF ⋅=( ) A .15B .16C .18D .2012.设1F ,2F 分别是双曲线2219y x -=的左右焦点.若点P 在双曲线上,且120PF PF ⋅=,则12PF PF +等于( )A .BC .D .13.已知双曲线E :22221x y a b-=(0a >,0b >)的左、右焦点分别为1F ,2F ,点M 在双曲线E 的右支上,若12,43F MF ππ⎡⎤∠∈⎢⎥⎣⎦,则12MF MF ⋅的取值范围是( )A .22,2b ⎤⎦B .222,1)b b ⎡⎤⎣⎦ C .221),b b ⎡⎤⎣⎦ D .221)b b ⎡⎤⎣⎦14.已知双曲线C 的焦点为1F ,2F ,点P 为双曲线上一点,若212PF PF =,1260PF F ∠=︒,则双曲线的离心率为( )A B .2C D .12+ 15.已知F 1,F 2是双曲线E :22221x y a b-=的左,右焦点,点M 在E 上,M F 1与x 轴垂直,sin 2113MF F ∠= ,则E 的离心率为( )A B .32C .2 16.已知1F ,2F 是双曲线E :22221(0,0)x y a b a b -=>>的左、右焦点,点M 在E 上,1MF 与x 轴垂直,211sin 4MF F ∠=,则双曲线E 的离心率为( )A B .53C .2D .317.已知椭圆22194x y +=的两个焦点是1F 、2F ,点M 是椭圆上一点,且122MF MF -=,则12F F M△的面积是______.18.设P 是椭圆221169x y +=上一点,12,F F 分别是椭圆的左、右焦点,若12||.||12PF PF =,则12F PF ∠的大小_____.19.已知12,F F 是椭圆222:13x y E a +=的左,右焦点,点M 在E 上,且1223F MF π∠=,则12F MF △的面积为______.。
有关圆锥曲线的焦点三角形面积公式的证明及其应用

圆锥曲线的焦点三角形面积问题比较常见,这类题目常以选择题、填空题、解答题的形式出现.圆锥曲线主要包括抛物线、椭圆、双曲线,每一种曲线的焦点三角形面积公式也有所不同,其适用情形和应用方法均不相同.在本文中,笔者对圆锥曲线的焦点三角形面积公式及其应用技巧进行了归纳总结,希望对读者有所帮助.1.椭圆的焦点三角形面积公式:S ΔPF 1F 2=b 2tan θ2若椭圆的标准方程为x 2a 2+y 2b2=1(a >b >0),∠F 1PF 2=θ,则三角形ΔF 1PF 2的面积为:S ΔPF 1F 2=b 2tan θ2.对该公式进行证明的过程如下:如图1,由椭圆的定义知||F 1F 2=2c ,||PF 1+||PF 2=2a ,图1可得||PF 12+2||PF 1||PF 2+||PF 22=4a 2,①由余弦定理可得||PF 12+||PF 22-2||PF 1||PF 2cos θ=4c 2,②①-②可得:2||PF 1||PF 2(1+cos θ)=4b 2,所以||PF 1||PF 2=2b 21+cos θ,则S ΔPF 1F2=12|PF 1||PF 2|sin θ=12×2b 21+cos θsin θ,=b 22sin θ2cos 2θ22cos 2θ2=b 2tan θ2.若已知椭圆的标准方程、短轴长、两焦点弦的夹角,则可运用椭圆的焦点三角形面积公式S ΔPF 1F 2=b 2tan θ2来求椭圆的焦点三角形面积.例1.(2021年数学高考全国甲卷理科)已知F 1,F 2是椭圆C :x 216+y 24=1的两个焦点,P ,Q 为椭圆C 上关于坐标原点对称的两点,且||PQ =||F 1F 2,则四边形PF 1QF 2的面积为________.解析:若采用常规方法解答本题,需根据椭圆的对称性、定义以及矩形的性质来建立关于||PF 1、||PF 2的方程,通过解方程求得四边形PF 1QF 2的面积.而仔细分析题意可发现四边形PF 1QF 2是一个矩形,且该矩形由两个焦点三角形构成,可利用椭圆的焦点三角形面积公式求解.解:S 四边形PF 1QF 2=2S ΔPF 1F 2=b 2tan θ2=2×4×tan π2=8.利用椭圆的焦点三角形面积公式,能有效地简化解题的过程,有助于我们快速求得问题的答案.例2.已知F 1,F 2是椭圆C:x 2a 2+y 2b2=1()a >b >0的两个焦点,P 为曲线C 上一点,O 为平面直角坐标系的原点.若PF 1⊥PF 2,且ΔF 1PF 2的面积等于16,求b的值.解:由PF 1⊥PF 2可得∠F 1PF 2=π2,因为ΔF 1PF 2的面积等于16,所以S ΔPF 1F 2=b 2tan θ2=b 2tan π2=16,解得b =4.有关圆锥曲线的焦点三角形面积公式的思路探寻48的面积,2.则ΔF 1PF 如|||PF 1-|得:|||PF 2cos θ即|由②所以则S Δ夹角、例3.双曲线C 是().A.72且)设双曲F 1,F 2,离△PF 1F 2=1.本题.运用该=p 22sin θ,且与抛S ΔAOB =图3下转76页)思路探寻49考点剖析abroad.解析:本句用了“S+Vt+动名词”结构,能用于此结构的及物动词或词组有mind ,enjoy ,finish ,advise ,consider ,practice ,admit ,imagine ,permit ,insist on ,get down to ,look forward to ,put off ,give up 等。
圆锥曲线焦点三角形推导
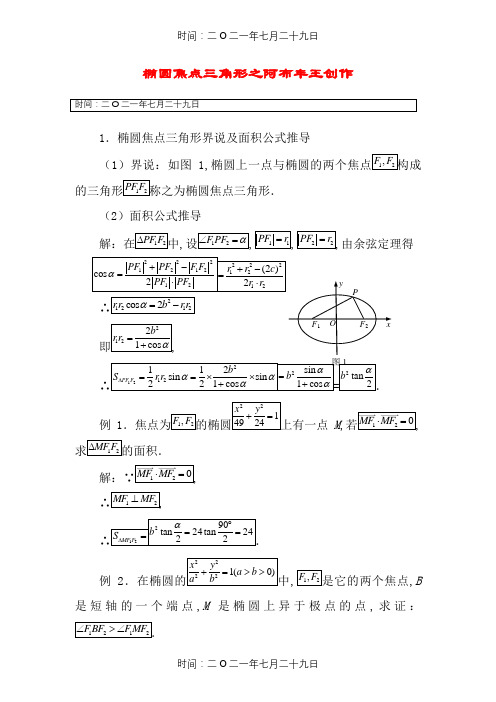
∴ ,
∴ .
例2.在椭圆的 中, 是它的两个焦点,B是短轴的一个端点,M是椭圆上异于极点的点,求证: .
证明:如图2,设M的纵坐标为 ,
∵ ,
∴ ,
即 ,
又 都是锐角,
故
从而有 .
2.双曲线焦点三角形界说及面积公式推导.
(1)界说:如图3,双曲线上一点P与双曲线的两个焦点 构成的三角形 称之为双曲线焦点三角形.
∵ ,
∴ ,
∴ .
开拓:从上例我们不难发现,若椭圆 和双曲线 有公共的焦点 和公共点P,那么 的面积 ,又 ,从而 ,即 .
时间:二O二一年七月二十九日
椭圆焦点三角形之阿布丰王创作
时间:ቤተ መጻሕፍቲ ባይዱO二一年七月二十九日
1.椭圆焦点三角形界说及面积公式推导
(1)界说:如图1,椭圆上一点与椭圆的两个焦点 构成的三角形 称之为椭圆焦点三角形.
(2)面积公式推导
解:在 中,设 , , ,由余弦定理得
∴
即 ,
∴ = .
例1.焦点为 的椭圆 上有一点M,若 ,求 的面积.
(2)面积公式推导:
解:在 中,设 , , ,由余弦定理得
∴
即 ,
∴ = .
例3、已知双曲线 ,设 是双曲线得两个焦点.点P在双曲线上, ,求 的年夜小.
解:双曲线的标准方程为 ,
∴ ,
从而有 = ,
∴ ,
∴ .
例4:椭圆 与双曲线 的公共焦点为 ,P是两曲线的一个交点,求 的值.
解:在椭圆和双曲线中异算 面积
专题15圆锥曲线焦点三角形微点3圆锥曲线焦点三角形内切圆问题

专题15 圆锥曲线焦点三角形微点3 圆锥曲线焦点三角形内切圆问题1e+图2二、椭圆焦点三角形内切圆的重要性质的应用(一) 定值问题1.已知椭圆2212516x y +=左、右焦点分别为PF F △的内心为I ,则2PI PF ⋅= (二) 轨迹问题4.已知椭圆()222210x y a b a b +=>>左、右焦点分别为动点,12PF F △的内心为I ,求点I 的轨迹方程.圆锥曲线的定义、曲线方程、性质存在着诸多联系,很多性质并不是孤立的,所以我们可以试着将椭圆焦点三角形内切圆性质研究思路应用到双曲线中,面我们研究双曲线焦点三角形内切圆的性质.图6 图7【性质2】双曲线C 的标准方程为焦点,P 为双曲线C 上异于实轴端点的任意一点,12PF F ∆三边相切于点,,D E H .设11,I x a F D F H a c ===+.参考答案:2.13【详解】设12,.PF n PF m ==则2m n +=根据垂心和内心的性质知(113PG PF PF =+故()()(112226IG c n m PF c m a c ⎡=+-++⎣+5.D【分析】设三角形内切圆的切点为A ,B ,C ,其中2121||||||||F C F C F A F B -=-,又AP PB =,所以2||F C 又2112||||||10F C F C F F +==,由此能求出圆心I 到y 轴的距离.【详解】解:因为双曲线221169x y -=,所以4,a b =设三角形内切圆的切点为A ,B ,C ,其中C 在由内切可得,1122||||,||||,|F B F C F A F C BP ==那么2121||||||||F C F C F A F B -=-,又1|||F P -所以21212F C F C F A F B F A AP -=-=+-又21122210,1F C F C F F c F C +====,7.C【分析】由已知点的坐标求得计算.【详解】()22,5P 在双曲线如图,设(),0M x ,内切圆与x 8.B【分析】设12PF F △的内切圆圆心为I 切线段长相等及双曲线的定义,可得段2OF 中点,可得2c a =,从而可得离心率根据椭圆的定义知122PF PF +=∴121PF PF F E PE PD DF +=-++12222F F F G a =+=, ∴22F G =∴点M 在x 轴上的射影是右顶点故选:A故I 是△1ABF 的重心,即11AIF BIF AIB S S S == ,又所以11222PIF F IF PIF S S S == ,而I 是12PF F △的内心,则由21212||||,||2c PF PF a F F -==,则2||2PF a =,故故选:D【点睛】关键点点睛:利用向量的线性关系构造重心,结合重心和内心的性质得到1122||||2||PF F F PF ==,再根据双曲线定义得到双曲线参数的齐次方程【详解】的内切圆圆心为I ,且与三边相切于点AN ,11F Q F M =,22F M F N =,由双曲线定义知:122AF AF a -=,212122AF F Q F N F M F M a =-=-=,又18.2【分析】首先确定P 点在左支上,作出PF △证明点A 为双曲线的左顶点,从而根据tan从而得到33c a c a +=-,求出离心率.【详解】因为1221tan3tan 22PF F PF F ∠∠=,所以所以122122PF F PF F ∠∠>,故P 点在左支上,2 12由三角形内切圆的性质知:12PF PF HF -=又122HF HF c +=②,11HF c =+③,由①②③得:1a =.∴223c a b =+=,故离心率3c e a==.故答案为:3。
焦点三角形问题(解析版)
第一篇圆锥曲线专题01焦点三角形问题焦点三角形的边角关系如下:三条边:122F F c =122PF PF a+==22a c +三角形周长ce a=222a b c =+三个角:随着动点P 的移动,三个角都在变化,可能为锐角,直角和钝角,这里我们只研究顶角P ∠,利用余弦定理,P ∠又和三边a,b,c 的大小有关系三角形的面积:12S ah =底为定值,面积最大时高最大1sin 2S ab c =面积和三边长有关系一、与焦点三角形边长有关的问题焦点三角形中三边长涉及a,c ,因此最直观的是可以根据三边关系求出离心率的值或取值范围,前提是三边之间存在可以转化的关系。
若单独分析三角形的两个腰长,则若能够构成三角形,则需满足1a c PF a c-≤≤+例1椭圆22221x y a b+=的右焦点为F ,其右准线与x 轴的交点为A ,在椭圆上存在一点P ,满足线段AP 的垂直平分线过点F ,则椭圆的离心率的取值范围是________.例2.已知12,F F 是椭圆22221x y a b+=的左右焦点,若在其右准线上存在点P ,使得线段1PF 的中垂线过点2F ,则椭圆的离心率的取值范围是________.【解析】求离心率的范围问题,需要根据条件列出不等式,在含有动点的题目中,需要找出动态的量和常量之间的大小关系。
题目中:2122PF F F c==因为点P 在右准线上下移动,2PF 虽然是常量,但由于不知道a,b,c 的关系,因此还是相对的变量。
本题的定值为22a F H c c=-在2RT PHF 中,222,2a PF F H c c c >≥-解得:313e ≤<例3.设12,F F 是双曲线2214x y -=的左右焦点,点P 在双曲线上,且满足1290F PF ︒∠=,则12PF F ∆的面积是________.方法一:方法二:此题目有更简单的做法,方法一只是为了巩固焦半径的知识,设12,PF x PF y ==则有:4x y -=,又因为2220x y +=解得:2xy =,因此面积等于1.上面两题都是关于焦点三角形中两条腰长的问题,在焦点三角形中两腰长之和为2a ,底边为2c ,因此三边之间暗含离心率的关系,因此在一些出现焦点三角形求离心率的问题中一般腰长和底边之间都存在一个可以互相转化的关系,通过这个关系可以求出离心率。
高中数学之圆锥曲线之焦点三角形面积知识点
高中数学之圆锥曲线之焦点三角形面积知识点
什么是焦点三角形?
定义:
椭圆(双曲线)上任意一点与两个焦点所组成的三角形叫做焦点三角形,它是由焦距和焦半径构成的特别的三角形。
其中焦点三角形的面积也是一个非常重要的几何量。
怎么求焦点三角形的面积呢?先看一道例题
公式推导:
同样的方法可以也可以证明得到双曲线的焦点三角形面积公式。
公式如下:
接下来在给出关于焦点三角形顶角的一个结论:
这个结论可以借助焦点三角形面积公式的推导过程来继续说明:
实战演练:。
圆锥曲线中焦点三角形几个问题的解法
刘 豪
(靖江市第三中学 ,江苏 泰州 214500)
摘 要 :焦点三角形是圆锥曲线的两个焦点与圆锥曲线上的任意一点组成的三角形 ,它在圆锥曲线中有着重要 的地位 。详细介绍如何求焦点三角形的周长 面积及和焦点三角形相关的最值问题 。
关键词 :圆锥曲线 ;焦点三角形 ;解法 中图分类号 : G633. 65 文献标志码 : A 文章编号 : 1008 - 6714 (2008) 04 - 0086 - 02
= b2
tan
θ ,
在双曲线里焦点三角形的面积
S
= b2
co t
θ。
2
2
注 : (1)此结论称为圆锥曲线焦点三角形面积公式。
( 2)此结论可用于客观题的解题 。在解圆锥曲线的问题
中 ,有些选择题或填空题 ,如果用常规方法去解题 , 无疑是
小题大做 ,这在考试特别是高考中 , 是非常不可取的 。运
用特殊解法 ,显得很重要 ,不但可以节省时间 , 还可提高答
PF1 - PF2 = ±2a
PF1 2 + PF2 2 - 2 PF1 · PF2 cos60°= ( 2c) 2 解得 PF1 · PF2 = 64
所以
S△PF1 F2
=
1 2
× PF1
·
PF2
sin60°= 1 2
×64 ×
3 2
= 16
3
如为客观题 , 可直接代入焦点三角形面积公式得 :
S△PF1F2 = 16 3 小结 : ( 1)求椭圆和双曲线的焦点三角形面积 , 需要
即 △F1 PF2 的周长无最大值 。 小结 :解和焦点三角形有关的最值问题 ,主要是利用
圆锥曲线的第一定义 ,并借助正弦定理 余弦定理以及均
焦点三角形公式推导
焦点三角形公式推导在我们学习圆锥曲线的时候,焦点三角形可是个经常出现的“家伙”。
今天咱们就来好好推导一下焦点三角形的公式,瞧瞧它背后的小秘密。
先来说说啥是焦点三角形。
在圆锥曲线中,比如椭圆或者双曲线,以两个焦点和曲线上一点构成的三角形就叫焦点三角形。
咱以椭圆为例来推导这个公式。
假设椭圆的标准方程是$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$($a>b>0$),两个焦点分别是$F_1$,$F_2$,椭圆上一点是$P$。
在推导之前,咱们先回忆一下椭圆的定义:椭圆上任意一点到两个焦点的距离之和等于长轴$2a$。
那在焦点三角形$PF_1F_2$中,根据余弦定理可得:$|F_1F_2|^2 = |PF_1|^2 + |PF_2|^2 - 2|PF_1||PF_2|\cos\theta$其中,$\theta$是$\angle F_1PF_2$。
因为$|PF_1| + |PF_2| = 2a$,所以$|PF_1|^2 + |PF_2|^2 + 2|PF_1||PF_2| = 4a^2$将其变形可得:$|PF_1|^2 + |PF_2|^2 = 4a^2 - 2|PF_1||PF_2|$把这个式子代入上面的余弦定理式子中:$4c^2 = 4a^2 - 2|PF_1||PF_2| - 2|PF_1||PF_2|\cos\theta$整理一下就得到:$|PF_1||PF_2| = \frac{2b^2}{1 + \cos\theta}$这就是焦点三角形在椭圆中的一个重要公式啦。
那双曲线中的焦点三角形公式又是咋样的呢?其实推导过程和椭圆有点类似。
假设双曲线的标准方程是$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$,两个焦点还是$F_1$,$F_2$,双曲线上一点是$P$。
同样根据双曲线的定义,双曲线上任意一点到两个焦点的距离之差的绝对值等于实轴$2a$,即$||PF_1| - |PF_2|| = 2a$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆焦点三角形
椭圆(双曲线)上一点和两焦点组成的三角形叫焦点三角形;有一个角为直角的焦点三角形叫焦点直角三角形。
1、椭圆焦点三角形中,顶点在椭圆上的点到另两点的张角中,以短轴端点到这两点的张角最大。
证法一:设P 是椭圆22
2
21x y a b += (0a b >>,c 为半焦距)上的一点,O 为原点,E 、F 是椭圆的两焦点,PE m =,PF n = 则222222244222cos 1122m n c b mn b b EPF mn mn mn a +--∠===-≥-,由余弦函数图象性质知EPF ∠的最大值为2
22arccos(1)
b a -,当且仅当P 在短轴端点时取到该最大值。
证法二:如图1,设M 的纵坐标为0y ,
∵21210212121
21MF F F BF S y F F b F F S ∆∆=⋅>⋅=,
∴221212tan tan 22F BF F MF b b ∠∠>, 即1212tan tan 22
F BF F MF
∠∠>,
又121211,22F BF F MF ∠∠都是锐角,故121211
22
F BF F MF ∠>∠ 从而有1212F BF F MF ∠>∠. 证法三:设),(o o y x P ,由焦半径公式可知:o ex a PF +=1,o ex a PF -=1
在21PF F ∆中,2
12
2
121212cos PF PF F F PF PF -+=
θ2
12
21221242)(PF PF c PF PF PF PF --+=
1))((2412442
2122--+=--=o o ex a ex a b PF PF c a =122
22
2--o
x e a b a x a ≤≤-0 22
a x o ≤∴
2、椭圆焦点三角形定义及面积公式推导
解:在12PF F ∆中,设12F PF α∠=,11PF r =,22PF r =,由余弦定理得
2
2
2
1212
12
cos 2PF PF F F PF PF α+-=
⋅222
12
12
(2)
2r r c r r +-=
⋅ 2
2
121212()242r r r r c r r +--=
2
2
1212
(2)242a rr c rr --=
2
2
12124()22a c r r r r --=
2
1212
2b r r r r -= ∴2
1212
cos 2rr b rr α=- 即2
1221cos b r r α=+, ∴12
2
12112sin sin 221cos PF F b S r r ααα
∆==⨯⨯+2sin 1cos b αα=+=2tan 2b α.
3、已知椭圆方程为),0(122
22>>=+b a b
y a x 两焦点分别为,,21F F 设焦点三角形21F PF 中,21θ=∠PF F 则
图2
F 1 x
y
O P
F 2
图1 F 1 x
y
O
M
F 2
B
.21cos 2e -≥θ
证明:设,,2211r PF r PF ==则在21PF F ∆中,由余弦定理得:
1222242)(2cos 2
12221221221212
212221--=--+=-+=r r c a r r c r r r r r r F F r r θ
.2112221)
2
(2222
2
2222122e a c a r r c a -=--=-+-≥ 4、已知椭圆方程为),0(122
22>>=+b a b
y a x 两焦点分别为,,21F F 设焦点三角形21F PF ,
,,1221βα=∠=∠F PF F PF 则椭圆的离心率β
αβαsin sin )
sin(++=
e 。
证明:
β
α
βαsin sin )
180sin(122
1PF PF F F o =
=
-- 由等比定理得:
β
αβαsin sin )
sin(2121++=
+PF PF F F
而
)sin(2)sin(2
1βαβα+=+c F F ,βαβαsin sin 2sin sin 21+=
++a PF PF ∴βαβαsin sin )sin(++==a c e 。
5、双曲线焦点三角形定义及面积公式推导.
解:在12PF F ∆中,设12F PF α∠=,11PF r =,22PF r =,由余弦定理得
2
2
2
1212
12
cos 2PF PF F F PF PF α+-=
⋅222
1212
(2)2r r c r r +-=
⋅ 22121212()242r r r r c r r -+-=22
1212(2)242a rr c r r +-=2212122()r r c a r r --=21212
2r r b r r -= ∴21212cos 2rr rr b α=-
即21221cos b r r α=-, ∴122
12112sin sin 221cos PF F b S r r ααα
∆==⨯⨯-2sin 1cos b αα=-=2cot 2b α.
图3
F 1 x
y
O
P
F 2。
