经典的滤波电路(值得收藏)
电源工程师必看:各种滤波电路合集!(很全)

电源工程师必看:各种滤波电路合集!(很全)整流电路输出电压是单向脉动性电压,不能直接给电子电路使用。
所以要对输出的电压进行滤波,消除电压中的交流成分,成为直流电后给电子电路使用。
在滤波电路中,主要使用对交流电有特殊阻抗特性的器件,如:电容器、电感器。
本文将对各种形式的滤波电路进行分析。
一、滤波电路种类滤波电路主要有下列几种:电容滤波电路,这是最基本的滤波电路;π型RC滤波电路;π型LC滤波电路;电子滤波器电路。
二、滤波原理1.单向脉动性直流电压的特点图1(a)所示是单向脉动性直流电压波形,从图中可以看出,电压的方向性无论在何时都是一致的,但在电压幅度上是波动的,就是在时间轴上,电压呈现出周期性的变化,所以是脉动性的。
但根据波形分解原理可知,这一电压可以分解成一个直流电压和一组频率不同的交流电压,如图1(b)所示。
在图1(b)中,虚线部分是单向脉动性直流电压U o中的直流成分,实线部分是U o中的交流成分。
图1:单向脉动性电压的分解2.电容滤波原理根据以上的分析,由于单向脉动性直流电压可分解成交流和直流两部分。
在电源电路的滤波电路中,利用电容器的“隔直通交”的特性和储能特性,或者利用电感“隔交通直”的特性可以滤除电压中的交流成分。
图2所示是电容滤波原理图。
图2(a)为整流电路的输出电路。
交流电压经整流电路之后输出的是单向脉动性直流电,即电路中的U o。
图2(b)为电容滤波电路。
由于电容C1对直流电相当于开路,这样整流电路输出的直流电压不能通过C1到地,只有加到负载R L上。
对于整流电路输出的交流成分,因C1容量较大,容抗较小,交流成分通过C1流到地端,而不能加到负载R L。
这样,通过电容C1的滤波,从单向脉动性直流电中取出了所需要的直流电压+U。
滤波电容C1的容量越大,对交流成分的容抗越小,使残留在负载R L上的交流成分越小,滤波效果就越好。
图2:电容滤波原理图3.电感滤波原理图3所示是电感滤波原理图。
常见的滤波电路有哪些

常见的滤波电路有哪些在电子领域中,滤波电路是一种能够选择性地传递或抑制特定频率组分的电路。
它在各种电子设备中都扮演着重要的角色,用于去除噪音、解调信号、分离频率等。
下面将介绍几种常见的滤波电路及其特点。
1. 低通滤波器低通滤波器是一种能够通过低频信号而抑制高频信号的电路。
它在音频设备、通信系统等领域有广泛应用。
常见的低通滤波器包括RC低通滤波器、LC低通滤波器以及巴特沃斯低通滤波器等。
RC低通滤波器简单实用,适用于一些简单的信号处理需求;LC 低通滤波器具有更好的性能,适用于高频信号的处理;巴特沃斯低通滤波器具有更陡的衰减特性,常用于要求严格的通信系统中。
2. 高通滤波器高通滤波器则是相反的,能够通过高频信号而抑制低频信号。
它在音频均衡器、高速数据传输系统等方面有应用。
常见的高通滤波器包括RC高通滤波器、LC高通滤波器以及巴特沃斯高通滤波器等。
它们在不同场景下发挥着各自的优势,如RC高通滤波器简单易实现,LC高通滤波器性能更稳定,而巴特沃斯高通滤波器衰减特性更陡。
3. 带通滤波器带通滤波器是一种只允许特定频率范围信号通过的滤波电路。
它在频率分割、通信系统等方面有广泛的应用。
常见的带通滤波器包括陷波滤波器、共振器等。
陷波滤波器能够抑制指定频率附近的信号,常用于噪声消除;共振器则能够放大特定频率的信号,常用于电子仪器的频率选择。
4. 带阻滤波器带阻滤波器是一种能够抑制特定频率范围内信号而放行其他频率的滤波电路。
它在信号捕获、频率选择等方面有重要应用。
常见的带阻滤波器包括陷波滤波器、巴特沃斯带阻滤波器等。
陷波滤波器能够抑制指定频率的信号,常应用于干扰抑制;巴特沃斯带阻滤波器具有更陡的衰减特性,适用于高要求的信号处理场合。
总结不同类型的滤波器在电子领域中各有其独特作用,可以根据具体需求选择合适的滤波电路。
除了上述提到的常见滤波器外,还有许多其他类型的滤波电路,如梳状滤波器、数字滤波器等。
熟练掌握各类滤波器的原理和特点,对于电子工程师而言是非常重要的。
常见运放滤波电路

滤波电路这节非常深入地介绍了用运放组成的有源滤波器。
在很多情况中,为了阻挡由于虚地引起的直流电平,在运放的输入端串入了电容。
这个电容实际上是一个高通滤波器,在某种意义上说,像这样的单电源运放电路都有这样的电容。
设计者必须确定这个电容的容量必须要比电路中的其他电容器的容量大100倍以上。
这样才可以保证电路的幅频特性不会受到这个输入电容的影响。
如果这个滤波器同时还有放大作用,这个电容的容量最好是电路中其他电容容量的1000 倍以上。
如果输入的信号早就包含了VCC/2 的直流偏置,这个电容就可以省略。
这些电路的输出都包含了VCC/2 的直流偏置,如果电路是最后一级,那么就必须串入输出电容。
这里有一个有关滤波器设计的协定,这里的滤波器均采用单电源供电的运放组成。
滤波器的实现很简单,但是以下几点设计者必须注意:1. 滤波器的拐点(中心)频率2. 滤波器电路的增益3. 带通滤波器和带阻滤波器的的Q值4. 低通和高通滤波器的类型(Butterworth 、Chebyshev、Bessell)不幸的是要得到一个完全理想的滤波器是无法用一个运放组成的。
即使可能,由于各个元件之间的负杂互感而导致设计者要用非常复杂的计算才能完成滤波器的设计。
通常对波形的控制要求越复杂就意味者需要更多的运放,这将根据设计者可以接受的最大畸变来决定。
或者可以通过几次实验而最终确定下来。
如果设计者希望用最少的元件来实现滤波器,那么就别无选择,只能使用传统的滤波器,通过计算就可以得到了。
3.1 一阶滤波器一阶滤波器是最简单的电路,他们有20dB 每倍频的幅频特性3.1.1 低通滤波器典型的低通滤波器如图十三所示。
图十三3.1.2 高通滤波器典型的高通滤波器如图十四所示。
图十四3.1.3 文氏滤波器文氏滤波器对所有的频率都有相同的增益,但是它可以改变信号的相角,同时也用来做相角修正电路。
图十五中的电路对频率是F 的信号有90 度的相移,对直流的相移是0度,对高频的相移是180度。
一阶rcr滤波电路

一阶rcr滤波电路一阶RCR滤波电路是一种经典的滤波电路,常用于对信号进行滤波和去噪。
在这篇文章中,我们将介绍一阶RCR滤波电路的原理、特点和应用。
一阶RCR滤波电路由一个电阻(R)、一个电容(C)和一个电感(L)组成。
它的原理是通过电阻、电容和电感的组合,实现对信号的频率进行选择性的衰减或增强。
具体来说,当信号的频率高于或低于一定的截止频率时,滤波电路会对信号进行衰减,从而实现对噪声的去除或信号的滤波。
一阶RCR滤波电路的特点有以下几个方面。
首先,它是一个线性滤波器,具有简单的电路结构和低成本的特点。
其次,它可以实现对特定频率范围内信号的滤波,具有较好的频率选择性。
此外,一阶RCR滤波电路还可用于对信号的幅度进行增益或衰减,具有一定的放大或衰减作用。
一阶RCR滤波电路在实际应用中具有广泛的用途。
首先,它常用于音频设备中,用于对音频信号进行去噪和滤波处理,提高音质和音量清晰度。
其次,一阶RCR滤波电路也常用于通信系统中,用于对信号进行预处理,提高信号质量和传输效果。
此外,一阶RCR滤波电路还可用于电源滤波,对电源信号进行稳压和去除纹波噪声。
在使用一阶RCR滤波电路时,需要注意一些问题。
首先,电阻、电容和电感的数值选择要合理,以满足滤波效果的要求。
其次,一阶RCR滤波电路的截止频率和衰减特性需要根据具体应用场景进行调整和优化。
此外,一阶RCR滤波电路对信号的相位会引起一定的延迟,需要在实际应用中进行补偿。
总结起来,一阶RCR滤波电路是一种常用的滤波电路,具有简单、低成本和频率选择性好的特点,广泛应用于音频设备、通信系统和电源滤波等领域。
在实际应用中,需要根据具体需求选择合适的电阻、电容和电感数值,并进行相应的调整和优化。
通过合理使用一阶RCR滤波电路,可以实现对信号的滤波、去噪和增益,提高信号质量和系统性能。
电子滤波器电路图大全(七款电子滤波器电路设计原理图详解)
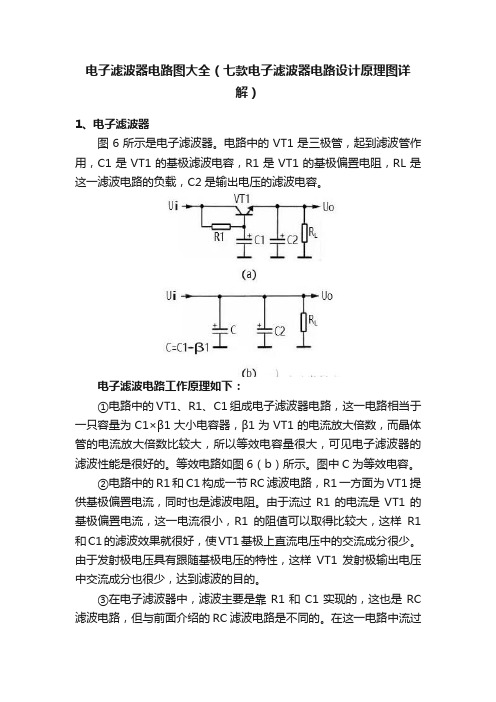
电子滤波器电路图大全(七款电子滤波器电路设计原理图详解)1、电子滤波器图6所示是电子滤波器。
电路中的VT1是三极管,起到滤波管作用,C1是VT1的基极滤波电容,R1是VT1的基极偏置电阻,RL是这一滤波电路的负载,C2是输出电压的滤波电容。
电子滤波电路工作原理如下:①电路中的VT1、R1、C1组成电子滤波器电路,这一电路相当于一只容量为C1×β1大小电容器,β1为VT1的电流放大倍数,而晶体管的电流放大倍数比较大,所以等效电容量很大,可见电子滤波器的滤波性能是很好的。
等效电路如图6(b)所示。
图中C为等效电容。
②电路中的R1和C1构成一节RC滤波电路,R1一方面为VT1提供基极偏置电流,同时也是滤波电阻。
由于流过R1的电流是VT1的基极偏置电流,这一电流很小,R1的阻值可以取得比较大,这样R1和C1的滤波效果就很好,使VT1基极上直流电压中的交流成分很少。
由于发射极电压具有跟随基极电压的特性,这样VT1发射极输出电压中交流成分也很少,达到滤波的目的。
③在电子滤波器中,滤波主要是靠R1和C1实现的,这也是RC 滤波电路,但与前面介绍的RC滤波电路是不同的。
在这一电路中流过负载的直流电流是VT1的发射极电流,流过滤波电阻R1的电流是VT1基极电流,基极电流很小,所以可以使滤波电阻R1的阻值设得很大(滤波效果好),但不会使直流输出电压下降很多。
④电路中的R1的阻值大小决定了VT1的基极电流大小,从而决定了VT1集电极与发射极之间的管压降,也就决定了VT1发射极输出直流电压大小,所以改变R1的大小,可以调整直流输出电压V的大小。
2、电子稳压滤波器图7所示是另一种电子稳压滤波器,与前一种电路相比,在VT1基极与地端之间接入了稳压二极管VD1。
电子稳压原理如下:在VT1基极与地端之间接入了稳压二极管VD1后,输入电压经R1使稳压二极管VD1处于反向偏置状态,此时VD1的稳压特性使VT1管的基极电压稳定,这样VT1发射极输出的直流电压也比较稳定。
经典常用滤波电路26页PPT

ห้องสมุดไป่ตู้
•
30、风俗可以造就法律,也可以废除 法律。 ——塞·约翰逊
经典常用滤波电路
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
•
26、我们像鹰一样,生来就是自由的 ,但是 为了生 存,我 们不得 不为自 己编织 一个笼 子,然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理,即使延续时 间再长 ,也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
•
29、在一切能够接受法律支配的人类 的状态 中,哪 里没有 法律, 那里就 没有自 由。— —洛克
常用滤波电路

常用滤波电路概述在电子电路设计中,滤波电路是非常重要的一部分。
它主要用于过滤信号中的杂散成分,提取出我们感兴趣的部分,保证信号传输的质量和可靠性。
常用滤波电路可以分为低通滤波、高通滤波、带通滤波和带阻滤波。
本文将详细介绍这些常用滤波电路的工作原理、电路结构以及在实际应用中的具体应用场景。
低通滤波器低通滤波器是一种将高频信号部分通过,而低频信号部分被抑制的滤波器。
它在实际电路设计中应用广泛,用于滤除高频噪声,提取出低频信号。
RC低通滤波器RC低通滤波器是一种简单的滤波电路,由一个电阻和一个电容组成。
其工作原理基于电容器对高频信号的阻抗较低,从而将高频信号绕过电阻,使之减小。
而对于低频信号,电容器的阻抗较高,导致大部分信号通过电阻流入地。
因此,RC低通滤波器可以将高频信号滤除,留下低频信号。
RC低通滤波器的传递函数为:H(s)=1 RC s+1RC其中,s为复变量,s=jω,j为虚数单位,ω为角频率。
LC低通滤波器LC低通滤波器由一个电感和一个电容组成。
其工作原理基于电容器对高频信号的阻抗较低,电感对高频信号的阻抗较高,从而将高频信号滤除。
与RC低通滤波器相反,LC低通滤波器的传递函数为:H(s)=1LCs2+RCs+1高通滤波器高通滤波器与低通滤波器相反,它主要用于滤除低频信号,保留高频信号。
RC高通滤波器与RC低通滤波器类似,RC高通滤波器也由一个电阻和一个电容组成。
但是,RC高通滤波器的电阻和电容的位置互换了。
其工作原理是对于低频信号,电容器的阻抗较高,导致大部分信号通过电容器流入地;而对于高频信号,电容器的阻抗较低,从而将其中的信号绕过电容器。
LC高通滤波器LC高通滤波器由一个电感和一个电容组成。
与LC低通滤波器相似,但是电感和电容的位置互换了。
其工作原理是对于低频信号,电感对其具有较高的阻抗,使之通过电容器流入地;而对于高频信号,由于电感对其具有较低的阻抗,使其通过电感器流入负载。
带通滤波器带通滤波器可以滤除某一频率范围之外的信号,保留其中的频率范围。
常见的滤波电路.ppt.ppt

有源滤波器实际上是一种具有特定频率响应的 放大器。它是在运算放大器的基础上增加一些 R 、 C等无源元件而构成的。 低通滤波器(LPF) 高通滤波器(HPF) 带通滤波器(BPF) 带阻滤波器(BEF)
低通滤波器的主要技术指标 (1)通带增益Avp
通带增益是指滤波器在通频带内的电压放大 倍数,性能良好的 LPF 通带内的幅频特性曲线 是平坦的,阻带内的电压放大倍数基本为零。
N节点的电流方程
R R f/ 1 A s 传递函数为 v 1 1 1 2 1 sC R R ( ) s C C R R 2 2 f 1 2 2 f R 1 R 2 R f A v p 频率响应为 A v f 2 1f 1 ( ) j 以上各式中 f Q f 0 0
0 0
A vp A v f 2 f 1( ) j3 f0 f0
fp 2 fp f f 当 p 时,上式分母的模 1 ( ) j3 2 f0 f0
解得截止频率
53 7 0 . 37 f f 0 . 37 f p 0 0 2 2 π RC 与理想的二阶波特图相比,在超过 f 0 以后,
RC低通 电压放大倍数 (传递函数)为
R C
n
+ V 1 1 o . A V V i 1 V j RC 1 SRC i
+ ), n 1 /( RC V o 称特征频率 .
1 V V 0 i 1 SRC
-
3.幅频响应
V A 0(s) A (s) 0 S V i (s) 1
反相型二阶lfp改进型反馈反相二阶lfp由图1n22osvrscsv??传递函数为??f2212f21f221f1111rrccsrrrrrscrrsav??????频率响应为020p1j1ffqffaavv????0fon2n1n1ni??????rsvsvrsvscsvrsvsvn节点的电流方程以上各式中1fprrav??f221021rrccf?2f21f21crrcrrrq?二阶压控型hpf有源高通滤波器由此绘出的频率响应特性曲线1通带增益1fp1rrav2传递函数2pp231scrscraascrsavvv???3频率响应令则可得出频响表达式3121p0vaqcrf???1j1020pffqffaavv????结论
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 f0 2π C1C2 R2 Rf
Rf C1 Avp Q ( R1 ∥ R2 ∥ Rf ) R2 Rf C2 R1
有源高通滤波器
(1)通带增益
Rf Avp = 1 + R1
(2)传递函数
Av ( s) = ( sCR ) 2 Avp 1 (3 Avp ) sCR ( sCR ) 2
二阶压控型低通滤波器
二阶压控型低通有源滤波器中的一个电容器C1原来是接 地的,现在改接到输出端。显然C1的改接不影响通带增益。
二阶压控型LPF
二阶压控型LPF的幅频特性
2.二阶压控型LPF的传递函数
Vo ( s) AvpV( ) ( s) 1 V( ) ( s) VN ( s) 1 sCR
3.频率响应
由传递函数可以写出频率响应的表达式 Avp Av f 2 f 1 ( ) j(3 - Avp ) f0 f0 当 f f 0 时,上式可以化简为
Av ( f f0 )
Avp j(3 - Avp )
定义有源滤波器的品质因数Q值为 f f 0 时的 电压放大倍数的模与通带增益之比
2.同相比例放大器
ui ~
测量u0=?,计算Auf = u0/ui 。
3.跟随器
ui ~
测量u0 =?,计算Auf = u0/ui 。
4.微分电路
ui ┌┑
观察 u0 的输出波形。
有 源 滤 波 电路
滤波器的用途 滤波器是一种能使有用信号通过,滤除信号中无 用频率,即抑制无用信号的电子装置。 例如,有一个较低频率的信号,其中包含一些较高 频率成分的干扰。
有源滤波电路的分类
有源滤波器实际上是一种具有特定频率响应的 放大器。它是在运算放大器的基础上增加一些R、 C等无源元件而构成的。 低通滤波器(LPF) 高通滤波器(HPF) 带通滤波器(BPF) 带阻滤波器(BEF)
RC低通 电压放大倍数 (传递函数)为
R + . Vi C
R1
n
Vo 1 1 AV Vi 1 jRC 1 SRC 1 V 0 Vi 1 SRC
+ n 1 /( RC), . Vo 称特征频率 -
3.幅频响应
V0 ( s) A0 A( s) Vi ( s) 1 S
二阶压控型HPF
(3)频率响应 1 1 ,Q , 则可得出频响表达式 令f 0 2π CR 3 Avp
Av
Avp f0 2 1 f0 1 ( ) j ( ) f Q f
由此绘出的频率响应特性曲线
结论:当 f f 0 时,
幅频特性曲线的斜率 为+40 dB/dec; 当 Avp ≥3时,电 路自激。
电路特点是电路简单,阻 带衰减太慢,选择性较差。
1.通带增益
当 f = 0时,电容视为开路,通 带内的增益为 R
A0 AVF 1
f
1 V P ( s ) Vi ( s ) 1 SRC 2.传递函数 A0 V0 ( s) 1 A( s) AVF Vi ( s) 1 SRC 1 S
(3)通带截止频率
将s换成 jω ,令 0 2π f 0 1/ RC,可得 当 f f p 时,上式分母的模 解得截止频率
Av 1 (
Avp f 2 f ) j3 f0 f0
1 (
fp f0
) j3
2
fp f0
2
53 7 0.37 fp f 0 0.37 f 0 2 2π RC 与理想的二阶波特图相比,在超过 f 0 以后, 幅频特性以-40 dB/dec的速率下降,比一阶的 下降快。但在通带截止频率 f p f 0之间幅频 特性下降的还不够快。
1 2.根据Q值求R1和 Rf ,因为 f f 0 时 Q 3 A 0.7, vP
Av P 1.57,根据 Av P与 R1 、R f 的关系,集成运放 P 1.57 R1
R1 // Rf R R 2R
解得: R 5.51 R, R 3.14 R, R 3.9 k 1 f
N节点的电流方程
Rf / R1 传递函数为 Av s 1 1 1 1 sC2 R2 Rf ( ) s 2C1C2 R2 Rf R1 R2 Rf Avp 频率响应为 Av f 2 1 f 1 ( ) j 以上各式中 f0 Q f0
Vi ( s) VN ( s) VN ( s) VN ( s) Vo ( s) VN ( s) sC1 0 R1 R2 Rf
N节点的电流方程:
VN ( s) V(+) ( s) Vi ( s) VN ( s) [VN ( s) Vo ( s)]sC 0 R R
联立求解以上三式,可得LPF的传递函数 Avp Vo s Av s 2 Vi s 1 (3 Avp )sCR sCR 上式表明,该滤波器的通带增益应小于3,才 能保障电路稳定工作。
二阶压控型HPF 频率响应
有源带通滤波器(BPF) 和带阻滤波器(BEF)
二阶压控型BPF
二阶压控型BEF
带通滤波器是由低通RC环节和高通RC环节组合而成的。要将 高通的下限截止频率设置的小于低通的上限截止频率。反之则为 带阻滤波器。 要想获得好的滤波特性,一般需要较高的阶数。滤波器的设计 计算十分麻烦,需要时可借助于工程计算曲线和有关计算机辅助 设计软件。
1 1 ∥ (R ) sC1 sC 2 VN s Vi ( s ) 1 1 R [ ∥ (R )] sC1 sC 2
通常有C1=C2=C,联立求解以上三式,可得 滤波器的传递函数 Avp VO s Av s VI s 1 3sCR sCR 2
低通滤波器的主要技术指标 (1)通带增益Avp
通带增益是指滤波器在通频带内的电压放大 倍数,性能良好的LPF通带内的幅频特性曲线 是平坦的,阻带内的电压放大倍数基本为零。
(2)通带截止频率fp
其定义与放大电路的上限截止频率相同。 通带与阻带之间称为过渡带,过渡带越窄,说 明滤波器的选择性越好。
一阶有源滤波器
1 Q 3 - Avp
Av
( f f0 )
QAvp
1 Q 3 Avp
Av ( f
f ) 0
QAvp
以上两式表明,当 2 Avp 3 时,Q>1,在 f f 0 处的电压增益将大于 Avp ,幅频特性在
f f 0 处将抬高。
当 Avp ≥3时,Q =∞,有源滤波器自激。由
n
V0 ( j ) A0 A( j ) Vi ( j ) 1 j ( )
n
A( j )
V0 ( j ) Vi ( j )
A0
2 1 ( ) n
一阶LPF的幅频特性曲线
简单二阶低通有源滤波器
为了使输出电压在高频段以更快的速率下降,以改 善滤波效果,再加一节RC低通滤波环节,称为二阶
R1 5.51 R 5.51 3.9 k 21.5 k Rf 3.14 R 3.14 3.9 k 12.2 k
实验八 运算放大器在信号方面的应用
调零电路 调整RW使输出为零。
1.反相比例放大器
ui ~
测量u0=?,计算Auf = u0/ui 。
例1:
要求二阶压控型LPF的f 0 400Hz,Q值为0.7, 试求电路中的电阻、电容值。
解:根据f 0 ,选取C再求R。 1. C的容量不易超过1μ F 。 因大容量的电容器体积大, 价格高,应尽量避免使用。 取 C 0.1μ F , 1k R 1M ,
1 1 f0 400 Hz 6 2π RC 2π R 0.110 计算出 R 3979 ,取 R 3.9 k
于将 接到输出端,等于在高频端给LPF加了 C1
一点正反馈,所以在高频端的放大倍数有所抬
高,甚至可能引起自激。
二阶反相型低通有源滤波器
二阶反相型LPF是在反相比例积分器的输入端再 加一节RC低通电路而构成。
反相型二阶LFP
改进型反馈反相二阶LFP
1 VN ( s) 由图 Vo ( s) sC2 R2
有源滤波电路。它比一阶低通滤波器的滤波效果更好。
二阶LPF
二阶LPF的幅频特性曲线
(1)通带增益
当 f = 0, 或频率很低时,各 电容视为开路,通带内的增 益为 Rf Avp 1 R1
(2)传递函数
Vo ( s ) AvpV( ) ( s ) V( ) ( s ) VN ( s ) 1 1 sC 2 R
