材料力学第一章
材料力学课件第1章绪论

自行车结构也有强度、 刚度和稳定问题
大型桥梁的强度 刚度 稳定问题
桥面结构
缆索与立柱
桥墩
南京长江大桥
上海南浦大桥
澳门桥
1940年11月,华盛顿州的Tacoma Narrows桥,由于桥面刚度太差, 在45 mph风速的情形下,产生“Galloping Gertie”(驰振)。
第一章 绪 论
一、材料力学的任务及与工程的联系 二、变形固体的性质及基本假设 三、外力及其分类 四、内力、截面法和应力 五、正应变与切应变 六、杆件变形的基本形式
§1-1、材料力学的任务及与工程的联系
材料力学:研究物体受力后的内在表现, 即,变形规律和破坏特征。
材料力学与工程设计密切相关。
强度、刚度、稳定性
扭转(torsion)
当作用在杆件上的力组成作用在垂直于杆轴 平面内的力偶Me时,杆件将产生扭转变形,即 杆件的横截面绕其轴相互转动 。
弯曲(bending)
当外加力偶M或外力作用于杆件的纵向平面内 时,杆件将发生弯曲变形,其轴线将变成曲线。
组合受力
由基本受力形式中的两种或两种以上所共同形成 的受力与变形形式即为组合受力与变形。
工程中的梁、杆结构
拉伸或压缩(tension or compression)
当杆件两端承受沿轴线方向的拉力或压力载荷 时,杆件将产生轴向伸长或压缩变形。
剪切(shearing)
在平行于杆横截面 的两个相距很近的平面 内,方向相对地作用着 两个横向力,当这两个 力相互错动并保持二者 之间的距离不变时,杆 件将产生剪切变形。
4、小变形假设:材料力学所研究的构件在载荷作用下的 变形与原始尺寸相比甚小,故对构件进行受力分析时 可忽略其变形。
(材料力学)第一章轴向拉伸和压缩

24
根据Saint-Venant原理:
25
7. 应力集中(Stress Concentration):
由于截面尺寸急剧变化而引起的局部应力增大的现象。
·应力集中因数
K max m
26
不同性质的材料对应力集中的敏感程度不同
1.脆性材料
σmax 达到强度极限,此位置开裂,所 以脆性材料构件对应力集中很敏感。
轴力图如右图 N
2P + –
3P
BC
PB
PC
N3
C
PC N4
5P
+
P
D PD D PD D PD
x
11
[例2] 图示杆长为L,受轴线方向均布力 q 作用,方向如图,试画
出杆的轴力图。 q
解:x 坐标向右为正,坐标原点在 自由端。
L
取左侧x 段为对象,内力N(x)为:
O x
N – qL
N(x)maxqL
2.塑性材料
应力集中对塑性材料在静载作用下的强度影响不 大,因为σmax 达到屈服极限,应力不再增加,未达 到屈服极限区域可继续承担加大的载荷,应力分布 趋于平均。
在静载荷情况下,不需考虑应力集中的影响;但 在交变应力情况下,必须考虑应力集中对塑性材料 的影响。
况、安全重要性、计算模型等等
16
依强度准则可进行三种强度计算:
①校核强度:
m ax
②设计截面尺寸:
Amin
Nmax
[ ]
③许可载荷:
N ma xA ;
Pf(Ni)
17
[例4] 已知三铰屋架如图,承受竖向均布载荷,载荷的分布 集度为:q =4.2kN/m,屋架中的钢拉杆直径 d =16 mm,许用
材料力学——精选推荐

材料力学第一章拉压一、构件设计应满足的要求:1、足够的强度:即抵抗破坏的能力;2、足够的刚度:即抵抗变形的能力;3、足够的稳定性:即保持平衡的能力;二、失稳:构件在一定外力的作用下,不能保持原有的平衡形式,称为失稳;细长杆件在压缩中容易产生失稳现象。
三、材料力学的基本假设:1、连续性假设:构件的整个体积内毫无空隙的充满了物质;2、均匀性假设:认为材料是均匀的,其力学性能与构件中的位置无关;(材料在外力作用下表现出来的性能,称为力学性能或机械性能)3、各项同性假设:沿各个方向均具有相同的力学性能;(相反,存在各向异性材料,常见的有碳纤维、玻璃纤维、环氧树脂、陶瓷等四、杆件变形的基本形式:拉伸或压缩、弯曲和扭转。
五、内力:外力作用下,构件内部相连两部分之间的相互作用力。
六、同一杆件在受力方式变化的情况下,即使只受轴向力作用,不同部分的轴向力大小也可能不同,如在杆端和杆中点均受力,切合力为0的情况。
七、设杆件的横截面积为A,轴力为N,且为均匀性材料,则横截面上各点处的正应力均为:Pa、Mpa、Gpa)。
八、圣维南原理:力作用于杆端的方式不同,只会使于杆端距离不大于杆横向尺寸的范围受其影响。
九、拉压杆上的最大剪应力发生在于杆轴成45°的斜截面上,其值为横截面正应力的一半。
十、单位长度的变形,称为正应变。
十一、材料的应力——应变曲线:工程中常用的材料的应力应变曲线分成以下几个阶段:1、线性阶段:在拉伸的初始阶段,应力——应变为一直线;此阶段的应力最高点,为材料的比例极限;2、屈服阶段:超过比例极限之后,应力和应变之间不再保持正比例关系。
此阶段内,应力几乎不变,但变形却极具增长,材料失去抵抗继续变形的能力,此种现象称为屈服。
相应的应力称为材料的屈服应力或屈服极限。
3、强化阶段:经过屈服阶段之后,材料又增强了抵抗变形的能力,此种现象称为强化。
强化节点最高点对应的应力称为材料的强度极限。
如果材料表面光滑,当材料屈服时,试样表面将出现于轴线成45°的线纹,作用有最大剪应力。
材料力学知识点总结
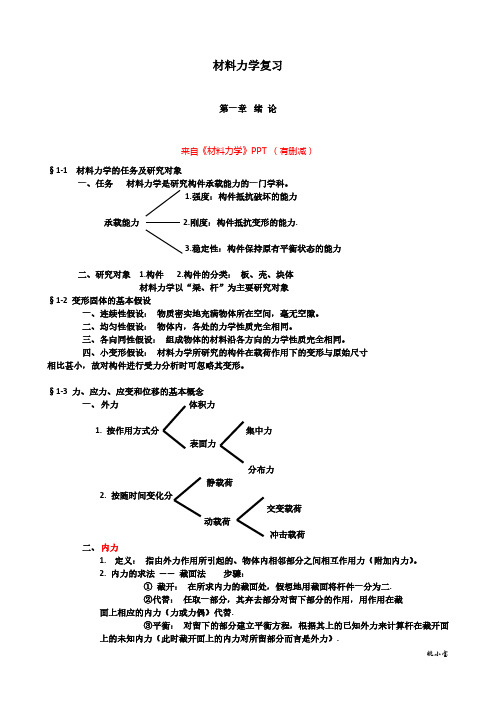
三、应力 1.定义 (Definition):由外力引起的内力的集度 2. 应力 ①平均应力
pm
=
ΔF ΔA
②全应力(总应力)
p lim ΔF dF ΔA0 ΔA dA
③全应力分解为 垂直于截面的应力称为“正应力”
lim ΔFN dFN ΔA0 ΔA dA
位于截面内的应力称为“切应力”
·§3-3 薄壁圆筒的扭转
1 10 r0
姚小宝
薄壁圆筒:壁厚
(r0—圆筒的平均半径)
3.推论 (1)横截面上无正应力,只有切应力;
(2)切应力方向垂直半径或 与圆周相切.
圆周各点处切应力的方向于圆周相切,且数值相等,近似的认为沿壁厚方向各点处
切应力的数值无变化.
4.推导
此式为薄壁圆筒扭转时横截面上切应力的计算公式. 薄壁筒扭转时横截面上的切应力均匀分布,与半径垂直,指向与扭矩的转向一致.
固定铰支座
固定端
5.静定梁的基本形式:
·§4-2 梁的剪力和弯矩
一、内力计算
简支梁 外伸梁
悬臂梁
求内力——截面法
姚小宝
二、内力的符号规定 1.剪力符号
2.弯矩符号
当 dx 微段的弯曲下凸(即该段的下 半部受拉 )时,横截面 m-m 上的弯矩为 正;
当 dx 微段的弯曲上凸(即该段的下半 部受压)时,横截面 m-m 上的弯矩为负.
2.平面假设
变形前为平面的横截面 ,变形后仍保持为平面.
3.几何关系 倾角 是横截面圆周上任一点 A 处的切应变, d 是 b-b 截面相对于 a-
a 截面象刚性平面一样绕杆的轴线转动的一个角度.
tan
材料力学课件第一章绪论

§1.3 外力及其分类 3 一、外力 周围物体对构件的作用。 周围物体对构件的作用。 二、外力分类 按作用方式划分: 1.按作用方式划分: 集中力 表面力 外力 线分布力 面分布力 体积力( 重力,惯性力) 体积力(如:重力,惯性力)
2.按作用趋势划分: .按作用趋势划分: 静载荷 主动力, 主动力,又称为载荷 动载荷 外力 约束力
∑ 由:
Fy = 0, F − FN = 0
o
∑M
= 0, Fa− M = 0
FN = F 得:
M = Fa
三、应力(stress) 应力 1 . 定义 截面内某一点处分布内力的集度称为该点的应力。 定义: 截面内某一点处分布内力的集度称为该点的应力。 2 . 定义式: 定义式:
∆F 平均应力: 平均应力: pm = ∆A
§1.6 杆件变形的基本形式
一、杆件(bar)的概念 杆件 的概念 1. 构件类型: 构件类型: 杆: 板: 壳: 块:
2. 杆件的两个要素: 杆件的两个要素: 轴线 3. 杆件分类: 杆件分类: 横截面 等截面直杆,变截面直杆,等截面曲杆,变截面曲杆。 等截面直杆,变截面直杆,等截面曲杆,变截面曲杆。 吊车图
MN → 0
M ′N ′ − MN ∆s = lim MN MN → 0 ∆ x
ቤተ መጻሕፍቲ ባይዱ
γ = lim
ML →0
π − ∠L′M ′N ′ MN →0 2
三、小变形问题的计算 1. 特点: 特点: 位移、变形和应变都是微小量。 位移、变形和应变都是微小量。 2. 采用简化计算: 采用简化计算: 原始尺寸法。 如:原始尺寸法。
∆F lim lim 应力: 应力: p = ∆A→0 pm = ∆A→0 ∆A
材料力学第一章知识归纳总结

材料力学
三、材料力学的任务 材料力学的任务就是在满足强度、刚度和 稳定性的要求下,为设计既经济又安全的构 件,提供必要的理论基础和计算方法。
若:构件横截面尺寸不足或形状 不合理,或材料选用不当 ——不满足上述要求,
不能保证安全工作。
若:不恰当地加大横截面尺寸或 选用优质材料 —— 增加成本,造成浪费
δ 1 < δ 2 << l
B
1 δ
A
FN 1
δ2
θ
A F
θ
C
F F
A1
FN 2
l
求FN1、 FN1 时,仍可 按构件原始尺寸计算。
材料力学
3、小变形前提保证叠加法成立 叠加法指构件在多个载荷作用下产生的变形—— 可以看作为各个载荷单独作用产生的变形之代数和
叠加法是材料力学中常用的方法。
材料力学
a a’
0.025
材料力学
第一章 §1-6 绪论 杆件变形的基本形式
构件的分类:杆件、板壳*、块体*
杆件——纵向尺寸(长度)远比横向尺寸大得多的 构件。 直杆——轴线为直线的杆 曲杆——轴线为曲线的杆 等截面直杆——横截面的 形状和大小不变的直杆
材料力学
板和壳:构件一个方向的尺寸(厚度)远小于其 它两个方向的尺寸。 块件:三个方向(长、宽、高)的尺寸相差不多 的构件。
}
研究构件的强度、刚度和稳定性,还需要了解材料的 力学性能。因此在进行理论分析的基础上,实验研究是 完成材料力学的任务所必需的途径和手段。
均不可取
材料力学
§1-2 变形固体的基本假设
一、变形固体: 在外力作用下可发生变形的固体。 二、变形固体的基本假设: 1、连续性假设: 认为变形固体整个体积内都被物质连续 地充满,没有空隙和裂缝。
材料力学电子教案

材料力学电子教案第一章:材料力学概述1.1 材料力学的定义和研究对象1.2 材料力学的发展简史1.3 材料力学的研究方法1.4 材料力学的应用领域第二章:内力、截面法和剪切力2.1 内力的概念及其计算2.2 截面法的基本原理与应用2.3 剪切力的概念及其计算2.4 剪切强度计算及剪切失效分析第三章:弯曲和扭转3.1 弯曲的基本概念3.2 纯弯曲梁的应力和应变3.3 弯曲强度计算3.4 扭转的基本概念3.5 扭转应力计算及扭转失效分析第四章:材料的基本力学性能4.1 弹性变形与弹性模量4.2 塑性变形与塑性极限4.3 材料的其他力学性能4.4 材料力学性能的测定方法第五章:应力-应变关系与胡克定律5.1 应力与应变的定义及关系5.2 胡克定律的表述及应用5.3 非线性材料的应力-应变关系5.4 弹性模量的测定方法及应用第六章:材料力学中的能量原理6.1 能量原理概述6.2 势能和弹性势能6.3 能量原理在材料力学中的应用6.4 能量原理在弹性问题求解中的应用第七章:材料力学中的强度理论7.1 强度理论概述7.2 强度条件及其应用7.3 安全系数的概念及其计算7.4 材料力学中的失效准则及应用第八章:梁的弯曲与扭转组合8.1 梁的弯曲与扭转组合问题概述8.2 纯弯曲梁的扭转应力8.3 扭转梁的弯曲应力8.4 弯曲与扭转组合问题的求解方法第九章:壳体力学9.1 壳体力学概述9.2 壳体的基本方程及其求解9.3 壳体的弯曲与轴向变形9.4 壳体的稳定性问题及其求解方法第十章:材料力学在工程中的应用10.1 材料力学在结构设计中的应用10.2 材料力学在机械设计中的应用10.3 材料力学在材料加工中的应用10.4 材料力学在其他工程领域的应用重点和难点解析1. 第一章中“材料力学的研究方法”是重点内容,因为它涉及到材料力学的基本研究方法和思维方式。
补充和说明:材料力学的研究方法包括实验研究、理论分析和数值模拟等。
材料力学第一章课件

受力如图:
M FN
38
列平衡方程:
Y 0 FN P Mo(F) 0
Pa M 0 M Pa
材料力学
第一章 绪论
➢ 内力的分类:
轴力:FN 剪力:FS ; 扭矩:T弯矩:My, Mz
剪力 FQz
剪力
FQy
y
z
FN x
FR 轴力
弯矩 Mz
弯矩 My
y
z 扭矩
T
x MO
39
材料力学
30
材料力学
第一章 绪论
§ 1.2 材料力学的基本假设
材料力学研究材料的宏观力学行为 材料力学主要研究钢材等金属材料
关于材料的基本假设:
连续性假设:认为材料无空隙地充满于整个构件。 ——力学量可以用坐标的连续函数表示。
均匀性假设:构件内每一处的力学性能相同。 ——通过试样得到的材料性能可用于构件的任何部位。 各向同性假设:构件某一处材料沿各个方向的力
26
材料力学
第一章 绪论
§1.1 材料力学的任务
1.1.1 研究对象和研究内容: 1) 强度 抵抗破坏的能力。
破坏 断裂 明显的塑性变形
27
材料力学
2) 刚度 抵抗变形的能力。
第一章 绪论
3) 稳定性 保持稳定的平衡状态的能力。
P
不
细
铅
倒
长
笔
翁
杆
28
材料力学
第一章 绪论
材料力学的任务:在满足上述强度、刚度和稳定性要求
2. 自行车负重爬坡出现“链条脱落”现象,并且无法安 装和继续前行,从力学的角度分析,此现象表明链条的
[A] 强度不足 [B] 刚度不足 [C] 稳定性不足
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章绪论1. 判断改错题1-1-1 铸铁结构由于没有屈服阶段,所以在静载作用时可以不考虑其应力集中的影响。
( × )应考虑其应力集中的影响。
因铸铁属脆性材料,因此构件在静载作用时,在尺寸突变处,没有明显的塑性变形来缓和应力的增加,应力集中使该处的应力远大于其它各处的应力,构件首先从该处破坏,所以静载作用时应该考虑应力集中的影响。
1-1-2 构件内力的大小不但与外力大小有关,还与材料的截面形状有关。
( × )。
静定构件内力的大小只与外力大小有关,与材料的截面无关。
1-1-3 钢筋混凝土柱中,钢筋与混凝土柱高度相同,受压后,钢筋与混凝土柱的压缩量相同,所以二者所受的内力也相同。
( × ) 它们的内力大小不一定相同。
钢筋混凝土柱受压后,由于钢筋的弹性模量E 1不等于混凝土的弹性模量E 2,钢筋横截面积A 1 也不等于混凝土的横截面积A 2,所以有 ,221121221112122221111,,,2A E AE N N A E N A E N l l A E l N l A E l N l ==∆=∆=∆=∆故在E 1 A 1=E 2 A 2 时,才有N 1=N 2 。
否则21N N ≠。
1-1-4 杆件的某横截面上,若各点的正应力均为零,则该截面上的轴力为零。
( √)1-1-5 只要构件的强度得到保证,则该构件就能正常的工作。
( × )。
只有构件的强度、刚度、稳定性都得到满足,构件才能正常工作。
1-1-6 两根材料、长度l 都相同的等直柱子,一根的横截面面积为A 1,另一根为A 2,且A 2>A 1.如图所示。
两杆都受自重作用。
则两杆的最大压应力相等,最大压缩量也相等。
( √ )。
自重作用时,最大压应力在两杆底端,即l AAlA N ννσ===max max也就是说,最大应力与面积无关,只与杆长有关。
所以两者的最大压应力相等。
最大压缩量为El EA lAl l 222max νν=⋅=∆ 即最大压缩量与面积无关,只与杆长有关。
所以两杆的最大压缩量也相等。
(a)A1A 2(b)题1-1-6图题1-1-7图1-1-7 如图所示桁架,两杆的抗拉刚度EA 相等,节点B 处受竖向荷载P 作用,则各杆的伸长量为EA Pl l AB =∆ ,EAPl l BC 34=∆。
( × )。
0,=∆=∆BC AB l EAPl l AB 杆的轴力N=P ,而BC 杆的轴力N=0。
1-1-8 直径为d 的圆截面拉伸试件,其标距是指试件两端面之间的距离。
( × )。
工作段内的距离。
1-1-9 低碳钢拉伸试件的强度极限是其拉伸试验中的最大实际应力值。
( × )。
强度极限不是真实最大应力值。
强度极限b σ=P b /A 。
A 为原来的横截面面积,而不是试件在P b 作用时的面积。
因此强度极限不是真实最大应力值。
1-1-10 建筑工地上把直径为10mm 的钢筋拉到8mm ,目的是为了减小钢筋的直径,宜于扎绑配筋。
( × )。
目的是为了增加钢筋的屈服极限、比例极限、改善工作性能。
建筑工地上把直径为10mm 的钢筋拉到8mm ,称为“冷拔”。
这实际上是把钢筋加载到强化阶段,然后卸载,是一种冷作硬化的处理。
1-1-11 受集中力轴向拉伸的等直杆,在变形中,任意两个横截面一定保持平行。
所以纵向纤维的伸长量都相等,从而在横截面上的内力是均匀分布的。
( × )。
在变形中,离开荷载作用处较远的两个横截面才保持平行。
在载荷作用处,横截面不再保持平面,纵向纤维伸长不相等,应力分布复杂,不是均匀分布的。
1-1-12 若受力物体内某点测得x 和y 方向都有线应变x ε和y ε,则x 和y 方向肯定有正应力x σ和y σ。
( × )。
x 和y 方向不一定有正应力x σ和y σ。
由于横向效应作用,轴在x 方向受拉(压),则有x σ ;y 方向不受力,但横向效应使y 方向产生线应变,x y νεεε-='=。
2.填空题1-2-1 轴向拉伸的等直杆,杆内任一点处最大剪应力的方向与轴线成 450 。
1-2-2 受轴向拉伸的等直杆,在变形后其体积将 改变(增大) 。
1-2-3 低碳钢经过冷作硬化处理后,它的 比例 极限得到了明显的提高。
1-2-4 工程上通常把延伸率>δ 5% 的材料称为塑性材料。
1-2-5 一空心圆截面直杆,其内、外径之比为α=0.8,两端轴受轴向拉力作用,如将内外径增加一倍,则其抗拉刚度将是原来的 4 倍。
1-2-6 两根长度及截面面积相同的等直杆,一根为钢杆,一根为铝杆,承受相同的轴向拉力。
比较二杆的正应力及伸长量大小,则钢杆的正应力 等于 铝杆的正应力,钢杆的伸长量 小于 铝杆的伸长量。
1-2-7在图示结构中,杆AB 为水平刚性杆,在求解二杆内力时,二杆的变形协调条件为=∆1l 4 2l ∆。
结构的变形图如题1-2-7解图。
'111'21130sin 22,CC CC l BB CCl BB l ==∆==∆=∆所以 Δl 1= 4 Δl 2。
1-2-8 截面 法是求杆件内力的基本方法。
3.选择题 1-3-1 下列结论正确的是( C )。
A .理论力学主要研究物体受力后的运动效应,但也考虑物体的变形效应B . 理论力学中的四个公理在材料力学中都能应用C . 材料力学主要研究杆件受力后的变形和破坏规律D .材料力学研究的问题主要是静止不动的荷载作用下的问题理论力学的研究对象是质点、质点系和刚体,不研究变形效应。
理论力学中的二力平衡公理、加减平衡力系公理及它们的力的可传性原理都适用于刚体,而不适用于变形体。
所以材料力学中不能用以上公理及原理。
材料力学中的荷载主要是静载,静载指的是荷载从零缓慢加载,产生的加速度不会影响材料的力学性能。
所以静载不是静止不动的载荷。
1-3-2 理论力学中的“力和力偶可传性原理”在下面成立的是( D )。
A .在材料力学中仍然处处适用B . 在材料力学中根本不能适用C . 在材料力学中研究变形是可以适用D .在材料力学中研究平衡问题时可以适用力与力偶可传性原理适用于刚体,所以在考虑变形时不适用。
但在求支座反力、杆的内力时不牵涉到变形,可以应用以上两个原理。
1-3-3下列结论中正确的是( B )。
A .外力是指作用于物体外部的力B . 自重是外力C . 支座约束反力不属于外力D .惯性力不属于外力外力指的是物体以外的其它物体对它的作用力。
外力可以作用在物体内、外部。
自重是物体受地球的引力,属于外力。
惯性力属于外力。
1-3-4下列结论正确的是( A )。
A .影响材料强度的是正应力和剪应力的大小B . 影响材料强度的是内力的大小C . 同一截面上的正应力必定是均匀分布的D .同一截面上的剪应力必定是均匀分布的 1-3-5下列结论正确的是( B )。
A .一个质点的位移可以分为线位移和角位移B . 一个质点可以有线位移,但没有角位移C . 一根线或一个面元素可以有角位移,但没有线位移D .一根线或一个面元素可以有线位移,但没有角位移1-3-6空心圆截面杆受轴向拉伸时,下列结论正确的是( B )。
题1-2-7图 题1-2-7图 1题1-4-1图题1-4-2图题1-4-2图解A .外径和壁厚都增大 B. 外径和壁厚都减小 C. 外径减小,壁厚增大 D .外径增大,壁厚减小设原管的外径为D ,内径为d ,则壁厚t=(D-d)/2。
轴向拉伸后,外径为D '=D -νD ,内径为D '=d -νd ,其中ν为泊松比。
壁厚t '为t t d D d d D D d D t <-=--=---=-=)1()1(22)()(2'''νννν所以外径和壁厚都减小。
1-3-7设低碳钢拉伸试件工作段的初始横截面面积为A 0,试件被拉断后断口的最小横截面面积为A 1,试件断裂前所能承受的最大荷载为P b 。
在下列结论中正确的是( B )。
A.材料的强度极限1/A P b b =σ B.材料的强度极限0/A P b b =σC.试件应力达到强度极限的瞬时,试件横截面面积为A 0D.试件开始段裂时,试件承受的荷载是P b 4.计算题1-4-1 求图示阶梯状直杆各横截面上的应力,并求杆的总伸长.材料的弹性模量E =200 GPa 。
横截面面积A 1=200 mm 2,A 2=300 mm 2,A 3=400 mm 2。
1-4-2 如图所示的桁架,两杆材料相同,AB 杆的横截面面积A 1=100 mm 2,AC 杆的横截面面积A 2=80 mm 2,弹性模量E=210 GPa ,铅垂力P =20kN 。
求A 点的位移。
Δl AB =0.805mm, Δl AC =0.871mm结构变形图如图。
x A =0.192m y A =1.04mmmm EA l N EA l N EA l N l MPa A N MPa A N MPa A N kN N kN N kN N CDCD BC BC AB AB AB AB AB CB CB CB CD CD CD BA CB CD 625.0254001010,3.333001010,1002001020101020333-=++=∆=⨯==-=⨯-==-=⨯-===-=-=σσσ︒=44.10γmmAA 058.11=题1-4-3图1-4-3 已知混凝土的容量3/22m kN =γ,许用压应力MPa 2][=σ。
试按强度条件确定图示混凝土柱所需的横截面面积A 1和A 2。
混凝土弹性模量E=20 GPa 。
并求柱顶A 的位移。
A 1m 576.0≥ 2A 2m 665.0≥ 2y A =Δl AC +Δl CB=(1.121+1.119)mm mm 24.2≈1-4-4 水平刚性横梁AB 与杆1和杆2及铰支座C 联接,杆1的长度做短了δ=1.5,如图所示。
杆1和杆2的材料、截面都相同,弹性模量E =200 GPa 。
求装配后两杆内正应力。
变形关系图如题1-4-4解图所示。
变形关系有121122BB l AA l =∆-=∆δ变形关系为MPaMPa l l 9.452.16222121==∆=∆-σσδ 1-4-5 图中横梁ABCD 设为刚体,由钢索拉住保持水平,钢索饶过无摩擦的滑轮,横截面面积A=76.4 mm 2,竖向荷载P=20kN ,钢索的弹性模量E=177 GPa 。
求钢索内的应力和C 点的位移。
1-4-6 图中,支架AB 和CD 可视为刚体,而拉杆DE 长l =2m ,横截面为圆,其直径d=15 mm ,弹性模量E=210GPa ,竖向力P=20kN 。
