求解中心天体质量和密度
万有引力专题02:中心天体质量和密度的估算
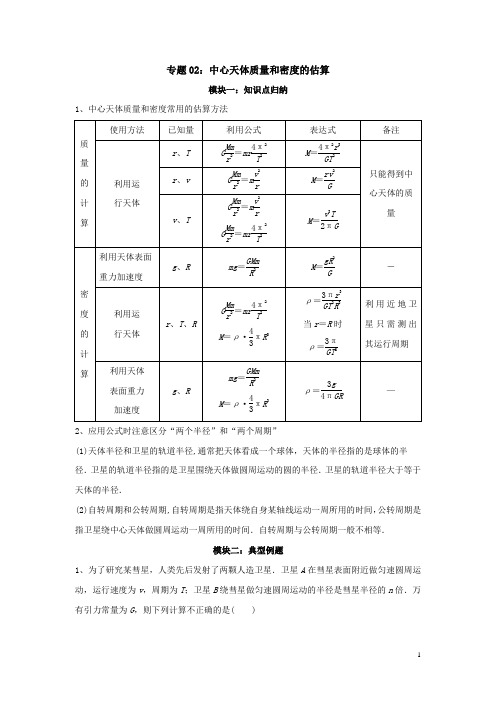
专题02:中心天体质量和密度的估算模块一:知识点归纳1、中心天体质量和密度常用的估算方法2、应用公式时注意区分“两个半径”和“两个周期”(1)天体半径和卫星的轨道半径,通常把天体看成一个球体,天体的半径指的是球体的半径.卫星的轨道半径指的是卫星围绕天体做圆周运动的圆的半径.卫星的轨道半径大于等于天体的半径.(2)自转周期和公转周期,自转周期是指天体绕自身某轴线运动一周所用的时间,公转周期是指卫星绕中心天体做圆周运动一周所用的时间.自转周期与公转周期一般不相等.模块二:典型例题1、为了研究某彗星,人类先后发射了两颗人造卫星.卫星A在彗星表面附近做匀速圆周运动,运行速度为v,周期为T;卫星B绕彗星做匀速圆周运动的半径是彗星半径的n倍.万有引力常量为G,则下列计算不正确的是( )A .彗星的半径为vT2π B .彗星的质量为v 3T4πGC .彗星的密度为3πGT2 D .卫星B 的运行角速度为2πT n32、我国计划于2019年发射“嫦娥五号”探测器,假设探测器在近月轨道上绕月球做匀速圆周运动,经过时间t (小于绕行周期),运动的弧长为s ,探测器与月球中心连线扫过的角度为θ(弧度),引力常量为G ,则( )A .探测器的轨道半径为 θtB .探测器的环绕周期为 πt θC .月球的质量为 s 3Gt 2θD .月球的密度为 3θ24Gt模块三:针对训练1、通过观测冥王星的卫星,可以推算出冥王星的质量。
假设卫星绕冥王星做匀速圆周运动,除了引力常量外,至少还需要两个物理量才能计算出冥王星的质量。
这两个物理量可以是( )A .卫星的速度和角速度B .卫星的质量和轨道半径C .卫星的质量和角速度D .卫星的运行周期和轨道半径2、近年来,人类发射了多枚火星探测器,对火星进行科学探究,为将来人类登上火星、开发和利用火星资源奠定了坚实的基础。
如果火星探测器环绕火星做“近地”匀速圆周运动,并测得该探测器运动的周期为T ,则火星的平均密度ρ的表达式为(k 是一个常数)( ) A .ρ=kTB .ρ=kTC .ρ=kT2D .ρ=k GT 23、火星成为我国深空探测的第二颗星球,假设火星探测器在着陆前,绕火星表面匀速飞行(不计周围其他天体的影响),宇航员测出飞行N 圈用时t ,已知地球质量为M ,地球半径为R ,火星半径为r ,地球表面重力加速度为g 。
万有引力与航天山东高考题总结

A.甲的周期大于乙的周期 B.乙的速度大于第一宇宙速度 C.甲的加速度小于乙的加速度 D.甲在运行时能经过北极的正上方 【解析】此题通过分析卫星的定轨运行,考查万有引力定律和圆周 运动知识。卫星绕地球做圆周运动,万有引力提供向心力,有 ,解得 。因为 ,所以 ,所以B项错误。 , ,
,A C选项正确。地球
万有引力与航天 山东高考题总结
淄博四中 吕昕珂 2014年7月18日
考点一、中心天体质量和密度的计算
1.估算中心天体的质量和密度的常见思路 (1)利用中心天体表面的重力加速度 g 和天体半径 R,质量为 m 的物 Mm 体在天体表面受到的重力近似等于万有引力,即 G R2 =mg 可得天体质 gR2 M M 3g 量 M= G ,进而求得 ρ= V =4 =4πGR. 3 π R 3 Mm 4π2 4π2r3 (2)利用环绕天体的轨道半径 r、周期 T,G r2 =m T2 r 即 M= GT2 . 若环绕天体绕中心天体表面做匀速圆周运动时,轨道半径 r=R,则 M 3π ρ= = 2. 4 3 GT πR 3
轨道二 轨道一
地球
P
A.飞船变轨前后的机械能相等 B.飞船在圆轨道上时航天员出舱前后都处于失重状态 C.飞船在此圆轨道上运动的角度速度大于同步卫星运动的角速度 D.飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨 道运动的加速度
【解析】飞船点火变轨,前后的机械能不守恒,所以A不正确。飞
船在圆轨道上时万有引力来提供向心力,航天员出舱前后都处于失
=
则Gliese 581c表面的重力加速度 = = 故飞船在Gliese 581c表面飞行的速度
vc gc Rc 10 10 g曲 R曲 7.9 km s 3 3
计算中心天体的质量和密度

计算天体的质量和密度知识梳理“天上”法“地上”法原理万有引力提供向心力:22m GMmv r r ==2m r ω=224m r T π=n ma万有引力等于重力:2GMmmg R=质量M=2324GT r π=2v r G =23rG ω=2n a r G2gR M G=需要已知量 G 、r 、T(或ω、v)G 、g 、R密度3233M r V GT R πρ==特例,当r=R 时:23GT πρ=34g GR ρπ=注意:计算天体质量需“一个中心、两个基本点”: “一个中心”即只能计算出中心天体的质量;“两个基本点” 即要计算中心天体的质量,除引力常量G 外,还要已知两个独立的物理量。
例题分析【例1】下列哪一组数据不能估算出地球的质量。
引力常量G 已知( )A.月球绕地球运行的周期与月地之间的距离B.地球表面的重力加速度与地球的半径C.绕地球运行卫星的周期与线速度D.地球表面卫星的周期与地球的密度【例2】已知引力常量G .月球中心到地球中心的距离R 和月球绕地球运行的周期T 。
仅利用这三个数据,可以估算出的物理量有( ) A .月球的质量 B .地球的密度C .地球的半径D .月球绕地球运行速度的大小【例3】(2006北京)一飞船在某行星表面附近沿圆轨道绕该行星飞行,认为行星是密度均匀的球体,要确定该行星的密度,只需要测量( )A.飞船的轨道半径B.飞船的运行速度C.飞船的运行周期D.行星的质量【例4】(2005广东)已知万有引力常量G ,地球半径R ,月球和地球之间的距离r ,同步卫星距地面的高度h ,月球绕地球的运转周期T 1,地球的自转周期T 2,地球表面的重力加速度g 。
某同学根据以上条件,提出一种估算地球质量M 的方法: 同步卫星绕地球作圆周运动,由得⑴请判断上面的结果是否正确,并说明理由。
如不正确,请给出正确的解法和结果。
⑵请根据已知条件再提出两种估算地球质量的方法并解得结果。
同步练习1.已知下面的哪组数据可以计算出地球的质量?引力常量G 已知( )A .月球绕地球运动的周期和月球的半径B .地球同步卫星离地面的高度C .地球绕太阳运动的周期和地球到太阳中心的距离D .人造卫星在地面附近的运动速度和周期2.下列哪一组数据能够估算出地球的密度。
专题26 中心天体质量密度的计算问题 (原稿版)

专题26 中心天体质量密度的计算问题专题导航目录常考点中心天体质量和密度常用的估算方法 (1)考点拓展练习 (4)常考点中心天体质量和密度常用的估算方法【典例1】宇宙中两颗靠得比较近的星球,只受到彼此之间的万有引力作用绕两球心连线上某点绕转,称之为双星系统。
设某双星系统中A、B两星球绕其连线上的某固定点O做匀速圆周运动。
若A、B的质量分别为M、m,则()A.星球A与星球B的轨道半径之比为M:mB.星球A与星球B的线速度大小之比为m:MC.星球A与星球B的周期大小之比为m:MD.若两星球间距离减小,则星球A做匀速圆周运动的周期变大【典例2】天问一号于2021年2月10日实施火星捕获,将于2021年5月择机实施降轨软着陆火星表面。
设天问一号距火星表面高度约为火星半径的n倍,其环绕周期为T,引力常量为G,则火星的密度为()A.B.C.D.【技巧点拨】1.中心天体质量和密度常用的估算方法质使用方法已知量利用公式表达式备注2.求天体质量和密度,警惕三个常见误区(1)不考虑自转问题时,有GMmR 2=mg ,其中g 为星球表面的重力加速度,若考虑自转问题,则在两极上才有:GMm R 2=mg ,而赤道上则有:GMm R 2-mg =m 4π2T2R 。
(2)利用G Mm r 2=m 4π2T 2r 计算天体质量时,只能计算中心天体的质量,不能计算绕行天体的质量。
(3)注意区分轨道半径r 和中心天体的半径R ,计算中心天体密度时应用ρ=M43πR 3而不是ρ=M43πr 3,但在表面附近绕行的卫星,可近似认为R =r 。
【变式演练1】(多选)如图所示,美国的“卡西尼”号探测器经过长达7年的“艰苦”旅行,进入绕土星飞行的轨道。
若“卡西尼”号探测器在半径为R 的土星上空离土星表面高h 的圆形轨道上绕土星飞行,环绕n 周飞行时间为t,已知引力常量为G,则下列关于土星质量M和平均密度ρ的表达式正确的是()A.M=B.M=C.ρ=D.ρ=【变式演练2】2020年7月23日,中国首个火星探测器“天问一号”在海南文昌卫星发射中心发射升空。
2020高考备考物理重难点《天体运动与人造航天器》(附答案解析版)

重难点05 天体运动与人造航天器【知识梳理】考点一 天体质量和密度的计算1.解决天体(卫星)运动问题的基本思路(1)天体运动的向心力来源于天体之间的万有引力,即ma r mv r T m r m rMm G ====2222)2(πω(2)在中心天体表面或附近运动时,万有引力近似等于重力,即2R MmG mg =(g 表示天体表面的重力加速度).(2)利用此关系可求行星表面重力加速度、轨道处重力加速度: 在行星表面重力加速度:2R Mm Gmg =,所以2R MG g = 在离地面高为h 的轨道处重力加速度:2)(h R Mm G g m +=',得2)(h R MG g +=' 2.天体质量和密度的计算(1)利用天体表面的重力加速度g 和天体半径R .由于2R Mm G mg =,故天体质量GgR M 2=天体密度:GRgV M πρ43==(2)通过观察卫星绕天体做匀速圆周运动的周期T 和轨道半径r .①由万有引力等于向心力,即r T m rMm G 22)2(π=,得出中心天体质量2324GT r M π=;②若已知天体半径R ,则天体的平均密度3233RGT r V M πρ== ③若天体的卫星在天体表面附近环绕天体运动,可认为其轨道半径r 等于天体半径R ,则天体密度23GTV M πρ==.可见,只要测出卫星环绕天体表面运动的周期T ,就可估算出中心天体的密度. 【重点归纳】 1.黄金代换公式(1)在研究卫星的问题中,若已知中心天体表面的重力加速度g 时,常运用GM =gR 2作为桥梁,可以把“地上”和“天上”联系起来.由于这种代换的作用很大,此式通常称为黄金代换公式. 2. 估算天体问题应注意三点(1)天体质量估算中常有隐含条件,如地球的自转周期为24 h ,公转周期为365天等. (2)注意黄金代换式GM =gR 2的应用. (3)注意密度公式23GTπρ=的理解和应用. 考点二 卫星运行参量的比较与运算 1.卫星的动力学规律由万有引力提供向心力,ma r mv r T m r m rMm G ====2222)2(πω2.卫星的各物理量随轨道半径变化的规律r GM v =;3r GM =ω;GMr T 32π=;2r GM a = (1)卫星的a 、v 、ω、T 是相互联系的,如果一个量发生变化,其它量也随之发生变化;这些量与卫星的质量无关,它们由轨道半径和中心天体的质量共同决定.(2)卫星的能量与轨道半径的关系:同一颗卫星,轨道半径越大,动能越小,势能越大,机械能越大.3.极地卫星和近地卫星(1)极地卫星运行时每圈都经过南北两极,由于地球自转,极地卫星可以实现全球覆盖. (2)近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫星,其运行的轨道半径可近似认为等于地球的半径,其运行线速度约为7.9 km/s. (3)两种卫星的轨道平面一定通过地球的球心. 【重点归纳】1.利用万有引力定律解决卫星运动的一般思路 (1)一个模型天体(包括卫星)的运动可简化为质点的匀速圆周运动模型. (2)两组公式卫星运动的向心力来源于万有引力:ma r mv r T m r m rMm G ====2222)2(πω在中心天体表面或附近运动时,万有引力近似等于重力,即:2R MmGmg = (g 为星体表面处的重2.卫星的线速度、角速度、周期与轨道半径的关系⎪⎪⎩⎪⎪⎨⎧⇒⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫====减小增大减小减小增大时当半径a T v r r GM a GM r T r GM r GM v ωπω2332 考点三 宇宙速度 卫星变轨问题的分析1.第一宇宙速度v 1=7.9 km/s ,既是发射卫星的最小发射速度,也是卫星绕地球运行的最大环绕速度.2.第一宇宙速度的两种求法:(1)r mv r Mm G 212=,所以r GMv =1 (2)rmv mg 21=,所以gR v =1.3.第二、第三宇宙速度也都是指发射速度.4.当卫星由于某种原因速度突然改变时(开启或关闭发动机或空气阻力作用),万有引力不再等于向心力,卫星将变轨运行:(1)当卫星的速度突然增加时,r mv rMm G 22<,即万有引力不足以提供向心力,卫星将做离心运动,脱离原来的圆轨道,轨道半径变大,当卫星进入新的轨道稳定运行时由rGMv =可知其运行速度比原轨道时减小.(2)当卫星的速度突然减小时,r mv rMm G 22>,即万有引力大于所需要的向心力,卫星将做近心运动,脱离原来的圆轨道,轨道半径变小,当卫星进入新的轨道稳定运行时由rGMv =可知其运行速度比原轨道时增大.卫星的发射和回收就是利用这一原理.1.处理卫星变轨问题的思路和方法(1)要增大卫星的轨道半径,必须加速;(2)当轨道半径增大时,卫星的机械能随之增大.2.卫星变轨问题的判断:(1)卫星的速度变大时,做离心运动,重新稳定时,轨道半径变大.(2)卫星的速度变小时,做近心运动,重新稳定时,轨道半径变小.(3)圆轨道与椭圆轨道相切时,切点处外面的轨道上的速度大,向心加速度相同.3.特别提醒:“三个不同”(1)两种周期——自转周期和公转周期的不同(2)两种速度——环绕速度与发射速度的不同,最大环绕速度等于最小发射速度(3)两个半径——天体半径R和卫星轨道半径r的不同【限时检测】(建议用时:30分钟)1.(2019·新课标全国Ⅰ卷)在星球M上将一轻弹簧竖直固定在水平桌面上,把物体P轻放在弹簧上端,P由静止向下运动,物体的加速度a与弹簧的压缩量x间的关系如图中实线所示。
求中心天体的质量与密度
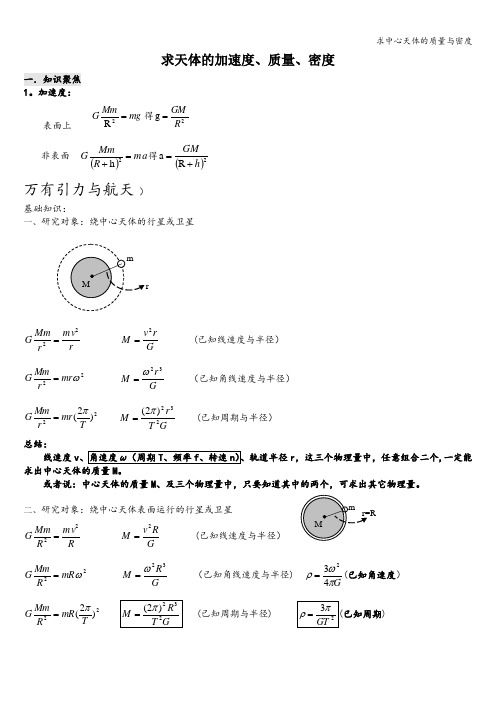
求天体的加速度、质量、密度一.知识聚焦 1。
加速度:表面上 mg MmG=2R得2g R GM = 非表面 ()m a R MmG=+2h 得)(2R a h GM +=万有引力与航天 )基础知识:一、研究对象:绕中心天体的行星或卫星r m v r Mm G 22= G r v M 2= (已知线速度与半径)22ωmr r Mm G = G r M 32ω= (已知角线速度与半径) 22)2(T mr r Mm G π= GT r M 232)2(π= (已知周期与半径) 总结:线速度vr ,这三个物理量中,任意组合二个,一定能求出中心天体的质量M 。
或者说:中心天体的质量M 、及三个物理量中,只要知道其中的两个,可求出其它物理量。
二、研究对象:绕中心天体表面运行的行星或卫星R m v RMm G 22= G R v M 2= (已知线速度与半径)22ωmR R Mm G = G R M 32ω= (已知角线速度与半径) G πωρ432=(已知角速度) 22)2(T mR R Mm G π=已知周期与半径已知周期)如果绕中心天体表面运转,三、研究对象:距离地面h 高处的物体,万有引力等于重力mg h R MmG =+2)( G h R g M 2)(+= (已知某高度处的重力加速度与距离)四、研究对象:地球表面的物体,万有引力等于重力mg R Mm G =2 G gR M 2= (已知中心天体表面的重力加速度与半径) GRgπρ43=训练题(真题)1宇航员站在一星球表面上的某高处,沿水平方向抛出一小球,经过时间t,小球落在星球表面,测得抛出点与落地点之间的距离为L ,若抛出时的初速度增大到2倍,则抛出点与落地点间的距离为3L ,已知两落地点在同一水平面上,该星球的半径为R ,引力常量为G,求该星球的质量M 和密度ρ.图21[解析]此题的关键就是要根据在星球表面物体的运动情况求出星球表面的重力加速度,再根据星球表面物体的重力等于物体受到的万有引力求出星球的质量和星球的密度.根据平抛运动的特点得抛出物体竖直方向上的位移为221gt y =设初始平抛小球的初速度为v ,则水平位移为x=vt .有2222)()21(L vt gt =+ 错误!当以2v 的速度平抛小球时,水平位移为x'= 2vt .所以有2222)3()2()21(L vt gt =+ ②在星球表面上物体的重力近似等于万有引力,有mg=G 2RMm③联立以上三个方程解得22332Gt LR M =而天体的体积为334R V π=,由密度公式V M =ρ得天体的密度为RGt L 223πρ=。
高考物理考题一 天体质量(密度)的估算
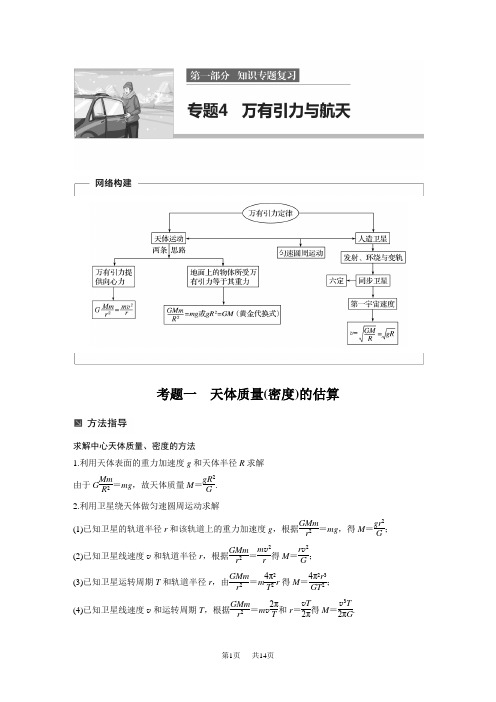
考题一 天体质量(密度)的估算求解中心天体质量、密度的方法1.利用天体表面的重力加速度g 和天体半径R 求解 由于G Mm R 2=mg ,故天体质量M =gR 2G .2.利用卫星绕天体做匀速圆周运动求解(1)已知卫星的轨道半径r 和该轨道上的重力加速度g ,根据GMm r 2=mg ,得M =gr 2G ;(2)已知卫星线速度v 和轨道半径r ,根据GMm r 2=m v 2r 得M =r v 2G ;(3)已知卫星运转周期T 和轨道半径r ,由GMm r 2=m 4π2T 2r 得M =4π2r 3GT 2;(4)已知卫星线速度v 和运转周期T ,根据GMm r 2=m v 2πT 和r =v T 2π得M =v 3T 2πG.3.天体密度的估算一般在质量估算的基础上,利用M =ρ·43πR 3进行.例1 宇宙中有两颗相距无限远的恒星S 1、S 2,半径均为R 0.图1分别是两颗恒星周围行星的公转周期T 2与半径r 3的图象,则( )图1A.恒星S 1的质量大于恒星S 2的质量B.恒星S 1的密度小于恒星S 2的密度C.恒星S 1的第一宇宙速度大于恒星S 2的第一宇宙速度D.距两恒星表面高度相同的行星,S 1的行星向心加速度较大解析 两颗恒星周围的行星绕恒星做匀速圆周运动,万有引力提供向心力,G Mm r 2=m 4π2T 2r ,变形得T 2r 3=4π2GM .故图象的斜率越大,质量越小.故恒星S 1的质量小于恒星S 2的质量.故A 错.因为两颗恒星的半径相等,所以体积相等,故恒星S 1的密度小于恒星S 2的密度,故B 对.由G MmR 2=m v 2R变形后得第一宇宙速度v = GMR,即质量越大,第一宇宙速度越大.故恒星S 1的第一宇宙速度小于恒星S 2的第一宇宙速度,故C 错.行星向心加速度a =GMr 2,行星距两恒星表面高度相同,故质量越大,加速度越大,故D 错. 答案 B 变式训练1.地质勘探发现某地区表面的重力加速度发生了较大的变化,怀疑地下有空腔区域.进一步探测发现在地面P 点的正下方有一球形空腔区域储藏有天然气,如图2所示.假设该地区岩石均匀分布且密度为ρ,天然气的密度远小于ρ,可忽略不计.如果没有该空腔,地球表面正常的重力加速度大小为g ;由于空腔的存在,现测得P 点处的重力加速度大小为kg (k <1).已知引力常量为G ,球形空腔的球心深度为d ,则此球形空腔的体积是( )图2A.kgd GρB.kgdGρ C.(1-k )gd GρD.(1-k )gd 2Gρ答案 D解析 如果将近地表的球形空腔填满密度为ρ的岩石,则该地区重力加速度便回到正常值,因此,如果将空腔填满,地面质量为m 的物体重力为mg ,没有填满时是kmg ,故空腔填满后引起的引力为(1-k )mg ;由万有引力定律,有:(1-k )mg =G ρVmd 2,解得:V =(1-k )gd 2Gρ,D对.2.某行星外围有一圈厚度为d 的发光带(发光的物质),简化为如图3甲所示模型,R 为该行星除发光带以外的半径.现不知发光带是该行星的组成部分还是环绕该行星的卫星群,某科学家做了精确地观测,发现发光带绕行星中心的运行速度与到行星中心的距离r 的关系如图乙所示(图中所标量为已知),则下列说法正确的是( )图3A.发光带是该行星的组成部分B.该行星的质量M =v 20RGC.行星表面的重力加速度g =v 20RD.该行星的平均密度为ρ=3v 20R4πG (R +d )3答案 BC解析 若发光带是该行星的组成部分,则其角速度与行星自转角速度相同,应有v =ωr ,v 与r 应成正比,与图不符,因此该发光带不是该行星的组成部分,故A 错误,发光带是环绕该行星的卫星群,由万有引力提供向心力,则有:G Mm r 2=m v 2r 得该行星的质量为:M =v 2r G;由题图知,r =R 时,v =v 0,则有:M =v 20R G .故B 正确.当r =R 时有mg =m v 2R ,得行星表面的重力加速度g =v 20R ,故C 正确.该行星的平均密度为ρ=M 43πR 3=3v 204πGR 2,故D 错误,故选B 、C.3.“嫦娥二号”绕月卫星于10月1日18时59分57秒在西昌卫星发射中心发射升空,并获得了圆满成功.“嫦娥二号”新开辟了地月之间的“直航航线”,即直接发射至地月转移轨道,再进入距月面约h =1×105 m 的圆形工作轨道,开始进行科学探测活动.设月球半径为R ,月球表面的重力加速度为g 月,万有引力常量为G ,则下列说法正确的是( ) A.由题目条件可知月球的平均密度为3g 月4πGRB.“嫦娥二号”在工作轨道上绕月球运行的周期为2π R G 月C.“嫦娥二号”在工作轨道上的绕行速度为g 月(R +h )D.“嫦娥二号”在工作轨道上运行时的向心加速度为(R R +h )2g 月答案 AD解析 在月球表面重力与万有引力相等,由G mM R 2=mg 月可得月球质量M =g 月R 2G ,据密度公式可得月球密度ρ=MV =g 月R 2G 43πR 3=3g 月4πGR,故A 正确;根据万有引力提供圆周运动的向心力有 G Mm (R +h )2=m (R +h )4π2T 2,可得周期T = 4π2(R +h )3GM= 4π2(R +h )3g 月R 2,故B 错误;根据万有引力提供圆周运动的向心力有 G mM(R +h )2=m v 2R +h可得“嫦娥二号”绕行速度v =GMR +h= g 月R 2R +h,故C 错误; 根据万有引力提供圆周运动的向心力有 G mM (R +h )2=ma , 可得“嫦娥二号”在工作轨道上的向心加速度 a =GM (R +h )2=(R R +h)2g 月,故D 正确. 考题二 人造卫星问题解答卫星问题的三个关键点 1.根据G Mmr2=F向=m v 2r =mrω2=mr 4π2T2=ma ,推导、记忆v = GMr、ω= GMr 3、T = 4π2r 3GM 、a =GMr2等公式. 2.理解掌握第一宇宙速度的意义、求法及数值、单位.3.灵活应用同步卫星的特点,注意同步卫星与地球赤道上物体的运动规律的区别与联系.例2 (·江苏·7)如图4所示,两质量相等的卫星A 、B 绕地球做匀速圆周运动,用R 、T 、E k 、S 分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的有( )图4A.T A >T BB.E k A >E k BC.S A =S BD.R 3A T 2A =R 3B T 2B解析 由GMm R 2=m v 2R =m 4π2T 2R 和E k =12m v 2可得T =2π R 3GM, E k =GMm 2R ,因R A >R B ,则T A >T B ,E k A <E k B ,A 对,B 错; 由开普勒定律可知,C 错,D 对. 答案 AD 变式训练4.(·全国丙卷·14)关于行星运动的规律,下列说法符合史实的是( ) A.开普勒在牛顿定律的基础上,导出了行星运动的规律 B.开普勒在天文观测数据的基础上,总结出了行星运动的规律C.开普勒总结出了行星运动的规律,找出了行星按照这些规律运动的原因D.开普勒总结出了行星运动的规律,发现了万有引力定律 答案 B解析 开普勒在天文观测数据的基础上总结出了开普勒天体运动三定律,找出了行星运动的规律,而牛顿发现了万有引力定律.5.水星或金星运行到地球和太阳之间,且三者几乎排成一条直线的现象,天文学称为“行星凌日”.已知地球的公转周期为365天,若将水星、金星和地球的公转轨道视为同一平面内的圆轨道,理论计算得到水星相邻两次凌日的时间间隔为116天,金星相邻两次凌日的时间间隔为584天,则下列判断合理的是( ) A.地球的公转周期大约是水星的2倍 B.地球的公转周期大约是金星的1.6倍 C.金星的轨道半径大约是水星的3倍D.实际上水星、金星和地球的公转轨道平面存在一定的夹角,所以水星或金星相邻两次凌日的实际时间间隔均大于题干所给数据 答案 BD解析 水星相邻两次凌日的时间间隔为t =116天, 设水星的周期为T 1,则有:2πT 1t -2πT 2t =2π, 代入数据解得T 1≈88天,可知地球公转周期大约是水星的4倍,故A 错误; 金星相邻两次凌日的时间间隔为584天,设金星的周期为T 3,则有:2πT 3t -2πT 2t =2π,代入数据解得T 3≈225天,可知地球的公转周期大约是金星的1.6倍,故B 正确; 根据G Mm r 2=mr (2πT )2,得r = 3GMT 24π2,因为水星的公转周期大约是金星的0.4倍,则水星的轨道半径大约是金星的0.5倍,故C 错误;由所给资料,若运行轨道平面不存在夹角,那么行星凌日间隔时间会与理论时间一致,而实际与理论不同,故运行轨道平面必然存在夹角,故D 正确.考题三 双星与多星问题1.双星问题的模型构建对于做匀速圆周运动的双星问题,双星的角速度(周期)以及向心力大小相等,基本方程式为G M 1M 2L 2=M 1r 1ω2=M 2r 2ω2,式中L 表示双星间的距离,r 1,r 2分别表示两颗星的轨道半径,L =r 1+r 2.2.做匀速圆周运动的双星问题中需要注意的几个关键点(1)双星绕它们连线上的某点做匀速圆周运动,两星轨道半径之和与两星距离相等; (2)双星做匀速圆周运动的角速度必相等,因此周期也必然相等;(3)双星做匀速圆周运动的向心力由双星间相互作用的万有引力提供,大小相等;(4)列式时须注意,万有引力定律表达式中的r 表示双星间的距离,而不是轨道半径(双星系统中两颗星的轨道半径一般不同).抓住以上四个“相等”,即向心力、角速度、周期相等,轨道半径之和与两星距离相等,即可顺利求解此类问题.例3 (12分)天体A 和B 组成双星系统,围绕两球心连线上的某点做匀速圆周运动的周期均为T .天体A 、B 的半径之比为2∶1,两天体球心之间的距离为R ,且R 远大于两天体的半径.忽略天体的自转,天体A 、B 表面重力加速度之比为4∶1,引力常量为G ,求A 天体的质量. [思维规范流程]每式各2分. 变式训练6.美国在2月11日宣布“探测到引力波的存在”.天文学家通过观测双星轨道参数的变化来间接验证引力波的存在,证实了GW150914是一个36倍太阳质量的黑洞和一个29倍太阳质量的黑洞合并事件.假设这两个黑洞绕它们连线上的某点做圆周运动,且这两个黑洞的间距缓慢减小.若该黑洞系统在运动过程中各自质量不变且不受其他星系的影响,则关于这两个黑洞的运动,下列说法正确的是( ) A.这两个黑洞运行的线速度大小始终相等B.这两个黑洞做圆周运动的向心加速度大小始终相等C.36倍太阳质量的黑洞轨道半径比29倍太阳质量的黑洞轨道半径大D.随两个黑洞的间距缓慢减小,这两个黑洞运行的周期也在减小 答案 D解析 这两个黑洞共轴转动,角速度相等,根据v =ωr 可知,由于不知道两个黑洞的转动半径关系,所以线速度大小不一定相等,故A 错误;根据a =ω2r 可知,由于不知道两个黑洞的转动半径关系,所以向心加速度大小不一定相等,故B 错误;两个黑洞都是做圆周运动,则Gm 1m 2r 2=m 1ω2r 1=m 2ω2r 2,可以得到半径与质量成反比关系,质量大的半径小,故选项C 错误;根据G m 1m 2r 2=m 14π2r 1T 2可得,m 2=4π2r 2GT 2r 1,根据G m 1m 2r 2=m 24π2r 2T 2可得,m 1=4π2r 2T 2r 2,所以m 1+m 2=4π2r 2GT 2(r 1+r 2)=4π2r 3GT 2,当m 1+m 2不变时,r 减小,则T 减小,即双星系统运行周期会随间距减小而减小,故D 正确.7.由三颗星体构成的系统,叫做三星系统.有这样一种简单的三星系统:质量刚好都相同的三个星体a 、b 、c 在三者相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O 在三角形所在的平面内做相同周期的圆周运动,若三个星体的质量均为m ,三角形的边长为a ,万有引力常量为G ,则下列说法正确的是( ) A.三个星体做圆周运动的轨道半径为a B.三个星体做圆周运动的周期均为2πaa3GmC.三个星体做圆周运动的线速度大小均为3GmaD.三个星体做圆周运动的向心加速度大小均为3Gma 2答案 B解析 由几何关系知,它们的轨道半径为r =a 232=33a ,故A 错误;根据合力提供向心力有:2·Gm 2a 2cos 30˚=ma ′=m v 2r =mr 4π2T 2,得星体做圆周运动的周期为:T =2πa a3Gm,线速度为:v =Gm a ,向心加速度为:a ′=3Gma2,故B 正确,C 、D 错误. 专题规范练1.有研究表明,目前月球远离地球的速度是每年3.82±0.07 cm.则10亿年后月球与现在相比( )A.绕地球做圆周运动的周期变小B.绕地球做圆周运动的加速度变大C.绕地球做圆周运动的线速度变小D.地月之间的引力势能变小 答案 C解析 对月球进行分析,根据万有引力提供向心力,则:GMm r 2=m (2πT)2r ,则:T =4π2r 3GM,由于半径变大,故周期变大,故选项A 错误.根据GMm r 2=ma ,则:a =GMr 2,由于半径变大,故加速度变小,故选项B 错误;根据GMmr 2=m v 2r,则v =GMr,由于半径变大,故线速度变小,故选项C 正确;由于月球远离地球,万有引力做负功,故引力势能变大,故选项D 错误.2.3月8日,马来西亚航空公司从吉隆坡飞往北京的航班MH370失联,MH370失联后多个国家积极投入搜救行动,在搜救过程中卫星发挥了巨大的作用.其中我国的北斗导航系统和美国的GPS 导航系统均参与搜救工作,北斗导航系统包含5颗地球同步卫星,而GPS 导航系统由运行周期为12小时的圆轨道卫星群组成,下列说法正确的是( ) A.发射人造地球卫星时,发射速度只要大于7.9 km/s 就可以 B.北斗同步卫星的线速度与GPS 卫星的线速度之比为312C.北斗同步卫星的机械能一定大于GPS 卫星的机械能D.卫星向地面上同一物体拍照时,GPS 卫星的拍摄视角小于北斗同步卫星的拍摄视角 答案 B解析 发射不同的人造地球卫星,发射速度要求是不相同的,故A 错;北斗同步卫星的周期是24 h ,GPS 导航系统卫星的周期为12小时,根据开普勒第三定律可得半径比为34,万有引力提供向心力,由v =GMr ,得线速度之比为312,B 对;不知道北斗同步卫星和GPS 卫星的质量,无法比较机械能,C 错;GPS 卫星半径小于北斗同步卫星运动半径,得GPS 卫星的拍摄视角大于北斗同步卫星的拍摄视角,D 错.3.(多选)我国志愿者王跃曾与俄罗斯志愿者一起进行“火星 500”的模拟实验活动.假设王跃登陆火星后,测得火星的半径是地球半径的12,质量是地球质量的19.已知地球表面的重力加速度是g ,地球的半径为R ,王跃在地球表面能竖直向上跳起的最大高度为h ,忽略自转的影响.下列说法正确的是( ) A.火星的密度为2g3πGRB.火星的第一宇宙速度与地球的第一宇宙速度相等C.火星表面的重力加速度为4g 9D.王跃在火星表面能竖直向上跳起的最大高度为9h4答案 ACD4.(·四川理综·3)国务院批复,自起将4月24日设立为“中国航天日”.1970年4月24日我国首次成功发射的人造卫星东方红一号,目前仍然在椭圆轨道上运行,其轨道近地点高度约为440 km ,远地点高度约为2 060 km ;1984年4月8日成功发射的东方红二号卫星运行在赤道上空35 786 km 的地球同步轨道上.设东方红一号在远地点的加速度为a 1,东方红二号的加速度为a 2,固定在地球赤道上的物体随地球自转的加速度为a 3,则a 1、a 2、a 3的大小关系为( ) A.a 2>a 1>a 3 B.a 3>a 2>a 1 C.a 3>a 1>a 2 D.a 1>a 2>a 3答案 D解析 由于东方红二号卫星是同步卫星,则其角速度和赤道上的物体角速度相等,根据a =ω2r ,r 2>r 3,则a 2>a 3;由万有引力定律和牛顿第二定律得,G Mmr 2=ma ,由题目中数据可以得出,r 1<r 2,则a 2<a 1;综合以上分析有,a 1>a 2>a 3,选项D 正确.5.(·天津理综·3)如图1所示,我国即将发射“天宫二号”空间实验室,之后发射“神舟十一号”飞船与“天宫二号”对接.假设“天宫二号”与“神舟十一号”都围绕地球做匀速圆周运动,为了实现飞船与空间实验室的对接,下列措施可行的是( )图1A.使飞船与空间实验室在同一轨道上运行,然后飞船加速追上空间实验室实现对接B.使飞船与空间实验室在同一轨道上运行,然后空间实验室减速等待飞船实现对接C.飞船先在比空间实验室半径小的轨道上加速,加速后飞船逐渐靠近空间实验室,两者速度接近时实现对接D.飞船先在比空间实验室半径小的轨道上减速,减速后飞船逐渐靠近空间实验室,两者速度接近时实现对接 答案 C解析 若使飞船与空间实验室在同一轨道上运行,然后飞船加速,所需向心力变大,则飞船将脱离原轨道而进入更高的轨道,不能实现对接,选项A 错误;若使飞船与空间实验室在同一轨道上运行,然后空间实验室减速,所需向心力变小,则空间实验室将脱离原轨道而进入更低的轨道,不能实现对接,选项B 错误;要想实现对接,可使飞船在比空间实验室半径小的轨道上加速,然后飞船将进入较高的空间实验室轨道,逐渐靠近空间实验室后,两者速度接近时实现对接,选项C 正确;若飞船在比空间实验室半径小的轨道上减速,则飞船将进入更低的轨道,不能实现对接,选项D 错误.6.(多选)已知地球自转周期为T 0,有一颗与同步卫星在同一轨道平面的低轨道卫星,自西向东绕地球运行,其运行半径为同步轨道半径的四分之一,该卫星两次在同一城市的正上方出现的时间间隔可能是( ) A.T 04 B.3T 04 C.3T 07 D.T 07答案 CD解析 设地球的质量为M ,卫星的质量为m ,运动周期为T ,因为卫星做圆周运动的向心力由万有引力提供,有:GMm r 2=4π2mrT2,解得:T =2πr 3GM. 同步卫星的周期与地球自转周期相同,即为T 0.已知该人造卫星的运行半径为同步卫星轨道半径的四分之一,所以该人造卫星与同步卫星的周期之比是:T T 0=r 3(4r )3=18,解得T =18T 0.设卫星至少每隔t 时间才在同一地点的正上方出现一次,根据圆周运动角速度与所转过的圆心角的关系θ=ωt 得:2πT t =2n π+2πT 0t ,解得t =nT 07,当n =1时t =T 07,n =3时t =3T 07,故A 、B 错误,C 、D 正确.7.据新华社北京3月21日电,记者21日从中国载人航天工程办公室了解到,已在轨工作1 630天的“天宫一号”目标飞行器在完成与三艘神舟飞船交会对接和各项试验任务后,由于超期服役两年半时间,其功能已于近日失效,正式终止了数据服务.根据预测,“天宫一号”的飞行轨道将在今后数月内逐步降低,并最终进入大气层烧毁.若“天宫一号”服役期间的轨道可视为圆且距地面h (h ≈343 km),运行周期为T ,地球的半径为R ,下列关于“天宫一号”的说法正确的是( )A.因为“天宫一号”的轨道距地面很近,其线速度小于同步卫星的线速度B.女航天员王亚平曾在“天宫一号”中漂浮着进行太空授课,那时她不受地球的引力作用C.“天宫一号”进入外层稀薄大气一小段时间内,克服气体阻力的功小于引力势能的减小量D.由题中信息可知地球的质量为4π2R 3GT 2答案 C解析 根据万有引力提供向心力可知:G Mmr 2=m v 2r,解得:v =GMr,由于“天宫一号”的轨道半径小于同步卫星的半径,则其线速度大于同步卫星的线速度,故A 错误;航天员在“天宫一号”中处于失重状态,地球对她的万有引力提供她随“天宫一号”围绕地球做圆周运动的向心力,不是不受地球的引力作用,故B 错误;根据动能定理可知引力与空气阻力对“天宫一号”做的总功应为正值,而引力做的功等于引力势能的减少,即“天宫一号”克服气体阻力做的功小于引力势能的变化,故C 正确; 根据万有引力提供向心力可知, G Mm(R +h )2=m 4π2(R +h )T 2, 解得:M =4π2(R +h )3GT 2,故D 错误.8.宇宙间是否存在暗物质是物理学之谜,对该问题的研究可能带来一场物理学的革命.为了探测暗物质,我国在12月17日成功发射了一颗被命名为“悟空”的暗物质探测卫星.已知“悟空”在低于同步卫星的轨道上绕地球做匀速圆周运动,经过时间t (t 小于其运动周期),运动的弧长为L ,与地球中心连线扫过的角度为θ(弧度),引力常量为G ,则下列说法中正确的是( )A.“悟空”的质量为L 3Gθt 2B.“悟空”的环绕周期为2πtθC.“悟空”的线速度大于第一宇宙速度D.“悟空”的向心加速度小于地球同步卫星的向心加速度 答案 B解析 “悟空”绕地球做匀速圆周运动,根据万有引力提供向心力,只能求出地球质量,不能求出“悟空”的质量,故A 错误;“悟空”经过时间t (t 小于“悟空”的周期),它运动的弧长为L ,它与地球中心连线扫过的角度为θ(弧度),则“悟空”的角速度为:ω=θt ,周期T=2πω=2πtθ,故B 正确;“悟空”在低于地球同步卫星的轨道上绕地球做匀速圆周运动,万有引力提供向心力,则有:GMmr 2=m v 2r,得v =GMr,可知卫星的轨道半径越大,速率越小,第一宇宙速度是近地卫星的环绕速度,故“悟空”在轨道上运行的速度小于地球的第一宇宙速度,故C 错误;由GMm r 2=ma 得:加速度a =G Mr 2,则知“悟空”的向心加速度大于地球同步卫星的向心加速度,故D 错误.9.一半径为R 、密度均匀的自行旋转的行星,其赤道处的重力加速度为极地处重力加速度的n 倍(n <1).求该行星的同步卫星距离地面的高度.答案 (311-n-1)R 解析 设行星的质量为M ,自转的角速度为ω,其极地处的重力加速度为g .对质量为m 1的物体位于极地和赤道时,根据万有引力定律 G Mm 1R2=m 1g G Mm 1R2-nm 1g =m 1Rω2 设同步卫星的质量为m 2,距离地面的高度为h ,根据万有引力定律 G Mm 2(R +h )2=m 2(R +h )ω2 整理得h = (311-n-1)R . 10.假设某天你在一个半径为R 的星球上,手拿一只小球从离星球表面高h 处无初速度释放,测得小球经时间t 落地.若忽略星球的自转影响,不计一切阻力,万有引力常量为G .求: (1)该星球的质量M ;(2)在该星球上发射卫星的第一宇宙速度大小v . 答案 (1)2hR 2Gt 2 (2)2hRt解析 (1)根据h =12gt 2可知g =2ht 2由GMmR 2=mg 可得M =2hR 2Gt2(2)根据GMmR 2=mg =m v 2R可得v =2hRt.。
万有引力定律

点击进入相应模块
5.(2012·门头沟一模)我国成功地发射了“嫦娥一号”探月 卫星,其轨道示意图如图所示。卫星进入地球轨道后还需要对 卫星进行10次点火控制。第一次点火,抬高近地点,将近地点 抬高到约600 km处,第二、三、四次点火,让卫星不断变轨加
速,经过三次累积,卫星加速到11.0 km/s的速度进入地月转
A.该卫星的发射速度必定小于11.2km/s
B.卫星在椭圆轨道Ⅰ运行的过程中,经过A点的速度大 于经过B点的速度
C.卫星沿轨道Ⅱ运动的周期小于沿轨道І运动的周期
D.卫星在椭圆轨道Ⅰ经过B点时的机械能大于在圆轨道 Ⅱ经过B点时的机械能
A Ⅱ Ⅰ O B
点击进入相应模块
2.我国未来将建立月球基地,并在绕月轨道上建造空间站。如
4 2 r 3 C.月球的质量为 M GT 2
)
D.月球的第一宇宙速度为 2r
T
点击进入相应模块
如图所示,a为地球赤道上的物体;b为沿地球表面附近做匀 速圆周运动的人造卫星;c为地球同步卫星。关于a、b、c做 匀速圆周运动的说法中正确的是 A.角速度的大小关系为
a c b
B.向心加速度的大小关系为 a a a a b c C.线速度的大小关系为 v a vb vc D.周期关系为 T T T a c b
点击进入相应模块
移轨道向月球飞去。后6次点火的主要作用是修正飞行方向和 被月球捕获时的紧急刹车,最终把卫星送入离月面200 km高的 工作轨道(可视为匀速圆周运动)。已知地球质量是月球质量的 81倍,R月=1 800 km,R地=6 400 km,卫星质量为2 350 kg ,地球 表面重力加速度g取10 m/s2。(涉及开方可估算,结果保留一 位有效数字)求:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
G
Mm r2
m
2
T
2
r
M
4 2r3
GT 2
球体的体积公式:V 4 R3
3
三、计算天体的密度 求解中心天体质量和密度
创新微课
已知太阳某行星的公转周期T、轨道半径r, 太阳的半径R,求太阳的密度?
F引=Fn
G
Mm r2
m
2
T
2
r
M
4 2r3
F引=Fn
只可求出中心天体的质量, 求不出环绕体的质量。
求解中心天体质量和密度
创新微课
这种方法可以计算中心天体的质量
如已知:
月亮周期:
T
月亮轨道半径: r
求 地球的质量 M?
F引=Fn
求解中心天体质量和密度
创新微课
二、计算中心天体的质量
如果不知道环绕体的公转周期,而知
道环绕体的线速度或角速度及其轨道半径,
黄金代换:GM=gR 2
2.将行星(或卫星)的运动看成 是匀速圆周运动.
3.万有引力充当向心力 F引=F向
明确各个物理量 求解中心天体质量和密度
创新微课
转动天体m
轨道半经r
中心天体M 天体半经R
同学,下节再见
创新微课 现在开始
行星运动的三定律
求解中心天体质量和密度
创新微课
一、“称量地球的质量” 求解中心天体质量和密度
创新微课
黄金代换:GM=gR 2
g---半径
求解中心天体质量和密度
二、计算太阳的质量
创新微课
我们可以测出太阳某行星的公转周期T、轨道半径r, 能不能由此求出太阳的质量M?
②
得:
求解中心天体质量和密度
思考讨论
创新微课
2020年我们班的某同学驾驶 着神州20号宇宙飞船飞近某一 不知名的行星,并进入靠近该行星 表面的圆形轨道运行, 对该行星进 行观测.需要测定该行星的密度 请同学们帮他想想办法.
二、计算天体的密度 求解中心天体质量和密度
创新微课
已知太阳某行星的公转周期T、轨道半径r, 太阳的半径R,求太阳的密度?
能不能求出中心天体的质量?
F引=Fn
G
Mm r2
m
v r
2
G
Mm r2
m
2r
练习 求解中心天体质量和密度
创新微课
登月密封舱在离月球表面h处的空中沿圆 形轨道运行,周期是T,已知月球的半径是R, 万有引力常数是G,据此试计算月球的质量。
r R
解:登月密封舱相当于月 球的卫星,对密封舱有:
①
r = R +h
GT 2
3r 3
GT 2R3
三、计算天体的密度 求解中心天体质量和密度
创新微课
已知地球的一颗人造卫星的公转周期T、轨 道半径r,地球的半径R,求地球的密度?
3r 3
GT 2 R3
此卫星是一近地卫星,地球的密度又是多少呢?
3
GT 2
小结:基本思路 求解中心天体质量和密度
创新微课
1. 在星体表面附近 F引=G重
