6.3实数(第1课时)(作业)
人教版七年级数学下册第6章习题课件6.3.1 实数及其分类

6.3 实数 第1课时 实数及其分类
提示:点击 进入习题
1 无理数 (1)开不尽 2D
3D 4B 5 见习题
6D 7A 8 见习题
答案显示
9 一一对应;实数;实数
10 D
提示:点击 进入习题
11 C 12 C 13 见习题 14 见习题 15 见习题
16 见习题 17 见习题
答案显示
12.(2019·包头) 实数 a,b 在数轴上的对应点的位置如图所示,
下列结论正确的是( C )
A.a>b C.-a>b
B.a>-b D.-a<b
13.面积为 7 的正方形的边长为 x. 请你回答下列问题: (1)x 的整数部分是多少? (2)把 x 的值精确到十分位是多少?精确到百分位呢? (3)x 是有理数吗? 解:设正方形的面积为 S,则 S=x2=7. 当 2<x<3 时,4<S<9; 当 2.6<x<2.7 时,6.76<S<7.29;
16.小明同学在学习了本章的内容后设计了如下问题: 定义:把形如 a+b m和 a-b m (a,b 为有理数且 b≠0,m 为正整数且开方开不尽)的两个实数称为共轭实数.
(1)请你写出一对共轭实数. 解:答案不唯一,如:3+2 2与 3-2 2等.
(2)3 2与-2 3是共轭实数吗?-2 3与 2 3是共轭实数吗? 解:因为 3 2与-2 3的被开方数不相同, 所以 3 2与-2 3不是共轭实数; 而-2 3与 2 3的被开方数都是 3,且 a=0,b=2 或 b=-2, 所以-2 3与 2 3是共轭实数.
所以 b=-2,a=3. 所以 ba=(-2)3=-8. 问题:设 x,y 都是有理数,且满足 x2-2y+ 5y=10+3 5, 求 x+y 的值. 解:原式可化为(x2-2y-10)+ 5(y-3)=0, 因为 x,y 都是有理数,所以 x2-2y-10,y-3 也是有理数. 因为 5是无理数,所以 y-3=0,x2-2y-10=0. 解得 y=3,x=±4,故 x+y=7 或-1.
七年级数学下册(人教版)6.3.1实数的相关概念及分类(第一课时)优秀教学案例

五、案例亮点
1.生活情境的创设:通过购物找零的实际例子,让学生感受到实数的实际意义,激发学生的学习兴趣,提高学生对实数的理解和运用能力。
2.问题导向的设计:通过设计具有启发性和针对性的问题,引导学生进行思考和探究,激发学生的思维活力,培养学生的解决问题的能力。
4.运用实际例子,引导学生将实数知识应用到生活中,培养学生的实践能力和创新意识。
(三)情感态度与价值观
1.培养学生对数学的兴趣和热情,使学生感受到数学的趣味性和魅力,激发学生学习数学的内在动力。
2.培养学生的团队合作意识,使学生在合作交流中体验到学习的乐趣,增强学习的自信心。
3.培养学生严谨治学的态度,使学生养成认真思考、细致观察的学习习惯,提高学生的学习效果。
2.利用数轴情境导入:在数轴上标出几个关键点,如0, 1, -1等,引导学生观察实数在数轴上的位置,引出实数的分类。
3.利用故事情境导入:讲述“兔子与胡萝卜”的故事,引发学生对实数的思考,如兔子每天跑的距离是无理数,胡萝卜的数量是有理数,引出实数的概念和分类。
(二)讲授新知
1.实数的定义和分类:讲解实数的概念,引导学生理解实数是包括有理数和无理数两大类的数,并讲解实数与数轴的关系。
5.教学策略的灵活运用:结合学生的认知水平和学习兴趣,设计丰富的教学活动,注重引导学生通过自主探究、合作交流,深入理解实数的本质特征和分类依据,提高实数知识的系统性和灵活运用能力。同时,运用多媒体教学手段,直观地展示实数的性质和规律,帮助学生更好地理解和掌握实数知识。
(二)过程与方法
1.通过自主探究、合作交流,培养学生的动手操作能力和思维能力,提高学生对实数概念和分类的理解。
2019年春七年级数学下册实数第1课时实数的概念同步练习(新版)新人教版

6.3 第1课时 实数的概念知识点 1 无理数的定义 1.下列说法正确的是( ) A .无限小数是无理数 B .有根号的数是无理数 C .无理数是开方开不尽的数D .无理数包括正无理数和负无理数 2.任何一个有理数都可以写成________________的形式,反过来,任何________________都是有理数.3.下列各数中:-14,3.14159,-π,π5,0,0.3,15,5.2·01·,2.121122111222…,其中无理数有________________________.知识点 2 实数的定义与分类 4.能够组成全体实数的是( ) A .自然数和负数 B .整数和分数 C .有理数和无理数D .正数和负数 5.下列说法正确的是( ) A .正实数和负实数统称实数 B .正数、零和负数统称为有理数 C .带根号的数和分数统称实数 D .无理数和有理数统称为实数6.按大小分,实数可分为________、________、________三类. 7.把下列各数分别填入相应的数集里.-13π,-2213,7,327,0.324371,0.5,39,-0.4,16,0.8080080008… 无理数集合{ …}; 有理数集合{ …}; 分数集合{ …}; 负实数集合{ …}.知识点 3 实数与数轴的关系8.和数轴上的点成一一对应关系的数是( ) A .自然数 B .有理数 C .无理数 D .实数9.如图6-3-1,数轴上的A ( )A .点AB .点BC .点CD .点D知识点 4 实数的相反数、绝对值 10.2的相反数是( )A .- 2 B. 2 C.12D .211.若m ,n 互为相反数,则式子|m -5+n |=________. 12.在数轴上表示-6的点到原点的距离为________. 13.求下列各数的相反数和绝对值.(1)-2; (2)-364; (3)π-3.14.求下列各式中的x . (1)|x |=35; (2)|x |=17.15.下列各组数中互为相反数的是( ) A .5和(-5)2B .-|-5|和-(-5)C .-5和3-125 D .-5和1516.实数a 对应的点在数轴上的位置如图6-3-2所示,则a ,-a ,1a的大小关系为( )图6-3-2A.1a <a <-a B .-a <1a<aC .a <1a <-a D.1a<-a <a17.已知a 为实数,则下列四个数中一定为非负数的是( )A .a B.3a C .|-a | D .-|-a |18.如图6-3-3,数轴上A ,B 两点表示的数分别为2和5.1,则A ,B 两点之间表示整数的点共有( )图6-3-3A .6个B .5个C .4个D .3个19.3-2的相反数是________,绝对值是________.20.有九个数:0.1427,(-0.5)3,3.1416,121,327,2.5,227,-2π,0.2020020002…,若无理数的个数为x ,整数的个数为y ,非负数的个数为z ,则x +y +z =________.21.如图6-3-4,A 是硬币圆周上一点,硬币与数轴相切于原点O (点A 与点O 重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A 恰好与数轴上的点A ′重合,则点A ′对应的实数是________.图6-3-422.已知实数a ,b 在数轴上的对应点的位置如图6-3-5所示,试化简:(a -b )2-|a +b |.图6-3-523.已知实数a ,b ,c ,d ,e ,f ,且a ,b 互为倒数,c ,d 互为相反数,e 的绝对值为2,f 的算术平方根是8,求12ab +c +d 5+e 2+3f 的值.24.先阅读下面的文字,再解答问题.大家知道2是无理数,而无理数是无限不循环小数,因此2的小数部分我们不可能全部地写出来,于是小明用2-1来表示2的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为2的整数部分是1,将这个数减去其整数部分,差就是小数部分.已知:10+3=x+y,其中x是整数,且0<y<1,求x-y的值.教师详解详析1.D [解析] A 项不正确,无限不循环小数是无理数.B 项不正确,有根号的数不一定是无理数,如4,38等.C 项不正确,π及类似1.010010001…(两个1之间0的个数逐次加1)的数也是无理数.2.有限小数或无限循环小数 有限小数或无限循环小数3.-π,π5,2.121122111222…4.C 5.D 6.正实数 0 负实数7.解:无理数集合{-13π,7,39,-0.4,0.8080080008…,…};有理数集合{-2213,327,0.324371,0.5,16,…};分数集合{-2213,0.324371,0.5,…};负实数集合{-13π,-2213,-0.4,…}.8.D [解析] ∵任何实数都可以用数轴上的点来表示,数轴上的任何一点都表示一个实数,∴和数轴上的点成一一对应关系的数是实数. 故选D . 9.B [解析] ∵3≈1.732, ∴-3≈-1.732.∵点A ,B ,C ,D 表示的数分别为-3,-2,-1,2,∴与数-3表示的点最接近的是点B.故选B . 10.A11. 5 [解析] 由题意m ,n 互为相反数,可知m +n =0,则|m -5+n|= 5.12. 6 [解析] 数轴上表示-6的点到原点的距离为-6的绝对值,|-6|= 6. 13.解:(1)-2的相反数为2,绝对值为||-2= 2. (2)-364的相反数为364=4,绝对值为⎪⎪⎪⎪-364=364=4.(3)π-3的相反数为3-π,因为π>3,所以绝对值为||π-3=π-3.14.解:(1)x =±35.(2)x =±17.15.B [解析] 只有符号不同的两个数互为相反数,它们的和为0,由此可判定选项.A 中(-5)2=5,两个数相等,故错误;B 中-|-5|=-5,-(-5)=5,-5与5互为相反数,故正确;C 中3-125=-5,两个数相等,故错误;D 中-5和15既不是相反数,也不是倒数,故错误.故选B .16.A [解析] 采用特殊值法来解决.不妨设a =-12,则-a =12,1a =-2.因为-2<-12<12,所以1a<a <-a.故选A .17.C [解析] 选项A 中的a 可以表示任何实数.选项B 中的3a 的符号与a 相同,所以也可以表示任何实数.选项C 中的|-a|表示-a 的绝对值,根据绝对值的意义,可知|-a|为非负数.选项D 中的-|-a|表示|-a|的相反数,由于|-a|为非负数,所以-|-a|为非正数.故选C .18.C [解析] 因为1<2<2,5<5.1<6,所以A ,B 两点之间表示整数的点有表示2,3,4,5的点,共有4个.故选C .19.2- 3 3- 2 [解析] 3-2的相反数是-(3-2)=-3+2=2-3.3-2是一个正实数,正实数的绝对值等于它本身.20.12 [解析] 无理数有 2.5,-2π,0.2020020002…,所以x =3.整数有121,327,所以y =2.非负数有0.1427,3.1416,121,327, 2.5,227,0.2020020002…,所以z=7,所以x +y +z =3+2+7=12.21.π [解析] 将硬币沿数轴正方向滚动一周,点A 恰好与数轴上的点A′重合,则点A 转过的距离是圆的周长,即π,因而点A′对应的实数是π.22.解: 根据数轴可得出:a -b >0,a +b <0,∴(a -b )2-|a +b|=(a -b)+(a +b)=2a. 23.解:因为a ,b 互为倒数,所以ab =1. 因为c ,d 互为相反数,所以c +d =0. 因为e 的绝对值为2,所以e =±2,所以e 2=(±2)2=2.因为f 的算术平方根是8,所以f =64,所以3f =364=4,所以12ab +c +d 5+e 2+3f =12+0+2+4=612.24.解:由1<3<2,得11<10+3<12.由x 是整数,且0<y<1,得x =11, y =10+3-11=3-1,从而x -y =11-(3-1)=12- 3.。
6.3实数

运用新知
例题2、把下列各数填入相应的集合内:
15 ,4
,
16
,2
,3
27
,0.15
,
7.5
,
π
,0
•
,2.3
.
3
①有理数集合:{
…};
②无理数集合:{
…};
③正实数集合:{
…};
④负实数集合:{
…}.
5 0.5 9
有限小数和无限循环小数叫有理数
探究新知
把下列各数写成小数的形式:
2 1.4142 3 3 1.442
3 1.7320
3 5 1.710
5 2.2360 3 7 1.913
3.14159265
无限不循环小数叫无理数
探究新知
思考:π是无理数吗?1.010 010 001 00001…
运用新知
例3 在数轴上表示下列各点,比较它们的大小, 并用“<”连接它们.
1 2 -2 5 3
-2 -1 0 1 2 3
-2< 3 < 1< 2 < 5
例4 估计 5 1 位于( B )
A.0~1之间 B.1~2之间 C.2~3之间
D.3~4之间
归纳 熟记一些常见数的算术平方根;或用计算器估计.
旧知回顾
3、有理数包括哪些数?
整数
正有理数
有理数
分数
有理数
零 负有理数
像 5,
2 5
,
27
8,
6
13
11 , 90 ,
8
9.
《实数》第一课时练习题(含答案)
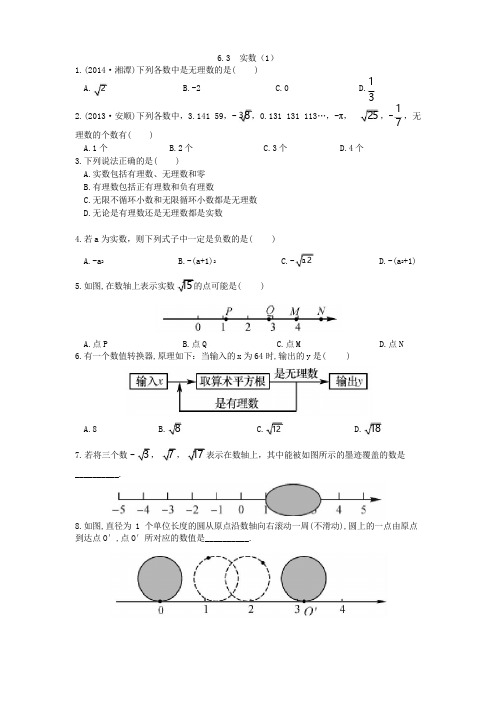
6.3实数(1)1.(2014·湘潭)下列各数中是无理数的是()A.2B.-2C.0D.132.(2013·安顺)下列各数中,3.14159,-38,0.131131113…,-π,25,-理数的个数有()A.1个B.2个C.3个D.4个3.下列说法正确的是()A.实数包括有理数、无理数和零B.有理数包括正有理数和负有理数C.无限不循环小数和无限循环小数都是无理数D.无论是有理数还是无理数都是实数4.若a为实数,则下列式子中一定是负数的是()17,无A.-a2B.-(a+1)2C.-a2D.-(a2+1)5.如图,在数轴上表示实数15的点可能是()A.点PB.点QC.点MD.点N6.有一个数值转换器,原理如下:当输入的x为64时,输出的y是()A.8B.8C.12D.187.若将三个数-3,7,17表示在数轴上,其中能被如图所示的墨迹覆盖的数是__________.8.如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周(不滑动),圆上的一点由原点到达点O′,点O′所对应的数值是__________.9.有六个数:0.1427,(-0.5)3,3.1416,227,-2π,0.1020020002…,若无理数的个数为x,整数的个数为y,非负数的个数为z,求x+y+z的值.10.小明知道了2是无理数,那么在数轴上是否能找到距原点距离为2的点呢?小颖在数轴上用尺规作图的方法作出了在数轴上到原点距离等于2的点,如图.小颖作图说明了什么?参考答案1.A2.B3.D4.D5.C6.B7.78.π9.由题意得无理数有2个,所以x=2;整数有0个,所以y=0,非负数有4个,所以z=4,所以x+y+z=2+0+4=6.10.①每一个无理数都可以用数轴上的一个点表示出来,也就是数轴上的点有些表示有理数,有些表示无理数;②到原点距离等于某一个数的实数有两个.。
同步训练015——6.3实数第一课时

同步训练015——6.3实数第一课时方案一一.选择题:(48分) 1. 9的平方根是 ( )A .3 B.-3 C. ±3 D. 81 2. 下列各数中,不是无理数的是 ( )A 7B 0.5C 2πD 0.151151115…)个之间依次多两个115( 3. 下列说法正确的是( )A. 有理数只是有限小数B. 无理数是无限小数C. 无限小数是无理数D. 3π是分数4. 下列说法错误的是( )A. 1的平方根是1B. –1的立方根是-1C. 2是2的平方根D. –3是2)3(-的平方根5. 若规定误差小于1, 那么60的估算值为( )A. 3B. 7C. 8D. 7或8 6. 和数轴上的点一一对应的是( )A 整数B 有理数C 无理数D 实数 7. 下列说法正确的是( )A.064.0-的立方根是0.4B.9-的平方根是3±C.16的立方根是316 D.0.01的立方根是0.000001 8. 若a 和a -都有意义,则a 的值是( )A.0≥aB.0≤aC.0=aD.0≠a 9. 边长为1的正方形的对角线长是( )A. 整数B. 分数C. 有理数D. 不是有理数 10. 38-=( ) A .2 B .-2C .±2D .不存在11a =-,则实数a 在数轴上的对应点一定在( )A .原点左侧B .原点右侧C .原点或原点左侧D .原点或原点右侧 12.下列说法中正确的是( )A. 实数2a -是负数 B. a a =2C. a -一定是正数D. 实数a -的绝对值是a 二. 填空题:(32分)13. 9的算术平方根是 ;3的平方根是 ; 0的平方根是 ;-2的平方根是 .14. –1的立方根是 ,271的立方根是 , 9的立方根是 . 15. 2的相反数是 , 倒数是 , -36的绝对值是 . 16. 比较大小填“>”或“<”)17. =-2)4( ;=-33)6( ; 2)196(= .18. 37-的相反数是 ; 32-=19.若2b +和5的立方根,则a = ,b =20.a 的两个平方根是方程223=+y x 的一组解,则a = ,2a 的立方根是三. 解答题:(20分)21.求下列各数的平方根和算术平方根:① 1; ②0.0004 ③ 256 ④8125 22. 求下列各数的立方根:①21627; ②610--.23.求下列各式的值:①44.1; ②3027.0-; ④649; ⑤44.1-21.1; ⑦)32(2+ 附加题:(20分) 24.若03)2(12=-+-+-z y x ,求z y x ++的值。
人教版初中数学七年级下册《6.3实数》同步练习(含答案)(最新整理)
(2) 3 2 ;
(3) 3 1 . 125
课后作业
8
9.下列说法正确的是( ) A.两个无理数的和一定是无理数 B.无理数的相反数是无理数 C.两个无理数的积一定是无理数 D.无理数与有理数的乘积是无理数
10.已知三个数:-π,-3, 7 ,它们按从小到大的顺序排列为( ) A. 3 7 B. 3 7 C. 7 3 D. 7 3 11.设实数 a、b 在数轴上对应的位置如图所示,且|a|>|b|,则化简 a2 | a b | 的结果是( )
A.2a+b B.-2a+b C.b D.2a-b
12.计算:(1) 3 5 2 5 ________ ; (2) 3 4 | 3 4 | ________ . 13. 7 2 的相反数是________,绝对值是________.
5 14.已知 a 是小于 3 5 的整数,且|2-a|=a-2,那么 a 的所有可能值是________.
6.把下列各数填在相应的表示集合的大括号内.
2
22
-6,π,- ,-|-3|, ,-0.4,1.6,
6 ,0,1.101 001 000 1…
3
7
整数:{
,…},
负分数:{
,…},
无理数:{
,…}.
5
7.下列结论正确的是( ) A.数轴上任一点都表示唯一的有理数 B.数轴上任一点都表示唯一的无理数 C.两个无理数之和一定是无理数 D.数轴上任意两点之间还有无数个点
6
3
(1)有理数集合:{ …};
(2)无理数集合:{ …};
(3)正实数集合:{ …}:
(4)负实数集合:{ …}.
课后作业
7.下列说法正确的是( )
七年级-人教版-数学-下册-[基础诊断]第1课时-实数的概念与表示
6.3 实数(第1课时)1.下列各数中是无理数的是( ).A .3.14B C D .172.给出下列结论:①数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.其中正确的是( ).A .①②B .②③C .③④D .②③④ 3.实数a 在数轴上的对应点的位置如图所示,若实数b 满足-a <b <a ,则b 的值可以是( ).A .2B .-1C .-2D .-34.计算-|=_______.5_______2的绝对值是_______.6.如图,根据实数a ,b 的对应点在数轴上的位置,试比较a ,-a ,b ,-b 的大小,按从小到大的顺序排列为__________________.7.将下列各数填入相应的集合中:2.161 661,2.161,237,-311,π2,0 无理数集合:{ …};负实数集合:{ …};非负有理数集合:{ …}.参考答案1.【答案】C【解析】对于选项A,3.14是有理数,不符合题意;对于选项B=3,3是有理数,不符合题意;对于选项C对于选项D,17是有理数,不符合题意.2.【答案】B【解析】数轴上的点既能表示无理数,也能表示有理数,故①错误;任何一个无理数都能用数轴上的点表示,故②正确;实数与数轴上的点一一对应,故③正确;有理数有无限个,无理数有无限个,故④错误.3.【答案】B【解析】因为-a<b<a,所以|b|<a.又因为1<a<2,所以b的值可以是-1.4【解析】-|5.【答案】-323,3.2<0,所以2|=-2)=26.【答案】a<-b<b<-a【解析】由实数a,b的对应点在数轴上的位置,可得a<-1,0<b<1,所以-a>1,-1<-b<0,所以a <-b <b <-a .7.【答案】解:无理数集合:π2⎧⎫⎨⎬⎩⎭;负实数集合:311⎧⎫--⎨⎬⎩⎭,; 非负有理数集合:232.1616612.16107⎧⎫⎨⎬⎩⎭,,,,.。
人教版七年级下册《6.3第1课时实数的概念》同步练习(含答案)
6.3实数第1课时实数的有关概念关键问答①无理数有几种常见的表现形式?②数轴上的每一点都可以表示一个什么样的数?1.①2017·滨州下列各数中是无理数的是()A. 2B.0 C.12017D.-12.②如图6-3-1,半径为1个单位长度的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr),把圆片沿数轴向左滚动1周,点Q到达数轴上点A的位置,则点A表示的数是________,属于__________(填“有理数”或“无理数”).图6-3-1命题点1无理数[热度:90%]3.③下列说法正确的是()A.无理数就是无限小数B.无理数就是带根号的数C.无理数都是无限不循环小数D.无理数包括正无理数、0和负无理数易错警示③(1)无理数的特征:无理数的小数部分位数无限且不循环,不能表示成分数的形式.(2)常见的无理数有三种表现形式:化简后含π的数;有规律的无限不循环小数,如:1.3131131113…;含有根号且开方开不尽的数,如5,36.4.④在下列各数:0.51525354…,0,0.2,3π,227,9,39,13111,27中,是无理数的有________________________.方法点拨④一个数不是有理数就是无理数,识别一个数是不是有理数,只需看其是不是整数或分数即可.5.有一个数值转换器,原理如图6-3-2所示:当输入的x 为256时,输出的y 是________.图6-3-26.⑤在1,2,3,…,100这100个自然数的算术平方根和立方根中,无理数共有多 少个?方法点拨⑤分别找出1~100这100个自然数的算术平方根和立方根中有理数的个数,即可得出无理数的个数.命题点 2 实数的概念与分类 [热度:95%] 7.⑥下列说法中,正确的是( ) A .正整数、负整数统称整数 B .正数、0、负数统称有理数C .实数包括无限小数与无限不循环小数D .实数包括有理数与无理数 易错警示⑥实数包括有理数和无理数,即有限小数、无限循环小数、无限不循环小数. 8.⑦有下列说法:①两个无理数的和还是无理数;②无理数与有理数的积是无理数;③有理数与有理数的和不可能是无理数;④无限小数是无理数;⑤不是有限小数的数不是有理数.其中正确的有( )A .0个B .1个C .2个D .3个 解题突破⑦两个无理数的和或差不一定是无理数.9.⑧实数13,24,π6中,分数有( )A .0个B .1个C .2个D .3个 方法点拨⑧分数是两个整数作商,不能整除的数. 10.下列说法错误的是( ) A.14是有理数 B.2是无理数 C .-3-27是正实数 D.22是分数11.在数轴上,表示实数2与10的点之间的整数点有________个;表示实数2与10之间的实数点有________个.12.将下列各数填在相应的集合里: 3512,π,3.1415926,-0.456,3.030030003…(从左到右相邻的两个3之间0的个数逐渐加1),0,511,-321,(-13)2,0.1.有理数集合:{_____________________________________________…};无理数集合:{_____________________________________________…};正实数集合:{_____________________________________________…};整数集合:{_______________________________________________…}.命题点3实数与数轴[热度:98%]13.下列说法中正确的是()A.每一个整数都可以用数轴上的点表示,数轴上的每一个点都表示一个整数B.每一个有理数都可以用数轴上的点表示,数轴上的每一个点都表示一个有理数C.每一个无理数都可以用数轴上的点表示,数轴上的每一个点都表示一个无理数D.每一个实数都可以用数轴上的点表示,数轴上的每一个点都表示一个实数14.⑨如图6-3-3,数轴上的A,B,C,D四个点表示的数中,与-3最接近的是()图6-3-3A.点A B.点B C.点C D.点D解题突破⑨-3介于哪两个连续的整数之间?这两个连续的整数中哪个整数的平方与3的差的绝对值小?15.2018·宁晋县期中如图6-3-4,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将该圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是()图6-3-4A.π-1 B.-π-1C.-π-1或π-1 D.-π-1或π+116.⑩在同一数轴上表示2的点与表示-3的点之间的距离是________.方法点拨⑩数轴上两点间的距离等于右边的点表示的数减去左边的点表示的数.17.⑪如图6-3-5所示,按下列方法将数轴的正半轴绕在一个圆(该圆的周长为3个单位长度,且在圆周的三等分点处分别标上了数字0,1,2)上.先让原点与圆周上0所对应的点重合,再将数轴的正半轴按顺时针方向绕在该圆周上,使数轴上1,2,3,4,…所对应的点分别与圆周上1,2,0,1,…所对应的点重合,这样数轴的正半轴上的整数就与圆周上的数字建立了一种对应关系.图6-3-5(1)圆周上数字a与数轴上的数字5对应,则a=__________;(2)数轴绕过圆周100圈后,一个整数点落在圆周上数字2所对应的位置,这个整数是________.模型建立⑪数轴绕过圆周n圈(n为正整数)后,一个整数落在圆周上数字2所对应的位置,这个整数是3n+2.18.阅读下面的文字,解答问题.大家都知道2是无理数,而无理数是无限不循环小数,因此2的小数部分我们不可能全部写出来,于是小明用2-1来表示2的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为2的整数部分是1,所以将2减去其整数部分,差就是其小数部分.(1)你能求出5+2的整数部分和小数部分吗?(2)已知10+3=x +y ,其中x 是整数,且0<y <1,请求出x -y 的相反数.19.⑫定义:可以表示为两个互质整数的商的形式的数称为有理数,整数可以看作是分母为1的有理数;反之为无理数.如2不能表示为两个互质的整数的商,所以2是无理数.可以这样证明:设2=a b ,a 与b 是互质的两个整数,且b ≠0,则2=a 2b 2,a 2=2b 2.因为b 是整数且不为0,所以a 是不为0的偶数.设a =2n (n 是整数),所以b 2=2n 2,所以b 也是偶数,这与a ,b 是互质的两个整数矛盾,所以2是无理数.仔细阅读上文,求证:5是无理数.方法点拨⑫从结论的反向出发,经推理,推得与基本事实、定义、定理或已知条件相矛盾的结果,这样的方法称为反证法.典题讲评与答案详析1.A 2.-2π无理数 3.C4.0.51525354…,3π,39,27[解析] 因为0是整数,0.2可化成分数,9=3,是整数,13111,227是分数,所以这五个数都是有理数.0.51525354…,3π,39,27都是无理数.5.2[解析] 由题图中所给的程序可知,把256取算术平方根,结果为16,因为16是有理数,所以再取算术平方根,结果为4,是有理数.再取4的算术平方根,结果为2,是有理数.再取算术平方根,结果为2,2是无理数,所以y= 2.6.解:∵12=1,22=4,32=9,…,102=100,∴1,2,3,…,100这100个自然数的算术平方根中,有理数有10个,∴无理数有90个.∵13=1,23=8,33=27,43=64,53=125,且64<100,125>100,∴1,2,3,…,100这100个自然数的立方根中,有理数有4个,∴无理数有96个,∴1,2,3,…,100这100个自然数的算术平方根和立方根中,无理数共有90+96=186(个).7.D[解析] 正整数、负整数、0统称为整数;有理数分为正有理数、0和负有理数;有理数包括无限循环小数和有限小数;实数包括有理数和无理数.8.B[解析] 两个无理数的和不一定是无理数,如2和-2;无理数与有理数的积也不一定是无理数,如2和0;有理数与有理数的和一定是有理数;无限不循环小数是无理数;有限小数和无限循环小数是有理数.9.B [解析] 分数是两个整数作商,不能整除的数,因此只有13是分数.10.D [解析]A 项,14=12是有理数,故选项正确;B 项,2是无理数,故选项正确;C 项,-3-27=3是正实数,故选项正确;D 项,22是无理数,故选项错误.故选D.11.2 无数12.有理数集合:{3512,3.1415926,-0.456,0,511,(-13)2,…};无理数集合:{π,3.030030003…(从左到右相邻的两个3之间0的个数逐渐加1),-321,0.1,…};正实数集合:{3512,π,3.1415926,3.030030003…(从左到右相邻的两个3之间0的个数逐渐加1),511,(-13)2,0.1,…};整数集合:{3512,0,(-13)2,…}.13.D [解析] 实数与数轴上的点具有一一对应的关系. 14.B15.C [解析]∵圆的直径为1个单位长度,∴此圆的周长=π,∴当圆向左滚动时点A ′表示的数是-1-π;当圆向右滚动时点A ′表示的数是π-1.16.2+3 [解析] 在同一数轴上表示2的点与表示-3的点之间的距离是2+||-3=2+ 3.17.(1)2 (2)302 [解析] (1)∵数轴上1,2,3,4,…所对应的点分别与圆周上1,2,0,1,…所对应的点重合,∴圆周上的数字a 与数轴上的数字5对应时,a =2.(2)∵数轴上1,2,3,4,…所对应的点分别与圆周上1,2,0,1,…所对应的点重合,∴圆周上的数字0,1,2与数轴的正半轴上的整数0,1,2,3,4,5,6,7,8,…每3个一组分别对应,∴数轴绕过圆周100圈后,一个整数点落在圆周上数字2所对应的位置,这个整数是302.18.解:(1)∵4<5<9,∴2<5<3,∴5的整数部分是2,小数部分是5-2,∴5+2的整数部分是2+2=4,小数部分是5-2.(2)∵3的整数部分是1,小数部分是3-1,∴10+3的整数部分是10+1=11,小数部分是3-1,∴x=11,y=3-1,∴x-y的相反数是y-x=3-12.19.证明:设5=ab,a与b是互质的两个整数,且b≠0,则5=a2b2,a2=5b2.因为b是整数且不为0,所以a不为0且为5的倍数.设a=5n(n是整数),所以b2=5n2,所以b也为5的倍数,这与a,b是互质的两个整数矛盾,所以5是无理数.【关键问答】①无理数有三种常见的表现形式:一是含有根号且开方开不尽的数;二是化简后含π的数;三是人为创造的一些无限不循环小数.②数轴上的每一点都可以表示一个实数.。
6.3.1 实数的相关概念及分类(第一课时)七年级数学下册(人教版)
自学导航
有理数和无理数统称为实数.
(1)按定义分
有理数
正有理数
0
有限小数或者无限循环小数
负有理数
实数
正无理数
无理数
无限不循环小数
负无理数
自学导航
有理数和无理数统称为实数.
(2)按性质分
正有理数
正实数
实数
正无理数
0
负有理数
无理数π可以用数轴上的点来表示出.
合作探究
如图,以单位长度为边长画一个正方形,以原点为圆心,正方形
对角线为半径画弧,与正半轴的交点就表示 2,与负半轴的交点就表示
- 2.(为什么)
合作探究
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数以后,实数与数轴上的点是一一对应的,即
1.了解实数的意义,并能将实数按要求进行分
类;
2.熟练掌握实数大小的比较方法;(重点)
3.了解实数和数轴上的点一一对应,能用数轴
上的点表示无理数.(难点)
自学导航
我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,
它们有什么特征?
5 3 27 11 9
, , , , .
2 5 4 9 11
5
2.5
2
3
0.6
5
27
6.75
4
.
11
1. 2
9
. .
9
0. 81
11
它们都可以写成有限小数或者无限循环小数的形式.
整数能写成小数的形式吗?3可以看成是3.0吗?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.3实数(第1课时)课后作业
1.下列各数中是无理数的是( )
B.-2
C.0
D.
13
2.下列各数中,
3.141 59,,0.131 131 113…,-,-17
,无理数的个数有( ) A.1个 B.2个 C.3个 D.4个
3.下列说法正确的是( )
A.实数包括有理数、无理数和零
B.有理数包括正有理数和负有理数
C.无限不循环小数和无限循环小数都是无理数
D.无论是有理数还是无理数都是实数
4.有一个数值转换器,原理如下:当输入的x 为64时,输出的y 是( )
A.8 5.实数可分为正实数,零和__________.正实数又可分为__________和__________,负实数又可分为__________和__________.
6.把下列各数填在相应的表示集合的大括号内.
-6,π,-23,-|-3|,227
,-0.4,1.6,0,1.101 001 000 1… 整数:{ ,…},
负分数:{ ,…},
无理数:{ ,…}.
7.下列结论正确的是( )
A.数轴上任一点都表示唯一的有理数
B.数轴上任一点都表示唯一的无理数
C.两个无理数之和一定是无理数
D.数轴上任意两点之间还有无数个点
8.若将三个数表示在数轴上,其中能被如图所示的墨迹覆盖的数是__________.
9.如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周(不滑动),圆上的一点由原点到达点O ′,点O ′所对应的数值是__________.
10.有六个数:0.142 7,(-0.5)3,3.141 6,
227
,-2π,0.102 002 000 2…,若无理数的个数为x,整数的个数为y,非负数的个数为z,求x+y+z 的值.
挑战自我
11.是无理数,的点呢?小颖在数轴上用尺规作图的方法作出
的点,如图.小颖作图说明了什么?。
