中职数学第二章复习课
合集下载
人教版(2021)中职数学基础模块上册第二章《不等式》复习课课件

5.含有绝对值不等式 (1)|x|≤a⇔-a≤x≤a; (2)|x|>a⇔x<-a或x>a.
6.均值定理 若a>0,b>0,则 a b ab,当且仅当a=b时,等号成立.
2
7.不等式的应用 四步骤:(1)阅读题意;(2)建立模型;(3)求解;(4)评价还原.
二、典型例题
1.不等式的基本性质与证明
C.{x|1<x<3}
D.R
【答案】D 【解析】由x无论取何值时,有|x-2|≥0,故|x-2|>-1恒成立.
9.已知不等式3x-10≥-6+ax的解集是{x|x≤-2},则a的值为 ( )
A.4
B.5
C.6
D.7
【答案】B 【解析】将x=-2代入方程3x-10=-6+ax,得-6-10=-6+(-2a),即a=5.
第二章 不等式 复习课
一、知识梳理 1.不等式的基本性质.
2.证明不等式的常用方法 作差法: (1)a-b=0⇔a=b; (2)a-b>0⇔a>b; (3)a-b<0⇔a<b.
3.一元一次不等式ax>b的解法: (1)当a>0时,解集是{x|x>b ,x∈R}.
a
(2)当a<0时,解集是{x|x< b ,x∈R}.
2x
3
7.不等式|3-2x|>7的解集是 ( A.(-2,5) C.(-∞,-2)∪(5,+∞)
) B.(-5,5) D.(-∞,-1)∪(5,+∞)
【答案】C 【解析】由|3-2x|>7得3-2x>7或3-2x<-7,则x<-2或x>5.
8.不等式|x-2|>-1的解集是 ( )
人教版(中职)数学基础模块上册同步课件 第二章 不等式 本单元复习与测试

03
不等式包括大于、小于、大于等于、小于等于四种关系
04
不等式的解集是指满足不等式关系的所有可能的解的集合
不等式的定义
不等式的分类
对数不等式:不等式的两边都是对数形式分式不等式:不等式的两边至少有一边是分式指数不等式:不等式的两边都是指数形式含参不等式:不等式的两边含有参数
线性不等式:含有一个未知数的一次不等式
3
利用不等式的性质:利用不等式的基本性质,如加法、乘法、乘方等,将分式不等式转化为整式不等式
4
分式不等式的解法
1
绝对值不等式的定义:含有绝对值的不等式,如|x|>a,|x|<a等。
2
绝对值不等式的解法:首先,将绝对值符号转化为等价的符号,如|x|>a可以转化为x>a或x<-a。
3
绝对值不等式的求解:根据不等式的性质,求解含有绝对值的不等式。
题型一:不等式性质
题型四:不等式应用
题型二:不等式求解
题型五:不等式综合
题型三:不等式证明
题型六:不等式拓展
本单元测试题解析
传递性:如果a>b,b>c,那么a>c
对称性:如果a&g法性质:如果a>b,c>0,那么a/c>b/c
传递性:如果a>b,c>d,那么a+c>b+d
平方根不等式性质:如果a>b,那么sqrt(a)>sqrt(b)
绝对值不等式:|x| ≤ a,其中a为常数
人教版(中职)数学基础模块上册同步课件 第二章 不等式 本单元复习与测试
可爱/纯真/童年/烂漫
CONTENTS
Contents
不等式的概念和性质
第二章不等式复习课件-2023-2024学年高一上学期高教版(2021)中职数学基础模块上册

所组成的集合称为区间,这两个点称为区
间端点.
设 a ,b R ,且 a b ,那么:
[a, b],称为闭区间;
x
(1)满足不等式 a ≤ x ≤ b的实数 的集合表示为
(2)满足不等式 a x b的实数 x 的集合表示为 (a, b) ,称为开区间;
(3)满足不等式 a ≤ x b的实数 x 的集合表示为 [a, b) ,称为左闭右开区间;
当 > 0时,含有绝对值的不等式的解集归纳总结见表:
例题辨析
A知识巩固
一、判断题
1、若a>b,则a+8>b+7.(
)
2、若a>b,c=d,则ac>bd.(
3、若a>b>0,则4a-b>3b.(
)
)
4、不等式 x<2的解集在数轴上可表示为到原点的距离小于2的点的集合.(
5、已知集合A的数轴表示如图所示,则它的区间表示为(2,4).( )
B.[2,3]
C.(-∞,-2)∪(3,+∞)
D.(2,3)
11.不等式|x+5|≤0的解集是(
)
A.R
B.∅
C.{-5}
D.(-∞,-5)∪(-5,+∞)
A知识巩固
例题辨析
三、填空题
2− ≥5
12.不等式组
,的解集是
3 − 1<2
13.设全集为R,集合A=(-∞,-2],则∁A=
A知识巩固
例题辨析
都称为无穷区间.
归纳见表
2.3一元二次不等式
像这样,含有一个未知数,并且未知数的最高次数为2的不等式,
称为一元二次不等式.其一般形式为
ax bx c .
0
a0
中职教育-数学(基础模块)上册 第2章 不等式.ppt

2.2.1 有限区间
实数与数轴上的点之间是一一对应的关系,如集合 {x|-3<x<2}可以用数轴上位于-3与2之间的一条线段 (不包括端点)来表示,如图2-1所示.
图2-1
由数轴上两点之间的全部实数所组成的集合称为区间,其 中这两个点称为区间端点.
不含端点的区间称为开区间.含有两个端点的区间称为闭区 间.只含左端点的区间称为右半开区间;只含右端点的区间称为 左半开区间.
(2)依次单击函数图像与x轴的相交处,构造出两个 交点.
(3)单击选中左侧的交点,然后选择“度量”>“横 坐标”菜单,标记出左侧交点A的横坐标;再选择“度 量”>“纵坐标”菜单,标记出左侧交点A的纵坐标.
(4)用同样的方法标记出右侧交点B的横、纵坐标.
例2 k为何值时,方程2x2-kx+x+8=0无实数解.
(3)当Δ=b2-4ac<0时,方程ax2+bx+c=0(a>0)没有 实数解,对应函数y=ax2+bx+c(a>0)的图像与x轴没有交点, 如图2-8(c)所示.此时不等式ax2+bx+c>0(a>0)的解集 为R,不等式ax2+bx+c<0(a>0)的解集为∅ .
软件学习 几何画板是学习数学的好帮手,我们将采用几何画板5.05 版带领大家一起来学习这款软件的用法.
2.1.2 不等式的基本性质
性质1(传递性) 如果a>b,b>c,则a>c.
性质2(加法性质) 如果a>b,则a+c>b+c.
性质3(乘法性质) 如果a>b,c>0,则ac>bc ;如果a>b, c<0,则ac<bc.
2.2 区间
不等式的解集是数集,对应着数轴上的一条或多条线段, 也就是说它们是数轴的一部分.为了应用的方便,我们引入 “区间”的概念.
解 2x2-kx+x+8=0可化为2x2+(1-k)x+8=0 .依题意 知,此方程的判别式Δ=b2-4ac<0,即
实数与数轴上的点之间是一一对应的关系,如集合 {x|-3<x<2}可以用数轴上位于-3与2之间的一条线段 (不包括端点)来表示,如图2-1所示.
图2-1
由数轴上两点之间的全部实数所组成的集合称为区间,其 中这两个点称为区间端点.
不含端点的区间称为开区间.含有两个端点的区间称为闭区 间.只含左端点的区间称为右半开区间;只含右端点的区间称为 左半开区间.
(2)依次单击函数图像与x轴的相交处,构造出两个 交点.
(3)单击选中左侧的交点,然后选择“度量”>“横 坐标”菜单,标记出左侧交点A的横坐标;再选择“度 量”>“纵坐标”菜单,标记出左侧交点A的纵坐标.
(4)用同样的方法标记出右侧交点B的横、纵坐标.
例2 k为何值时,方程2x2-kx+x+8=0无实数解.
(3)当Δ=b2-4ac<0时,方程ax2+bx+c=0(a>0)没有 实数解,对应函数y=ax2+bx+c(a>0)的图像与x轴没有交点, 如图2-8(c)所示.此时不等式ax2+bx+c>0(a>0)的解集 为R,不等式ax2+bx+c<0(a>0)的解集为∅ .
软件学习 几何画板是学习数学的好帮手,我们将采用几何画板5.05 版带领大家一起来学习这款软件的用法.
2.1.2 不等式的基本性质
性质1(传递性) 如果a>b,b>c,则a>c.
性质2(加法性质) 如果a>b,则a+c>b+c.
性质3(乘法性质) 如果a>b,c>0,则ac>bc ;如果a>b, c<0,则ac<bc.
2.2 区间
不等式的解集是数集,对应着数轴上的一条或多条线段, 也就是说它们是数轴的一部分.为了应用的方便,我们引入 “区间”的概念.
解 2x2-kx+x+8=0可化为2x2+(1-k)x+8=0 .依题意 知,此方程的判别式Δ=b2-4ac<0,即
中职数学总复习课件(同济版)第二章

D.若a>b,且c>d,则ac>bd
解析
对于本题选项A ,若c = 0 ,则 ac = bc = 0 ,A选项不成立 ;
对于选项B和选项D ,可以通过特殊值来判断,令a=0,b=1,c=-2,d=-3,可排除选项B和D.
本题选项C正确.
技巧
点拨
解答此类题目,要注意不等式性质的正确应用,同时也
要考虑其他知识 另外也可用特殊值法来判断.
(2)利用数轴求出这些不等式的解集的公共部分,即可求出这个不等式组的解集.
注意
(1)利用数轴表示不等式的解集时,要注意表示数的点的位置上是空心圆圈,还是
实心圆点.
(2)若不等式组中各个不等式的解集没有公共部分,则这个不等式组无解.
3.由两个一元一次不等式组成的不等式组的解集的情况
由两个一元一次不等式组成的不等式组的解集的情况见表2-1.
①当Δ>0时,求出两根
且
• 写出相应的方程
计算判别式Δ.
(注意灵活运用因式分解法和配方法).
②当Δ=0时,求根
• 根据不等式,写出解集.
③当Δ<0时,方程无解.
考点三 含绝对值不等式的求解
1.绝对值的定义
代数意义
一个数的绝对值是非负数,即
几何意义
一个数的绝对值|a|表示这个数a在数轴上对应的点到原点的距离.
性质3
如果a >b ,c >0,那么ac >bc ;如果a >b ,c <0,那么ac <bc
(同向不等式可加性)
(异向不等式可减性)
推论
知识点二 区间
设a,b∈R,且a<b,我们规定:
(1){x|a≤x≤b}=[a,b],[a,b]称为闭区间.
解析
对于本题选项A ,若c = 0 ,则 ac = bc = 0 ,A选项不成立 ;
对于选项B和选项D ,可以通过特殊值来判断,令a=0,b=1,c=-2,d=-3,可排除选项B和D.
本题选项C正确.
技巧
点拨
解答此类题目,要注意不等式性质的正确应用,同时也
要考虑其他知识 另外也可用特殊值法来判断.
(2)利用数轴求出这些不等式的解集的公共部分,即可求出这个不等式组的解集.
注意
(1)利用数轴表示不等式的解集时,要注意表示数的点的位置上是空心圆圈,还是
实心圆点.
(2)若不等式组中各个不等式的解集没有公共部分,则这个不等式组无解.
3.由两个一元一次不等式组成的不等式组的解集的情况
由两个一元一次不等式组成的不等式组的解集的情况见表2-1.
①当Δ>0时,求出两根
且
• 写出相应的方程
计算判别式Δ.
(注意灵活运用因式分解法和配方法).
②当Δ=0时,求根
• 根据不等式,写出解集.
③当Δ<0时,方程无解.
考点三 含绝对值不等式的求解
1.绝对值的定义
代数意义
一个数的绝对值是非负数,即
几何意义
一个数的绝对值|a|表示这个数a在数轴上对应的点到原点的距离.
性质3
如果a >b ,c >0,那么ac >bc ;如果a >b ,c <0,那么ac <bc
(同向不等式可加性)
(异向不等式可减性)
推论
知识点二 区间
设a,b∈R,且a<b,我们规定:
(1){x|a≤x≤b}=[a,b],[a,b]称为闭区间.
职高数学基础模块各章节复习提纲(2020年整理).pptx
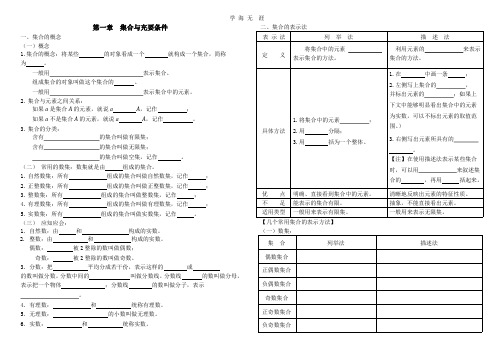
第一章 集合与充要条件
学海无 涯 二、集合的表示法
一、集合的概念
表 示法
列举法
(一)概念 1.集合的概念:将某些
为
。
的对象看成一个
就构成一个集合,简称
将集合中的元素 定 义 表示集合的方法。
一般用
表示集合。
组成集合的对象叫做这个集合的
。
一般用
表示集合中的元素。
2. 集合与元素之间关系: 如果 a 是集合 A 的元素,就说 a 如果 a 不是集合 A 的元素,就说 a
3
CU (CU A) ;
(4) CU ( A B)
五、充要条件
(2) A CU A ; ; (5) CU ( A B)
(一)相关概念:
1. 命题:判断一件事情的语句叫做命题。 2. 命题的表示方法:使用小写英语字母 p、q、r、s 等表示命题。
3. 真命题:成立(正确)的命题是真命题。
4. 假命题:不成立(错误)的命题是假命题。
A,记作 A,记作
3. 集合的分类: 含有
的集合叫做有限集;
含有
的集合叫做无限集;
; 。
具体方法
1.将集合中的元素
;
2.用
分隔;
3.用
括为一个整体。
的集合叫做空集,记作
。
(二) 常用的数集:数集就是由
组成的集合。
1. 自然数集:所有
组成的集合叫做自然数集,记作
;
2. 正整数集:所有
组成的集合叫做正整数集,记作
。 【注】在使用描述法表示某些集合
时,可以用
来叙述集
合的
,再用
括起来。
清晰地反映出元素的特征性质。 抽象,不能直接看出元素。 一般用来表示无限集。
学海无 涯 二、集合的表示法
一、集合的概念
表 示法
列举法
(一)概念 1.集合的概念:将某些
为
。
的对象看成一个
就构成一个集合,简称
将集合中的元素 定 义 表示集合的方法。
一般用
表示集合。
组成集合的对象叫做这个集合的
。
一般用
表示集合中的元素。
2. 集合与元素之间关系: 如果 a 是集合 A 的元素,就说 a 如果 a 不是集合 A 的元素,就说 a
3
CU (CU A) ;
(4) CU ( A B)
五、充要条件
(2) A CU A ; ; (5) CU ( A B)
(一)相关概念:
1. 命题:判断一件事情的语句叫做命题。 2. 命题的表示方法:使用小写英语字母 p、q、r、s 等表示命题。
3. 真命题:成立(正确)的命题是真命题。
4. 假命题:不成立(错误)的命题是假命题。
A,记作 A,记作
3. 集合的分类: 含有
的集合叫做有限集;
含有
的集合叫做无限集;
; 。
具体方法
1.将集合中的元素
;
2.用
分隔;
3.用
括为一个整体。
的集合叫做空集,记作
。
(二) 常用的数集:数集就是由
组成的集合。
1. 自然数集:所有
组成的集合叫做自然数集,记作
;
2. 正整数集:所有
组成的集合叫做正整数集,记作
。 【注】在使用描述法表示某些集合
时,可以用
来叙述集
合的
,再用
括起来。
清晰地反映出元素的特征性质。 抽象,不能直接看出元素。 一般用来表示无限集。
中职数学第二章复习课

(1)满足x a的全体实数,记作 a, ; (2)满足x a的全体实数,记作 a, ; (3)满足x a的全体实数,记作 , a ; (4)满足x a的全体实数,记作 , a
四、含有绝对值的不等式
x m m x m; x m x m或x m
三、不等式的解集与区间
用区间表示不等式的解集
设a, b R, 且a b, 则:
(1)满足a x b的全体实数x的集合,叫做闭区间,记作a, b;
(2)满足a x b的全体实数x的集合,叫做开区间,记作 a, b ;
(3)满足a x b或a x b的全体实数x的集合,叫做半开半闭区间, 记作 a, b 或 a, b ;
五、一元二次不等式
1、定义:只含有一个未知数,并且未知数的最高次数是
2的整式不等式叫做一元二次不等式.
2、当m 0时,
x 2 m 2 x m; x 2 m 2 x m.
二、不等式的基本性质
1、实的大小:
a b 0 a b; a b 0 a b; a b 0 a b.
2、不等式的基本性质:
a b a c b c(a c b c ); a b a b, c 0 ac bc( ); c c a b a b, c 0 ac bc( ); c c 对于a 0, b 0, 有a b a 2 b 2 .
一、一元二次方程
1、定义:只含有一个未知数,并且未知数的最高次数是
2的整式方程叫做一元二次方程.
2、一般形式:ax² +bx+c=0
(a ≠0)
3、用配方法解一元二次方程 4、用公式法解一元二次方程
中职数学第二章不等式第三节复习课件

课堂探究
1.探究问题 【探究1】一组学生乘汽车去旅游,预计共需车费120元,后来多了2人, 车费仍不变,这样每人可少摊3元,原来这组学生共有多少人?
答案: 120 120 3 , x=8 . x x2
【探究2】如何判断二次函数图像与x轴的位置关系?一元二次方程的根 与对应的二次函数图像与x轴交点有何关系?
课堂探究
1.探究问题
【探究1】如何分析一元二次方程ax2+bx+c=0根的情况?
【探究2】如何分析一类含参的一元二次不等式的恒成立问题?
2.知识链接:
(1)一般地,若不等式ax2+bx+c<0(a≠0)的解集为(-∞,x1) ∪ (x2 ,+ ∞) 或
(x1, x2 ) ,则x1,x2是方程 ax2 bx c 0
R
;
y≤0的解集为
.
例2 求下列不等式的解集 (1)x2-2x-3>0; (2) 9x2-6x+1≤0; (3) -x2+2x-2<0; (4) x2+x+1<0.
答案: (1)(-∞,-1)∪(3,+ ∞);(2){1/3};
(3)R;(4) .
例3 问实数 m取何值时,关于x 的一元二次方程 x2+mx-m=0. (1)有实根;(2)无实根.
课堂探究
1.探究问题
【探究】据气象部门预报,在距离其码头南偏东45°方向600km处的热带风 暴中心正以20km/h的速度向正北方向移动,距风暴中心450km以内的地区都 将受到影响,影响时间大约为多长?
答案:15小时
2.知识链接: (1)关于一元二次不等式应用的一般解题思路: ①审题:把文字语言翻译成数学语言,设出来知量并写出对应关系式. ②列式:根据题意列出不等式并解,即建立数学模型. ③作答:将数学问题的解转化为实际问题的解,并根据实际判断是否符 合现实情况. (2)对实际应用问题的处理,关键是把实际问题转化成数学问题,列好目 标函数关系式是求最值的基本保证.运用数学知识解决实际问题的一般步 骤:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)满足x a的全体实数,记作 a, ; (2)满足x a的全体实数,记作 a, ; (3)满足x a的全体实数,记作 , a ; (4)满足x a的全体实数,记作 , a
四、含有绝对值的不等式
x m m x m; x m x m或x m
一、一元二次方程
1、定义:只含有一个未知数,并且未知数的最高次数是
2的整式方程叫做一元二次方程.
2、一般形式:ax² +bx+c=0
(a ≠0)
3、用配方法解一元二次方程 4、用公式法解一元二次方程
2 b b 4ac 2 =b 4ac 0, x ; 2a b =b 2 4ac 0, x1 x2 ; 2a =b 2 4ac 0, 原方程无实数根.
五、一元二次不等式
1、定义:只含有一个未知数,并且未知ቤተ መጻሕፍቲ ባይዱ的最高次数是
2的整式不等式叫做一元二次不等式.
2、当m 0时,
x 2 m 2 x m; x 2 m 2 x m.
三、不等式的解集与区间
用区间表示不等式的解集
设a, b R, 且a b, 则:
(1)满足a x b的全体实数x的集合,叫做闭区间,记作a, b;
(2)满足a x b的全体实数x的集合,叫做开区间,记作 a, b ;
(3)满足a x b或a x b的全体实数x的集合,叫做半开半闭区间, 记作 a, b 或 a, b ;
二、不等式的基本性质
1、实数的大小:
a b 0 a b; a b 0 a b; a b 0 a b.
2、不等式的基本性质:
a b a c b c(a c b c ); a b a b, c 0 ac bc( ); c c a b a b, c 0 ac bc( ); c c 对于a 0, b 0, 有a b a 2 b 2 .
