温度预测模型研究.
温度变化对大气环境影响研究及其预测模型建立

温度变化对大气环境影响研究及其预测模型建立随着全球气候变化问题的引起人们的关注,温度和大气环境受到了广泛的关注。
温度变化会对大气环境产生什么样的影响?科学家已经做出了一系列的研究,并建立了一些预测模型。
本文将探讨温度变化对大气环境的影响以及相关的预测模型建立。
一、温度变化对大气环境的影响温度变化会对大气环境产生多方面的影响。
首先,温度升高将导致海平面上升,从而引发大规模的海岸侵蚀、海水入侵和低陆地淹没等影响。
其次,温度升高还会对生态系统产生影响,包括物种的分布和生态系统的稳定性。
此外,温度变化还会加剧自然灾害的发生频率和严重程度。
其中,最为重要的是温度变化对大气环境的影响。
温度的升高将导致大气层的热量分配发生改变,温度梯度增加,从而导致风的强度和方向发生变化。
此外,温度的升高还可以加剧干旱、风暴、洪水等自然灾害的发生频率和严重程度,导致大气环境的混乱和不稳定。
因此,深入研究温度变化对大气环境的影响,对于减少大气环境的危害和保护人类安全具有非常重要的意义。
二、相关研究为深入了解温度变化对大气环境的影响,科学家们已经开展了大量的研究。
其中,复杂的气候模拟和长期的气候数据分析是其中的两个主要方法。
一方面,科学家们通过复杂的气候模拟来模拟大气环境的变化。
这些模拟模型基于空气动力学、热力学、化学物理等多种科学原理,并结合具体的地理位置、气象数据等因素,以预测未来气候趋势。
另一方面,科学家们通过长期的气候数据分析来研究温度变化对大气环境的影响。
他们收集来自全球各地长达数十年的气象数据,并使用各种数据分析技术进行处理和分析,以查看温度变化对大气环境的影响。
三、建立预测模型了解温度变化对大气环境的影响是非常重要的,但是如何建立一个准确的预测模型来预测未来的气候变化是更加关键的。
预测模型的建立需要考虑多种因素,包括大气环境的物理、化学、生态等因素。
目前,科学家们已经开发了各种预测模型,包括统计模型、物理模型、机器学习模型等。
ARIMA模型---时间序列分析---温度预测
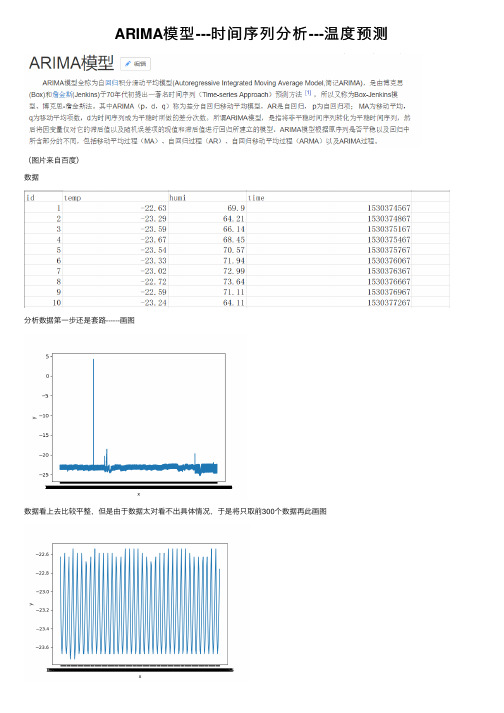
ARIMA模型---时间序列分析---温度预测(图⽚来⾃百度)数据分析数据第⼀步还是套路------画图数据看上去⽐较平整,但是由于数据太对看不出具体情况,于是将只取前300个数据再此画图这数据看上去很不错,感觉有隐藏周期的意思代码#coding:utf-8import csvimport matplotlib.pyplot as pltdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1]))aim_list_2.append(data[3])returndef plot_picture(x, y):plt.xlabel('x')plt.ylabel('y')plt.plot(x, y)plt.show()returnif__name__ == '__main__':temp = []tim = []file_name = 'C:/Users/lichaoxing/Desktop/testdata.csv'read_csv_data(temp, tim, file_name)plot_picture(tim[:300], temp[:300])使⽤ARIMA模型(ARMA)第⼀步观察数据是否是平稳序列,通过上图可以看出是平稳的如果不平稳,则需要进⾏预处理,⽅法有对数变换差分对于平稳的时间序列可以直接使⽤ARMA(p, q)模型进⾏拟合ARMA (p, q) : AR(p) + MA(q)此时参数p和q的确定可以通过观察ACF和PACF图来确定通过观察PACF图可以看出,阶数为9也就是p=9,这⾥ACF图看出⾃相关呈现震荡下降收敛,但是怎么决定出q,我没太明⽩,这⾥姑且拍脑袋才⼀个吧就q=3但是这⾥我遇到了⼀个问题,没有搞懂,就是平稳的序列,如果我进⾏⼀阶差分后应该仍然是平稳的序列,但是这个时候我⼜画了⼀个ACF 与PACF图,竟然是下图这样,lag的范围是-0.04到0.04(不懂)lag的范围是-0.04到0.04的问题原因(修改于再次使⽤此模型)原因:当时,我使⽤的是⼀阶差分,也就是让数据的后⼀个值减去前⼀个值得到新的值,这样就会导致第⼀个值变为缺失值(下⾯的数据是再此使⽤此模型时的数据,与原博客数据⽆关)就是因为此处的值为缺失值,导致绘制ACF与PACF时数据有问题⽽⽆法成功显⽰解决办法,在绘制上述图形前,将第⼀个数据去除:dta= dta.diff(1)dta = dta.truncate(before= ym[1])#删除第⼀个缺失值其实还有就是使⽤ADF检验,得到的结果如图,这个p值很⼩===》平稳画图代码def acf_pacf(temp, tim):x = timy = tempdta = pd.Series(y, index = pd.to_datetime(x))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=50,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=50,ax=ax2)show()ADF检验代码def test_stationarity(timeseries):dftest = adfuller(timeseries, autolag='AIC')return dftest[1]这⾥先使⽤ARMA(9,3)来实验测试⼀下效果,取前300个数据中的前250个作为train,后⾯的作为test 效果可以说这个模型是真的强⼤,预测的还是⼗分准确的代码def test_300(temp, tim):x = tim[0:300]y = temp[0:300]dta = pd.Series(y[0:249], index = pd.to_datetime(x[0:249]))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=30,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=30,ax=ax2)arma_mod = sm.tsa.ARMA(dta, (9, 3)).fit(disp = 0)predict_sunspots = arma_mod.predict(x[200], x[299], dynamic=True)fig, ax = plt.subplots(figsize=(9, 6))ax = dta.ix[x[0]:].plot(ax=ax)predict_sunspots.plot(ax=ax)show()其实,可以通过代码来⾃动的选择p和q的值,依据BIC准则,⽬标就是bic越⼩越好代码def proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModel遇到的问题,预测时predict函数没怎么使⽤明⽩当写于某些预测区间的时候,会报 “start”或“end”的相关错误,还有⼀个函数forcast,这个函数使⽤就是forcast(N):预测后⾯N个值返回的是预测值(array型)标准误差(array型)置信区间(array型)还有:对于构造时间序列,时间可以是时间格式:如 “2018-01-01” 或者就是个时间戳,在⽤时间戳的时候,其实在序列⾥它会⾃动识别时间戳,并加上起始时间1970-01-01 00:00:01形式附录(代码)预测⼀序列中某⼀点的值#coding:utf-8import csvimport timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport argparseimport warningswarnings.filterwarnings('ignore')def timestamp_datatime(value):value = time.localtime(value)dt = time.strftime('%Y-%m-%d %H:%M',value)return dtdef time_timestamp(my_date):my_date_array = time.strptime(my_date,'%Y-%m-%d %H:%M')my_date_stamp = time.mktime(my_date_array)return my_date_stampdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1])) #1:温度 2:湿度dt = int(data[3])aim_list_2.append(dt)returndef proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q)) #bugtry:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModeldef test_300(temp, tim, time_in):x = []y = []end_index = len(tim)for i in range(0, len(tim)):if (time_in - (tim[i]) < 300):end_index = ibreakif (end_index < 100):x = tim[0: end_index]y = temp[0: end_index]else:x = tim[end_index - 100: end_index]y = temp[end_index - 100: end_index]tidx = pd.DatetimeIndex(x, freq='infer')dta = pd.Series(y, index = tidx)print(dta)arma_mod = proper_model(dta, 9)predict_sunspots = arma_mod.forecast(1)return predict_sunspots[0]def predict_temperature(file_name, time_in):temp = []tim = []read_csv_data(temp, tim, file_name)result_temp = test_300(temp, tim, time_in)return result_tempif__name__ == '__main__':parser = argparse.ArgumentParser()parser.add_argument('-f', action='store', dest='file_name')parser.add_argument('-t', action='store', type = int, dest='time_')args = parser.parse_args()file_name = args.file_nametime_in = args.time_result_temp = predict_temperature(file_name, time_in)print ('the temperature is %f ' % result_temp)在上⾯的代码中,预测某⼀点的值我采⽤序列中此点的前100个点作为训练集如果给出待预测的多个点,由于每次都要计算模型的p和q以及拟合模型,时间会很慢,于是考虑将给定的待预测时间点序列切割成⼩段,使每⼀段中最⼤与最⼩的时间间隔在某⼀范围内在使⽤forcast(n)函数⼀次预测多点,然后在预测值中找到与待预测的时间值相近的值,速度⼤⼤提升,思路如图代码#coding:utf-8import csv#import timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport warningswarnings.filterwarnings('ignore')def proper_model(timeseries, maxLag):init_bic = 1000000000init_p = 1init_q = 1for p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_p = pinit_q = qinit_bic = bicreturn init_p, init_qdef read_csv_data(file_name, clss = 1):i = 0aim_list_1 = [] #temperature(1) or humidity(2)aim_list_2 = [] #timecsv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[clss]))dt = int(data[3])aim_list_2.append(dt)tidx = pd.DatetimeIndex(aim_list_2, freq = None)dta = pd.Series(aim_list_1, index = tidx)init_p, init_q = proper_model(dta[:aim_list_2[100]], 9)return init_p, init_q, aim_list_2, dtadef for_kernel(p, q, tim, dta, tmp_time_list, result_dict):interval = 20end_index = len(tim) - 1for i in range(0, len(tim)):if (tmp_time_list[0]["time"] - tim[i] < tim[1] - tim[0]):end_index = ibreakif (end_index < 100):dta = dta.truncate(after = tim[end_index])else:dta = dta.truncate(before= tim[end_index - 101], after = tim[end_index])arma_mod = ARMA(dta, order=(p, q)).fit(disp = 0, method='css')#为未来interval天进⾏预测,返回预测结果,标准误差,和置信区间predict_sunspots = arma_mod.forecast(interval)####################################for tim_i in tmp_time_list:for tim_ in tim:if tim_i["time"] - tim_ >= 0 and tim_i["time"] - tim_ < tim[1] - tim[0]:result_dict[tim_i["time"]] = predict_sunspots[0][tim.index(tim_) - end_index] returndef kernel(p, q, tim, dta, time_in_list):interval = 20time_first = time_in_list[0]det_time = tim[1] - tim[0]result_dict = {}tmp_time_list = []for time_ in time_in_list:if time_first["time"] + det_time * interval > time_["time"]:tmp_time_list.append(time_)continuetime_first = time_for_kernel(p, q, tim, dta, tmp_time_list, result_dict)tmp_time_list = []tmp_time_list.append(time_first)for_kernel(p, q, tim, dta, tmp_time_list, result_dict)return result_dictdef predict_temperature(file_name, time_in_list, clss = 1):p, q, tim, dta = read_csv_data(file_name, clss)result_temp_dict = kernel(p, q, tim, dta, time_in_list)return result_temp_dictdef predict_humidity(file_name, time_in_list, clss = 2):p, q, tim, dta = read_csv_data(file_name, clss)result_humi_dict = kernel(p, q, tim, dta, time_in_list)return result_humi_dictif__name__ == '__main__':file_name = "testdata.csv"time_in = [{"time":1530419271,"temp":"","humi":""},{"time":1530600187,"temp":"","humi":""},{"time":1530825809,"temp":"","humi":""}] #time_in = [{"time":1530600187,"temp":"","humi":""},]result_temp = predict_temperature(file_name, time_in)print(result_temp)由于后续⼜改动了需求,需要预测温度以及湿度,完成了项⽬在github。
转子温度模型估算精度和意义-概述说明以及解释

转子温度模型估算精度和意义-概述说明以及解释1.引言1.1 概述转子温度模型估算是一种重要的技术手段,用于预测和估计转子在工作过程中的温度变化。
随着工业技术的不断发展,转子的温度变化对于机械设备的性能和寿命有着重要的影响。
因此,精确地估算转子的温度变化对于设备的正常运行和维护具有重要的意义。
在本文中,我们将介绍转子温度模型估算方法的基本原理和流程。
首先,我们会对不同的转子温度模型进行介绍,并分析它们的优缺点。
然后,我们将详细说明转子温度模型的估算方法和步骤,包括输入数据的获取、数学模型的建立以及模型参数的优化等。
为了评估转子温度模型的估算精度,我们将进行数值模拟和实际测试。
通过与实际测量数据进行对比,我们可以对转子温度模型的估算精度进行评估和分析。
同时,我们还会探讨不同因素对温度模型估算精度的影响,以及如何进一步提高模型的准确性和可靠性。
转子温度模型的估算具有重要的工程应用意义。
首先,它可以帮助监测和预测机械设备的性能和寿命,提前发现潜在的故障和问题。
其次,它可以指导设备的运行和维护,合理调整工作参数,提高设备的运行效率和安全性。
最后,转子温度模型的估算结果可以为设计优化提供参考,改进设备结构和材料的选取,提高设备的整体性能和可靠性。
总结而言,本文将重点介绍转子温度模型估算的方法和精度分析,探讨其在工程实践中的意义和应用。
通过深入研究和分析,我们希望能够提供有关转子温度模型估算精度和应用的全面理解,为转子温度模型估算和相关领域的研究工作提供有益的参考和启示。
1.2 文章结构本文将以转子温度模型的估算精度和意义为主题,分为引言、正文和结论三个部分。
引言部分将概述转子温度模型估算的背景和意义,介绍转子温度模型估算方法的重要性和现状。
同时,明确本文的目的,即通过对转子温度模型估算精度和意义的分析,为相关领域的研究和应用提供参考和指导。
正文部分将分为三个小节。
首先,介绍转子温度模型估算方法的基本原理和常用方法,包括传统的热传导模型和基于机器学习的模型等。
基于线性逐步回归的夏季草莓大棚内地温预测模型研究

Journal of Agricultural Catastrophology 2023, Vol.13 No.9基于线性逐步回归的夏季草莓大棚内地温预测模型研究黄龙斐1,王 忠1,张 靓2,王 涛1,周志恒31.阿坝州气象探测中心,四川马尔康 624000;2.阿坝州气象局,四川马尔康624000;3.阿坝州气象台,四川马尔康 624000摘要 收集2018年8—9月塑料大棚内观测的气象数据,构建了基于线性逐步回归的草莓生产大棚内的地温预测模型,采用1号大棚内的地面温度、气温、风速、总辐射,构建1个模拟方程,在构建的过程中,逐一剔除不显著的自变量。
将通过信度为0.05水平的显著性检验的要素模拟出地温模型。
通过2号棚的相应数据验证模型。
该模型所需参数少,实用性强,模拟精度较好,可为设施夏季草莓气象服务和环境调控提供数据依据。
关键词 线性逐步回归;地温;模拟模型;夏季草莓中图分类号:S625.3 文献标识码:B 文章编号:2095–3305(2023)09–0112-03草莓为蔷薇科,属多年生草本植物,有“水果皇后”的美誉,营养价值、经济价值都较高。
作为短日照、喜冷凉气候作物,我国出产的草莓主要为冬春草莓,出产时间为每年12月—翌年5月,批发价格20~40元/kg。
每年6—11月是我国草莓生产空白期,只有南半球可出产优质草莓,但受限于交通运输,目前国内优质夏季鲜食草莓市场暂为空白[1]。
川西北高原位于四川省西北部的阿坝藏族羌族自治州、甘孜藏族自治州境内,平均海拔在3 000~4 000 m以上,是四川省地势最高地区;大部分地区年均温为0~6 ℃,极端最低温在-20 ℃以下,10 ℃以上活动积温1 000~1 500 ℃·d,全年长冬无夏,春秋相连,为四川热量最低地区。
而太阳年辐射量和年日照时数均为四川省最高值,丰富的光能资源在一定程度上弥补了地高天寒、热量不足的缺陷[2-6]。
通过利用高原的夏季模拟平原冬季气候,“蓝迦梅朵”团队前期经不同栽培试验,目前已成功在6—10月产出了优质鲜食草莓,并于松潘高原种植基地成功投入生产。
小井眼超深井井筒温度预测模型及降温方法研究

小井眼超深井井筒温度预测模型及降温方法研究
刘涛;何淼;张亚;陈鑫;阚正玉;王世鸣
【期刊名称】《钻采工艺》
【年(卷),期】2024(47)3
【摘要】顺北区块超深小井眼钻井井底高温问题突出,明确井筒温度场分布规律并探讨高效降温方法对于保障该地区钻井安全具有重要工程意义。
文章基于超深小井眼钻井工艺,综合考虑钻井液黏性耗散、钻柱偏心和旋转及钻头破岩等多种热源项对井筒温度的影响,建立了适用于小井眼超深井的井筒瞬态传热模型,并提出针对性的降温方法,然后采用MWD实测数据及商业软件Drillbench进行对比验证,本模型预测值与随钻数据更为吻合,误差在2%以内;钻柱隔热可降低井底温度33℃,钻井提速、增加排量等其它方法可使井底温度降低3~10℃,采用地面降温法的降温效率呈现显著的边际递减效应,即井越深其降温能力越有限。
针对单一降温方法降温效果不够显著,建议综合多种降温方法有效降低井筒温度。
本研究成果可为小井眼超深井的井筒温度准确预测和降温方法优选提供理论指导。
【总页数】8页(P65-72)
【作者】刘涛;何淼;张亚;陈鑫;阚正玉;王世鸣
【作者单位】长江大学石油工程学院;油气钻采工程湖北省重点实验室•长江大学;荆州嘉华科技有限公司;天津汇铸石油设备科技有限公司;天津市油气与地热完井工具重点实验室
【正文语种】中文
【中图分类】TE2
【相关文献】
1.超深井掺稀降黏井筒温度分布模拟研究
2.深水超深井钻井井筒温度剖面预测
3.顺北一区小井眼超深井井筒温度场特征研究与应用
4.超深井井筒温度数值模型与解析模型计算精度对比研究
5.深井超深井注入过程井筒温度场模型研究及应用
因版权原因,仅展示原文概要,查看原文内容请购买。
转炉炼钢终点温度预报模型的研究

转炉炼钢终点温度预报模型的研究转炉炼钢是一种重要的钢铁生产过程,其终点温度的预报是关键的决策因素之一。
为了提高转炉炼钢的质量和效率,研究转炉炼钢终点温度预报模型已成为研究的热点。
本文将介绍转炉炼钢终点温度预报模型的研究内容和研究现状,探讨其应用价值和未来发展方向。
一、研究内容转炉炼钢终点温度预报模型的研究内容主要包括以下几个方面:1、数据采集和处理:利用物理、化学参数和历史数据等信息,建立炉内温度、氧气含量、碳含量等变量的数据采集系统,并进行数据预处理,以保证数据的质量和可靠性。
2、模型建立:基于数据采集和处理的结果,建立转炉炼钢终点温度预报模型,以实现对炉内不同区域温度的预测和控制。
常见的预测模型包括神经网络、支持向量机和逻辑回归等。
3、模型评估:通过比较不同模型的预测结果,评估模型的准确性、稳定性和实用性,确定最优模型并进行后续验证。
4、应用实践:利用建立的预报模型,实现对转炉炼钢过程中终点温度的预测和控制。
通过实践应用,逐步提高模型的适应性和预测精度,为钢铁生产提供可靠的技术支持。
二、研究现状目前,国内外对于转炉炼钢终点温度预报模型的研究已经取得了一定的成果。
国内一些钢铁企业对于该问题进行了探索和应用,开展了一些基于统计学和人工智能算法的研究。
例如,多个钢铁企业采用了支持向量机算法来预测炉内温度,取得了良好的预测效果。
国际上,美国、日本等国家也在该领域进行了长期的研究,目前已有许多文献探讨了转炉炼钢终点温度预测的基础理论、实验研究以及预测模型的应用等方面。
以美国为例,该国的许多大型钢铁企业都在转炉炼钢领域具有深厚的技术积累和应用经验,其预测模型的准确性已经达到了相当高的水平。
三、应用价值转炉炼钢终点温度预报模型的研究具有重要的应用价值。
首先,该模型可以预测炉内不同区域的温度分布,实现对炉温的精准控制,提高炼钢的质量和效率。
其次,该模型可以帮助钢铁企业降低生产成本,减少资源浪费,提高经济效益。
航空高速齿轮服役温度预测模型研究

2024年第48卷第2期Journal of Mechanical Transmission航空高速齿轮服役温度预测模型研究陈玉灵1朱加赞2陈泰民1朱才朝1魏沛堂1徐永强2(1 重庆大学高端装备机械传动全国重点实验室,重庆400044)(2 中国航发四川燃气涡轮研究院机械系统技术研究室,四川成都610500)摘要随着高速重载下航空传动服役温度的不断提高,齿轮胶合失效成为制约飞行器性能的关键因素。
为高效预测航空齿轮服役温度,针对某航空发动机齿轮提出了一种基于顺序耦合的齿轮温度仿真分析方法,考虑固-液-气多相对流换热及不同齿面散热系数等因素,模拟了航空齿轮在不同工况下的本体温度和齿面闪温。
经验证说明,该数值方法与ISO/TS 6336-20闪温法标准计算结果吻合良好,不同工况下接触温度最大偏差控制在10%以内;当传动系统输入转速为22 400 r/min、转矩为119.4 N·m时,分流大齿轮的接触温度达到242.6 ℃,齿轮胶合安全系数为1.22,存在胶合失效风险。
所提出的仿真分析方法能有效预测航空等领域高速齿轮服役温度,为评估航空齿轮胶合失效风险提供了高效可靠的方法。
关键词航空齿轮齿轮胶合温度仿真本体温度接触温度Study on Operating Temperature Prediction Model of Aero High-speed GearsChen Yuling1Zhu Jiazan2Chen Taimin1Zhu Caichao1Wei Peitang1Xu Yongqiang2(1 State Key Laboratory of Mechanical Transmission for Advanced Equipment, Chongqing University, Chongqing 400044, China)(2 Laboratory of Mechanical Systems Technology, AEEC Sichuan Gas Turbine Establishment, Chengdu 610500, China)Abstract With the continuous improvement of the operating temperature of aero transmission under the high-speed and high load, gear scuffing failure has become a key factor restricting the performance of aircrafts. To efficiently predict the operating temperature of aero gears, a sequential coupling numerical analysis method of the gear temperature is proposed for an aero engine gear, which simulates the bulk temperature and flash tem⁃perature under different working conditions, considering factors such as solid-liquid-gas multi-state flow heat exchange and heat dissipation coefficients of different tooth surfaces. The simulated gear contact temperature is compared with calculation results of ISO/TS 6336-20 and shows consistency, the largest deviation between which under different working conditions is controlled within 10%. When the input speed is 22 400 r/min and the torque is 119.4 N∙m, the split large gear contact temperature reaches 242.6 ℃, the scuffing safety factor is 1.22, and there is a risk of scuffing failure. The proposed simulation analysis method can effectively predict the operating temperature of aero high-speed gears, and provide an efficient and reliable method for assessing the risk of aero gear scuffing failure.Key words Aero gear Gear scuffing Temperature simulation Bulk temperature Contact tempera⁃ture0 引言航空发动机朝着高马赫数、高推重比、高可靠性和长寿命方向发展,这给航空发动机机械传动系统研制带来了更加严峻的挑战。
基于GA-BP神经网络的温室温度预测研究

第13卷㊀第9期Vol.13No.9㊀㊀智㊀能㊀计㊀算㊀机㊀与㊀应㊀用IntelligentComputerandApplications㊀㊀2023年9月㊀Sep.2023㊀㊀㊀㊀㊀㊀文章编号:2095-2163(2023)09-0168-04中图分类号:S625;TP183文献标志码:A基于GA-BP神经网络的温室温度预测研究李其操,董自健(江苏海洋大学电子工程学院,江苏连云港222005)摘㊀要:温度对于温室内作物的生长起着重要的作用,为了更精准的管理和控制温室内的温度,提出了基于遗传算法优化的BP神经网络预测模型(GA-BP),对温室内温度进行预测㊂本文利用遗传算法对BP神经网络的权值和阈值进行优化,使模型避免出现局部最优,有效改善了传统BP神经网络预测模型的性能,使预测出的温度更加精准㊂实验证明,选择隐藏层节点数为7时,GA-BP神经网络预测模型的预测结果最佳,平均绝对误差(MAE)㊁均方误差(MSE)和平均绝对百分比误差(MAPE)分别为0.441㊁0.276㊁0.525㊂与传统BP神经网络预测模型相比分别提升了13.2%㊁38.4%㊁21.5%㊂关键词:遗传算法;BP神经网络;温室温度;预测模型GreenhousetemperaturepredictionbasedonGA-BPneuralnetworkLIQicao,DONGZijian(SchoolofElectronicEngineering,JiangsuOceanUniversity,LianyungangJiangsu222005,China)ʌAbstractɔTemperatureplaysanimportantroleinthegrowthofcropsinthegreenhouse.Inordertomanageandcontrolthetemperatureinthegreenhousemoreaccurately,ageneticalgorithm-optimizedBPneuralnetworkpredictionmodel(GA-BP)wasproposedtopredictthetemperatureinthegreenhouse.Inthispaper,thegeneticalgorithmisusedtooptimizetheweightsandthresholdsoftheBPneuralnetwork,sothatthemodelavoidslocaloptimization,effectivelyimprovestheperformanceofthetraditionalBPneuralnetworkpredictionmodel,andmakesthepredictedtemperaturemoreaccurate.Experimentsshowthatwhenthenumberofhiddenlayernodesisselectedtobe7,thepredictionresultoftheGA-BPneuralnetworkpredictionmodelisthebest,andthemeanabsoluteerror(MAE),meansquareerror(MSE)andmeanabsolutepercentageerror(MAPE)are0.441,0.276,and0.525respectively.ComparedwiththetraditionalBPneuralnetworkpredictionmodel,ithasincreasedby13.2%,38.4%,and21.5%respectively.ʌKeywordsɔgeneticalgorithm;BPneuralnetwork;greenhousetemperature;predictionmodel作者简介:李其操(1997-),男,硕士研究生,主要研究方向:农业物联网;董自健(1973-),男,博士,教授,主要研究方向:检测与控制㊁通信技术㊂通讯作者:董自健㊀㊀Email:dzjian@126.com收稿日期:2022-10-200㊀引㊀言中国是排在世界前列的农业生产大国,温室的面积占据着世界首位㊂温室内的环境因素对于作物的生长有着至关重要的影响[1-2]㊂目前,温室的调控方式大多是凭借工人的生产经验,通过获得的传感器数据,进行预判性的调控㊂因此,能够精准的预测出温室内的温度情况,对温室调控系统有很大的帮助㊂近年来,许多学者提出了针对温度预测的方法㊂如:左志宇[3]提出采用时序分析法建立温度预测模型的方法;徐意[4]构建了基于RBF神经网络的温室温度预测模型;徐宇[5]构建了基于复数神经网络的温室温度预测模型;王红君[6]利用贝叶斯正则化算法对BP神经网络进行改进,降低了影响温度的因子之间的耦合度等㊂但是,上述预测模型都容易出现陷入局部最优的情况㊂因此,本文利用遗传算法,对BP神经网络的初始权值和阈值进行优化,使预测模型避免出现局部最优的情况,从而对温室内温度进行更精准的预测㊂1㊀GA-BP神经网络预测模型的构建1.1㊀BP神经网络BP神经网络的主要思想是:训练数据通过前馈网络训练后得到输出数据,将输出数据与期望数据进行对比得到误差,反向传播网络将得到的误差反向输入输出层,对网络的连接权值和阈值进行反复训练,缩小网络输出和期望输出之间的误差㊂输入㊁输出层为单层结构,而隐藏层可以是单层或多层㊂输入层㊁隐藏层㊁输出层之间的神经元都是相互连接的,为全连接㊂BP神经网络结构如图1所示㊂uy输入层节点隐藏层节点输出层节点图1㊀BP神经网络结构图Fig.1㊀StructureofBPneuralnetwork㊀㊀假设输入层节点数为n,隐藏层节点数为l,输出层节点数为m,输入层到隐藏层的权重为ωij,隐藏层到输出层的权重为ωjk,输入层到隐藏层的阈值为aj,隐藏层到输出层的阈值为bk,学习速率为η,激励函数为g(x)㊂其中,激励函数为g(x)取sigmoid函数㊂形式如式(1)所示:gx()=11+e-x(1)㊀㊀隐藏层的输出如式(2)所示:Hj=gðni=1ωijxi+aj()(2)㊀㊀输出层的输出如式(3)所示:Ok=ðlj=1Hjωjk+bk(3)㊀㊀网络误差如式(4)所示:ek=Yk-Ok(4)㊀㊀其中,Yk为期望输出㊂输入层到隐藏层权值的更新公式如式(5)所示:㊀㊀ωij=ωij+ηHj1-Hj()xiðmk=1ωjkek(5)隐藏层到输出层权值的更新公式如式(6)所示:ωjk=ωjk+ηHjek(6)㊀㊀隐藏层节点阈值的更新公式如式(7)所示:aj=aj+ηHj1-Hj()ðmk=1ωjkek(7)㊀㊀输出层节点阈值的更新公式如式(8)所示:bk=bk+ηek(8)㊀㊀由于BP神经网络的初始连接权值和阈值是随机选定,可能会使网络陷入局部极值,权值收敛到局部最小值,从而出现网络训练失败,模型的预测精度不高的结果㊂因此,本文采用遗传算法对BP神经网络进行优化,得到权值和阈值的最优解,使模型能够更高效的训练和更精准的预测㊂1.2㊀遗传算法(1)初始化种群㊂种群中的个体由BP神经网络中输入层到隐藏层的权值㊁隐藏层的阈值㊁隐藏层到输出层的权值和输出层的阈值编码而成㊂(2)适应度函数㊂适应度函数用于表明BP神经网络中权值和阈值的优劣性,个体适应度值为训练数据预测误差绝对值之和㊂适应度函数的计算公式如式(9)所示:Fi=kðni=1absyi-oi()()(9)式中:k为系数,n为神经网络输出节点数量,yi为神经网络第i个节点的期望输出,oi为神经网络第i个节点的预测输出㊂(3)选择操作㊂选择操作从旧群体中以一定概率选择优良个体组成新的种群,以繁殖得到下一代个体,本文采用轮盘赌法,每个个体i被选择的概率pi如式(10)所示:pi=FiðNj=1Fi(10)式中:N为种群规模,Fi为第i个个体适应度值㊂(4)交叉操作㊂交叉操作是指从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体,由于个体采用实数编码,所以交叉操作采用实数交叉法[7]㊂第j个个体Sj和k个个体Sk在i位的交叉过程如式(11)所示:Sj,i=Sj,i1-b()+Sk,i㊃bSk,i=Sk,i1-b()+Sj,i㊃b{(11)式中b为[0,1]区间内的随机数㊂(5)变异操作㊂为了防止遗传算法在优化过程中陷入局部最优解,在搜索过程中,需要对个体进行变异㊂经过交叉操作后得到新的染色体后,随机选择染色体上的若干个基因,将这若干个基因的值进行随机修改,从而更新了染色体的基因,突破了搜索的限制,更有利于获取全局最优解[8]㊂选择第i个961第9期李其操,等:基于GA-BP神经网络的温室温度预测研究个体的第j个基因aij进行变异,操作过程如式(12)㊁式(13)所示:aij=aij+amax-aij()㊃fs()r>0.5aij-aij-amin()㊃fs()rɤ0.5{(12)fs()=r1-sGmaxæèçöø÷(13)式中:amax㊁amin分别是个体i的最大值和最小值,s是迭代次数,Gmax是最大进化次数,r为[0,1]区间内的随机数㊂1.3㊀GA-BP神经网络预测模型GA-BP神经网络预测模型由遗传算法(GeneticAlgorithms,GA)优化部分和BP神经网络两部分组成㊂由于种群中的每个个体都包含了BP神经网络的初始权值和阈值,遗传算法部分的作用是优化BP神经网络的权值和阈值㊂通过计算BP神经网络的误差,得到个体适应度值㊂经过遗传算法的选择㊁交叉和变异操作找到最优适应度值的个体㊂对最优个体进行解码,得到权值和阈值,赋值给BP神经网络,再使用反向传播进行训练㊂GA-BP神经网络预测模型的执行过程如图2所示㊂输出预测结果满足终止条件更新权值和阈值计算误差获取最优权值和阈值确定B P 神经网络初始权值和阈值满足终止条件选择、交叉、变异计算适应度值初始化种群对权值和阈值编码YNNY图2㊀遗传算法优化BP神经网络流程图Fig.2㊀FlowchartofgeneticalgorithmtooptimizeBPneuralnetwork2㊀实验与结果分析2.1㊀样本数据采集本文实验数据采集自连云港赣榆葡萄园第6号温室,选用温度㊁湿度㊁二氧化碳浓度㊁土壤氮含量㊁土壤磷含量和土壤钾含量作为样本数据㊂每15min采集一次数据,共采集了2292组样本数据㊂为了实验测试更方便,本文选用其中2000组数据,并将前80%的样本数据作为训练样本,剩余的20%样本数据作为测试样本㊂部分样本数据见表1㊂表1㊀部分样本数据Tab.1㊀Partialsampledata日期时间温度/ħ湿度/%二氧化碳浓度/(ppm)土壤氮含量/%土壤磷含量/%土壤钾含量/%2022/8/2118:40:3828.28736125.226702022/8/2119:19:4127.88635925.225702022/8/2119:34:5527.88636025.126702022/8/2119:50:1027.68635925.225702022/8/2120:05:2427.68635825.225702022/8/2120:20:3927.58635825.225682.2㊀模型参数设定2.2.1㊀BP神经网络结构根据所获得的样本数据,将输入层节点设定为5,即5个特征,分别为湿度㊁二氧化碳浓度㊁土壤氮含量㊁土壤磷含量和土壤钾含量数据;输出层节点为1个,特征为温度数据;通过试凑法确定隐藏层节点为7个㊂因此,BP神经网络的结构为5-7-1㊂2.2.2㊀遗传算法参数设定由于过多的迭代次数会影响模型的训练效率,且适应度曲线在迭代50次后的变化幅度不大,因此本实验将进化迭代次数设定为50次,种群规模为30,交叉概率为0.3,变异概率为0.1㊂图3为遗传算法的适应度曲线㊂10410310210110099980102030405060进化代数适应度平均适应度适应度曲线终止代数=50图3㊀遗传算法适应度曲线Fig.3㊀Geneticalgorithmfitnesscurve071智㊀能㊀计㊀算㊀机㊀与㊀应㊀用㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第13卷㊀2.3㊀模型评价标准为了评定预测模型的性能,本文以平均绝对误差(MAE)㊁均方误差(MSE)和平均绝对百分比误差(MAPE)作为评判预测模型性能优劣的标准㊂各评估误差指标的计算公式如式(14) 式(16)所示:MAE=1nðni=1y^i-yi(14)MSE=1nðni=1y^i-yi()2(15)MAPE=1nðni=1y^i-yiyi(16)式中:y^i为模型的预测值,yi为真实值,n为样本数㊂所得的值越小,则模型的性能越优异㊂2.4㊀预测结果及分析通过MATLAB软件对GA-BP神经网络预测模型和传统BP神经网络预测模型进行验证,得到的预测对比结果如图4所示㊂预测结果实际值282726252423222120050100150200250300350400样本编号温度(a)GA-BP网络预测输出预测结果实际值282726252423222120050100150200250300350400样本编号温度(b)BP网络预测输出图4㊀GA-BP与BP训练效果对比图Fig.4㊀ComparisonofGA-BPandBPtrainingeffects㊀㊀由图4可知,GA-BP神经网络预测模型与传统BP神经网络预测模型相比,GA-BP的预测效果更优,预测结果更贴近实际值㊂评价结果见表2㊂可以看出,GA-BP预测模型的各项误差指标均小于传统BP预测模型㊂实验证明,GA-BP神经网络预测模型具有更好的预测效果㊂表2㊀模型的评价指标对比Tab.2㊀Comparisonofevaluationindicatorsofthemodels评价指标GA-BPBPMAE0.4410.508MSE0.2760.448RMSE0.5250.6693㊀结束语本文以温室内湿度㊁二氧化碳浓度和土壤氮磷钾含量与温度有关的影响因子作为输入量,以温度作为输出量,通过遗传算法优化BP神经网络的权值和阈值,构建了GA-BP神经网络预测模型㊂实验证明,GA-BP神经网络预测模型能够更精准的进行温室内温度预测,对于温室管理有一定的参考价值㊂参考文献[1]王军伟.苏北地区日光温室构型优化㊁室内温湿度分析及应用效果初探[D].南京:南京农业大学,2015.[2]王克安,李絮花,吕晓惠,等.不同结构日光温室温湿度变化规律及其对番茄产量和病害的影响[J].山东农业科学,2011,235(3):33-36.[3]左志宇,毛罕平,张晓东,等.基于时序分析法的温室温度预测模型[J].农业机械学报,2010,41(11):173-177,182.[4]徐意,项美晶.基于RBF神经网络的温室温度调控研究[J].农机化研究,2010,32(3):74-76.[5]徐宇,冀荣华.基于复数神经网络的智能温室温度预测研究[J].中国农机化学报,2019,40(4):174-178.[6]王红君,史丽荣,赵辉,等.基于贝叶斯正则化BP神经网络的日光温室温度预测模型[J].湖北农业科学,2015,54(17):4300-4303.[7]曹雪丽.配送中心订单分批处理随机服务系统模型与优化研究[D].北京:北京物资学院,2012.[8]高基旭,王珺.一种基于遗传算法的多边缘协同计算卸载方案[J].计算机科学,2021,48(1):72-80.171第9期李其操,等:基于GA-BP神经网络的温室温度预测研究。
