数字电路和数字电子技术课后答案解析第七章
数字电子技术基础习题册答案7-11

第7章 时序逻辑电路【7-1】已知时序逻辑电路如图7.1所示,假设触发器的初始状态均为0。
(1 )写出电路的状态方程和输出方程。
(2) 分别列出X =0和X =1两种情况下的状态转换表,说明其逻辑功能。
(3) 画出X =1时,在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形。
1J 1KC11J 1KC1Q 1Q 2CPXZ1图7.1解:1.电路的状态方程和输出方程n 1n2n 11n 1Q Q Q X Q +=+ n 2n 11n 2Q Q Q ⊕=+ CP Q Q Z 21=2.分别列出X =0和X =1两种情况下的状态转换表,见题表7.1所示。
逻辑功能为 当X =0时,为2位二进制减法计数器;当X =1时,为3进制减法计数器。
3.X =1时,在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形如图7.1(b)所示。
题表7.1Q Q Z图7.1(b)【7-2】电路如图7.2所示,假设初始状态Q a Q b Q c =000。
(1) 写出驱动方程、列出状态转换表、画出完整的状态转换图。
(2) 试分析该电路构成的是几进制的计数器。
Q c图7.2解:1.写出驱动方程1a a ==K J ncn a b b Q Q K J ⋅== n b n a c Q Q J = n a c Q K = 2.写出状态方程n a 1n a Q Q =+ n a n a n a n a n c n a 1n b Q Q Q Q Q Q Q +=+ nc n a n c n b n a 1n b Q Q Q Q Q Q +=+3.列出状态转换表见题表7.2,状态转换图如图7.2(b)所示。
图7.2(b)表7.2状态转换表CP na nbc Q Q Q 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 16 0 0 0n4.由FF a 、FF b 和FF c 构成的是六进制的计数器。
(全)数字电子技术基础课后答案夏路易

《数字电子技术基础教程》习题与参考答案(2010.1)第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101 解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
数字电路第七章答案

数字电路第七章答案第七章可编程逻辑器件第一节基本内容一、基本知识点(一)可编程逻辑器件基本结构可编程逻辑器件是70年代发展起来的新型逻辑器件,相继出现了只读存储器、可编程只读存储器、可编程逻辑阵列、可编程阵列逻辑、通用阵列逻辑和可擦写编程逻辑器件等多个品种,它们的组成和工作原理基本相似。
的基本结构由与阵列和或阵列构成。
与阵列用来产生有关与项,或阵列把所有与项构成“与或”形式的逻辑函数。
在数字电路中,任何组合逻辑函数均可表示为与或表达式,因而用“与门-或门”两级电路可实现任何组合电路,又因为任何时序电路是由组合电路加上存储元件(触发器)构成的,因而的“与或”结构对实现数字电路具有普遍意义。
在中,输入电路中为了适应各种输入情况,每一个输入信号都配有一缓冲电路,使其具有足够的驱动能力,同时产生原变量和反变量输出,为与门阵列提供互补信号输入。
输出电路的输出方式有多种,可以由或阵列直接输出,构成组合方式输出,也可以通过寄存器输出,构成时序方式输出。
输出既可以是低电平有效,也可以是高电平有效;既可以直接接外部电路,也可以反馈到输入与阵列,由此可见的输出电路根据不同的可编程逻辑器件有所不同。
(二)可编程逻辑器件分类1.按编程部位分类有着大致相同的基本结构,根据与阵列和或阵列是否可编程,分为三种基本类型:(1)与阵列固定,或阵列可编程(2)与或阵列均可编程(3)与阵列可编程,或阵列固定归纳上述的结构特点,列于表7-1。
表7-1 各种的结构特点2.按编程方式分类(1)掩膜编程(2)熔丝与反熔丝编程(3)紫外线擦除、电可编程(4)电擦除、电可编程(5)在系统编程()(三)高密度可编程逻辑器件通常衡量可编程逻辑器件芯片的密度是以芯片能容纳等效逻辑门的数量,一般是以2000为界限,即芯片容纳等效逻辑门小于2000门,称它为低密度可编程逻辑器件或简单的可编程逻辑器件(),若大于2000等效逻辑门,称为高密度可编程逻辑器件()。
数字电子技术第七章习题答案

第七章D/A 和A/D 转换器7.1填空1、8位D/A转换器当输入数字量只有最高位为高电平时输出电压为5V,若只有最低位为高电平,则输出电压为40mV 。
若输入为10001000,则输出电压为5.32V 。
2、A/D转换的一般步骤包括采样、保持、量化和编码。
3、已知被转换信号的上限频率为10kH Z,则A/D转换器的采样频率应高于20kH Z。
完成一次转换所用时间应小于50μs。
4、衡量A/D转换器性能的两个主要指标是精度和速度。
5、就逐次逼近型和双积分型两种A/D转换器而言,双积分型抗干扰能力强;逐次逼近型转换速度快。
7.2CPU O-0.625V-1.25V-1.875V-2.5V7.32R 2R 2R 2R2R R R R 2R Q0 Q1 Q2 Q33RRRU O&-+-+CP ui+ -四位二进制计数器RdV AG首先将二进制计数器清零,使U o=0。
加上输入信号(U i>0),比较器A输出高电平,打开与门G,计数器开始计数,U o增加。
同时U i亦增加,若U i>U o,继续计数,反之停止计数。
但只要U o未达到输入信号的峰值,就会增加,只有当U o=U imax 时,才会永远关闭门G,使之得以保持。
7.41、若被检测电压U I(max)=2V,要求能分辨的最小电压为0.1mV,则二进制计数器的容量应大于20000;需用15位二进制计数器2、若时钟频率f CP=200kH Z,则采样时间T1=215×5μs=163.8ms3、TRC2V5V1⨯=RC=409.5ms7.5 1、完成一次转换需要36μs2、A/D转换器的输出为0100111118。
数字电子技术习题答案

习题答案第一章数制和码制1.数字信号和模拟信号各有什么特点?答:模拟信号——量值的大小随时间变化是连续的。
数字信号——量值的大小随时间变化是离散的、突变的(存在一个最小数量单位△)。
2.在数字系统中为什么要采用二进制?它有何优点?答:简单、状态数少,可以用二极管、三极管的开关状态来对应二进制的两个数。
3.二进制:0、1;四进制:0、1、2、3;八进制:0、1、2、3、4、5、6、7;十六进制:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。
4.(30.25)10=( 11110.01)2=( 1E.4)16。
(3AB6)16=( 0011101010110110)2=(35266)8。
(136.27)10=( 10001000.0100)2=( 88.4)16。
5.B E6.ABCD7.(432.B7)16=( 010*********. 10110111)2=(2062. 556)8。
8.二进制数的1和0代表一个事物的两种不同逻辑状态。
9.在二进制数的前面增加一位符号位。
符号位为0表示正数;符号位为1表示负数。
这种表示法称为原码。
10.正数的反码与原码相同,负数的反码即为它的正数原码连同符号位按位取反。
11.正数的补码与原码相同,负数的补码即为它的反码在最低位加1形成。
12.在二进制数的前面增加一位符号位。
符号位为0表示正数;符号位为1表示负数。
正数的反码、补码与原码相同,负数的反码即为它的正数原码连同符号位按位取反。
负数的补码即为它的反码在最低位加1形成。
补码再补是原码。
13.A:(+1011)2的反码、补码与原码均相同:01011;B: (-1101)2的原码为11101,反码为10010,补码为10011.14.A: (111011)2 的符号位为1,该数为负数,反码为100100,补码为100101. B: (001010)2 的符号位为0,该数为正,故反码、补码与原码均相同:001010.15.两个用补码表示的二进制数相加时,和的符号位是将两个加数的符号位和来自最高有效数字位的进位相加,舍弃产生的进位得到的结果就是和的符号。
数字电子技术第7章习题答案

数字电子技术第7章习题答案
1. 什么是逻辑门?
答:逻辑门是数字电路中的基本组件,用于对输入进行逻辑运算并产生输出。
2. 列举几种常见的逻辑门。
答:与门、或门、非门、异或门、与非门、或非门等。
3. 什么是真值表?
答:真值表是一种用来展示逻辑函数输入与输出关系的表格,其中列出了所有可能的输入和对应的输出。
4. 什么是逻辑电路?
答:逻辑电路是指由逻辑门组成的电路,用于对输入进行逻辑运算并产生输出。
5. 什么是卡诺图?
答:卡诺图是一种用于最小化逻辑函数的图形化工具,通过将函数的真值表转化为图形,可快速找到最小化的逻辑表达式。
6. 什么是多路复用器?
答:多路复用器是一种数字电路,可以选择不同的输入并将其发送到一个输出线上。
7. 什么是解码器?
答:解码器是一种数字电路,用于将二进制数字输入转换为对应的输出,通常用于驱动其他数字电路中的寄存器、计数器等。
8. 什么是编码器?
答:编码器是一种数字电路,用于将多个输入端连接到一个二进制数字输出端,也可以实现将多个开关等输入转换为一个数字信号输出。
9. 什么是计数器?
答:计数器是一种数字电路,可用于记录电路所经过的时间或事件数量,通常用于计时器、频率计等应用。
10. 什么是触发器?
答:触发器是一种数字电路,可用于存储和控制数字信号,通常用于存储器、寄存器等应用。
《数字电路-分析与设计》第七章习题及解答(部分1) 北京理工大学出版社
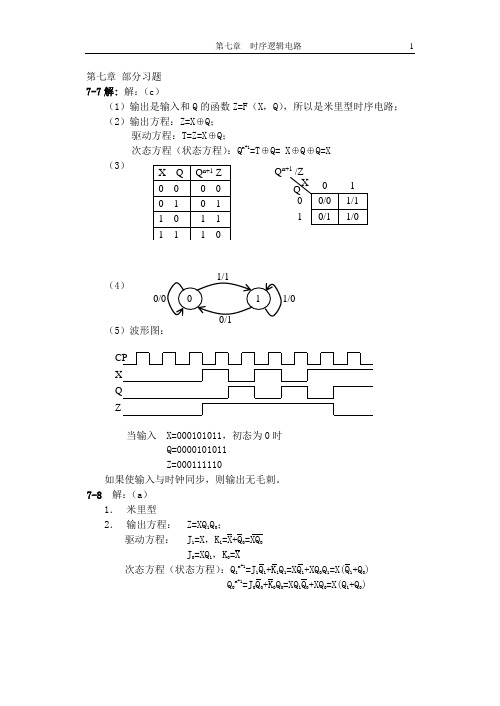
第七章 部分习题 7-7解: 解:(c )(1)输出是输入和Q 的函数Z=F (X ,Q ),所以是米里型时序电路; (2)输出方程:Z=X ⊕Q ;驱动方程:T=Z=X ⊕Q ;次态方程(状态方程):Q n+1=T ⊕Q= X ⊕Q ⊕Q=X(3)(4)(5)波形图:当输入 X=000101011,初态为0时 Q=0000101011 Z=000111110如果使输入与时钟同步,则输出无毛刺。
7-8 解:(a ) 1. 米里型2. 输出方程: Z=XQ 1Q 0;驱动方程: J 1=X ,K 1=X+Q 0=XQ 0J 0=XQ 1,K 0=X次态方程(状态方程):Q 1n+1=J 1Q 1+K 1Q 1=XQ 1+XQ 0Q 1=X(Q 1+Q 0)Q 0n+1=J 0Q 0+K 0Q 0=XQ 1Q 0+XQ 0=X(Q 1+Q 0)Q n+1CP X Q Z3.4.7-12某同步时序电路的逻辑方程如下:驱动方程:nQ X T 01⊕=,n Q X T 10=;输出方程:n Q X Z 1=。
要求: 解:1.同步时序电路的逻辑图示于图,这是米里型的状态机。
2.(a )状态方程: Q 1n+1=T 1⊕Q 1=X ⊕Q 0⊕Q 1Q 0n+1=T 0⊕Q 0=XQ 1⊕Q 0=XQ 1Q 0+XQ 0+Q 1Q 0(b )状态转换表: (c )状态转换图:(Q 1Q 0n+1Q7-15解:(a )“11”检测器,不重叠。
S 0:初始状态,输出0; S 1:输入一个“1”,输出0; S 2:输入两个“1”,输出1;(b ) “101”检测器,可重叠。
S 0:初始状态;S 1:输入序列为“1”;S 2:输入序列为“10”;S 3:输入序列为“101”;(c )(d )略7-34 “011”序列检测器,可重叠。
解:1.采用D(a ) 米里型状态图: S 0:初始状态;S 1:输入序列为“0”; S 2:输入序列为“01”;S 3:输入序列为“011”; (b ) 状态表(两种画法均可):(c ) 状态化简:由观察法知,S 0、S 3等价。
《数字电路-分析与设计》第七章习题及解答(部分2) 北京理工大学出版社

第七章 习题答案7-111、米里型状态机2、输出方程: 01Q XQ Z =驱动方程: 011Q Q X D = 10Q X D =状态方程: 01111Q Q X D Q n ==+ 1010Q X D Q n ==+ 3、状态转换表:4、状态转换图:5、时序图:已知:X=1011111001110 初始: 0001=Q Q0/0X Q 1n Q 0n ZCP7-147-32 一、次态K 图,D 触发器: 1、根据状态转换表,有:1212313Q XQ Q Q Q X Q n +=+1212122312Q XQ Q Q X Q Q X Q Q X Q n +++=+ 111Q X Q n =+2、求驱动方程:对于D 就是状态方程: 12123133Q XQ Q Q Q X Q D n +==+12121223122Q XQ Q Q X Q Q X Q Q X Q D n +++==+ 1111Q X Q D n ==+3、检查启动特性:Z Q Q Q n n n /111213+++能够自启动。
二、次态K 图,JK 触发器:1、求状态方程:1212313Q XQ Q Q Q X Q n +=+ 1212122312Q XQ Q Q X Q Q X Q Q X Q n +++=+ 111Q X Q n =+与采用D 触发器一样。
与JK 触发器的特性方程相比Q K Q J Q n +=+1 2、得JK 触发器的驱动方程: 12312313Q Q Q X Q Q Q X Q n +=+∴ )(123Q Q X J ⊕= 13=K132XQ Q X J += 1112Q X Q X Q X K ⊕=+= X J =1 11=K 3、检查启动特性: (与前相同,略)7-38 设计一个二位多功能计数器: 1、列状态转换驱动表:2、从四变量K 图求驱动方程:00100011Q C C Q C Q C J ++=其它K 图略: 001001001011Q C C Q C C Q C C C C K +++= 1110Q C Q J += 1110Q C C K +=逻辑电路图,略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 时序逻辑电路
1.电路如图P7.1所示,列出状态转换表,画出状态转换图和波形图,分析电路功能。
图P7.1 解:
(1)写出各级的W.Z 。
D 1=21Q Q ,D 2=Q 1,Z=Q 2CP
( 2 ) 列分析表
( 3 ) 状态转换表
(4)状态转换图和波形图。
Q 2 Q 1 D 2 D 1 Q 2n+1 Q 1n+1 Z 0 0 0 1 0 1 0 0 1 1 0 1 0 0 1 0 0 0 0 0 1 1 1 1 0 1 0 1
Q 2 Q 1 Q 2n+1 Q 1n+1 Z 0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 1 1 1 0 1
CP
CP Q 1 0 Q 1 0
Z
( b )
Q 2 Q 1 /Z
( a )
01/0
11/1 10/1
00/0
图7.A1
本电路是同步模3计数器。
2. 已知电路状态转换表如表P7.1所示,输入信号波形如图P7.2所示。
若电路的初始状态为Q2Q1 = 00,试画出Q2Q1的波形图(设触发器的下降沿触发)。
解:由状态转换表作出波形图
3. 试分析图P7.3所示电路,作出状态转换表及状态转换图,并作出输入信号为0110111110相应的输出波形(设起始状态Q2Q1 = 00)。
( a )
表P7.1
X
Q2 Q1
0 1
00
01
10
11
01/1
10/0
10/0
01/1
11/1
10/0
11/0
00/1
Q2n+1 Q1n+1/Z
CP
X
Q1 0
Q2 0
Z
图P7.2
CP
X
Q1 0
Q1 0
Z
图P7.A2
( b )
解:(1)写W.Z 列分析表
J 1 = XQ 2 1Q Q X K 1 = X
( 2 ) 作出状态转换表及状态转换图
(3)作出输出波形图:
1 根据状态转换表,作出状态的响应序列,设y = Q 2Q 1 X : 0 1 1 0 1 1 1 1 1 0 y n : 0 0
2 1 0 2 1
3 3 3 y n+1: 0 2 1 0 2 1 3 3 3 0
Z : 1 1 1 1 1 1 1 0 0 1
2 根据状态响应序列画响应的输出波形。
4. 设计一个“1 1 1 1”序列信号检测器,设输入信号为X ,输出信号为Z 。
X :0 0 1 1 0 0 0 1 1 1 1 1 0 1 … Z :0 0 0 0 0 0 0 0 0 0 1 1 0 0 … 解:
(1)建立原始的状态转换图和状态转换表 设:A --- 输入“0”以后的状态。
B --- 输入1个“1”以后的状态。
C --- 输入2个“1”以后的状态。
D --- 输入3个“1”以后的状态。
E --- 输入4个“1”以后的状态。
(2)状态化简:画出化简后的状态转换图和状态转换表。
(3)状态分配:画出分配后的状态转换表和状态转换图
设:A —00 B —01 C —11 D —
(4)画出动作卡诺图,触发器选型,确定电路激励输入,确定外输出Z 。
图P7.A4( d )
选用JK 触发器,J 是a 必圈0必不圈,其余无关,K 是β必圈1必不圈,其余无关。
J 2 = XQ 1 J 2 =2Q X Z =12Q Q X K 2 =X K1=X +Q 2 =2Q X (5)画出逻辑电路图
图P7.A4( e )
5. 已知某计数器电路中图P7.4所示,分析它是几进制计数器,并画出工作波形,设电路初始状态Q 2Q 1 = 00。
图P7.4
解:列出分析表:D 1=1Q ,D 2=21Q ⊕Q
设计数器为4进制计数器,画出工作波形图如下:
Q 2 Q 1 D 2 D 1 Q 2n+1 Q 1n+1 0 0 0 1 0 1 0 1 1 0 1 0 1 0 1 1 1 1 1 1 0 0 0 0
图P7.A5( a )
00
01 11 10 CP Q 1 0 Q 1 0
图P7.A5 ( b )
6. 分析图P
7.5所示计数器电路,画出状态转换图,说明是几进制计数器,有无自启功能。
图P7.5
解:(1)写出激励函数,列分析表
J 1=32Q Q J2=1Q J 3=Q 2Q 1 K 1=1 K2= 31Q Q =Q 1+Q 3 K 3=1
Q 3 Q 2 Q 1 J 3 K 3 J 2 K 2 J 1 K 1 Q 3n+1 Q 2n+1 Q 1n+1
0 0 0 0 1 0 0 1 1 0 0 1 0 0 1 0 1 1 1 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 1 1 0 1 1 1 1 1 1 0 1 1 0 0 1 0 0 0 1 0 1 1 1 0 0 1 1 0 1 0 1 1 1 1 1 0 1 0 1 1 0 0 1 0 1 0 1 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0。
