2019-2020年高中数学 第三章 第1课 平均变化率教学案 苏教版选修1-1
江苏省连云港市灌云县四队中学高中苏教版数学选修1-1教案:《平均变化率》
(备课人: 吴利霞 学科: 高二数学 )备课
时间
3.28 教学 课题 教时 计划 1 教学 课时 1 教学
目标 通过大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,体会导数的思想及其内涵。
重点难
点
平均变化率的意义
教学过程 一、问题情境
1、情境:
某市2008年4月20日最高气温为33.4℃,而4月19日和4月18日的最高气温分别为24.4℃和18.6℃,短短两天时间,气温陡增14.8℃,闷热中的人们无不感叹:“天气热得太快了!”
时间
4月18日 4月19日 4月20日 日最高气温 18.6℃ 24.4℃ 33.4℃
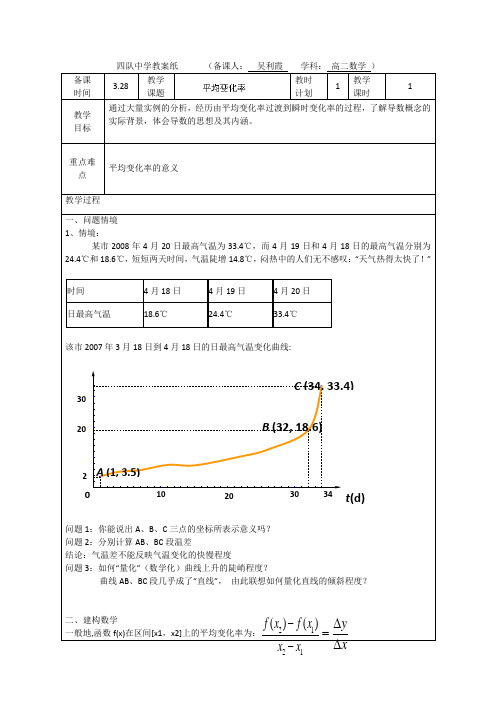
该市2007年3月18日到4月18日的日最高气温变化曲线:
问题1:你能说出A 、B 、C 三点的坐标所表示意义吗?
问题2:分别计算AB 、BC 段温差
结论:气温差不能反映气温变化的快慢程度
问题3:如何“量化”(数学化)曲线上升的陡峭程度?
曲线AB 、BC 段几乎成了“直线”, 由此联想如何量化直线的倾斜程度?
二、建构数学
一般地,函数f(x)在区间[x1,x2]上的平均变化率为: t (d)
20 30 34 2
10 20 30
A (1, 3.5)
B (32, 18.6)
0 C (34, 33.4) T (℃)
2 10 2121
()()f x f x x x --x y ∆∆=。
高中数学新苏教版精品教案《苏教版高中数学选修1-1 3.1.1 平均变化率》18

课题:平均变化率江阴市华士高级中学 孟勇教学目标:知识与技能:1.理解并掌握平均变化率的概念,会求函数在指定区间上的平均变化率,能利用平均变化率解决或说明生活中的实际问题;2.理解平均变化率的意义,为后续建立瞬时变化率和导数的数学模型提供丰富的背景;过程与方法:通过从实际生活背景中引出数学模型的过程来引入平均变化率,学会数学抽象思维,注重数形结合的思想方法;情感意志和价值观:1培养学生分析问题、归纳综合的能力;2通过数学文化的渗透,激发学习热情,培养优秀的数学学习品质 教学重点:平均变化率的概念、平均变化率的实际意义和数学意义 教学难点:理解平均变化率的概念及其实际意义 教学过程: 一、引言只有微分学才能使自然科学有可能用数学来不仅仅表明状态,而且也表明过程:运动。
------恩格斯 二、情景引入1江阴10月问题1:10月24日,11月22日最高气温分别是___________设计意图:引导学生读懂表格信息,为下面的问题做准备。
问题2:A 、B 、C 三段气温变化有什么共同特点? 问题3:A 、B 、C 三轮降温哪一轮更容易感冒? 问题4:A 、C 比较呢?设计意图:通过问题串,引导学生从时间增量、温度增量两个方面比较三段降温人体的感觉,认识错误!的实际意义:单位时间内温度的变化量。
22 “数缺形时少直观,形离数时难入微” ---华罗庚设计意图:(1)两个引例都来自于生活,分别代表了函数的两种表现形式:列表法、图像法。
(2)让学生理解平均变化率的实际意义,平均变化率是从具体的模型中抽象出来的一个概念,在具体的问题中它的意义会更具体化,比如引例1中即为:“单位时间内的温度变化量”,引例2中即为:“单位长度内高度的变化量”,还有在平均速率中为“单位时间内路程的变化量”三、构建新知:从“单位时间内的温度变化量”, “单位长度内高度的变化量”, “单位时间内路程的变化量”这些概念,抽象出“平均变化率”的概念四、数学应用例1、某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月以及第6个月到第12个月该婴儿体重的平均变化率问题5:从视觉角度,AB ,BC 两段曲线有什么区别?问题6:如何量化陡峭程度呢? 数学思想方法总结: 1直线斜率近似量化曲线的陡峭程度 ------以直代曲2平均变化率是曲线的陡峭程度的“数量化”, 曲线陡峭程度是平均变化率的“视觉化” ------数形结合设计意图:让学生了解比较变化的过程可以从两个方面,“数”与“形”例2、已知函数f=21, 分别计算f在区间[-3 , -1] , [0 , 5]上的平均变化率口答:1已知函数g=-2 ,分别计算g在区间[-3 , -1] , [0 , 5]上的平均变化率2已知函数f=21, g=-2,计算在区间[m , n]上f及g的平均变化率思考:=b在区间[m,n]上的平均变化率有什么特点?结论:一次函数=b在区间[m,n]上的平均变化率为斜率设计意图:巩固平均变化率的公式,提炼数学思想:特殊到一般数学文化链接:哥德巴赫猜想例3、已知函数f=2,分别计算f在下列区间上的平均变化率:(1)[1,3];(2)[1,2];(3)[1,];(4)[1,]变式:(5)[,1];(6)[,1];(7)[,1]设计意图:深化平均变化率公式的运用,引导学生发现规律,为下一节课瞬时变化率、导数的学习做好铺垫五、深化理解思考:平均变化率相等,曲线陡峭程度一定相同吗?结论:用平均变化率来量化曲线的陡峭程度是“粗糙不精确”的。
苏教版高中数学选修(1-1)课件3.1.1《平均变化率》

平均速度的数学意义是什么?
ks5u精品课件
现有南京市某年3月和4月某天日最高气温记载
时间 日最高气 温
3月18 日 3.5℃
4月18 4月20 日 日 18.6℃ 33.4℃
温差15.1℃ 温差14.8℃
“气温陡增”这一句生活用语,用数学方法如何刻
画?
ks5u精品课件
1、平均变化率
[ x1 , x2 ] 一般的,函数 f ( x)在区间上的平均变化率为
高中数学课件
灿若寒星整理制作
3.1.1平均变化率
ks5u精品课件
法国《队报》网站的文章称刘翔以不可思议的速度统治 了赛场。这名21岁的中国人跑的几乎比炮弹还快,赛道 上显示的12.94秒的成绩已经打破了12.95奥运会记录,但 经过验证他是以12.91秒平了世界纪录,他的平均速度 达到8.52m/s。
f ( x1 ) f ( x2 ) x1 x2
2、平均变化率是曲线陡峭程度的“数量化”,是一种粗 略 的刻画
ks5u精品课件
由本例得到什么结论?
一次函数y=kx+b在区间[m,n]上的 平均变化率就等于k.
ks5u精品课件
f ( x) 3x 1 练习2、已知函数,分别计算在下 列区间上的平均变化率: f ( x)
(1)[-1,2]; (3) (2)[-1,1]; (3) (3) (3)[-1,-0.9];
ks5u精品课件
2 例4、已知函数,分别计算在下列 f ( x) x
区间上的平均变化率: f ( x)
4 (2)[1,2]; 3 (3)[1,1.1] 2.1
(1)[1,3];
(4)[1,1.001]
ks5u精品课件
2.001
高中数学第3章导数及其应用3.1.1平均变化率课件苏教版选修1-1

1.函数 y=x2+ax+b,当自变量由 0 变化到 1 时,函数值的变化量为________. 【解析】 函数值的变化量为 f(0+1)-f(0)=(0+1)2+a(0+1)+b-02-a·0-b =1+a. 【答案】 1+a
我还有这些不足: (1) ________________________________________________________ (2) ________________________________________________________ 我的课下提升方案: (1) ________________________________________________________ (2) ________________________________________________________
图 3-1-1
1.若已知函数的图象,可从函数的图象上大致分析函数的变化快慢. 2.利用平均变化率的计算公式可以对函数的平均变化快慢进行具体精确的分 析,在实际问题中,平均变化率具有更为具体的现实意义.
求函数的平均变化率
已知函数 f(x)=x12, (1)求 f(x)在 x0 到 x0+Δx 之间的平均变化率.(x0≠0); (2)求 f(x)在 2 到 2.1 之间的平均变化率.
阶
阶
段
段
一
三
3.1 导数的概念
3.1.1 平均变化率
学
阶 段 二
业 分 层 测
评
1.理解并会求具体函数的平均变化率.(重点) 2.会在具体的环境中说明平均变化率的实际意义.(难点)
[基础·初探] 教材整理 平均变化率 阅读教材 P67~P68 例 1 以上部分,完成下列问题. 平均变化率
2019-2020学年度最新高中数学苏教版选修1-1课件:3.1.1平均变化率课件(13张)-优质PPT课件
程度. 曲线越“陡峭”,说明变量变越化快;
曲线越“平缓”,说明变量变越慢.
作业:
1、已知函数 f (x) x2 x 在区间[1,t]上的
平均变化率为2,求t的值. 2、十七大报告中首次提出2020年人均GDP将比2000年翻两番.通 过互联网收集有关中国GDP增长的数据,并比较GDP增长的平均 变化率,从而了解近几年中国经济发展的趋势.
的平均变化率为 g(1) g(3) 2
(1) (3)
函数 f (x)在区间[0,5]上的平均。 函数 g( x) 在区间[0,5]上的平
变化率为
f (5) f (0) 2 50
均变化率为
g(5) g(0) 2 50
一次函数 y=kx+b在区间 [m , n] (m <n) 上的平均变 化率有什么特点?
甲 乙
应用五
已知函数 f ( x) 2x 1, g( x) 2x计算在区间[-3,-1],
[0,5]上 f (x) 及 g(x)的平均变化率.
解: 函数 f (x)在区间[-3,-1]上的 函数 g( x) 在区间[-3,-1]上
平均变化率为
f (1) f (3) 2
(1) (3)
W
W1(t )
W2 (t)
标准
o
t0 t
应用三
甲、乙两人从事某种经营活动所得利润如下图 ,试 比较并评价两人的经营效果.
S(万元) 24
B
乙
2
A
05
甲 60
t(月)
应用四
水经过虹吸管从容器甲中流向容器乙,t s后
容器甲中水的体积 V (t) 5 e0.1t (单位: cm3), 计算第一个10 s内V 的平均变化率. (已知: e 2.718 , e1 0.368 )
【精品】高中数学苏教版选修1-1课件:3.1.1平均变化率课件(15张)

“量化”BC段曲线 的陡峭程度吗?
o 1
32
34
t /d
T (℃ )
C (34, 33.4)
30
20 10 A (1, 3.5) 2 0 2
B (32, 18.6)
10
20
30
34
t(d)
气温在区间【1,32】 的平均变化率为:
你能据此归 纳出“函数f(x) y y 1 8 . 6 3 . 51 5 . 1 B A 0 . 5 , 在区间[x ,x ]上 1 2 x x 3 2 1 3 1 B A 的平均变化率” 气温在区间【32,34】 的平均变化率为: 的一般性定义 y y 3 3 . 4 1 8 . 61 4 . 8 吗? C B
T/oC 33.4
时间
日最高气温
3月18日 4月18日 4月20日 3.5℃ 18.6℃ 33.4℃
联想 直线? 气温变化慢
C(34,33.4) B(32,18.6)
陡 峭问题3] 你能用数学语言来
18.6
A(1,3.5) 3.5
平缓
xC-xB
气温曲线
[情境1]下图是一段登山路线。
y/m
[ 问题 1] 同样是 登山,但是从 A
yC
登山路线
C
yC-yB
处到 B 处会感觉
比较轻松,而 从 B 处到 C 处会
yB A o [问题2] xB
B
xC-xB
感觉比较吃力。
想想看,为什 么?
xC
x/m
“陡峭” 是生活用语,如何量化线段BC的陡峭程度呢?
[情境2] 下面是 某市2004年3月 18日到4月20日 期间的日最高气 温变化曲线图.
高中数学 3.1.1 平均变化率学案(无答案)苏教版选修1-1(2021年整理)

江苏省镇江市丹徒镇高中数学3.1.1 平均变化率学案(无答案)苏教版选修1-1编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江苏省镇江市丹徒镇高中数学3.1.1 平均变化率学案(无答案)苏教版选修1-1)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江苏省镇江市丹徒镇高中数学3.1.1 平均变化率学案(无答案)苏教版选修1-1的全部内容。
平均变化率●三维目标1.知识与技能通过丰富的实例,让学生经历平均变化率概念的形成过程,体会平均变化率是刻画变量变化快慢程度的一种数学模型.2.过程与方法理解平均变化率的概念,了解平均变化率的几何意义,会计算函数在某个区间上的平均变化率.3.情感、态度与价值观感受数学模型刻画客观世界的作用,进一步领会变量数学的思想,提高分析问题、解决问题的能力.●重点难点重点:平均变化率的概念.难点:平均变化率概念的形成过程.【问题导思】1.物体从某一时刻开始运动,设s表示此物体经过时间t走过的路程,显然s是时间t 的函数,表示为s=s(t).在运动的过程中测得了一些数据,如下表.t/s025101315…s/m069203244…物体在0~2 s和10~13 s这两段时间内,哪一段时间运动得快?如何刻画物体运动的快慢?2.某病人吃完退烧药,他的体温变化如图所示.比较时间x从0 min到20 min和从20 min到30 min体温的变化情况,哪段时间体温变化较快?如何刻画体温变化的快慢?一般地,函数f(x)在区间[x1,x2]上的平均变化率为。
【题型分类】【类型一】平均变化率的概念及意义的应用例1、在经营某商品中,甲挣到10万元,乙挣到2万元,如何比较和评价甲,乙两人的经营成果?变式:在经营某商品中,甲用5年时间挣到10万元,乙用5个月时间挣到2万元,如何比较和评价甲,乙两人的经营成果?例2、水经过虹吸管从容器甲中流向容器乙,t s后容器甲中水的体积0.1=⨯(单位:3()52tV t-cm),计算第一个10s内V的平均变化率。
名师教学设计《平均变化率》完整教学教案

对教学过程的反思
课堂教学中发现,学生的反应与自己的预想相差甚远。
经了解实际情况,原因是学生还不知道两点连线的斜率公式,从而导致“思考:观察函数的图象平均变化率
表示什么”的教学设计意图不能完全展现。
这是借班上课容易出现的问题,但从另一个侧面说明了教学中关注学生的认知基础是成功地实施课堂教学的前提。
课堂实施过程中,虽然在形式上没有将知识直接抛给学生,但自己的“引导具”有明显的“牵”的味道。
在教学过程中,虽然能关注到适当的计算量,但激发学生思维的好问题不多。
整堂课学生的思维量不够,学生缺少思辩,同时留给学生判断和分析的成分、时间都不够。
例如,在分析“气球膨胀率问题”中的函数变式时,目的仅仅为了推导变式函
数,虽然有些学生也有一定的思考,但为了赶时间、赶任务,并没有进行更深入的分析。
教学的预设目标基本完成,特别是知识目标,学生能较好地掌握“平均变化率”这一概念,并会利用概念求平均变化率。
当然也存在很多不足:对呼之欲出的“瞬时变化率”没有及时给出,缺乏联系性,没有用发展的眼光来处理教材;有关数学思想与方法的落实有所欠缺;等。
如果对教材挖掘得更到位些,更深入地体会教材的编写意图,那么相信这堂课就会上得更成功些。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年高中数学 第三章 第1课 平均变化率教学案 苏教版选修
1-1
班级:高二( )班 姓名:____________
教学目标:
1.通过对一些实例的直观感知,构建平均变化率的概念,并初步运用和加深
理解利用平均变化率来刻画变量变化得快与慢的原理;
2.通过从实际生活背景中构建数学模型来引入平均变化率,领会以直代曲
和数形结合的思想,培养学生的抽象思维与归纳综合的能力,提升学生的数学思维与数学素养;
3.培养学生关注身边的数学,并能从数学的视角来分析问题、解决问题,
体验数学发展的历程,感受数形统一的辨证思想.
教学重点:会利用平均变化率来刻画变量变化得快与慢.
教学难点:对平均变化率概念的本质的理解;对生活现象作出数学解释.
教学过程:
一、问题情境
1.问题情境.
法国《队报》网站的文章称刘翔以不可思议的速度统治了赛场.这名21岁的中国人跑的几乎比炮弹还快,赛道上显示的12.94秒的成绩已经打破了12.95秒的奥运会纪录,但经过验证他是以12.91秒的成绩追平了世界纪录,他的平均速度达到了8.52m/s .
某人走路的第1秒到第34秒的位移时间图象如图所示:
观察图象,回答问题:
问题1 从A 到B 的位移是多少?从B 到C 的位移是多少?
问题2 从A 到B 这一段与从B 到C 这一段,你感觉哪一段的位移变化得较快?
2.学生活动.
案例中,从B 到C 位移“陡增”,这是我们从图象中的直观感觉,那么如何量化陡峭程度呢?
(1)由点B 上升到C 点必须考察的大小,但仅注意到的大小能否精确量化BC 段陡峭的程度?为什么?
(2)还必须考察什么量?在考察的同时必须考察.
(3)曲线上BC 之间的一段几乎成了直线,由此联想到如何量化直线倾斜程度?
二、建构数学
1.一般地,函数在区间上的平均变化率为.
注意:平均变化率不能脱离区间而言.
s
2.平均变化率是曲线陡峭程度“数量化”.曲线陡峭程度是平均变化率“视觉化”.思考:
(1)若设,即将看作是对于的一个增量, ,
则在平均变化率为
x
x
f
x
x
f
x
y
x
x
x
f
x
f
∆
-
∆
+
=
∆
∆
=
-
-)
(
)
(
)
(
)
(
1
1
1
2
1
2
.
(2)在平均变化率的几何意义即为区间两端点连线所在直线斜率.
三、数学运用
例1某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到
第3个月以及第6个月到第12个月该婴儿体重的平均变化率.
问题(1)如何解释例1中从出生到第3个月,婴儿体重平均变化率为1(月)?问题(2)本题中两个不同平均变化率的实际意义是什么?
讲评在不同的区间上平均变化率可能不同.
例2水经过虹吸管从容器甲流向容器乙,s后容器甲中的水的体积
(单位:),试计算第一个内的平均变化率.
例3已知函数
x
x
g
x
x
f2
)
(
,1
2
)
(-
=
+
=,分别计算在区间上,
函数及的平均变化率.
问题你在解本题的过程中有没有发现什么?
讲评一次函数在区间上的平均变化率等于它的斜率.例4已知函数,分别计算在下列区间上的平均变化率:
① ② ③ ④
【巩固练习】
1.函数y =f(x)的平均变化率的几何意义是指函数y =f(x)图象上两点,
P1(x1,f(x1)),P2(x2,f(x2))连线的 .
2.在曲线上取点及它的附近点,
那么为
班级:高二( )班 姓名:____________
1.某物体位移公式为s =s(t),从t0至t0+Δt 这段时间内,下列说法正确的
有________.
①(t0+Δt)-t0称为函数增量; ②t0即为函数增量
③Δs =s(t0+Δt)-s(t0)称为函数增量; ④Δs Δt 称为函数增量
2.设函数,当自变量由到时,函数的改变量 。
3.函数在区间[,]上的平均变化率为
4.在经营某商品中,甲用5年时间挣到10万元,乙用5个月时间挣到2万元,如何比较和评价甲,乙两人的经营成果?
5.物体运动的方程为(位移单位是m ,时间单位是s ),
求物体在2 s 到3 s 的平均速度.
6.已知自由落体运动的方程是,求落体在到这段时间的平均速度.
7.已知函数,分别计算在下列区间上的平均变化率:
(1)[1,2];(2)[1,1.5]。
2019-2020年高中数学第三章第2课瞬时变化率—导数(曲线上一点处
切线)教学案苏教版选修1-1
班级:高二()班姓名:____________
教学目标:
1.理解并掌握曲线在某一点处的切线的概念;
2.理解并掌握曲线在一点处的切线的斜率的定义以及切线方程的求法;
3.理解切线概念的实际背景,培养学生解决实际问题的能力和培养学生转
化问题的能力及数形结合思想.
教学重点:理解并掌握曲线在一点处的切线的斜率的定义以及切线方程的求法.
教学难点:用“无限逼近”、“局部以直代曲”的思想理解某一点处切线的斜率.
教学过程:
一、问题情境
1.问题情境.
如何精确地刻画曲线上某一点处的变化趋势呢?
如果将点P附近的曲线放大,那么就会发现,曲线在点P附近看上去有点像是直线.
P P
如果将点P附近的曲线再放大,那么就会发现,曲线在点P附近看上去几乎成了直线.事实上,如果继续放大,那么曲线在点P附近将逼近一条确定的直线,该直线是经过点P的所有直线中最逼近曲线的一条直线.
因此,在点P附近我们可以用这条直线来代替曲线,也就是说,点P附近,
曲线可以看做直线(即在很小的范围内以直代曲).
2.探究活动.
如图所示,直线为经过曲线上一点P的两条直线.
试判断哪一条直线在点P附近更加逼近曲线;
在点P附近能作出一条比更加逼近曲线的直线吗?
在点P附近能作出一条比更加逼近曲线的直线吗?
二、建构数学
切线定义:如图,设Q为曲线C上不同于P的一点,直线PQ称为曲线的割线.随着点Q 沿曲线C向点P运动,割线PQ在点P附近逼近曲线C,当点Q无限逼近点P时,
直线PQ最终就成为经过点P处最逼近曲线的直线l,这条直线l也称为曲线在点P处的切线.这种方法叫割线逼近切线.
思考:如上图,P为已知曲线C上的一点,如何求出点P处的切线方程?
三、数学运用
例1.试求在点(2,4)处的切线斜率.
小结求曲线上一点处的切线斜率的一般步骤:
(1)找到定点P的坐标,设出动点Q的坐标;
(2)求出割线PQ的斜率;
(3)当时,割线逼近切线,那么割线斜率逼近切线斜率.
思考:如上图,P 为已知曲线C 上的一点,如何求出点P 处的切线方程? 解:设))(,()),(,(0000x x f x x Q x f x P ∆+∆+
x x f x x f x x x x f x x f k PQ ∆-∆+=-∆+-∆+=∴)()()()()(000000
例2.已知,求曲线在处的切线斜率和切线方程;
练习1.试求在x =1处的切线斜率.
练习2.已知,求曲线在处的切线斜率和切线方程.
2.已知曲线y =12x2-2上一点P(1,-32),则过点P 的切线的倾斜角为________
3.函数在点(12,-2)处的切线方程为________.
4.函数的图像在处的切线的斜率是
5.判断曲线y =x3+1在点P(-1,0)处是否有切线,如果有,求出切线的方程.。
