§ 各配分函数的求法及其对热力学函数的贡献
配分函数与热力学函数的关系

第七章统计热力学基础教学目的与要求:通过本章的教学使学生初步了解统计热力学的基本研究方法,各种独立子系统的微观状态数的求法,不同系统的统计规律,系统的各热力学函数的表示式,配分函数的计算,固体的热容理论导出的基本思路。
重点与难点:统计热力学的基本研究方法,不同系统的微观状态数的计算,玻尔兹曼分布律的含义,系统的热力学函数的表示式,配分函数的计算,不同的固体热容理论的基本方法。
§7.1 概论统计热力学的研究任务和目的统计力学的研究对象是大量微观粒子所构成的宏观系统。
从这一点来说,统计热力学和热力学的研究对象都是一样的。
但热力学是根据从经验归纳得到的四条基本定律,通过演绎推理的方法,确定系统变化的方向和达到平衡时的状态。
由于热力学不管物质的微观结构和微观运动形态,因此只能得到联系各种宏观性质的一般规律,而不能给出微观性质与宏观性质之间的联系。
而统计热力学则是从物质的微观结构和基本运动特性出发,运用统计的方法,推导出系统的宏观性质,和变化的可能方向。
统计力学的研究方法是微观的方法,它根据统计单位(微粒)的力学性质如速度、动量、位置、振动、转动等,用统计的方法来推求系统的热力学性质,例如压力、热容、熵等热力学函数。
统计力学建立了体系的微观性质和宏观性质之间的联系。
从这个意义上,统计力学又可称为统计热力学。
相对于热力学,统计力学对系统的认识更深刻,它不但可以确定系统的性质,变化的方向和限度,而且还能确定系统的性质的微观根源,这一点要比热力学要深刻。
对于简单系统,应用统计热力学的方法进行处理,其结果是令人满意的。
当然统计热力学也有自身的局限性,由于统计力学要从微观粒子的基本运动特性出发,确定系统的状态,这就有一个对微观粒子的运动行为的认识问题。
由于人们对于物质结构的认识不断深化,不断地修改充实物质结构的模型,所对统计理论和统计方法也要随之修改,所以统计理论是一种不断发展和完善的。
同时模型本身也有近似性,所以由此得到的结论也有近似性。
07_统计热力学基础小结

核的总配分函数等于各原子的核配分函数的乘积。 q n ,total = (2s n + 1)(2 s n '+1)(2 s n "+1)... = ∏ (2 s n + 1) i
i
仅在此种近似下,核配分函数才与温度 T 无关,此时有: H n = U n = CV (n) = 0 p = -(∂An/∂V)T,n=0 An = − NkT ln qn ∂A S n = − n = Nk ln q n ∂T V , N Gn = − NkT ln qn = An 分子全配分函数 q = q t ⋅ q r ⋅ qV ⋅ qe ⋅ q n 化学反应体系的公共能量标度 按公共能量标度, q ' = ∑ g i e −(ε 0 +εi ) / kT =e −ε 0 / kT ∑ g i e −ε i / kT = e −ε 0 / kT ⋅ q 能量标度的改变只对具能量单位的量 U、H、F、G 有影响,即多一项 U0 例如:对非定位系 A = − kT ln qN + U0 N!
1
二.波尔兹曼能量分布式 N i* = N gi e − εi / kT ∑ gi e−εi /kT
i
最可几分布时 i 能级上的粒子数 e −ε i / kT 称波尔兹曼因子
Ni g e − ε i / kT = i − ε i / kT N ∑ gie
i
i 能级上的粒子数占总粒子数之比,也称能级分布数
同左
同左
CV =
∂ ln q p = NkT ∂V T , N
同左
对来自第一定律的函数(H、U、CV、p)表达式相同 对来自第二定律的函数(S、A、G)表达式不同
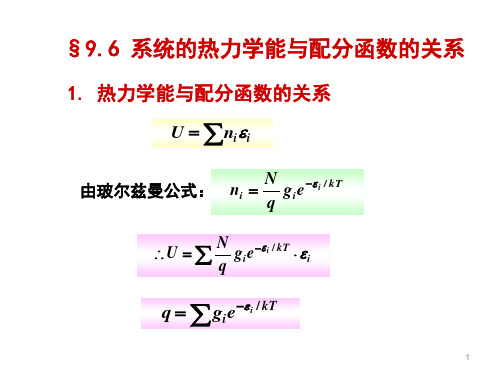
§9.6 系统的热力学能与配分函数的关系
T
V
NkT 2 ln qt NkT 2 d ln qr NkT 2 d ln qvT VdT NhomakorabeadT
NkT 2 d ln qe NkT 2 d ln qn
dT
dT
Ut Ur Uv Ue Un
(因为q = qt qr qv qe qn ,只有qt 与V 有关,所以必须
写成偏导数, 其它均可写成全导数。)
1
kT 2
g e i / kT ii
移项得:
kT 2 q T V
i giei / kT
带入热力学能公式: U
N q
gi e i / kT i
得:
U N kT 2 q NkT 2 ln q
q T V
T V
2
将 q = qt qr qv qe qn 代入,则;
U NkT 2 ln qtqrqvqeqn
NkT 2
d
ln
1
1 e
ΘV
/T
dT
1 NkΘV ev /T 1
a)通常情况下,v>>T,量子化效应较突出
ΘV 1 T
,
qV0 1
,
U
0 V
0
振动基本都处于基态,对Uv0无贡献
8
b)v /T<<1 (高温或低V) 时
eΘV /T 1 ΘV T
U
0 v
NkΘV
1 eΘv /T
1
NkΘV
U
0 r
0
,
U
0 V
0
3 Um 2 RT U0,m
低温:振动能级未开放:
5 Um 2 RT U0,m
(U
0 v
0)
08-4 配分函数的计算

e,0
kT
)[1
e,1 e,0
kT
电子能级间隔也很大, (e,1 e,0 ) 400 kJ mol-1 , 除F, Cl 少数元素外,方括号中第二项也可略去。虽然温度很高时,电 子也可能被激发,但往往电子尚未激发,分子就分解了。所以 通常电子总是处于基态,则:
1 (v ) v / T 2
qv
e
1 (v ) v / T 2
ev / 2T (1 ev / T )1
e vv / T (1 ev / T )
n0 基态分子分数 f 0 1 ev / T N
300 K 时
激发态 fex 1 f0 ev / T
物理化学II
7
统计热力学基础
配分函数的计算
2 h2 nx qt, x exp( 2) 8mkT a nx 1
exp( n )
nx 1 2 x
h (设 ) 2 8mkTa
2
因为 是一个很小的数值,所以求和号用积分号代替, 得:
2 qt,x exp( nx )dnx 0
配分函数的计算
配分函数的分离
t r q [ g t exp( )] [ g r exp( )] k BT k BT v e [ g v exp( )] [ g e exp( )] k BT k BT n [ g n exp( )] k BT
qt qr qv qe qn qt q内
平动, 转动,振动,电子,核运动
简并度 g i = gt •gr • gv • ge • gn
i / kBT
则
热力学 配分函数

热力学配分函数热力学中,配分函数是一个非常重要的概念。
它是一种函数,用于描述一个系统处于不同的能量状态下的概率分布。
在统计物理学中,配分函数通常用于计算热力学量,如内能、熵和自由能等。
配分函数的定义与系统的哈密顿量有关。
对于一个具有N个粒子的系统,其哈密顿量可以表示为H = ∑i=1N hi其中,hi是每个粒子的能量。
假设系统总能量为E,那么系统的所有可能状态数可以用下面的式子计算:Ω(E) = ∫···∫d3Nq1···d3NqNδ(EH(q1,...,qN))其中,q1,...,qN是系统所有粒子的位置和动量,δ是狄拉克δ函数。
这个式子的意义是,系统总能量为E的所有可能状态数,等于所有粒子的位置和动量满足哈密顿量为E的状态数之和。
在统计物理学中,我们通常更关注系统的宏观性质,而不是具体的粒子位置和动量。
因此,我们需要将Ω(E)转化为一个更容易处理的函数。
这个函数就是配分函数Z,它定义为Z = ∫···∫d3Nq1···d3NqNeβH(q1,...,qN)其中,β=1/kBT,T是系统的温度,kB是玻尔兹曼常数。
配分函数的物理意义是,它描述了系统处于不同能量状态的概率分布。
具体来说,系统处于能量为E的状态的概率可以用下面的式子计算:P(E) = Ω(E) eβE / Z其中,Ω(E)是系统总能量为E的所有可能状态数。
配分函数的作用是将所有可能的状态数归一化,使得概率分布满足归一化条件。
配分函数不仅可以用来计算概率分布,还可以用来计算热力学量。
例如,系统的内能可以用下面的式子计算:U = lnZ/β系统的熵可以用下面的式子计算:S = kB lnZ + βU系统的自由能可以用下面的式子计算:F = U TS = kB T lnZ配分函数是热力学中非常重要的一个概念,它在理论物理、化学、材料学等领域都有广泛的应用。
配分函数及其对热力学函数的贡献

4. G定位 F pV F V (F / V )T , N
ln q kT ln q NVkT ( )T , N V
N
Tankertanker Design
5.
H定位 G TS U pV
ln q ln q NkT ( )V , N NkTV ( )T , N T V
g e
e 0
e e 0 / kT 0
e 0 /kT
g e
e 1 e 0
e / kT e 1 1
)
g e
e 0
e 0 / kT
g (1 e g
e 1 e 0 kT
若取基态能量为能量零点时,则 电子基态能级简并度
e 0
q g
e 0
e 0
g 2 j 1
U非定位 F TS
Tankertanker Design
q q 2 ln q kT ln kT ln NkT ( )V ,N N! N! T
N N
ln q NkT ( )V , N T
2
4. 5.
F ln q p ( )T , N NkT ( )T , N V V
级上粒子的分布数。
Tankertanker Design
∵
Ng i e N i / kT gi e
i
i / kT
Ng i e
i
0 0 i kT 0 0 i kT
g e
Tankertanker Design
N
g e
i
gi e
0 / kT
e
i 0 / kT
h =6.626×10-34J· sec-1
物理化学电子教案.doc

物理化学电子教案第七章统计热力学基础物理化学教研室【基本概念·基本知识】1、统计热力学系统的分类:独立/非独立粒子系统、可别/不可别粒子系统2、独立粒子系统的分布、最可几分布、平衡态分布3、系统的微观状态4、粒子的配分函数5、转动特征温度,振动特征温度6、焓函数、吉布斯自由能函数7、统计熵、量热熵【基本定律与基本理论】1、等几率假设2、玻兹曼分布定律(推导和表达式的意义)3、Maxwall 速率分布的意义及与平动有关的各种统计平均值4、粒子配分函数与热力学函数的关系5、最低能级能量数值的选取对配分函数的影响6、双原子分子转动、振动、平动的能级公式7、波兹曼公式:ln S k =Ω8、热力学定律的统计解释【基本计算与基本方法】1、独立可别与不可别粒子系统Ω的计算2、用波兹曼分布定律计算简单系统的粒子分布3、单原子分子、双原子分子各种运动形式的配分函数4、单原子及双原子分子各种运动形式对热力学性质的贡献5、分别用配分函数和自由能函数计算简单理想气体反应的平衡常数第一讲:统计热力学概论·Boltzmann 统计一、统计热力学概论(一)、统计热力学的基本任务1、统计热力学的基本任务回 顾:A 、 经典热力学的任务:a )解决某一过程的能量衡算;b )过程的方向判断据; 基础:热力学三定律;优点:着眼与系统的状态而不依赖系统的微观结构,高度可靠; 缺点:无法描述系统的微观结构和微观运动规律B 、统计热力学的任务:用统计学的原理,从系统的微观结构和运动状态出发,揭示系统宏观性质的本质。
物质的宏观性质本质上是微观粒子不停地运动的客观反映,虽然每个粒子都遵守力学定律,但是无法用力学中的微分方程去描述整个系统的运动状态,所以必须用统计学的方法。
根据对物质结构的某些基本假定,以及实验所得的光谱数据,求得物质结构的一些基本常数,如核间距、键角、振动频率等。
利用这些数据可以计算分子配分函数,再根据配分函数求出物质的热力学性质,这就是统计热力学的基本任务。
第三章统计热力学基础

4. 振动配分函数
双原子分子
qv
1
h i
1
V
1 e kT 1 e T
线型多原子分子 非线型多原子分子
q v
3n5
i1 1
1
h i
e kT
qv
3n6 1
i 1
1
h i
e kT
5.电子配分函数
qe
ge,0
exp( e,0 )
kT
若将 视为零,则 e,0
1e T
v
hv k
hc
k
2273K
T
qv
1
V
1
2273K
1.00
1 e T 1 e 298K
电子:
1
qe ge,0 ge,1e kT
3
2
exp[
1.57331019 s (1.381023 JK 1)(298K
)
]
3.00
零点后,F、G、H、U的表示式中均多了一个
U0项(U0=N 0)
2.从自由能函数计算平衡常数
G(T ) U0 Nk ln q
T
N
G(T ) Uo 称为自由能函数
T
D+E
G+H
rGmθ (T )
RT
ln Kθ
(
Gmθ
(T
)
H
θ m
(0)
)
rU
θ m
(0)
T
T
T
T
称为热函函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
原子核配分函数 电子配分函数
平动配分函数
单元子理想气体的热力学函数
转动配分函数
振动配分函数
20.03.2020
1
原子核配分函数
q ng n ,0e x p (k n T ,0) g n ,1e x p (k n T ,1)
g n ,0ex p (k n T ,0)[1g g n n ,,0 1ex p (n ,1 k Tn ,0) ]
kTlnkTkTlnp
对1 mol气体分子而言,各项均乘以阿伏伽
德罗常数 L, Lk R, 则1 mol气体化学势为
20.03.2020
19
(5)化学势
L(n,0e,0)RTlngn,0ge,0RTln(2m hk3T)32)
RTlnkTRTlnp
当处于标准态时,p p ,则:
L(n,0e,0)RTlngn,0ge,0RTln(2m hk3T)32)
2sn
1 i
i
由于核自旋配分函数与温度、体积无关,所以
对热力学能、焓和等容热容没有贡献。
但对熵、Helmholtz自由能和Gibbs自由能有相 应的贡献。
从化学反应的角度看,一般忽略核自旋配分函
数的贡献,仅在计算规定熵时会计算它的贡献。
20.03.2020
4
电子配分函数
q eg e ,0ex p (k e T ,0)g e ,1ex p (k e T ,1)
设分子作只有一种频率 的简谐振动,振
动是非简并的,g i ,v 1 ,其振动能为:
v(v1 2)h v0,1,2,
式中v为振动量子数,当v=0时, v , 0 称为零点振动能
v,0
1 2
h
20.03.2020
27
qv
i
gi,v
exp(i,v)
kT
(v 1)h
exp[ 2 ]
v0
kT
e x p 1 2 k h T e x p 3 2 k h T e x p 5 2 k h T L
r J(J1)8 h2 2I
J0, 1 , 2,
式中J是转动能级量子数,I是 转动惯量,设双原子质量分别
为 m , 20.03.12020 m2,r为核间距,则:
I ( m1m2 )r2 m1 m2
22
转动角动量在空间取向也是量子化的,所以能
级简并度为:
gi,r 2J 1
qr i
gi,r
f t 为平动自由度, f r 为转动自由度
n 为分子中原子总数
因此,线型多原子分子的 q v 为:
20.03.2020
kT
如将核基态能级能量选为零,则上式可简化为:
qn gn,0 2sn1
即原子核的配分函数等于基态的简并度,它来
源于核的自旋作用。式中 sn 是核的自旋量子数。
20.03.2020
3
对于多原子分子,核的总配分函数等于各原子 的核配分函数的乘积
q n ,总 2 s n 1 2 s n ' 12 s n '' 1 L
是非简并的。如有一个未配对电子,可能有两种不同
的自旋,如 N a , 它的
j
1 2
,
ge,0
2
。
20.03.2020
6
电子配分函数
电子配分函数对热力学函数的贡献为
Ue He CV,e 0 Ae NkTlnqe Ge NkTlnqe Se Nklnqe
20.03.2020
7
平动配分函数
设质量为m的粒子在体积为 abc 的立方体
qr
T
r
13Tr
L
20.03.2020
25
对于同核双原子和线性多原子分子,还要
除以对称数
qr
8 2 IkT h2
对于非线性多原子分子,转动配分函数为
qr 82( 2hk3T)32(IxIyIz)12
Ix,Iy 和Iz分别为三个轴上的转动惯量。
20.03.2020
26
振动配分函数
双原子分子的 q v
qe
ge,0
exp(e,0
kT
)
20.03.2020
5
电子配分函数
qe
ge,0
exp(e,0 )
kT
若将 e , 0 视为零,则 qe ge,0 2j1
式中 j 是电子总的角动量量子数。电子绕核运动 总动量矩也是量子化的,沿某一选定轴上的分量可能 有 2j+1个取向。
某些自由原子和稳定离子的 j 0, ge,0 1,
用统计热力学的方法可以导出理想气体 状态方程,这是经典热力学无法办到的。
20.03.2020
21
转动配分函数
单原子分子的转动配分函数等于零,异核双原子 分子、同核双原子分子和线性多原子分子的q r 有类似 的形式,而非线性多原子分子的 q r 表示式较为复杂。
(1)异核双原子分子的 q r ,设其为刚性转子绕质 心转动,能级公式为:
3lnT5] 22
这公式也称为Sachur-Tetrode公式。
可用来计算单原子理想气体的熵
20.03.2020
17
(3)热力学能 U
因为q n , q e 对热力学能没有贡献,只有平动
能有贡献,所以:
UUt NkT2( lnTqt)V,N
3 2
N kT
(4)定容热容 CV
CVCV,t (U Tt)V,N
5 2
这就是Sackur-Tetrode公式,用来计算理想气
2体0.03.的2020平动熵
12
对于1 mol 理想气体,Sackur-Tetrode 公式为
St,mRln 2m Lh kT 3 3/2Vm 5 2R
根据 UATS
Ut NkT2 ln Tqt V,N3 2NkT
CV,t
U Tt
V
3Nk 2
根据热力学函数之间的关系,可以得到 G t , H t
20.03.2020
13
根据热力学函数之间的关系,可以得到 G t , H t
Ht Ut pV
Gt At pV
A
p
( V
)T,N
代入相应的 U t , A t 表示式即得。
20.03.2020
14
单原子理想气体热力学函数
1x
则q v 的表示式为:
qvexp 1 2k hT 1e1 h /kT
将零点振动能视为零,
即v,0
1 h
2
0
,
则:
qv'
v0,1,2,L
expvkhT
h 2h
(1ekTekT L)
1
h
1 e kT
20.03.2020
30
多原子分子的 q v
多原子分子振动自由度 f v fv 3nft fr
e x p 1 2k h T 1 e x p k h T e x p 2 k h T L
令
h
k
2v0称.03.2为020 振动特征温度,也具有温度量纲,则上式为28
qv
ex p (v)ex p3(v)ex p5(v)
2T
2T
2T
ex p (v)1[ex p (v)ex p2(v)]
这个结论与经典的能量均分原理的结果是一
致的,单原子分子只有三个平动自由度,每个自
k N k 由度贡献 1 ,则N个粒子共有 3
20.03.2020
2
2
18
(5)化学势
(NA)T,V
对于理想气体,V NkT ,代入 A 的表示式,得: p
(n,0e,0)kTlngn,0ge,0kTln(2m hk3T)32
RTlnkTRTlnp
从该式可看出,p 一定时, 只是T的函数。
两式相减得:
(T ,p )(T ) R T ln (p /p)
20.03.2020
20
(6)状态方程式
dA
p
( dV
)T , N
将A的表示式代入,由于其它项均与体积 无关,只有平动项中有一项与V有关,代入即 得理想气体状态方程。
p[(N kV TlnV)]T,NN V kT
qr0 (2J1 )exJ p (J( T 1 ) r)dJ
令: x J ( J 1 ),d x ( 2 J 1 ) d J
代入上式后,得:
20.03.2020
24
q r
exp(
0
x r ) dx T
T exp( x r )
r
T 0
T r
8 2 IkT h2
对于转动特征温度较高的分子,应该使用下式
式中 n,0 , n,1分别代表原子核在基态和第
一激发态的能量,g n,0 , g n,1 分别代表相应能级的
简并度。
20.03.2020
2
由于化学反应中,核总是处于基态,另外基态 与第一激发态之间的能级间隔很大,所以一般把方 括号中第二项及以后的所有项都忽略不计,则:
qn
gn,0
exp(n,0 )
由于单原子分子内部运动没有转动和振动, 所以只有原子核、电子和外部的平动对热力学函 数有贡献。
理想气体是非定位系统,所以它的一系列热 力学函数用配分函数的计算式分别分列如下:
(1)Helmholtz自由能 A
AAnAeAt N kTlnqnN kTlnqekTlnq N tN !
20.03.2020
exp(i,r )
kT
J(J1)h2
(2J1)exp(
)
J0
82IkT
令r
h2
8 2Ik
