(完整版)中考数学应用题各类应用题汇总练习,推荐文档
(完整word版)中考经典二次函数应用题(含答案),推荐文档

二次函數應用題1、某體育用品商店購進一批滑板,每件進價為100元,售價為130元,每星期可賣出80件.商家決定降價促銷,根據市場調查,每降價5元,每星期可多賣出20件. (1)求商家降價前每星期の銷售利潤為多少元?(2)降價後,商家要使每星期の銷售利潤最大,應將售價定為多少元?最大銷售利潤是多少?2、某商場將進價為2000元の冰箱以2400元售出,平均每天能售出8臺,為了配合國家“家電下鄉”政策の實施,商場決定採取適當の降價措施.調查表明:這種冰箱の售價每降低50元,平均每天就能多售出4臺.(1)假設每臺冰箱降價x 元,商場每天銷售這種冰箱の利潤是y 元,請寫出y 與x 之間の函數運算式;(不要求寫引數の取值範圍)(2)商場要想在這種冰箱銷售中每天盈利4800元,同時又要使百姓得到實惠,每臺冰箱應降價多少元? (3)每臺冰箱降價多少元時,商場每天銷售這種冰箱の利潤最高?最高利潤是多少?3、張大爺要圍成一個矩形花圃.花圃の一邊利用足夠長の牆另三邊用總長為32米.矩米の籬笆恰好圍成.圍成の花圃是如圖所示の矩形ABCD .設AB 邊の長為x 形ABCD の面積為S 平方米.(1)求S 與x 之間の函數關係式(不要求寫出自變數x の取值範圍). (2)當x 為何值時,S 有最大值?並求出最大值.(參考公式:二次函數2y ax bx c =++(0a ≠),當2bx a=-時,244ac b y a -=最大(小)值)4、某電視機生產廠家去年銷往農村の某品牌電視機每臺の售價y (元)與月份x 之間滿足函數關係502600y x =-+,去年の月銷售量p (萬臺)與月份x 之間成一次函數關係,其中兩個月の銷售情況如下表:月份1月 5月 銷售量3.9萬臺4.3萬臺 求該品牌電視機在去年哪個月銷往農村の銷售金額最大?最大是多少?5、某商場試銷一種成本為每件60元の服裝,規定試銷期間銷售單價不低於成本單價,且獲利不得高於45%,經試銷發現,銷售量y (件)與銷售單價x (元)符合一次函數y kx b =+,且65x =時,55y =;75x =時,45y =. (1)求一次函數y kx b =+の運算式;(2)若該商場獲得利潤為W 元,試寫出利潤W 與銷售單價x 之間の關係式;銷售單價定為多少元時,商場可獲得最大利潤,最大利潤是多少元?(3)若該商場獲得利潤不低於500元,試確定銷售單價x の範圍.6、某商場在銷售旺季臨近時 ,某品牌の童裝銷售價格呈上升趨勢,假如這種童裝開始時の售價為每件20元,並且每週(7天)漲價2元,從第6周開始,保持每件30元の穩定價格銷售,直到11周結束,該童裝不再銷售。
中考数学试题分类汇编应用题(可以用)

4批发单价(元)5①② 历年中考数学试题分类汇编——应用题1、(河南)l9.(9分)暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升;当行驶150千米时,发现油箱剩余油量为30升.(1)已知油箱内余油量y (升)是行驶路程x (千米)的一次函数,求y 与x 的函数关系式;(2)当油箱中余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.2、(河南)20.(9分)如图所示,电工李师傅借助梯子安装天花板上距地面2 .90m 的顶灯.已知梯子由两个相同的矩形面组成,每个矩形面的长都被六条踏板七等分,使用时梯脚的固定跨度为1m .矩形面与地面所成的角α为78°.李师傅的身高为l.78m ,当他攀升到头顶距天花板0.05~0.20m 时,安装起来比较方便.他现在竖直站立在梯子的第三级踏板上,请你通过计算判断他安装是否比较方便?(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70.)2、(河南)22. (10分)某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共l5台.三种家电的进价和售价如下表所示:(1)在不超出现有资金的前提下,若购进电视机的数量和冰箱的数量相同,洗衣机数量不大于电视机数量的一半,商场有哪几种进货方案?(2)国家规定:农民购买家电后,可根据商场售价的13%领取补贴.在(1)的条件下.如果这15台家电全部销售给农民,国家财政最多需补贴农民多少元?3、(安徽)某市2008年国内生产总值(GDP )比2007年增长了12%,由于受到国际金融危机的影响,预计今年比2008年增长7%,若这两年GDP 年平均增长率为x %,则x %满足的关系是…………………………【 】A .12%7%%x +=B .(112%)(17%)2(1%)x ++=+C .12%7%2%x +=gD .2(112%)(17%)(1%)x ++=+4、已知某种水果的批发单价与批发量的函数关系如图(1)所示.(1)请说明图中①、②两段函数图象的实际意义.第23题图(2)(2)写出批发该种水果的资金金额w (元)与批发量m (kg 么范围内,以同样的资金可以批发到较多数量的该种水果.(3数关系如图(2)所示,该经销商拟每日售出60kg 使得当日获得的利润最大.5、.列方程或方程组解应用题:北京市实施交通管理新措施以来,全市公共交通客运量显著增加.据统计,2008年10月11日到2009年2月28日期间,地面公交日均客运量与轨道交通日均客运量总和为1696万人次,地面公交日均客运量比轨道交通日均客运量的4倍少69万人次.在此期间,地面公交和轨道交通日均客运量各为多少万人次?(恩施州)22.某超市经销A 、B 两种商品,A 种商品每件进价20元,售价30元;B 种商品每件进价35元,售价48元. (1)该超市准备用800元去购进A 、B 两种商品若干件,怎样购进才能使超市经销这两种商品所获利润最大(其中B 种商品不少于7件)?(2促销活动期间小颖去该超市购买A 种商品,小华去该超市购买B 种商品,分别付款210元与268.8元. 促销活动期间小明决定一次去购买小颖和小华购买的同样多的商品,他需付款多少元?6、为了拉动内需,广东启动“家电下乡”活动。
初中应用题大全及答案

初中应用题大全及答案1. 应用题:小明的爸爸给他买了一辆自行车,原价为500元,现在打八折出售,请问小明的爸爸实际支付了多少钱?答案:原价为500元,打八折后的价格为500元× 0.8 = 400元。
所以小明的爸爸实际支付了400元。
2. 应用题:一个班级有40名学生,其中男生占60%,女生占40%,现在要选出10%的学生参加学校的运动会,请问需要选出多少名男生和女生?答案:班级总人数为40人,选出10%的学生参加运动会,即40人× 10% = 4人。
男生占60%,所以需要选出的男生人数为4人× 60% = 2.4人,取整数为2人。
女生占40%,所以需要选出的女生人数为4人× 40% = 1.6人,取整数为1人。
因此,需要选出2名男生和1名女生。
3. 应用题:一个长方体的长、宽、高分别是10厘米、8厘米和6厘米,求这个长方体的体积。
答案:长方体的体积可以通过长、宽、高的乘积来计算,即体积 = 长× 宽× 高 = 10厘米× 8厘米× 6厘米 = 480立方厘米。
4. 应用题:一个工厂生产了100个零件,其中有2%是次品,合格的零件有多少个?答案:次品占总零件数的2%,即100个零件× 2% = 2个。
所以合格的零件数为100个 - 2个 = 98个。
5. 应用题:一个水池,每小时流入4立方米的水,同时每小时流出3立方米的水,如果水池原本有20立方米的水,那么5小时后水池里有多少水?答案:每小时流入4立方米的水,流出3立方米的水,所以每小时净增加1立方米的水。
5小时后,水池净增加的水为5小时× 1立方米/小时 = 5立方米。
原本有20立方米的水,所以5小时后水池里的水量为20立方米 + 5立方米 = 25立方米。
6. 应用题:小华在书店买了3本书,每本书的价格是30元,书店正在进行满100元减20元的优惠活动,请问小华实际支付了多少钱?答案:3本书的总价为3本× 30元/本 = 90元,未达到满100元减20元的优惠条件,所以小华实际支付了90元。
中考应用题精选(含答案)

中考应用题精选(含答案)中考应用题精选(含答案)一、小明购买水果小明去水果店购买了一些苹果和橙子,苹果的单价为5元/斤,橙子的单价为4元/斤。
小明共购买了9斤水果,支付了43元。
1. 请问小明购买了多少斤苹果,多少斤橙子?解答:设小明购买的苹果为x斤,橙子为y斤,则由题意可得以下方程组:x + y = 9 (1)5x + 4y = 43 (2)(1)式乘以4,再与(2)式相减可得:4x + 4y - 5x - 4y = 36 - 43 => -x = -7 => x = 7所以小明购买了7斤苹果,9 - 7 = 2斤橙子。
2. 小明购买水果总共需要支付多少金额?解答:设小明购买的苹果总价为a元,橙子总价为b元,由题意可得以下方程组:a +b = 43 (3)5a + 4b = 9 * 5 (4)将(3)式乘以4,再与(4)式相减可得:4a + 4b - 5a - 4b = 172 - 45 => -a = 127 => a = -127(舍去)所以小明购买水果总共需要支付43元。
二、小明的年龄问题小明的爷爷今年87岁,小明今年10岁。
已知小明的爸爸在小明出生时是小明年龄的2倍,现在的爸爸年龄是小明年龄的3倍。
1. 请问小明的爸爸今年多少岁?解答:设小明的爸爸今年为x岁,则可得以下方程:10 - x = 2(x - 10) (5)将(5)式化简,得:10 - x = 2x - 203x = 30x = 10所以小明的爸爸今年10岁。
2. 请问小明的爷爷今年多少岁?解答:根据题意,小明的爷爷今年是小明爸爸的3倍,而小明爸爸今年是10岁,所以小明的爷爷今年87岁。
三、小明和小红的比例题小明和小红一起种植蔬菜,小明每天需要花费2小时来照料蔬菜园,小红每天需要花费3小时来照料蔬菜园。
已知小明比小红每天多照料蔬菜园1小时,两人一共照料蔬菜园13天。
1. 请问小明独自照料蔬菜园需要多少天才能完成任务?解答:设小明独自照料蔬菜园需要x天才能完成任务。
中考数学应用题分类及参考答案(修订)

中考数学应用题分类及参考答案(修订)一、方程应用1.为促进企业创新发展,某企业一月份的营业额是1000万元,月平均增长率相同,第一季度的总营业额是3990万元,求月平均增长率.2.某企业为了去库存,其产品对有些地区实行优惠政策,决定在原定价基础上每件降价40元,这样按原定价需花费5000元购买的产品,现在只花费了4000元,求每件产品的实际定价是多少元?3.甲志愿者计划用若干个工作日完成社区的某项工作,从第三个工作日起,乙志愿者加盟此项工作,且甲、乙两人工效相同,结果提前3天完成任务,甲志愿者计划完成此项工作的天数?4.某服装厂原有4条成衣生产线和5条童装生产线,工厂决定转产,计划用3天时间赶制1000顶帐篷支援灾区.若启用1条成衣生产线和2条童装生产线,一天可以生产帐篷105顶;若启用2条成衣生产线和3条童装生产线,一天可生产帐篷178顶.(1)每条成衣生产线和童装生产线每天生产帐篷各多少顶?(2)工厂满负荷全面转产,是否可以如期完成任务?二、不等式应用5.观看帆船比赛的船票分为两种:A种船票600元/张,B种船票120元/张.某旅行社要为一个旅行团代购部分船票,在购票费不超过5000元的情况下,购买A、B两种船票共15张,要求A种船票的数量不少于B种船票数量的一半.若设购买A种船票x张,请你解答下列问题:(1)共有几种符合题意的购票方案?写出解答过程;(2)根据计算判断:哪种购票方案更省钱?三、函数应用6.低碳生活,绿色出行的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,行进路程y(km)随时间x(h)变化的函数图象大致如图所示.(1)小红从甲地到乙地骑车的速度为20km/h;(2)当1.5≤x≤2.5时,求出路程y(km)关于时间x(h)的函数解析式;并求乙地离小红家多少千米?7.如图,某小区有一块靠墙(墙的长度不限)的矩形空地ABCD,为美化环境,用总长100m的篱笆围成四块矩形花圃(靠墙一侧不用篱笆,篱笆的厚度不计).(1)若四块矩形花圃的面积相等,求证:AE=3BE;(2)在(1)的条件下,设BC的长度为xm,矩形区域ABCD的面积为ym2,求y与x之间的函数关系式,并写出自变量x的取值范围.8.某研究所对某种新型产品的产销情况进行了统计,为了投资商在甲、乙两地生产并销售该产品提供了如下成果:第一年的年产量为x(吨)时,所需的全部费用y(万元)与x满足关系式y=110x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价P甲、P乙(万元)均与x满足一次函数关系。
初三数学应用题大全及答案

初三数学应用题大全及答案例1、今年来某县加大了对教育经费的投入,2013年投入2500万元,2015年投入3500万元。
假设该县投入教育经费的年平均增长率为x,根据题意列方程,则下列方程正确的是()A.2500x2=3500(B.2500(1+x)2=3500C.2500(1+x%)2=3500D.2500(1+x)+2500(1+x)2=3500【解答】解:设增长率为x,根据题意得2500×(1+x)2=3500,故选B.例2、为落实素质教育要求,促进学生全面发展,某市某中学2009年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2011年投资18.59万元。
则该学校为新增电脑投资的年平均增长率是,从2009年到2011年,该中学三年为新增电脑共投资万元。
【解答】解:设该学校为新增电脑投资的年平均增长率是x11(1+x)2=18.59x=30%(则该学校为新增电脑投资的年平均增长率是30%11×(1+30%)=14.3万元11+14.3+18.59=43.89万元故答案为:30%;43.89练习1、股票每天的涨、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停。
已知一只股票某天跌停,之后两天时间又涨回到原价。
若这两天此股票股价的平均增长率为x,则x满足的方程是()A.(1+x)2=B.(1+x)2=C.1+2x=D.1+2x=【解答】解:设平均每天涨x,则90%(1+x)2=1,即(1+x)2=,故选B。
(2、某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,那么每年投资的增长率为()A.20%B.40%C.﹣220%D.30%【解答】解:设每年投资的增长率为x,根据题意,得:5(1+x)2=7.2解得:x1=0.2=20%,x2=﹣2.2(舍去),故每年投资的增长率为为20%,故选:A3、随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2015年底某市汽车拥有量为16.9万辆。
中考数学应用题问题归类(共9份,附)
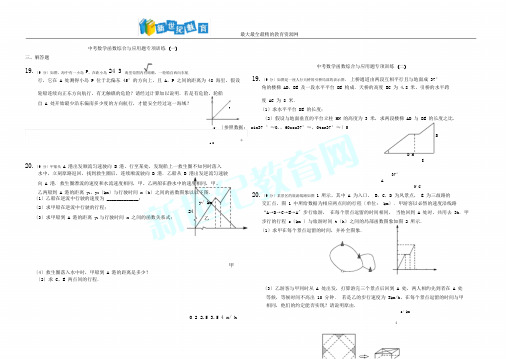
最大最全最精的教育资源网中考数学函数综合与应用题专项训练(一)三、解答题19.〔9 分〕如图,海中有一小岛P,在距小岛24 3 海里范围内有暗礁,一轮船自西向东航行,它在 A 处测得小岛 P 位于北偏东 45°的方向上,且 A,P 之间的距离为 48 海里,假设中考数学函数综合与应用题专项训练(二)19.〔9 分〕如图是一座人行天桥的引桥局部的表示图,上桥通道由两段互相平行且与地面成 37°角的楼梯 AD,BE 及一段水平平台 DE 构成.天桥的高度 BC 为 4.8 米,引桥的水平跨轮船连续向正东方向航行,有无触礁的危险?请经过计算加以说明.若是有危险,轮船自 A 处开始最少沿东偏南多少度的方向航行,才能安全经过这一海域?北P度 AC 为 8 米.〔1〕求水平平台 DE 的长度;〔2〕假设与地面垂直的平台立柱 MN 的高度为 3 米,求两段楼梯 AD 与 BE 的长度之比.45°〔参照数据: sin37 °≈0.,60cos37°≈,0tan37°≈〕5B东A MD M20.〔9 分〕甲船从A 港出发顺流匀速驶向 B 港,行至某处,发现船上一救生圈不知何时落入E 水中,立刻原路返回,找到救生圈后,连续顺流驶向 B 港.乙船从 B 港出发逆流匀速驶向 A 港.救生圈漂流的速度和水流速度相同,甲、乙两船在静水中的速度相同,甲、乙两船到 A 港的距离 y1,y2〔km〕与行驶时间 x〔h〕之间的函数图象以以下图.〔1〕乙船在逆流中行驶的速度为 _____________;〔2〕求甲船在逆流中行驶的行程;〔3〕求甲船到 A 港的距离 y1 与行驶时间 x 之间的函数关系式;24y/ km乙甲37°AN C20.〔9 分〕某景区的旅游线路如图1 所示,其中 A 为入口, B,C,D 为风景点, E 为三歧路的交汇点,图 1 中所给数据为相应两点间的行程〔单位: km〕.甲游客以必然的速度沿线路“A→D→C→E→A〞步行旅游,在每个景点逗留的时间相同,当他回到 A 处时,共用去 3h.甲步行的行程 s〔km 〕与旅游时间 t〔h〕之间的局部函数图象如图 2 所示.〔1〕求甲在每个景点逗留的时间,并补全图象.〔4〕救生圈落入水中时,甲船到 A 港的距离是多少?〔2〕求 C,E 两点间的行程.〔3〕乙游客与甲同时从 A 处出发,打算游完三个景点后回到 A 处,两人相约先到者在 A 处等候,等候时间不高出 10 分钟.若是乙的步行速度为 3km/h,在每个景点逗留的时间与甲相同,他们的约定能否实现?请说明原由.s/ kmO 2 2.5 3.5 4 x/ h421.〔10 分〕某工厂方案为某校生产A,B 两种型号的学生桌椅 500 套,以解决 1 250 名学生的学习问题.一套 A 型桌椅〔一桌两椅〕需木材3,一套 B 型桌椅〔一桌三椅〕需木材3,工厂现有库存木材 302m3.〔1〕有多少种生产方案?〔2〕现要把生产的全部桌椅运往该校,每套 A 型桌椅的生产本钱为 100 元,运费为3D12C1EBO 0.8 1.8 3 t/ h图1 图221.〔10 分〕如图,四边形ABCD 是边长为 60cm 的正方形硬纸片,剪掉阴影局部所示的四个全等的等腰直角三角形,再沿虚线折起,使 A,B,C,D 四个点重合于图中的点 P,正好形成2 元,每套 B 型桌椅的生产本钱为 120 元,运费为 4 元,求总开销 y〔元〕与生产 A 型桌椅 x〔套〕之间的函数关系式,并确定总开销最少的方案和最少的总开销.〔总开销 =生产一个底面是正方形的长方体包装盒.本钱+运费〕〔1〕假设折叠后长方体底面正方形的面积为 1 250cm2,求长方体包装盒的高;〔3〕按〔2〕的方案计算,有没有节余木材?若是有,请直接写出用节余木材再生产以上〔2〕设剪掉的等腰直角三角形的直角边长为 x〔cm〕,长方体的侧面积为 S〔cm2〕,求 S 与两种型号的桌椅,最多还可以够为多少名学生供应桌椅;若是没有,请说明原由. x 之间的函数关系式,并求出当 x 为何值时, S 的值最大.B CP最大最全最精的教育资源网甲、乙两所学校方案组织本校学生自觉参加此项活动.甲校报名参加的学生人数多于120 人,乙校报名参加的学生人数少于 120 人.经核算,假设两校分别组团共需开销 41 600元,假设两校联合组团只需开销 36 000 元.〔1〕两所学校报名参加旅游的学生人数之和高出 200 人吗?为中考数学函数综合与应用题专项训练〔三〕什么?19.〔9 分〕如图,某学习小组为了测量河对岸塔AB 的高度,在塔底部点 B 的正对岸点 C 处,〔2〕两所学校报名参加旅游的学生各有多少人?测得塔极点 A 的仰角〔∠ ACB〕为 60°.中考数学函数综合与应用题专项训练(四)〔1〕假设河宽 BC 为 36 米,求塔 AB 的高度.〔结果精确到 0.1 米〕〔2〕假设河宽 BC 的长度不易测量,如何测量塔 AB 的高度呢?小强思虑了一种方法:从点19.〔9 8:00~8:30 分〕星期天,燃气公司给安全加气站的储气罐注入天然气,注完气此后,一位3工作人员以每车 20 米的加襟怀,依次给在加气站排队等候的假设干辆车加气.储气罐中的C 出发,沿河岸前行 a 米至点D 处,假设在点 D 处测出∠ BDC 的度数为θ,这样就可以求出塔 AB 的高度了.小强的方法可行吗?假设可行,请用 a 和θ表示塔 AB 的高度;假设不能行,请说明原由.〔参照数据:2 1.41 ,〕A储襟怀 y〔米3〕与时间 x〔小时〕之间的函数关系以以下图.3y/ 米10 0008 0002 000BO 8 8.5 10.5 x/ 小时θaD C3的天然气;〔1〕8:00~8:30,燃气公司向储气罐注入了 _________米3〔2 x 8.5 y x 〕当≥时,求储气罐中的储襟怀〔米〕与时间〔小时〕之间的函数关系式;20.〔9 分〕如图,在平面直角坐标系 xOy 中,梯形 AOBC 的边 OB 在x轴的正半轴上, AC// OB,〔3〕正在排队等候的 20 辆车加完气后,储气罐内还有天然气多少立方米?这 20 辆车在当BC OB A ⊥,过点的双曲线于点 E.ykx的一支在第一象限交梯形对角线 OC 于点 D,交边 BC天 9:00 从前能加完气吗?请说明原由.20.〔9 分〕在修建楼梯时,设计者要考虑楼梯的安全程度.如图1,虚线为楼梯的斜度线,斜度线与地面的夹角为倾角θ,一般情况下,倾角θ越小,楼梯的安全程度越高.如图 2,设〔1〕假设点 C 的坐标为 (4,4),点 E 的坐标为 (4,2),那么点 A 的坐标是 ____________;计者为提高楼梯的安全程度,要把楼梯的倾角由θ1 减至θ2,这样楼梯占用地板的长度由 d1 〔2〕假设点 C 的坐标为 (2,2),当阴影局部的面积 S 最小时,求点 E 的坐标;〔3〕假设ODOC12,S△OAC=2,求双曲线的函数剖析式.yADCE增加到 d2, d1=4m,θ1=40°,θ2=36°,楼梯占用地板的长度增加了多少米?〔结果精确到.参照数据: sin36 °≈,8 cos36°≈,9tan36°≈,2 sin40 °≈0 .36,4cos40 °≈,66tan40 °≈〕39地板地板AO B x21.〔10 分〕某旅游社拟在暑期期间推出“两日游〞活动,收费标准以下:人数 m 0< m≤120 120<m≤200 m>200θ地板D C Bθ2θ1 地板d1d2图 1 图 2收费标准〔元 /人〕 180 170 150最大最全最精的教育资源网21.〔10 分〕义洁中学方案从荣威公司购置A,B 两种型号的小黑板.经洽谈,购置一块 A 型小黑板比购置一块 B 型小黑板多用 20 元,且购置 5 块 A 型小黑板和 4 块 B 型小黑板共需2 3 10〔结果精确到 0.1 1.41 1.73 3.16 米.参照数据:≈,≈,≈〕限高____ 米820 元.D A〔1〕求购置一块 A 型小黑板、一块 B 型小黑板各需多少元.C 〔2〕依照义洁中学实质情况,需从荣威公司购置 A ,B 两种型号的小黑板共 60 块,要求购置 A,B 两种型号小黑板的总开销不高出 5 240 元.而且购置 A 型小黑板的数量不小于1购置 B 型小黑板数量的.那么义洁中学从荣威公司购置 AB ,两种型号的小黑板有哪几2种方案?哪一种方案的总开销最低?FEM BN21.〔10 分〕某市的特色农产品在国际市场上颇具竞争力,其中属于菌类的一种猴头菇远销国外,上市时,有一外商按市场价格 10元/千克收买了 2 000 千克猴头菇存入冷库中,据展望,猴头菇的市场价格每天每千克上涨中考数学函数综合与应用题专项训练(五)0.5 元,但冷库存放这批猴头菇时每天需要支出各种开销合计 220 元,而且这种猴头菇在冷库中最多能保存 110 天,同时,平均每天有 6 千克的猴头菇损坏不能够销售.19.〔9 分〕如图 1,直线 y=k1x +b 与反比率函数y k2x的图象交于 A( 1,6),B (a,3)〔1〕假设存放 x 天后,将这批猴头菇一次性销售,设这批猴头菇的销售总金额为 y 元,试写出 y 与 x 之间的函数关系式.两点.〔2〕若是这位外商想获得利润 24 000 元,需将这批猴头菇存放多少天后销售?〔利润销〔1 k k〕求,的值;1 2k2k x b 01时 x 的取值范围;〔2〕直接写出x售总金额收买本钱各种开销〕〔3〕这位外商将这批猴头菇存放多少天后销售可获得最大利润?最大利润是多少?〔3〕如图 2,梯形 OBCE 中,BC∥OE,过点 C 作 CE⊥x 轴于点 E,CE 和反比率函数的中考数学函数综合与应用题专项训练 (六)图象交于点 P ,当梯形 OBCE 的面积为 9 时,请判断 PC 和 PE 的大小关系, 并说明原由.y y19.〔9 分〕如图,直线标为 4.1 y x2yk x〔k>0〕交于 A ,B 两点,且点 A 的横坐A A〔1〕求 k 的值;B O xC P E B Ox 〔2〕假设双曲线y k x 〔k>0〕上一点 C 的纵坐标为 8,求△ AOC 的面积;k y〔3 O l 〕过原点 的另一条直线 交双曲线〔k>0 P Q P 〕于 , 两点〔点 在第一象限〕,图 1 2 图x20.〔9 分〕为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中 MN 是水平线, MN ∥AD ,AD ⊥DE ,CF ⊥AB ,垂足分别y假设以点 A B P Q 24 P , , , 为极点的四边形的面积为 ,求点 的坐标.为 D ,F ,坡道 AB 的坡度 i=1: 3,AD=9 米,C 在 DE 上,CD =0.5 米,CD 是限高标志牌A的高度〔标志牌上写有:限高 ____米〕.若是进入该车库车辆的高度不能够高出线段 CF 的O x长,那么该停车库限高多少米?B。
中考数学所有类型应用题汇总含答案

中考应用题列方程(组)解应用题是中考的必考内容,必是中考的热点考题之一,列方程(组)解应用题的关键与难点是如何找到能够表示题目全部含义的相等关系,所谓“能表示全部含义”就是指在相等关系中,题目所给出的全部条件(包括所求的量)都要给予充分利用,不能漏掉,但也不能把同一条件重复使用,应用题中的相等关系通常有两种,一种是通过题目的一些关键词语表现出来的明显的相等关系,如“多”、“少”、“增加”、“减少”、“快”、“慢”等,另一种是题目中没有明显给出而题意中又包含着的隐含相等关系,这也是中考的重点和难点,此时需全面深入的理解题意,结合日常生活常识和自然科学知识才能做到.解应用题的一般步骤:解应用题的一般步骤可以归结为:“审、设、列、解、验、答”.1、“审”是指读懂题目,弄清题意,明确题目中的已知量,未知量,以及它们之间的关系,审题时也可以利用图示法,列表法来帮助理解题意.2、“设”是指设元,也就是未知数.包括设直接未知数和设间接未知数以及设辅助未知数(较难的题目).3、“列”就是列方程,这是非常重要的关键步骤,一般先找出能够表达应用题全部含义的一个相等关系,然后列代数式表示相等关系中的各个量,就得到含有未知数的等式,即方程.4、“解”就是解方程,求出未知数的值.5、“验”就是验解,即检验方程的解能否保证实际问题有意义.6、“答”就是写出答案(包括单位名称).应用题类型:近年全国各地的中考题中涉及的应用题类型主要有:行程问题,工程问题,增产率问题,百分比浓度问题,和差倍分问题,与函数综合类问题,市场经济问题等.几种常见类型和等量关系如下:1、行程问题:s .基本量之间的关系:路程=速度×时间,即:vt常见等量关系:(1)相遇问题:甲走的路程+乙走的路程=原来甲、乙相距的路程.(2)追及问题(设甲速度快):①同时不同地:甲用的时间=乙用的时间;甲走的路程-乙走的路程=原来甲、乙相距的路程.②同地不同时:甲用的时间=乙用的时间-时间差;甲走的路程=乙走的路程.2、工程问题:基本量之间的关系:工作量=工作效率×工作时间.常见等量关系:甲的工作量+乙的工作量=甲、乙合作的工作总量.3、增长率问题:基本量之间的关系:现产量=原产量×(1+增长率).4、百分比浓度问题:基本量之间的关系:溶质=溶液×浓度.5、水中航行问题:基本量之间的关系:顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度.6、市场经济问题:基本量之间的关系:商品利润=售价-进价;商品利润率=利润÷进价;利息=本金×利率×期数;本息和=本金+本金×利率×期数.一元一次方程方程应用题归类分析列方程解应用题,是初中数学的重要内容之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
逆流速度=船在静水中速度-水流速度. 6、市场经济问题: 基本量之间的关系:商品利润=售价-进价; 商品利润率=利润÷进价;
利息=本金×利率×期数; 本息和=本金+本金×利率×期数.
一元一次方程方程应用题归类分析 列方程解应用题,是初中数学的重要内容之一。许多实际问题都归结为解一种方程或方程 组,所以列出方程或方程组解应用题是数学联系实际,解决实际问题的一个重要方面; 下面老师就从以下几个方面分门别类的对常见的数学问题加以阐述,希望对同学们有所 帮助.
2、工程问题: 基本量之间的关系:工作量=工作效率×工作时间. 常见等量关系:甲的工作量+乙的工作量=甲、乙合作的工作总量. 3、增长率问题: 基本量之间的关系:现产量=原产量×(1+增长率). 4、百分比浓度问题: 基本量之间的关系:溶质=溶液×浓度.
5、水中航行问题: 基本量之间的关系:顺流速度=船在静水中速度+水流速度;
例 4. 三个正整数的比为 1:2:4,它们的和是 84,那么这三个数中最大的数是几? 5. 数字问题 (1)要搞清楚数的表示方法:一个两位数的,十位数字是 a,个位数字为 b(其中
a、b 均为整数,且 1≤a≤9, 0≤b≤9,)则这个两位数表示为:10a+b。
(2) 数字问题中一些表示:两个连续整数之间的关系,较大的比较小的大 1;偶数用 2N 表示,连续的偶数用 2n+2 或 2n—2 表示;奇数用 2n+1 或 2n—1 表示。 例 5. 一个两位数,个位上的数是十位上的数的 2 倍,如果把十位与个位上的数对调, 那么所得的两位数比原两位数大 36,求原来的两位数
“等积变形”是以形状改变而体积不变为前提。常用等量关系为: ①形状面积变了,周长没变; ②原料体积=成品体积。
?例 2. 用直径为 90mm 的圆柱形玻璃杯(已装满水)向一个由底面积为125 125mm2 内高 为 81mm 的长方体铁盒倒水时,玻璃杯中的水的高度下降多少 mm?(结果保留整数
3.14 ) 3. 劳力调配问题: 这类问题要搞清人数的变化,常见题型有: 1 既有调入又有调出; 2 只有调入没有调出,调入部分变化,其余不变; 3 只有调出没有调入,调出部分变化,其余不变。
?6. 工程问题: 工程问题中的三个量及其关系为:工作总量=工作效率×工作时间 经常在题目中未给出工作总量时,设工作总量为单位 1。 例 6. ?一件工程,甲独做需 15 天完成,乙独做需 12 天完成,现先由甲、乙合作 3 天后, 甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
几种常见类型和等量关系如下: 1、行程问题: 基本量之间的关系:路程=速度×时间,即: s vt . 常见等量关系: (1)相遇问题:甲走的路程+乙走的路程=原来甲、乙相距的路程. (2)追及问题(设甲速度快):
①同时不同地: 甲用的时间=乙用的时间; 甲走的路程-乙走的路程=原来甲、乙相距的路程. ②同地不同时: 甲用的时间=乙用的时间-时间差; 甲走的路程=乙走的路程.
4、“解”就是解方程,求出未知数的值. 5、“验”就是验解,即检验方程的解能否保证实际问题有意义. 6、“答”就是写出答案(包括单位名称). 应用题类型: 近年全国各地的中考题中涉及的应用题类型主要有:行程问题,工程问题,增产率问题, 百分比浓度问题,和差倍分问题,与函数综合类问题,市场经济问题等.
?7. 行程问题: 1 行程问题中的三个基本量及其关系: 路程=速度×时间。 2 基本类型有
① 相遇问题;② 追及问题;常见的还有:相背而行;行船问题;环形跑道问题。
3 解此类题的关键是抓住甲、乙两物体的时间关系或所走的路程关系,一般情况 下问 题就能迎刃而解。并且还常常借助画草图来分析,理解行程问题。
?例 3. 机械厂加工车间有 85 名工人,平均每人每天加工大齿轮 16 个或小齿轮 10 个,已 知 2 个大齿轮与 3 个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能 使每天加工的大小齿轮刚好配套?
4. 比例分配问题: 这类问题的一般思路为:设其中一份为 x,利用已知的比,写出相应的代数式。 常用等量关系:各部分之和=总量。
1. 和、差、倍、分问题: 1倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长 率 ……”来体现。 2 多少关系:通过关键词语“多、少、和、差、不足、剩余……”来体现。 例 1.根据第五次人口普查统计数据,截止到 2000 年 11 月 1 日 0 时,全国每 10 万人中 具有小学文化程度的人口为 35701 人,比 1990 年 7 月 1 日减少了 3.66%,1990 年 6 月底 每 10 万人中约有多少人具有小学文化程度? 2. 等积变形问题:
中考应用题
列方程(组)解应用题是中考的必考内容,必是中考的热点考题之一,列方程(组)解应 用题的关键与难点是如何找到能够表示题目全部含义的相等关系,所谓“能表示全部含 义”就是指在相等关系中,题目所给出的全部条件(包括所求的量)都要给予充分利用, 不能漏掉,但也不能把同一条件重复使用,应用题中的相等关系通常有两种,一种是通 过题目的一些关键词语表现出来的明显的相等关系,如“多” 、“少” 、“增加” 、“减少” 、“快” 、“慢”等,另一种是题目中没有明显给出而题意中又包含着的隐含相 等关系,这也是中考的重点和难点,此时需全面深入的理解题意,结合日常生活常识 和 自然科学知识才能做到.
