理想弹塑性线性强化模型的身管残余应力分析

合集下载

ANSYS命令流学习笔记11-厚壁压力容器弹塑性变形后的残余压力分析

!ANSYS命令流学习笔记11-厚壁压力容器弹塑性变形后的残余压力分析!学习重点：!1、从材料的几何、静力平衡、物理（广义胡克定律）出发，推算厚壁容器的弹塑性区，并计算受力状态。

理解残余应力的产生与计算此部分过于复杂，不便于展开。

但是基本道理十分简单，刘鸿文老师的书也是十分简洁明了。

参考刘鸿文老师的《材料力学（第4版）Ⅱ》中的第16章和第18章。

!2、复习四大强度理论、莫尔强度理论四大强度理论，这里主要应用第三强度理论，即最大切应力理论。

此理论使用简单，在金属材料方面广泛应用。

σ1 - σ3 ≤[σs]此理论解释了低碳钢在拉伸状态下，沿45°角断裂的问题。

很好地解释了三向均匀下（即静水压力）塑性材料不破坏的问题。

没有考虑σ2，所以解释不了三向均拉下塑性材料的破坏。

再此对四大强度理论做一个小结：第一强度理论：最大拉应力理论。

适用于脆性材料的二向拉伸与扭转状态，解释了铸铁等脆性材料在拉伸时垂直拉力方向断裂，扭转时与力矩成45°角断裂。

只考虑最大主应力Mises考虑了σ1。

σ1 ≤[σs]第二强度理论：最大拉应变理论。

使用与脆性材料的二向力状态，且二向力分别对应为拉应力和压应力，如脆性材料铸铁的压缩，弥补第一强度理论不能解释压缩破坏。

但是这个理论不能解释二向拉伸，二向压缩，三向压缩等情况，一般有限元分析中也很少用到此理论。

ε 1 ≤[εu]默认第三和第四强度理论已经非常熟悉了，这里总结一下小知识点：(1) 一般情况下，脆性材料用第一、第二理论；塑性材料用第三、第四理论(2) 无论脆塑，三向均匀拉应力状态下，均按照第一强度理论解释(3) 无论脆塑，三向均匀压应力状态下，均按照第三或者第四强度理论解释；如容器内冰块膨胀不破碎，海底石头不能被压碎(4) 脆性或塑性会改变；低温变脆，高温变塑；高速动载变脆，低速静载保持塑性等!3、复习Tresca、Mises屈服准则，联系强度理论综合应用Tresca屈服准则对应第三强度理论，Mises屈服准则对应第四强度理论。

材料弹塑阶段性质及残余应力的测定

材料弹塑阶段性质及残余应力的测定关雪涛苏铮铮张莉何琳北京工业大学000112班指导教师：张亦良摘要本文报导了由普通碳钢构成的四点弯曲梁试件，在加、卸载过程中弹性、塑性阶段应力应变的全过程及塑性变形后表面的残余应力状况。

通过弯曲梁正反两面粘贴电阻应变片，详细记录了加、卸载过程中弹塑性的应力应变曲线，特别是记录了梁进入塑性阶段初期并形成塑性铰的过程，得到了弹塑性泊松比曲线。

结果发现，材料泊松比并不是常量，在弹性阶段近似为0.3左右，而进入塑性以后，数值不断增大，最终为0.5左右。

卸载后，梁出现了不可恢复的塑性变形，用X射线法测量了试件两面的残余应力，与弹塑性理论解基本相符。

研究了加工应力沿深度的分布，为准确测定表面残余应力提供了实验依据。

关键词：弹塑性应力；残余应力；X射线法；泊松比一、引言在工程中，多数材料用于弹性范围。

但是，就钢材这类塑性材料而言，其塑性性能很好，在弹性以外，仍有广阔用途，如塑性加工、锻造成型等等。

对于横截面应力非均匀分布的塑性材料杆件，当危险点应力达到屈服极限时，并未丧失工作能力，按塑性极限法设计，可提高承载能力，节省原材料，在建筑行业中已得到广泛应用。

这就是说，我们不可避免的要接触到材料在弹塑性区域的性质。

在压力容器行业中，所应用的球罐都是由冷加工成型的，事先压成瓜片，再由焊接而成。

由于材料的塑性变形，不可避免的带来残余应力。

而如何计算残余应力、找出残余应力的最大值，是至关重要的。

因为残余应力与工作应力叠加，才是容器真正的应力。

容器应力水平的大小与评估，对于设备的安全运行来说十分重要。

在我们材料力学的学习中，关于塑性区及残余应力的内容介绍很少。

为了能更好地研究并了解材料在这一区间的性质，以及当材料发生塑性变形后的特性，我们选择了“弹塑性应力及电测法的综合实验”这样一个综合性较强的实验。

通过这个实验，希望能在我们并不熟悉的领域里发现一些现象，解决一些有关于工程实际的问题。

同时我们也希望能通过这个实验锻炼我们独立思考和动手能力，因为指导老师曾多次告诉我们这个实验有一定难度，由于是破坏实验，难以重复，因此在加载时要十分小心。

厚壁圆筒__弹塑性力学知识

2. 弹塑性阶段：（1）弹性区：r r b
(1 )a 2 pe u E (b 2 a 2 ) b2 r (1 2 )r
a2 pe 1 2 2 b
ss

内半径为r ，外半径为b，在 r = r 处承受内压的厚壁筒
sq r
r rb
sq
p
r
sq r
a p
b
sq r
r b2 p a2 1 2 s s 1 l n 2 2 a b a r 2 2 2 s r a p b s 1 2 2 2 2 2 b b a r
通解：
s r C1 C2 r 2
s q C1 C2 r 2
一、弹性分析
2. 解答
通解：
s r C1 C2 r 2
s q C1 C2 r 2
er
1 1 C1 1 C 2 r 2 E 1 1 C1 1 C 2 r 2 eq E 1 1 C1r 1 C 2 r 1 u E 1 2 2 C1 2 a p b p2 1 2 b a a 2b 2 p2 p1 C2 2 2 b a
u
e
rr
u
p
rr
(1 ) r 2s s 2 2 C b ( 1 2 ) r 2 Eb 2

(1 ) r 2s s 2 2 u b ( 1 2 ) r 2 Eb 2 r

=1/2
3 r 2s s u 4 Er ul ue b2 2 a
弹性极限状态:
a p1

基于统一强度理论的自紧身管残余应力分析

基于统一强度理论的自紧身管残余应力分析
佟海生;樊江涛;李强
【期刊名称】《火炮发射与控制学报》
【年(卷),期】2024(45)2
【摘要】基于统一强度理论,考虑材料拉压异性和鲍辛格效应的影响,采用双线性强化材料模型对身管进行自紧分析,推导了身管加载应力、卸载应力、残余应力及工作应力的解析解,得到了弹塑性交界面半径、反向屈服半径的计算公式,提出了最佳自紧度和自紧压力的计算方法,通过与实验数据进行对比,验证了本文理论解的正确性,分析了材料拉压强度比、中间应力系数等参数对身管残余应力、弹塑性交界面半径、反向屈服半径和最佳自紧压力的影响。

结果表明,反向屈服半径、弹塑性交界面半径、弹塑性交界面处残余应力与材料拉压强度比成正比,与中间应力系数成反比;最佳自紧压力与材料拉压强度比成反比,与中间应力系数成正比。

【总页数】9页(P97-104)
【作者】佟海生;樊江涛;李强
【作者单位】内蒙古北方重工业集团有限公司;中北大学机电工程学院
【正文语种】中文
【中图分类】TJ304
【相关文献】
1.基于统一强度理论的井简围岩应力分析
2.基于统一强度理论的非均匀应力场圆形巷道围岩塑性区分析
3.基于双向强度理论计算钛容器的焊接残余应力
4.基于统一强度理论的灰土挤密桩应力分析
5.不同强度理论下自紧身管应力数值仿真
因版权原因，仅展示原文概要，查看原文内容请购买。

塑性力学复习题

塑性力学复习题一、填空题1．塑性变形不仅与当前的应力状态有关，还和（）有关。

2．对一般金属，体积应变完全是（）的，静水压力不产生（）。

它对屈服极限的影响（）。

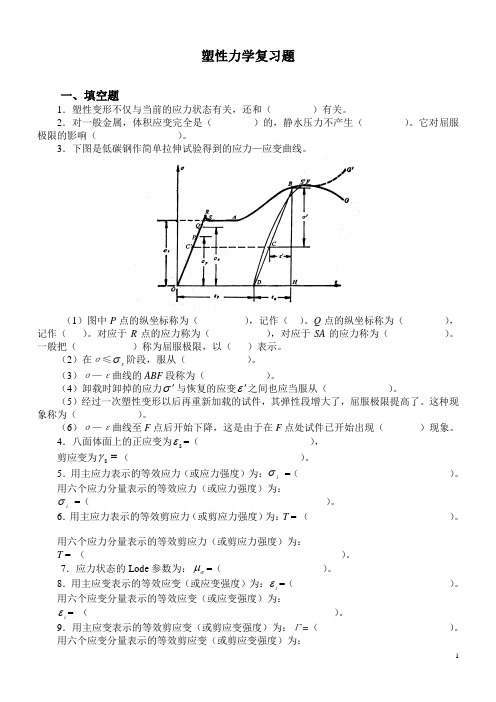
3．下图是低碳钢作简单拉伸试验得到的应力—应变曲线。

（1）图中P点的纵坐标称为（），记作（）。

Q点的纵坐标称为（），记作（）。

对应于R点的应力称为（），对应于SA的应力称为（）。

一般把（）称为屈服极限，以（）表示。

σ阶段，服从（）。

（2）在σ≤s（3）σ—ε曲线的ABF段称为（）。

（4）卸载时卸掉的应力σ'与恢复的应变ε'之间也应当服从（）。

（5）经过一次塑性变形以后再重新加载的试件，其弹性段增大了，屈服极限提高了。

这种现象称为（）。

（6）σ—ε曲线至F点后开始下降，这是由于在F点处试件已开始出现（）现象。

ε=（），4．八面体面上的正应变为8γ（）。

剪应变为=8σ=（）。

5．用主应力表示的等效应力（或应力强度）为：i用六个应力分量表示的等效应力（或应力强度）为：σ=（）。

i6．用主应力表示的等效剪应力（或剪应力强度）为：T = （）。

用六个应力分量表示的等效剪应力（或剪应力强度）为：T = （）。

μ=（）。

7．应力状态的Lode参数为：σε=（）。

8．用主应变表示的等效应变（或应变强度）为：i用六个应变分量表示的等效应变（或应变强度）为：ε= （）。

i9．用主应变表示的等效剪应变（或剪应变强度）为：Γ=（）。

用六个应变分量表示的等效剪应变（或剪应变强度）为：Γ=（）。

10．表示应变状态特征的Lode 参数为：εμ=（）。

11．第一应力不变量为：1I =（）=（）。

第二应力不变量为：2I =（）=（）。

第三应力不变量为：3I =（）=（）。

12．第一应变不变量为：1I '=（）=（）。

第二应变不变量为：2I '=（）=（）。

第三应变不变量为：='3I （）=（）。

13．应力偏张量的第一不变量为：=1J （）。

身管自紧残余应力

二：弹塑性阶段圆筒静力平衡方程：
d r dr
r
r
0
Mises屈服条件为等效应力

3 2
= s
( r ) s

通过上面两个式子可以求得 r C
2 3
s ln r
又因为
r a 时 r P
代入上式可以求得
C
将C带入上式，最终求得：
弹性区域：
s rs 2 a2P b2 2 )(1 2 ) r ( 2 2 b a r 3b s rs 2 a2P b2 2 )(1 2 ) ( 2 2 b a r 3b s rs 2 a2P 2 z 2 b a2 3b
r P P P z
rs
2 3 2 3 2 3
s ln
r a r
s (1 ln )
a
s ( ln )
2 a
1
r
为弹塑性交界区域的半径，此处所受力为弹塑性极限力： rs rs 2 s 2 Ps ( r ) r rs p s ln (1 2 ) 2 a b b 3
1 2
( r ) 2 ( z ) 2 ( r z ) 2

3 2
( r ) 3 P
a22 2b2源自2b a rs
通过上式可以看出：等效应力与半径成反比，所以半径最小处（r=a）首先发生屈服，由此求得弹性极限压力为：
a2 s Pe (1 2 ) b 3
最终求得：
rs 2 2 rs 1 P ln (1 2 ) b 3 a 2

ansys分析三杆结构塑性卸载后的残余应力

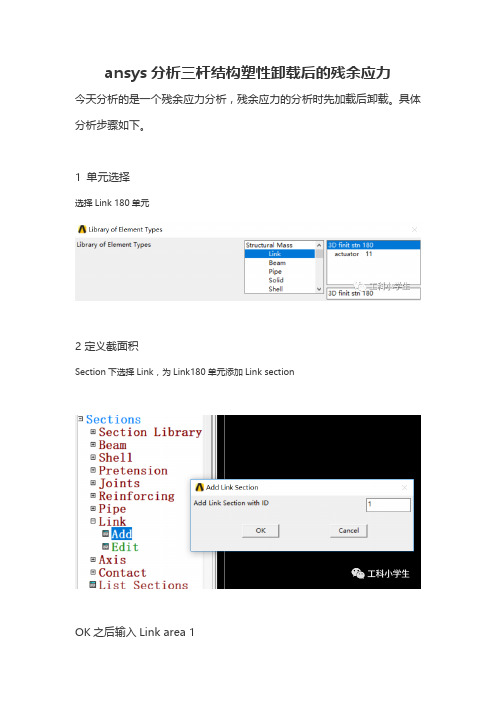
ansys分析三杆结构塑性卸载后的残余应力今天分析的是一个残余应力分析，残余应力的分析时先加载后卸载。

具体分析步骤如下。

1 单元选择选择Link 180单元2 定义截面积Section下选择Link，为Link180单元添加Link sectionOK之后输入Link area 13 定义材料参数ANSYS Main Menu: Preprocessor→Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX：30e6（定义弹性模量）→OK，Nolinear （定义屈服应力）→Inelastic →Rate Independent →Kinematic Hardening Plasticity →Mises Plasticity→Bilinear →Yield Stss：30000→OK→Close（关闭材料定义窗口）4 定义参数及指定角度单位ANSYS Utility Menu: Parameters →Scalar Parameters..…（出现Scalar Parameters 对话框）→Selection下输入L=100→Accept→输入THETA=30→Accept→CloseANSYS Utility Menu: Parameters→Angular Units...→Units for angular: Degrees DEG →OKANSYS Utility Menu: Parameters →Scalar Parameters..…（出现Scalar Parameters 对话框）→Selection下输入XLOC=L*TAN(THETA）→Accept→Close5 生成模型ANSYS Main Menu: Preprocessor→Modeling→Create→Nodes→In Active CS→NODE Node number：1：X，Y，Z Location in active CS:-XLOC，0→Apply →NODE Node number：3；X，Y，Z Location in active CS: XLOC，0→OK→Nodes-Fill between Nds→选择节点1和3→OK（出现Create Nodes Between 2 Nodes对话框）→OK→Nodes-In Active CS →NODE Node number：4；X，Y，Z Location in active CS：0,-L →OK →Elements→Auto Numbered →Thru Nodes（出现Elements.…对话框）→选择节点1和4→Apply→选择节点2和4→Apply→选择节点3和4→OK6 设置求解输出控制ANSYS Main Menu: Preprocessor→Loads →Load Step Opts →Output Ctrls →Solu Printout（出现Solution Printout Controls 对话框）→FREQ Print frequency:Every Nth substep；Value ofN：1→OK7 模型加约束及载荷ANSYS Main Menu: Preprocessor→Loads→Define Loads →Apply →Structural→Displacement→On Nodes →选择节点1、2和3→OK（出现Apply U，ROT on Nodes 对话框）→Lab2：All DOF；VALUE: 0；→OKANSYS Main Menu: Preprocessor→Loads →Define Loads →Apply →Structural→Force/Moment→On Nodes →选择节点4→OK（出现Apply F/M on Nodes对话框）→Lab: FY；VALUE：-51961.5→OK8 求解ANSYS Main Menu: Solution →Solve →Current LS出现Solve Curent Load Step 对话框，关闭/STATUS Command记事本）→OK→Close（关闭出现的Solution is done 消息框）9 提取4节点位移，赋值给变量DEFANSYS Utility Menu: Parameters →Get Scalar Data..…（出现Get Scalar Data 对话框）→选择Result data，Nodal results→OK（出现Get Nodal results Data对话框）→Name: DEF；Node number N：4；Reseluts data to be retrieved: DOF solution，UY→OK10 再次设置求解及输出控制ANSYS Main Menu: FinishANSYS Main Menu: Solution →Analysis Type →Sol'n Controls →Basic（出现Solution Controls对话框）→Time Control，Automatic time stepping: On; Number of substeps：10；Write Items to Results File：All solution items；Frequeney: Write every Nth substep，N：10→OK11 施加载荷ANSYS Utility Menu: Plot →Multi-Plots ANSYS Main Menu: Solution→Define Loads →Apply →Structural→Force/Moment→On Nodes →选择节点4→OK（出现Apply F/M on Nodes 对话框）→Lab:FY:VALUE:-81961.5→OK12 求解（施加F2求解）ANSYS Main Menu: Solution →Solve →Current LS（出现Solve Curent Load Step 对话框，关闭/STATUS Command记事本）→OK→Close（关闭出现的Solution is done 消息框）13 设置求解及输出控制ANSYS Main Menu: Solution →Analysis Type →Sol'n Controls →Basic（关闭出现的Warning对话框，出现Solution Controls对话框）→Time Control，Number of substeps：5，Frequency: Write every Nth substep，N：5→OK14 施加载荷ANSYS Utility Menu: Plot →Multi-PlotsANSYS Main Menu: Solution→DefineLoads→Apply→Structural→Force/Moment→On Nodes →选择节点4→OK（出现Apply F/M on Nodes对话框）→Lab: FY: VALUE: 0→OK15求解（卸载求解）ANSYS Main Menu: Solution →Solve →Current LS（出现Solve Current Load Step 对话框，关闭/STATUS Command 记事本）→OK→Close（关闭出现的Solution is done 消息框）16 提取单元2的应力，赋给变量STRSSANSYS Main Menu: General Postproc →Element Table →Define Table（出现Element Table Data对话框）→press Add..…（出现Define Additional Element Table Items对话框）→Lab: STRS；Item，Comp：LS.1→OK→CLOSE（关闭Element Table Data 对话框）ANSYS Utility Menu: Parameters →Get Scalar Data..…（出现Get Scalar Data对话框）→选择Result data，Elem table data-OK（出现Get Element Table Data对话框）→Name: STRSS；Element numberN：2→OK17 列出所有参数值ANSYS Utility Menu: List →Status→Parameters →All Parameters（出现一文本文件列出所以的参数）18 结果与讨论1）4节点的垂直位移是-0.07533in，2号杆单元的轴向应力是-5650.344psi2）本次案例共加载了两次载荷，第一次载荷是查看4节点的y方向位移，第二次载荷加载是查看2号杆单元的轴向应力。

欧盟压力容器标准EN13445分析设计标准概述定稿

为了克服弹塑性增量有限元法的困难，提出了许多求极限载荷的简化分析方法：
(1) R. Seshadri提出的广义的局部应力应变节点重新分布法[GLOSS] 与真实的极限载荷差别较大
(2) D. Mackenzie和J. T. Boyle首先提出的弹性补偿法求得极限载荷的值比用弹塑性分析求得的值小11%~20%，其准确性受网格密度和单元阶的影响非常大
分析设计最初引入时，在承压设备设计中主要的分析方法是薄壳不连续分析，它是基于薄壳理采用有限元法进行承压设备响应分析计算后，由于有限元分析是基于弹性理论而不是薄壳理论得到应力数值解，除壳体特别薄以外，应力沿壁厚呈非线性分布。
以Hechmer和Hollinger等为代表的美国压力容器研究委员会（PVRC）开展了三维应力数值解评估技术研究，但难以取得突破性进展。究其原因，是迄今为止仍未解决以下几个问题：
1.2.1 极限分析
1.2.2 塑性分析
1.2.1 极限分析
极限分析是假设材料为理想弹塑性（或理想刚塑性）、结构处于小变形状态时，研究塑性极限状态下的结构特性。
极限分析的上、下限定理可以用来确定结构的极限载荷，通常是根据下限定理来求结构的下限极限载荷。只有比较简单的问题如轴对称结构的简单容器、环板才能求得其极限载荷。对一些复杂的结构还无法求出极限载荷的解析解。数值解多数是根据有限元法和数学规划法相结合而建立的。
（7）三倍弹性变形准则
Schroeder将弹性响应的变形取为切线交点变形，并定义塑性载荷为载荷—变形曲线上测定变形等于3倍弹性变形时的载荷。
（8）塑性功准则
该准则是由Gerdeen于1979年提出的。他建议参数选择原则是：载荷参数与相对应的变形参数的乘积表示功，例如：力和位移、弯矩和转角。这时，载荷—变形曲线下的面积就表示载荷对容器所做的功，总的功由弹性功和塑性功组成。塑性功可

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第３４卷第４期２０１３年４月
兵
ＮＯ．４
ＡＣＴＡＡＲＭＡＭＥＮＴＡＲＩＩ
Ａｐｒ．
２０１３
理想弹塑性线性强化模型的身管残余应力分析
常列珍，潘玉田，李魁武，马新谋
（１．中北大学力学系，山西太原０３００５１；２．中北大学动力机械系，山西太原０３００５１；
中图分类号：ＴＢ１２５文献标志码：Ａ文章编号：１０００－１０９３（２０１３）０４－０３８５ — ０７
ＤＯＩ：１０．３９６９／ｊ．ｉｓｓｎ．１０００ — １０９３．２０１３．０４．００１
（１．ＤｅｐａｒｔｍｅｎｔｏｆＭｅｃｈａｎｉｃｓ，ＮｏｒｔｈＵｎｉｖｅｒｓｉｔｙｏｆＣｈｉｎａ，Ｔａｉｙｕａｎ０３００５１，Ｓｈａｎｘｉ，Ｃｈｉｎａ；
２．ＤｅｐａｒｔｍｅｎｔｏｆＰｏｗｅｒＭｅｃｈａｎｉｃａｌＥｎｇｉｎｅｅｒｉｎｇ，ＮｏｒｔｈＵｎｉｖｅｒｓｉｔｙｏｆＣｈｉｎａ，Ｔａｉｙｕａｎ０３００５１，Ｓｈａｎｘｉ；Ｃｈｉｎａ
ＲｅｓｉｄｕａｌＳｔｒｅｓｓＡｎａｌｙｓｉｓｏｆＧｕｎＢａｒｒｅｌｗｉｔｈＢｉ－ｌｉｎｅａｒＭａｔｅｒｉａｌＭｏｄｅｌ
ＣＨＡＮＧＬｉｅ．ｚｈｅｎ，ＰＡＮＹｕ— ｔｉａｎ，ＬＩＫｕｉ．ＷＵ，ＭＡＸｉｎ— ｍｏｕ
ｈａｒｄｅｎｉｎｇｍａｔｅｒｉａｌｍｏｄｅｌ，ｔｈｅｅｌａｓｔｉｃｉｔｙａｎｄｐｌａｓｔｉｃｉｔｙｏｆｂａｒｒｅｌｄｕｒｉｎｇｌｏａｄｉｎｇａｎｄｕｎｌｏａｄｉｎｇａｒｅａｎａｌｙｚｅｄｂａｓｅｄｏｎｔｈｅｔｈｅｏｒｙｏｆｅｌａｓｔｉｃ－ｐｌａｓｔｉｃｍｅｃｈａｎｉｃｓａｎｄｓｏｍｅａｓｓｕｍｐｔｉｏｎｓ．Ａｎｄｔｈｅｆｏｒｍｕｌａｓｏｆｐｌａｓｔｉｃｒａｄｉ－ＵＳ，ｌｏａｄｉｎｇａｎｄｕｎｌｏａｄｉｎｇｓｔｒｅｓｓ — ｓｔｒａｉｎｓ，ａｎｄｒｅｖｅｒｓｅｙｉｅｌｄｉｎｇｒａｄｉｕｓｏｆｓｗａｇｅａｕｔｏｆｒｅｔｔａｇｅｇｕｎｂａｒｒｅｌａｒｅｄｅｒｉｖｅｄ．Ｔｈｅｒｅｓｉｄｕａｌｓｔｒｅｓｓｆｏｒｍｕｌａｓｗｉｔｈａｎｄｗｉｔｈｏｕｔｒｅｖｅｒｓｅｙｉｅｌｄｉｎｇａｒｅｏｂｔａｉｎｅｄｂｙｕｓｉｎｇｌｏａｄｉｎｇａｎｄｕｎｌｏａｄｉｎｇｓｔｒｅｓｓｅｓｏｆｇｕｎｂａｒｒｅｌ，ｒｅｓｐｅｃｔｉｖｅｌｙ．Ｉｎｏｒｄｅｒｔｏｖｅｒｉｆｙｔｈｅａｃｃｕｒａｃｙ，ｔｈｅｐｌａｓｔｉｃｒａｄｉｕｓ，ｒｅｖｅｒｓｅｙｉｅｌｄｉｎｇｒａｄｉｕｓａｎｄｒｅｓｉｄｕａｌｓｔｒｅｓｓｏｆｂａｒｒｅｌａｒｅｃａｌｃｕｌａｔｅｄｂｙｕｓｉｎｇｔｈｅｐｒｅｓｅｎｔｅｄｆｏｒｍｕｌａｓ．Ｔｈｅｒｅｓｕｌｔｓｓｈｏｗｔｈａｔｔｈｅｔｈｅｏｒｅｔｉｃａｌｖａｌｕｅｓａｒｅｇｏｏｄａｇｒｅｅｍｅｎｔｗｉｔｈｔｈｅｅｘｐｅｒｉｍｅｎｔｒｅｓｕｌｔｓ．
３．ＮｏｒｔｈｗｅｓｔＩｎｓｔｉｔｕｔｅｏｆＭｅｃｈａｎｉｃａｌａｎｄＥｌｅｃｔｒｉｃａｌＥｎｇｉｎｅｅｒｉｎｇ，Ｘｉａｎｙａｎｇ７１２０９９，Ｓｈａａｎｘｉ，Ｃｈｉｎａ）Ａｂｓｔｒａｃｔ：Ｔｏｄｅｒｉｖｅｔｈｅｒｅｓｉｄｕａｌｓｔｒｅｓｓｏｆｓｗａｇｅａｕｔｏｆｒｅｔｔａｇｅｇｕｎｂａｒｒｅｌｗｉｔｈｅｌａｓｔｉｃｐｅｒｆｅｃｔｌｙ－ｐｌａｓｔｉｃｌｉｎｅａｒ
卸载过程中的应力应变、反向屈服半径的计算公式。利用机械自紧身管加载和卸载过程中的应力，
给出了身管有反向屈服和无反向屈服两种情况下残余应力的计算公式。应用这些公式计算了一个模拟管的塑性半径、反向屈服半径和残余应力，结果表明理论值与实验值吻合良好。关键词：固体力学；机械自紧；残余应力；塑性半径；反向屈服；反向屈服半径
３．西北机电工程研究所，陕西咸阳７１２０９９）
摘要：为计算理想弹塑性线性强化模型机械自紧身管的残余应力，基于弹塑性力学和一些基本假设，通过对加载和卸载过程中的身管做弹塑性分析，得到了机械自紧身管的塑性半径、加载和