MBA数学致胜十大法宝
MBA数学技巧讲义-推荐下载

对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置各试时类卷,管调需路控要习试在题验最到;大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资,常料要工试加况卷强下安看与全22过,22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
制胜法宝还是致胜法宝

制胜法宝还是致胜法宝
制胜法宝还是致胜法宝?
答:“致胜法宝”是错误用法,应该是制胜法宝。
制胜法宝的意思:比喻用对方意料不到的方法取得胜利。
制胜:读音为[zhì shèng]意思是以制服对方来取得胜利。
出自《孙子·虚实》:“人皆知我所以胜之形,而莫知吾所以制胜之形。
”
法宝是意为佛教心法、规则、智慧和修行解脱法门,道教意为长生法门。
宝:佛教意为智慧的结晶,道教意为诀窍。
后来,演变成了神话传说中能降妖伏魔的宝贝。
比喻有特效的武器、方法或经验。
MBA数学笔记-完整版
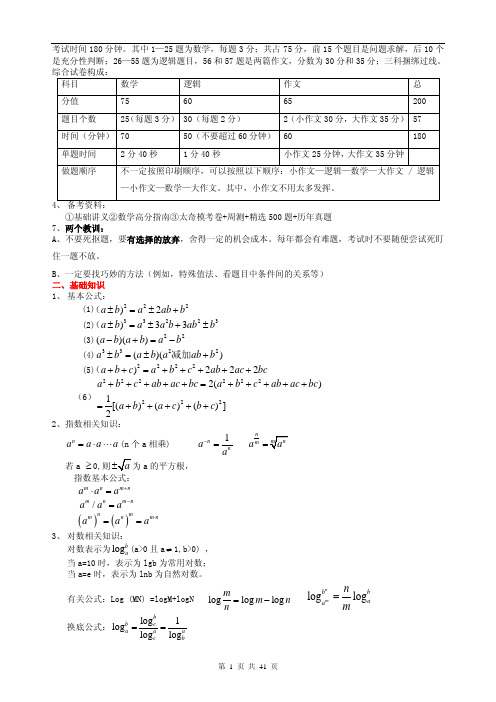
a 2 (升次)
| x1 − x2 =|
2 2
( x1 − x2 ) 2 =
a a ≥ 0 −a a < 0
( x1 + x2 ) 2 − 4 x1 x2
(2) | a | = a (去绝对值符号) (3) a = | a =|
2
非负性(重点):归纳具有非负性的量
第 4 页 共 41 页
1
1
| a |≥ 0, a 2 ......a 2 n ≥ 0, a 2 ......a 2 n ≥ 0
a −2 , a −4 ......a −2 n > 0
− 1 1 1 − − 2 , a 4 .......a 2 n
>0 | x| x 1 6、重要公式 = = x | x | −1 a
1 = n a
a = m an
n m
若 a ≥ 0,则 ± a 为 a 的平方根, 指数基本公式:
a ) (= a ) (=
m n n m
am ⋅ an = a m+n a m / a n = a m−n
a m⋅ n
3、 对数相关知识: 对数表示为 log a (a>0 且 a ≠ 1,b>0) ,
b
当 a=10 时,表示为 lgb 为常用对数; 当 a=e 时,表示为 lnb 为自然对数。 有关公式:Log (MN) =logM+logN
m log = log m − log n n
= log b am
n
n b log a m
log b 1 c 换底公式: log = = a a log c log b
S1 + S 2 ⇒ P则题目选C S1 + S 2 ≠> P则题目选E
MBA、MPAcc管理类考试数学备考规划.doc

题方法掌握不好。
二、强化阶段一般需要两个月左右,在复习中要注重公式应用,要以做题为主,充分利用历年试题,重视总结归纳解题思路、套路和经验。
数学考试不需背诵,也不要自由发挥,全部任务就是解题,而基本概念、公式、结论等也只有在反复练习中才会真正理解与巩固。
数学试题千变万化,其知识结构却基本相同,题型也相对固定,往往存在明显的解题套路。
三、冲刺阶段在考试前一个月左右,要注意查缺补漏,针对考纲看看哪些知识点没有复习到,尤其是考纲上新增的考点。
有了前两个阶段的复习,要进行综合性试题和应用题训练,考试会出现一些应用到多个知识点的综合性试题和应用型试题。
这类试题比较灵活,难度也要大一些。
在强化阶段复习期间,可不将它们作为重点,但也应逐步进行一些训练,积累解题思路,同时这也有利于对所学知识的消化吸收,彻底弄清楚有关知识的纵向与横向联系,转化为自己真正掌握的思维定势。
考前要提高做题速度,也即是要注重解题技巧,尤其是针对做选择题的技巧。
因为对于选择题,所要做的只是将正确选项挑出来即可,没必要一步步去计算求解。
综上所述,将以上复习阶段简要归纳如下:基础阶段:梳理考点公式,切记急于求成,对应看看数学高分指南的基础题目即可。
强化阶段:培养和建立数学思维,归纳和总结考试题型、考法,对知识点、题型、方法和技巧进行系统完整的归纳,对应看看数学高分指南的提高题目。
冲刺阶段:最好以周为单位,做做历年真题,把知识点理成一条条线,再有线织成一张合理、清晰、有效的知识网。
总之,数学并不可怕,基础也不是制约高分的瓶颈,只要方法对路,会提高很快。
所以在复习时,一定要充满信心。
遇到难题时千万不要气馁,只要踏踏实实复习,在经过一段时间的磨练后,会发现数学命题规律,找到高分捷径。
此外,考试心态很重要,无论题目容易还是难,不喜不悲,沉着冷静答题,不受外界干扰。
当答题状态不佳或遇到难题时,可以深呼吸或喝口水调整一下,再全力以赴答题。
试卷下发后,先做强项,先把该拿的分拿到。
最全MBA必备数学公式

最新最全版MBA 必备数学公式①基本公式:(1)222)2a b a ab b ±=±+( (2)33223)33a b a a b ab b ±=±+±( (3)22()()a b a b a b -+=-(4)3322()()a b a b a ab b ±=±+减加(5)2222)222a b c a b c ab ac bc ++=+++++( (6)2222222222()1[()()()]2a b c ab ac bc a b c ab ac bc a b a c b c +++++=+++++=+++++②指数相关知识:na a a a =⋅⋅⋅⋅(n 个a 相乘) 1nn aa-= nm n m a a = 若a ≥0,则a ±为a 的平方根, 指数基本公式: ③ 对数相关知识:对数表示为log b a (a>0且a ≠1,b>0) , 当a=10时,表示为lgb 为常用对数; 当a=e 时,表示为lnb 为自然对数。
有关公式:Log (MN) =logM+logN log log log m m n n=- log log nmb ba a n m= 换底公式:log 1log log log b b ca a ac b== 单调性:a>1 0<a<1 ④ 有关充分性判断:题型为给出题干P ,条件① 1S ② 2S若1S P ⇒,而2S ≠>P 则题目选A 若1S ≠>P,而2S P ⇒ 则题目选B 若1S P ⇒,而2S P ⇒ 则题目选D 若1S ≠>P,而2S ≠>P 但1212S S P C S S P E+⇒⎧⎨+≠>⎩则题目选则题目选形象表示:① √ ② × (A) ① × ② √ (B) ① × ② × ① ②联(合)立 √ (C) ① √ ② √ (D)① × ② × ① ②联(合)立 × (E) 特点:(1)肯定有答案,无“自检机会”、“准确性高” (2)准确度 解决方案:(1) 自下而上带入题干验证(至少运算两次) (2)自上而下,(关于范围的考题)法宝:特值法,注意只能证“伪”不能证“真” 图像法,尤其试用于几何问题第一章实数(1)自然数:自然数用N 表示(0,1,2-------)(2)0Z +-⎧⎪⎨⎪⎩正整数 Z 整数负整数 Z(3)质数和合数:质数:只有1和它本身两个约数的数叫质数,注意:1既不是质数也不是合数最小的合数为4,最小的质数为2;10以内质数:2、3、5、7;10以内合数4、6、8、9。
MBA数学考题分布及复习方法

【经典资料,WORD文档,可编辑修改】【经典考试资料,答案附后,看后必过,WORD文档,可修改】华宏解析2015MBA数学考题分布及复习方法为帮助考生更好进行2012年MBA考试复习,使广大考生都能够更加合理、有效的安排好自己的复习重点,制定更好的复习计划,上海华宏MBA培训中心周志恒老师为考生分析2012年MBA考题分布、复习方法及最新大纲解析。
一、管理类联考分析:1、综合能力(200分)(上午3个小时)数学(75分)+逻辑(60分)+作文(65分)题量 25题目+30题目+2题目(1300字)时间:70分钟+40分钟+60分钟=170分钟 10分钟涂卡2、英语(100分)二、最新大纲解析:(一)算术:(1)整数:整数及其运算、整除、公倍数、公约数、奇数与偶数、质数与合数(2)分数、小数、百分数(3)比与比例(4)数轴与绝对值(二)代数:那么08年MBA数学考什么?应该从哪几方面复习?11年MBA数学主要考查以下几个方面,一是考查对基础知识的理解,基础知识包括基本概念、基本理论、基本运算等,二是考查简单的分析综合能力,三是考查数学理论在实际生活中运用,四是考查考生解题速度和解题的准确程度。
MBA数学没有通常意义下的所谓“难题”。
所以考生在数学复习中一定要重视基础知识。
对概念和性质一定要理解其内涵和外延,对各个知识点一定要弄清楚其区别和联系。
同时要做一定数量的题目,要逐步提高运算的速度和准确度。
逐步培养解答MBA数学试题的解题技巧。
考试内容与题型?综合能力考试由条件充分性判断、问题求解,逻辑推理和写作四部分组成。
旨在综合测试考生的数学基础知识及运用能力、逻辑推理能力、综合归纳能力、分析论证能力和写作能力。
其中数学题型:(一)条件充分性判断题条件充分性判断题的测试的形式为单项选择,要求考生在给定的5个选择项中,选择一个作为答案。
(二)问题求解题问题求解题的测试形式为单项选择,要求考生在给定的5个选择项中,选择1个作为答案。
MBA数学各科知识点汇总

初等数学部分1:21%)(1%)%%%%4:1a b a b a b b a p a p p p p p a c a mc a cm b d b md b -≤+≤+≤≥≥−−−→+−−−→--⇔=⇔=•±±===±±原值a原值a 考点:若干个具有非负性质的数之和等于零时,则每个非负数必然为零。
:三角不等式,即 左边等号成立的条件:ab 0且a 右边等号成立的条件:ab 03:增长率p%现值( 下降率p%现值甲乙注意:甲比乙大,甲是乙的甲乙乙合分比定理:5:11,d c e a c e ad f b d f b a a m ab b n b b n ++==⇒=+++><+<>+a 等比定理:b 增减性:,a a+m 0<b11126:,,,,,,(......n nn n i X X n X X X x nX X ≥>===当为当且仅当 72(0),8a bab ab b an n +≥>::个正数的算术平均值与几何平均值相等时,则这个正数相等,且等于算术平均值222122129,,0,400,100(0),/0(0)/a b c R ac X aX bX c a X X X b a aX bX c a X X c a∈>⎧⎪∆-=⎨⎪<⎩++=≠+=-++=≠=211:判别式()两个不相等的实根 =b ,两个相等的实根无实根:根与系数的关系X ,是方程的两个根,则X 是方程的两根1221211:1X X X X X ++=1利用韦达定理可以求出关于两个根的对称轮换式的数值来:1 (1)X212122221221X X X X X X X +-+=21()1 (2)X ()0111111110;12n n n n n n n n n nk n k k n C a C a b L C ab C b k T C a n a n b n ----+=+++++=+−−−→n 逐渐减二项式定理:公式(a+b)所表示的通项公式:第项为项数:展开总共项指数:的指数:由; 各项a 与b 的指数之和为n 展开式的最大系数:当n :二项式展开式的特征4135132,222,n n n n n n n n n C C C C C -⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪+⎪⎪⎪⎪⎩+==++=n+1和项)2;即奇数项系数和等⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩系数和微积分部分212212)()()(),()X X X f X f X f X f X D ∈<≤≥111:单调性:设有函数y=f(x),x D,若对于D 中任意两点X ,(),都有f(X 或则称函数在上单调上升(或单调下降)。
MBA数学必备公式(打印版)

MBA联考数学基本概念和必备公式(一)初等数学部分一、绝对值1、非负性:即|a| ≥ 0,任何实数a 的绝对值非负。
归纳:所有非负性的变量(1) 正的偶数次方(根式) 0,,,,412142≥a a a a(2) 负的偶数次方(根式) 112424,,,,0a a a a---->(3) 指数函数 a x(a > 0且a ≠1)>0考点:若干个具有非负性质的数之和等于零时,则每个非负数必然为零。
2、三角不等式,即|a| - |b| ≤ |a + b| ≤ |a| + |b| 左边等号成立的条件:ab ≤ 0且|a| ≥ |b|右边等号成立的条件:ab ≥ 03、 要求会画绝对值图像 二、比和比例1、%(1%)ap a p −−−→+原值增长率现值%)1(%p a p a -−−→−现值下降率原值%%%%p p p p ⋅=⇔=-⇔乙甲,甲是乙的乙乙甲注意:甲比乙大 2、 合分比定理:d b ca m mdb mc ad c b a ±±=±±==1等比定理:.a c e a c e a b d f b d f b++==⇒=++ 3、增减性1>b a b a m b m a <++ (m>0) , 01a b << ba mb m a >++ (m>0) 4、 注意本部分的应用题 三、平均值1、当n x x x ,⋯⋯,,21为n 个正数时,它们的算术平均值不小于它们的几何平均值,即),1 0( ·2121n i x x x x nx x x i nn n ,=>+++⋯⋯≥⋯当且仅当时,等号成立=n x x x ⋯⋯==21。
2、 2ab b a ≥+⎪⎩⎪⎨⎧>>等号能成立另一端是常数,00b a 3、2(0)a bab ab b a≥>+ ,同号 4、n 个正数的算术平均值与几何平均值相等时,则这n 个正数相等,且等于算术平均值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MBA数学致胜十大法宝
文件排版存档编号:[UYTR-OUPT28-KBNTL98-UYNN208] MBA数学致胜十大法宝 ? 选择题根本原则:用最少的条件找出正确或错误的选项,若无法从正面直接找到正确答案,可以从反面排除错误答案,剩下的那个答案就是正确答案了。 ? 充分性判断:找等价转化,一般用逆向思维 问题求解:反命题,排除法,一般用代特值的方法 ? 法宝一:巧妙运用特值法 这种方法适合题目中的参数没有范围限制,提干中的命题对于有限范围的值都是成立的,所以我们可以取特定的值进行验证,一般通过这种方法去找题干中的反例来排除选项,属于排除法的范畴。具体又可以分为以下两种情况。 ? (1) (1)?????? 代入简单的特殊值进行排除
例 3122baba ( ) (2003年MBA考题第4题) (1)2a,1, 2b成等差数列 (2)a1,1,b1成等比数列 答案E 解析:对于条件(1)和条件(2),都可以设a=b=1,这时条件(1)和条件(2)都满足,但题目的结论并不满足。所以,这两个条件单独或者联立起来都不是充分的。 (2)一遇到选择变量范围的题目(一般在初数和微积分中常见),立即用特值进行排除。选取特值的优先顺序如下: 特值:X=0,1,-1,边界值a, b,其它具有分辨性的数值
29211)(29211)( 29)(29211)(211)() (10431xxExDxCxBxAxx或
解为: 不等式例
解: 选x = 0 7<10 OK! 从而排除C、E、A 再代入边界值! 1010 29 NOx 从而排除 D 于是答案不言自明,选B
的取值范围对一切实数都成立,则、不等式例kkkxkx011222( )
250)(kA 250)(kkB或
2150)(kC
2150)(kkD或
均不正确DCBAE,,,)( 解:代入k = 0 , 1>0, OK! 满足题干,故选E,只需5秒钟
? 例3.若a (b – c ) , b(c – a), c(a – b) 组成以q为公比的等比数列( ) (1)a≠b≠c且 (2) b≠c 解:代入a = 0 因为等比数列的任何一个元素都不可能为零 NO! 选(E) 例4.不等式5≤|x2-4|≤x+2的解为( ) A)x=-3 B)x=2 C)x=3 D)x∈[1,3] E)(-∞,-3)∪(3,+∞) 解: 代入 x=2 5≤0≤4 NO! 排除B、D 代入 x=3 5≤5≤5 OK! 排除A、E 此时只剩正确答案(C) 练习:方程09323axxx有三个不同实根,则a的取值为( ) (A)-2< a <25 (B)2< a <27 (C)0< a <25
(D)-25< a <2 (E)A,B,C,D都不正确 ? 法宝二:变限积分 ? 解题提示:一遇到变限积分的题目和求极值的题目,立即对等式两边进行求导。也就是说,当你遇到一道变限积分的题目的时候,不知道如何下手解题,你可以对它进行求导,然后观察看看能否出现待求的表达式。
)(·))(()(·))((')()()(''xxfxxfdttfxx求导公式 注意:若被积函数中若含有求导参量x,要先进行换元,转化成乘积的导数。 备注:2004年新大纲微积分部分新增了一个考点:变上限积分,望加以重视。 ?
1ln2)()2ln2)()121)ln1(2)(01= += = = +-,=-:例attfeatttfxxdttf
x
2ln21)ln1(211·21·)(xxxxf=++-=-解: 求导:
xxxxxfxxxfln2ln)(ln)(2=== xaxaxaxadttttttdttdtt1·lnlnln2222-==
2lnln22axaaxx---=
a=e 22222eee=-+- a=1 1/2
以上都不对 - - - =,则-=满足: 设连续函数例--)21)21))21))()2(02)(21021EeeDeCeBeAdxxfeedttfxxf
xxx xxexfexf--=-=-解: 2)(2·)22( 10110)1(212121-==----eedxexx
+- +- +- +- + 为,则-+=: 例xxExxDxCxxBxAxfxxdxxfx1))1())1(1)1)11))()(211)(3322223
10
22)1(1)1)(1(xxxf+=-解: )()(,ln)(0)()(4 为则上连续,且满足,-在: 例xfxxdueuxfxxf
u
=-,-=解: 令dtduuxtdtetfxxt--)(0 xxdtetfxedtetfxtxxtln)(0)(0==--- exxxdtetfxt·ln)(0=
xxxxfexxeexexfxxxxln1ln)(·ln·ln)(++=++=
0)()2)()()1)()()(.300TxdxxfxfTxfTdttfxFxf 的周期函数是周期为连续,则 设例
)( )()()()()()()( 000xFdttfdttfdttfdttfdttfdttfTxfTxTTxxTxxxTx 分析: xxTxTduufduuTfuTtdttf 00)()()(
xTxxduufdttfdttfTxF 00)()()()(
0000)()()()( xTxxdttfdttfdttfdttf TdttfxF 0)()( 若(1),(2)联合起来,=>F(x+T)=F(x) 故应选(C)
?
xxxxxdttftftEdttftftDdttftftCdttfBdttfAxf 数中为偶函数的是为连续函数,则下列函设例02000202 )]()([) )]()([) )]()([) )() )()
)( .4
分析:f(x)=1=>排除(A)、(B)、(E) f(x)=x=>排除(C) 故选(D) 1)0(')2( ,0)0(1 21))(1ln(lim .5200ffxdttfxx )(设连续函数,例
21 2))(1ln(lim00 ))(1ln(lim 0200xxfxdttfxxx 分析: 0(0)(0)]ln[1 ff 21)0('210)0()(lim212)(lim2)](1ln[lim 000fxfxfxxfxxf
xxx原式于是:
故应选(C)
22)a 11)a 1)()( 1ln111)( .60处可导在点则,,设例 xdttfxFxxxxaxfx
存在处连续在若分析:)1('1)( Fxxf 1)1( )1( 111lim)(lim11faaxaxfxx, 211aa
故应选(B)
xxfxxfxxxxdttfxx11)()2( )1ln()()1(
1)1ln(2]')( .7202 例
xxxxfxdttfxxxxdttfxxx1)1ln(2(x)·)(2x 1)1ln(2]')([ 220202+分析:
充分非充分 11(x) 2) )1ln((x) 1) xfxf
故应选(B)
均不正确、、、个个个个内的根有,在开区间,则方程〕上连续,且,在闭区间〔设例 DCBAEDCBAbadttfdttfxfbaxfxbxa) 3) 2) 1) 0) )( 0)(1)(0)()( .8
〕上连续,可导,在〔:分析badttfdttfxFxbxa )(1)()( 0 )()( 0 )(1 -)(1)( babaabdttfbFdttfdttfaF且 内有根,在)()(baxF 0)(1)()('xfxfxF又
内根必唯一,在)(0)(baxF
故应选(B)
?
练习.函数xuxfxxdueuxfxf 0 )(ln)(),()(为,则函数上连续,且满足在
(A)xxxxlnln (B)xxxxlnln (C)xxln1 (D)xxxlnln1 (E)xxxlnln1 ? ? 法宝三:抽象函数 ? 解题提示:一遇到抽象函数f(x)的题目,立即将其具体化。因为如果微积分的概念掌握的不够牢固,那么在做抽象函数的题目的时候很容易出错,所以我们可以找一个满足题干的具体函数进行判断选项的正误。 具体化的优先顺序:f(x)=x, x2,x3,x-1,, ?
都不对 有时,,则当,,轴对称,当二阶可导,关于: 已知例)0)(''0)(')0)(''0)(')0)(''0)(')0)(''0)('))(00)(''0)('0)(1ExfxfDxfxfCxfxfBxfxfAxxfxfxyxf
解:f(x)=x2 2)(''2)('= =xfxxf
无法确定 有,则,+ ,可导,若互为反函数,且均二阶与: 例)0)(''0)(')0)(''0)(')0)(''0)(')0)(''0)('))()0(0)(''0)(')()(2ExgxgDxgxgCxgxgBxgxgAxfxfxgxf
解:取f(x)=x1/3 g(x)=x3
xxgxxg6)(''03)('2= = ?
法宝四 定积分 ? 解题提示:一遇到被积函数表达式已给定的定积分,可以按照以下的优先顺序进行求解: (1)利用被积函数放缩 (2利用对称区间积分性质 (3)利用图形面积解题 放缩技巧:找与之最相近的(整)数,因为整数的积分值最容易判断。
y ? ? a b o x
