材料力学习题册答案-第9章-压杆稳定
第九章材料力学压杆稳定

映承载能力的强弱, Fcr越高,稳定性越好,承 载能力越强;
材料力学
中南大学土木建筑学院
14
(5)临界载荷Fcr与外部轴向压力的大小无关。
②弯曲挠曲线 w Asin kx Asin p x l
(1) wmax = A,数值不能确定,是由于采用了挠曲 线近似微分方程,若采用精确微分方程,可以 确定最大挠度值。
EIw″=-M
导出 欧拉公式
适用条件:材料服从胡克定律;小变形。
因此,应力超过材料的比例极限sp后,
欧拉公式不再成立。
欧拉公式的适用范围是 scr≤sp 。
s cr
p2 E
2
sp
p2 E
sp
p
材料力学
中南大学土木建筑学院
31
p
p2 E
sp
压杆 柔度
ml
i
p
大柔度杆细长杆
材料固有柔度值, 与实际压杆无关。
F= Fcr
材料力学
中南大学土木建筑学院
l
x
F
y
F
11
M =Fcrw
EIw〞=-M =-Fcrw
w Fcr w 0 记 k 2 Fcr; k2 w = 0
通解 w=Asinkx+Bcoskx
边界条件Ⅰ: x = 0,w = 0
B=0
w=Asinkx
材料力学
中南大学土木建筑学院
x
x
材料力学
中南大学土木建筑学院
39
二、稳定(折减)因数法
s
F A
[s w ]
s cr
nst
scr、nst与压杆柔度有关,[sw]是的 函数。
[sw]=j [s ]
第9章 压杆稳定 (材料力学)

µ l是各种支承条件下,细长压杆失稳时,挠曲线中相当于 是各种支承条件下,细长压杆失稳时 挠曲线中相当于 失稳时,
半波正弦曲线的一段长度 半波正弦曲线的一段长度. 长度.
(Buckling of Columns)
(2)横截面对某一形心主惯性轴的惯性矩 I 若杆端在各个方向的约束情况相同(如球形铰等),则 I 若杆端在各个方向的约束情况相同(如球形铰等),则 ), 应取最小的形心主惯性矩. 应取最小的形心主惯性矩. 取 Iy ,Iz 中小的一个计算临界力. 中小的一个计算临界力. 若杆端在各个方向的约束情况不同(如柱 若杆端在各个方向的约束情况不同( 形铰),应分别计算杆在不同方向失稳时的临 形铰),应分别计算杆在不同方向失稳时的临 ), 界压力. 为其相应中性轴的惯性矩. 界压力. I 为其相应中性轴的惯性矩. 即分别用 Iy ,Iz 计算出两个临界压力. 然 计算出两个临界压力. 后取小的一个作为压杆的临界压力. 后取小的一个作为压杆的临界压力. x y z
压杆 平衡状态 应力 平衡方程 极限承载能力 强度问题 直线平衡状态不变 达到限值 变形前的形状、尺寸 变形前的形状、 实验确定 稳定问题 平衡形式发生变化 小于限值 σ<σσ 变形后的形状、尺寸 变形后的形状、 理论分析计算
压杆什么时候发生稳定性问题,什么时候产生强度问题呢? 压杆什么时候发生稳定性问题,什么时候产生强度问题呢?
•两端简支压杆的挠曲轴 两端简支压杆的挠曲轴
y = Asin
πx
l
•压杆在临界状态时的平衡是一种有条件的随遇平衡 压杆在临界状态时的平衡是一种有条件的随遇平衡—— 压杆在临界状态时的平衡是一种有条件的随遇平衡 可有任意的微弯程度, 但轴线形状一定。 可有任意的微弯程度, 但轴线形状一定。 •临界载荷(欧拉临界载荷)与截面抗弯刚度成正比, 临界载荷(欧拉临界载荷)与截面抗弯刚度成正比, 临界载荷 与杆长的平方成反比。 与杆长的平方成反比。
材料力学答案- 压杆稳定
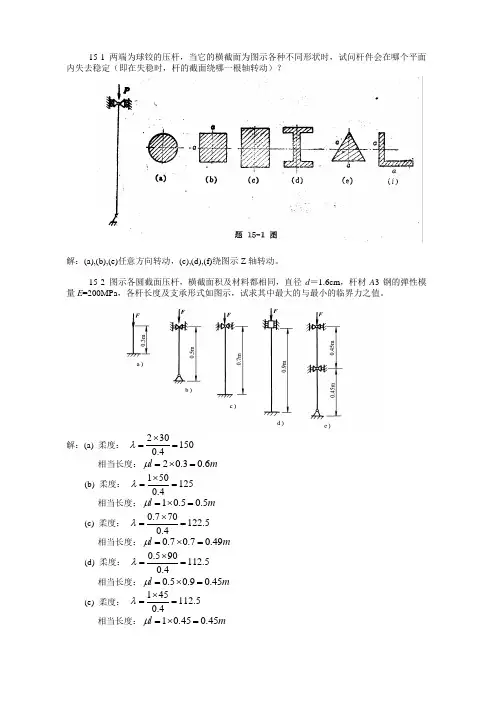
15-1 两端为球铰的压杆,当它的横截面为图示各种不同形状时,试问杆件会在哪个平面内失去稳定(即在失稳时,杆的截面绕哪一根轴转动)?解:(a),(b),(e)任意方向转动,(c),(d),(f)绕图示Z 轴转动。
15-2 图示各圆截面压杆,横截面积及材料都相同,直径d =1.6cm ,杆材A 3钢的弹性模量E =200MPa ,各杆长度及支承形式如图示,试求其中最大的与最小的临界力之值。
解:(a) 柔度: 2301500.4λ⨯== 相当长度:20.30.6l m μ=⨯=(b) 柔度: 1501250.4λ⨯== 相当长度:10.50.5l m μ=⨯=(c) 柔度: 0.770122.50.4λ⨯== 相当长度:0.70.70.49l m μ=⨯=(d) 柔度: 0.590112.50.4λ⨯== 相当长度:0.50.90.45l m μ=⨯=(e) 柔度: 145112.50.4λ⨯== 相当长度:10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出:各压杆的临界力可用欧拉公式计算。
即:()22cr EIF l πμ=各压杆的EJ 均相同,故相当长度最大的压杆(a)临界力最小,压杆(d)与(e)的临界力最大,分别为:()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ,s σ=274MPa ,E =200GPa ,直线公式λσ22.1338-=cr ,试计算该材料压杆的P λ及S λ值,并绘制1500≤≤λ范围内的临界应力总图。
解:92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆,其外径和内径分别为,12mm 和10mm ,杆长为383mm ,两端为铰支座,材料的E =210GPa ,P σ=288MPa ,试求此挺杆的临界力cr F 。
单辉祖材料力学-第九章 压杆稳定

i
I min A
47 .26 1.68cm 2 8.367
150 89.3 p 100 i 1.68
所以,应由经验公式求临界压力。 σcr=304-1.12λ=304-1.12*89.3=204(MPa)
2E p cr p cr 2 p
2E p
2E p (临界柔度) A3钢λ p=100,λ s=61.6 p
则1:大柔度杆(细长压杆)采用欧拉公式计算。 2 EI 2E p ( p ) Fcr cr 2 2 ( l ) 2:中柔度杆(中长压杆)采用经验公式计算。
2 [25.6 12.74 (1.52 a / 2)2 ]
即:
198 .3 25.6 12.74(1.52 a / 2) 2 时合理
a=4.32cm
28
2、求临界力:
L
i
0.7 6 Iz 2 A1
0.7 6 396 .6 10 2 12 .74 10 4
A1 12 .74 cm , z0 1.52 cm,
I z1 198 .3cm4 , I y1 25 .6cm4
两根槽钢图示组合之后, (z1) I 2 I 2 198.3 396.6cm4
Z Z1
I y 2[ I y1 A1 ( z0 a / 2) 2 ]
边界条件为: w
Fcr
w
m0
Fcr m0
14
m0 c , d 0, kL 2n F
为求最小临界力, “ n”应取除零以外的最小值,即取:
刘鸿文《材料力学》复习笔记和课后习题(含考研真题)详解(压杆稳定)【圣才出品】

所示。
表 9-1-2
3 / 63
圣才电子书 十万种考研考证电子书、题库视频学习平台
(2)关于欧拉公式的讨论 ①相当长度 μl 的物理意义 压杆失稳时,挠曲线上两拐点间的长度就是压杆的相当长度 μl,它是各种支承条件下, 细长压杆失稳时,挠曲线中相当于半波正弦曲线的一段长度。 ②横截面对某一形心主惯性轴的惯性矩 I 杆端在各个方向的约束情况相同(如球形铰等),则 I 应取最小的形心主惯性矩;杆端 在各个方向的约束情况不同(如柱形铰),应分别计算杆在不同方向失稳时的临界压力,I 为其相应中性轴的惯性矩。 三、欧拉公式的适用范围及临界应力总图 1.相关概念
图 9-1-1
选取坐标系如图 9-1-1 所示,距原点为 x 的任意截面的挠度为 w,则弯矩 M=-Fw。
根据压杆变形后的平衡状态,得到杆的挠曲线近似微分方程
d2w dx2
M EI
2 / 63
圣才电子书 十万种考研考证电子书、题库视频学习平台
通过对该方程的求解可得到使压杆保持微小弯曲平衡的最小压力,即两端铰支细长压杆 临界力为
π 2 EI Fcr l 2
上述计算公式称为两端铰支压杆的欧拉公式。
2.欧拉公式的普遍形式
Fcr
π 2 EI
l 2
式中,μl 为相当长度;μ 为长度因数,与压杆的约束情况有关;I 为横截面对某一形心
主惯性轴的惯性矩。
(1)各种支承情况下等截面细长压杆的长度因数及临界压力的欧拉公式,如表 9-1-2
对比项目 平衡状态
应力 平衡方程 极限承载能力
强度问题 直线平衡状态不变
达到限值 变形前的形状、尺寸
实验确定
稳定问题 平衡形式发生变化
可能小于限值 变形后的形状、尺寸
第九章压杆的稳定习题

第九章压杆的稳定习题第九章 压杆的稳定习题一、填空题1、对于大柔度杆,用 计算临界压力;对于中柔度杆,用 计算临界压力2、对于大柔度杆,用来计算临界压力的欧拉公式为 ;对于中柔度杆,用来计算临界压力的经验公式为 。
3、求临界应力的公式22cr Eλπσ=。
式中的λ称为压杆的 ,根据λ数值由大 到小, 把压杆具体分为 , 和 。
二、计算题1、如图有一截面为圆形的大柔度压杆,杆长2.5m ,截面直径为40mm 。
杆的一端固定,一端铰支,材料的弹性模量E =210G pa 。
试求杆的临界压力P cr 。
2、如图所示,某液压作动筒的活塞杆,长度l =1800mm ,直径d =60mm ,承受轴向载荷F =120kN,可认为两端铰支。
活塞杆材料的弹性模量E =210Gpa ,λp =100。
若规定稳定安全系数[n st ]=3,试对活塞杆的稳定性进行校核。
图图3、图示托架中杆AB的直径d=40mm,长度l=800mm,两端可视为铰支,材料是Q235钢。
材料的弹性模量E=210Gpa。
(1)试按杆AB的稳定条件求托架的临界压力F cr。
(2)若已知实际载荷F=70kN,稳定安全系数[n st]=2,问此托架是否安全。
(注:Q235钢,a=310Mpa b=1.14Mpa λp=100 λs=60)图4、如图一截面为12×20cm2的矩形木柱为大柔度杆,杆长L=4m,在最小刚度平面内弯曲时,长度系数μ=1,木材的弹性模量E=10Gpa,试求木柱的临界压力。
图5、如图一横截面为圆的大柔度杆,横截面直径d=16cm,杆长L=5m,材料的弹性模量E=210Gpa。
杆的两端铰支,长度系数μ=1。
试求杆的临界压力P cr。
图6、某型柴油机的挺杆为大柔度压杆,该挺杆长为l =257mm,圆形横截面的直径d =8mm 。
所用钢材的E =210 GPa 。
试求该挺杆的临界力。
(提示:挺杆的两端可简化为铰支座)7、某轧钢车间使用的螺旋推钢机的示意图如图所示。
材料力学 第九章 压杆的稳定
欧拉公式一般表达式
Fcr
EI l2
Fcr
EI (2l )2
Fcr
EI
l / 22
Fcr
EI (0.7l )2
Fcr
π EI
(l )2
1
2 1
2
0.7
l - 相当长度-相当的两 - 长度因数-代表支持方
端铰支细长压杆的长度
式对临界载荷的影响
§9-3 欧拉公式的适用范围 中小柔度杆的临界应力
临界状态特点-压杆可在任意微弯状态保持平衡
其他形式的稳定问题
F Fcr
§9-2 细长压杆的临界力
一、两端铰支压杆的临界力
求解思路 Fcr-使压杆在微弯条件下保持平衡的最小轴向压力 方法:使压杆微弯, 再求能 保持其平衡的最小轴向压力
临界力公式
微弯, 且 max p 时
d2w dx 2
M(x EI
(0 < < p )
a1, b1值与材料有关 适用于结构钢与低合金结构钢等
15
例题
例 9-1 硅钢活塞杆, d = 40 mm, E = 210 GPa, p= 100,
求Fcr
解:
2
i
I A
πd 4 64
4 πd
2
d 4
1.0
102
m
l
i
200
> p 大柔度杆
Fcr
π 2 EI
(l )2
cr=235 MPa-(0.00669 MPa) p=100
解:
FN
M A0, FN 30.9 kN
FN 30.9 kN
i
I A
(
D4 64
d
4
建筑力学第9章压杆稳定
• 为了说明压杆平衡状态的稳定性,我们取一根细长的直杆进行压缩试 验,如图9-1所示。
上一页 下一页 返回
第一节 压杆稳定的概念
• 压杆的平衡状态可以分为三种。图9-1(a)中,当压力P不太大时, 用一微小的横向力干扰它,压杆微弯,当横向力撤去后,压杆能自动 恢复原有的直线形状,这时压杆处于稳定的平衡状态。图9-1(b) 中,当压力P增大到某一特定值Pcr时,微小的横向干扰力撤去后, 压杆在微弯状态下维持新的平衡,这时压杆处于临界平衡状态,这个 特定值Pcr叫作临界力。图9-1(c)中,当压力P超过临界力Pcr 后,干扰力作用下的微弯会越来越大直至压杆弯断,此时压杆丧失了 稳定性。
• σcr=π2E/λ2≤σP
• ■四、中长杆的临界应力计算———经验公式
• 当压杆的柔度小于λP时,称为中长杆或中柔度杆。中长杆的临界应 力σcr大于材料的比例极限σP,此时欧拉公式不再适用。工程中对 这类压杆一般采用经验公式计算临界力或临界应力。常用的经验公式 有两种:直线公式和抛物线公式。
上一页
• Pcr=π2EI/(μl)2(9-1) • 式中 • E———材料的弹性模量; • I———压杆横截面的最小惯性矩; • EI———压杆的抗弯刚度;
下一页 返回
第二节 临界力和临界应力
• l———压杆的实际长度; • μ———压杆的长度系数,见表9-1; • μl———压杆的计算长度。 • ■二、临界应力 • 在临界力作用下,细长压杆横截面上的平均压应力叫作压杆的临界应
• 从前面几节内容可知,影响压杆稳定性的主要因素有:压杆的截面形 状、长度、两端的约束条件以及材料的性质等。要提高压杆的稳定性 ,可采取以下四个措施。
上海理工材料力学习题解答(压杆稳定)
. 某型柴油机的挺杆长为l =257 mm ,圆形横截面的直径d =8 mm 。
所用钢材的E =210 GPa ,σp =240 MPa 。
挺杆所受的最大压力P = kN 。
规定n st =2~5。
试校核挺杆的稳定性。
解:(1) 求挺杆的柔度挺杆的横截面为圆形,两端可简化为铰支座,μ=1,i =d /4 计算柔度91614410.257128.50.0082101092.924010P ll id Eμμλλππσλλ⨯⨯====⨯===⨯∴挺杆是细长压杆,使用欧拉公式计算临界压力 (2) 校核挺杆的稳定性()()4410422910220.008 2.0110 646421010 2.0110 6.3110.257cr d I m EI P KNl ππππμ--⨯===⨯⨯⨯⨯⨯===⨯工作安全系数max 6.313.591.76cr P n P === 所以挺杆满足稳定性要求。
. 图示蒸汽机活塞杆AB 所受压力为P =120 kN ,l =1.8 m ,截面为圆形d =75 mm 。
材料为Q275钢,E =210 GPa ,s =240 MP 。
规定n st =8。
试校核活塞杆的稳定性。
解:(1) 求柔度极限值9162101092.924010PEλπσ⨯===⨯ 压杆的柔度11 1.8960.075/4liμλλ⨯====压杆是大柔度杆 (2) 压杆的临界压力()()44642296220.075 1.55310 646421010 1.55310993 1 1.8cr d I m EI P kNl ππππμ--⨯===⨯⨯⨯⨯⨯===⨯BAPPlp(3) 压杆的稳定性9938.275120cr st P n n P ===压杆稳定。
10.6. 三根圆截面压杆,直径均为d =160 mm 材料为Q235钢,E =200 GPa ,p =200 MPa ,s =240 MPa 。
三杆均为两端铰支,长度分别为l 1、l 2和l 3,且l 1=2l 2=4l 3=5m 。
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-压杆稳定(圣才出品)
2.压杆分类(见表 9-1-4) 表 9-1-4 压杆分类
3.折减弹性模量理论(见表 9-1-5)
3 / 40
圣才电子书 十万种考研考证电子书、题库视频学习平台
表 9-1-5 折减弹性模量理论
4.压杆的临界应力总图 压杆临界应力 σcr 与柔度 λ 的关系曲线称为压杆的临界应力总图。当压杆的柔度很小时, 以屈服界限 σs 作为临界应力。临界应力总图的绘制如图 9-1-1 所示。
图 9-1-1 临界应力总图
4 / 40
圣才电子书 十万种考研考证电子书、题库视频学习平台
四、实际压杆的稳定因数 实际压杆的稳定许用应力与稳定因数的确定见表 9-1-6。
表 9-1-6 稳定许用应力与稳定因数
五、压杆的稳定计算·压杆的合理截面 1.压杆的稳定计算(见表 9-1-7)
6 / 40
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 9-2-1 令 k2=Fcr/EI,可得:w″+k2w=k2Me/Fcr。则该微分方程的通解:w=Asinkx+ Bcoskx+Me/Fcr。 其一阶导为:w′=Akcoskx-Bksinkx,由边界条件 x=0,w=0,w′=0 可确定积分 常数:A=0,B=-Me/Fcr。故方程的通解:w=-Mecoskx/Fcr+Me/Fcr。 又由 x=l,w=0 得:-Mecoskx/Fcr+Me/Fcr=0,即 coskl=1,kl=2nπ(n=1, 2,3…),取其最小解 kl=2π,则压杆的临界力 Fcr 的欧拉公式 Fcr=4π2EI/l2=π2EI/ (0.5l)2。 9-2 长 5m 的 10 号工字钢,在温度为 0℃时安装在两个固定支座之间,这时杆不受 力。已知钢的线膨胀系数 αl=125×10-7(℃)-1,E=210GPa。试问当温度升高至多少 度时,杆将丧失稳定? 解:设温度升高 Δt 时,杆件失稳。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 九 章 压 杆 稳 定 一、选择题 1、一理想均匀直杆受轴向压力P=PQ时处于直线平衡状态。在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( A )。 A、弯曲变形消失,恢复直线形状; B、弯曲变形减少,不能恢复直线形状; C、微弯状态不变; D、弯曲变形继续增大。 2、一细长压杆当轴向力P=PQ时发生失稳而处于微弯平衡状态,此时若解除压力P,则压杆的微弯变形( C ) A、完全消失 B、有所缓和 C、保持不变 D、继续增大 3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( D )来判断的。 A、长度 B、横截面尺寸 C、临界应力 D、柔度 4、压杆的柔度集中地反映了压杆的( A )对临界应力的影响。 A、长度,约束条件,截面尺寸和形状; B、材料,长度和约束条件; C、材料,约束条件,截面尺寸和形状; D、材料,长度,截面尺寸和形状; 5、图示四根压杆的材料与横截面均相同, 试判断哪一根最容易失稳。答案:( a ) 6、两端铰支的圆截面压杆,长1m,直径50mm。其柔度为 ( C ) A.60; B.66.7; C.80; D.50 7、在横截面积等其它条件均相同的条件下,压杆采用图( D )所示截面形状,其稳定性最好。
8、细长压杆的( A ),则其临界应力σ越大。 A、弹性模量E越大或柔度λ越小; B、弹性模量E越大或柔度λ越大; C、弹性模量E越小或柔度λ越大; D、弹性模量E越小或柔度λ越小; 9、欧拉公式适用的条件是,压杆的柔度( C )
A、λ≤ PE B、λ≤sE
C、λ≥ PE D、λ≥sE 10、在材料相同的条件下,随着柔度的增大( C ) A、细长杆的临界应力是减小的,中长杆不是; B、中长杆的临界应力是减小的,细长杆不是; C、细长杆和中长杆的临界应力均是减小的; D、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( A ) A. 临界应力一定相等,临界压力不一定相等; B. 临界应力不一定相等,临界压力一定相等; C. 临界应力和临界压力一定相等; D. 临界应力和临界压力不一定相等; 12、在下列有关压杆临界应力σe的结论中,( D )是正确的。 A、细长杆的σe值与杆的材料无关;B、中长杆的σe值与杆的柔度无关; C、中长杆的σe值与杆的材料无关;D、粗短杆的σe值与杆的柔度无关; 13、细长杆承受轴向压力P的作用,其临界压力与( C )无关。 A、杆的材质 B、杆的长度 C、杆承受压力的大小 D、杆的横截面形状和尺寸 二、计算题 1、 有一长l=300 mm,截面宽b=6 mm、高h=10 mm的压杆。两端铰接,压杆材料为Q235钢,E=200 GPa,试计算压杆的临界应力和临界力。 解:(1)求惯性半径i 对于矩形截面,如果失稳必在刚度较小的平面内产生,故应求最小惯性半径
mm 732.1126121123minminbbhhbAIi (2)求柔度λ λ=μl/i,μ=1, 故 λ=1×300/1.732=519>λp=100 (3)用欧拉公式计算临界应力
MPa 8.652.1731020ππ24222cr
E
(4)计算临界力 Fcr=σcr×A=65.8×6×10=3948 N=3.95 kN
2、一根两端铰支钢杆,所受最大压力KNP8.47。其直径mmd45,长度mml703。
钢材的E=210GPa,p=280MPa,2.432。计算临界压力的公式有:(a) 欧拉公式;(b)
直线公式cr=461-2.568(MPa)。 试 (1)判断此压杆的类型; (2)求此杆的临界压力; 解:(1) 1 8621PE 5.624dlil 由于12,是中柔度杆。 (2)cr =461-2.568MPa KNAPcrcr478
3、活塞杆(可看成是一端固定、一端自由),用硅钢制成,其直径d=40mm,外伸部分的最大长度l=1m,弹性模量E=210Gpa, 1001。 试(1)判断此压杆的类型;(2)确定活塞杆的临界载荷。
解:看成是一端固定、一端自由。此时2
,而 ,所以, 。
故属于大柔度杆- 用大柔度杆临界应力公式计算。
4、托架如图所示,在横杆端点D处受到P=30kN的力作用。已知斜撑杆AB两端柱形约束(柱形较销钉垂直于托架平面),为空心圆截面,外径D=50mm、内径d=36mm,材料为A3钢,E=210GPa、p=200MPa、s=235MPa、a=304MPa、b=1.12MPa。若稳定安全系数nw=2,试校
杆AB的稳定性。
1.5m0.5mPCABD第第第第30o
解 应用平衡条件可有 0AM,107N5.05.11040230sin5.123PNBDkN
2cm837.32A,4cm144yI,cm04.2yi,4cm1910xI
cm64.7xi A3钢的 4.99P
,1.57S
压杆BA的柔度
Sxxil7.220764.0
30cos
5.11
Pyyil9.820209.0
30cos
5.11
因x、y均小于P,所以应当用经验公式计算临界载荷 N109.8212.130400329.0)(6ycrcrbaAAP
695kN
压杆的工作安全系数
55.6107695stnn BA压杆的工作安全系数小于规定的稳定安全系数,故可以安全工作。
5、 如图所示的结构中,梁AB为No.14普通热轧工字钢,CD为圆截面直杆,其直径为d=20mm,二者材料均为Q235钢。结构受力如图所示,A、C、D三处均为球铰约束。若已知pF=25kN,
1l=1.25m,2l=0.55m,s=235MPa。强度安全因数sn=1.45,稳定安全因数st[]n=1.8。试校
核此结构是否安全。
解:在给定的结构中共有两个构件:梁AB,承受拉伸与弯曲的组合作用,属于强度问题;杆CD,承受压缩荷载,属稳定问题。现分别校核如下。 (1) 大梁AB的强度校核。大梁AB在截面C处的弯矩最大,该处横截面为危险截面,其上的弯矩和轴力分别为 3maxp1(sin30)(25100.5)1.25MFl° 315.6310(Nm)15.63(kNm) 3Npcos302510cos30FF°° 321.6510(N)21.65(kN) 由型钢表查得14号普通热轧工字钢的
333222102cm10210mm21.5cm21.510mmzWA 由此得到 33maxNmax392415.631021.6510102101021.51010zMFWA
6163.210(Pa)163.2(MPa) Q235钢的许用应力为
ss235[]162(MPa)1.45n
max略大于[],但max([])100%[]0.7%5%,工程上仍认为是安全的。 (2) 校核压杆CD的稳定性。由平衡方程求得压杆CD的轴向压力为
Npp2sin3025(kN)CDFFF°
因为是圆截面杆,故惯性半径为 5(mm)4IdiA 又因为两端为球铰约束1.0,所以 p31.00.55110101510li 这表明,压杆CD为细长杆,故需采用式(9-7)计算其临界应力,有 222932Pcrcr2220610(2010)41104EdFA
352.810(N)52.8(kN) 于是,压杆的工作安全因数为 crPcrwstwN52.82.11[]1.825CDFnnF
这一结果说明,压杆的稳定性是安全的。 上述两项计算结果表明,整个结构的强度和稳定性都是安全的。 6、一强度等级为TC13的圆松木,长6m,中径为300mm,其强度许用应力为10MPa。现将圆木用来当作起重机用的扒杆,试计算圆木所能承受的许可压力值。
解:在图示平面内,若扒杆在轴向压力的作用下失稳,则杆的轴线将弯成半个正弦波,长度系数可取为1。于是,其柔度为 168010.34li 根据80,求得木压杆的稳定因数为 22110.39880116565
从而可得圆木所能承受的许可压力为 62[][]0.398(1010)(0.3)281.34FA(kN) 如果扒杆的上端在垂直于纸面的方向并无任何约束,则杆在垂直于纸面的平面内失稳时,只能视为下端固定而上端自由,即2。于是有
2616010.34li
求得 22280028000.109160
62[][]0.109(1010)(0.3)774FA(kN) 显然,圆木作为扒杆使用时,所能承受的许可压力应为77 kN,而不是281.3 kN。
7、 如图所示,一端固定另一端自由的细长压杆,其杆长l = 2m,截面形状为矩形,b = 20 mm、h = 45 mm,材料的弹性模量E = 200GPa 。试计算该压杆的临界力。若把截面改为b = h =30 mm,而保持长度不变,则该压杆的临界力又为多大? 解:(一)、当b=20mm、h=45mm时 (1)计算压杆的柔度 22000692.82012li>123c(所以是大柔度杆,可应用
欧拉公式) (2)计算截面的惯性矩 由前述可知,该压杆必在xy平面内失稳,故计算惯性矩
4433100.312204512mmhbIy
(3)计算临界力 μ = 2,因此临界力为 kNNlEIFcr70.337012210310200289222
