现代控制-状态反馈控制系统的设计与实现
现代控制理论基础实验报告

紫金学院计算机系实验报告现代控制理论基础实验报告专业:年级:姓名:学号:提交日期:实验一 系统能控性与能观性分析1、实验目的:1.通过本实验加深对系统状态的能控性和能观性的理解;2.验证实验结果所得系统能控能观的条件与由它们的判据求得的结果完全一致。
2、实验内容:1.线性系统能控性实验;2. 线性系统能观性实验。
3、实验原理:系统的能控性是指输入信号u 对各状态变量x 的控制能力。
如果对于系统任意的初始状态,可以找到一个容许的输入量,在有限的时间内把系统所有的状态变量转移到状态空间的坐标原点。
则称系统是能控的。
系统的能观性是指由系统的输出量确定系统所有初始状态的能力。
如果在有限的时间内,根据系统的输出能唯一地确定系统的初始状态,则称系统能观。
对于图10-1所示的电路系统,设i L 和u c 分别为系统的两个状态变量,如果电桥中4321R R R R ≠,则输入电压u 能控制i L 和u c 状态变量的变化,此时,状态是能控的;状态变量i L 与u c 有耦合关系,输出u c 中含有i L 的信息,因此对u c 的检测能确定i L 。
即系统能观的。
反之,当4321R R =R R 时,电桥中的c 点和d 点的电位始终相等, u c 不受输入u 的控制,u 只能改变i L 的大小,故系统不能控;由于输出u c 和状态变量i L 没有耦合关系,故u c 的检测不能确定i L ,即系统不能观。
1.1 当4321R RR R ≠时u L u i R R R R C R R R R R R R R L R R R R R R C R R R R R R R R L u i C L C L ⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⨯⎪⎪⎪⎪⎪⎭⎫+++-+-+-⎝⎛+-+-+++-=⎪⎪⎭⎫ ⎝⎛01)11(1)(1)(1)(143214343212143421243432121 (10-1)y=u c =[01]⎪⎪⎪⎭⎫⎝⎛c L u i (10-2)由上式可简写为bu Ax x+= cx y =式中⎪⎪⎭⎫ ⎝⎛=C L u i x ⎪⎪⎪⎪⎪⎭⎫+++-+-+-⎝⎛+-+-+++-=)11(1)(1)(1)(143214343212143421243432121R R R R C R R R R R R R R L R R R R R R C R R R R R R R R L A⎪⎪⎪⎭⎫⎝⎛=01L b 1] [0=c由系统能控能观性判据得][Ab brank =2 2=⎥⎦⎤⎢⎣⎡cA c rank故系统既能控又能观。
现代控制理论_第5章_状态反馈与状态观测器

y 10 0 0 x
状态反馈阵
k k k k 1 2 0
状态反馈系统特征方程:
2 1 j 1 j 3 4 2 6 4 0
、x 、x 根据两特征方程同次项系数相等的条件,可求出由x1 2 3 引出的反馈系数为:
x x 0 1 0 10 1 1 0 0 -2 x 10 u x 2 2 0 1 3 0 x x 3 3
二、用状态反馈使闭环极点配置在任意位置上的充要条 件是:受控对象能控 证明: 若式(5-1)所示对象可控,定可通过变换化为能 控标准形,有
0 0 A 0 a 0
1 0 0
0 0 0
a a 1 2
0 1 a n1
G C sI A 1
1 b
10
11 q1
1,n1
1 sn a sn1 a s a n1 1 0 q0
q,n1
I A bk n a
k n1 a k 2 a k 1 n1 2 1 1 n 2 1 a k 0 0 0 (5-9)
, k ,可使特征方程的 显见,任意选择k 阵的 n 个元素 k0, n1 个系数满足规定要求,能保证特征值(即闭环极点)任意配 置。
课件-现代控制理论-刘豹第三版-第5章

能控性与能观性的判别方法
能观性判别方法
能控性判别方法
表示系统是否可以通过输入控制实现任意状态转移。若系统完全能控,则可以通过设计合适的控制器实现任意状态轨迹的跟踪或镇定;若部分能控或不能控,则存在状态无法被有效控制的风险。
能控性的物理意义
表示系统状态是否可以通过输出完全反映出来。若系统完全能观,则可以通过观测输出信号来准确估计系统状态;若部分能观或不能观,则存在状态无法被准确观测的风险,进而影响控制性能的实现。
控制系统稳定性分析是控制理论的核心内容之一,对于确保控制系统的正常运行具有重要意义。
章节内容结构
稳定性概念及定义
介绍稳定性的基本概念和定义,包括Lyapunov稳定性和BIBO稳定性等。
线性系统稳定性判据
详细阐述线性系统稳定性的判据,如Routh-Hurwitz判据、Nyquist判据和Bode图等。
图解法
状态转移矩阵的计算方法
1
2
3
状态转移矩阵反映了系统在时间间隔内从初始状态到最终状态的动态变化过程。
描述系统状态的动态变化过程
若系统稳定,则状态转移矩阵将逐渐趋于零,表示系统状态将逐渐趋于稳定。
反映系统稳定性
状态转移矩阵是进行系统分析和设计的重要工具,可用于研究系统的稳定性、能控性、能观性等性质。
非线性系统稳定性分析
介绍非线性系统稳定性分析方法,如相平面法、Lyapunov直接法等。
熟练掌握线性系统稳定性的判据和分析方法,能够应用所学知识分析和设计线性控制系统。
了解非线性系统稳定性分析方法的基本原理和应用范围,能够运用所学知识分析和设计简单的非线性控制系统。
掌握稳定性的基本概念和定义,理解不同稳定性定义之间的联系与区别。
现代控制理论基础 第7章 状态空间分析法在工程中的应用

h2
特征多项式
1 0
0 1
1
w
0
u
h02 h1 h0h1 h2
y
11 0 1 h0h2 11h1
h0
x1
w
h1
y
h2
I (A11 hA21) 3 h02 (11 h1) (11h0 h2 )
期望极点-3, -2+j, -2-j;期望特征方程
g0 9, g1 42, g2 148, g3 492
状态反馈
12
五、降维观测器设计
由于小车位移z可测,无需估计,可用降维观测器进行设计。重新排列系统状 态变量次序,把需由降维观测器估计的变量与可观测的变量分开,则状态方程 和输出方程为
d dt
•
z
•
--z--
0 1 0 0
第七章 状态空间分析法在工程中的应用
第一节 单倒置摆系统的状态空间设计 第二节 大型桥式吊车行车系统的状态空间设计 第三节 液压伺服电机最优控制系统
1
线性控制理论在工程设计中应用最广泛的是状态空 间综合方法,也就是状态反馈与状态观测器的相关理论 与方法。本章通过三个工程实例予以说明状态空间分析 方法的具体应用。
3
若不给小车施加控制力,是一个不稳定系统。 控制的目的是,当倒置摆无论出现向左或向右倾倒时,通过控制直
流电动机使小车在水平方向运动,将倒置摆保持在垂直位置上。
4
一、倒置摆的状态空间描述
根据牛顿定律
M d 2z m d 2 (z l sin ) u
dt 2
dt 2
由于绕摆轴旋转运动的惯性力矩应与重力矩平衡,因而有
(6-3) (6-4)
联立求解
..
现代控制理论

现代控制理论1.举出几个你在实践中遇到的开环控制系统和闭环控制系统的例子,说明什么工作原理并画出方块图。
●开环控制系统:如果系统的输出端和输入端之间不存在反馈回路,输出量对系统的控制作用没有影响,这样的系统成为开环控制系统。
如:原始的数控机床的进给系统就是开环控制系统。
指令输入计算机控制系统之中,带动步进电机运动,是工作台移动,产生位移输出。
在日常生活中,许多控制系统都可以理解成开环控制系统,如电风扇的转速是由档位决定的,不能根据环境温度自动调节。
●闭环控制系统:反馈控制系统也叫闭环控制系统,输出量对控制作用有直接影响。
如:自动调温空调,当环境温度高于设定温度时,空调制冷系统自动开启,调定室温到设定值。
自动电热水壶工作原理:分析:加热:瓶内注满水,插上电源,超温保险器、主加热器、保温加热器构成回路,加热指示灯亮。
由于温控器并联于保温加热器和保温指示灯两端,因而保温加热器不发热保温指示灯也不亮。
接通电源后主加热器发热升温,当水温达到沸腾温度时,超温保险器自动跳开,加热指示灯熄灭,保温:一旦测温装置获得的水温低于设定的温度,保温指示灯亮,此时主加热器与保温加热器串联,而主加热器的电阻远比保温加热器小,所以保温加热器发热,进行保温。
2.试分析反馈控制系统中反馈的性质和作用。
基于反馈原理建立的自动控制系统。
所谓反馈原理,就是根据系统输出变化的信息来进行控制,即通过比较系统行为(输出)与期望行为之间的偏差,并消除偏差以获得预期的系统性能。
在反馈控制系统中,不管出于什么原因(外部扰动或系统内部变化),只要被控制量偏离规定值,就会产生相应的控制作用去消除偏差。
因此,它具有抑制干扰的能力,对元件特性变化不敏感,并能改善系统的响应特性。
但反馈回路的引入增加了系统的复杂性,而且增益选择不当时会引起系统的不稳定。
为提高控制精度,在扰动变量可以测量时,也常同时采用按扰动的控制(即前馈控制)作为反馈控制的补充而构成复合控制系统。
现代控制理论ppt课件

5.2 极点配置
设状态反馈系统希望的极点为 s1, s2, , sn
其特征多项式为
n
Δ*K (s) (s si ) sn an*1sn1 a1*s a0* i 1
选择 k使i 同次幂系数相同。有
K a0* a0 a1* a1 an*1 an1
而状态反馈矩阵 K KP k0 k1 kn1 9
βn-1sn1 βn-2sn2 β1s sn an-1sn1 a1s a0
β0
(s) (s)
引入状态反馈 u V Kx V KP1x V Kx
令
K KP 1 k0 k1 kn1
其中 k0 , k1, , kn1为待定常数
7
5.2 极点配置
0 1
0 0
5
5.2 极点配置
证明:充分性
线性定常系统
x Ax Bu
y
Cx
经过线性变换 x P1x ,可以使系统具有能控标准形。
0 1 0 0
x
0
0
1
0
0
x
u
0
0 0
1
a0 a1 an1
0 1
y β0 β1 βn1 x
6
5.2 极点配置
系统传递函数:g(s) C[sI A]1b C [sI A]1b
0 0 1 P 0 1 12
16
1 18 144
5.2 极点配置
0 0 1
k kP 4 66 140 1 12
1 18 144
14 186 1220
17
5.2 极点配置
方法二:
k k1 k2 k3
s k1 k2
k3
a*
(
s)
现代控制理论课后答案(俞立)第五章
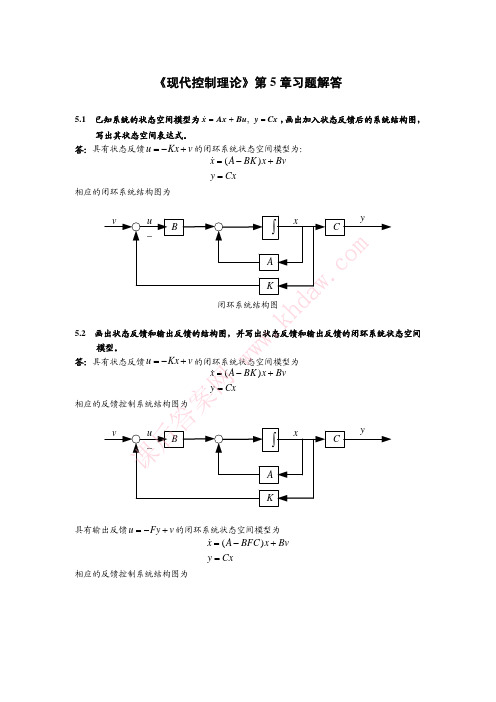
《现代控制理论》第5章习题解答5.1 已知系统的状态空间模型为Cx y Bu Ax x =+=, ,画出加入状态反馈后的系统结构图,写出其状态空间表达式。
答:具有状态反馈的闭环系统状态空间模型为:u Kx =−+v ()xA BK x Bv y Cx=−+=相应的闭环系统结构图为闭环系统结构图5.2画出状态反馈和输出反馈的结构图,并写出状态反馈和输出反馈的闭环系统状态空间模型。
答:具有状态反馈的闭环系统状态空间模型为u Kx =−+v ()xA BK x Bv y Cx=−+=相应的反馈控制系统结构图为具有输出反馈的闭环系统状态空间模型为u Fy =−+v ()x A BFC x Bv y Cx=−+=相应的反馈控制系统结构图为后案网 ww w.kh d5.3 状态反馈对系统的能控性和能观性有什么影响?输出反馈对系统能控性和能观性的影响如何?答:状态反馈不改变系统的能控性,但不一定能保持系统的能观性。
输出反馈不改变系统的能控性和能观性。
5.4 通过检验能控性矩阵是否满秩的方法证明定理5.1.1。
答:加入状态反馈后得到闭环系统K S ,其状态空间模型为()x A BK x Bv y Cx=−+=开环系统的能控性矩阵为0S 1[,][]n c A B BAB A B −Γ="闭环系统K S 的能控性矩阵为 1[(),][()()]n cK A BK B B A BK B A BK B −Γ−=−−"由于222()()()()(A BK B AB BKBA BKB A ABK BKA BKBK B)A B AB KB B KAB KBKB −=−−=−−+=−−−#以此类推,总可以写成的线性组合。
因此,存在一个适当非奇异的矩阵U ,使得()m A BK B −1,,,m m A B A B AB B −[(),][,]cK c A BK B A B U Γ−=Γ由此可得:若rank([,])c A B n Γ=,即有个线性无关的列向量,则n [(),]cK A BK B Γ−也有个线性无关的列向量,故n rank([(),])cK A BK B n Γ−=5.5 状态反馈和输出反馈各有什么优缺点。
状态反馈控制

本科毕业论文(设计)题目状态反馈控制学院计算机与信息科学学院专业自动化(控制方向)年级2009级学号222009321042049 姓名王昌洪指导老师何强成绩2013 年4 月18 日状态反馈控制王昌洪西南大学计算机与信息科学学院,重庆400715摘要:现代控制理论的特色为状态反馈控制,状态反馈控制经过近几十年的发展演变,在现实控制系统中应用越来越是广泛,由于系统的内部特性可以由状态变量全面的反应出来,因而相对于输出反馈控制,状态反馈更加的有利于改善系统的控制性能。
但是,在实际的系统中,状态变量由于其难于直接测量,所以进行状态反馈总是很难实现。
本论文将论述状态反馈基本原理,并通过举例说明状态反馈控制的优越性,同时将对状态反馈控制进行Matlab仿真,使系统满足提出的设计要求。
关键词:状态反馈;极点配置;Matlab仿真;时域指标State Feedback ControlWang changhongSouthwest university school of computer and information science, chongqing, 400715Abstract:Modern control theory, the characteristics for the state feedback control, state feedback control through decades of development and evolution, in the real control system is applied more and more widely, because the internal characteristics of the system can be fully reflected by the state variables,So relative to the output feedback control, state feedback are more favorable to improve the control performance. However, in practical systems, the state variable because of its difficult to measure directly, so the state feedback is always difficult to achieve.This paper will describe the state feedback principle, and illustrates the superiority of the state feedback control, at the same time, the state feedback control for Matlab simulation, the system meets the requirements of the design.Key words:State feedback;Pole assignment;Matlab simulation;Time domain index目录1 引言 (1)2 状态反馈控制原理 (2)3 状态反馈矩阵可控性和可观性 (2)3.1 状态反馈系统的可控性 (2)3.2状态反馈系统的可观性 (3)4 极点配置问题 (4)5 极点配置 (5)6 状态反馈控制实例 (6)7 加入干扰信号后的状态反馈系统 (12)7.1 系统输入端产生干扰信号 (12)7.2 系统中产生干扰信号(1) (12)7.3 系统中产生干扰信号(2) (13)8 分析与总结 (15)参考文献: (16)1 引言随着状态观测器理论与状态估计方法的发展,卡尔曼-布什滤波方法的出现,以及计算机仿真技术的越来越成熟,状态反馈控制方法应用越来越广泛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制工程学院课程实验报告:
现代控制原理课程实验报告
实验题目:状态反馈控制系统的设计与实现
一、实验目的及内容
实验目的:
1.掌握极点配置定理及状态反馈控制系统的设计方法;
2.比较输出反馈与状态反馈的优缺点
3.训练Matlab程序设计能力
实验内容:
1.针对一个二阶系统,分别设计输出反馈和状态反馈控制器;
2.分别测出两种情况下系统的阶跃响应;
3.对实验结果进行对比分析。
二、实验设备
装有Matlab7.1版本的PC机一台
三、实验原理
1.闭环系统的动态性能与系统的特征根密切相关,在状态空间的分析中可利用状态反馈来配置系统的闭环极点。
这种校正手段能提供更多的校正信息,在形成最优控制率、抑制或消除扰动影响、实现系统解耦等方面获得广泛应用。
2.为了实现状态反馈,需要状态变量的测量值,而在工程中,并不是状态变量都能
测量到,而一般只有输出可测,因此希望利用系统的输入输出量构成对系统状态变量的估计。
解决的方法是用计算机构成一个与实际系统具有同样动态方程的模拟系统,用模拟系统的状态向量作为系统状态向量的估值。
状态观测器的状态和原系统的状态之间存在着误差,而引起误差的原因之一是无法使状态观测器的初态等于原系统的初态。
引进输出误差的反馈是为了使状态估计误差尽可能快地衰减到零。
3.若系统是可控可观的,则可按极点配置的需要选择反馈增益阵k,然后按观测器的动态要求选择H,H 的选择并不影响配置好的闭环传递函数的极点。
因此系统的极点配置和观测器的设计可分开进行,这个原理称为分离定理。
4.由于引入反馈,系统状态的系数矩阵发生了变化,对系统的可控性、可观测性、稳定性、响应特性等均有影响。
状态反馈的引入不改变系统的可控性,但可能改变系统的可观测性。
输出至状态微分反馈的引入不改变系统的可观测性,但可能改变系统的可控性。
状态反馈和输出反馈都能影响系统的稳定性。
加入反馈,使得通过反馈构成的闭环系统成为稳定系统,并且都能够改变闭环系统的极点位置。
四、实验步骤
在实验中,我首先随意假设了一个传递函数G(s)=2S+1/S2-3S-1,对传递函数进行Matlab 语言编程,其编程语言如下
%%本程序用于求解形如Y(s)/U(s)=num/den闭环传递函数%%
%% 极点配置问题,包括状态反馈阵<K>和输出反馈阵<H> %%
%%如:Y(s)/U(s) = 2s+1/ s^2 - 3s - 1
clc %清屏
num = [3]; %闭环传递函数分子多项式
den = [1 -3 -1]; %闭环传递函数分母多项式
P=[-1+j -1-j]; %希望配置的闭环极点
[A,B,C,D]=tf2ss(num,den); %求状态空间表达式
[str K]=pdctrb(A,B,P) %求状态反馈阵<K>
[str H]=pdobsv(A,C,P) %求输出反馈阵<H>
同时,对状态反馈的可控和输出反馈的可观进行Matlab语言的编程,其编程结果如下
状态反馈可控编程:
%%-------------------------------------%%
%%程序功能:系统可控性判断以及求解状态反馈阵
%%输入量:系数矩阵A
%% 输入矩阵B
%% 配置极点P
%%输出量:可控性判断结果
%% 状态反馈矩阵K
%%-------------------------------------%%
function [str K] = pdctrb(A,B,P) %定义函数pdctrb
S = ctrb(A,B); %求可控性判别矩阵S
R = rank(S); %求可控性判别矩阵S的秩
L = length(A); %求系数矩阵A的维数
if R == L %判断rank(S)是否等于A的维数str = '系统是状态完全可控的!'; %输出可控性判断结果
K =acker(A,B,P); %求状态反馈矩阵K
else
str = '系统是状态不完全可控的!';
end
输出反馈可观编程:
%%-------------------------------------%%
%%程序功能:系统可观性判断以及求解输出反馈阵
%%输入量:系数矩阵A
%% 输出矩阵B
%% 配置极点P
%%输出量:可观性判断结果
%% 输出反馈矩阵H
%%-------------------------------------%%
function [str H] = pdobsv(A,C,P) %定义函数pdobsv
V = obsv(A,C); %求可观性判别矩阵V
R = rank(V); %求可观性判别矩阵V的秩
L = size(A,1); %求系数矩阵A的维数
if R == L %判断rank(V)是否等于A的维数str = '系统是状态完全可观的!'; %输出可观性判断结果
K = acker(A',C',P);
H = K'; %求输出反馈矩阵H
else
str = '系统是状态不完全可观的!';
通过Matlab实现编程之后,可以算出状态反馈的B值和输出反馈的H值,在siumlink下进行仿真:
五、实验结果
原系统结构图波形:
加入状态反馈后的系统波形:
加入输出反馈系统的波形:
H值和K值运算结果如下:str =
系统是状态完全可控的!
K =
5 3
str =
系统是状态完全可观的!
H =
6.0000
1.6667
>>
六、结果分析
本次实验做了3次的实验对比可以看出,原系统就是一个稳定的系统,假如状态反馈以后,系统转台的系数矩阵发生了变化,对系统的可控性、可观测性、稳定性、响应特性等均有影响。
1、状态反馈的引入不改变系统的可控性,但是改变了系统的可观测性。
2、输出至状态微分反馈的引入不改变系统的可观测性,但是改变了系统的可控性 3、由上面三图可看出系统的输出量均发生了变化响应时间由原来的7秒到后来的3.5秒。
输出至微分反馈的响应时间由原来的7秒到后来的3秒。
可以看出这两种的反馈均能提高原系统的动态特性七、教师评语。
