数学建模多元回归模型作业1
多元回归模型数学建模论文

多元回归模型数学建模论文研究方案:1. 研究背景与目的:多元回归模型是数学建模中一种常用的分析工具,它可以帮助研究者探索多个自变量对因变量的影响关系。
本研究旨在通过构建合适的多元回归模型,分析自变量对因变量的影响,并提出新的观点和方法,为解决实际问题提供有价值的参考。
2. 研究对象与变量选择:选择合适的研究对象是研究模型的基础,本研究选择某企业的销售额作为因变量,自变量包括广告投入、产品价格、产品质量等。
变量的选择应基于实际情况和理论基础,以获得可靠的研究结果。
3. 方案实施情况:在实施研究方案前,需要进行数据采集和整理,以及模型的建立和分析。
具体步骤如下:步骤一:数据采集通过企业相关部门提供销售数据、广告投入数据、产品价格数据、产品质量数据等,并对其进行有效性和可靠性检验。
步骤二:数据整理与探索性分析对采集到的数据进行清洗、整理和变量转换,包括缺失值处理、异常值处理、变量标准化等。
然后进行探索性分析,包括描述性统计、变量相关性分析等,以了解数据的基本情况和变量之间的关系。
步骤三:模型建立与系数估计根据变量之间的关系和实际问题,选择适当的多元回归模型,并进行模型的建立和系数估计。
可以采用最小二乘法或其他合适的方法进行参数估计。
步骤四:模型评估与优化通过模型评估指标,如残差分析、F检验、标准化系数等,对建立的多元回归模型进行评估和优化,以获得更准确和稳定的模型。
步骤五:创新和发展在已有研究成果的基础上,提出新的观点和方法,如引入其他自变量、改进模型结构等,以提高模型的预测精度和解释能力。
数据采集与分析:根据研究方案,我们采集了某企业2019年到2021年的销售额、广告投入、产品价格和产品质量等数据,共计N个样本。
通过数据整理与探索性分析,我们了解到各个变量的分布情况和相关性。
在进行多元回归分析之前,我们首先对变量进行了标准化处理,以消除量纲差异对模型估计的影响。
然后,我们采用最小二乘法估计多元回归模型的系数。
第四章 多元回归模型
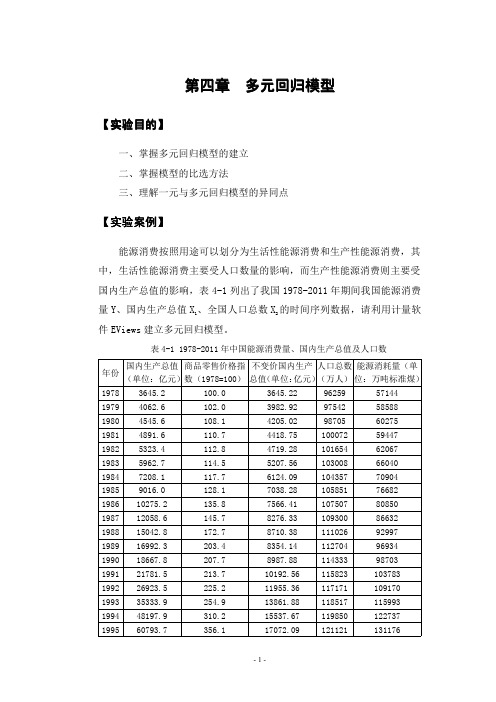
第四章多元回归模型【实验目的】一、掌握多元回归模型的建立二、掌握模型的比选方法三、理解一元与多元回归模型的异同点【实验案例】能源消费按照用途可以划分为生活性能源消费和生产性能源消费,其中,生活性能源消费主要受人口数量的影响,而生产性能源消费则主要受国内生产总值的影响,表4-1列出了我国1978-2011年期间我国能源消费量Y、国内生产总值X1、全国人口总数X2的时间序列数据,请利用计量软件EViews建立多元回归模型。
表4-11978-2011年中国能源消费量、国内生产总值及人口数年份国内生产总值(单位:亿元)商品零售价格指数(1978=100)不变价国内生产总值(单位:亿元)人口总数(万人)能源消耗量(单位:万吨标准煤)19783645.2100.03645.229625957144 19794062.6102.03982.929754258588 19804545.6108.14205.029********* 19814891.6110.74418.7510007259447 19825323.4112.84719.2810165462067 19835962.7114.55207.5610300866040 19847208.1117.76124.0910435770904 19859016.0128.17038.2810585176682 198610275.2135.87566.4110750780850 198712058.6145.78276.3310930086632 198815042.8172.78710.3811102692997 198916992.3203.48354.1411270496934 199018667.8207.78987.8811433398703 199121781.5213.710192.56115823103783 199226923.5225.211955.36117171109170 199335333.9254.913861.88118517115993 199448197.9310.215537.67119850122737 199560793.7356.117072.09121121131176199671176.6377.818839.75122389138948 199778973.0380.820738.72123626138173 199884402.3370.922756.07124761132214 199989677.1359.824924.14125786130119 200099214.6354.427995.08126743138553 2001109655.2351.631187.48127627143199 2002120332.7347.034678.01128453151797 2003135822.8346.739175.87129227174990 2004159878.3356.444859.24129988203227 2005184937.4359.351471.57130756224682 2006216314.4362.959607.17131448246270 2007265810.3376.770562.86132129265583 2008314045.4398.978727.86132802285000 2009340902.8394.186501.60133450306647 2010401512.8406.398821.76134091324939 2011472881.6426.2110952.97134735348002数据来源:中国统计年鉴-2012【实验步骤】一、建立工作文件启动EViews软件,在主菜单上依次点击File\New\Workfile,在弹出的对话框中对数据的时间频率(Frequency)、起始期(Start Date)、终止期(End Date)进行定义并对工作文件(WF)进行命名。
计量经济学多元线性回归模型(老师作业要求范本)范文

计量经济学·多元线性回归模型应用作业一、概述在当今市场上,一国的原油产量与多个因素存在着紧密的联系,例如民用汽车拥有量、宏观经济等都是影响一国原油产量的重要因素。
本次将以中国1990-2006年原油产量与国内民用汽车拥有量、GDP等因素的数据,通过建立计量经济模型来分析上述变量之间的关系,强调的重要性,从而促进国内原油产业的发展。
二、模型构建过程⒈变量的定义解释变量:X1民用汽车拥有量,X2电力产量,X3国内生产总值,X4能源消费总量。
被解释变量:Y 原油产量建立计量经济模型:解释原油产量与民用汽车拥有量、电力产量、国内生产总值、以及能源消费总量之间的关系。
⒉模型的数学形式设定原油产量与五个解释变量相关关系模型,样本回归模型为:∧Y i=∧β+∧β1X i1+∧β2X i2+∧β3X i3+∧β4X i4+e i⒊数据的收集该模型的构建过程中共有四个变量,分别是中国从1990-2006年民用汽车拥有量、电力产量、国内生产总值以及能源消费总量,因此为时间序列数据,最后一个即2006年的数据作为预测对比数据,收集的数据如下所示:⒋用OLS法估计模型回归结果,散点图分别如下:Y=20425.46-2.1872X1-0.1981X2+0.0823X3+0.0011X4 id.f.=12 ,R 2=0.9933 ,Se=(531.1592) (0.4879) (0.1123) (0.0082) (0.0057) t=(38.4545) (-4.4825) (-1.7635) (10.0106) (0.1998)三、 模型的检验及结果的解释、评价⒉拟合优度检验及统计检验R 2=0.9933,可以看到模型的拟合优度非常高,说明原油产量与上述四个解释变量之间总体线性关系显著。
● 模型总体性检验(F 检验):给定显著水平α=0.05,查自由度为(4,12)的F 分布表,得F(4,12)=3.26,可见该模型的F 值远大于临界值,因此该回归方程很明显是显著的。
数学建模作业-统计回归模型

统计回归模型摘要本文通过两个关于统计归回问题的解决,理解有关回归问题的解决办法,和对处理统计回归问题是的数学知识加以学习、巩固,学会用MA TLAB处理有关数学模型问题。
通过对数据的统计分析,找出与数据拟合最好的模型;其中,回归模型是用统计分析方法建立的最常用的一类模型,不涉及回归分析的数学原理和方法,通过实例讨论如何选择不同类型的模型,对软件得到的结果进行分析,对模型进行改进。
(当然,这是我初次用MA TLAB做回归问题,里面肯定会有很多不理想之处,就请老师多多指点。
)问题一:是有关牙膏的销售量问题。
问题二:软件开发人员的薪金问题。
一、问题的提出问题一一家技术公司人事部门为研究软件开发人员的薪金与他们的资历、管理责任、教育程度等因素之间的关系,要建立一个数学模型,以便分析公司人事策略的合理性,并作为新聘用人员薪金的参考。
他们认为目前公司人员的薪金总体上是合理的,可以作为建模的依据,于是调查来46名软件开发人员的档案资料,如表4,其中资历一列指从事专业工作的年数,管理一列中1表示管理人员,0表示非管理人员,教育一列中1表示中学程度,2表示大学分析与假设 按照常识,薪金自然随着资历的增长而增加,管理人员的薪金应高于非管理人员,教育程度越高薪金也越高。
薪金记作y ,资历记作x1,为了表示是否管理人员,定义:210,x ⎧=⎨⎩,管理人员非管理人员为了表示3种教育程度,定义:31,0,x ⎧⎨⎩中学其它41,0,x ⎧⎨⎩大学其它这样,中学用x3=1,x4=0表示,大学用x3=0,x4=1表示,研究生则用x3=0,x4=0表示。
为简单起见,我们假定资历对薪金的作用是线性的,即资历每加一年,薪金的增长是常数;管理责任、教育程度、资历诸因素之间没有交互作用,建立线性回归模型。
基本模型 薪金y 与资历x1,管理责任x2,教育程度x3,x4之间的多元线性回归模型为011223344y a a x a x a x a x ε=+++++ (1)其中014,,a a a …,是待估计的回归系数,ε是随机误差。
多元线性回归作业

0.7
0.9
1.2
报纸广告费 (万元)
0.1
0.2
0.5
0.8
销售额Y(万元)
712Biblioteka 1720试求Y对 , 的线性回归方程,并进行回归效果检验,找出最佳模型。
2.有一对夫妇用所拥有的一套面积为1800平方尺、每年房屋税为1500美元且配有游泳池的住房,向杰弗逊山谷银行提出抵押19万美元的申请,该银行搜集的房屋销售资料如下,试以此判断该银行能否接受这对夫妇的申请?
电台宣传费万元04070912报纸广告费万元01020508销售额121720有一对夫妇用所拥有的一套面积为1800平方尺每年房屋税为1500美元且配有游泳池的住房向杰弗逊山谷银行提出抵押19万美元的申请该银行搜集的房屋销售资料如下试以此判断该银行能否接受这对夫妇的申请
1.从某公司得到如下数据:
电台宣传费 (万元)
多元线性回归模型之数学建模实验报告

%y= 45.3636+0.3604*x1+3.0906*x2+11.8246*x3
rcoplot(r,rint)
x1=x(a,:)
y1=y(a)
[b1,bint1,r1,rint1,s1]=regress(y1',x1)
b1,bint1,s1
%y= 58.5101+0.4303*x1+2.3449*x2+10.3065*x3
30.0184 59.4982
-19.6030 32.7499
-28.9960 22.3987
-24.1742 26.8599
-23.8105 28.7839
-27.9825 22.9747
-22.6411 27.8754
-32.8481 18.0569
9.3635 48.2532
-30.5838 21.0099
-20.9189 30.3583
-35.7261 13.7317
x3=[0 1 0 1 1 0 1 0 1 0 1 0 0 0 0 1 0 0 0 0 01 0 0 1 1 0 1 0 1];
plot(x1,y,’>’)
plot(x2,y,’*’)
x=[ones(30,1), x1',x2',x3']
[b,bint,r,rint,s]=regress(y',x)
1.0000 53.0000 28.6000 1.0000
1.0000 63.0000 28.3000 0
1.0000 29.0000 22.0000 1.0000
1.0000 25.0000 25.3000 0
1.0000 69.0000 27.4000 1.0000
第三章多元线性回归模型习题答案
设是 0012:0H βββ=== C 、相关系数较大意味着两个变量存在较强的因果关系 D 、当随机误差项的方差估计量等于零时,说明被解释变量与解 释变量之间为函数关系 9、对于 01122????i i i k ki i Y X X X e ββββ=+++++…,如果原模型满足线性模型的基本 假设则 在零假设 0j β=下,统计量??()j j s ββ(其中?()j s β是 j β的标 准误差)服从 ( B ) A 、()t n k B 、(1)t n k -C 、(1,)F k n k -D 、(,1)F k n k -10、下列说法中正确的是 ( D ) A 、如果模型的 R 2 很高,我们可以认为此模型的质量较好 B 、如果模型的 R 2 很低,我们可以认为此模型的质量较差 C 、如果某一参数不能通过显著性检验,我们应该剔除该解释变 量 D 、如果某一参数不能通过显著性检验,我们不应该随便剔除该 解释变量 二、判断题 四、判断题、
B 、对回归模型的总体显著性检验没有必要 C 、总体回归方程与样本回归方程是有区别的 D 、决定系数 2 R 不可以用于衡量拟合优度 6、根据调整的可决系数 2R 与 F 统计量的关系可知,当 21R = 时,有 ( C ) A 、F=0 B 、F=-1 C 、F →+∞ D 、F=-∞ 7、线性回归模型的参数估计量?β是随机向量 Y 的 函数,即 1?()X X X Y β-''=。?β 是 (A) A 、随机向量 B 、非随机向量 C 、确定性向量 D 、常量 8、下面哪一表述是正确的 ( D ) A 、线性回归模型 01i i i Y X ββμ=++的零均值假设是指 1 10n i i n μ==∑ B 、对模型 01122i i i i Y X X βββμ=+++ 进行方程显著性检验(即 F 检验),检验的零假
数学建模模拟题,图论,回归模型,聚类分析,因子分析等 (1)
11.1抗生素显著性检验问题摘要在已知抗生素效果情况服从正态分布,且方差相同条件下。
通过用SPSS13.0软件编写程序,进行单因素方差分析。
检验五种抗生素之间是否存在明显差异。
关键词:抗生素方差分析显著性检验一问题重述抗生素注入人体后会与人体血浆蛋白质结合,以致减少了药效。
现在将常用的抗生素注入到牛的体内,得到抗生素与血浆蛋白质结合的百分比。
在总体服从正态分布,且方差相同的条件下分析五种抗生素效果是否存在显著性差异。
二问题分析题目显示各类抗生素效果情况服从正态分布,为了进一步说明抗生素使用效果的差异,需要检查不同抗生素是否有显著性差异,即对数据进行显著性检验。
首先,应该提出抗生素之间没有显著性差异的假设。
然后通过SPSS13.0版本软件进行单因素方差检验[1]。
验证假设是否成立。
三模型假设四符号说明五模型建立与求解题目显示各类抗生素与血浆蛋白质结合的百分比情况属于正态总体,要对各类抗生素是否存在显著性差异。
应用软件SPSS13.0进行单因素方差检验。
其检验步骤如下:Step1. 提出假设:H:各类抗生素之间没有显著性差异;H:各类抗生素之间有显著性差异。
1α0.05。
Step2. 选定显著性水平=Step3. 用软件SPSS13.0进行单因素方差检验用SPSS13.0编写程序得到问题的解:即不同抗生素效果明显不同。
(各抗生素之间具体分析见附录一)六模型评价与改进参考文献[1]薛薇 ,《SPSS统计分析方法及应用》,出版地:电子工业出版社,2009。
[编号] 作者,论文名,杂志名,卷期号:起止页码,出版年。
[编号] 作者,资源标题,网址,访问时间(年月日)。
附录附录一PSS13.0编写程序得到问题的解:11.2化肥与小麦种子的不同对小麦产量的影响问题摘要化肥与小麦的品种的差异将影响小麦的产量,进而影响农民的生活水平。
本文建立数学模型,就化肥的不同,小麦品种的不同这两种因素定量分析化肥与小麦品种对小麦实际产量的影响。
数学建模-多元线性回归分析
数学建模-多元线性回归分析引言多元线性回归是一种常用的数学建模方法,它用于分析多个自变量和一个因变量之间的关系。
通过寻找最佳的拟合直线,我们可以预测因变量的值,同时还可以了解每个自变量对因变量的贡献程度。
在本文档中,我们将介绍多元线性回归的基本原理、模型拟合和模型评估等内容。
基本原理多元线性回归的基本原理建立在最小二乘法的基础上。
我们假设因变量Y和自变量X之间存在线性关系,即:Y = β0 + β1X1 + β2X2 + … + βn*Xn其中,Y是因变量,X1、X2、…、Xn是自变量,β0、β1、β2、…、βn是回归系数。
我们的目标是求解最佳的回归系数,使得拟合直线与观测数据之间的残差平方和最小。
模型拟合为了拟合多元线性回归模型,我们首先需要收集足够的数据。
然后,我们可以使用各种统计软件或编程语言来进行模型拟合。
这些软件和语言通常提供了专门的函数或库,用于执行多元线性回归分析。
以Python语言为例,我们可以使用statsmodels库中的OLS函数进行多元线性回归拟合。
下面是一个示例代码:import pandas as pdimport statsmodels.api as sm# 读取数据data = pd.read_csv('data.csv')# 构建自变量矩阵X和因变量YX = data[['X1', 'X2', ... , 'Xn']]Y = data['Y']# 添加常数列X = sm.add_constant(X)# 拟合模型model = sm.OLS(Y, X)results = model.fit()# 输出回归结果print(results.summary())在上面的代码中,我们首先读取了数据集,然后构建了自变量矩阵X和因变量Y。
接下来,我们使用sm.add_constant()函数在自变量矩阵X中添加了一个常数列,用于拟合截距项。
数学建模多元线性回归分析
量 X j 对Y 的影响强度,通常在有统计学意义的前提下, 标准化回归系数的绝对值愈大说明相应自变量对 Y 的作 用愈大。
注意:
一般回归系数有单位,用来解释各自 变量对应变量的影响,表示在其它自变量保
持不变时, X 增j 加或减少一个单位时Y的平
均变化量 。不能用各 b来j 比较各 X对j Yˆ 的影响大小。
结果
t1
0.1424 0.3656
0.390
t3
0.2706 0.1214
2.229
结论
t2
0.3515 0.2042
1.721
t4
0.6382 0.2433
2.623
t0.05 / 2,22 2.074 , t4 | t3 | 2.074 , P 值均小于 0.05,说明b3 和 b4 有统计学意 义,而 b1 和 b2 则没有统计学意义。
标准化回归系数无单位,用来比较各 自变量对应变量的影响大小,bj 越大,X j 对 的Yˆ影响越大。
S1 1.5934 , S2 2.5748 , S3 3.6706, S4 1.8234 , SY 2.9257
b 1'
0.1424
1.5934 2.9257
0.0776
结
3.标准化回归系数 变量标准化是将原始数据减去相应变量的均数,
然后再除以该变量的标准差。
X
' j
(X
jX Sj
j)
计算得到的回归方程称作标准化回归方程,
相应的回归系数即为标准化回归系数。
b
' j
bj
l jj lYY
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模
1
多元回归模型
摘 要:本文主要以社会市场中的一个公司为例,来研究这个问题。综合近几年我国经济
发展状况,我国正处于经济高速发展的时期,各行业都展现处欣欣向荣的景象。而这篇文
通过多元线性回归分析,定量从销售价格,广告费用,销售量这三个方面来分析的。
文中结合题目所给数据,运用灰色关联分析模型法对公司产品销售进行关联分析,
得出公司生产的商品在市场一的销售价格情况,其顺序均按照时间顺序来写,并且注明了
月份,同时还对销售价格,广告费用,销售量做出了准确的计数,将他们用图表和公式的
方式将其直观展现出来,这样可以直观的看出价格于销售的关系。同时也能够直接的把公
司的运营情况看的清楚明白,
关键字:蓝色关联分析;分批要素推算法;产品销售价格;微分方程;模型
1 问题的背景及重述
1.1问题的背景
随着工业的发展,人们已经从以前的计划经济开始了市场经济,在这种状况下,人
们对经济的研究也越来越受人们关注,中国也已经从初步的市场经济开始转向国际贸易
了 ,在这种情况下,我们将不得不研究一下多元回归问题。因此,根据已有数据,运用
数学建模的方法,对这个实际的问题进行研究一下。
1.2 问题的重述
对于目前的经济发展状况,我只对一些简单的项目进行了一下研究,从中积累了一
些数据,对多元回归的研究也许能又一些帮助。这个文章主要是针对企业的经济发转状况
的一些前景做进一步的研究。对企业的未来目标做出一个深刻的认识。
2 模型假设
设某公司生产的商品在市场一的销售价格为1x(元/件)、用于商品的广告费用为2x(万
元)、销售量为y(万件)的连续12个月的统计数据如下表所示。
月份
销售价格1x 广告费用2x
销售量y
1 100 5.50 55
2 90 6.30 70
3 80 7.20 90
4 70 7.00 100
5 70 6.30 90
:多元回归模型
2
6 70 7.35 105
7 70 5.60 80
8 65 7.15 110
9 60 7.50 125
10 60 6.90 115
11 55 7.15 130
12 50 6.50 130
3 问题分析
问题要求从中国的实际情况和经济增长的新特点出发,参考相关数据资料,建立数学
模型,并由此对中国经济增长的中短期和长期趋势做出预测。为此,我们首先对数据进行
生产产品系统结构分析,并找出数据的特点以及这些数据所反映出的规律,特别是要从数
据中分析出对产品随季节变化的主要因素。在此基础上,提出公司生产的产品的中短期预
测模型和长期预测模型。
对于模型的建立,我们可以结合对数据的分析结果,兼顾近年来中国经济发展中出现
的一些新特点,先求出短期内影响公司经济发展的一些常用参数,如销售价格个广告效应
等。再利用这些常用参数以及相关数据对公司产品中短期发展趋势进行预测。
在长期预测模型的建立上,我们不仅要看现在公司产品的销售情况和价格走向,同时
也要兼顾市场的变化,以便能及时做出相应的反映,及时调整公司的生产计划,使公司一
直处于良好的发展状态下。
4 模型建立与求解
(1)○1y与x1,x2的关系求法如下:
数学建模
3
116.1571.308x111.246x2
的关系为所以销售量y与销售价格x1广告费用x2
y1.30811.246116.157x1x21y116.1571.308x111.246x2
Fx1x2()coeffx1x21
Fitx()interpvsXYx()
coeff1.30811.246116.157
coeffsubmatrixvs3500()
vsT3311.30811.246116.157()
vsregressXYk()k1
N12NrowsX()
Y5570901009010580110125115130130X10090807070707065606055505.506.307.207.006.307.355.607.157.506.907.156.50
销售量y的矩阵Y
定义商品销售价格x1和广告费用x2的数据矩阵X
:多元回归模型
4
y116.1571.308x111.246x2
的关系为所以销售量y与销售价格x1广告费用x2
y1.30811.246116.157x1x21y116.1571.308x111.246x2
Fx1x2()coeffx1x21
Fitx()interpvsXYx()
coeff1.30811.246116.157
coeffsubmatrixvs3500()
vsT3311.30811.246116.157()
vsregressXYk()k1
○
2使用matlab作图程序如下
x1=[100 90 80 70 70 70 70 65 60 60 55 50];
x2=[5.50 6.30 7.20 7.00 6.30 7.35 5.60 7.15 7.50 6.90 7.15 6.50];
y=116.157-1.308*x1+11.26*x2;
plot3(x1,x2,y);
图形为:
数学建模
5
说明销售量与销售价格和广告费用之间有显著相关关系
FF1
F8.022
FqF12N30.01
F109.589FSSR2SSEN3
进行F法检验求出F统计量和临界值
有高度相关关系求出的y与x1x2
这说明Hx1x2()116.1571.308x111.246x2
R0.98RSSRSST
按照复相关定义
SSR6.052103SSE248.49SST6.3103
SSRpredYmeanY()()2SSEpredYY()2SSTNvarY()
回归平方和及残差平方和为
为了检验回归方程的显著性设总离差平方和
predYiFitXTi
i0N1
现在对以上做法做统计上的误差分析对回归方程做显著性检验
所以预测第13个月该商品的销售量将是90.239万件
H807()90.239
Hx1x2()116.1571.308x111.246x2
2()
:多元回归模型
6
5 模型的评价与改进
本文依据题目所给出的条件因素和相关资料,建立了公司产品的中短期预测模型和长
期预测模型,总的来说,预测结果是比较好的,与公司发展战略上相应的数字很接近。
尽管通过这次对模型的初步建立,对公司的发展状况又了一定的了解。但是,我们还
不能仅凭一张模型来评论什么,这个知识对公司的一个大概统计,还有很多状况我们还需
要从实际考虑,来用实际问题做出更加深刻的研究。
