3D密码的Square攻击
密码芯片的物理攻击与防护对策

微电子学研究所 微电子与纳电子学系
近年来,涉及信息安全的密码芯片面临着越来 越严重的安全性挑战,已经出现了各种不同层次、 不同水平的攻击手段,概括起来主要可以划分为以 下几种: (1)窃听攻击方法(Eavesdropping) (2)软件攻击方法(Software Attacks) 非破坏 性攻击 破坏性 攻击
微电子学研究所 微电子与纳电子学系
物理攻击手段的主要步骤: (1)获取相关的密码电路芯片,这是对其实施各种 物理攻击的必要前提; (2)利用机械切割或化学腐蚀手段,打开芯片的封 装结构,再辅以聚焦离子束等微区刻蚀技术,对其 关键引出端口(例如电源、时钟信号,各种控制、 地址与数据信号总线以及芯片内部预留的测试焊盘 等)重新进行超声键合; (3)给密码电路芯片重新加载,必要时可以采用外 部的时钟和地址信号发生器,首先对密码芯片内部 的各类不挥发存储器直接进行访问和扫描读出,获 得其相关的存储信息;
微电子学研究所 微电子与纳电子学系
内容提要 密码芯片面临的安全性挑战 各种常见的物理攻击技术分析 针对不同物理攻击手段的防护对策 总结与展望
微电子学研究所 微电子与纳电子学系
物理攻击手段所需的主要设备条件: 进行密码芯片的物理攻击必须具备一定的硬件设 备条件,主要包括:化学腐蚀工作台、微区探针测试 台、超声压焊机、光学共焦显微镜、扫描电子显微镜 (SEM)、聚焦离子束(FIB)设备、激光微区切割 设备、微区精密定位装置(微动工作台)、CCD摄 像机、多通道示波器、时钟信号发生器、图形发生器、 逻辑分析仪、直流稳压电源,以及一台用于各种信号 采集和数据处理的高性能计算机。
微电子学研究所 微电子与纳电子学系
关于芯片表面物理防护的等级: • 普通的钝化保护:通常为二氧化硅、氮化硅等绝缘 介质或聚酰亚胺等高分子聚合物材料,其特点是工 艺技术兼容性好、寄生效应小、物理化学性质稳定, 存在问题是材料本身透明、易于腐蚀去除; • 中等的物理防护:表面可以选用合适的难熔金属薄 膜等不透明材料,能够抵御各种可见光、X射线、 红外线、紫外线的穿透,存在问题是可能会带来较 大的寄生效应,对于FIB刻蚀也是无能为力的; • 先进的物理防护:坚固、不透明材料,能够耐受各 种酸、碱溶液腐蚀且难以去除(或者在去除的同时 将引起芯片内部器件或电路结构的破坏),工艺技 术兼容性好、寄生效应小(???)。
square用法

square用法【最新版】目录1.Square 的定义与词性2.Square 的用法举例3.Square 的常见搭配4.Square 的近义词与反义词正文【square】是一个英文单词,既可以作名词,也可以作动词和形容词。
它主要有以下几种用法:1.作为名词,square 表示“广场”、“矩形”或“平方”。
例如:- Tomorrow we will meet at the square.(明天我们将在广场见面。
)- The picture is in the shape of a square.(这幅画是矩形的。
)- The area of the square is 100 square meters.(这个广场的面积是 100 平方米。
)2.作为动词,square 表示“使成方形”、“平方”或“对准”。
例如:- She squared the table with a ruler.(她用尺子使桌子成方形。
)- 4 squared is 16.(4 的平方是 16。
)- The company"s profits squared in the last quarter.(该公司在上个季度的利润翻了一番。
)3.作为形容词,square 表示“方形的”、“正方形的”或“平稳的”。
例如:- The square table is very stable.(这张方形的桌子非常稳定。
)- He has a square face with distinct features.(他有一张方形的脸,五官分明。
)4.Square 还有一些常见的搭配,如:- square dance(四方舞)- square meal(丰盛的正餐)- square up(对准;使成方形)5.Square 的近义词有:rectangle(矩形)、cube(立方体)、circle (圆形)等。
反义词则是没有特定的单词,但可以说成“non-square”(非方形的)。
squaretest 原理

squaretest 原理SquareTest原理是一种软件测试方法,旨在验证软件的功能、性能和安全性。
它通过对软件系统的各个方面进行全面测试,以确保软件的质量和可靠性。
在进行SquareTest之前,首先需要明确测试的目标和范围。
测试目标可以包括功能测试、性能测试、安全测试等。
测试范围可以根据软件的不同模块和功能来确定,以保证测试的全面性和有效性。
在功能测试中,SquareTest主要关注软件的各个功能是否能够正常运行并符合预期。
对于每个功能,测试人员需要设计相应的测试用例,包括输入数据、预期输出以及测试步骤等。
通过执行这些测试用例,可以验证软件的各项功能是否正常工作。
在性能测试中,SquareTest主要关注软件的性能指标,如响应时间、并发用户数、吞吐量等。
测试人员可以通过模拟实际使用场景,使用性能测试工具对软件进行压力测试和负载测试,以评估软件在不同负载下的性能表现。
在安全测试中,SquareTest主要关注软件的安全性,包括漏洞、安全漏洞、数据泄露等方面。
测试人员可以使用各种安全测试工具和技术,对软件进行渗透测试、代码审计等,以发现潜在的安全风险并提出相应的改进措施。
除了功能、性能和安全性,SquareTest还可以涉及其他方面的测试,如兼容性测试、易用性测试等。
通过对软件的全面测试,可以发现并解决软件中的潜在问题,提高软件的质量和可靠性。
在进行SquareTest时,测试人员需要遵循一定的测试方法和流程。
首先,需要进行测试计划和测试方案的编写,明确测试的目标、范围、方法和时间计划等。
然后,根据测试方案,设计测试用例并执行测试。
在测试执行过程中,需要记录测试过程和结果,以便后续分析和评估。
最后,根据测试结果,对软件进行问题分析和改进措施的制定。
SquareTest的原理在软件测试领域具有重要的意义。
通过全面测试软件的各个方面,可以发现潜在的问题并及时解决,提高软件的质量和可靠性。
同时,SquareTest也可以帮助开发人员和测试人员更好地理解软件的特性和性能,以便进行更有效的测试和优化。
代数攻击

线性化方法
eXtended Linearizations方法
N. Courtois, A. Klimov, J. Patarin, and A. Shamir. Efficient
algorithms for solving overdefined systems of multivariate polynomial equations, EUROCRYPT 2000
f 模P约化到g: f g f g mod Id(P) P f
p1
g1
g2 g =g p2 pk k
若g模P不能再约化了,则g称为f 模P的一个正规型 0 f Id(P) f P
23
Grö bner基方法
什么是Grö bner基
F2[x1, x2,..., xn]中理想的一组特殊的生成元
11
线性化方法
x1x2+x1x3+x0+x2 = 0 x0x2+x1x2+x2x3+x1+x3+1 = 0 x0x3+x2x3+x0+x1+x2 = 0 x0x1+x0x3+x1x3+x2+x3+1 = 0 x0x1+x0x2+x0+x3+1 = 0 x1x2+x1x3+x0 = 0 x0x2+x1x2+x2x3+x1 = 0 x0x3+x2x3+x2 = 0 x0x1+x0x3+x1x3+x1+x3+1 = 0 x0x1+x0x2+x0+x2 = 0
分组密码的主要攻击方法
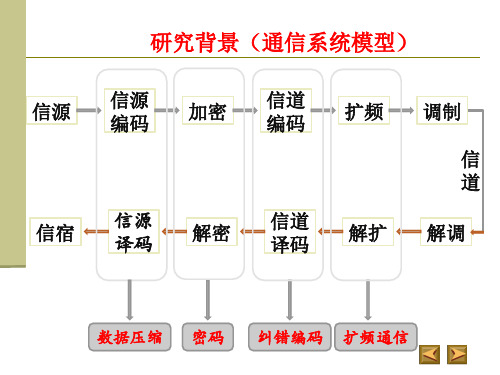
研究背景(序列密码) 研究背景(序列密码)
序列密码的主要攻击方法: 经典序列密码的攻击方法: 线性逼近攻击-非线性度 相关攻击-相关免疫度 代数攻击-代数免疫度
1 f ( x) = n 2
∑S
w∈F2n
f
( w)( −1)
wi x
布尔函数的Walsh变换 §1.2 布尔函数的 变换
第1章 布尔函数与向量值函数
☆ Walsh谱的基本性质 谱的基本性质 (1)循环Walsh谱与线性Walsh谱具有如下关系 循环Walsh谱与线性Walsh谱具有如下关系 Walsh谱与线性Walsh
第1章 布尔函数与向量值函数
●
非线性度
NL ( f ) = min d ( f , l ) = min wt ( f − l )
l∈ An l∈ An
(1) NL ( f ) = 2 (2 ) (3 ) (4)
n −1
1 − max | W f ( w) | w∈ 2 w∈F2n
n −1 2
NL ( f ) ≤ 2 n −1 − 2
定义3 为两个正整数, 定义3 设n和m为两个正整数,从F2n到F2m的映射称 和 为两个正整数 向量值函数, 为(n,m)函数,有时也称为向量值函数,多输出布 )函数,有时也称为向量值函数 尔函数或向量布尔函数. 尔函数或向量布尔函数. 向量值函数的表示方法: ☆ 向量值函数的表示方法: (1)分量函数表示法: 分量函数表示法:
4
代数攻击-代数次数 中间相遇攻击 相关密钥攻击
研究背景(序列密码) 研究背景(序列密码)
如何应对密码攻击

80
添加标题
哈希函数:将任意长度的输入 转换为固定长度的输出,常用 于密码存储和验证
添加标题
数字签名:使用私钥对消息进 行签名,接收方使用公钥验证 签名,确保消息的完整性和身
份认证
密码哈希技术
02
安全性:哈希函数的输
出应具有抗碰撞性、抗
01
预映像性等特性
哈希函数:将任意长度
的输入转换为固定长度
的输出
认证等
04
示例:使用字典攻击、彩虹表攻击等方法破
解密码。
字典攻击
原理:通过猜测密码可能的组合来破解密码 特点:简单、直接,但效率较低 应对策略:使用强密码、定期更换密码、使用多因素认证等 局限性:对于复杂的密码,字典攻击可能无法破解。
彩虹表攻击
原理:利用彩虹表技术, 通过预先计算并存储密码 哈希值,实现快速破解密
添加 标题
添加 标题
遵守密码法规的重要性: 保护个人和企业的信息安
全
密码法规的内容:包括密 码使用、管理、存储等方
面的规定
违反密码法规的后果:可 能面临罚款、刑事处罚等
法律后果
如何遵守密码法规:加强 密码管理,定期更新密码,
不泄露密码等措施。
加强密码教育和培训
提高员工对密码安全的认识 定期进行密码安全培训 制定密码使用规范和流程 加强密码管理,确保密码的保密性和安全性
密码政策和法规
制定密码政策
密码政策应符合 国家法律法规和
行业标准
密码政策应明确 密码的使用范围、
权限和管理要求
密码政策应定期 进行审查和更新,
以适应技术发展 和安全形势的变
化
密码政策应得到 组织内部的广泛 宣传和培训,确 保员工理解和遵
虐杀原形二操作方法
虐杀原形二操作方法
《虐杀原形2》是一款动作冒险游戏,在游戏中玩家扮演主角亚历克斯·黒任,可以使用各种超能力进行战斗和操纵环境。
以下是游戏的基本操作方法:
1. 移动:使用方向键或左摇杆控制角色移动。
2. 跳跃:按下跳跃键(通常为X键或A键)进行跳跃。
可以进行连续跳跃和墙壁跳跃。
3. 攻击:使用攻击键(通常为Square键或X键)进行近战攻击。
可以进行连续攻击和组合技。
4. 投掷:使用投掷键(通常为Circle键或B键)进行远程攻击。
可以抓取物体并投掷,或使用特殊能力进行攻击。
5. 超能力:通过特定按键组合或触发条件,可以使用各种超能力。
例如,使用变形能力进行快速移动,使用生化能力进行远程攻击等。
不同的超能力可以通过游戏中的任务和追踪系统获得。
6. 吞噬:亚历克斯有能力吞噬其他生物,获取他们的记忆和能力。
接近一个目标后,按下吞噬键(通常为Triangle键或Y键)进行吞噬。
7. 系统菜单:通过按下选项键(通常为Start键或菜单键)可以打开游戏菜单,其中包括存档、任务追踪和游戏设置等。
每个玩家可能对操作有所不同,可以根据自己的喜好和游戏习惯进行调整。
以上是《虐杀原形2》的基本操作方法,希望对你有所帮助!。
流密码算法Grain的立方攻击
软件学报ISSN 1000-9825, CODEN RUXUEW E-mail: jos@Journal of Software,2012,23(1):171-176 [doi: 10.3724/SP.J.1001.2012.03983] ©中国科学院软件研究所版权所有. Tel/Fax:+86-10-62562563流密码算法Grain的立方攻击*宋海欣1,2+, 范修斌1, 武传坤1, 冯登国11(中国科学院软件研究所信息安全国家重点实验室,北京 100190)2(中国科学院研究生院,北京 100049)Cube Attack on GrainSONG Hai-Xin1,2+, FAN Xiu-Bin1, WU Chuan-Kun1, FENG Deng-Guo11(State Key Laboratory of Information Security, Institute of Software, The Chinese Academy of Sciences, Beijing 100190, China)2(Graduate University, The Chinese Academy of Sciences, Beijing 100049, China)+ Corresponding author: E-mail: songhaixin@; shx_201@Song HX, Fan XB, Wu CK, Feng DG. Cube attack on Grain. Journal of Software, 2012,23(1):171-176. /1000-9825/3983.htmAbstract: At EUROCRYPT 2009, Dinur and Shamir proposed a new type of algebraic attacks named cube attack. Grain is one of the 3 final hardware-oriented stream ciphers in the eSTREAM portfolio, which takes an 80-bit secret key and a 64-bit initial vector as input and produces its keystream after 160 rounds of initialization. Applying cube attack on Grain with 70 initialization rounds, the study finds that 15-bit secret key can be recovered and can find 4 linear equations on another 23 bits of the secret key. Moreover, 1-bit secret key can be recovered by applying cube attack on Grain with 75 initialization rounds.Key words: eSTREAM project; stream cipher; Grain; cube attack; key recovery摘要: Dinur和Shamir在2009年欧洲密码年会上提出了立方攻击的密码分析方法.Grain算法是欧洲序列密码工程eSTREAM最终入选的3个面向硬件实现的流密码算法之一,该算法密钥长度为80比特,初始向量(initial vector,简称IV)长度为64比特,算法分为初始化过程和密钥流产生过程,初始化过程空跑160拍.利用立方攻击方法对Grain算法进行了分析,在选择IV攻击条件下,若算法初始化过程空跑70拍,则可恢复15比特密钥,并找到了关于另外23比特密钥的4个线性表达式;若算法初始化过程空跑75拍,则可恢复1比特密钥.关键词: eSTREAM工程;流密码算法;Grain;立方攻击;密钥恢复中图法分类号: TP309文献标识码: AeSTREAM工程[1]始于2004年11月,面向社会征集流密码算法,征集活动于2005年4月结束,一共征集到34种流密码算法.经过3个阶段的评选,选出4种适合软件实现的算法及4种适合硬件实现的算法.由于面向硬件实现的F-FCSR-H算法被成功破译[2],最终剩下7种算法.Grain算法[3]是由瑞典的Hell,Johansson和瑞士的Meier共同设计的一种面向硬件实现的流密码算法.针对*基金项目: 国家自然科学基金(60833008, 60902024)收稿时间:2010-10-26; 定稿时间: 2010-12-31CNKI网络优先出版: 2011-05-12 11:47, /kcms/detail/11.2560.TP.20110512.1147.002.html172 Journal of Software软件学报 V ol.23, No.1, January 2012该算法过滤函数所存在的弱点,文献[4]提出了密钥恢复攻击,文献[5]提出了区分攻击,针对该算法初始化过程所存在的弱点,文献[6]提出了滑动再同步攻击.为了解决该算法存在的安全性问题,设计者对Grain算法进行修改后又提交了Grain v1算法[7],算法密钥长度为80比特.此外,设计者还提交了128比特密钥版本的Grain算法Grain-128[8].Grain v1算法是eSTREAM工程最终入选的7种流密码算法之一.若无特别声明,本文中“Grain”均指Grain v1算法.目前,针对Grain算法最好的密码分析结果如下:2008年,文献[9]基于滑动再同步攻击的思想,对Grain算法的初始化过程进行了分析,比密钥穷举攻击快了1倍,时间复杂度由280降为279;2009年,文献[10]指出Grain算法在2144个密钥-IV空间中存在264个弱密钥,导致初始化过程完成后算法线性反馈移位寄存器LFSR的状态为全0,在这种条件下,恢复密钥将比穷举攻击更加有效.在2009年欧洲密码年会上,Dinur和Shamir提出了一种新型的代数攻击方法,称为立方攻击(cube attack)[11].它是一种密钥恢复攻击[12],只要有一个输出比特可以表示为密钥和初始向量(或明文)的低次数多变量多项式,它就可以用来攻击任何密码系统.在文献[11]中,作者对eSTREAM工程最终入选的另外一种适合硬件实现的流密码算法Trivium[13]进行了立方攻击,Trivium算法初始化过程空跑1 152拍,若初始化过程空跑735拍后即输出乱数,则在选择IV攻击条件下,他们找到了52个关于密钥的线性表达式,使恢复全部80比特密钥的时间复杂度降为230.Grain算法与Trivium算法相比,非线性次数较高.目前,公开文献上尚未有关于Grain算法立方攻击方面的分析结果.本文利用立方攻击密码分析方法,对减少初始化空跑拍数(由160拍减少至70拍和75拍)的Grain算法进行了分析.对初始化空跑拍数减少到70拍的Grain算法,我们可以恢复15比特密钥,并找到了关于另外23比特密钥的4个线性表达式;对初始化空跑拍数减少到75拍的Grain算法,我们可以恢复1比特密钥.本文第1节介绍Grain算法.第2节对立方攻击进行简要介绍.第3节介绍我们对Grain算法进行立方攻击分析的结果.第4节对本文进行总结.1 Grain算法简介1.1 算法描述Grain算法是由瑞典的Hell,Johansson和瑞士的Meier共同设计的一种流密码算法,算法分为密钥流产生过程和初始化过程,密钥长度为80比特,初始向量IV(initial vector)长度为64比特,适用于对硬件资源(如门电路数、能量消耗、内存)限制很大的环境[14],每个时钟周期产生1比特乱数.Grain算法由非线性反馈移位寄存器(NFSR)、线性反馈移位寄存器(LFSR)和输出函数h(x)等部分组成,算法结构如图1所示.Fig.1 Schematic view of Grain图1 Grain算法框图1.1.1 密钥流(keystream)产生过程1. 线性反馈移位寄存器(LFSR)LFSR为80级的线性反馈移位寄存器,反馈多项式为f(x)=1+x18+x29+x42+x57+x67+x80.宋海欣 等:流密码算法Grain 的立方攻击173LFSR 从右向左运动,每个时钟周期运动1拍,状态位从左至右按比特记为s t ,s t +1,s t +2,…,s t +79,状态位的更新可表示如下:s t +80=s t +62⊕s t +51⊕s t +38⊕s t +23⊕s t +13⊕s t .2. 非线性反馈移位寄存器(NFSR)NFSR 为80级的非线性反馈移位寄存器,反馈多项式为1820283543475259667180172043476571202835475259173552712028434717205965172028354347525965712835434752()1 g x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =++++++++++++++++++++++59.xNFSR 从右向左运动,每个时钟周期运动1拍,状态位从左至右按比特记为b t ,b t +1,b t +2,…,b t +79,LFSR 的状态位s t 参与NFSR 状态位的更新,NFSR 状态位的更新可表示如下:80626052453733282114963603733159605245332821634528960523733 t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t t b s b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b +++++++++++++++++++++++++++++++=+++++++++++++++++++636021156360524537332821159524537332821t t t t t t t t t t t t t t t t t t t b b b b b b b b b b b b b b b b b b b +++++++++++++++++++++++3. 过滤函数过滤函数为5入1出函数,表达式为14032334012023024124234(),h x x x x x x x x x x x x x x x x x x x x x x x x =⊕⊕⊕⊕⊕⊕⊕⊕⊕其中,x 0=s t +3,x 1=s t +25,x 2=s t +46,x 3=s t +64,x 4=s t +63.将过滤函数的输出记为h .4. 密钥流产生从NFSR 取7个比特b t +1,b t +2,b t +4,b t +10,b t +31,b t +43,b t +56及过滤函数输出的1个比特h 共计8个比特做模2加运算,得到1比特的密钥流,记为ks ,可表示如下:ks =b t +1⊕b t +2⊕b t +4⊕b t +10⊕b t +31⊕b t +43⊕b t +56⊕h .1.1.2 初始化过程记80比特密钥为k 0,k 1,k 2,…,k 79,记64比特IV 为v 0,v 1,v 2,…,v 63.首先,将密钥载入NFSR,即b t +i =k i (0≤i ≤79),将初始向量IV 作为前64比特状态载入LFSR,LFSR 后16位用1填充,即s t +i =v i (0≤i ≤63),s t +i =1(64≤i ≤79).然后,密钥流ks 与移位寄存器NFSR 及LFSR 的反馈进行模2加运算,运行“密钥流产生过程”160拍,完成初始化过程.初始化过程如图2所示.Fig.2 Initialization of Grain图2 Grain 算法初始化过程2 立方攻击简介立方攻击[11]是一种新型的代数攻击方法,旨在寻找密码算法的低次方程以恢复密钥或进行区分攻击.它吸收了饱和攻击[15]及高阶差分分析[16]的思想,该攻击方法主要基于下述定理:定理1[11]. 设f (x 1,x 2,…,x n )为含有n 个变量的布尔函数,I 为集合S ={x 1,x 2,…,x n }的真子集:f (x 1,x 2,…,x n )=p (I )⋅(P (x j |j ∈S -I ))⊕R (x j |j ∈S ),其中:()()i I i p I x ∈=∏;P (⋅)和R (⋅)均为代数标准型(ANF )表示的布尔函数,P (⋅)函数中的变量均取自集合I 的补集174 Journal of Software 软件学报 V ol.23, No.1, January 2012 S -I ,R (⋅)函数中的每一项均不含I 中的全部变量.那么,{|}12(,,...,)().i x i I n f x x x P ∈⊕=⋅举例如下:设12345123124245122355(,,,,)1,f x x x x x x x x x x x x x x x x x x x x =⊕⊕⊕⊕⊕⊕⊕它可以表示为1234512342453525(,,,,)(1)(1).f x x x x x x x x x x x x x x x x =⊕⊕⊕⊕⊕⊕⊕这里,1212342453525{|}1234534534534534534{,},(),()1,()1,(,,,,)(0,0,,,)(0,1,,,)(1,0,,,)(1,1,,,) 1i x i I I x x p I x x P x x R x x x x x x x f x x x x x f x x x f x x x f x x x f x x x x x ∈==⋅=⊕⊕⋅=⊕⊕⊕⊕⊕=⊕⊕⊕=⊕⊕ ().P =⋅在流密码算法中,初始向量IV 为公开变量,密钥为未知变量.若集合I 中的变量均为公开变量,P (⋅)为非常量 的线性表达式,我们就得到了关于未知变量(密钥)的一个线性方程{|}12()(,,...,),i x i I n P f x x x ∈⋅=⊕并称p (I )为极大 项(maxterm),称P (⋅)为超级多项式(superpoly).立方攻击为选择IV 攻击,攻击者把密码算法看作一个黑盒子,它是关于n 个未知变量和m 个公开变量的未知多项式,输出1个比特.对密码算法的立方攻击分为两个阶段:预处理阶段和密钥恢复阶段.在预处理阶段,攻击者可以改变公开变量及未知变量的值,并可以模拟算法的执行,目的是找到尽量多的关于未知变量的线性方程(超级多项式),预处理过程只进行1次.在密钥恢复阶段,攻击者只改变公开变量的值,通过在预处理阶段找到的超级多项式来恢复某些密钥比特.对分组密码来讲,在选择明文攻击的条件下,明文为公开变量,密钥为未知变量;对序列密码来讲,在选择IV 攻击的条件下,IV 为公开变量,密钥为未知变量.3 对Grain 算法的立方攻击在文献[11]中,Dinur 和Shamir 提出了立方攻击的分析方法,并对减少初始化空跑拍数的Trivum 算法进行了密码分析.若算法非线性次数不高,立方攻击将十分有效.Grain 算法与Trivium 算法相比,非线性次数较高, Grain 算法非线性反馈移存器的反馈多项式的非线性次数为6,过滤函数的非线性次数为3;而Trivium 算法非线性反馈移存器的反馈多项式的非线性次数为2,过滤函数是线性的.我们编程对初始化空跑拍数减少到70拍和75拍的Grain 算法进行了立方攻击.在攻击的预处理阶段,主要问题是如何找到极大项p (I )和超级多项式P ,并确定P 是关于哪些密钥比特的线性表达式,下面分别进行介绍.3.1 寻找极大项我们通过线性测试的方法寻找极大项,随机选择x ,y ∈{0,1}n ,验证P [0]⊕P [x ]⊕P [y ]=P [x ⊕y ]是否成立.具体步骤如下:(1) 随机选择公开变量的一个子集记为I ,将其他公开变量设置为0;(2) 随机选择两个密钥变量值x ,y ∈{0,1}n ,验证P [0]⊕P [x ]⊕P [y ]=P [x ⊕y ]是否成立.其中,函数P [x ]的计算方法为:密钥变量取值为x ,I 之外的公开变量取值为0,跑遍I 所有可能的取值,计算各函数值f (⋅),将得到的结果模2加即为P [x ]=⊕I f (⋅);(3) 若不成立,转步骤(1);若成立,转步骤(2)继续测试,直到连续通过N 次测试,输出结果.说明:关于测试次数N 的选择,若N 选择过大,则效率比较低;若N 选择过小,则会有大量的非线性多项式连续通过N 次测试.在实际编程过程中,我们采取了折衷的策略.若将测试次数N 设为100仍有大量的非线性多项式被误以为是线性的,经过不断实验,我们最终将测试次数N 设为200.虽然仍有很少量的非线性多项式被误以为是线性的,但效率较高.下一步,我们对检测通过的每一个多项式再进行连续10 000次测试,若均通过,则认为该多项式是线性的,否则淘汰该多项式.宋海欣等:流密码算法Grain的立方攻击1753.2 确定超级多项式若p(I)为极大项,确定P是关于哪些密钥比特的线性表达式的方法如下:(1)首先确定自由项,即表达式中有无⊕1:将I之外的所有变量(未知变量和公开变量)置为0,跑遍I,对结果求和,若为0,则无⊕1;若为1,则有⊕1;(2)确定P中变量x j的系数是0还是1:将I之外的所有变量(未知的和公开的)置为0,跑遍I,对结果求和得到a;将x j置为1,将I之外的所有其他变量(未知的和公开的)置为0,跑遍I,对结果求和得到b;若a=b,则系数为0;否则,系数为1.简言之,在一个线性表达式中,将所有变量置为0即得到自由项,若变量取值变反,运算结果也变反,则表达式中有该变量.3.3 实验结果及分析我们按照上述方法进行编程,在个人PC机上运行了两天,找到的极大项及超级多项式见表1.程序又持续运行了几个星期,找到一些新的极大项,但没有找到新的超级多项式.Table 1Cube attack results on Grain表1对Grain算法的立方攻击结果极大项集合I超级多项式空跑拍数{28,2,46,48,42,14,57} 1+k6370{31,17,42,32,2,48,47} 1+k6470{2,44,20,5,48,49,37,55} 1+k6670{24,19,41,18,39,2,50,48,16}1+k6770{28,48,42,10,51,14,61,2,39}1+k6870{25,17,12,54,13,14,52,48,2}1+k6970{5,48,42,28,2,44,36,53} 1+k7070{24,25,10,6,9,54,48,2,28,17}1+k7170{55,48,37,35,7,31,2} k7270{2,12,9,15,56,48,31} 1+k7370{32,2,12,1,35,48,31} k7470{56,37,26,48,29,31,58,2} k7570{17,48,59,63,2,6,7,38} k7670{48,35,61,32,37,2,26} 1+k7870{48,13,60,11,1,2,7,28,32} k7970{63,13,59,48,10,2,0,36} k2+k3+k5+k11+k32+k44+k5770{9,10,34,29,35,19,7} k3+k4+k6+k12+k33+k45+k5870{48,37,31,2,18,44,20} k4+k5+k7+k13+k34+k46+k5970{12,40,9,41,31,57,60,37} k5+k6+k8+k14+k35+k47+k6070{62,15,25,40,12,46,10,34} k6375从表1可以看出:对初始化空跑拍数减少到70拍的Grain算法,在选择IV攻击的条件下,我们可以直接恢复15比特密钥,并找到了关于另外23比特密钥的4个线性表达式;对初始化空跑拍数减少到75拍的Grain算法,我们可以直接恢复1比特密钥.表1中,极大项中公开变量的个数最少为7,最大为10;再随着初始化空跑拍数的增加,算法非线性次数增长很快,极大项中公开变量的个数也增加很快.对初始化空跑拍数减少到80拍的Grain算法,我们也编程进行了测试,极大项中公开变量的个数设置在32以下进行随机测试,在个人PC机上连续运行了几个月,仍未找到超级多项式.我们认为,初始化空跑拍数为160拍的Grain算法是可以抵抗立方攻击的.4 结束语本文应用立方攻击方法对减少初始化空跑拍数的Grain算法进行了密码分析,可以直接恢复部分密钥比特,从而极大地降低了密钥穷举量.如何改进和加速立方攻击算法是我们下一步研究工作的重点.致谢在此,我们向对本文的工作给予支持和建议的同行,尤其是冯登国教授领导的讨论班上的同学和老师表示衷心的感谢.176 Journal of Software软件学报 V ol.23, No.1, January 2012References:[1] eSTREAM-ECRYPT stream cipher project. /stream/[2] Hell M, Johansson T. Breaking the F-FCSR-H stream cipher in real time. In: Pieprzyk J, ed. Proc. of the ASIACRYPT 2008. LNCS5350, Heidelberg: Springer-Verlag, 2008. 557-569. [doi: 10.1007/978-3-540-89255-7_34][3] Hell M, Johansson T, Meier W. Grain—A stream cipher for constrained environments. eSTREAM-ECRYPT Stream Cipher ProjectReport, 2005/010, 2005. /stream/ciphers/grain/grain.pdf [doi: 10.1504/IJWMC.2007.013798][4] Berbain C, Gilbert H, Maximov A. Cryptanalysis of Grain. In: Robshaw MJB, ed. Proc. of the FSE 2006. LNCS 4047, Heidelberg:Springer-Verlag, 2006. 15-29. [doi: 10.1007/11799313_2][5] Khazaei S, Hassanzadeh M, Kiaei M. Distinguishing attack on Grain. eSTREAM-ECRYPT Stream Cipher Project Report,2005/071, 2005. /stream/papersdir/071.pdf[6] Kücük Ö. Slide resynchronization attack on the initialization of Grain 1.0. eSTREAM-ECRYPT Stream Cipher Project Report,2006/044, 2006. /stream/papersdir/2006/044.ps[7] Hell M, Johansson T, Maximov A, Meier W. The Grain family of stream ciphers. In: Robshaw M, Billet O, eds. Proc. of the NewStream Cipher Designs. LNCS 4986, Heidelberg: Springer-Verlag, 2008. 179-190. [doi: 10.1007/978-3-540-68351-3_14][8] Hell M, Johansson T, Meier W. A stream cipher proposal: Grain-128. eSTREAM-ECRYPT Stream Cipher Project. 2006./stream/grainp3.html [doi: 10.1109/ISIT.2006.261549][9] De Cannière C, Kücük Ö, Preneel B. Analysis of Grain’s initialization algorithm. In: Vaudenay S, ed. Proc. of the AFRICACRYPT2008. LNCS 5023, Heidelberg: Springer-Verlag, 2008. 276-289.[10] Zhang HN, Wang XY. Cryptanalysis of stream cipher Grain family. Cryptology ePrint Archive Report, 2009/109, 2009./2009/109/[11] Dinur I, Shamir A. Cube attacks on tweakable black box polynomials. In: Joux A, ed. Proc. of the EUROCRYPT 2009. LNCS 5479,Heidelberg: Springer-Verlag, 2009. 278-299. [doi: 10.1007/978-3-642-01001-9_16][12] Aumasson JP, Dinur I, Meier W, Shamir A. Cube testers and key recovery attacks on reduced-round MD6 and Trivium. In:Dunkelman O, ed. Proc. of the FSE 2009. LNCS 5665, Heidelberg: Springer-Verlag, 2009. 1-22. [doi: 10.1007/978-3-642- 03317-9_1][13] De Cannière C, Preneel B. TRIVIUM—A stream cipher construction inspired by block cipher design principles. eSTREAM-ECRYPT Stream Cipher Project Report, 2005/030, 2005. /stream/ciphers/trivium/trivium.pdf[14] Good T, Benaissa M. Hardware performance of eStream phase-III stream cipher candidates. In: Proc. of the SASC 2008. 2008./stvl/sasc2008/[15] Lucks S. The saturation attack—A bait for Twofish. In: Matsui M, ed. Proc. of the FSE 2001. LNCS 2355, Heidelberg: Springer-Verlag, 2002. 1-15. [doi: 10.1007/3-540-45473-X_1][16] Knudsen LR. Truncated and higher order differentials. In: Preneel B, ed. Proc. of the FSE’94. LNCS 1008, Heidelberg: Springer-Verlag, 1995. 196-211. [doi: 10.1007/3-540-60590-8_16]宋海欣(1976-),男,山东泗水人,博士生,主要研究领域为流密码.武传坤(1964-),男,博士,研究员,博士生导师,CCF高级会员,主要研究领域为密码学,信息安全.范修斌(1966-),男,博士,教授,博士生导师,主要研究领域为密码学,信息安全.冯登国(1965-),男,博士,研究员,博士生导师,CCF高级会员,主要研究领域为密码学,信息安全.。
密码破译方法和防止密码破译的措施(一)
密码破译方法和防止密码破译的措施(一)密码破译方法和防止密码破译密码是我们日常生活和工作中保护个人隐私和保密信息的重要工具。
然而,密码破译已经成为黑客和犯罪分子尝试获取未经授权访问的常见方法之一。
本文将介绍一些常见的密码破译方法以及我们可以采取的措施来防止密码被破解。
常见密码破译方法1. 字典攻击字典攻击是通过使用预先准备好的密码字典,尝试将这些密码逐个与目标密码进行匹配。
这些密码字典包含常见密码、常用单词、姓名等。
这种攻击方法通常相对简单,因为很多人习惯使用容易猜测的密码。
2. 暴力破解暴力破解是通过尝试所有可能的密码组合,直到找到正确的密码。
这种攻击方法需要耗费大量的时间和计算资源,但对于复杂密码也是可行的。
3. 社交工程社交工程是通过欺骗或诱使用户泄露密码来获取未经授权访问。
这种攻击方法通常通过钓鱼邮件、欺骗性网站或社交媒体信息等手段进行。
防止密码破译的措施1. 使用强密码使用强密码是防止密码破译的首要措施。
一个强密码应包含大小写字母、数字和特殊字符,长度应在8个字符以上。
避免使用常见的字典单词、个人信息或连续的数字作为密码。
2. 多因素身份验证多因素身份验证是一种有效的防止密码破译的方法。
通过结合密码和额外的验证因素,如指纹识别、短信验证码或硬件令牌,可以大大增加账户的安全性。
3. 定期修改密码定期修改密码可以降低密码被破译的概率。
建议每3-6个月更改一次密码,并避免在多个账户中使用相同的密码。
4. 使用密码管理器密码管理器是一个有用的工具,可以帮助我们创建并管理安全的密码。
它可以保存密码,生成强密码,并自动填充登录表单,避免使用相同的密码。
5. 注意钓鱼攻击钓鱼攻击是获取密码的常见手段之一。
我们应该警惕来自陌生发件人的可疑电子邮件,以及要求我们提供个人信息或密码的任何网站或应用程序。
6. 加密存储和传输对于存储在我们自己的设备或云端的密码,我们应该使用加密的存储方式。
同时,在传输密码时,应尽量使用加密的通信通道,如HTTPS。
密码硬解诈骗手法
THANKS
感谢观看
。
在密码硬解过程中,攻击者会使用专门 的破解工具,通过穷举、字典、混合攻
击等方式尝试猜测目标密码。
由于密码硬解需要大量的计算资源和时 间,因此通常适用于破解较短的密码或 弱密码。对于复杂长密码,密码硬解的
破解难度非常大。
密码硬解原理
01
穷举攻击
穷举攻击是一种最基本的密码破解方法,攻击者会尝试所有可能的密码
案例二:网络钓鱼诈骗案例
总结词
网络钓鱼诈骗是一种利用虚假网站或邮件骗 取受害者个人信息和密码的诈骗手法。
详细描述
犯罪分子通常会发送一封看似来自知名机构 或网站的邮件,诱导受害者点击其中的链接 或附件。当受害者访问这些虚假网站或下载 恶意软件时,犯罪分子便会盗取其个人信息 和密码。网络钓鱼诈骗通常针对个人和企业 ,利用人们对知名机构的信任进行欺诈。
虚拟货币诈骗
总结词
虚拟货币诈骗是一种利用虚拟货币进行密码硬解诈骗的手法。
详细描述
犯罪分子通常会以高回报为诱饵,诱骗受害人投资虚拟货币。在受害人投资后,犯罪分子可能会消失 匿迹,或者以各种理由拒绝兑现承诺的回报。此外,有些犯罪分子还会通过虚假交易、恶意挖矿等方 式骗取受害人的虚拟货币。
03
防范密码硬解诈骗的措施
提高安全意识
01
了解密码硬解诈骗的手法和常见 形式,提高对诈骗行为的警觉性 。
02
时刻保持头脑清醒,不轻易相信 陌生人和陌生信息,避免被诱导 泄露个人信息。
定期更换密码
定期更换密码,增加密码被破解的难 度。
使用复杂且难以猜测的密码组合,包 括数字、字母和特殊字符,以提高密 码的安全性。
使用安全软件
Hashcat
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第32卷第1期 2010年1月 电子与信息学报
Journal of Electronics&Information Technology Vo1.32NO.1
Jan.2010
3D密码的Square攻击 王美一 唐学海 李超 屈龙江 f国防科技大学数学与系统科学系 长沙410073) f东南大学移动通信国家重点实验室 南京210096)
摘要:3D密码是CANS 2008提出的新的分组密码算法,与以往的分组密码算法不同,该密码采用3维结构。 该文根据3D密码的结构特性,得到了3D密码的5.25轮和6.25轮新的Square区分器,重新评估了其抗Square 攻击的强度。攻击结果表明:新区分器对6轮3D密码攻击的数据复杂度和时间复杂度比已有的结果好,并且还可 应用到7轮,8轮和9轮的3D密码攻击中。 关键词:分组密码;3D密码;Square攻击 中图分类号:TN918.1 文献标识码:A 文章编号:1009.5896(2010)01—0157-05 DOI:10.3724/SP.J.1146.2008.01846
Square Attacks on 3D Cipher Wang Mei—yi①Tang Xue—hai①Li Chao① Qu Long-jiang①② (Department 01 Mathematics and System Science1 National University 0{Defense Technology Changsha 410073}China) (National Mobile Communications Research Laboratory,Southeast University,Nanjing 210096,China)
Abstract:3D cipher is a new block cipher proposed in CANS 2008.It is different from all known block cipher as it uses the three dimension structure.According to the structure properties of 3D cipher.a new 5.25一round and a new 6.25一round square distinguishers are presented.and the square attacks on reduced—round 3D are improved. Attacking results demonstrate that 6-round attack is better than the known square attacks in data complexity and time complexity.Moreover,these two new distinguishers can be applied to 7/8/9一round 3D cipher. Key words:Block cipher;3D cipher;Square attack
1 引言 3D密码是Nakahara Jr.J在CANS 2008上提 出的一种新的SPN型分组密码算法[1】'其主要设计 思想来源于AES密码[2】0在AES中,明文、密文、 中间状态都被表示为一个2维的4 X 4字节矩阵进行 处理。3D密码则把它们表示为4×4×4的3维字节 矩阵,因而可形象地把它们看作是一个立方体。作 者指出了3D密码由于具有3维结构特性,使得它 在密码设计、安全性和潜在的应用f哈希函数, MAC,流密码,伪随机数生成器1等方面都有很大 的改进。3D密码的安全性仅在原文中给出了粗略的 评估,主要的评估结果见表1。 Square攻击最初是由Knudsen等人在文献f3] 中提出来的,用来分析基于SPN结构的分组密码 Square。Lucks等将此攻击应用于具有Feistel结构 的Twofish密码[4】a此后,Square攻击被广泛地应 用到各种结构的分组密码中,并且取得了较好的结 果【 ,现在,Square攻击被普遍认为是最有效的 密码分析方法之一,抗Square攻击的强度已经成为 衡量新的分组密码安全性的重要标准。
2008-12—31收到,2009-06-29改回 国家自然科学基金(60803156)和东南大学移动通信国家重点实验室 开放基金(w200807)资助课题 通信作者:王美一tomorrow—selly@163.eom
表1文献【1】对3D密码的主要攻击结果 本文主要分析了3D密码的Square攻击,发现 了5.25轮和6.25轮新的Square区分器,并给出了 低轮3D密码的Square攻击,这些结果都优于原文 献,见表2。这表示低轮的3D密码对Square攻击 是不抵抗的,但这并不能表明完整的3D密码是不 安全的,其安全性有待进一步的研究。
2 3D密码简介 本文中所涉及到的符号如下: 为512.bit的 明文, 为512一bit的密文, 、为第i个密文的第 J个字节,7- 为i轮的轮函数,琏为第i轮的密钥, 为砖的第J个字节,f。g为表示函数,和g的复合 运算,即f O 9( )=ffg(z)1。 3D密码的分组长度和密钥长度均为512 bit, 都可表示为4×4X4的3维字节矩阵。 对于64个字节的数据分组,按照图1排列。 158 电子与信息学报 第32卷 表2 3D密码的Square攻击的比较
注:下标①表示应用的是5.25轮区分器,②表示应用的是6.25轮区 分器
Zn 4 8 X12 I%X9 j3 2 6 l0 14 7 l1 I5 X16 XI7 Xl8 19 Z2o 2I 22 3 24 5 26 7 茁28 X29 30 X31 32 X33 X34 35 36 37 38 3239 Z蛐 l X42 3 茁44 46 47 48 4口 茁5L) 51 52 53 54 55 Z56 5 58 9 60 l 62 63
3D密码的加密轮数是22轮。r轮(0<r 22) 的加密过程如下:设明文分组为 ,第i轮的轮函数 为 : ri( )=7r o 。d2+1。 o (X)=7r( 。d2+1 ( ( ( )))),0 i r一2。最后一轮没有7r但增加 了 ,即最后一轮的轮函数为7-r一】(X)= 。 ) od2+1 o7。 一1( )。其中 是将512一bit密钥 按比特位直接与数据进行异或; 是对数据的每一 个字节都进行相同的 盒操作,采用的是AES中的 盒;01, 相当于AES中的行移位操作;01把图1 变换为图2排列; 把图1变换为图3排列。
{) 10 5
Z4 3214 3 8 I3 2 Xl2 I 6 1 02。1。 1 。'。 2 4 o 。 。 。 16 I 26 1 20 30 19 9 18 3 B B B B B B B B B B 口 Z28 17 Z22
7 32 37 42 7 图2 36 Z4I 46 5 4l_ 34 3239 44 Z33 38 43 48 3 58 52 7 62 51 56 %1 50 55
60 9 54 %g
B B B B B B B B 0 Z4 8 X12 Z17 X21 25 2。 X X38 42 46 X51 Z55 5。 63 16茁20 02a 28 Z33 Z37 41 X45 气0 4屯8 62 3 7 】】 15 32 X36 40 Z X49 Z53 57 Z61 %X10墨4 Z】9 3223 Z27 m 图3 Z48 52 56 560 Xi Z5 Z0 Z13 0l8 2 6毛0 35 30 Z43 47 7r相当于AES中的列混合操作,这里使用的是 Anubis密码[9】中4×4的MDS矩阵。密钥扩展算法 与本文分析无关,不再赘述。 3 3D密码的Square攻击 首先给出/l集的概念: Square攻击和以集的概念是由Knudsen等人 在文献f31中引入的。记,集是一个字节集的256个 状态集。状态集的元素是i∈{0,1,…,255},其中 ,) 是 ( 的第J个字节。如果r集中的第J个字节各不 相同,即 ( ,力≠,y【 ),Vi,i ∈f0,1,.一,255}, i≠i , 称之为活跃字节。如果第J个字节保持不变,即 ,y( )= ’ ,Vi,i ∈f0 1一,255},i≠i ,称之为固 定字节,而如果第J个字节的模二加和为0,即 3/( )=0,则称之为平衡字节。为后续讨 ∈{0=}_=255) 论方便, 代表活跃字节,P代表固定字节,而B 代表平衡字节,其它字节用 表示。如果所有字节 为活跃字节和固定字节,称之为/l集。 下面给出文献[1】中的4.25轮区分器(图4),即 若选取明文为只有一个字节是活跃字节的以集,则 可得到以下4.25轮的区分器: A P P A P A P U c, U U U U U 图4文献【1]中的4.25轮区分器 P P P P P P P P r, r, U U U P 4 P A P A P U U U c, U U U P P P p P P P P U U 矿 c, U U U c厂 r, 『, 矿 U A J4 A A A U 扩 (厂 U U r, 矿 矿 U 『, 『, 矿
A A A A A U c厂 r, U U 『,
、IIIlllllP P P P P P P P P P P n_ P P P P P P P P P P P P p p P P P P A A P P P P A P
