2011年南京白下区一模试卷
2011年南京市鼓楼区数学一模试卷答案

3 这个二次函数的关系式为 y=- x2+3x+2. …………………………4 分 4 3 3 (2)y= (x-2)2-1.(或 y= x2-3x+2 ) 4 4 …………………………7 分
24. (本题 8 分) 解: (1)直线 BC 与⊙A 相切. 理由如下:过点 A 作 AD⊥BC,垂足为 D,…………………………1 分 在 Rt△ ADC,∠C=30° ,AC=2,
共有 6 种结果,它们出现的可能性相同.…………………………3 分 所有的结果中,摸到的 2 个球都是白球的结果有 2 种, 1 所以 P(摸出 2 个白球)= . 3 4 (2) …………………………6 分 9 ⑶ 4 …………………………7 分 9 …………………………4 分
数学答案
第 4 页(共 4 页)
O
2 2 2 2 2 2
M A N
D E G F N′ G B C M′
答:ON 至少为 4.5 米…题 10 分) BC 4 解: (1)在 Rt△ ABC 中,AB=4 3,BC=4,∠B=90° ,∴tan∠BAC= = . AB 4 3 ∴tan∠BAC= 3 .∵∠BAC 是锐角,∴∠BAC=30° . 3
(2)设 AB 所在直线的函数关系式为 y=kx+b, 将点 A(0,30),B(7.5,18)代入 y=kx+b 得:
b=30, 18k+b=7.5 b=30, 解得 k=-1.6
…………………………4 分
∴AB 所在直线的函数关系式为 y=-1.6x+30 …………………………6 分 答:AB 所在直线的函数关系式为 y=-1.6x+30. (3) 甲到达扶梯底端所需时间为 60÷ 2.4=25 s, 乙到达扶梯底端所需时间是 18.75 s,
2011年江苏省南京市中考数学试卷及答案(解析版)

南京市2011年初中毕业生学业考试数学数学注意事项:1.本试卷共6页,全卷满分120分,考试时间为120分钟,考生答题全部答在答题卡上,答在本试卷上无效.2.请认真核对监考教师在答题卡上所有粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米的黑色墨水签字笔填写在答题卡及本试卷上.3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需要改动,请用橡皮擦干净后,再选涂其他答案,答非选择题必须0.5毫米黑色墨水签字笔写在答题卡上指定位置,在其他位置答题一律无效.4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确的选项的字母代号填涂在答题卡相应位置.......上)1A.3B.-3C.±3D.【答案】A.【考点】算术平方根。
【分析】利用算术平方根的定义,直接得出结果2.下列运算正确的是A.a2+a3=a5 B.a2•a3=a6C.a3÷a2=a D.(a2)3=a8【答案】C.【考点】指数运算法则。
【分析】a3÷a2=a= a3-2= a3.在第六次全国人口普查中,南京市常住人口约为800万人,其中65岁及以上人口占9.2%.则该市65岁及以上人口用科学记数法表示约为A.0.736×106人B.7.36×104人C.7.36×105人D.7.36×106 人【答案】C.【考点】科学记数法。
【分析】利用科学记数法的定义,直接得出结果:8000000×9.2%=736000=7.36×105.4.为了解某初中学校学生的视力情况,需要抽取部分学生进行调查,下列抽取学生的方法最合适的是A.随机抽取该校一个班级的学生B.随机抽取该校一个年级的学生C.随机抽取该校一部分男生D.分别从该校初一、初二、初三年级中各班随机抽取10%的学生【答案】D.【考点】随机抽样样本的抽取。
2011江苏各地调研试卷试题汇编 . 导数3

江苏省2011百校大联考一模试题14.若函数()|sin |(0)f x x x =≥的图象与过原点的直线有且只有三个交点,交点中横坐标的最大值为α,则2(1)sin 2ααα+=______________.【解析】()|sin |(0)f x x x =≥与直线l 的三个交点如下图所示,令切点为3(,sin ),(,)2A παααπ-∈,在3(,)2ππ上,'()cos f x x =-,故sin cos ααα-=-,即tan αα=,故22(1)sin 2(1tan )sin 2sin 22tan sin cos ααααααααα++===.如东县2011届高三数学最后一次考前适应训练 14、已知函数21()f x x a x =++,33()21g x x a a =-++,若存在 121,[,](1)a a aξξ∈>,使得9|)()(|21≤-ξξg f ,则a 的取值范围是 ▲ .14、(]4,1南京金陵中学2011年高考数学预测卷213.已知函数()f x =3x +2(1)a x -+3x +b 的图象与x 轴有三个不同交点,且交点的横坐标分别可作为抛物线、双曲线、椭圆的离心率,则实数a 的取值范围是 .【解】由题意知,三个交点分别为(1,0),(1x ,0),(2x ,0),且0<1x <1<2x .由(1)f =0可知b =-a -3,所以()f x =3x +2(1)a x -+3x +b =(x -1)(2x +ax +a +3),故2x +ax +a +3=0的两根分别在(0,1),(1,+∞)内.令()g x =2x +ax +a +3,则(0)0(1)0g g >⎧⎨<⎩,得-3<a <-2.南师大附中2011届高三第四次模拟考试 2011、519、已知对任意的实数m ,直线都不与曲线相切. ⑴.求实数的取值范围;⑵.当时,函数y=f (x )的图象上是否存在一点P ,使得点P 到x 轴的距离不小于14.试证明你的结论.【解】⑴.,因对任意,直线都不与相切,故,,实数的取值范围是; ⑵.存在,证明方法1:问题等价于当时,,设,则在上是偶函数,故只要证明当时,, 0=++m y x )(3)(3R ∈-=a ax x x f a ]1,1[-∈x ),3[33)(2+∞-∈-='a a x x f R ∈m 0=++m y x )(x f y =),3[1+∞-∉-a a 31-<-a 31<a ]1,1[-∈x 41|)(|max ≥x f |)(|)(x f x g =)(x g ]1,1[-∈x ]1,0[∈x 41|)(|max ≥xf①当上单调递增,且,;②当,列表:时,,时,,故,由1(1)134f a=-≥及13a<<,解得14a<≤,此时(1)f f-≤成立.故max1()(1)134g x f a==-≥.由124f-=≥及13a<<,解得1143a≤<,此时(1)f f-≥成立.故max1()24g x f=-=≥.故在上至少存在一个,使得成立.②当,列表:]1,0[)(,0)(,0在时xfxfa≥'≤0)0(=f)()(xfxg=41131)1()(max>>-==afxg,310时<<a))((333)(2axaxaxxf-+=-=')3,0(ax∈)()(xfxg-=)1,3(ax∈)()(xfxg=)}(),1(max{)(maxaffxg-=]1,1[-∈xx41|)(|≥xf,310时<<a))((333)(2axaxaxxf-+=-='在上递减,在上递增,注意到(0)0f f ==,且,故时,,时,,故,注意到103a <<,由:,矛盾;,矛盾;故,与矛盾,故假设不成立,原命题成立.连云港市2011届高三年级调研考试20.已知函数222121451()ln ,()ln ,()2,6392f x ax x f x x x x f x x ax a R =+=++=+∈. ⑴.求证:函数()f x 在点(,())e f e 处的切线横过定点,并求出定点的坐标; ⑵.若2()()f x f x <在区间(1,)+∞上恒成立,求a 的取值范围; ⑶.当23a =时,求证:在区间(1,)+∞上,满足12()()()f x g x f x <<恒成立的函数()g x 有无穷多个.【解】⑴.因1()2f x ax x '=+,故()f x 在点(e,(e))f 处的切线的斜率为12k ae e=+,故()f x 在点(,())e f e 处的切线方程为21(2)()1y ae x e ae e =+-++,整理得11(2)()22e y ae x e -=+-,故切线恒过定点1(,)22e .(2) 令x ax x a x f x f x p ln 2)21()()()(22+--=-=<0,对(1,)x ∈+∞恒成立,因(1)[(21)1]()x a x p x x ---'=(*)令()0p x '=,得极值点1x 1=,2121x a =-,①当112a <<时,有1x x 12=>,即1a 21<<时,在(2x ,+∞)上有()0p x '>,此时)(x p 在区间2(,)x +∞上是增函数,并且在该区间上有)(x p ∈2((),)p x +∞,不合题意;②当1a ≥时,有211x x <=,同理可知,)(x p 在区间(1,)+∞上,有)(x p ∈((1),)p +∞,也不合题意;③当12a ≤时,有210a -≤,此时在区间(1,)+∞上恒有()0p x '<,从而)(x p 在区间(1,)+∞上是减函数;)(x f ),0(a )1,(a 13<<a a )3,0(a x ∈)()(x f x g -=)1,3(a x ∈)()(x f x g =)}(),1(max{)(max a f f x g -=⎪⎩⎪⎨⎧<-=-=≤-4131)1(31)1()(a f a f a f ⎪⎪⎩⎪⎪⎨⎧>≤<41410a a ⎪⎩⎪⎨⎧<=--=≥-412)(31)1()(a a a f af a f ⎪⎪⎩⎪⎪⎨⎧<≥4141a a ∀]1,1[-∈x 41|)(|0<x f 31<a要使0)(<x p 在此区间上恒成立,只须满足021)1(≤--=a p 12a ⇒≥-,故1122a -≤≤.综上可知a 的范围是11[,]22-. ⑶.当23a =时,221214514()ln ,()63923f x x x x f x x x =++=+,记22115()()ln ,(1,)39y f x f x x x x =-=-∈+∞.因225650399x x y x x-'=-=>,故21()()y f x f x =-在(1,)+∞上为增函数,故21211()()(1)(1)3f x f x f f ->-=,设11()(),(01)3R x f x λλ=+<<, 则12()()()f x R x f x <<,故在区间()1,+∞上,满足12()()()f x g x f x <<恒成立的函数()g x 有无穷多个.江苏省镇江市2011届高三统考2010年12月 17.已知函数xxx f ln )(=(0,1x x >≠). ⑴.求函数)(x f 的极值;⑵.若不等式axe x >对任意实数x 恒成立,求实数a 的取值范围. 【解】⑴.函数xx x f ln )(=的定义域为),1()1,0(+∞ ,2ln 1()ln x f x x -'=,令()0f x '=,解得e x =,列表);故极小值为)(e f =e ,无极大值.⑵.当0x ≤时,对任意0a ≠,不等式恒成立;当0x >时,在x ae x >两边取自然对数,得ln xx a>, 1当01x <≤时,ln 0x ≤,当0a >,不等式恒成立;如果0a <,ln 0x <, ln 0a x >,不等式等价于ln x a x<,由(1)得,此时(,0)ln xx ∈-∞,不等式不恒成立.2当1x >时,ln 0x >,则0a >,不等式等价于ln x a x <, 由(1)得,此时ln xx的最小值为e ,得0a e <<.综上:a 的取值范围是0a e <<.扬州市第一中学2010-2011学年度第一学期期末考试14.已知函数13()ln 44f x x x x=-++,2()2 4.g x x bx =-+若对任意1(0,2)x ∈,存在2[1,2]x ∈,使12()()f x g x ≥,则实数b 取值范围是 14、b 214≥ 8-20已知函数,其中。
南京市白下区2011届高三年级二模模拟考试数学试卷

图1南京市白下区2011届高三年级二模模拟考试数学试卷一.填空题:(本大题共14小题,每小题5分,共70分)1.已知集合2{|1},{|4}P x x Q x x =<==,则P Q = _________. 2.在复平面内,复数(1)i i -对应的点在第_________象限.3.甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下(单位:t / hm 2)其中产量比较稳定的小麦品种是_________. 4.函数sin()4y x π=-在[0,]π上的单调递增区间是_________.5.执行右边的流程图,最后输出的n 的值是_________.6.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出两个小球,则取出的小球上标注的数字之和为5或7的概率是_________.7.已知,41)6sin(=+πx 则)3(sin )65sin(2x x -+-ππ=_________. 8.已知点(2,)P t 在不等式组4030x y x y --≤⎧⎨+-≤⎩表示的平面区域内,则点(2,)P t 到直线34100x y ++=距离的最大值为_________.9.将一边长为4的正方形纸片按照图中的虚线所示的方法剪开后拼接为一正四棱锥,则该正四棱锥的体积为_________.10.在数列{}n a 中,111a =,且*1332()n n a a n +=-∈N ,则该数列中相邻两项乘积的最小值为_________.11.已知点1F ,2F 分别是双曲线22221 (0,0)x ya b a b -=>>的左、右焦点,过F 1且垂直于x 轴的直线与双曲线交于A ,B 两点,若2ABF ∆是锐角三角形,则该双曲线离心率的取值范围是_________. 12.设O 为坐标原点,给定一个定点(4,3)A , 而点)0,(x B 在x 正半轴上移动,)(x l 表示AB 的长,则△OAB 中两边长的比值)(x l x的最大值为_________. 13.若对[],1,2x y ∈且2xy =总有不等式24ax y-≥-成立,则实数a 的取值范围是_________. (第5题图)14.如果对于函数()f x 定义域内任意的两个自变量的值12,x x ,当12x x <时,都有12()()f x f x ≤,且存在两个不相等的自变量值12,m m ,使得12()()f m f m =,就称()f x 为定义域上的不严格的增函数.已知函数()g x 的定义域、值域分别为A 、B ,{1,2,3}A =,B A ⊆, 且()g x 为定义域A 上的不严格的增函数,那么这样的()g x 共有_________个.二.解答题:(本大题共6小题,共计90分,解答时应写出文字说明、证明或演算步骤) 15、(本小题满分14分)设已知(2cos sin 22a αβαβ+-= ,,(cos 3sin 22b αβαβ+-= ,,其中(0,)αβπ∈、. (1)若32πβα=+,且2a b = ,求βα、的值;(2)若52a b ⋅= ,求βαtan tan 的值.16.(本小题满分14分)如图,四棱锥P-ABCD 中,底面ABCD 为菱形,且60BAD ∠=,侧面PAD 是正三角形,其所在的平面垂直于底面ABCD ,点G 为AD 的中点. (1)求证:BG ⊥面PAD ;(2)E 是BC 的中点,在PC 上求一点F ,使得PG //面DEF.17.(本小题满分15分)某企业有两个生产车间分别在A ,B 两个位置,A 车间有100名员工,B 车间有400名员工,现要在公路AC 上找一点D ,修一条公路BD ,并在D 处建一个食堂,使得所有员工均在此食堂用餐,已知A ,B ,C 中任意两点间的距离均有1 km ,设∠BDC =α,所有员工从车间到食堂步行的总路程为S . (1)写出S 关于α的函数表达式,并指出α的取值范围; (2)问食堂D 建在距离A 多远时,可使总路程S 最少? 18.(本小题满分15分) 如图,椭圆C 的中心在原点,焦点在x 轴上,12,F F 分别是椭圆C 的左、右焦点,M 是椭圆短轴的一个端点,过1F 的直线l 与椭圆交于,A B两点,12MFF ∆的面积为4,2ABF ∆的周长为 (1)求椭圆C 的方程;(2)设点Q 的坐标为(1,0),是否存在椭圆上的点P 及以Q 为圆心的一个圆,使得该圆与直线12,PF PF 都相切,如存在,求出P 点坐标及圆的方程,如不存在,请说明理由. 19.(本小题满分16分) 已知数列{}n a 满足:1n a ≠±,112a =,2213(1)2(1)n n a a +-=-,记数列21n n b a =-,221n n n c a a +=-(n N *∈).FEGDCB AP(1)证明数列{}n b 是等比数列; (2)求数列{}n c 的通项公式;(3)是否存在数列{}n c 的不同项,,i j k c c c (i j k <<)使之成为等差数列?若存在请求出这样的不同项,,i j k c c c (i j k <<);若不存在,请说明理由. 20.(本小题满分16分)已知函数32(1)()ln (1)x x bx c x f x a xx ⎧-+++<=⎨≥⎩的图象过点(1,2)-,且在点(1,(1))f --处的切线与直线510x y -+=垂直.(1)求实数,b c 的值;(2)求()f x 在[1,]e -(e 为自然对数的底数)上的最大值;(3)对任意给定的正实数a ,曲线()y f x =上是否存在两点,P Q ,使得POQ ∆是以O 为直角顶点的直角三角形,且此三角形斜边中点在y 轴上?21.(1)选修4—2:矩阵与变换变换1T 是逆时针旋转2π的旋转变换,对应的变换矩阵是1M ;变换2T 对应的变换矩阵是21101M ⎡⎤=⎢⎥⎣⎦. (ⅰ)求点(2,1)P 在变换1T 作用下的点'P 的坐标;(ⅱ)求函数2y x =的图象依次在变换1T ,2T 作用下所得曲线的方程.22.一投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.经过多次试验,某人投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋. (1)求该人在4次投掷中恰有三次投入红袋的概率; (2)求该人两次投掷后得分ξ的数学期望E ξ.23.设)0,1(F ,点M 在x 轴上,点P 在 y 轴上,且⊥=,2 (1)当点P 在y 轴上运动时,求点N 的轨迹C 的方程;(2)设),(),,(),,(332211y x D y x B y x A 是曲线C 上的点,且|||,||,|成等差数列,当AD 的垂直平分线与x 轴交于点)0,3(E 时,求B 点坐标.参考答案二、解答题:15.解:(1)∵32πβα=+,∴a = (1,)3sin(πα-),b = (21,)3sin(3πα-).由2a b = ,得0)3sin(=-πα,(0,)απ∈,∴33ππαβ==,(k ∈Z).(2)∵a ·b = 2cos 22)cos(13)cos(12sin 3)2cos(22βαβαβαβα--⨯+++=--+=5cos()2αβ++- 3cos()2αβ-,∴25)cos(23)cos(25=--++βαβα,即 )cos(23)cos(βαβα-=+整理得βαβαcos cos sin sin 5=-, ∵A ∈βα、,∴51tan tan -=βα.16.(1)证明:连结BD ,因为四边形ABCD 为菱形,且60BAD ∠=,所以三角形ABD 为正三角形,又因为点G 为AD 的中点,所以BG ⊥AD ;因为面PAD ⊥底面ABCD ,且面PAD 底面ABCD=AD ,所以BG ⊥面PAD .(2)解:当点F 为PC 的中点时,PG //面DEF .连结GC 交DE 于点H .因为E 、G 分别为菱形ABCD 的边BC 、AD 的中点,所以四边形DGEC 为平行四边形,所以点H 为DE 的中点,又点F 为PC 的中点,所以FH 时三角形PGC 的中位线,所以PG //FH . 因为FH ⊂面DEF ,PG ⊄面DEF ,所以PG //面DEF .综上可知,当点F 为PC 的中点时,PG //面DEF . 17.解:(1)在△BCD 中,∵sin 60sin sin(120)BD BC CD αα==︒︒-,∴2sin BD α=,sin(120)sin CD αα︒-=. 则sin(120)1sin AD αα︒-=-,S=sin(120)2400100[1]sin sin ααα︒-⋅+⋅-=cos 450sin αα--,其中π3≤α≤2π3.(2)2sin sin (cos 4)cos sin S ααααα-⋅--'=-=214cos sin αα-. 令S '=0,得1cos 4α=.当1cos 4α>时,S '<0,S 是α的单调减函数;当1cos 4α<时,S '>0,S 是α的单调增函数.∴当1cos 4α=时,S取得最小值.此时,sin α=1sin sin(120)12211sin sin 2AD ααααα+︒-=-=-==11122=(答略)18.解:(1)由题意知:,4,4221==⨯⨯bc b c 22,284==a a ,解得2==c b .∴椭圆的方程为14822=+y x(2)假设存在椭圆上的一点),(00y x P ,使得直线21,PF PF 与以Q 为圆心的圆相切,则Q 到直线21,PF PF 的距离相等,)0,2(),0,2(21F F -1PF :02)2(000=+--y x y y x 2PF:02)2(000=--+y x y y x 2220022001)2(|3|)2(||d y x y y x y d =++=+-=化简整理得083240820020=++-y x x∵ 点在椭圆上,∴822020=+y x 解得20=x 或 80=x (舍).当20=x 时,20±=y ,1=r , ∴ 椭圆上存在点P ,其坐标为)2,2(或)2,2(-,使得直线21,PF PF 与以Q 为圆心的圆1)1(22=+-y x 相切.19.(1)证明:由已知)(0,1*N n b a n n ∈≠±≠,431=b ,)1(2)1(3221n n a a -=-+,)(32*1N n b b nn ∈=+ 所以}{n b 是43为首项,32为公比的等比数列. (2)解:)()32(43*1N n b n n ∈⋅=- ,)()32(4311*12N n b a n n n ∈⋅-=-=- )()32(41*1221N n a a c n n n n ∈⋅=-=-+.(3)解:假设存在k j i c c c ,,满足题意成等差数列,k i j c c c +=2代入得111)32(41)32(41)32(412---⋅+⋅=⋅⋅k i j ,则1232j i j i k j i -+-+-=+,1223j i k j i j i -++---=,左偶右奇不可能成立.所以假设不成立,这样三项不存在.20.解:(1)当1x <时,2'()32f x x x b =-++,由题意得(1)2'(1)5f f -=⎧⎨-=-⎩,即22325b c b -+=⎧⎨--+=-⎩, 解得0b c ==.(2)由(1)知:32(1)()ln (1)x x x f x a xx ⎧-+<=⎨≥⎩①当11x -≤<时,'()(32)f x x x =--.由'()(32)0f x x x =--=得:0x =或23x =;解'()0f x >得203x <<;解'()0f x <得10x -<<或213x <<∴()f x 在(10)-,和2(,1)3上单减,在2(0)3,上单增.∵24(1)2()(0)0(1)0327f f f f -====,,,,∴()f x 在[1,1)-上的最大值为2.②当1x e ≤≤时,()ln f x a x =,当0a ≤时,()0f x ≤;当0a >时,()f x 在[1,]e 单调递增.∴()f x 在[1,]e 上的最大值为a .∴当2a ≥时,()f x 在[1,]e -上的最大值为a ;当2a <时,()f x 在[1,]e -上的最大值为2.(3)假设曲线()y f x =上存在两点,P Q 满足题意,则,P Q 只能在y 轴两侧,不妨设(,())(0)P t f t t >,则32(,)Q t t t -+,且1t ≠.∵POQ 是以O 为直角顶点的直角三角形,∴0OP OQ =,即232()()0t f t t t -++=(*).是否存在,P Q 等价于方程(*)是否有解.①若01t <<,则32()f t t t =-+,代入方程(*)得:23232()()0t t t t t -+-++=,即:4210t t -+=,而此方程无实数解,从而1t >,∴()ln f t a t =,代入方程(*)得:232ln ()0t a t t t -++= ,即:1(1)ln t t a=+, 设()(1)ln (1)h x x x x =+≥,则1'()l n 10h x x x=++>在[1,)+∞恒成立,∴()h x 在[1,)+∞上单调递增,从而()(1)0h x h ≥=,则()h x 的值域为[0,)+∞.∴当0a >时,方程1(1)ln t t a=+有解,即方程(*)有解.∴对任意给定的正实数a ,曲线()y f x =上总存在两点,P Q ,使得POQ 是以O 为直角顶点的直角三角形,且此三角形斜边中点在y 轴上. 21.(1)解:(ⅰ)10110M -⎡⎤=⎢⎥⎣⎦,12012111012M --⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦,所以点(2,1)P 在1T 作用下的点'P 的坐标是'(1,2)P -.(ⅱ)211110M M M -⎡⎤==⎢⎥⎣⎦,设x y ⎡⎤⎢⎥⎣⎦是变换后图像上任一点,与之对应的变换前的点是00x y ⎡⎤⎢⎥⎣⎦,则00x x M y y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,也就是⎧⎨⎩000x y x x y -==,即⎧⎨⎩00x yy y x ==-,所以,所求曲线的方程是2y x y -=. (2)解:1sin 322πρθρθθ-由sin(-)=3得:()=3,660y y ∴=-+=, 由2cos 2sin x y θθ=⎧⎨=⎩得224x y +=∴圆心到直线l 的距离632d ==,所以,P 到直线l 的距离的最大值为5d r +=.22.解:(1)“飞碟投入红袋”,“飞碟投入蓝袋”,“飞碟不入袋”分别记为事件A ,B ,C .则4110025)()(,2110050)(=====C P B P A P .因每次投掷飞碟为相互独立事件,故4次投掷中恰有三次投入红袋的概率为41)211()21()3(3344=-=C P .(2)两次投掷得分ξ的得分可取值为0,1,2,3,4则161)()()0(===C P C P P ξ,8141412)()()1(12=⨯⨯===C P B P C P ξ,165)()()()()2(12=+==B P B P C P A P C P ξ, 41)()()3(12===C P A P C P ξ,41)()()4(===A P A P P ξ, 2541441316528111610=⨯+⨯+⨯+⨯+⨯=∴ξE . 23.解:(1)设(,)N x y ,则由2MN MP = 得P 为MN 中点,所以)2,0(),0,(yP x M -.又PF PM ⊥得0PM PF ⋅= ,)2,1(),2,(yy x PM -=--=,所以x y 42=(0≠x ). (2)由(1)知)0,1(F 为曲线C 的焦点,由抛物线定义知,抛物线上任一点),(000y x P 到F 的距离等于其到准线的距离,即2||00p x F P +=,所以2||,2||,2||321px p x p x +=+=+=,根据|||,||,|成等差数列,得2312x x x =+,直线AD 的斜率为312123131313444y y y y y y x x y y +=--=--,所以AD 中垂线方程为)3(431-+-=x y y y ,。
2011年南京市中考数学试卷
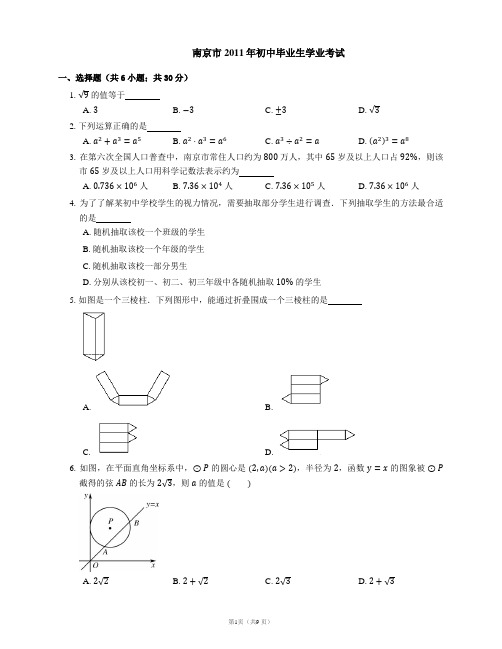
南京市2011年初中毕业生学业考试一、选择题(共6小题;共30分)1. 的值等于A. B. C. D.2. 下列运算正确的是A. B. C. D.3. 在第六次全国人口普查中,南京市常住人口约为万人,其中岁及以上人口占,则该市岁及以上人口用科学记数法表示约为A. 人B. 人C. 人D. 人4. 为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的是A. 随机抽取该校一个班级的学生B. 随机抽取该校一个年级的学生C. 随机抽取该校一部分男生D. 分别从该校初一、初二、初三年级中各随机抽取的学生5. 如图是一个三棱柱.下列图形中,能通过折叠围成一个三棱柱的是A. B.C. D.6. 如图,在平面直角坐标系中,的圆心是,半径为,函数的图象被截得的弦的长为,则的值是A. B. C. D.二、填空题(共10小题;共50分)7. 的相反数是.8. 如图,过正五边形的顶点作直线,则.9. 计算:.10. 等腰梯形的腰长为,它的周长是,则它的中位线长为.11. 如图,以为圆心,任意长为半径画弧,与射线交于点,再以为圆心,长为半径画弧,两弧交于点,画射线,则的值等于.12. 如图,菱形的边长是,是的中点,且,则菱形的面积为.13. 如图,海边立有两座灯塔,,暗礁分布在经过,两点的弓形(弓形的弧是的一部分)区域内,.为了避免触礁,轮船与,的张角的最大值为.14. 如图,,分别是正方形的边,上的点,,连接,.将绕正方形的中心按逆时针方向旋转到,旋转角为(),则.15. 设函数与的图象的交点坐标为,则的值为.16. 甲、乙、丙、丁四位同学围成一圈依序循环报数,规定:①甲、乙、丙、丁首次报出的数依次为,,,,接着甲报,乙报,按此规律,后一位同学报出的数比前一位同学报出的数大.当报到的数是时,报数结束;②若报出的数为的倍数,则报该数的同学需拍手一次.在此过程中,甲同学需拍手的次数为.三、解答题(共8小题;共104分)17. 解不等式组并写出不等式组的整数解.18. 计算:.19. 解方程.20. 某校部分男生分组进行引体向上训练.对训练前后的成绩进行统计分析,相应数据的统计图如下.(1)求训练后第一组平均成绩比训练前增长的百分数;(2)小明在分析了图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的,所以第二组的平均成绩不可能提高个这么多.”你同意小明的观点吗?请说明理由;(3)你认为哪一组的训练效果最好?请提供一个解释来支持你的观点.21. 从名男生和名女生中随机抽取 2014 年南京青奥会志愿者.求下列事件的概率:(1)抽取名,恰好是女生;(2)抽取名,恰好是名男生和名女生.22. 已知函数(是常数).(1)求证:不论为何值,该函数的图象都经过轴上的一个定点;(2)若该函数的图象与轴只有一个交点,求的值.23. 如图,某数学课外活动小组测量电视塔的高度.他们借助一个高度为的建筑物进行测量,在点处测得塔顶的仰角为,在点处测得的仰角为(,,三点在一条直线上).求电视塔的高度.(参考数据:,,)24. 如图1,为内一点,连接,,,在,和中,如果存在一个三角形与相似,那么就称为的自相似点.(1)如图2,已知中,,,是上的中线,过点作,垂足为.试说明是的自相似点;(2)在中,.(i)如图 3,利用尺规作出的自相似点(写出作法并保留作图痕迹);(ii)若的内心是该三角形的自相似点,求该三角形三个内角的度数.答案第一部分1. A2. C3. C 【解析】因为万,所以首先确定为,再根据的位数为位可得,所以用科学记数法表示为.4. D 【解析】根据抽查的特点,对照每个选项的具体内容可得,答案选择D.这是因为分别从该校初一、初二、初三年级中各班随机抽取的学生,能够确保每位学生都有被抽到的可能,从而保证了抽查的全面性和随机性.5. B【解析】动手操作用纸片去折,看能不能折成三棱柱,观察就能得出答案选择 B.本题也可以直接发挥空间想象能力,通过观察所给四个选项中的展开图,得出答案.6. B 【解析】作,轴,垂足分别为,,交于点,连接.可得.根据勾股定理可得.因为的圆心是,所以,当时,,所以,所以,所以,所以,所以,所以,所以,所以.第二部分7.8.【解析】如图,连接.因为五边形是正五边形,所以,,所以.又因为,,所以,根据两直线平行,内错角相等可得.9.【解析】.10.11.【解析】根据作图过程可知,所以三角形是等边三角形,所以,所以.12.【解析】因为在菱形中,所以.因为是中点,所以.又因为,所以,所以菱形的面积为.13.【解析】首先根据题意确定张角的最大值的情况是点正好在圆周上.根据同弧所对的圆周角等于圆心角的一半,可得弧所对的圆周角为.再根据圆外角小于圆周角可得为了避免触礁,轮船与,的张角的最大值为.14.15.【解析】因为函数与的图象的交点坐标为,所以,,所以,.故.16.【解析】本题难度中等,考查学生探究数的规律的能力.根据①可知:甲报到的数除以余数为,即为,,,,.再根据②若报出的数为的倍数,则报该数的同学需拍手一次,所以甲同学需要拍手的次数为.第三部分17. 解不等式,得解不等式,得所以,不等式组的解集是.不等式组的整数解是,,.18.19. 移项,得配方,得由此可得20. (1)训练后第一组平均成绩比训练前增长的百分数是.(2)我不同意小明的观点,因为第二组的平均成绩增加(个).(3)我认为第一组训练效果最好,因为训练后第一组平均成绩比训练前增长的百分数最大.21. (1)抽取名,恰好是女生的概率是.(2)分别用男、男、男、女、女表示这位同学.从中任意抽取名,所有可能出现的结果有(男,男),(男,男),(男,女),(男,女),(男,男),(男,女),(男,女),(男,女),(男,女),(女,女),共有种,它们出现的可能性相同.所有的结果中,满足抽取名,恰好是名男生和名女生(记为事件)的结果有种,所以.22. (1)当时,.所以不论为何值,函数的图象都经过轴上的一个定点.(2)(i)当时,函数的图象与轴只有一个交点;(ii)当时,若函数的图象与轴只有一个交点,则方程有两个相等的实数根.所以,.综上,若函数的图象与轴只有一个交点,则的值为或.23. 在中,,.在中,,.在中,,..答:电视塔的高度约为.24. (1)在中,,是上的中线,...,...是的自相似点.(2)(i)如图所示,作法如下:①在内,作;②在内,作,交于点.则为的自相似点.(ii)连接,.是的内心,,.为的自相似点,.,,.,..该三角形三个内角的度数分别为,,.。
2011年江苏省南京市中考数学试卷

2011年江苏省南京市中考数学试卷一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(2分)的值等于()A.3B.﹣3C.±3D.2.(2分)下列运算正确的是()A.a2+a3=a5B.a2•a3=a6C.a3+a2=a D.(a2)3=a6 3.(2分)在第六次全国人口普查中,南京市常住人口约为800万人,其中65岁及以上人口占9.2%,则该市65岁及以上人口用科学记数法表示约为()A.0.736×106人B.7.36×104人C.7.36×105人D.7.36×106人4.(2分)为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的是()A.随机抽取该校一个班级的学生B.随机抽取该校一个年级的学生C.随机抽取该校一部分男生D.分别从该校初一、初二、初三年级中各随机抽取10%的学生5.(2分)如图是一个三棱柱.下列图形中,能通过折叠围成一个三棱柱的是()A.B.C.D.6.(2分)如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是()A.2B.2+C.2D.2+二、填空题(本大题共10小题,每小题2分,共20分,不需写出解答过程,请把答案直接填写在答题卡相应位置上)7.(2分)﹣2的相反数是.8.(2分)如图,过正五边形ABCDE的顶点A作直线l∥CD,则∠1=.9.(2分)计算(+1)(2﹣)=.10.(2分)等腰梯形的腰长为5cm,它的周长是22cm,则它的中位线长为cm.11.(2分)如图所示,以O为圆心,任意长为半径画弧.与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于.12.(2分)如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为cm2.13.(2分)如图,海边立有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°.为了避免触礁,轮船P与A、B的张角∠APB的最大值为.14.(2分)如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则∠α=.15.(2分)设函数y=与y=x﹣1的图象的交点坐标为(a,b),则﹣的值为.16.(2分)甲、乙、丙、丁四位同学围成一圈依序循环报数,规定:①甲、乙、丙、丁首次报出的数依次为1、2、3、4,接着甲报5,乙报6…按此规律,后一位同学报出的数比前一位同学报出的数大1.当报到的数是50时,报数结束;②若报出的数为3的倍数,则报该数的同学需拍手一次.在此过程中,甲同学需拍手的次数为.三、解答题(本大题共12小题,共88分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.(6分)解不等式组>,并写出不等式组的整数解.18.(6分)计算(﹣)÷.19.(6分)解方程:x2﹣4x﹣1=0.20.(7分)某校部分男生分3组进行引体向上训练.对训练前后的成绩进行统计分析,相应数据的统计图如下.(1)求训练后第一组平均成绩比训练前增长的百分数;(2)小明在分析了图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均成绩不可能提高3个这么多.”你同意小明的观点吗?请说明理由;(3)你认为哪一组的训练效果最好?请提供一个解释来支持你的观点.21.(7分)如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.(1)求证:△ABF≌△ECF;(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.22.(7分)小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中的折线表示小亮在整个行走过程中y与x的函数关系.(1)小亮行走的总路程是m,他途中休息了min;(2)①当50≤x≤80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?23.(7分)从3名男生和2名女生中随机抽取2014年南京青奥会志愿者.求下列事件的概率:(1)抽取1名,恰好是女生;(2)抽取2名,恰好是1名男生和1名女生.24.(7分)已知函数y=mx2﹣6x+1(m是常数).(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;(2)若该函数的图象与x轴只有一个交点,求m的值.25.(7分)如图,某数学课外活动小组测量电视塔AB的高度.他们借助一个高度为30m的建筑物CD进行测量,在点C处测得塔顶B的仰角为45°,在点E 处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)26.(8分)如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.(1)当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;(2)已知⊙O为△ABC的外接圆.若⊙P与⊙O相切,求t的值.27.(9分)如图①,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.(1)如图②,已知Rt△ABC中,∠ACB=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE丄CD,垂足为E.试说明E是△ABC的自相似点;(2)在△ABC中,∠A<∠B<∠C.①如图③,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.28.(11分)【问题情境】已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?【数学模型】设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+)(x>0).【探索研究】(1)我们可以借鉴以前研究函数的经验,先探索函数y=x+(x>0)的图象和性质.①填写下表,画出函数的图象;②观察图象,写出该函数两条不同类型的性质;③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=x+(x>0)的最小值.【解决问题】(2)用上述方法解决“问题情境”中的问题,直接写出答案.2011年江苏省南京市中考数学试卷参考答案与试题解析一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(2分)的值等于()A.3B.﹣3C.±3D.【解答】解:∵=3,故选:A.2.(2分)下列运算正确的是()A.a2+a3=a5B.a2•a3=a6C.a3+a2=a D.(a2)3=a6【解答】解:A、a2与a3不是同类项,不能合并,故本选项错误;B、a2•a3=a2+3=a5≠a6,故本选项错误;C、a3与a2不是同类项,不能合并,故本选项错误;D、(a2)3=a2×3=a6,故本选项正确.故选:D.3.(2分)在第六次全国人口普查中,南京市常住人口约为800万人,其中65岁及以上人口占9.2%,则该市65岁及以上人口用科学记数法表示约为()A.0.736×106人B.7.36×104人C.7.36×105人D.7.36×106人【解答】解:该市65岁及以上人口:8000000×9.2%=736000(人)将736 000人用科学记数法表示7.36×105人.故选:C.4.(2分)为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的是()A.随机抽取该校一个班级的学生B.随机抽取该校一个年级的学生C.随机抽取该校一部分男生D.分别从该校初一、初二、初三年级中各随机抽取10%的学生【解答】解:因为要了解初中的视力情况范围较大、难度较大,所以应采取抽样调查的方法比较合适,本题考查的是调查方法的选择,正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析,故只有D符合实际并具有普遍性,故选:D.5.(2分)如图是一个三棱柱.下列图形中,能通过折叠围成一个三棱柱的是()A.B.C.D.【解答】解:A、折叠后有二个侧面重合,不能得到三棱柱;B、折叠后可得到三棱柱;C、折叠后有二个底面重合,不能得到三棱柱;D、多了一个底面,不能得到三棱柱.故选:B.6.(2分)如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是()A.2B.2+C.2D.2+【解答】解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.∵PE⊥AB,AB=2,半径为2,∴AE=AB=,PA=2,根据勾股定理得:PE==1,∵点A在直线y=x上,∴∠AOC=45°,∵∠DCO=90°,∴∠ODC=45°,∴△OCD是等腰直角三角形,∴OC=CD=2,∴∠PDE=∠ODC=45°,∴∠DPE=∠PDE=45°,∴DE=PE=1,∴PD=.∵⊙P的圆心是(2,a),∴a=PD+DC=2+.故选:B.二、填空题(本大题共10小题,每小题2分,共20分,不需写出解答过程,请把答案直接填写在答题卡相应位置上)7.(2分)﹣2的相反数是2.【解答】解:﹣2的相反数是:﹣(﹣2)=2,故答案为:2.8.(2分)如图,过正五边形ABCDE的顶点A作直线l∥CD,则∠1=36°.【解答】解:∵多边形ABCDE是正五边形,∴∠BAE==108°,∠ABE=∠AEB,又∵∠2=∠ABE,∠1=∠AEB,∴∠1=∠2=(180°﹣∠BAE),即2∠1=180°﹣108°,∴∠1=36°.故答案为:36°.9.(2分)计算(+1)(2﹣)=.【解答】解:(+1)(2﹣),=2﹣×+1×2﹣1×,=2﹣2+2﹣,=.故答案为:.10.(2分)等腰梯形的腰长为5cm,它的周长是22cm,则它的中位线长为6 cm.【解答】解:∵等腰梯形的腰长为5cm,它的周长是22cm,∴AD+BC=22﹣5﹣5=12,∵EF为梯形的中位线,∴EF=(AD+BC)=6.故答案为:6.11.(2分)如图所示,以O为圆心,任意长为半径画弧.与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于.【解答】解:连接AB,由图可知:OA=0B,AO=AB∴OA=AB=OB,即三角形OAB为等边三角形,∴∠AOB=60°,∴cos∠AOB=cos60°=.故答案是:.12.(2分)如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为2cm2.【解答】解:∵E是AB的中点,∴AE=1cm,∵DE丄AB,∴DE==cm.∴菱形的面积为:2×=2cm2.故答案为:2.13.(2分)如图,海边立有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°.为了避免触礁,轮船P与A、B的张角∠APB的最大值为40°.【解答】解:∵海边立有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°.∴当P点在圆上时,不进入经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,轮船P与A、B的张角∠APB的最大,此时为∠AOB=80°的一半,为40°.故答案为:40°.14.(2分)如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则∠α=90°.【解答】解:∵四边形ABCD是正方形.∴∠AOB=90°,故α=90°.故答案是:90°.15.(2分)设函数y=与y=x﹣1的图象的交点坐标为(a,b),则﹣的值为﹣.【解答】解:∵函数y=与y=x﹣1的图象的交点坐标为(a,b),∴b=,b=a﹣1,∴ab=2,b﹣a=﹣1,∴﹣==﹣.故答案为:﹣.16.(2分)甲、乙、丙、丁四位同学围成一圈依序循环报数,规定:①甲、乙、丙、丁首次报出的数依次为1、2、3、4,接着甲报5,乙报6…按此规律,后一位同学报出的数比前一位同学报出的数大1.当报到的数是50时,报数结束;②若报出的数为3的倍数,则报该数的同学需拍手一次.在此过程中,甲同学需拍手的次数为4.【解答】解:∵甲、乙、丙、丁首次报出的数依次为1、2、3、4,接着甲报5,乙报6…按此规律,后一位同学报出的数比前一位同学报出的数大1.当报到的数是50时,报数结束;∴50÷4=12余2,∴甲共报数13次,分别为1,5,9,13,17,21,25,29,33,37,41,45,49,∴报出的数为3的倍数,则报该数的同学需拍手一次.在此过程中,甲同学需报到:9,21,33,45这4个数时,应拍手4次.故答案为:4.三、解答题(本大题共12小题,共88分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.(6分)解不等式组>,并写出不等式组的整数解.,【解答】解:>由①得:x≥﹣1,由②得:x<2,∴不等式组的解集为:﹣1≤x<2,∴不等式组的整数解是:﹣1,0,1.18.(6分)计算(﹣)÷.【解答】解:原式=(﹣)•=(﹣)•(﹣),=﹣•,=﹣.19.(6分)解方程:x2﹣4x﹣1=0.【解答】解:∵x2﹣4x﹣1=0,∴x2﹣4x=1,∴x2﹣4x+4=1+4,∴(x﹣2)2=5,∴x=2±,∴x1=2+,x2=2﹣.20.(7分)某校部分男生分3组进行引体向上训练.对训练前后的成绩进行统计分析,相应数据的统计图如下.(1)求训练后第一组平均成绩比训练前增长的百分数;(2)小明在分析了图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均成绩不可能提高3个这么多.”你同意小明的观点吗?请说明理由;(3)你认为哪一组的训练效果最好?请提供一个解释来支持你的观点.【解答】解:(1)训练后第一组平均成绩比训练前增长的百分数是×100%≈67%;(2)我不同意小明的观点,设第二组男生的人数为x人,第二组的平均成绩增加(8×10%•x+6×20%•x+5×20%•x+0×50%•x)÷x=3个.故不同意小明的观点;(3)本题答案不唯一,下列解法供参考.我认为第一组的训练效果最好;训练后每组的平均成绩比训练前增长的百分数分别为:第一组:×100%≈67%,第二组:×100%=50%,第三组:×100%≈22%,训练后第一组的平均成绩比训练前增长的百分数最大,所以第一组的训练效果最好.21.(7分)如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.(1)求证:△ABF≌△ECF;(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,∴∠ABF=∠ECF,∵EC=DC,∴AB=EC,在△ABF和△ECF中,∵∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,∴△ABF≌△ECF(AAS).(2)∵AB=EC,AB∥EC,∴四边形ABEC是平行四边形,∴FA=FE,FB=FC,∵四边形ABCD是平行四边形,∴∠ABC=∠D,又∵∠AFC=2∠D,∴∠AFC=2∠ABC,∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB,∴FA=FE=FB=FC,∴AE=BC,∴四边形ABEC是矩形.22.(7分)小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中的折线表示小亮在整个行走过程中y与x的函数关系.(1)小亮行走的总路程是3600m,他途中休息了20min;(2)①当50≤x≤80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?【解答】解:(1)3600,20;(2)①当50≤x≤80时,设y与x的函数关系式为y=kx+b,根据题意,当x=50时,y=1950;当x=80时,y=3600∴解得:∴函数关系式为:y=55x﹣800.②缆车到山顶的线路长为3600÷2=1800米,缆车到达终点所需时间为1800÷180=10分钟小颖到达缆车终点时,小亮行走的时间为10+50=60分钟,把x=60代入y=55x﹣800,得y=55×60﹣800=2500.∴当小颖到达缆车终点时,小亮离缆车终点的路程是3600﹣2500=1100米.23.(7分)从3名男生和2名女生中随机抽取2014年南京青奥会志愿者.求下列事件的概率:(1)抽取1名,恰好是女生;(2)抽取2名,恰好是1名男生和1名女生.【解答】解:(1)5名学生中有2名女生,所以抽取1名,恰好是女生的概率为;(2)由树形图可得出:共有20种情况,恰好是1名男生和1名女生的情况数有12种,所以概率为.24.(7分)已知函数y=mx2﹣6x+1(m是常数).(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;(2)若该函数的图象与x轴只有一个交点,求m的值.【解答】解:(1)当x=0时,y=1.所以不论m为何值,函数y=mx2﹣6x+1的图象都经过y轴上一个定点(0,1);(2)①当m=0时,函数y=mx2﹣6x+1的图象与x轴只有一个交点;②当m≠0时,若函数y=mx2﹣6x+1的图象与x轴只有一个交点,则方程mx2﹣6x+1=0有两个相等的实数根,所以△=(﹣6)2﹣4m=0,m=9.综上,若函数y=mx2﹣6x+1的图象与x轴只有一个交点,则m的值为0或9.25.(7分)如图,某数学课外活动小组测量电视塔AB的高度.他们借助一个高度为30m的建筑物CD进行测量,在点C处测得塔顶B的仰角为45°,在点E 处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)【解答】解:在Rt△ECD中,tan∠DEC=,∴EC=≈=40(m),在Rt△BAE中,tan∠BEA=,∴=0.75,∴h=120(m),答:电视塔的高度约为120m.26.(8分)如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.(1)当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;(2)已知⊙O为△ABC的外接圆.若⊙P与⊙O相切,求t的值.【解答】解:(1)直线AB与⊙P相切,如图,过P作PD⊥AB,垂足为D,在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm,∴AB=10cm,∵P为BC中点,∴PB=4cm,∵∠PDB=∠ACB=90°,∠PBD=∠ABC,∴△PBD∽△ABC,∴,即,∴PD=2.4(cm),当t=1.2时,PQ=2t=2.4(cm),∴PD=PQ,即圆心P到直线AB的距离等于⊙P的半径,∴直线AB与⊙P相切;(2)∵∠ACB=90°,∴AB为△ABC的外接圆的直径,∴BO=AB=5cm,连接OP,∵P为BC中点,PO为△ABC的中位线,∴PO=AC=3cm,∵点P在⊙O内部,∴⊙P与⊙O只能内切,∴当⊙P在⊙O内部时:5﹣2t=3,当⊙O在⊙P内部时2t﹣5=3,∴t=1或4,∴⊙P与⊙O相切时,t的值为1或4.27.(9分)如图①,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.(1)如图②,已知Rt△ABC中,∠ACB=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE丄CD,垂足为E.试说明E是△ABC的自相似点;(2)在△ABC中,∠A<∠B<∠C.①如图③,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.【解答】解:(1)在Rt△ABC中,∠ACB=90°,CD是AB上的中线,∴CD=AB,∴CD=BD,∴∠BCE=∠ABC,∵BE⊥CD,∴∠BEC=90°,∴∠BEC=∠ACB,∴△BCE∽△ABC,∴E是△ABC的自相似点;(2)①如图所示,作法:①在∠ABC内,作∠CBD=∠A,②在∠ACB内,作∠BCE=∠ABC,BD交CE于点P,则P为△ABC的自相似点;②∵P是△ABC的内心,∴∠PBC=∠ABC,∠PCB=∠ACB,∵△ABC的内心P是该三角形的自相似点,∴∠PBC=∠A,∠BCP=∠ABC=2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,∴∠A+2∠A+4∠A=180°,∴∠A=,∴该三角形三个内角度数为:,,.28.(11分)【问题情境】已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?【数学模型】设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+)(x>0).【探索研究】(1)我们可以借鉴以前研究函数的经验,先探索函数y=x+(x>0)的图象和性质.①填写下表,画出函数的图象;②观察图象,写出该函数两条不同类型的性质;③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=x+(x>0)的最小值.【解决问题】(2)用上述方法解决“问题情境”中的问题,直接写出答案.【解答】解:(1)①故答案为:,,,2,,,.函数y=x+的图象如图:②答:函数两条不同类型的性质是:当0<x<1时,y 随x的增大而减小,当x>1时,y 随x的增大而增大;当x=1时,函数y=x+(x>0)的最小值是2.③y=x+==+2=+2,∵x>0,所以≥0,所以当x=1时,的最小值为0,∴函数y=x+(x>0)的最小值是2.(2)答:矩形的面积为a(a为常数,a>0),当该矩形的长为时,它的周长最小,最小值是4.。
2011年江苏省南京市中考数学试卷及答案(解析版)
2011年江苏省南京市中考数学试卷及答案(解析版)南京市2011年初中毕业生学业考试数学数学注意事项:1.本试卷共6页,全卷满分120分,考试时间为120分钟,考生答题全部答在答题卡上,答在本试卷上无效.2.请认真核对监考教师在答题卡上所有粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米的黑色墨水签字笔填写在答题卡及本试卷上.3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需要改动,请用橡皮擦干净后,再选涂其他答案,答非选择题必须0.5毫米黑色墨水签字笔写在答题卡上指定位置,在其他位置答题一律无效.4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确的选项的字母代号填涂在答题卡相应位置.......上)13B.-3C.±3D.【答案】A.【考点】算术平方根。
【分析】利用算术平方根的定义,直接得出结果2.下列运算正确的是A.a2+a3=a5 B.a2•a3=a6C.a3÷a2=aD.(a2)3=a8【答案】C.【考点】指数运算法则。
【分析】a3÷a2=a= a3-2= a3.在第六次全国人口普查中,南京市常住人口约为800万人,其中65岁及以上人口占9.2%.则该市65岁及以上人口用科学记数法表示约为A.0.736×106人B.7.36×104人C.7.36×105人D.7.36×106 人【答案】C.【考点】科学记数法。
【分析】利用科学记数法的定义,直接得出结果:8000000×9.2%=736000=7.36×105.4.为了解某初中学校学生的视力情况,需要抽取部分学生进行调查,下列抽取学生的方法最合适的是A.随机抽取该校一个班级的学生B.随机抽取该校一个年级的学生C.随机抽取该校一部分男生D.分别从该校初一、初二、初三年级中各班随机抽取10%的学生【答案】D.【考点】随机抽样样本的抽取。
2011年江苏省南京市中考数学试题(word版及答案)
南京市2011年初中毕业生学业考试数学数学注意事项:1.本试卷共6页,全卷满分120分,考试时间为120分钟,考生答题全部答在答题卡上,答在本试卷上无效.2.请认真核对监考教师在答题卡上所有粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米的黑色墨水签字笔填写在答题卡及本试卷上.3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需要改动,请用橡皮擦干净后,再选涂其他答案,答非选择题必须0.5毫米黑色墨水签字笔写在答题卡上指定位置,在其他位置答题一律无效.4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确的选项的字母代号填涂在答.题卡相应位置......上)1A.3B.-3C.±3D.2.下列运算正确的是A.a2+a3=a5 B.a2•a3=a6C.a3÷a2=a D.(a2)3=a83.在第六次全国人口普查中,南京市常住人口约为800万人,其中65岁及以上人口占9.2%.则该市65岁及以上人口用科学记数法表示约为A.0.736×106人B.7.36×104人C.7.36×105人D.7.36×106 人4.为了解某初中学校学生的视力情况,需要抽取部分学生进行调查,下列抽取学生的方法最合适的是A.随机抽取该校一个班级的学生B.随机抽取该校一个年级的学生C.随机抽取该校一部分男生D.分别从该校初一、初二、初三年级中各班随机抽取10%的学生5.如图是一个三棱柱,下列图形中,能通过折叠围成一个三棱柱的是6.如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P的弦AB的长为a的值是A.B.2+C.D.2A.B.D.(第5题)二、填空题(本大题共10小题,每小题2分,共20分,不需要写出解答过程,请把答案直接填写在答题卡相应位置.......上) 7.-2的相反数是________.8.如图,过正五边形ABCDE 的顶点A 作直线l ∥CD ,则∠1=____________.9.计算1)(2=_______________.10.等腰梯形的腰长为5㎝,它的周长是22㎝,则它的中位线长为___________㎝.11.如图,以O 为圆心,任意长为半径画弧,与射线OM 交于点A ,再以A 为圆心,AO 长为半径画弧,两弧交于点B ,画射线OB ,则cos ∠AOB 的值等于___________.12.如图,菱形ABCD 的连长是2㎝,E 是AB 中点,且DE ⊥AB ,则菱形ABCD 的面积为_________㎝2.13.如图,海边有两座灯塔A 、B ,暗礁分布在经过A 、B 两点的弓形(弓形的弧是⊙O 的一部分)区域内,∠AOB =80°,为了避免触礁,轮船P 与A 、B 的张角∠APB 的最大值为______°.14.如图,E 、F 分别是正方形ABCD 的边BC 、CD 上的点,BE =CF ,连接AE 、BF ,将△ABE 绕正方形的中心按逆时针方向转到△BCF ,旋转角为a (0°<a <180°),则∠a =______. 15.设函数2y x =与1y x =-的图象的交战坐标为(a ,b ),则11a b-的值为__________. 16.甲、乙、丙、丁四位同学围成一圈依序循环报数,规定:①甲、乙、丙、丁首次报出的数依次为1、2、3、4,接着甲报5、乙报6……按此规律,后一位同学报出的数比前一位同学报出的数大1,当报到的数是50时,报数结束; ②若报出的数为3的倍数,则报该数的同学需拍手一次,在此过程中,甲同学需要拍手的次数为____________.三、解答题(本大题共12小题,共88分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)(第12题)(第8题)l(第11题)BA MO(第12题)A(第14题)ABCDF17.(6分)解不等式组523132x x x +⎧⎪+⎨⎪⎩≥>,并写出不等式组的整数解.18.(6分)计算221()a b a b a b b a-÷-+-19.(6分)解方程x 2-4x +1=0 20.(7分)某校部分男生分3组进行引体向上训练,对训练前后的成绩进行统计分析,相应数据的统计图如下.⑴求训练后第一组平均成绩比训练前增长的百分数; ⑵小明在分析了图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均数不可能提高3个这么多.”你同意小明的观点吗?请说明理由;⑶你认为哪一组的训练效果最好?请提出一个解释来支持你的观点.21.(7分)如图,将□ABCD 的边DC 延长到点E ,使CE =DC ,连接AE ,交BC 于点F .⑴求证:△ABF ≌△ECF⑵若∠AFC =2∠D ,连接AC 、BE .求证:四边形ABEC 是矩形.①训练后第二组男生引体向上增加个数分布统计图增加85个②(第20题)B D (第21题)22.(7分)小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.⑴小亮行走的总路程是____________㎝,他途中休息了________min.⑵①当50≤x≤80时,求y与x的函数关系式;②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?23.(7分)从3名男生和2名女生中随机抽取2014年南京青奥会志愿者.求下列事件的概率:⑴抽取1名,恰好是女生;⑵抽取2名,恰好是1名男生和1名女生.24.(7分)已知函数y=mx2-6x+1(m是常数).⑴求证:不论m为何值,该函数的图象都经过y轴上的一个定点;⑵若该函数的图象与x轴只有一个交点,求m的值.25.(7分)如图,某数学课外活动小组测量电视塔AB的高度,他们借助一个高度为30m 的建筑物CD进行测量,在点C处塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)Bh (第25题)(第22题)26.(8分)如图,在Rt △ABC 中,∠ACB =90°,AC =6㎝,BC =8㎝,P 为BC 的中点.动点Q 从点P 出发,沿射线PC 方向以2㎝/s 的速度运动,以P 为圆心,PQ 长为半径作圆.设点Q 运动的时间为t s .⑴当t =1.2时,判断直线AB 与⊙P 的位置关系,并说明理由; ⑵已知⊙O 为△ABC 的外接圆,若⊙P 与⊙O 相切,求t 的值.27.(9分)如图①,P 为△ABC 内一点,连接P A 、PB 、PC ,在△P AB 、△PBC 和△P AC 中,如果存在一个三角形与△ABC 相似,那么就称P 为△ABC 的自相似点.⑴如图②,已知Rt △ABC 中,∠ACB =90°,∠ACB >∠A ,CD 是AB 上的中线,过点B 作BE ⊥CD ,垂足为E ,试说明E 是△ABC 的自相似点.⑵在△ABC 中,∠A <∠B <∠C .①如图③,利用尺规作出△ABC 的自相似点P (写出作法并保留作图痕迹); ②若△ABC 的内心P 是该三角形的自相似点,求该三角形三个内角的度数.28.(11分)问题情境已知矩形的面积为a (a 为常数,a >0),当该矩形的长为多少时,它的周长最小?最小值是多少?数学模型设该矩形的长为x ,周长为y ,则y 与x 的函数关系式为2()(0)a y x x x=+>.探索研究⑴我们可以借鉴以前研究函数的经验,先探索函(第26题)①②③(第27题)数1(0)y x x x=+>的图象性质. ① 填写下表,画出函数的图象: ②②观察图象,写出该函数两条不同类型的性质;③在求二次函数y =ax 2+bx +c (a ≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数1y x x=+(x >0)的最小值. 解决问题⑵用上述方法解决“问题情境”中的问题,直接写出答案.答案:一.选择题:ACCDBB 二.填空:7. 2 8. 36 9.10. 6 11.1212. 13. 40 14. 90 15. 12-16. 4 17.解:解不等式①得:1x ≥- 解不等式②得:2x <所以,不等式组的解集是12x -≤<. 不等式组的整数解是1-,0,1. 18.221)a ba b a b b a-÷-+-解:(()()()()a a b b a b a b a b a b b a ⎡⎤-=-÷⎢⎥+-+--⎣⎦()()b b aa b a b b -=⋅+- 1a b=-+ 19. 解法一:移项,得241x x -=-.配方,得24414x x -+=-+, 2(2)3x -=由此可得2x -=12x =22x =解法二:1,4, 1.a b c ==-=224(4)411120b ac -=--⨯⨯=>,2x ==±12x =,22x =.20.解:⑴训练后第一组平均成绩比训练前增长的百分数是53100%3-⨯≈67%. ⑵不同意小明的观点,因为第二组的平均成绩增加8×10%+6×20%+5×20%+0×50%=3(个).(3)本题答案不唯一,我认为第一组训练效果最好,因为训练后第一组平均成绩比训练前增长的百分数最大.21.证明:⑴∵四边形ABCD 是平行四边形,∴AB ∥CD,AB=CD .∴∠ABF=∠ECF . ∵EC=DC , ∴AB=EC .在△ABF 和△ECF 中,∵∠ABF=∠ECF ,∠AFB=∠EFC ,AB=EC , ∴⊿ABF ≌⊿ECF .(2)解法一:∵AB=EC ,AB ∥EC ,∴四边形ABEC 是平行四边形.∴AF=EF , BF=CF . ∵四边形ABCD 是平行四边形,∴∠ABC=∠D ,又∵∠AFC=2∠D ,∴∠AFC=2∠ABC . ∵∠AFC=∠ABF+∠BAF ,∴∠ABF=∠BAF .∴F A=FB . ∴F A=FE=FB=FC , ∴AE=BC .∴口ABEC 是矩形.解法二:∵AB=EC ,AB ∥EC ,∴四边形ABEC 是平行四边形. ∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠D=∠BCE . 又∵∠AFC=2∠D ,∴∠AFC=2∠BCE ,∵∠AFC=∠FCE+∠FEC ,∴∠FCE=∠FEC .∴∠D=∠FEC .∴AE=AD . 又∵CE=DC ,∴AC ⊥DE .即∠ACE=90°.∴口ABEC 是矩形. 22. 解⑴3600,20.⑵①当5080x ≤≤时,设y 与x 的函数关系式为y kx b =+. 根据题意,当50x =时,1950y =;当80x =,3600y =.所以,y 与x 的函数关系式为55800y x =-.②缆车到山顶的路线长为3600÷2=1800(m ), 缆车到达终点所需时间为1800÷180=10(min ).小颖到达缆车终点时,小亮行走的时间为10+50=60(min ). 把60x =代入55800y x =-,得y=55×60—800=2500.所以,当小颖到达缆车终点时,小亮离缆车终点的路程是3600-2500=1100(m ). 23. 解⑴抽取1名,恰好是女生的概率是25. ⑵分别用男1、男2、男3、女1、女2表示这五位同学,从中任意抽取2名,所有可能出现的结果有:(男1,男2),(男1,男3),(男1,女1),(男1,女2),(男2,男3),(男2,女1),(男2,女2),(男3,女1),(男3,女2),(女1,女2),共10种,它们出现的可能性相同,所有结果中,满足抽取2名,恰好是1名男生和1名女生(记为事件A )的结果共6种,所以P (A )=63105=. 24.解:⑴当x =0时,1y =.所以不论m 为何值,函数261y mx x =-+的图象经过y 轴上的一个定点(0,1). ⑵①当0m =时,函数61y x =-+的图象与x 轴只有一个交点;②当0m ≠时,若函数261y mx x =-+的图象与x 轴只有一个交点,则方程2610mx x -+=有两个相等的实数根,所以2(6)40m --=,9m =.综上,若函数261y mx x =-+的图象与x 轴只有一个交点,则m 的值为0或9. 25.在Rt ECD ∆中,tan DEC ∠=DCEC. ∴EC =tan DC DEC ∠≈30400.75=(m ).在Rt BAC ∆中,∠BCA =45°,∴BA CA =在Rt BAE ∆中,tan BEA ∠=BA EA .∴0.7540hh =+.∴120h =(m ).答:电视塔高度约为120m .26.解⑴直线AB 与⊙P 相切.如图,过点P 作PD ⊥AB , 垂足为D . 在Rt △A BC 中,∠ACB =90°,∵AC =6cm ,BC =8cm ,∴10AB cm ==.∵P 为BC 的中点,∴PB =4cm .∵∠P DB =∠ACB =90°,∠PBD =∠ABC .∴△PBD ∽△ABC . ∴PD PB AC AB =,即4610PD =,∴PD =2.4(cm) . 当 1.2t =时,2 2.4PQ t ==(cm)∴PD PQ =,即圆心P 到直线AB 的距离等于⊙P 的半径. ∴直线AB 与⊙P 相切.⑵ ∠ACB =90°,∴AB 为△ABC 的外切圆的直径.∴152OB AB cm ==. 连接OP .∵P 为BC 的中点,∴132OP AC cm ==. ∵点P 在⊙O 内部,∴⊙P 与⊙O 只能内切. ∴523t -=或253t -=,∴t =1或4. ∴⊙P 与⊙O 相切时,t 的值为1或4.27. 解⑴在Rt △ABC 中,∠ACB =90°,CD 是AB 上的中线,∴12CD AB =,∴CD =BD . ∴∠BCE =∠ABC .∵BE ⊥CD ,∴∠BEC =90°,∴∠BEC =∠ACB .∴△BCE ∽△ABC . ∴E 是△ABC 的自相似点. ⑵①作图略. 作法如下:(i )在∠ABC 内,作∠CBD =∠A ; (ii )在∠ACB 内,作∠BCE =∠ABC ;BD 交CE 于点P . 则P 为△ABC 的自相似点.②连接PB 、PC .∵P 为△ABC 的内心,∴12PBC ABC ∠=∠,12PCB ACB ∠=∠. ∵P 为△ABC 的自相似点,∴△BCP ∽△ABC .∴∠PBC =∠A ,∠BCP =∠ABC=2∠PBC =2∠A , ∠ACB =2∠BCP=4∠A .∵∠A +∠ABC+∠ACB =180°. ∴∠A +2∠A+4∠A =180°. ∴1807A ∠=.∴该三角形三个内角的度数分别为1807、3607、7207.28. 解⑴①174,103,52,2,52,103,174. 函数1y x x=+(0)x >的图象如图.②本题答案不唯一,下列解法供参考.当01x <<时,y 随x 增大而减小;当1x >时,y 随x 增大而增大;当1x =时函数1y x x =+(0)x >的最小值为2. ③1y x x =+=22+=22+-=22+=0,即1x =时,函数1y x x =+(0)x >的最小值为2.。
【VIP专享】南京宣武区2011年中考数学一模试题及答案
,110°40D ∠=°在它的图象上;② 它的图象在
时,随的增大而减
y x (第16题)
图书种类
工具书小说漫画
诗歌80
56
24
100
20轴交于A ,两点,B
C
A
B
请你求出FG的长度.
(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG
向右平移,至F点与B重合时停止.在平移过程中,设
纸片重叠部分面积为.y,求在平移的整个过程中,y与
叠部分面积为10时,平移距离x的值.
(2)的操作中,小明发现在平移过程中,虽然有时平移的距离不等,但两纸片重叠的面积却是相等的;而有时候平移的距离不等,两纸片重叠部分的面积也
等.请探索这两种情况下重叠部分面积y的范围(直接写出结果
,此时概率最小C
A
B
D。
南京市江宁区2011年中考数学一模试卷(含答案)
南京市江宁区2011年中考数学一模试卷(含答案)2011年江宁区初三第二学期一模数学试卷(考试时间:120分钟考试分值:120分)一、选择题(每题2分,共16分) 1.-2的相反数是(▲)11 C. D.2222.要使代数式x?2有意义,则x的取值范围是(▲)A.x?2 B.x?2 C.x?2 D. x??2A.-2 B.?3.在圆锥、长方体、圆柱、正方体这四个几何体中,主视图、左视图和俯视图完全相同的几何体是(▲) A.圆锥 B.长方体 C.圆柱 D.正方体4.南京市深入实施环境污染整治,全市经济开发区的40家化工企业中已关停、整改32家,每年排放的污水减少了167000吨.将167000用科学记数法且保留两个有效数字表示为(▲) A.1.6?105 B.16?104C.1.7?105D.0.17?1065.△ABC中,∠C=90°,AC=8,BC=6,则cosA的值是(▲)A.4 5 B.3 5 C.43 D. 346.如图,利用标杆BE测量建筑物DC的高度,如果标杆BE长为1.5米,测得AB=2米, BC=10米,且点A、E、D在一条直线上,则楼高CD是(▲) A.8米 B.7.5米 C.9米 D.9.5米 7.已知x?3,那么在数轴上与实数x 对应的点可能是(▲)2A.P1B.P4C.P2或P3D. P1或P48.如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2010次输出的结果为(▲) A.3 B.6 C.AE B第6题C第8题322006 D.1 x2321003?3?1003x为偶数 D输入x x为奇数输出 x+3 二、填空题(每空3分,共30分)9.如果x?1是方程x?2a?3的解,那么a? ▲.110.请你写出一个满足不等式2x-1。
