2010年水文水资源硕士复试试卷
工程水文学试题-考试专用复习(客观题)

一、概念题(一)填空题1。
水文学的含义是研究自然界各种水体的存在、分布、循环和物理化学性质及其他环境因素的变化规律,预测、预报各种水文现象的变化情势。
2。
工程水文学的含义是水文学的一个重要分支,为工程规划设计、施工、运营管理提供水文依据的一门科学。
(二) 选择题1.水文现象的发生[D ]。
a。
完全是偶然性的 b。
完全是必然性的c。
完全是随机性的 d。
既有必然性也有随机性4。
水资源是一种[B ]。
a.取之不尽、用之不竭的资源b.再生资源c。
非再生资源 d。
无限的资源9。
水文现象的发生、发展,都具有偶然性,因此,它的发生和变化[B ]。
a杂乱无章。
b。
具有统计规律c。
具有完全的确定性规律 d。
没有任何规律10。
水文现象的发生、发展,都是有成因的,因此,其变化[C].a。
具有完全的确定性规律 b. 具有完全的统计规律c.具有成因规律d. 没有任何规律(三) 判断题3.水文现象的产生和变化,都有其相应的成因,因此,只能应用成因分析法进行水文计算和水文预报.[ F]4。
水文现象的产生和变化,都有某种程度的随机性,因此,都要应用数理统计法进行水文计算和水文预报。
[F]6。
水文现象的变化,如河道某一断面的水位、流量过程,具有完全肯定的多年变化周期、年变化周期和日变化周期。
[F ]8。
水文现象的变化,既有确定性又有随机性,因此,水文计算和水文预报中,应根据具体情况,采用成因分析法或数理统计法,或二者相结合的方法进行研究。
[ T]第二章水文循环与径流形成一、概念题(五)填空题4. 按水文循环的规模和过程不同,水文循环可分为__大_____循环和__小______循环。
11. 一条河流,沿水流方向,自上而下可分为河源、上游、中游、下游、河口五段。
38. 降雨初期的损失包括___蒸发___,__植物截留_____, ___填洼___, ___补充土壤水分。
39。
河川径流的形成过程可分为__产流___________过程和 ____汇流________过程。
2010年工程硕士(GCT)语文真题试卷(题后含答案及解析)

2010年工程硕士(GCT)语文真题试卷(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 阅读理解题选择题(15题,每小题2分)下列每题给出的四个选项中,只有一个选项符合题目要求。
1.下面没有错别字的一句是:A.光阴荏苒,岁月流逝,大学毕业到现在,转眼40多年过去了。
B.与李伯元火辣辣的挖苦讽刺不同,他对社会现实的批判是棉里藏针。
C.万里长堤锁住了桀傲不驯的江河,捍卫着沿江人民的生命财产安全。
D.日军攻占南京后,制造了震惊中外的“南京大屠杀”,30万同胞惨遭杀戳。
正确答案:A解析:(本题考查错别字辨析。
B“棉里藏针”应为“绵里藏针”;C“桀傲不驯”应为“桀骜不驯”;D“杀戳”应为“杀戮”。
)2.下面加下划线的词,意义相同的一组是:A.①这种不良现象的产生往往是受,狭隘利益驱动的结果。
②“边境有边,边贸无边”是对狭隘地域观念的否定。
B.①他似乎生性就很淡漠,对周围的人和事好像从不在意。
②刚刚有些淡漠的卢嘉川的影子,竞又闯入了她的心头。
C.①就是这样可怜的要求,范素云一年也难能满足儿子几次。
②他忙中出错当成抹布,可怜的白围巾成了深灰色的破布。
D.①我恍惚觉得此刻不是身在新疆,而是在江南的什么地方。
②他拖着铅一样沉重的脚步,神情恍惚地回到自己的家中。
正确答案:A解析:(本题考查相同的词在不同语境中的意义辨析。
B①“淡漠”指没有热情,冷淡,②“淡漠”指记忆淡薄,印象不深;C①“可怜”指数量少,②“可怜”为本义;D①“恍惚”为比喻义,“好像”的意思,②“恍惚”指本义。
)3.下面各组成语中,加下划线的意义四个都不相同的一组是:A.沽名钓誉徒有虚名不可名状师出无名B.栉风沐雨捕风捉影移风易俗附庸风雅C.横生枝节起死回生无中生有妙笔生花D.动人心弦兴师动众动辄得咎惊心动魄正确答案:B解析:(本题考查对成语的辨析。
A“沽名钓誉”、“徒有虚名”的“名”同为“名誉”之义;B“栉风沐雨”之“风”为自然之风,“捕风捉影”之“风”为消息,“移风易俗”之“风”为风俗,“附庸风雅”之“风”为诗歌,都不相同;C“横生枝节”、“妙笔生花”的“生”同为“生出”之义;D“动人心弦”、“惊心动魄”的“动”同为“打动”之义。
水高考题整理(修改版)
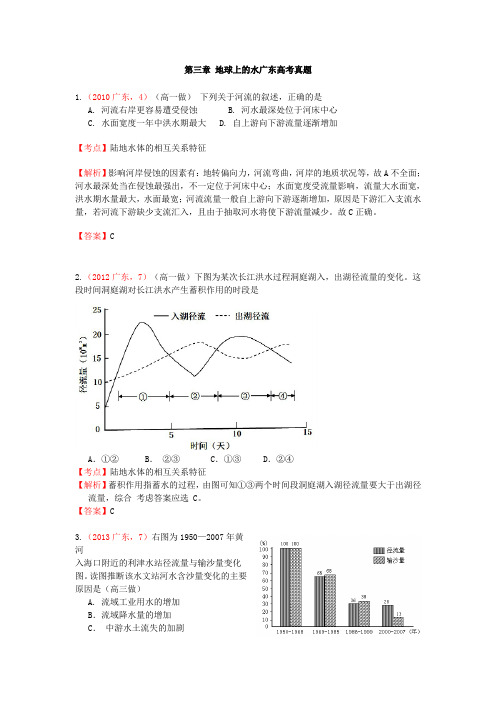
第三章地球上的水广东高考真题1.(2010广东,4)(高一做)下列关于河流的叙述,正确的是A. 河流右岸更容易遭受侵蚀B. 河水最深处位于河床中心C. 水面宽度一年中洪水期最大D. 自上游向下游流量逐渐增加【考点】陆地水体的相互关系特征【解析】影响河岸侵蚀的因素有:地转偏向力,河流弯曲,河岸的地质状况等,故A不全面;河水最深处当在侵蚀最强出,不一定位于河床中心;水面宽度受流量影响,流量大水面宽,洪水期水量最大,水面最宽;河流流量一般自上游向下游逐渐增加,原因是下游汇入支流水量,若河流下游缺少支流汇入,且由于抽取河水将使下游流量减少。
故C正确。
【答案】C2.(2012广东,7)(高一做)下图为某次长江洪水过程洞庭湖入,出湖径流量的变化。
这段时间洞庭湖对长江洪水产生蓄积作用的时段是A.①② B.②③ C.①③ D.②④【考点】陆地水体的相互关系特征【解析】蓄积作用指蓄水的过程,由图可知①③两个时间段洞庭湖入湖径流量要大于出湖径流量,综合考虑答案应选 C。
【答案】C3.(2013广东,7)右图为1950—2007年黄河入海口附近的利津水站径流量与输沙量变化图。
读图推断该水文站河水含沙量变化的主要原因是(高三做)A. 流域工业用水的增加B.流域降水量的增加C.中游水土流失的加剧D.上中游水库的增建【考点】陆地水体的相互关系特征【解析】本题以统计图为切入点,考察影响河流水文特征的因素。
读图可知,该水文站河水含沙量逐年减少,而流域内工业用水的增加,不会导致河流含沙量的变化,所以A项错误。
流域内降水量的增加,中游水土流失的加剧导致河水含沙量增大,故B,C项错误。
上中游水库的增建拦蓄了更多的内啥,会导致下游含沙量减少,故C正确。
【答案】D4.(2014广东,7)(高三做)随着我国南方地区部分江河水库主要功能的退化,大坝将被拆除。
当河流生态系统稳定之后,与拆坝前相比,将会出现的变化有A.坝址上游枯水期平均水位上升B.坝址上游汛期出现的季节提前C.坝址下游径流量年际变化减少D.坝址下游汛期洪峰流量增大【考点】陆地水体的相互关系【解析】水库的主要作用即为洪水期时降低洪峰流量。
中山大学2010年硕士研究生入学考试复试基本分数线
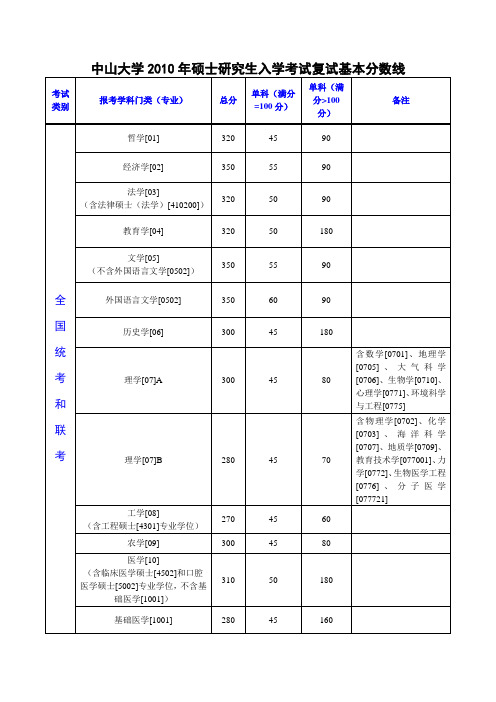
一、关于复试分数线的相关说明
思想政治理论、外国语满分为100分;教育学[04]、历史学[06]、医学[10](含临床医学硕士[4502]、公共卫生硕士[5101]和口腔医学硕士[5002])门类业务课一满分为300分;工商管理硕士、公共管理硕士、会计硕士管理类联考综合能力满分为200分,会计硕士业务课二满分为100分,其他门类业务课一及业务课二满分均为150分。
二、“少数民族高层次骨干人才计划”复试基本分数要求
1、参照国家统一划定的“少数民族高层次骨干人才计划”复试基本分数要求。
2、具有复试资格的“少数民族高层次骨干人才计划”考生,复试前须向中山大学研究生招生办公室提交《报考2010年“少数民族高层次骨干人才计划”硕士研究生考生登记表》。
三、“大学生志愿服务西部计划”复试基本分数要求
参加“大学生志愿服务西部计划”并完成服务期、考核合格的志愿者,在服务期满后三年内的考生,总分可加10分。
考生须提前向报考院系提出申请,复试时须出具全国大学生志愿服务西部计划项目管理办公室统一制作颁发的《大学生志愿服务西部计划志愿服务证》、《志愿服务鉴定书》和服务单位证明。
四、关于复试名单及复试的有关事项
复试名单、学校及招生院系的复试办法将于3月底网上公布。
复试的有关事项近期将在网上告示,请考生务必留意我校研究生招生网上的相关公告。
专业知识(水利水电)考试试卷(含五卷)含答案解析

专业知识(水利水电)考试试卷(一)一、单项选择题(每小题2分,共100分)1、每一个需要安置的农业人口的安置补助费标准,为该耕地被征用前()o但是,每公顷被征用耕地的安置补助费,最高不得超过被征用前三年平均年产值的15倍。
A、3年平均年产值的3~6倍B、3年平均年产值的4~6倍C、4年平均年产值的3~6倍I)、4年平均年产值的4~6倍2、用历史流量法计算河口生态需水量时,以干流()保证率水文条件下的年人海水量的()作为河口生态需水量。
A、60%,50%~80%B、50%,50%~80%C、60%,60%~80%D、50%,60%~80%3、导流建筑物级别划分时,当其他三项指标中至少有1项满足3级指标,失事后果为淹没重要城镇、工矿企业、交通干线或推迟总工期及第一台(批)机组发电而造成重大灾害和损失时,导流建筑物的级别为()级。
A、2B、3C、4I)、54、设置环境监测项目、点位和频率应()A、根据现有监测数据确定B、根据区域环境管理计划确定C、根据工程分析确定D、根据受影响的主要环境要素及因子确定5、整体式闸室结构在闸墩中间设()A、顺水流向的永久缝B、垂直水流向的永久缝C、顺水流向的施工缝I)、垂直水流向的施工缝6、()是指其所含粘性土颗粒在水中散凝呈悬浮状,易被雨水或渗流冲蚀带走。
A、固结土B、粉土C、分散性土D、吹填土7、当山区、丘陵地区的水利水电工程永久性水工建筑物的挡水高度低于(),且上下游最大水头差小于()时,其洪水标准宜按平原、滨海区标准确定。
()A、10m;5mB、15m;5mC、15m;IOmD、10m;15m8、()时,防洪库容和兴利库容部分重叠。
A、防洪限制水位在正常蓄水位与死水位之间,防洪高水位在正常蓄水位之上B、防洪限制水位在正常蓄水位与死水位之间,防洪高水位在正常蓄水位之下C、防洪限制水位在正常蓄水位与死水位之间,防洪高水位与正常蓄水位重D、防洪限制水位和正常蓄水位重合,防洪高水位在正常蓄水位之下9、控制段的闸墩的顶部高程在宣泄校核洪水时不应()校核洪水位加安全超高值。
2010年全国硕士研究生入学统一考试数学三试题及答案

- ⎪ ⎪ ) lim 1一、选择题2010 年全国硕士研究生入学统一考试数学三试题参考答案(1) 【答案】 (C). 【解析】lim ⎛ 1 ⎛ 1 - a ⎫ e x ⎫ = lim 1 (1- e x (1- a x )) = l im 1 (1- e x + axe x = ⎛ 1- e x axe x ⎫ + ⎪ x →0 ⎝ x ⎝ x ⎭ ⎭ x →0 x x →0 x x →0 ⎝ xx ⎭所以a = 2 .(2) 【答案】 (A).= lim x →0 1- e x x + lim x →0 axe xx= -1+ a = 1 【解析】因λ y 1 - μ y 2 是 y ' + P ( x ) y = 0 的解,故(λ y 1 - μ y 2 )' + P (x )(λ y 1 - μ y 2 ) = 0 ,所以λ ⎡ y ' + P ( x ) y ⎤ - μ ⎡ y ' + p (x ) y ⎤ = 0 ,⎣ 11⎦ ⎣ 22⎦而由已知 y ' + P (x ) y = q (x ), y ' + P (x ) y = q (x ) ,所以 1122(λ - μ ) q ( x ) = 0 ,①又由于一阶次微分方程 y ' +λ - μ = 0 .p ( x ) y = q ( )x 是非齐的,由此可知 q ( x ) ≠ 0 , 所以由于λ y 1 + μ y 2 是非齐次微分方程 y ' + P ( x ) y = q ( x ) 的解,所以(λ y 1 + μ y 2 )' + P ( x )(λ y 1 + μ y 2 ) = q ( x ),整理得λ ⎡ y ' + P ( x ) y ⎤ + μ ⎡ y ' + P ( x ) y ⎤ = q ( x ) ,⎣ 11⎦ ⎣ 22⎦即(λ + μ ) q ( x ) = q (x ) ,由q ( x ) ≠ 0 可知λ + μ = 1, ②由①②求解得λ = μ = ,故应选(A).2(3) 【答案】 (B).【解析】{ f [g (x )]}' = f '[g (x )]⋅ g '(x ),{ f [g (x )]}' = { f '[g (x )]⋅ g '(x )}' = f '[g (x )]⋅[g '(x )]2+ f '[g (x )]⋅ g '(x )由于 g (x 0 ) = a 是 g (x ) 的极值,所以 g '(x 0 ) = 0 .所以= 10 ⋅9 2 limln x x →+∞ x ,αr ) ≤ r (β1, , βs ) ≤ s Λ 1{ f [g (x 0)]}'' = f '[g (x 0 )]⋅ g '(x 0 ) = f '(a )⋅ g '(x 0 )由于 g ''(x 0 ) < 0 ,要使{ f [g (x )]}'' < 0 ,必须有 f '(a ) > 0 ,故答案为 B.(4)【答案】 (C). h (x )xe10x 1 【解析】因为 lim= lim= lim e 10= +∞ ,所以,当 x 充分大时, h (x ) > g (x ) . x →+∞g (x )x →+∞ x x →+∞10又因为 lim f (x ) = limln x = lim 10 ln 9 x ⋅ 1 9x = 10 lim ln x x →+∞g (x )x →+∞xx →+∞1ln 8 x ⋅ 1x →+∞x= 10 ⋅9 limx = = 10! lim = 0 .x →+∞ 1x →+∞ x所以当 x 充分大时, f (x ) < g (x ) ,故当 x 充分大, f (x ) < g (x ) < h (x ).(5) 【答案】 (A).【解析】由于向量组I 能由向量组II 线性表示,所以r (I) ≤ r (II) ,即r (α1,若向量组 I 线性无关, 则 r (α1, ,αr ) = r , 所以 r = r (α1, , 即r ≤ s ,选(A).(6) 【答案】 (D).【解析】设λ 为 A 的特征值,由于 A 2 + A = O ,所以λ2+ λ = 0 ,即(λ +1)λ = 0 ,这样 A 的特征值只能为-1 或 0. 由于 A 为实对称矩阵, 故 A 可相似对角化, 即 A ,⎛ -1 ⎫ -1 ⎪ ⎛ -1 ⎫-1 ⎪ r (A ) = r (Λ) = 3,因此, Λ= ⎪ ,即 A Λ= ⎪ . -1 ⎪ 0 ⎪ -1 ⎪ 0⎪⎝ ⎭ ⎝ ⎭(7) 【答案】 (C).【解析】离散型随机变量的分布函数是跳跃的阶梯形分段函数,连续型随机变量的分布函数是连续函数.观察本题中 F (x ) 的形式,得到随机变量 X 既不是离散型随机变量,也不是连续 型随机变量,所以求随机变量在一点处的概率,只能利用分布函数的定义.根据分布函数的定义,函数在某一点的概率可以写成两个区间内概率的差,即P {X = 1} = P {X ≤ 1} - P {X < 1} = F (1) - F (1- 0) = 1- e -1 - 1 = 1- e -1 , 故本题选2 2(C).(8) 【答案】 (A).,αr ) ≤ r (β1, , βs ) ≤ s10⎨ ⎰ ⎰⎰2 4 +∞ ⎝ ⎭1 - x 2⎧1 ,-1 ≤ x ≤ 3 【解析】根据题意知, f 1 ( x ) e 2( -∞ < x < +∞ ), f 2( x ) = ⎪ 4 ⎪⎩0, 其它+∞利用概率密度的性质:-∞f ( x ) d x = 1,故 f ( x ) d x = 0af ( x ) dx + +∞bf ( x )dx =a +∞f ( x )dx + b31 dx = a + 3b = 1⎰-∞⎰-∞1⎰22 ⎰-∞1⎰42 4所以整理得到2a + 3b = 4 ,故本题应选(A). 二、填空题 (9) 【答案】-1. 【解析】x + ye -t2dt = x xsin t 2dt ,令 x = 0 ,得 y = 0 ,等式两端对 x 求导:e -(x + y )2 (1+ dy) = ⎰x sin t 2dt + x sin x 2 .dx将 x = 0 , y = 0 代入上式,得1+π 2x =0= 0 .所以 dy dx x =0 = -1. (10) 【答案】 .4【解析】根据绕 x 轴旋转公式, 有V = ⎰+∞ π y 2dx = ⎰+∞πdxeex (1+ l n 2 x )= π d ln x = π ⋅ ⎡arctan (ln x )⎤ +∞= π ⎛ π - π ⎫ = π2.⎰e 1+ ln 2 x 1(P 3-1)⎣ ⎦e ⎪ (11) 【答案】 p ⋅ e 3.dR p3dR ⎛ 1 2 ⎫ 1 2 【解析】由弹性的定义,得 ⋅ = 1+ p ,所以 R = p + p ⎪ dp ,即ln R = ln p + 3 p + C ,dp R1⎝ ⎭1 1 1( p 3 -1)又 R (1) = 1,所以C =- .故ln R = ln p + 3p - ,因此 R = p ⋅e 3 .3 3 (12) 【答案】b = 3 .【解析】函数为 y = x 3 + ax 2 + bx +1 , 它的一阶导数为 y ' = 3 x 2 + 2ax + b ;二阶导数为y '' = 6x + 2a ,又因为(-1, 0) 是拐点,所以 y ''= 0 ,得- a= -1 ,所以a = 3,又因为曲线 x =-13过点(-1, 0) ,所以将 x = -1, y = 0 代入曲线方程,得b = 3 .dydx +∞4= = 1+ y 22 y1x (13) 【答案】3.【解析】由于 A (A -1 + B )B -1 = (E + AB )B -1 = B -1 + A ,所以A +B -1 = A (A -1 + B )B -1 = A A -1 + B B -1因为 B = 2 ,所以 B -1-11B,因此 2A +B -1 = A(14)【答案】σ 2 + μ2 .A -1 +B B -1 = 3⨯ 2⨯ = 3 . 2⎛ 1 n 2 ⎫ 1 ⎛ n 2 ⎫ 12 2 2 2【解析】 E (T ) = E ∑ X i ⎪ = E ∑ X i ⎪ = nE ( X ) = E ( X ) = σ + μ .三、解答题⎝ n i =1 ⎭ n ⎝ i =1 ⎭ n⎛ 1 ⎫ ⎛ 1 ⎫ ⎛ ln x ⎫1 ln x x -1⎪ln x x -1⎪ ln e x -1⎪1 ⎪ ⎪ ⎛ - ⎫ln x⎝ ⎭ lim ⎝ ⎭ lim ⎝ ⎭(15) 【解析】 lim x x 1⎪ = lim eln x= ex →+∞ ln x= e x →+∞ln x x →+∞⎝ ⎭其中x →+∞lim ln(e x-1) = lim (e x-1)-1 ln x x⋅1- ln x = limln x x⋅1- ln x= lim e ln x ( 1 -1) = -1. x →+∞ ln xx →+∞1 x x 2x →+∞ ln x xxx →+∞ ln x故原式= e -1 .(16) 【解析】积分区域 D = D 1,其中 D 1 ={( x , y ) 0 ≤ y ≤ 1, 2 y ≤ x ≤1+ y 2}D 2= {( x , y ) -1 ≤ y ≤ 0, - 2 y ≤ x ≤ 1+ y 2}⎰⎰( x + y )3dxdy = ⎰⎰(x 3 + 3x 2 y + 3xy 2 + y 3 )dxdy DD因 为 区 域 D 关于 x 轴对称 , 被 积 函 数 ⎰⎰(3x 2 y + y 3 )dxdy = 0 .D3x 2 y+ y 3 是 y 的 奇 函 数 , 所以 33 2 3 2⎡ 1 3 2⎤⎰⎰( x + y ) dxdy = ⎰⎰(x + 3xy )dxdy = 2⎰⎰(x + 3xy )dxdy = 2 ⎢⎰0dy ⎰2 y(x + 3xy )dx ⎥DDD 1⎣⎦= 21⎛ 1 x 4 + 3 x 2 y 2 ⎫dy = 2 1⎛- 9 y 4 + 2 y 2+ 1 ⎫ dy = 14 .⎰0 4 2 ⎪ ⎰0 4 4 ⎪ 15 ⎝ ⎭⎝ ⎭(17) 【解析】令 F( x , y , z , λ ) = xy + 2yz + λ (x 2 + y 2 + z 2 -10),用拉格朗日乘数法得1+ y 2 D 2 ln x ln xe e20 0 1⎧Fx ' = y + 2λ x = 0, ⎪F ' = x + 2z + 2λ y = 0, ⎪ y⎨F ' = 2 y + 2λ z = 0, ⎪ z⎪⎩F λ' = x 2 + y 2 + z 2 -10 = 0,求解得六个点:A (1, 5, 2), B (-1, - 5, -2),C (1, - 5, 2),D (-1, 5, -2),E (2 2, 0, - 2 ),F (-2 2, 0, 2 ).由于在点 A 与 B 点处, u = 5 5 ;在点C 与 D 处, u = -5 5 ;在点 E 与 F 处, u =0 . 又因为该问题必存在最值,并且不可能在其它点处,所以u max = 5 5 , u min = -5 5 .(18) 【解析】 (I)当0 < x < 1时0 < ln(1+ x ) < x ,故[ln(1+ t )]n< t n ,所以ln t [ln(1+ t )]n< ln t t n ,则⎰1ln t [ln(1+ t )]ndt < ⎰1ln t t n dt (n = 1, 2, ) .(II)1 ln t t n dt = - 1 ln t ⋅t ndt = - 11 ln td (t n +1 ) = 1 ,故由⎰⎰n +1 ⎰0(n +1)20 < u n < 1ln t t ndt =1(n +1)2根据夹逼定理得0 ≤ lim u n ≤ lim2= 0 ,所以lim u n = 0 .n →∞n →∞(n +1)n →∞(19)【解析】(I) 因为2 f (0) =⎰2f (x )dx ,又因为 f ( x ) 在[0, 2] 上连续,所以由积分中值定理得,至少有一点η ∈[0, 2] ,使得⎰0f ( x )dx = f (η )⋅(2 - 0)即2 f (0) = 2 f (η ) ,所以存在η ∈[0, 2] ,使得 f (η ) = f (0) .(Ⅱ)因为 f (2) + f (3) = 2 f (0) ,即f (2) + f (3)= f (0) ,又因为 f ( x ) 在[2, 3] 上连2续,由介值定理知,至少存在一点η1 ∈[2,3]使得 f (η1 ) = f (0).⎰ ,⎪ 1 ⎝ a 1 λ → 0 ⎭ ⎝ ⎝ ⎭⎝ ⎪⎭ ⎝ ⎪ ⎪ ⎝ ⎪ ⎭⎪⎭ ⎝⎪因为 f ( x ) 在[0, 2] 上连续,在[0, 2] 上可导,且 f (0) = f(2) ,所以由罗尔中值定理知,C存在ξ1 ∈(0, 2) ,有 f '(ξ1 ) = 0 .又因为 f ( x ) 在[2,η1]上连续,在(2,η1 ) 上可导,且 f (2) = f (0) = f (η1) ,所以由罗尔中值定理知,存在ξ2 ∈(2,η1 ) ,有 f (ξ2 ) = 0 .又因为 f ( x ) 在[ξ1,ξ2 ]上二阶可导,且 f '(ξ1 ) = f '(ξ2 ) =0 ,所以由罗尔中值定理,至少有一点 Ax = b ⊂ (0,3) ,使得 f ''(ξ ) = 0 .(20)【解析】因为方程组有两个不同的解,所以可以判断方程组增广矩阵的秩小于 3,进而可以通过秩的关系求解方程组中未知参数,有以下两种方法.方法 1:( I )已知 Ax = b 有 2 个不同的解,故r ( A ) = r (A ) < 3 ,对增广矩阵进行初等行变换,得⎛ λ 1 1a ⎫ ⎛ 1 1 λ 1 ⎫A = 0 λ -1 0 1 ⎪ → 0 λ -1 0 ⎪1 1 λ ⎪ 1 1 ⎭ ⎛ 1 1λ 1 ⎫ ⎛ 1 1 λ 1 ⎫ → 0 λ -1 0 ⎪ 1 ⎪ λ -1 0 1 ⎪ 0 1- λ 1- λ 2 a - λ ⎪ 0 0 1- λ 2 a - λ +1⎪⎛ 1 1 1 当λ = 1时, A →0 0 0 0 0 0 1 ⎫ ⎛ 1 1 1 1 ⎪ → 0 0 0 a ⎪ 0 0 0 1 ⎫1 ⎪ ,此时, r (A ) ≠ r ( A ) ,故 Ax = b 无解(舍去).⎪ ⎭ ⎛ 1 1 -1 1 ⎫ 当λ = -1时, A → 0 -2 0 1 ⎪,由于r (A ) = r (A ) < 3 ,所以a = -2 ,故λ = -1 , a = -2 .0 0 0 a + 2⎪方法 2:已知 Ax = b 有 2 个不同的解,故r ( A ) = r (A ) < 3 ,因此 A = 0 ,即λA = 0 1 1λ -1 0= (λ -1)2 (λ +1) = 0 ,11λ知λ = 1或-1.当 λ = 1时, r ( A ) = 1 ≠ r ( A ) = 2 ,此时, Ax = b 无解,因此λ = -1 .由 r ( A ) = r ( A ) ,得a = -2 .( II ) 对增广矩阵做初等行变换1 6 ⎪2 1 ⎪⎛ - 1 1 1 -2 ⎫ ⎛ 1-1 -1 2 ⎫ ⎛1 0 -13 ⎫ ⎪ A = 0 -2 0 1 ⎪ → 0 2 0 -1⎪ → 0 1 0 - 1 ⎪ 2 ⎪ 1 1 -1 1 ⎪ 0 0 0 0 ⎪ ⎪ ⎝ ⎭ ⎝ ⎭ 0 0 0⎝0 ⎪ ⎭⎛ 3 ⎫⎧ 3 ⎛x ⎫ ⎛ 1 ⎫ 2 ⎪ ⎪x 1 - x 3 = 2 ⎪ ⎪ ⎪ 1 可知原方程组等价为⎨ ,写成向量的形式,即 x ⎪ = x 0 ⎪ + - ⎪ .⎪x =- 1x ⎪ 1 ⎪ 2 ⎪ ⎩⎪ 2 2 ⎝ 3 ⎭ ⎝ ⎭ 0 ⎪⎛ 1 ⎫ ⎪⎝ ⎭⎛ 3 ⎫ 2 ⎪⎪ 因此 Ax = b 的通解为 x = k 0 ⎪ + - 1 ⎪ ,其中k 为任意常数. ⎪ 2 ⎪ 1 ⎪ ⎝ ⎭ 0⎪ ⎝ ⎭⎛ 0 -1 4 ⎫ (21)【解析】由于A =-1 3 a ⎪ ,存在正交矩阵Q ,使得Q T AQ 为对角阵,且Q 的第一 ⎪ 4 a 0 ⎪ ⎝ ⎭列为 (1, 2,1)T ,故 A 对应于λ 的特征向量为ξ =(1, 2,1)T .1 1⎛ 1 ⎫ ⎛ 1 ⎫6 ⎪ 6 ⎪ ⎪ ⎪根据特征值和特征向量的定义,有 A 2 ⎪ = λ 2 ⎪ ,即6 ⎪ 1 6 ⎪ ⎪ ⎪ 1 ⎪ 1 ⎪ 6 ⎪ 6 ⎪⎛ 0 -1 4 ⎫⎛1 ⎫ ⎛1 ⎫ ⎝ ⎭ ⎝ ⎭⎛ 0 -1 4 ⎫ -1 3 a ⎪ 2 ⎪ = λ 2 ⎪ ,由此可得a = -1, λ = 2 .故 A =-1 3 -1⎪ .⎪ ⎪ 1 ⎪ 1 ⎪ 4 a 0 ⎪1 ⎪ 1⎪ 4 -1 0 ⎪ ⎝ ⎭⎝ ⎭ ⎝ ⎭ ⎝ ⎭λ1 -4由 λE - A = 1λ - 3 1 = (λ + 4)(λ - 2)(λ - 5) = 0 ,-4 1 λ可得 A 的特征值为λ1 = 2, λ2 = -4, λ3 = 5 .2 3 1 6ξ1 1 6 1 2 1 2 6 1 61 2 1 3 π2 3 +∞ 6 - 3 ⎛ -4 1 -4 ⎫⎛ x 1 ⎫ 由(λ E - A )x = 0 ,即1 -7 1 ⎪ x ⎪ = 0 ,可解得对应于 λ = -4 的线性无关的2 ⎪ 2 ⎪ 2 -4 1-4 ⎪ x ⎪⎝ ⎭⎝ 3 ⎭特征向量为ξ = (-1, 0,1)T .⎛ 5 1 -4 ⎫⎛ x 1 ⎫ 由 (λ E - A )x = 0 , 即1 2 1 ⎪ x ⎪ = 0 , 可解得对应于 λ = 5 的特征向量为3 ⎪ 2 ⎪ 3 -4 15 ⎪ x ⎪⎝ ⎭⎝ 3 ⎭ξ = (1,- 1, 1T).由于 A 为实对称矩阵, ξ1,ξ2,ξ3 为对应于不同特征值的特征向量,所以ξ1,ξ2,ξ3 相互正 交,只需单位化:η =ξ1= (1, 2,1)T ,η = ξ2 = (-1, 0,1)T ,η = ξ3 =(1, -1,1)T , 12⎛ 1 1 ⎫ ⎪ ⎪ 21 T 3⎛ 2 ⎫ ⎪ 取Q = (η ,η ,η ) = 0 - ⎪ ,则Q AQ = Λ = -4 ⎪ . 1 2 3 3 ⎪ 5⎪ ⎪ ⎝ ⎭⎪ ⎪⎝ ⎭(22)【解析】当给出二维正态随机变量的的概率密度 f (x , y ) 后,要求条件概率密度f (x , y )f Y |X ( y | x ) ,可以根据条件概率公式 f Y |X ( y | x ) =A 要根据概率密度的性质求解,具体方法如下.f X (x )来进行计算.本题中还有待定参数,f ( x ) = f ( x , y ) d y = A +∞ e -2 x 2 +2 x y - y 2 dy = A+∞e -( y -x )2-x 2dy = Ae - x 2+∞e -( y -x )2dyX⎰-∞= A ⎰-∞πe -x2, -∞ < x < +∞ .⎰-∞⎰-∞根据概率密度性质有 1 =+∞-∞f X( x )dx = A+∞e - x 2dx = A π ,即 A = π -1 ,-∞故 f X (x ) = 1 e -x 2, -∞ < x < +∞.当-∞ < x < +∞时,有条件概率密度f (x , y ) Ae -2 x 2+2xy - y 21 2 2 1 2f ( y x ) = = = e - x +2xy - y = e -(x -y ) , -∞ < x < +∞, -∞ < y < +∞ .Y X X (x ) ξ2 ξ3 1 3π A π e -x 2 π π⎰ ⎰f{ = = } =C = 6 6 6 (23)【解析】(I) X 的所有可能取值为0,1 , Y 的所有可能取值为0,1, 2 .C 23 1 P {X = 0,Y = 0} = 3= = ,其中 X = 0,Y = 0 表示取到的两个球都是黑球;2 6C 1C 115 5 6 2 P {X = 0,Y = 1} = 23 = = ,其中 X = 0,Y = 1表示取到的一个是白球,一个是黑球;215 5C 2 1 P {X = 0,Y = 2} = 2= ,其中 X = 0,Y = 2 表示取到的两个球都是白球; 2 15C 1C 1 3 1 P {X = 1,Y = 0} = 1 3= = ,其中 X = 1,Y = 0表示取到的一个是红球,一个是黑球;2 6C 1C 115 52 P {X = 1,Y = 1} = 1 2= ,其中 X = 1,Y = 1表示取到的一个是红球,一个是白球;215P X 1,Y 2 2 0 , 6因此二维离散型随机变量( X ,Y ) 的概率分布为(II) Cov ( X ,Y ) = E ( XY ) - E ( X ) E (Y ) ,222 1 1E ( XY ) = 1⨯1⨯ = , E ( X ) = 0⨯ +1⨯ = ,15 15 3 3 3 E (Y ) = 0⨯ 2 +1⨯ 8 + 2⨯ 1 = 25 15 15 32 1 2 4Cov ( X ,Y ) = E ( XY ) - E ( X ) E (Y ) = - ⨯ = - .15 3 3 45Y 0 1 2X2 311 32 58 1512 15 1 51 152 5 1 5 C C C C C。
《水文与水资源学》习题
《水文与水资源学》部分习题
1.某流域面积F=194Km2,L=3
2.1Km,J=0.00932,H24.1%=214mm,n=0.75,m=0.96,u=
3.0mm/h
求Q m1%=?
2
3.已知统计参数Q=100m3/s,Cv=0.5,Cs=2.5Cv,试绘理论频率曲线。
并确定频率P=1%,P=2%,P=5%时的设计流量。
若Cs=3.5Cv,试绘理论频率曲线,并与Cs=2.5Cv时的理论频率曲线进行比较。
4.设有A,B两站的洪峰流量(m3/s),利用A站的资料展延B站的资料
5.某河某水文站的流域面积为1077km2,年平均流量为15.5m3/s,流域平均降水量为1033mm,试求其年径流总量、径流模数、径流深度及径流系数。
6. 某站有35年最大流量资料,试求最大流量的理论濒率曲线及相应于P=1%和P=0.1%的最大流量值。
7. 某水库的泄洪建筑物为开敞式的河岸式溢洪道,溢洪道堰定高程为116m,相应的库容为247×106m3,溢洪道顶宽B=45m,流量系数m1=1.6。
设计洪水过程线见表。
水位库容关系线如表,取△t=12h,求最大下泄流量q m,放洪库容V防和设计洪水位Z。
水文模拟试卷(1)
水文与水利水电规划模拟试题一、填空题(每空1分,共10分)1、闭合流域的多年平均水量平衡方程 E=H 。
2、水文资料的“三性审查”是指审查水文资料的 可靠性 、 一致性和 代表性 。
3、自然界的水文循环按规模和过程分为外循环和内循环。
其中内循环又分为 和 。
4、河流某出口断面以上的 集水区域 所包围的面积,称为该断面所控制的流域面积。
5、 死 水位与 正常蓄 水位之间的库容称为兴利库容。
6、理论频率曲线是指用 数学方程 表示的频率曲线。
二、选择题(每题2分,共20分)1、使水资源具有可再生性的原因,是由于自然界的所引起(B ) A 、径流 B 、水循环 C 、蒸发 D 、降水2、流域围湖造田和填湖造田,将使流域蒸发(B )A 、增加B 、减少C 、不变D 、难以肯定3、某流域(为闭合流域)上有一场暴雨洪水,其净雨量将(C ) A 、等于其相应的降雨量 B 、大于其相应的径流量 C 、等于其相应的径流量 D 、小于其相应的径流量4、一条垂线上测三点流速计算垂线平均流速时,应,分别施测相对水深(ACD )处的流速。
A. 0.2B. 0.4C. 0.6D. 0.8 5、典型洪水同频率放大的次序是(D )。
A.短历时洪量、长历时洪量、峰B. 峰、长历时洪量、短历时洪量C.短历时洪量、峰、长历时洪量D. 峰、短历时洪量、长历时洪量 6、水文现象中,大洪水出现机会比中、小洪水出现机会小,其频率密度曲线为考场号 系别 班级 姓名 学号密 封线注意:密封线内不要答题密封线外不要写姓名学号班级违者试卷作零分处理( C )。
A、负偏;B、对称;C、正偏;D、双曲函数曲线。
7、百年一遇洪水,是指( B )。
A、大于等于这样的洪水每隔100年必然会出现一次;B、大于等于这样的洪水平均100年可能出现一次;C、小于等于这样的洪水正好每隔100年出现一次;D、小于等于这样的洪水平均100年可能出现一次;8、相关系数R的取值范围是(C)。
浙江师范大学普通物理_力学与电磁学_2010年复试试题
页
共,页
2
2
图 题
3
O m
2
第
O m′ v m, l
大?
(2) 若棒转动时受到大小为 Mr = 4.0 N· 的 m
恒定阻力矩作用,棒能转过多大的角度θ?
3. 如图所示,一空气平行板电容器,极板面积为
S ,两极板之间距离为 d ,其中平行地放有一层
t
S d
厚度为 t ( (t < d ) 、 相对介电常量为 ε r 的各向同性
图 题
L
)
6. 在一均匀磁场中,若带电粒子的速度 v 与磁感应强度 B 斜交成 θ 角, θ ≠ 则带电粒子的运动轨道是一螺旋线。( )
π
,
2
7. 质点作简谐振动时,从平衡位置运动到最远点需 1/4 周期,因此走过该距离 的一半需 1/8 周期。 ( ) 8. 质点系中的内力不能改变质点系的总动量。 ( 二、计算题(共 6 小题,每小题 21 分,共 126 分) 计算题 1.一半径为 R 的无限长半圆柱面型导体,与轴线上的长 直导线载有等值相反的电流 I,如图所示.求半无限长圆 柱面电流单位长度上所受的力.(21 分) 2. 一根放在水平光滑桌面上的匀质棒,可绕通过其一端
图 题
5
6. 甲乙两人所乘飞行器沿 X 轴作相对运动。甲测得两个事件的时空坐标为
x1=6×104m , y1=z1=0,t1=2×10-4s ; x2=12×104m, y2=z2=0, t2=1×10-4 s,若
乙测得这两个事件同时发生于 t ′ 时刻, 求: 1)乙对于甲的运动速度是多少? ( (2)乙所测得的两个事件的空间间隔是多少?
均匀电介质。略去边缘效应,试求其电容值。
4. 质量为 m 的钢球系在长为 l 的绳子的一端, 另一端固定在 O 点。 现把绳子拉到水平位置后将 球由静止释放, 球在最低点和一原来静止的、 质 量为 m'的钢块发生完全弹性碰撞,求碰后钢球
中级职称考试题库-水资源
中级职称考试题库(水资源)一、填空题1、研究河流泥沙的目的,在于预估未来工程运用期内河流泥沙的和,为水利工程规划设计提供有关泥沙的资料和数据。
2、河流中的泥沙,按其运动形式可分为、和三类。
工程实际中,主要估计和。
3、当缺乏实测悬移质资料时,其多年平均输沙量只能采用法、法、法粗略估算。
4、流域地表的侵蚀与、、、、等有着密切的关系。
5、泥沙颗粒分析的方法很多,目前常用的有、、、等。
6、在相同的实验条件下,独立地重复多次随机试验,每一次试验结果是时间t的某种函数,我们称这些随时间变化的函数为。
7、当随机函数随时间t连续地取有限区间内的值时,称为;当随机函数随时间t取离散值时,则称为。
8、年降水量、年径流、年蒸发量序列等以年为时间尺度的水文序列,在相当长时间内具有一定稳定性,均可近似作为。
9、月径流序列受年径流周期变化影响,变化较大,一般同时包括和。
10、模型中的参数必须通过实测序列资料进行估计。
估计参数可采用、和等方法。
11、设计永久性建筑物采用的洪水标准,分为正常运用和非常运用两种情况,并分别称为和。
12、与年径流资料的审查一样,洪水资料的审查也包括、和的审查。
13、洪水样本系列的组成,一般由两部分组成,即和。
14、历史洪水的洪峰和洪量的推算方法有、和等方法,历史洪水的考证可分为、和实测期。
15、针对调洪作用大的水库,设计洪水计算中用进行典型洪水的放大。
16、水文分析与计算分为设计年径流计算、、、、河流泥沙分析等多个内容。
17、、是水文分析与计算最核心的内容,其关键是参数估计法。
18、随着系统科学和计算机模拟技术的发展,出现了一些新的水文分析计算方法,如、、和非线性分析法等。
19、水文站只有布设测验断面,才能观测各种水文要素。
测验断面可分为、、和比降断面。
(基本水尺断面、流速仪测流断面、浮标测流断面)20、水位资料的整理有日平均水位、月平均水位和年平均水位等。
关于日平均水位,其计算方法有、。
21、流量资料整编中所用的方法很多,是流量资料整编中最常用、最基本的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机密★启用前秘密★启用后请将所有答案写在报考点提供的专用答题纸上河海大学2010年攻读硕士学位研究生入学考试复试笔试试题
共3页第1页
共3页第2页
4.某流域3h10mm单位线如表3,该流域7月23日发生一次降雨,时段长为3h的地面净雨
过程列也于表3,洪水基流为40m3/s。
试求:
(1)该流域的面积;
(2)该次暴雨在流域出口形成的洪水过程(列表计算)。
(10分)
表3 某流域3h10mm单位线和一次地面净雨过程
时间(日.时)23.2 23.5 23.8 23.11 23.14 23.17 23.20
单位线(m3/s)0 20 75 50 35 10 0
地面净雨(mm) 8 30
三、综合题(共20分,每题10分)
1.阐述在水文测验中采用分析法计算河道断面流量的主要步骤。
2.某流域欲修建一座水库,需推求水库坝址断面的设计年径流,已了解到的资料条件如下:
水库坝址断面有A水文站,自1991年设站以来已有18年流量观测资料,其下游约40km 处设有B水文站,自1974年设站以来已连续观测流量35年。
试根据以上信息拟出该水库设计年径流及年内分配计算的工作步骤。
共3页第3页。
