2009年上期永州市高 一 数 学期末检测试卷
2009年八年级(上)期末学业水平检测.
2009年八年级(上)期末学业水平检测数学试卷【温馨提示】本卷满分100分,附加题10分。
考试时间100分。
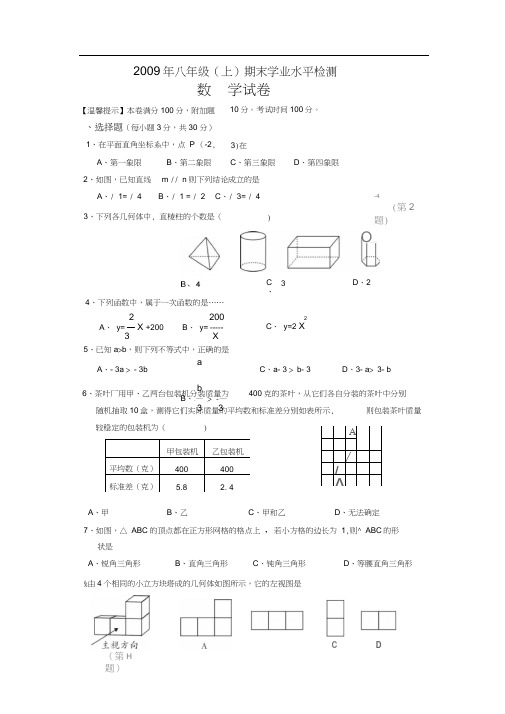
、选择题(每小题3分,共30 分)1、在平面直角坐标系中,点P (-2, 3)在A、第一象限B、第二象限C、第三象限D、第四象限2、如图,已知直线m // n则下列结论成立的是A、/ 1= / 4B、/ 1 = / 2C、/ 3= / 43、下列各几何体中, 直棱柱的个数是(-4(第2题))OC、3D、24、下列函数中,属于一次函数的是……2 200A、y= —X +200B、y= -----3 X2C、y=2 X5、已知a>b,则下列不等式中,正确的是abB、-— > -—3 3A、- 3a > - 3b C、a- 3 > b- 3 D、3- a> 3- b6、茶叶厂用甲、乙两台包装机分装质量为400克的茶叶,从它们各自分装的茶叶中分别随机抽取10盒,测得它们实际质量的平均数和标准差分别如表所示,较稳定的包装机为(甲包装机乙包装机平均数(克)400400标准差(克) 5.8 2. 4)A、甲B、乙C、甲和乙则包装茶叶质量A//AD、无法确定7、如图,△ ABC的顶点都在正方形网格的格点上,若小方格的边长为1,则^ ABC的形状是A、锐角三角形B、直角三角形C、钝角三角形D、等腰直角三角形&由4个相同的小立方块塔成的几何体如图所示,它的左视图是C D(第H题)X5的平均数是5,则另一组数据X1+3, X2+3,小镇A、B、C三点的连线恰好构成一个直角三角形,A、B之间的距离为17、已知水箱中储水150米3,每小时流出的水量为7米3,则水箱中剩余的水量y(米3)18、如图,C表示灯塔,轮船从A处出发以每小时20海里的速度向正北(AN )方向航行,2小时后到达B处。
测得C在A的北偏东30°方向上,并在B的北偏东9、如图,已知一次函数y=k x+b的图象经过第一、四象限,贝U k、b的符号为A、k> 0, b >0B、k > 0, b v 0C、k v 0, b v0D、k v 0, b > 010、已知等边△ ABC,点A在坐标原点,B点的坐标为(6, 0),则点C的坐标为A、(3, 3)B、( 3, 2 晶)C、(2J3 , 3)D、( 3,3^3 )二、填空题(每小题4分,共32分)11、如图,若/ 1= / 2,则//12、用不等式表示:’X与y的和小于O[第11题)13、请写出一个三视图都相同的几何体:X3+3,X 4+3 , X 5+3的平均数是40km,景点D恰好位于AB的中点,则景点D与小镇C的距离是km。
人大附中 高一期末数学测试题

人大附中2009-2010学年度第一学期高一年级数学必修1模块考核试卷20XX 年11月4日制卷人: 审卷人 : 成绩: 卷一 (共90分)说明:本试卷,卷一共三道大题,17道小题,卷二共二道大题,6道小题,共6页;满分120分,考试时间90分钟;请在密封线内填写个人信息。
一、选择题:(本大题共10小题,每小题4分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的请将正确答案填涂在答题卡上.)1.已知集合A = {1,2},B = {1,2,3},C = {2,3,4},则(A ∩B )∪C = ( ) A .{1,2,3} B .{1,2,4} C .{2,3,4} D .{1,2,3,4}2. 将322化成分数指数幂的形式是( ) .A .122- B .122 C . 132 D .5623.若函数()3x f x =的反函数是1()y f x -=,则1(3)f -的值是( ).A .1B .0C .13 D .34.函数y =1-11-x 的图象是 ( )5.已知集合[]0,4A =,集合[]0,2B =,按照对应法则f 能建立从A 到B 的一个映射是( ).A .:f x y x →=±B .:2f x y x →=-C .1:2f x y x →=D .1:f x y x →= 6.已知()x x x f 422-=-,那么()x f =( ).A .284x x -- B .284x x -+ C . 28x x + D .42-x7.若函数()x f 的定义域为[]4,0,则函数()2x f 的定义域为( ).A .[]2,0B .[]16,0C .[]2,2-D .[]0,2-8. 已知函数()1+=ax x f ,存在0x (1,1)∈-,使()00=x f ,则a 的取值范围是( ) .A .11<<-aB .1>aC .1-<aD .11>-<a a 或9.当函数()2x f x m -=-的图象与x 轴有交点时,实数m 的取值范围是( ).A .01m <≤,B .01m ≤≤,C .10m -≤<;D .1m ≥10.函数 y=f(x),y=g(x)的图象如下,f(1)=g(2)=0,不等式0)()(≥x g x f 的解集是( ).A .{}{}21|21|<<⋃><x x x x x 或B .{}21|<≤x xC .{}{}21|21|<<⋃>≤x x x x x 或D .{}21|≤≤x x二、填空题:(本大题共4小题,每小题4分,共16分. 请把答案填在答题表中)11. 已知集合{1,2,}A a =,集合{1,7}B =,若B A ⊆,则实数a 的值是 .12. 设0.80.52 1.514,8,()2a b c -===,则,,a b c 从小到大的顺序是 .13. 已知函数()f x 是奇函数,当0x ≤时,2()2f x x x =-,那么当0x >时,()f x 的解析式是 .14.函数432--=x x y 的定义域是],0[m ,值域是]4,[425--,则m 的取值范围是 .人大附中2009-2010学年度第一学期高一年级数学必修1模块考核试卷答题纸一、DBABC DCDAB二、填空题(每题4分,共16分)11.__7________________ 12.___c<b<a_________________13.2()2f x x x =--_______ 14._3[,3]2__________________三、解答题(本大题共3小题,共34分,解答应写出文字说明证明过程或演算步骤).15.(本题10分)设函数)32lg()(-=x x f 的定义域为集合M ,函数()g x =N . 求:(1)集合M ,N ;(2)集合N M ,R C N .解:(Ⅰ)};23|{}032|{>=>-=x x x x M -----------------------------------2分 {|13}N x x x =<≥或 -----------------------------------5分(Ⅱ)3{|1}2MN x x x =<>或 ----------------------------------8分{|13};R C N x x =≤< ----------------------------------10分16.(本题12分) 某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?解:(1)当每辆车的月租金定为3600元时,未租出的车辆数为:5030003600- =12,所以这时租出了88辆车. --------------------4分 (2)设每辆车的月租金定为x 元,则租赁公司的月收益为f (x )=(100-503000-x )(x -150)-503000-x ×50,(3000,50,x x k k Z ≥=∈) -------------8分整理得:f (x )=-502x +162x -21000=-501(x -4050)2+307050.所以,当x =4050时,f (x )最大,其最大值为f (4050)=307050 --------------------10分即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元.---12分17.(本题12分)已知点在幂函数()f x 的图像上,点1(2,)4-在幂函数()g x 的图像上(1)求函数()f x ,()g x 的解析式;(2)判断函数()g x 的单调性并用定义证明; (3)问x 为何值时有()()f x g x ≤.略解:(1)2()f x x = ,2()g x x -= ------------------------------4分 (2)()(,0)(0,)g x -∞+∞函数在上是增函数,在上是减函数----------6分证明略 ----------------10分 (3)()22()f x g x x x -≤∴≤故当110x x -≤≤≠且时,()()f x g x ≤ -----------12分卷二 (共30分)一、填空题(本题共4小题,每题4分,共16分)1. 计算:log2.56.25+lg1001+ln e +3log 122+= 162. 2. 已知函数⎪⎩⎪⎨⎧<+≥⎪⎭⎫ ⎝⎛=,4),1(,4,21)(x x f x x f x则)3log 2(2+f 的值为 124 .3. 若函数y =在(,1]-∞总有意义,则a 的取值范围 [1-+∞,)4.定义在(-∞,+∞)上的偶函数f (x )满足:f (x +1)=-f (x ),且在[-1,0]上是增函数,下面关于f (x )的判断:①f (2)=f (0);②f (x )的图象关于直线x =1对称;③f (x )在[0,1]上是增函数;④f (x )在[1,2]上是减函数;其中正确的判断是__①_②______(把你认为正确的判断的序号都填上);二、解答题(本题共2小题,共14分)5、(本题8分)设函数2()1f x ax bx =++ (a,b 为实数), (1)0f -=且对任意实数x 均有()0f x ≥成立, (1)求()f x 表达式;(2)若()()g x f x kx =-,在区间[]2,2-上是单调函数, 则实数k 的取值范围;(3)若 F(x)= ⎩⎨⎧<->)0()()0()(x x f x x f ,当x []2,0)(0,2∈-时,求F(x)的值域;解:(1) f(-1)=0∴1+=a b --------------1分 由f(x)≥0恒成立 知a=0或a>0且△=b 2-4a=(a+1)2-4a=(a-1)≤20 -------2分 ∴a=1从而f(x)=x 2+2x+1 --------3分(2)由(1)可知f(x)=x 2+2x+1∴g(x)=f(x)-kx=x 2+(2-k)x+1由于g(x)在[]2,2-上是单调函数,知 -222-≤-k 或-222≥-k--------------5分 得k ≤-2或k ≥6 -------------6分(3)由题意F(x)=22(1)(0)(1)(0)x x x x ⎧+>⎪⎨-+<⎪⎩ ----------------7分故F(x)的值域为[10]19]-,(, ---------------8分 6.(本题满分6分)对于函数()f x ,若()f x x =,则称x 为()f x 的“不动点”;若[]()f f x x =,则称x 为()f x 的“周期点”,函数()f x 的“不动点”和“周期点”的集合分别记为A 和B 即{}[]{}(),()A x f x x B x f f x x ====.(1)求证:A ⊆B(2)若2()1f x ax =- (),a R x R ∈∈,且A B =≠∅,求实数a 的取值范围. 解:(1)若A=∅,则A ⊆B 显然成立,若,A ≠∅∈设t A 则f (t)=t, f [f (t)]=f [t]=t,即t ∈B从而A ⊆B ---------------2分(2)A 中元素是方程()f x x =的根,即21ax x -=的根由A ≠∅,∴0a =或0140a a ≠⎧⎨=+≥⎩即14a ≥-B 中元素是方程22(1)1a ax x --=即3422210a x a x x a --+-=的根由A ⊆B ,则方程可化为222(1)(1)0ax x a x ax a --+-+= 要使A=B ,即使方程2210a x ax a +-+= ①/无实根,或实根是方程210ax x --= ②/的根若①无实根,则224(1)0a a a =--<解得34a <若①有实根,且①的实根是②的实根,由②有22a x ax a =+代入①得210ax +=,由此解得12x a=-,再代入②得111042a a +-= ∴34a =故a 的取值范围是13[,]44- -----6分。
高一数学上学期期末综合试卷含答案

高一数学上学期期末综合试卷含答案一、选择题1.已知全集U =R ,集合{}12M x x =-≤,则U M 等于( ) A .{}13x x -<< B .{}13x x -≤≤ C .{1x x <-或}3x >D .{1x x ≤-或}3x ≥2.已知函数()f x =()()3y f x f x =+-的定义域是( ) A .[-5,4]B .[-2,7]C .[-2,1]D .[1,4]3.已知α是第三象限角,且cos cos22αα=-,则2α是( ) A .第一象限角 B .第二象限角 C .第三象限角D .第四象限角4.已知0a <,角α的终边上一点(,2)a a -,则sin α=( )A B .C D .5.函数2()ln f x x x=-的零点所在的大致区间是( ) A .(1,2)B .1(1,)eC .(3,4)D .(2,3)6.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画1描绘了筒车的工作原理.假定在水流稳定的情况下,简车上的每一个盛水筒都做匀速圆周运动.如图2,将筒车抽象为一个几何图形(圆),筒车的半径为4m ,筒车转轮的中心O 到水面的距离为2m ,筒车每分钟沿逆时针方向转动4圈.规定:盛水筒M 对应的点P 从水中浮现(即0P 时的位置)时开始计算时间,且以水轮的圆心O 为坐标原点,过点O 的水平直线为x 轴建立平面直角坐标系xOy .设盛水筒M 从点0P 运动到点P 时所经过的时间为(t 单位:s),则点P 第一次到达最高点需要的时间为( )A .7sB .132s C .6s D .5s7.若函数26,3()ln(2)9,3x x x f x x x ⎧-≤=⎨--->⎩,则()26(1)f x f x >+的解集为( )A .11,32⎛⎫ ⎪⎝⎭B .1,12⎛⎫ ⎪⎝⎭C .1,12⎛⎫- ⎪⎝⎭D .11,32⎛⎫- ⎪⎝⎭8.已知()f x 是定义在[]1,1-上的奇函数,且()11f -=-,当,1,1a b且0a b +≠时()()0f a f b a b+>+.已知,22ππθ⎛⎫∈- ⎪⎝⎭,若()243sin 2cos f x θθ<+-对[]1,1x ∀∈-恒成立,则θ的取值范围是( )A .,62ππ⎛⎫- ⎪⎝⎭B .,23ππ⎛⎫-- ⎪⎝⎭C .,32ππ⎛⎫- ⎪⎝⎭D .,26ππ⎛⎫- ⎪⎝⎭二、填空题9.下列命题是真命题的是( ) A .若幂函数()a f x x 过点1,42⎛⎫⎪⎝⎭,则12α=-B .(0,1)x ∃∈,121log 2xx ⎛⎫> ⎪⎝⎭C .(0,)x ∀∈+∞,1123log log x x> D .命题“x ∃∈R ,sin cos 1x x +<”的否定是“x ∀∈R ,sin cos 1x x +≥” 10.21x ≤的一个充分不必要条件是( ) A .10x -≤<B .1≥xC .01x <≤D .11x -≤≤11.下列命题不正确的( ) A .110||||a b a b<<⇒> B .ab a b cc>⇒>C .33110a b a b ab ⎫>⇒<⎬>⎭D .22110a b a bab ⎫>⇒<⎬>⎭12.关于函数()cos 2cos 236f x x x ππ⎛⎫⎛⎫=-++ ⎪ ⎪⎝⎭⎝⎭,其中正确命题是( )A .()y f x =的最大值为2B .()y f x =是以π为最小正周期的周期函数C .将函数2cos 2y x =的图像向左平24π个单位后,将与已知函数的图像重合 D .()y f x =在区间13,2424ππ⎛⎫⎪⎝⎭上单调递减 三、多选题13.若命题“()0x ∃∈+∞,,使得24ax x >+成立”是假命题,则实数a 的取值范围是_________. 14.2log 3a c =,1log 2ab c =,则log b c =________ 15.已知函数()221f x x ax =-+,[]1,x a ∈-,且()f x 最大值为f a ,则a 的取值范围为______.16.定义域为R 的函数()2x F x =可以表示为一个奇函数()f x 和一个偶函数()g x 的和,则()f x =_________;若关于x 的不等式()()f x a bF x +≥-的解的最小值为1,其中,R a b ∈,则a 的取值范围是_________.四、解答题17.已知集合{}()(23)0A x x m x m =+-+<,其中m ∈R ,集合203x B xx ⎧⎫-=>⎨⎬+⎩⎭. (1)当1m =-时,求A B ;(2)若B A ⊆,求实数m 的取值范围.18.已知函数()2sin()0,02f x x πωϕωϕ⎛⎫=+><< ⎪⎝⎭的部分图像如图所示,P 为该图像的最高点.(1)若2πω=,求cos APB ∠的值;(2)若PAB 45∠=︒,P 的坐标为()1,2,求()f x 的解析式. 19.已知函数2()(1)1(0)f x ax a x a =-++>.(1)若()f x 的单调递减区间是(,1]-∞,求a 的值并证明你的结论; (2)解关于x 的不等式()0(0)f x a <>.20.如图,已知正方形ABCD 的边长为1,点P ,Q 分别是边BC ,CD 上的动点(不与端点重合),在运动的过程中,始终保持4PAQ π∠=不变,设BAP α∠=.(1)将APQ 的面积表示成α的函数,并写出定义域; (2)求APQ 面积的最小值.21.已知函数()xf x a =(0a >,且1a ≠).(1)证明:()()()1212222f x f x f x x +≥+;(2)若()12f x =,()23f x =,()128f x x =,求a 的值; (3)x ∀∈R ,()212xx f x -+≤恒成立,求a 的取值范围.22.已知2()ln ,()241()f x x g x x ax a a R ==-+-∈.(Ⅰ)若函数(())f g x 在[1,3]上单调递增,求实数a 的取值范围; (Ⅱ)若函数(())g f x 在区间1,e e ⎡⎤⎢⎥⎣⎦上的最大值为()M a ,最小值为()m a ,令()()()k a M a m a =-,求()k a 的解析式及其最小值(注:e 为自然对数的底数).【参考答案】一、选择题 1.C 【分析】解绝对值不等式求出集合M ,再利用集合的补运算即可求解. 【详解】因为集合{}{}1213M x x x x =-≤=-≤≤,全集U =R , 所以{U 1M x x =<-或}3x >, 故选:C. 2.D 【分析】由函数解析式可得2820x x +-≥,解不等式可得24x -≤≤,再由24234x x -≤≤⎧⎨-≤-≤⎩即可求解.【详解】由()f x =2820x x +-≥, 解得24x -≤≤,所以函数()()3y f x f x =+-的定义域满足24234x x -≤≤⎧⎨-≤-≤⎩,解得14x ≤≤, 所以函数的定义域为[1,4]. 故选:D 3.B 【分析】由α是第三象限角,知2α在第二象限或在第四象限,再由cos cos 22αα=-,知cos 02α≤,由此能判断出2α所在象限. 【详解】α是第三象限角,()180360270360k k k Z α∴+⋅<<+⋅∈, ()901801351802k k k Z α∴+⋅<<+⋅∈.当k 是偶数时,设()2k n n =∈Z ,则()903601353602n n n Z α+⋅<<+⋅∈,此时2α为第二象限角; 当k 是奇数时,设()21k n n Z =+∈,则()2703603153602n n n Z α+⋅<<+⋅∈,此时2α为第四象限角. 综上所述,2α为第二象限角或第四象限角,coscos22αα=-,cos02α∴≤,2α∴为第二象限角.故选:B . 【点睛】本题考查角所在象限的判断,属于基础题,关键在于由所在的象限,得出关于α的不等式,再求出2α的范围. 4.C 【分析】首先根据三角函数的定义求出tan α,再根据同角三角函数的基本关系计算可得; 【详解】解:因为角α的终边上一点(,2)a a -,所以tan 2α,又22sin tan 2cos sin cos 1ααααα⎧==-⎪⎨⎪+=⎩,解得sin α=,由0a <可知α在第二象限,故sin α= 故选:C . 5.D 【分析】 函数2()ln f x x x=-在(0,)+∞上是连续增函数,根据()()230f f <,根据零点存在定理可得零点所在的大致区间. 【详解】解:对于函数2()ln f x x x=-在(0,)+∞上是连续增函数, 由于()2ln 210f =-<,()23ln 303f =->, 所以()()230f f <,根据零点存在定理可知,函数2()ln f x x x=-的零点所在的大致区间是(2,3), 故选:D . 6.D 【分析】设点P 离水面的高度为()sin()f t A t ωϕ=+,根据题意求出,,A ωϕ,再令()4f t =可求出结果. 【详解】设点P 离水面的高度为()sin()f t A t ωϕ=+, 依题意可得4A =,826015ππω==,6πϕ=-, 所以2()4sin()156f t t ππ=-, 令2()4sin()4156f t t ππ=-=,得2sin()1156t ππ-=,得221562t k ππππ-=+,k Z ∈,得155t k =+,k Z ∈,因为点P 第一次到达最高点,所以2015215t ππ<<=, 所以0,5s k t ==. 故选:D 7.D 【分析】首先作出分段函数()f x 的单调性,根据单调性去掉f 即可求解. 【详解】作出26,3()ln(2)9,3x x x f x x x ⎧-≤=⎨--->⎩的图象如图:由图知,函数()f x 在R 单调递减,由()26(1)f x f x >+可得261x x <+,即2610x x --<,解得:1132x -<<,所以()26(1)f x f x >+的解集为11,32⎛⎫- ⎪⎝⎭,故选:D 【点睛】关键点点睛:本题解题的关键点是判断()f x 的单调性,利用单调性解不等式. 8.A 【分析】由奇偶性分析条件可得()f x 在[]1,1-上单调递增,所以()max 1f x =,进而得2143sin 2cos θθ<+-,结合角的范围解不等式即可得解. 【详解】因为()f x 是定义在[]1,1-上的奇函数, 所以当,1,1a b且0a b +≠时()()()()00()f a f b f a f b a b a b +-->⇔>+--,根据,a b 的任意性,即,a b -的任意性可判断()f x 在[]1,1-上单调递增, 所以()max (1)(1)1f x f f ==--=,若()243sin 2cos f x θθ<+-对[]1,1x ∀∈-恒成立,则2143sin 2cos θθ<+-,整理得(sin 1)(2sin 1)0θθ++>,所以1sin 2θ>-,由,22ππθ⎛⎫∈- ⎪⎝⎭,可得,62ππθ⎛⎫∈- ⎪⎝⎭,故选:A. 【点睛】关键点点睛,本题解题的关键是利用()()()()00()f a f b f a f b a b a b +-->⇔>+--,结合变量的任意性,可判断函数的单调性,属于中档题.二、填空题9.BD 【分析】根据幂函数的定义判断A ,结合图象判断BC ,根据特称命题的否定为全称命题可判断D . 【详解】解:对于A :若幂函数()a f x x 过点1,42⎛⎫ ⎪⎝⎭,则142解得2α=-,故A 错误;对于B :在同一平面直角坐标系上画出12xy ⎛⎫= ⎪⎝⎭与12log y x=两函数图象,如图所示由图可知(0,1)x ∃∈,121log 2xx ⎛⎫> ⎪⎝⎭,故B 正确;对于C :在同一平面直角坐标系上画出13log y x=与12log y x=两函数图象,如图所示由图可知,当(0,1)x ∈时,1123log log x x>,当1x =时,1123log log x x=,当(1,)x ∈+∞时,1123log log x x<,故C 错误;对于D :根据特称命题的否定为全称命题可知,命题“x ∃∈R ,sin cos 1x x +<”的否定是“x ∀∈R ,sin cos 1x x +≥”,故D 正确; 故选:BD【点睛】本题考查指数函数对数函数的性质,幂函数的概念,含有一个量词的命题的否定,属于基础题. 10.AC 【分析】由不等式21x ≤,求得11x -≤≤,结合充分条件、必要条件的判定方法,即可求解. 【详解】由不等式21x ≤,可得11x -≤≤,结合选项可得: 选项A 为21x ≤的一个充分不必要条件; 选项B 为21x ≤的一个既不充分也不必要条件; 选项C 为21x ≤的一个充分不必要条件; 选项D 为21x ≤的一个充要条件, 故选:AC. 11.ABD 【分析】利用不等式的性质,结合特殊值法、比较法逐一判断即可. 【详解】 A :1100ab a b <<∴>且110a b ->->,因此110ab ab ab a b-⋅>-⋅>⋅,即00b a b a b a ->->⇒->->⇒>,故本命题不正确; B :因为4822>--,显然48>不成立,所以本命题不正确; C :由332233()()0b a b a b a b b a a ⇒-=-++>>,而0ab >, 所以有a b >,而11110b a a b ab a b--=<⇒<,故本命题正确; D :若2,1a b =-=-,显然220a b ab ⎧>⎨>⎩成立,但是1121<--不成立,故本命题不正确, 故选:ABD 【点睛】方法点睛:关于不等式是否成立问题,一般有直接运用不等式性质法、特殊值法、比较法. 12.ABD 【分析】先把()cos 2cos 236f x x x ππ⎛⎫⎛⎫=-++ ⎪ ⎪⎝⎭⎝⎭化为()5212f x x π⎛⎫=+ ⎪⎝⎭,直接对四个选项一一验证. 【详解】()cos 2cos 236f x x x ππ⎛⎫⎛⎫=-++ ⎪ ⎪⎝⎭⎝⎭cos 2cos 2626x x πππ⎛⎫⎛⎫=+-++ ⎪ ⎪⎝⎭⎝⎭sin 2cos 266x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭264x ππ⎛⎫=++ ⎪⎝⎭5212x π⎛⎫=+ ⎪⎝⎭ 显然A 、B 选项正确C 选项:将函数2y x =的图像向左平24π个单位得到212y x π⎛⎫=+ ⎪⎝⎭,图像不会与原图像重合,故C 错误;D 选项:当13,2424x ππ⎛⎫∈ ⎪⎝⎭,则532,1222x πππ⎛⎫+∈ ⎪⎝⎭,∴()y f x =在区间13,2424ππ⎛⎫ ⎪⎝⎭上单调递减成立. 故选:ABD 【点睛】(1)三角函数问题通常需要把它化为“一角一名一次”的结构,借助于sin y x =或cos y x =的性质解题;(2)求单调区间,最后的结论务必写成区间形式,不能写成集合或不等式.三、多选题 13.(],4-∞【分析】由题意可知,命题“()0x ∀∈+∞,,使得24ax x ≤+成立”是真命题,可得出4a x x≤+,结合基本不等式可解得实数k 的取值范围. 【详解】若命题“()0x ∃∈+∞,,使得24ax x >+成立”是假命题, 则有“()0x ∀∈+∞,,使得24ax x ≤+成立”是真命题. 即4a x x ≤+,则min 4a x x ⎛⎫≤+ ⎪⎝⎭,又44x x+≥=,当且仅当2x =时取等号,故4a ≤. 故答案为:(],4-∞ 14.2 【分析】 根据2log 3a c =,1log 2ab c =,找到a 、b 、c 的关系,计算log b c . 【详解】 ∵2log 3a c =,1log 2ab c =, ∴()2132a c ab c ==,, ∴()2132=a ab ,化简得:1162=a b ,即3=a b , ∴2=c b ,∴2log log 2b b c b ==.故答案为:2 【点睛】 对数运算技巧: (1)应用常用对数值; (2)灵活应用对数的运算性质; (3) 逆用法则、公式;(4) 应用换底公式,化为同底结构.15.[)2,+∞【分析】由题知1a >-,进而得函数的对称轴[]14,a ax ∈-=,再根据函数开口向上,()f x 最大值为f a 得144a aa -≥+,解不等式即可得答案. 【详解】解:因为[]1,x a ∈-,所以1a >-, 因为函数的对称轴为[]14,a ax ∈-=,开口向上,()f x 最大值为f a 所以144a aa -≥+,解得2a ≥,所以a 的取值范围为[)2,+∞ 故答案为; [)2,+∞ 16.()1222xx -- 1a ≥- 【分析】先根据()f x 为奇函数,()g x 为偶函数,求出()F x -,再与()F x 联立即可求出()f x ;先将()(),f x F x -代入()()f x a bF x +≥-,即可得到()12222xxx a b --≥--,将其转化为()1max1222,1x x a b x --⎡⎤⎛⎫≥+- ⎪⎢⎥⎭⎣⎦≥⎝,令()()11222,1x x h x x b --⎛⎫+- ⎪⎝⎭=≥,求出()max h x 即可求出a 的取值范围. 【详解】解:由题意知:()()()2xF x f x g x =+=()f x 为奇函数,()g x 为偶函数,()()()(),f x f x g x g x ∴-=--=, ()()()()()2x F x f x g x f x g x -=-+-=-+=()()()()()()()222x xF x F x f x g x f x g x f x ---=+--+==-⎡⎤⎣⎦,即()()1222x xf x -=-, ()()f x a bF x +≥-,即()12222xx x a b ---+≥⋅, 即()12222xxx a b --≥--, 即11222x x a b --⎛⎫≥+- ⎪⎝⎭,关于x 的不等式()()f x a bF x +≥-的解的最小值为1, 等价于()1max 1222,1x x a b x --⎡⎤⎛⎫≥+- ⎪⎢⎥⎭⎣⎦≥⎝, 令()()11222,1x x h x x b --⎛⎫+- ⎪⎝⎭=≥,当12b =-时,()()1,21x h x x --=≥易知:()12x h x -=-在[)1,+∞单调递减,()()0max 121h x h ==-=-,故1a ≥-,当12b >-时,102b +>,()11222x x b h x --⎛⎫+- ⎪⎝⎭=在[)1,+∞单调递减,()()10max 13122224b h x h b -⎛⎫==+⨯-=- ⎪⎝⎭,当b 趋近于+∞时,()max h x 趋近于+∞, 故()1max 1222,1x x a b x --⎡⎤⎛⎫≥+- ⎪⎢⎥⎭⎣⎦≥⎝无解,当12b <-时,102b +<,当1≥x 时,1022x-≤≤, 1202x b -⎛⎫+< ⎪⎝⎭,112x --<-, 故()121122x x h x b --⎛⎫+- ⎪⎝⎭=<-,即1a ≥-, 综上所述:1a ≥-. 故答案为:()1222xx --;1a ≥-. 【点睛】关键点点睛:本题解题的关键是将关于x 的不等式()()f x a bF x +≥-的解的最小值为1,转化为()1max1222,1x x a b x --⎡⎤⎛⎫≥+- ⎪⎢⎥⎭⎣⎦≥⎝.四、解答题17.(1){}52x x -<<;(2)(,2][3,)-∞-⋃+∞ 【分析】(1)先分别求出集合,A B ,再根据集合间的运算即可求解; (2)由B A ⊆知:A ≠∅,对m 进行讨论即可求解. 【详解】 解:(1)由203xx ->+, 解得:32x -<<,故{}20323x B x x x x ⎧⎫-=>=-<<⎨⎬+⎩⎭∣, 当1m =-时,()(23)0x m x m +-+<可化为:(5)(1)0x x +-<, 解得:51x -<<,∴集合{}51A x x =-<<,故{}52A B x x ⋃=-<<; (2)显然A ≠∅,即1m ≠, 当23m m -<-,即1m 时,{}23A x m x m =-<<-, 又B A ⊆,13232m m m >⎧⎪∴-≤-⎨⎪-≥⎩, 解得:3m ≥; 当23m m ->-,即1m <时,{}23A x m x m =-<<-, 又B A ⊆,12332m m m <⎧⎪∴-≤-⎨⎪-≥⎩, 解得:2m ≤-,综上所述:实数m 的取值范围为(,2][3,)-∞-⋃+∞. 18.(12)()2sin 44f x x ππ⎛⎫=+ ⎪⎝⎭.【分析】 (1) 由2πω=,则2242AB πππω===,由周期可分别求出,AQ BQ ,进一步求出,AP BP ,由余弦定理可得答案.(2)由条件可得2AQ QP ==,即8T =,所以4πω=,又(1)2sin()24f πϕ=+=可得答案.【详解】解析:(1)由题设可知,由2πω=,则2242AB πππω===在APB △中,max ()2PQ f x ==,则14T AQ ==,334T BQ == 所以222145AP AQ PQ =+=+=,222223213BP PQ BQ =+=+=,由余弦定理可得:2225131665cos 2652513AP PB AB APB AP BP+-+-∠===⋅⋅⨯⨯.(2)由PAB 45∠=︒,P 的坐标为()1,2,所以在APQ ,2AQ QP == 易知24T=,8T =,所以4πω=, 又(1)2sin()24f πϕ=+=,则2,42k k Z ππϕπ+=+∈又02πϕ<<,所以4πϕ=,所以()2sin 44f x x ππ⎛⎫=+ ⎪⎝⎭.19.(1)1a =,证明见解析;(2)当01a <<时,不等式的解集为1|1x x a ⎧⎫<<⎨⎬⎩⎭;当=1a 时,不等式的解集为∅;当1a >时,不等式的解集为1|1x x a ⎧⎫<<⎨⎬⎩⎭.【分析】(1)先求出a 的值,并利用单调性的定义进行证明; (2)对1a和1 的大小进行分类讨论,解不等式即可. 【详解】(1)函数2()(1)1(0)f x ax a x a =-++>的图像为抛物线,开口向上,对称轴为12a x a+=. 因为()f x 的单调递减区间是(,1]-∞,所以1=12a a+,解得:1a =. 此时2()21f x x x =-+,下面证明2()21f x x x =-+在区间(,1]-∞单调递减: 任取121x x <≤,则()()12212122()()2121f f x x x x x x -=-+--+()222121=2x x x x --- ()()1212=2x x x x -+-因为121x x <≤,所以12x x <,1220x x +-<,所以()()121220x x x x -+->. 所以12()()f f x x >,所以2()21f x x x =-+在区间(,1]-∞单调递减;(2)关于x 的不等式()0(0)f x a <>可化为:()()110x ax --<. 当01a <<时,解得:11x a<<; 当=1a 时,原不等式无解; 当1a >时,解得:11x a<<; 综上所述:当01a <<时,不等式的解集为1|1x x a ⎧⎫<<⎨⎬⎩⎭;当=1a 时,不等式的解集为∅;当1a >时,不等式的解集为1|1x x a ⎧⎫<<⎨⎬⎩⎭.【点睛】(1)单调性的证明通常用定义法;(2)解含参数的不等式通常需要分类讨论,分类的标准:①最高次项系数是否为0;②关于x 的方程()=0f x 是否有根;③()=0f x 的几个根的大小比较. 20.(1)1124APQSπα=⎛⎫+ ⎪⎝⎭;定义域为0,4π⎛⎫⎪⎝⎭;(21 【分析】(1)在Rt ABP 与Rt ADQ 中,利用正方形的边长,求出,AP AQ ,根据三角形的面积公式即可求解.(2)由(1)利用三角函数的性质即可求解. 【详解】(1)由BAP α∠=,4PAQ π∠=,则244ADQ πππαα∠=--=-,正方形的边长为1,在Rt ABP 中,1cos AP α=, 在Rt ADQ 中,1cos 4AQ πα=⎛⎫- ⎪⎝⎭,所以1111sin 242cos cos 4APQSAP AQ ππαα=⋅⋅=⋅⋅⎛⎫- ⎪⎝⎭()211112cos cos sin 2cos cos sin αααααα=⋅=⋅++12121cos 2sin 2124ααπα=⋅=++⎛⎫+ ⎪⎝⎭,由图可知04πα<<,所以函数的定义域为0,4π⎛⎫⎪⎝⎭. (2)由04πα<<,则32444πππα<+<,1124APQS πα=⎛⎫+ ⎪⎝⎭,当sin 214πα⎛⎫+= ⎪⎝⎭,即8πα=时,APQ 面积的最小,即APQ 1=. 【点睛】方法点睛:求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤: 第一步:三角函数式的化简,一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式;第二步:由x 的取值范围确定x ωϕ+的取值范围,再确定()sin x ωϕ+(或()cos x ωϕ+)的取值范围;第三步:求出所求函数的值域(或最值).21.(1)见详解;(23)(]1,11,28⎡⎫⎪⎢⎣⎭【分析】(1)根据函数解析式,直接作差比较()()1222f x f x +与()122f x x +的大小,即可证明结论成立;(2)根据题中条件,由指数幂运算性质,直接计算,即可得出结果; (3)先由不等式恒成立,得到x ∀∈R ,212x xx a -+≤恒成立;不等式两边同时取对数,得到x ∀∈R ,22log 1x a x x ≤-+恒成立,讨论0x =,0x >,0x <三种情况,分别求出对应的a 的范围,再求交集,即可得出结果.【详解】(1)因为()xf x a =,所以()()()()111222222121222220x x x x x x f x f x f x x a a a a a ++-+=+-=-≥显然恒成立, 所以()()()1212222f x f x f x x +≥+;(2)由()12f x =,()23f x =得1223x x a a ⎧=⎨=⎩,所以()212122x x x x x a a ==,又()1221228x x xf x x a ===,所以23x =,则233x a a ==,因此a =(3)若x ∀∈R ,()212xx f x -+≤恒成立,即x ∀∈R ,212x xx a -+≤恒成立;则x ∀∈R ,2122log log 2x xx a -+≤恒成立,即x ∀∈R ,22log 1x a x x ≤-+恒成立,当0x =时,不等式可化为01<,显然恒成立;所以0a >,且1a ≠; 当0x >时,不等式可化为21log 1a x x ≤+-,而1111y x x =+-≥=在0x >上恒成立,当且仅当1x =时,取等号;所以只需2log 1a ≤,解得12a <≤或01a <<; 当0x <时,不等式可化为21log 1a x x≥+-,而()111113y x x x x ⎡⎤⎛⎫=+-=--+--≤-=- ⎪⎢⎥⎝⎭⎣⎦在0x <上恒成立,当且仅当1x =-时,取等号;所以只需2log 3a ≥-,解得118a ≤<或1a >,综上,118a ≤<或12a <≤,即a 的取值范围是(]1,11,28⎡⎫⎪⎢⎣⎭【点睛】 关键点点睛:求解本题第三问的关键在于将不等式两边同时取对数,化为22log 1x a x x ≤-+恒成立,再对x 分段讨论,求解a 的范围,即可得解.22.(Ⅰ)(]0,1;(Ⅱ)224,121,10()21,014,1a a a a a k a a a a a a -<-⎧⎪-+-≤≤⎪=⎨++<≤⎪⎪>⎩,1.【分析】(Ⅰ)由复合函数的单调性得函数2()241g x x ax a =-+-在[1,3]上单调递增,则1(1)0a g ≤⎧⎨>⎩,解出即可; (Ⅱ)由题意得[]()ln 1,1f x x =∈-,设()t f x =,则2(())()241g f x g t t at a ==-+-22()41t a a a =--+-,[]1,1t ∈-,再分类讨论即可得到224,121,10()21,014,1a a a a a k a a a a a a -<-⎧⎪-+-≤≤⎪=⎨++<≤⎪⎪>⎩,再根据函数()k a 的单调性即可求出最小值.【详解】解:(Ⅰ)∵函数(())f g x 在[1,3]上单调递增, 函数()ln f x x =在[1,3]上单调递增,,∴函数2()241g x x ax a =-+-在[1,3]上单调递增,∴1(1)0a g ≤⎧⎨>⎩,解得01a <≤, ∴实数a 的取值范围是(]0,1;(Ⅱ)∵1,x e e ⎡⎤∈⎢⎥⎣⎦,∴[]()ln 1,1f x x =∈-,设()t f x =,则2(())()241g f x g t t at a ==-+-22()41t a a a =--+-,[]1,1t ∈-, ①当1a <-时,函数()g t 在[]1,1-上单调递增, ∴最大值()()12M a g a ==,最小值()()16m a g a =-=, ∴()264k a a a a =-=-;②当10a -≤≤时,函数()g t 在[]1,a -上单调递减,在[],1a 上单调递增,∴最大值()()12M a g a ==,最小值()2()41m a g a a a ==-+-,∴()22()24121k a a a a a a =--+-=-+;③当01a <≤时,函数()g t 在[]1,a -上单调递减,在[],1a 上单调递增,∴最大值()()16M a g a =-=,最小值()2()41m a g a a a ==-+-,∴()22()64121k a a a a a a =--+-=++;④当1a >时,函数()g t 在[]1,1-上单调递减,∴最大值()()16M a g a =-=,最小值()()12m a g a ==, ∴()624k a a a a =-=;综上,224,121,10()21,014,1a a a a a k a a a a a a -<-⎧⎪-+-≤≤⎪=⎨++<≤⎪⎪>⎩,∴()k a 在(],0-∞上单调递减,在[)0,+∞上单调递增, 当0a =时,()k a 取最小值1. 【点睛】本题主要考查复合函数的单调性,考查含参的二次函数在闭区间上的最值,考查计算能力,考查分类讨论的方法,属于难题.。
2009年江西省新余市高一上期末质量检测数学试题(必修1 必修2)

高一上学期期末质量检测数学试题一、、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中的横线上)13.函数)1(log 1)(2-=x x f 的定义域是 。
14.幂函数k x k k y ---=112)22(在(0,+∞)上是减函数,则k =__________。
15. 如图正△ABC 的斜二测画法的水平放置图形的直观图,若C B A '''∆的面积为3,那么△ABC 的面积为_______________。
16.关于函数()),0(1lg 2R x x xx x f ∈≠+=有下列命题: ①函数)(x f y =的图象关于y 轴对称;②在区间)0,(-∞上,函数)(x f y =是减函数;③函数)(x f 的最小值为2lg ;④在区间),1(∞上,函数)(x f 是增函数.其中正确命题序号为_______________.三、解答题(本大题6小题,共74分,解答应写出文字说明,证明过程或演算步骤)18.(本小题满分12分)如图,已知三角形的顶点为)3,2),2,0(),4,2(--C B A 求:(Ⅰ)AB 边上的中线CM 所在直线的方程;(Ⅱ)求△ABC 的面积.19.(本小题满分12分)如图,在四棱锥P-ABCD 中,底面ABCD 是正方形,侧棱PD⊥底面ABCD ,PD =DC =2,E 是P C 的中点,作EF ⊥PB 交PB 于点F .(1)证明 P A //平面EDB ;(2)证明PB ⊥平面EFD ;(3)求EFD B V -.21.(本小题满分12分)已知函数()f x ,当,x y R∈时,恒有()()f x y f x f y +=+. (1). 求证: ()()0;f x f x +-=(2). 若(3),f a -=试用a 表示(24);f15题图(3). 如果0>x 时,()0,f x <且1(1)2f =-,试求()f x 在区间[2,6]-上的最大值和最小值. 22.(本小题满分14分)已知正实数y x ,满足等式(3)1log 11log 1y x y x +⎡⎤⎛⎫⎡⎤-+= ⎪⎢⎥⎣⎦⎝⎭⎣⎦ (1)试将y 表示为x 的函数()x f y =,并求出定义域和值域。
2009-2014年湖南省普通高中学业水平考试数学试卷(含答案)

2014年湖南省普通高中学业水平考试数学试卷本试卷包括选择题、填空题和解答题三部分,共5页。
时量120分钟,满分100分.一、选择题:本大题共10小题,每小题4分,满分40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图是一个几何体的三视图,则该几何体为 A.圆柱 B.圆锥 C.圆台 D.球2.已知元素{0,1,2,3}a ∈,且{0,1,2}a ∉,则a 的值为 A.0 B.1 C.2 D.33.在区间[0,5]内任取一个实数,则此数大于3的概率为A.15 B. 25 C.35 D.454.某程序框图如图所示,若输入x 的值为1,则输出y 的值是A.2B.3C.4D.55.在△ABC 中,若0AB AC ⋅=u u u r u u u r,则△ABC 的形状是A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形 6.sin120o的值为A.2 B.1- C.3 D. 2-7.如图,在正方体1111ABCD A B C D -中,异面直线BD 与11A C 的位置关系是 A.平行 B.相交 C.异面但不垂直 D. 异面且垂直 8.不等式(1)(2)0x x +-≤的解集为A.{|12}x x -≤≤B. {|12}x x -<<C. {|12}x x x ≤-≥或D. {|12}x x x <->或9.点(,1)P m 不在不等式02<-+y x 表示的平面区域内,则实数m 的取值范围是 A.1m < B. 1m ≤ C.1m ≥ D.1m >10.某同学从家里骑车一路匀速行驶到学校,只是在途中遇到一次交通堵塞,耽误了一些时间,下列函数的图像最能符合上述情况的是二、填空题:本大题共5小题,每小题4分,满分20分. 11.样本数据2,0,6,3,6-的众数是 .12.在ABC ∆中, 角A 、B 、C 所对应的边分别为a 、b 、c ,已知11,2,sin 3a b A ===,则sin B = .13.已知a 是函数()22log f x x =-的零点, 则实数a 的值为 . 14.已知函数sin (0)y x ωω=>在一个周期内的图像如图所示,则ω的值为 .15.如图1,矩形ABCD 中,2,,AB BC E F =分别是,AB CD 的中点,现在沿EF 把这个矩形折成一个二面角A EF C --(如图2)则在图2中直线AF 与平面EBCF 所成的角为 .三、解答题:本大题共5小题,满分40分. 解答应写出文字说明、证明过程或演算步骤 . 16.(本小题满分6分)已知函数,[0,2],()4,(2,4].x x f x x x∈⎧⎪=⎨∈⎪⎩(1)画出函数()f x 的大致图像;(2)写出函数()f x 的最大值和单调递减区间.某班有学生50人,其中男同学30人,用分层抽样的方法从该班抽取5人去参加某社区服务活动.(1)求从该班男、女同学中各抽取的人数;(2)从抽取的5名同学中任选2名谈此活动的感受,求选出的2名同学中恰有1名男同学的概率. 18.(本小题满分8分) 已知等比数列{}n a 的公比2q =,且234,1,a a a +成等差数列. (1)求1n a a 及;(2)设n n b a n =+,求数列{}n b 的前5项和5S .已知向量(1,sin ),(2,1).a b θ==r r(1)当6πθ=时,求向量2a b +r r的坐标;(2)若a r ∥b r ,且(0,)2πθ∈,求sin()4πθ+的值.20.(本小题满分10分) 已知圆22:230C x y x ++-=. (1)求圆的圆心C 的坐标和半径长;(2)直线l 经过坐标原点且不与y 轴重合,l 与圆C 相交于1122(,),B(,)A x y x y 两点,求证:1211x x +为定值; (3)斜率为1的直线m 与圆C 相交于,D E 两点,求直线m 的方程,使△CDE 的面积最大.2014年湖南省普通高中学业水平考试数学试卷参考答案及评分标准题号 1 2 3 4 5 6 7 8 9 10 答案CDBBACDACA二 、填空题(每小题4分,满分20分) 11.6 12.23 13.4 14.2 15. 45o (或4π)三 、解答题(满分40分)16. 解:(1)函数()f x 的大致图象如图所示; ……………………………2分 (2)由函数()f x 的图象得出,()f x 的最大值为2, ………………4分其单调递减区间为[]2,4.…………6分17. 解: (1)305350⨯=(人), 205250⨯=(人), 所以从男同学中抽取3人, 女同学中抽取2人; ……………………………………4分 (2)过程略. 3()5P A =. ……………………………………………………………………………8分18. 解: (1)12n n a -=; ………………………………………………………………4分 (2)546S =. ……………………………………………………………………………8分 19. 解: (1)()4,2; …………………………………………………………………4分 (2)26+. ………………………………………………………………………8分 20. 解: (1)配方得()2214x y ++=, 则圆心C 的坐标为()1,0-,……………………2分 圆的半径长为2; ………………………………………………………………………4分 (2)设直线l 的方程为y kx =, 联立方程组22230x y x y kx ⎧++-=⎨=⎩,消去y 得()221230k x x ++-=, ………………………………………………5分则有: 1221222131x x k x x k ⎧+=-⎪⎪+⎨⎪=-⎪+⎩ ………………………………………………6分 所以1212121123x x x x x x ++==为定值. ………………………………………………7分 (3)解法一 设直线m 的方程为y kx b =+, 则圆心C 到直线m 的距离d =所以DE ==, …………………………………8分()2241222CDEd d S DE d d ∆-+=⋅=≤=,当且仅当d =,即d =时, CDE ∆的面积最大, …………………………9分=解之得3b =或1b =-, 故所求直线方程为30x y -+=或10x y --=.……………………………………10分解法二 由(1)知2CD CE R ===, 所以1sin 2sin 22CDE S CD CE DCE DCE ∆=⋅⋅∠=∠≤,当且仅当CD CE ⊥时, CDE ∆的面积最大,此时DE = ………………………………………………………8分 设直线m 的方程为y x b =+ 则圆心C 到直线m的距离d =…………………………………………………9分由DE ==,得d =,=得3b =或1b =-,故所求直线方程为30x y -+=或10x y --=.……………………………………10分(第3题图)俯视图侧视图正视图2013年湖南省普通高中学业水平考试试卷数 学本试题卷包括选择题、填空题和解答题三部分,共5页。
2009高考真题数学试卷

2009高考真题数学试卷2009年高考数学真题试卷一、选择题1. 已知函数f(x)=2^x,g(x)=log<sub>2</sub>x,则f(g(16))的值为多少?A. 3B. 4C. 5D. 62. 已知函数f(x)=x^2-4x+3,g(x)=ax+b,且f(g(x))=x^2+x-1,则a的值为多少?A. 3B. 2C. 1D. 03. 若1+sinx=cos(π/6+x),则x=?A. -7π/6B. -5π/6C. -π/6D. π/64. 若集合A={x|-3≤x≤3},集合B={x|1≤x≤5},则A∪B的值为?A. [-3,5]B. [1,5]C. [-3,3]D. [-3,3)∪[1,5]5. 一辆汽车以每小时40公里的速度行驶,一辆以每小时50公里的速度行驶的汽车比其每小时行驶时间多5小时,则这段路长多少公里?A. 200B. 240C. 250D. 300二、填空题1. 已知函数f(x)=2sin2x,则f(π/6)的值为多少?2. 直线3x+4y=9与y轴交于点A,与x轴交于点B,点A到原点的距离为多少?3. 若集合A={1,2,3,4},集合B={3,4,5,6},则A∩B的值为多少?4. 若直角三角形的两条直角边分别为3和4,则斜边长多少?5. 若log3x=1,求x的值。
三、解答题1. 如图所示,已知AD=BC=5,AB=CD=3,则矩形ABCD的面积为多少?2. 求方程2cosx-√3sinx=1的通解。
3. 一块铁板长12米,宽8米,要做成一个矩形的圆筒,问直径为多少时圆筒的容积最大?4. 某班级中男女比为2:3,若男生人数增加10%,女生人数减少10%,则男女比为多少?5. 一球从3米高的地方自由下落,碰到地面后反弹到高度的3/4,再落下。
求球共经过的路程。
以上是2009年高考数学真题试卷的部分内容,希朝考生认真答题,把握好考试时间,取得优异成绩。
湖南省永州市2023-2024学年高一上学期期末质量监测数学试卷含解析
永州市2023年下期高一期末质量监测试卷数学(答案在最后)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{}1,2,3,4U =,{}1,2A =,则U A =ð()A.{}1,2 B.{}1,3 C.{}3,4 D.{}2,3,4【答案】C 【解析】【分析】由集合补运算求集合.【详解】由{}1,2,3,4U =,{}1,2A =,则U A =ð{}3,4.故选:C2.命题p :x ∀∈R ,210x ->的否定是()A.x ∀∈R ,210x -<B.x ∀∈R ,210x -≤C.x ∃∈R ,210x -≤D.x ∃∈R ,210x ->【答案】C 【解析】【分析】根据含有一个量词的命题的否定的方法即可求解.【详解】命题p :x ∀∈R ,210x ->的否定是:x ∃∈R ,210x -≤.故选:C.3.“02a <<”是“24a <”成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】解一元二次不等式求参数范围,结合充分、必要性定义判断条件间的关系.【详解】由24a <,可得22a -<<,故“02a <<”是“24a <”成立的充分不必要条件.故选:A4.已知幂函数y =f (x )的图象经过点(4,2),则f (2)=()A.14B.4C.2D.【答案】D 【解析】【分析】利用待定系数法求出函数的解析式,再代入求值即可.【详解】设f (x )=x a ,因为幂函数图象过(4,2),则有24a =,∴a 12=,即12()f x x =,∴f (2)122==故选:D【点睛】本题考查了待定系数法求函数解析式,考查了求函数值,属于基础题.5.扇形的面积为4,周长为8,则扇形的圆心角的弧度数为()A.1B.2C.3D.4【答案】B 【解析】【分析】利用扇形的面积、弧长公式列方程求半径、弧长,即可求扇形的圆心角.【详解】令扇形半径为r ,弧长为l ,则1824228428rl r rl r l l r l ⎧===⎧⎧⎪⇒⇒⎨⎨⎨+==⎩⎩⎪+=⎩,所以扇形的圆心角的弧度数为2lr=.故选:B6.已知2sin cos 0θθ-=,则cos sin cos sin θθθθ+=-()A.1 B.32C.2D.3【答案】D 【解析】【分析】由题设得1tan 2θ=,化弦为切求目标式的值.【详解】由题设1tan 2θ=,又cos sin 1tan 3cos sin 1tan θθθθθθ++==--.故选:D7.已知ln2ln5a =,1512b ⎛⎫= ⎪⎝⎭,0.5log 0.2c =,则()A.c b a << B.b<c<aC.a b c<< D.b a c<<【答案】C 【解析】【分析】由对数运算性质有1ac =,进而有1202c a >>>>,再由指数函数性质求b ,即可得答案.【详解】由5ln2log 2ln5a ==,0.52log 0.2log 5c ==,则1ac =,所以1202c a >>>>,又151(,1)122b ⎭∈⎛⎫= ⎪⎝,综上,a b c <<.故选:C8.已知函数()12141,211log ,22xx f x x x ⎧-≤⎪⎪=⎨⎪+>⎪⎩,若方程()()0f f x a -=有5个不同的实数解,则a 的取值范围是()A.()0,1 B.10,2⎛⎫ ⎪⎝⎭C.30,2⎛⎫ ⎪⎝⎭D.1,12⎛⎫ ⎪⎝⎭【答案】B 【解析】【分析】根据分段函数解析式,结合指对数函数性质画出函数大致图象,令()t f x =并讨论t 判断对应方程根的个数,再由()f t a =有5个不同的实数解,讨论a 范围,结合对应t 的分布确定根的个数,即可得范围.【详解】由解析式得函数大致图象如下,由1211(1)log 122f =+=,令1|41|2x -=,可得12x =-或21(log 31)2x =-,令()t f x =,当0t <或312t <<时有1个解;当0=t 或1t =时有2个解;当01t <<时有3个解;当32t ≥时无解;要使()f t a =有5个不同的实数解,若a<0,则2t >,此时方程有1解;若0a =,则10t =有2个解,22t =有1解,此时方程共有3个解;若102a <<,则1102t -<<有1个解,2210(log 31)2t <<-有3解,312t <<有1解,此时方程共有5个解;若12a =,则112t =-有1个解,221(log 31)2t =-有3解,31t =有2解,此时方程共有6个解;若112a <<,则112t <-有1个解,2211(log 31)22t -<<有3解,3212t <<有3解,此时方程共有7个解;若1a =,则112t =有3个解,222t =有3个解,此时方程共有6个解;若312a <<,则1222t <<有3个解,此时方程共有3个解;若32a ≥,没有对应t ,此时方程无解;综上,102a <<.故选:B【点睛】关键点点睛:根据函数图象研究()t f x =对应根的个数,再数形结合讨论()f t a =范围研究根的个数.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.9.若a b c d >>>,则下列不等式成立的是()A.a c b d +>+B.ad bc> C.33a c > D.22a b>【答案】ACD 【解析】【分析】由不等式性质判断A 、B 、C ,根据指数函数单调性判断D.【详解】由a b c d >>>,则a c b d +>+,33a c >,A 、C 对;若2,1,0,2a b c d ====-,此时ad bc <,B 错;由2x y =单调递增,故22a b >,D 对.故选:ACD10.在下列函数中,既是偶函数又在区间()0,1上单调递增的有()A.3y x =B.cos y x=- C.tan y x= D.2xy =【答案】BCD 【解析】【分析】根据指数、幂函数及三角函数性质判断函数奇偶性、区间单调性,即可得答案.【详解】由3y x =为奇函数,A 不符;由cos y x =-定义域为R ,且cos()cos x x --=-,为偶函数,在区间()0,1上单调递增,B 符合;由tan y x =定义域为π{|π},Z 2x x k k ≠+∈,且tan()|tan ||tan |x x x -=-=,为偶函数,在区间()0,1上单调递增,C 符合;由2xy =定义域为R ,且22x x -=,为偶函数,在区间()0,1上单调递增,D 符合;故选:BCD11.定义域为R 的偶函数()f x 满足()()20f x f x -+=,且[]0,1x ∈时,()()21f x x =-,则()A.3124f ⎛⎫-=- ⎪⎝⎭B.()()4f x f x +=C.()f x 的图象关于直线3x =对称D.()f x 在区间[]2023,2024上单调递增【答案】ABD 【解析】【分析】由题设关系得3122f f ⎛⎫⎛⎫=-⎪ ⎪⎝⎭⎝⎭,结合区间解析式求值判断A ;根据已知有()()f x f x -==()2f x --,即()(2)f x f x =-+,利用递推关系即可判断B ;由已知可得()(6)f x f x =--即可判断C ;根据周期性,区间[]2023,2024与区间[]1,0-的单调性相同,结合已知区间单调性及偶函数判断D.【详解】由33111222224f f f f⎛⎫⎛⎫⎛⎫⎛⎫-==-=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,A 对;由题设()()f x f x -==()2f x --,即()(2)(4)f x f x f x =-+=+,B 对;由()(2)f x f x =--,则()4(6)f x f x +=--,综上()(6)f x f x =--,即()f x 关于(3,0)对称,C 错;根据周期性,区间[]2023,2024上单调性与区间[]1,0-上单调性相同,又[]0,1x ∈时,()()21f x x =-,即在[]0,1上()f x 上递减,又()f x 是偶函数,所以()f x 在区间[]1,0-上递增,故()f x 在区间[]2023,2024上单调递增,D 对.故选:ABD12.已知函数()()πsin 03f x x ωω⎛⎫=-> ⎪⎝⎭在区间[]0,π上有且仅有两个不同的零点,则()A.()f x 在区间[]0,π上有两条对称轴B.ω的取值范围是47,33⎡⎫⎪⎢⎣⎭C.()f x 在区间π0,3⎛⎫⎪⎝⎭上单调递增D.若()()0πf f =,则53ω=【答案】BC 【解析】【分析】由题设有sin y t =在ππ[,π]33t ω∈--有且仅有两个不同的零点,结合正弦函数性质求得4733ω≤<,再由各项描述逐项判断各项正误.【详解】区间[]0,π上πππ[,π333t x ωω=-∈--且0ω>,故sin y t =在ππ[,π33t ω∈--有且仅有两个不同的零点,所以πππ2π3ω≤-<,可得4733ω≤<,B 对;当43ω=时π[,π]3t ∈-,此时sin y t =只有一条对称轴,即()f x 在[]0,π上可能只有一条对称轴,A 错;区间π0,3⎛⎫ ⎪⎝⎭上()πππ,1333x ωω⎡⎤-∈--⎢⎥⎣⎦,而ππ4π(1)[,399ω-∈,所以()f x 在区间π0,3⎛⎫⎪⎝⎭上单调递增,C 对;由()()0πf f =,即ππsin πsin 332ω⎛⎫⎛⎫-=-=- ⎪ ⎪⎝⎭⎝⎭,又πππ2π3ω≤-<,所以π4ππ33ω-=或π5ππ33ω-=,可得53ω=或2ω=,D 错.故选:BC【点睛】关键点点睛:应用换元法,将问题化为sin y t =在ππ[,π]33t ω∈--有且仅有两个不同的零点求参数范围为关键.三、填空题:本题共4小题,每小题5分,共20分.13.()3348log 4log 3-+⋅=______.【答案】511-【解析】【分析】利用换底公式计算不同底数的对数运算,再与-8的立方求和即得.【详解】()334lg 4lg 38log 4log 35125121511lg 3lg 4-+⋅=-+=-+=- 故答案为:-511.14.函数1()2(0,1)x f x a a a -=+>≠的图象恒过定点_____________.【答案】(1,3)【解析】【分析】根据指数函数的性质,即可得答案.【详解】令10x -=,可得1x =,所以0(1)23f a =+=,即()f x 图象恒过定点(1,3).故答案为:(1,3)15.已知0a >,0b >,则21b a a b++的最小值为______.【答案】【解析】【分析】两次应用基本不等式求目标式最小值,注意取值条件.【详解】由题设21112b a b a b b b ++≥=+≥,当且仅当2b a a=,即a b =时第一个等号成立,当且仅当12b b =,即2b =时第二个等号成立,综上,2a b ==时目标式有最小值为.故答案为:16.若函数()y f x =在定义域内存在实数x 使得()()f x kf x -=-,其中k ∈Z ,则称函数()y f x =为定义域上的“k 阶局部奇函数”,对于任意的实数(],3t ∈-∞,函数()22f x x x t =-+恒为R 上的“k 阶局部奇函数”,则k 的取值集合是______.【答案】{}3,2,1---【解析】【分析】由题意,建立方程,利用分类讨论思想,结合一元二次方程有解问题,可得答案.【详解】由题意得,函数()22f x x x t =-+恒为R 上的“k 阶局部奇函数”,即()()0f x k f x -+⋅=在R 上有解,则有()()22()220x x t k x x t ---++-+=,即()()()212210k x k x k t ++-++=有解,当1k =-时,0R x =∈,满足题意;当1k ≠-时,对于任意的实数(],3t ∞∈-,22Δ(22)4(1)0k k t =--+≥,变形可得224(1)3(22)0k k +⋅--≤,解可得:22k -≤≤-+,由Z k ∈,故{}3,2,1k ∈---.故答案为:{}3,2,1---.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知函数()af x x x=+(1)若2a =,求()()1ff 的值;(2)若a<0,判断()f x 在区间()0,∞+上的单调性,并用定义证明.【答案】(1)113;(2)()f x 在区间()0,∞+上递增,证明见解析.【解析】【分析】(1)由()()1(3)ff f =,将自变量代入求值即可;(2)设120x x >>,应用作差法比较()()12,f x f x 证明单调性.【小问1详解】由题设()2f x x x =+,则()13f =,故()()2111(3)333f f f ==+=;【小问2详解】()f x 在区间()0,∞+上递增,证明如下:令120x x >>,则()()1212121212()()()(1)a a af x f x x x x x x x x x -=+-+=--,又a<0,则1210->ax x ,且120x x ->,所以()()12f x f x >,即()f x 在区间()0,∞+上递增.18.已知集合{}2430A x x x =-+≤,{}2log 1B x x =>(1)求A B ⋂;(2)已知集合{}1C x x a =<<,若C A ⊆,求实数a 的取值范围.【答案】(1){|23}x x <≤;(2)3a ≤.【解析】【分析】(1)解一元二次不等式求集合A ,解对数不等式求集合B ,再应用集合交运算求结果;(2)由包含关系,讨论C =∅、C ≠∅列不等式求参数范围.【小问1详解】由题设{}(1)(3)0{|13}A x x x x x =--≤=≤≤,{|2}B x x =>,所以{|23}A B x x ⋂=<≤;【小问2详解】由C A ⊆,若C =∅,则1a ≤满足题设;若C ≠∅,则13a a >⎧⎨≤⎩,即13a <£;综上,3a ≤.19.已知函数()π12sin cos 62f x x x ⎛⎫=++ ⎪⎝⎭.(1)求()f x 的最小正周期;(2)将函数()f x 的图象向右平移π6个单位长度,再把横坐标缩小为原来的12(纵坐标不变),得到函数()y g x =的图象,求()g x 在π0,2⎡⎤⎢⎥⎣⎦上的单调递增区间.【答案】(1)π;(2)单调递增区间为π[0,]6和5ππ[,]122.【解析】【分析】(1)利用三角恒等变换化简函数式得π()sin(2)6f x x =+,即可求最小正周期;(2)根据图象平移得π()sin(4)6g x x =-,由正弦函数性质,应用整体法求递增区间.【小问1详解】由题设()23111312sin (cos sin )3sin cos sin sin 2cos 2222222f x x x x x x x x x =-+=-+=+πsin(2)6x =+,所以()f x 的最小正周期2ππ2T ==;【小问2详解】图象向右平移π6个单位长度,得ππ()sin(2)66f x x -=-,把横坐标缩小为原来的12(纵坐标不变),得π()sin(4)6g x x =-,在π0,2⎡⎤⎢⎥⎣⎦上ππ11π4[,]666x -∈-,显然πππ4662x -≤-≤或3ππ11π4266x ≤-≤,所以π06x ≤≤或5ππ212x ≤≤,故()g x 在π0,2⎡⎤⎢⎥⎣⎦上的单调递增区间为π[0,]6和5ππ[,]122.20.为响应“湘商回归,返乡创业”的号召,某企业回永州投资特色农业,为了实现既定销售利润目标,准备制定一个激励销售人员的奖励方案:按销售利润进行奖励,总奖金额y (单位:万元)关于销售利润x (单位:万元)的函数的图象接近如图所示,现有以下三个函数模型供企业选择:①()0y kx b k =+>②()20x y k m k =⋅+>③()3log 303x y k n k ⎛⎫=++> ⎪⎝⎭(1)请你帮助该企业从中选择一个最合适的函数模型,并说明理由;(2)根据你在(1)中选择的函数模型,如果总奖金不少于6万元,则至少应完成销售利润多少万元?【答案】(1)③,理由见解析(2)72万元【解析】【分析】(1)根据已知条件,结合函数所过的点,以及函数的增长速度,即可求解.(2)根据(1)的结论,将对应的点代入,即可求解函数表达式,列不等式求解即可.【小问1详解】对于模型①,y kx b =+,图象为直线,故①错误,由图可知,该函数的增长速度较慢,对于模型②,指数型的函数是爆炸型增长,故②错误,对于模型③,对数型的函数增长速度较慢,符合题意,故选项模型③,【小问2详解】由(1)可知,选项模型③,所求函数过点(0,0),(18,3),则33log 30log (63)3k n k n +=⎧⎨++=⎩,解得3k =,3n =-,故所求函数为33log (3)33x y =+-,∴33log (3)363x +-≥,即3log (3)33x +≥,∴3273x +≥,∴72x ≥,∴至少应完成销售利润72万元.21.在平面直角坐标系xOy 中,角π4及锐角α的终边分别与单位圆交于A ,B 两点.(1)若B 点的横坐标为35,求()()3πsin tan π2cos πααα⎛⎫-+ ⎪⎝⎭--的值:(2)设角π4α+的终边与单位圆交于点C ,AP ,BQ ,CR 均与x 轴垂直,垂足分别为P ,Q ,R ,请判断以线段AP ,BQ ,CR 为边能否构成三角形,并说明理由.【答案】(1)43(2)利用见解析【解析】【分析】(1)利用三角函数的定义,结合诱导公式化简计算即可;(2)由α,π4α+范围,得cos (0,1)α∈,πcos()4α+<于第三边.【小问1详解】已知α是锐角,则34,55B ⎛⎫ ⎪⎝⎭,根据三角函数的定义,得3cos 5α=,4sin 5α=,4tan 3α=,()()3πsin tan πcos tan 42tan cos πcos 3ααααααα⎛⎫-+ ⎪-⎝⎭===---.【小问2详解】能构成三角形,理由如下:由三角函数的定义得,πsin 42AP ==,sin BQ α=,πsin()4CR α=+,因为π(0,)2α∈,所以cos (0,1)α∈,于是有ππππsin()sin cos cos sin sin sin 4444αααα+=+<+,①故CR AP BQ <+,又因为ππ3π(,444α+∈,所以πcos()4α<+<ππππππππsin sin(())sin()cos cos()sin sin(sin 44444444ααααα=+-=+⋅-+⋅<++,②故BQ AP CR<+同理,ππsin sin(sin 44αα<++,③,由①,②,③可得,以AP ,BQ ,CR 的长为三边长能构成三角形.22.已知函数()lg f x x =,()2e e x x g x a =-.(1)若对[]11,10x ∀∈,[)20,x ∀∈+∞都有()()12f x g x ≤,求实数a 的取值范围;(2)若函数()()()h x g x g x =+-,求函数()h x 的零点个数.【答案】(1)2a ≥;(2)答案见解析.【解析】【分析】(1)将问题化为()()12max min f x g x ≤,令2[1,)e x t ∈=+∞,结合对数函数单调性求最值得21at t -≥在[1,)t ∈+∞上恒成立,进而化为max 211(a t t ≥+求参数范围;(2)令2e e x x μ-+=≥转化为研究22a μμ=-在[2,)μ∈+∞上解的个数,求出右侧范围,再讨论参数a ,确定对应μ,结合e e x x μ-=+函数性质确定()h x 的零点个数.【小问1详解】对[]11,10x ∀∈,[)20,x ∀∈+∞都有()()12f x g x ≤,只需()()12max min f x g x ≤,由()11lg f x x =在[]11,10x ∈上递增,故()1max (10)1f x f ==,由()2222e e x x g x a =-,在[)20,x ∈+∞上有2[1,)e x t ∈=+∞,所以()22g x y at t ==-且[1,)t ∈+∞,故有21at t -≥在[1,)t ∈+∞上恒成立,所以2max max 211111([()]24a t t t ≥+=+-,而1(0,1]t ∈,即2a ≥.【小问2详解】由题设()2222e e e )e e e e ()(e x x x x x x x x h a x a a ----=--=+-++,令2e e x x μ-=≥=+,当且仅当0x =时等号成立,则2222()2e e e e x x x x μ--+=+=+,即2222e e x x μ-+=-,所以()2()2a a h x ϕμμμ==--且[2,)μ∈+∞,令2()20a a ϕμμμ=--=,则问题等价于2122a μμμμ==--在[2,)μ∈+∞上解的个数,又12y μμ=-在[2,)μ∈+∞上递减,故(0,1]y ∈,当1a >或0a ≤时,22a μμ=-在[2,)μ∈+∞上无解,即()h x 无零点;当1a =时,22(1)(2)0μμμμ--=+-=在[2,)μ∈+∞上有2μ=,所以2e e x x μ-+==,即0x =,故()h x 有1个零点;当01a <<时,220a a μμ--=在[2,)μ∈+∞上有11822a μ+=>(负值舍),又e e x x μ-=+为偶函数,此时()h x 有2个零点;综上,1a >或0a ≤时,()h x 无零点;1a =时,()h x 有1个零点;01a <<时,()h x 有2个零点;【点睛】关键点点睛:第一问,问题化为()()12max min f x g x ≤,令2[1,)e x t ∈=+∞进一步化为max 211()a t t ≥+;第二问,令2e e x x μ-+=≥转化为研究22a μμ=-在[2,)μ∈+∞上解的个数为关键.。
2008-2009学年(上)期末考试七年级数学试卷(答案)
2008-2009学年(上)期末考试七年级数学试卷(答案)[]923)6()1(3224)1(322949)1(-=⎪⎭⎫ ⎝⎛-⨯-⨯-=⎪⎭⎫ ⎝⎛-÷--⨯-=⎪⎭⎫ ⎝⎛-÷⎥⎦⎤⎢⎣⎡-⨯-⨯-=2008-2009学年(上)期末考试七年级数学试卷(答案)一、DCABDBDABC二、1、小; 2、4 ; 3、35 ;4、8×108 ;5、150 °;6、20% ;7、144°;8、70三、1、原式=(-9)×5+6×5+3×11 (2分) =-45+30+33 (2分) =18 (1分)2、原式(2分)(2分)(1分)3、原式=4a 2-18b -15a 2+12b=-11a 2-6b (3分) 把a=-2,b=-2代入 ,原式=-32 (2分)4、 去分母,得 6 (x+15)=15-10(x-7)去括号,得 6x+90=15-10x+70 (2分)移项,得 6x+10x=15+70-90合并同类项,得 16x=-5 (2分)系数化为1,得x=165 (1分)四、1、两种情况各3分 m=7或m=12、求得∠MOC =55°(2分)求得∠NOC =15°(2分)求得∠MON =40°(2分)3、平均数增加1的可能性最大。
理由如下:由于平均数增加1的区域最大,转动转盘时指针落在这一区域的可能性最大(2分)。
设添加一个数X,则14 (2+3+7+X) =13(2+3+7) +1,解得X=8。
(2分)因此添加8的可能性最大(2分)4、每问2分。
最少8块 最多11块五、1、(1).60÷30%=200, 本次一共调查了200名学生(3分)2008—2009(上)期末试题七年英语试卷参考答案(满分100分)听力部分20分Ⅰ. 1——20 B C A C C A C B B A B A C A CTennis ; science ; watches TV ; at six/6:00 ;on Sunday afternoon笔试部分80 分Ⅱ. 21——35 共15分,每题1分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009高一数学满分:120分 时量:120分钟第I 卷一、选择题(本大题共10小题,每小题4分,共40只有一项符合题目要求,请将正确选项的代号填入第II 卷卷首的答题栏内.) 1. tan120的值为A .33-B .33 C .3 D .3-2. 下列选项那个是正确的A .PRINT 4*xB .INPUT A ;BC .INPUT B =3D .PRINT y =2*x +1 3. 一个公司共有300名员工,现采用分层抽样方法从全体员工中抽取一个容量为20的样本,已知某部门有60名员工,那么从这一部门抽取的员工人数是 A .4 B .5 C .6 D .8 4. 若函数()f x 满足()cos f x x =()x R ∈,则()2f x π+=A .sin xB .sin x -C .cos xD .x cos -5.袋中有红、蓝、黑、白4个除颜色以外完全相同的球,甲、乙、丙、丁四人依次各摸一球,则事件“甲摸得白球”与事件“乙摸得白球”是 A .对立事件 B .互斥但不对立事件 C .不可能事件 D .以上都不对6. 如右图,已知CA a = ,CB b = ,2AD DB =,用a 、b 表示CD 为A .5233CD a b =-B .1233CD a b =+C .CD =3132+D .CD =b a 3121+7. 函数)sin(ϕω+=x A y (0,0,0A ωϕπ>><<)在一个周期内的图象如右图,此函数的解析式为 A .)322sin(2π+=x y B .)32sin(2π+=x y C .)32sin(2π-=x y D .)32sin(2π-=x y8. 阴影部分.较短的直角边长为2,现向大正方形靶盘投掷飞镖,则飞镖落在阴影区域的概率为 A .134 B .132DxC .131 D .133 9. 在区间[]0,2π上满足21sin ≥x 的x 的取值范围是 A .⎥⎦⎤⎢⎣⎡6,0πB .⎥⎦⎤⎢⎣⎡65,6ππ C .⎥⎦⎤⎢⎣⎡32,6ππD .⎥⎦⎤⎢⎣⎡ππ,6510. 甲、乙两人玩数字游戏的规则如下:甲、乙两人都从集合{}1,2,3,4中任选一个数写在纸上,并分别记为a 、b ,若1a b -≤,则称甲、乙两人“心有灵犀”,那么甲、乙两人在一次游戏中“心有灵犀”的概率为 A .38B .716C .58D .712二、填空题(本大题共5小题,每小题4分,满分20分)11.已知(2,1)a = ,(1,)b λ=-,且//a b ,则λ= .12.某学校号召学生在暑假期间至少参加一次社会公益活动(以下简称活动).该校文学社共有100名学生,他们参加活动的次数统计如图所示.则该文学社学生参加活动的人均次数为 .13.15sin 15cos 3-的值等于 . 14. 阅读以下程序:INPUT x IF 0x < THEN*2*6y x x x =-+ ELSE()()1*1y x x =-- END IFPRINT y END若输出9y =, 则输入的x 值应该是 . 15.给出下列命题: ① 函数)225sin(x y -=π)(R x ∈是偶函数; ② 函数21()cos 2f x x =-)(R x ∈的周期为π;③ 函数)4sin(π+=x y 在闭区间]2,2[ππ-上是增函数;④ 将函数)32cos(π-=x y )(R x ∈的图象向左平移3π个单位,得到函数x y 2cos =的图象. 其中正确的命题的序号是 .11.12.13.14.15.第II 卷三、解答题(本大题共6小题,共60分,解答应写出文字说明、证明过程或演算步骤) 16. (本小题8分)在2008年奥运会上甲、乙两名射击运动员在比赛中打出如下成绩:甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8; 乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1; (I) 请用茎叶图表示甲,乙两人成绩;(II)根据茎叶图分别求出他们的中位数,并分析甲、乙两人的成绩.17. (本小题10分)已知tan 34πα⎛⎫+=⎪⎝⎭,计算: (Ⅰ) tan α; (Ⅱ)αααcos sin 2sin +.18. (本小题10分)在一个匣内有大小完全相同的1个白球、2个红球和2个黑球,现从中任取两球,分别求下列事件的概率:(Ⅰ) 恰有一个红球;(Ⅱ) 至少有一个红球;(Ⅲ) 没有黑球.19. (本小题10分)已知1e 、2e 是单位向量,1e 与2e 的夹角为3π,122a e e =-,122+b e e λ= . (Ⅰ)若1λ=-,求 a b ⋅ 及向量a 与b 的夹角θ的大小; (Ⅱ)λ取何值时, a b ⊥.20. (本小题10分)设计一个求100991321211⨯++⨯+⨯的值的程序框图.21. (本小题12分)已知向量(2cos ,2sin )m x x = ,(cos ,)n x x =,函数()f x am n b a =⋅+-(a 、b 为常数且x ∈R ).(Ⅰ) 当==2a b 1,时,求()f x 的最小值; (Ⅱ) 是否存在非零整数a b 、,使得当0,2x π⎡⎤∈⎢⎥⎣⎦时,()f x 的值域为[]2,8.若存在,求出a b 、的值;若不存在,说明理由.高一数学参考答案及评分标准二、填空题(本大题共5小题,每小题4分,满分20分) 11.-2112. 2.2 13.2 14.-1,4 15.①②三、解答题(本大题共6小题,共60分,解答应写出文字说明、证明过程或演算步骤) 16. 解:(I)如图所示,茎表示成绩的整数环数,叶表示小数点后的数字4分(II)甲的中位数是9.05,乙的中位数是9.156分乙的成绩大致对称,可看出乙发挥稳定性好,甲波动性大. 8分17.解:(Ⅰ)由已知,得3tan 1tan 1=-+αα,解得21tan =α;5分(Ⅱ)解法一:原式==+⨯=+1212211tan 2tan αα4110分解法二:(1) 若α在第一象限,则sin 5α=、cos 5α=121212==⨯+41;7分(2) 若α在第三象限,则sin 5α=-、cos 5α=-,121212==⨯+419分综上所述 αααcos sin 2sin +=4110分18. 解:把2个红球记为:红1、红2,把2个黑球记为: 黑1、黑2,总事件共有10个基本事件: 1分 {白,红1}{白,红2}{白,黑1}{白,黑2}{红1,黑1}{红2,黑1} {红1,黑2}{红2,黑2}{红1,红2}{黑1,黑2}, 2分(Ⅰ)恰有一个红球含有6个基本事件:{白,红1}{白,红2}{红1,黑1}{红2,黑1}{红1,黑2}{红2,黑2},故P 1=63104=; 4分{Ⅱ} 至少有一个红球含有7个基本事件:{白,红1}{白,红2}{红1,黑1}{红2,黑1}{红1,黑2}{红2,黑2}{红1,红2},故P 2=710; 7分{Ⅲ} 没有黑球含有3个基本事件:{白,红1}{白,红2}{红1,红2},故P 3=310. 10分19.(本小题10分)解:(Ⅰ) λ=-1,122a e e = -,122b e e =- ,1212e e ⋅=1分 a b ⋅ =12(2)e e ⋅ -12(2)e e - =111222252e e e e e e ⋅-⋅+⋅ =542-=32;3分2||a =a a ⋅ =1212(2)(2)e e e e ⋅--=11122244e e e e e e ⋅-⋅+⋅=3,||a =, 4分同理||b cos θ=312||||a b a b ⋅==⋅,cos θ=12; 又[0,]θπ∈,所以θ=3π. 6分 (Ⅱ)由 a b ⊥ 知: 0a b ⋅=,7分a b ⋅ =12(2)e e ⋅ -12(2)e e λ+ =1112222(4)2e e e e e e λλ⋅+-⋅-⋅=132(4)2022λλλ+--=-=,故0λ= 10分20. (本小题10分)解:程序框图如下: 或A BCD10分21.(本小题12分)解:(Ⅰ)函数a b n m a x f -+⋅=)(=a (2cos ,2sin )x x⋅(cos ,)x x +b -a=22cos cos sin a x x x ++b -a=cos2sin 2a x x b +=2sin (2)6a xb π++,3分当a =1,b =2时,()2sin (2)=2sin (2)266f x a x b x ππ=++++,又x ∈R ,所以f(x)的最小值为05分(Ⅱ)假设存在非零整数a 、b ,使得f(x)的值域为[2, 8],∵x ∈[0 ]2π,∴7(2)[,]666x πππ+∈, 即2sin (2)6x π+[1,2]∈-由(I)知=)(x f 2sin (2)6a xb π++7分①当a >0时,则有2=8=2a b a b ⎧⎨⎩+-+ ,求得24a b ⎧⎨⎩==9分②当a <0时,则有2=2=8a b a b ⎧⎨⎩+-+ ,求得26a b ⎧⎨⎩=-=11分 所以,存在2a =、4b =或2a =-、6b =,使得f(x)的值域为[2,8] .12分。
