人教版初三数学上册二次函数中的面积问题课后作业

合集下载

初中数学中考二轮6二次函数中的面积问题(1)

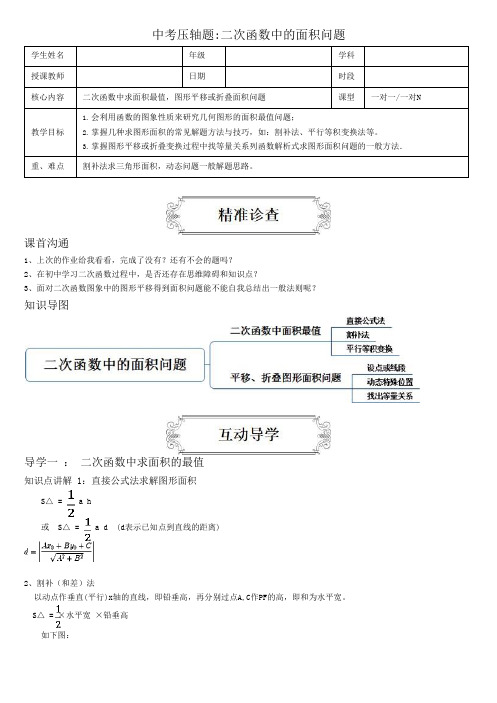
中考压轴题:二次函数中的面积问题学生姓名年级学科授课教师日期时段核心内容二次函数中求面积最值，图形平移或折叠面积问题课型一对一/一对N教学目标1.会利用函数的图象性质来研究几何图形的面积最值问题；2.掌握几种求图形面积的常见解题方法与技巧，如：割补法、平行等积变换法等。

3.掌握图形平移或折叠变换过程中找等量关系列函数解析式求图形面积问题的一般方法．重、难点割补法求三角形面积，动态问题一般解题思路。

课首沟通1、上次的作业给我看看，完成了没有？还有不会的题吗？2、在初中学习二次函数过程中，是否还存在思维障碍和知识点？3、面对二次函数图象中的图形平移得到面积问题能不能自我总结出一般法则呢？知识导图导学一：二次函数中求面积的最值知识点讲解 1：直接公式法求解图形面积S△ = a ha d (d表示已知点到直线的距离)2、割补（和差）法以动点作垂直(平行)x轴的直线，即铅垂高，再分别过点A,C作PF的高，即和为水平宽。

S△ = ×水平宽×铅垂高如下图：或S△ =3、平行线等积变换①等底等高的两个三角形面积相等．②底在同一条直线上并且相等，该底所对角的顶点是同一个点或在与底平行的直线上，这两个三角形面积相等．如图，AD∥BC中，AC与BD交点O，则S△ABC= S△DBC，S△AOB =S△COD例 1. （2015潍坊中考改编）如图，在平面直角坐标系中，抛物线y＝mx2－8mx＋4m＋2（m＞0）与y轴的交点为A，与x轴的交点分别为B（x1，0），C（x2，0），且x2－x1＝4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y轴的直线l与抛物线，直线AD的交点分别为P，Q．（1）求抛物线的解析式；（2）当0＜t≤8时，求△APC面积的最大值．【学有所获】图形面积的求法常见有三种，分别是：(1)(2)(3)[学有所获答案] (1) 直接公式求法(2) 割补法(3) 平行线等积变换法我爱展示1.（2014海珠一模）如图，已知抛物线y＝x2＋bx＋c与轴交于A，B两点（点A 在点B的左侧）与轴交于点C（0，－3），对称轴是直线x＝1，直线BC与抛物线的对称轴交于点D，点E为y轴上一动点，CE的垂直平分线交抛物线于P，Q两点（点P在第三象限）（1）求抛物线的函数表达式和直线BC的函数表达式；（2）当△CDE是直角三角形，且∠CDE＝90°时，求出点P的坐标；（3）当△PBC的面积为时，求点E的坐标．2.（2015越秀期末考试）如图，已知抛物线y＝x2＋ax＋4a与x轴交于点A，B，与y轴负半轴交于点C且OB＝OC，点P为抛物线上的一个动点，且点P位于x轴下方，点P与点C不重合．（1）求该抛物线的解析式；（2）若△PAC的面积为，求点P的坐标；（3）若以A，B，C，P为顶点的四边形面积记作S，则S取何值时，对应的点P有且只有2个?导学二：二次函数中的图形平移、折叠问题知识点讲解 1：二次函数、一次函数图象平移法则将（）的图像如何平移到的图像。

压轴题07 二次函数中三种面积最值问题(学生版) 2023-2024学年九年级数学上册培优(人教版)

压轴题07 二次函数中三种面积最值问题目录解题知识必备..............................................................Error! Bookmark not defined.压轴题型讲练 (2)题型一、三角形面积最值 (2)题型二、四边形面积最值 (9)题型三、面积和差最值 (18)压轴能力测评（17题） (27)二次函数中的面积最值问题通常有以下3种解题方法：1）当所求图形的面积没有办法直接求出时，通常采用分割或补全图形的方法表示所求图形的面积，如下：一般步骤为：①设出要求的点的坐标；②通过割补将要求的图形转化成通过条件可以表示的图形面积和或差；③列出关系式求解；④检验是否每个坐标都符合题意．2）用铅垂定理巧求斜三角形面积的计算公式：三角形面积等于水平宽和铅锤高乘积的一半.3）利用平行线间的距离处处相等，根据同底等高，将所求图形的面积转移到另一个图形中，如图所示：一般步骤为：①设出直线解析式，两条平行直线k 值相等；②通过已知点的坐标，求出直线解析式；③求出题意中要求点的坐标；④检验是否每个坐标都符合题意．题型一：三角形面积最值问题【例1】．（23-24九年级上·福建莆田·期末）已知抛物线()21231y mx m x m =++--与x 轴交于不同的两点．(1)求m 的取值范围；(2)证明该抛物线经过象限内的某个定点P ，并求点P 的坐标；(3)设抛物线与x 轴的两个交点分别是A ，B ，当184m -£<-时，ABP V 的面积是否有最大值或最小值？若有，求出该最大值或最小值及对应的m 的值；若没有，请说明理由．交y 轴于点C ，点P 是线段OA 上一动点，PN x ^轴，交直线AC 于点M ，交抛物线于点N ．(1)求抛物线的函数表达式；(2)连接,AN CN ，求四边形ANCO 面积的最大值．【变式2】．（23-24九年级上·新疆伊犁·期末）如图，抛物线()230y ax bx a =++¹的对称轴为直线1x =-，抛物线交x 轴于A ，C 两点，与直线1y x =-交于A ，B 两点，直线AB 与抛物线的对称轴交于点E ．(1)求抛物线的解析式；(2)求一次函数值大于二次函数值的x 的取值范围；(3)点P 在直线AB 上方的抛物线上运动，若ABP V 的面积最大，求此时点P 的坐标．与y 轴交于点B ，且2,4OA OC OB ===．(1)求这个二次函数的解析式，并求出顶点D 的坐标；(2)若点M 为第一象限内抛物线上一点，求M 点坐标为多少时，BCM V 的面积最大，并求出这个最大面积．题型二：四边形面积最值问题【例2】．（23-24九年级上·海南海口·期末）如图，直线122y x =-+交y 轴于点A ，交x 轴于点C ，抛物线214y x bx c =-++经过点A ，点C ，且交x 轴于另一点B ．(1)直接写出：点A 坐标，点C 坐标；(2)求该抛物线的解析式；(3)在直线AC 上方的抛物线上是否存在点M ，使四边形ABCM 面积最大？若存在，求出该最大值；若不存在，请说明理由；(4)将线段OA 绕x 轴上的动点(,0)P m 顺时针旋转90°得到线段O A ¢¢，若线段O A ¢¢与抛物线只有一个公共点，请结合函数图象，求m 的取值范围．【变式1】．（23-24九年级上·云南保山·期末）如图，已知抛物线()220y ax bx a =+-¹与x 轴交于A 、()4,0B -两点，与y 轴交于C 点，直线BD 交抛物线于点()2,3D ．(1)求抛物线的解析式；(2)已知点M 为抛物线上一动点，且在第三象限，求四边形BMCA 面积的最大值；并直接写出M 点的坐标．【变式2】．（22-23九年级上·广东惠州·期中）如图，已知二次函数2y x bx c =++的图象与x 轴交于点(1,0)A ，(3,0)B ，与y 轴交于点C ．(1)求二次函数的解析式；(2)点E 是二次函数第四象限图象上一点，过点E 作x 轴的垂线，交直线BC 于点D ，求四边形AEBD 面积的最大值及此时点E 的坐标；(3)若点P 为抛物线上的一点，点F 为对称轴上的一点，且以点A ，B ，P ，F 为顶点的四边形为平行四边形，直接写出点P 的坐标．【变式3】．（23-24九年级上·山东枣庄·期中）已知，如图抛物线2(0)y x bx c a =++>与y 轴交于点C ，与x 轴交于A ，B 两点，点A 在点B 左侧．点B 的坐标为(1,0)，3OC OB =．(1)求抛物线的解析式．(2)点M 是抛物线对称轴l 上的一个动点，当MB MC +的值最小时，求点M 的坐标．(3)若点D 是线段AC 下方抛物线上的动点，求四边形ABCD 面积的最大值．题型三：面积和差最值问题【例3】．（23-24九年级上·广东东莞·期末）如图，抛物线26y ax bx =+-与x 轴交于A (−2,0)，()6,0B ，交y 轴于点C ，点P 是线段BC 下方抛物线上一动点，过点P 作PQ AC ∥交BC 于点Q ，连接AQ ，OQ ，PA ，PB ．(1)求抛物线的函数解析式；(2)求AOQ △周长的最小值；(3)假设PAQ △与PBQ V 的面积分别为1S ，2S ，且12S S S =+，求S 的最大值．【变式1】（2024·安徽合肥·一模）已知抛物线()2222230y a x a x a a =--¹与x 轴交于A 、B 两点（点A 在点B的左侧），与y 轴交于点C ，直线y ax b =+经过点A ．(1)求A 、B 两点的坐标;(2)若直线y ax b =+与抛物线222223y a x a x a =--的对称轴交于点E ．①若点E 为抛物线的顶点，求a 的值；②若点E 在第四象限并且在抛物线的上方，记ACE △的面积为1S ，记ABE V 的面积为2S ，21S S S =-，求S 与x 的函数表达式，并求出S 的最大值．【变式2】（2024·安徽淮北·模拟预测）已知抛物线()()24y a x x =+-（a 为常数，且a<0）与x 轴交于A B ，两点（点A 在点B 的右侧），与y 轴交于点C ，经过点B 的直线12y x b =+与抛物线的另一交点为点D ，与y 轴的交点为点E ．(1)如图1，若点D 的横坐标为3，试求抛物线的函数表达式；(2)如图2，若DE BE =，试确定a 的值；(3)如图3，在（1）的情形下，连接AC BC ，，点P 为抛物线在第一象限内的点，连接BP 交AC 于点Q ，当APQ BCQ S S -△△取最大值时，试求点P 的坐标．【变式3】（2024·广东广州·一模）综合应用如图，抛物线2y x bx c =-++与x 轴交于点()1,0A B ，，与y 轴交于点()0,3C ．(1)求抛物线的解析式；(2)直线y x =-与抛物线在第二象限交于点M ，若动点N 在OM 上运动，线段CN 绕点N 顺时针旋转，点C 首次落在x 轴上时记为点D ，在点N 运动过程中，判断CND Ð的大小是否发生变化？并说明理由．(3)在（2）的条件下，连接CD ，记CND △的外接圆的最小面积为1S ，记CND △的外接圆的最大面积为2S ，试求21S S -的值（结果保留p ）．1．（23-24九年级上·广东梅州·期末）已知二次函数223y x x =--+的图象和x 轴交于点A 、B ，与y 轴交于点C ，点P 是直线AC 上方的抛物线上的动点．(1)求直线AC 的解析式．(2)当P 是抛物线顶点时，求APC △面积．(3)在P 点运动过程中，求APC △面积的最大值．2 ．（23-24九年级上·海南省直辖县级单位·期末）如图，抛物线2y x bx c =++经过()3,0B 、C (0,−3)两点，与x 轴的另一个交点为A ，顶点为D ．(1)求该抛物线的解析式；(2)点E 为该抛物线上一动点（与点B 、C 不重合），①当点E 在直线BC 的下方运动时，求CBE △的面积的最大值；②在①的条件下，点M 是抛物线的对称轴上的动点，点P 是抛物线上的动点，若以C 、E 、P 、M 为顶点的四边形是平行四边形，请直接写出所有符合条件的点P 的坐标．3．（23-24九年级上·江西赣州·期末）抛物线()223y x m x m =-++++与x 轴交于点A ，B （点A 在点B 左侧），与y 轴交于点C ，点P 是抛物线上一点，其横坐标为a ．(1)已知点()0,5C ，求抛物线的解析式．(2)若1m =，①如图，当点P 位于第二象限时，过点P 分别作PM BC ^于点E ，PN y ^轴于点N ，当PM PN +取得最大值时，求a 的值；②在①的条件下，连接PB ，PC ，判断此时PBC △的面积是否为最大，并说明理由．4．（23-24九年级上·广东深圳·期末）如图，在平面直角坐标系xOy 中，直线122y x =+与x 轴交于点A ，与y 轴交于点C ．抛物线2y ax bx c =++的对称轴是32x =-，且经过A C 、两点，与x 轴的另一交点为点B ．(1)求抛物线解析式．(2)若点P 为直线AC 上方的抛物线上的一点，连接PA PC ，．求PAC V 的面积的最大值，并求出此时点P 的坐标．5．（23-24九年级下·山东临沂·期中）如图，抛物线234y x bx c =-++与x 轴交于A 、B 两点，与y 轴交于点C ，直线334y x =+经过A 、C 两点，点D 是第二象限内抛物线上一点.(1)求抛物线的解析式；(2)连接AD 、CD ，求ACD V 面积的最大值；(3)若点D 关于直线BC 的对称点D ¢恰好落在直线AC 上，求点D 的坐标.6．（22-23九年级上·广东湛江·期中）已知抛物线2y x bx c =--+的图像与x 轴交于点()3,0A -和点C ，与y 轴交于点B (0,3)．(1)求抛物线的解析式；(2)设点P 为抛物线的对称轴上一动点，当PBC △的周长最小时，求点P 的坐标；(3)在第二象限的抛物线上，是否存在一点Q ，使得ABQ V 的面积最大？若存在，求出点Q 的坐标；若不存在，请说明理由．7．（23-24九年级上·广西柳州·期中）如图，已知抛物线22y x mx m =-++-的顶点为A ，且通过点()3,3B -．(1)求顶点A 的坐标；(2)点C 为直线AB 上方抛物线上一动点，求ABC V 面积的最大值；(3)在抛物线上存在一点P ，使得PAB 45Ð=°，求点P 坐标．8．（23-24九年级上·四川自贡·期末）将拋物线()212y x =-+平移到图中2l 的位置，且与直线1l 交于A (0,−1)，B (2,1)两点．(1)抛物线2l 是由抛物线()212y x =-+向左平移______个单位，再向下平移______个单位得到的；(2)求抛物线2l 的顶点坐标；(3)动点P 在直线1l 下方的抛物线2l 上，求以点O A P B ，，，为顶点的四边形的最大面积．9．（23-24九年级上·甘肃兰州·期末）如图，在平面直角坐标系中，二次函数243y ax x =+-图象的顶点是A ，与x 轴交于B ，C 两点，与y 轴交于点D ，点B 的坐标是10（，）．(1)求A ，C 两点的坐标．(2)平移该二次函数的图象，使点D 恰好落在点A 的位置上，求平移后图象所对应的二次函数的表达式．(3)在直线CD 上方的抛物线上是否存在点P ，使PCD △的面积最大？若存在，求P 点的坐标及PCD △面积的最大值．10．（23-24九年级上·辽宁抚顺·期末）如图，抛物线22y ax bx =++与x 轴交于点(1,0)A -和点(4,0)B ，与y 轴交于点C ，连接BC ，点D 在抛物线上．(1)求抛物线的解析式；(2)如图1，点D 在第一象限内的抛物线上，连接BD ，CD ，请求出BCD △面积的最大值；(3)点D 在抛物线上移动，连接CD ，存在DCB ABC Ð=Ð，请直接写出点D 的坐标．11．（22-23九年级上·天津河西·期末）如图所示，在ABC V 中，90B Ð=°，5cm AB =，7cm BC =，点P 从点A 开始沿AB 边向点B 以1cm /s 的速度运动，点Q 从点B 开始沿BC 边向点C 以2cm /s 的速度运动．P 、Q 分别从A 、B 同时出发，当P 、Q 两点中有一点停止运动时，则另一点也停止运动．设运动的时间为s t ．(0)t ≥(1)当t 为何值时，PQ 的长度等于5cm ；(2)求出V BPQ S 关于t 的函数解析式，计算P 、Q 出发几秒时，V BPQ S 有最大值，并求出这个最大面积？12．（22-23九年级上·海南海口·期末）如图1，抛物线23 2y ax x c=++与x轴交于点A、B(4,0)（A点在B点左侧），与y轴交于点C(0,6)，点P是抛物线上一个动点，连接PB，PC，BC(1)求抛物线的函数表达式；(2)若点P的横坐标为3，求BPCV的面积；(3)如图2所示，当点P在直线BC上方运动时，连接AC，求四边形ABPC面积的最大值，并写出此时P点坐标．(4)若点M是x轴上的一个动点，点N是抛物线上一动点，P的横坐标为3．试判断是否存在这样的点M，使得以点B，M，N，P为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由．13．（22-23九年级上·辽宁沈阳·期末）已知，抛物线22y ax bx =++与x 轴交于A ，B 两点（点A 在点B 左侧），与y 轴交于点C ，抛物线过()2,3D --，()3,2E ，点P 为第一象限内抛物线上一动点：(1)求抛物线的函数表达式和直线DE 的函数表达式；(2)在y 轴上取F (0,1)，连接PF ，PB ，当OBPF S 四边形面积最大时，求点P 横坐标；(3)当7OBPF S =四边形时，点P 在抛物线对称轴右侧时，直线DE 上存在两点MN （M 在N 上方），MN =动点Q 从P 出发，沿P M N A ®®®运动到终点A ，当Q 运动路程最短时，直接写出点N 坐标．14．（23-24九年级上·天津·期中）已知如图，抛物线22(0)y ax ax c a =++>与y 轴交于点C ，与x 轴交于A B 、两点，点A 在点B 的左侧，点B 的坐标为(1,0)，点C 的坐标()0,3-(1)求抛物线的解析式；(2)若点D 是线段AC 下方抛物线上的动点，求四边形ABCD 面积的最大值；(3)若点E 在x 轴上，点P 在抛物线上，是否存在以A C E P 、、、为顶点，且以AC 为一边的平行四边形呢？若存在，直接写出点P 的坐标；若不存在，请说明理由．15．（22-23九年级上·海南海口·期中）如图①，已知二次函数23y ax bx =+-与x 轴相交于()1,0A -、()3,0B 两点，与y 轴相交于点C ．(1)求二次函数的表达式；(2)如图②，连结AC 、BC ．①求直线BC 的表达式；②在对称轴上是否存在一个点P ，使PAC V 的周长最小？若存在，请求出点P 的坐标和此时PAC V 的周长；若不存在，请说明理由；③点D 为抛物线在第四象限内图象上一个动点，是否存在点D ，使得BDC V 的面积最大？若存在，请求出点D 的坐标和此时BDC V 面积的最大值；若不存在，请说明理由．16．（22-23九年级上·贵州黔南·期中）已知，如图抛物线()20y ax bx c a =++>与y 轴交于点()0,4C -，与x轴交于A (−4,0)、()1,0B 两点．(1)求抛物线的解析式；(2)若点D 是线段AC 下方抛物线上的动点，求四边形ABCD 面积的最大值．(3)点P 是抛物线对称轴上一动点，点Q 是直线AC 上一动点，且以点A B Q P 、、、为顶点的四边形是平行四边形，请直接写出点Q 的坐标．17．（23-24九年级上·湖北襄阳·期中）如图，抛物线214y x bx c =++经过点B (−2,0)和点()0,2C -，与x 轴交于点A ．(1)求抛物线的解析式；(2)点M 是第四象限内抛物线上的动点，求四边形AOCM 的面积的最大值和此时点M 的坐标；(3)点()0,P n 是y 轴上的一个动点，将线段OB 绕点P 顺时针旋转90°，得到线段O B ¢¢，若线段O B ¢¢与抛物线有一个公共点，结合函数图像，请直接写出n 的取值范围．。

人教版九年级数学上典中点课后作业22.1.1二次函数(A)(含答案)

22.1.1 二次函数课后作业：方案（A）一、教材题目：P41复习巩固T1、T2、T81．一个矩形的长是宽的2倍，写出这个矩形的面积关于宽的函数解析式，2．某种商品的价格是2元，准备进行两次降价．如果每次降价的百分率都是x，经过两次降价后的价格y(单位：元)随每次降价的百分率x的变化而变化，y与x之间的关系可以用怎样的函数来表示？8．如图，在△ABC中，∠B＝90°，AB＝12 mm，BC＝24 mm，动点P从点A开始沿边AB向点B以2 mm/s的速度移动，动点Q从点B开始沿边BC向点C以4 mm/s的速度移动．如果P，Q两点分别从A，B两点同时出发，那么△PBQ的面积S随出发时间t如何变化？写出S关于t的函数解析式及t的取值范围．（第8题）二、补充题目：来源于《典中点》6．下列说法中，正确的是( )A ．二次函数中两个变量的值是非零实数B ．二次函数中自变量的值可以是所有实数C ．形如y ＝ax 2＋bx ＋c 的函数叫二次函数D ．二次函数y ＝ax 2＋bx ＋c 中a ，b ，c 的值均不能为零 7．对于任意实数m ，下列函数一定是二次函数的是( ) A ．y ＝mx 2＋3x －1 B ．y ＝(m －1)x 2 C ．y ＝(m －1)2x 2 D ．y ＝(－m 2－1)x 210．(2015·温州)如图，∠AOB ＝90°，在∠AOB 的平分线ON 上依次取点C ，F ，M ，过点C 作DE ⊥OC ，分别交OA ，OB 于点D ，E ，以FM 为对角线作菱形FGMH ，已知∠DFE ＝∠GFH ＝120°，FG ＝FE.设OC ＝x ，图中阴影部分面积为y ，则y 与x 之间的函数关系式是( )(第10题)A ．y ＝32x 2B ．y ＝3x 2C ．y ＝23x 2D ．y ＝33x 211．下列函数关系中，不是二次函数的是( ) A ．边长为x 的正方形的面积y 与边长x 的函数关系B ．一个直角三角形两条直角边长的和是6，则这个直角三角形的面积y 与一条直角边长x的函数关系C．在边长为5的正方形内挖去一个边长为t的小正方形，剩余面积S与t的函数关系D．多边形的内角和m与边数n的函数关系13．已知函数y＝(m2－m)x2＋(m－1)x＋m＋1.(1)若这个函数是关于x的一次函数，求m的值；(2)若这个函数是关于x的二次函数，则m的值应是多少？14．一直角三角形两直角边长之和为15，其中一条直角边长为x，求它的面积S关于x 的函数关系式，并写出自变量的取值范围．17．某广告公司设计一幅周长为12 m的矩形广告牌，设计费为每平方米1 000元，设矩形一边的长为x m，面积为S m2.(1)求S与x之间的函数关系式，并确定自变量x的取值范围；(2)若要求设计的广告牌边长为整数，请你填写下表，并探究当x取何值时，广告牌的设计费最多．18．如图，正方形ABCD的边长为4 cm，动点P，Q同时从点A出发，以1 cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动．设运动时间为x s，由点P，B，D，Q 确定的图形的面积为y cm2，求y与x(0≤x≤8)之间的函数关系式．(第18题)答案一、教材1．解：设矩形的面积为S ，宽为x ，矩形的面积关于宽的函数解析式为S ＝2x·x ，即S ＝2x 2. 2．解：y ＝2(1－x)2.8．解：动点P 从点A 到点B 所需时间为：122＝6(s )，动点Q 从点B 到点C 所需时间为：244＝6(s )，所以0＜t ＜6.因为AP ＝2t ，所以BP ＝12－2t.又因为BQ ＝4t ，所以S ＝12·BP·BQ ＝12×(12－2t)·4t ＝－4t 2＋24t(0＜t ＜6)．点拨：本题注意时间t 的取值范围．二、典中点6.B7.D 10.B 11.D13．解：(1)若y ＝(m 2－m)x 2＋(m －1)x ＋m ＋1是关于x 的一次函数，则⎩⎪⎨⎪⎧m 2－m ＝0，m －1≠0，解得m ＝0. (2)若y ＝(m 2－m)x 2＋(m －1)x ＋m ＋1是关于x 的二次函数，则m 2－m≠0，解得m≠0且m≠1.∴m 可以是除了1和0的所有实数． 14．解：S ＝12x(15－x)＝－12x 2＋152x.自变量的取值范围为0＜x ＜15.点拨：最终的结果要化成二次函数的一般形式，且自变量的取值要符合题意． 17．解：(1)S ＝x ⎝⎛⎭⎫122－x ＝－x 2＋6x(0＜x ＜6)． (2)18．解：由题意可知，当0≤x≤4时，AP ＝AQ ＝x cm ， y ＝4×4－12×4×4－12x 2，即y ＝8－12x 2；当4＜x≤8时，CQ ＝CP ＝(8－x)cm ，y ＝4×4－12×4×4－12(8－x)2，即y ＝－12x 2＋8x －24.综上可知，所求的函数关系式为y ＝2218(04),21824(48).2x x x x x ⎧-≤≤⎪⎪⎨⎪-+-<≤⎪⎩。

第22章二次函数知识点过关练习题二次函数与几何图形面积问题2021-2022人教九年级上册数学

人教版九年级上册数学《二次函数》知识点过关精准练（二次函数与几何图形面积问题）知识储备：1.对于二次函数y=-2x2+4x-5,当x=______时,y有最_______值,最_______值是_______.2.应用二次函数解决面积最值问题的步骤1.分析题中的变量与常量、几何图形的基本性质.2.找出等量关系,建立函数模型.3.结合函数图象及性质,考虑实际问题中自变量的取值范围,常采用配方法求出,或根据二次函数顶点坐标公式求出面积的最大或最小值.知识点过关精准练一、选择题。

1.用长40 m的篱笆围成一个矩形菜园,则围成的菜园的最大面积为( )A.400 m2B.300 m2C.200 m2D.100 m22. 如图,小明想用长为12 m的栅栏(虚线部分),借助围墙围成一个矩形花园ABCD,则矩形ABCD的最大面积是( )A.16 m2B.18 m2C.20 m2D.24 m23.已知在直角三角形中两条直角边的和为18,则当三角形的面积最大时,其中一条直角边长为( )A.8B.9C.10D.124.如图所示,在矩形ABCD的各边AB,BC,CD和DA上分别选取点E,F,G,H(不与A,B,C,D各点重合),使得AE=AH=CF=CG,如果AB=60,BC=40,那么四边形EFGH的最大面积是( )A.1 350B.1 300C.1 250D.1 2005. 已知一个直角三角形两直角边之和为20 cm,则这个直角三角形的最大面积为( )A.25 cm2B.50 cm2C.100 cm2D.不确定6.如图,△ABC是直角三角形,∠A=90°,AB=8 cm,AC=6 cm.点P从点A出发,沿AB方向以2 cm/s的速度向点B运动,同时点Q从点A出发,沿AC方向以1 cm/s 的速度向点C运动,其中一个动点到达终点时则另一个动点也停止运动,则△APQ 的最大面积是( )A.0 cm2B.8 cm2C.16 cm2D.24 cm27. 用长为12 m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=x m,五边形ABCDE的面积为S m2.则S的最大值为 ( )A.12√3 m2B.12 m2C.24√3 m2D.没有最大值二、填空题。

中考数学：二次函数三角形面积问题习题

1、（2012•岳阳）我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为6dm ，锅深3dm ，锅盖高1dm （锅口直径与锅盖直径视为相同），建立直角坐标系如图①所示，如果把锅纵断面的抛物线记为C 1，把锅盖纵断面的抛物线记为C 2．（1）求C 1和C 2的解析式；（2）如图②，过点B 作直线BE ：131-=x y 交C 1于点E （-2，25-）），连接OE 、BC ，在x 轴上求一点P ，使以点P 、B 、C 为顶点的△PBC 与△BOE 相似，求出P 点的坐标；（3）如果（2）中的直线BE 保持不变，抛物线C 1或C 2上是否存在一点Q ，使得△EBQ 的面积最大？若存在，求出Q 的坐标和△EBQ 面积的最大值；若不存在，请说明理由．2、（2012•湘潭）如图，抛物线2232--=x ax y (a ≠0)的图象与x 轴交于A 、B 两点，与y 轴交于C 点，已知B 点坐标为（4，0）．（1）求抛物线的解析式；（2）试探究△ABC 的外接圆的圆心位置，并求出圆心坐标；（3）若点M 是线段BC 下方的抛物线上一点，求△MBC 的面积的最大值，并求出此时M 点的坐标．3、（2012•梧州）如图，抛物线y=-x2+12x-30的顶点为A，对称轴AB与x轴交于点B．在x 上方的抛物线上有C、D两点，它们关于AB对称，并且C点在对称轴的左侧，CB⊥DB．（1）求出此抛物线的对称轴和顶点A的坐标；（2）在抛物线的对称轴上找出点Q，使它到A、C两点的距离相等，并求出点Q的坐标；（3）延长DB交抛物线于点E，在抛物线上是否存在点P，使得△DEP的面积等于△DEC 的面积？若存在，请你直接写出点P的坐标；若不存在，请说明理由．4、（2012•铜仁地区）如图已知：直线y=-x+3交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c 经过A、B、C（1，0）三点．（1）求抛物线的解析式；（2）若点D的坐标为（-1，0），在直线y=-x+3上有一点P，使△ABO与△ADP相似，求出点P的坐标；（3）在（2）的条件下，在x轴下方的抛物线上，是否存在点E，使△ADE的面积等于四边形APCE的面积？如果存在，请求出点E的坐标；如果不存在，请说明理由．5、（2012•遂宁）已知：如图，直线y=mx+n 与抛物线c bx x y ++=231交于点A （1，0）和点B ，与抛物线的对称轴x=-2交于点C （-2，4），直线f 过抛物线与x 轴的另一个交点D 且与x 轴垂直．（1）求直线y=mx+n 和抛物线的解析式；（2）在直线f 上是否存在点P ，使⊙P 与直线y=mx+n 和直线x=-2都相切．若存在，求出圆心P 的坐标，若不存在，请说明理由；（3）在线段AB 上有一个动点M （不与点A 、B 重合），过点M 作x 轴的垂线交抛物线于点N ，当MN 的长为多少时，△ABN 的面积最大，请求出这个最大面积．6、（2012•衢州）如图，把两个全等的Rt △AOB 和Rt △COD 分别置于平面直角坐标系中，使直角边OB 、OD 在x 轴上．已知点A （1，2），过A 、C 两点的直线分别交x 轴、y 轴于点E 、F ．抛物线y=ax 2+bx+c 经过O 、A 、C 三点．（1）求该抛物线的函数解析式；（2）点P 为线段OC 上一个动点，过点P 作y 轴的平行线交抛物线于点M ，交x 轴于点N ，问是否存在这样的点P ，使得四边形ABPM 为等腰梯形？若存在，求出此时点P 的坐标；若不存在，请说明理由．（3）若△AOB 沿AC 方向平移（点A 始终在线段AC 上，且不与点C 重合），△AOB 在平移过程中与△COD 重叠部分面积记为S ．试探究S 是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．7、（2012•沈阳）已知，如图，在平面直角坐标系中，点A 坐标为（-2，0），点B 坐标为（0，2），点E 为线段AB 上的动点（点E 不与点A ，B 重合），以E 为顶点作∠OET=45°，射线ET 交线段0B 于点F ，C 为y 轴正半轴上一点，且OC=AB ，抛物线n mx x y ++-=22的图象经过A ，C 两点．（1）求此抛物线的函数表达式；（2）求证：∠BEF=∠AOE ；（3）当△EOF 为等腰三角形时，求此时点E 的坐标；（4）在（3）的条件下，当直线EF 交x 轴于点D ，P 为（1）中抛物线上一动点，直线PE 交x 轴于点G ，在直线EF 上方的抛物线上是否存在一点P ，使得△EPF 的面积是△EDG 面积的（22+1）？若存在，请直接写出点P 的坐标；若不存在，请说明理由．8、（2012•黔西南州）如图，在平面直角坐标系xOy 中，已知抛物线经过点A （0，4），B （1，0），C （5，0），抛物线的对称轴l 与x 轴相交于点M ．（1）求抛物线对应的函数解析式和对称轴；（2）设点P 为抛物线（x ＞5）上的一点，若以A 、O 、M 、P 为顶点的四边形的四条边的长度为四个连续的正整数，请你直接写出点P 的坐标；（3）连接AC ，探索：在直线AC 下方的抛物线上是否存在一点N ，使△NAC 的面积最大？若存在，请你求出点N 的坐标；若不存在，请说明理由．9、（2012•黔东南州）如图，已知抛物线经过点A （-1，0）、B （3，0）、C （0，3）三点．（1）求抛物线的解析式．（2）点M 是线段BC 上的点（不与B ，C 重合），过M 作MN ∥y 轴交抛物线于N ，若点M 的横坐标为m ，请用m 的代数式表示MN 的长．（3）在（2）的条件下，连接NB 、NC ，是否存在m ，使△BNC 的面积最大？若存在，求m 的值；若不存在，说明理由．10、（2012•攀枝花）如图，在平面直角坐标系xOy 中，四边形ABCD 是菱形，顶点A 、C 、D 均在坐标轴上，且AB=5，sinB=54．（1）求过A 、C 、D 三点的抛物线的解析式；（2）记直线AB 的解析式为y 1=mx+n ，（1）中抛物线的解析式为y 2=ax 2+bx+c ，求当y 1＜y 2时，自变量x 的取值范围；（3）设直线AB 与（1）中抛物线的另一个交点为E ，P 点为抛物线上A 、E 两点之间的一个动点，当P 点在何处时，△PAE 的面积最大？并求出面积的最大值．11、（2012•宁德）如图，矩形OBCD 的边OD 、OB 分别在x 轴正半轴和y 轴的负半轴上，且OD=10，OB=8，将矩形的边BC 绕点B 逆时针旋转，使点C 恰好与x 轴上的点A 重合（1）直接写出点A 、B 的坐标：A （，）、B （，）；（2）若抛物线c bx x y ++-=231经过A 、B 两点，则这条抛物线的解析式是；（3）若点M 是直线AB 上方抛物线上的一个动点，作MN ⊥x 轴于点N ，问是否存在点M ，使△AMN 与△ACD 相似？若存在，求出点M 的横坐标；若不存在，说明理由；（4）当27≤x≤7时，在抛物线上存在点P ，使△ABP 得面积最大，求△ABP 面积的最大值．12、（2012•内江）如图，已知点A （-1，0），B （4，0），点C 在y 轴的正半轴上，且∠ACB=90°，抛物线y=ax 2+bx+c 经过A 、B 、C 三点，其顶点为M ．（1）求抛物线y=ax 2+bx+c 的解析式；（2）试判断直线CM 与以AB 为直径的圆的位置关系，并加以证明；（3）在抛物线上是否存在点N ，使得S △BCN =4？如果存在，那么这样的点有几个？如果不存在，请说明理由．13、（2012•乐山）如图，在平面直角坐标系中，点A 的坐标为（m ，m ），点B 的坐标为（n ，-n ），抛物线经过A 、O 、B 三点，连接OA 、OB 、AB ，线段AB 交y 轴于点C ．已知实数m 、n （m ＜n ）分别是方程x 2-2x-3=0的两根．（1）求抛物线的解析式；（2）若点P 为线段OB 上的一个动点（不与点O 、B 重合），直线PC 与抛物线交于D 、E 两点（点D 在y 轴右侧），连接OD 、BD ．①当△OPC 为等腰三角形时，求点P 的坐标；②求△BOD 面积的最大值，并写出此时点D 的坐标．14、（2012•兰州）如图，Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上，O 为坐标原点，A 、B 两点的坐标分别为（-3，0）、（0，4），抛物线c bx x y ++=232经过点B ，且顶点在直线25=x 上．（1）求抛物线对应的函数关系式；（2）若把△ABO 沿x 轴向右平移得到△DCE ，点A 、B 、O 的对应点分别是D 、C 、E ，当四边形ABCD 是菱形时，试判断点C 和点D 是否在该抛物线上，并说明理由；（3）在（2）的条件下，连接BD ，已知对称轴上存在一点P 使得△PBD 的周长最小，求出P 点的坐标；（4）在（2）、（3）的条件下，若点M 是线段OB 上的一个动点（点M 与点O 、B 不重合），过点M 作∥BD 交x 轴于点N ，连接PM 、PN ，设OM 的长为t ，△PMN 的面积为S ，求S 和t 的函数关系式，并写出自变量t 的取值范围，S 是否存在最大值？若存在，求出最大值和此时M 点的坐标；若不存在，说明理由．15、（2012•济宁）如图，抛物线y=ax 2+bx-4与x 轴交于A （4，0）、B （-2，0）两点，与y 轴交于点C ，点P 是线段AB 上一动点（端点除外），过点P 作PD ∥AC ，交BC 于点D ，连接CP ．（1）求该抛物线的解析式；（2）当动点P 运动到何处时，BP 2=BD•BC ；（3）当△PCD 的面积最大时，求点P 的坐标．16、2012•呼和浩特）如图，抛物线y=ax 2+bx+c （a ＜0）与双曲线y xk 相交于点A ，B ，且抛物线经过坐标原点，点A 的坐标为（-2，2），点B 在第四象限内，过点B 作直线BC ∥x 轴，点C 为直线BC 与抛物线的另一交点，已知直线BC 与x 轴之间的距离是点B 到y 轴的距离的4倍，记抛物线顶点为E ．（1）求双曲线和抛物线的解析式；（2）计算△ABC 与△ABE 的面积；（3）在抛物线上是否存在点D ，使△ABD 的面积等于△ABE 的面积的8倍？若存在，请求出点D 的坐标；若不存在，请说明理由．17、（2012•河南）如图，在平面直角坐标系中，直线y 21 x+1与抛物线y=ax 2+bx-3交于A 、B 两点，点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上一动点（不与A 、B 点重合），过点P 作x 轴的垂线交直线AB 于点C ，作PD ⊥AB 于点D ．（1）求a 、b 及sin ∠ACP 的值；（2）设点P 的横坐标为m ．①用含有m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；②连接PB ，线段PC 把△PDB 分成两个三角形，是否存在适合的m 的值，直接写出m 的值，使这两个三角形的面积之比为9：10？若存在，直接写出m 的值；若不存在，说明理由．18、（2012•广西）已知抛物线y=ax 2+2x+c 的图象与x 轴交于点A （3，0）和点C ，与y 轴交于点B （0，3）．（1）求抛物线的解析式；（2）在抛物线的对称轴上找一点D ，使得点D 到点B 、C 的距离之和最小，并求出点D 的坐标；（3）在第一象限的抛物线上，是否存在一点P ，使得△ABP 的面积最大？若存在，求出点P 的坐标；若不存在，请说明理由．。

人教版九年级上册数学第二十二章二次函数含答案

人教版九年级上册数学第二十二章二次函数含答案一、单选题(共15题，共计45分)1、如图，正三角形ABC的边长为3+ ，在三角形中放入正方形DEMN和正方形EFPH，使得D，E，F在边AB上，点P、N分别在边CB、CA上，设两个正方形的边长分别为m，n，则这两个正方形的面积和的最小值为（）A. B. C.3 D.2、已知二次函数y＝2 x2＋9x+34，当自变量x取两个不同的值x1、x2时，函数值相等，则当自变量x取x1＋x2时的函数值与（）A.x＝1时的函数值相等B.x＝0时的函数值相等C.x＝时的函数值相等D.x＝－时的函数值相等3、抛物线y=2x2+1的顶点坐标是（）A.（2，1）B.（0，1）C.（1，0）D.（1，2）4、已知抛物线与x轴交于点A，B两点（A在原点O左侧，B 在原点O右侧），与y轴交于点C，若OC=OB，则点A的横坐标为（）A. B. C. D.-25、二次函数的图象如图所示，对称轴为直线，下列结论①②③④（m为任意实数）其中不正确的个数是（）A.1个B.2个C.3个D.4个6、抛物线可以由抛物线平移而得到，下列平移正确的是（）.A.先向左平移1个单位，再向上平移2个单位B.先向左平移1个单位，再向下平移2个单位C.先向右平移1个单位，再向上平移2个单位 D.先向右平移1个单位，再向下平移2个单位7、抛物线y=（x-2）2+3的对称轴是（）A.直线x=-3B.直线x=-2C.直线x=2D.直线x=38、二次函数的顶点坐标为（-1，n），其部分图象如图所示．以下结论错误的是（）．A. B. C. D.关于的方程无实数根9、抛物线y＝x2﹣x+m与x轴至少有一个公共点，则m的取值范围是（）A.mB.m＞C.m≤D.m＜10、对于二次函数的图象，下列说法正确的是（）A.开口向下B.对称轴C.顶点坐标是D.与轴有两个交点11、如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与y轴交于点B （0，﹣2），点A（﹣1，m）在抛物线上，则下列结论中错误的是（）A.ab＜0B.一元二次方程ax 2+bx+c＝0的正实数根在2和3之间 C.a＝ D.点P1（t，y1），P2（t+1，y2）在抛物线上，当实数t＞时，y1＜y212、已知二次函数y=x2+（m﹣1）x+1，当x＞1时，y随x的增大而增大，而m 的取值范围是（）A.m=﹣1B.m=3C.m≤﹣1D.m≥﹣113、抛物线y=3 ＋5的顶点坐标是（）A.（－2，5）B.（－2，－5）C.（2，5）D.（2，－5）14、向空中发射一枚炮弹，经x秒后的高度为y米，且时间与高度的关系为y=ax2+bx+c（a≠0）．若此炮弹在第7秒与第14秒时的高度相等，则在下列时间中炮弹所在高度最高的是（）A.第8秒B.第10秒C.第12秒D.第15秒15、已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①a，b同号；②当x=1和x=3时，函数值相等；③4a+b=0；④当y=﹣2时，x 的值只能取2；⑤当﹣1＜x＜5时，y＜0．其中正确的有（）A.2个B.3个C.4个D.5个二、填空题(共10题，共计30分)16、二次函数的顶点坐标是________．17、如图，抛物线关于点B的中心对称得________。

人教版九年级数学上册《用定值周长围成的图形面积问题》练习 (1)

实际问题与二次函数1：用定值周长围成图形面积问题教学目标：1、学会用二次函数方法研究几何面积问题；2、体会一元二次方程与二次函数内在关系；3、面积最值的基本求法教学过程：一、问题引入1、用长为100cm的金属铝制成一个矩形方框，能否制成面积是600cm2的矩形框？2、同样的条件，能否制800cm2的矩形方框问1：预设学生的做法：设金属丝矩形方框一边长是x cm，另一边为（50－x）cm，得x(50－x)=600，答：可以制成面积为600cm2的矩形方框问2：预设有的说能，有的说不能，还有学生只作判断不说理由，老师要求说明理由。

则上述方程为：x(50－x)=800x2－50x+800=0△=b2－4ac=－700＜0原方程无实根，即没有这样的实数，使矩形面积为800cm，所以不能制成。

问3：面积是600cm2可以制成，面积是800cm2不能制成，同学们有何想法？学生：面积不能太大师问：面积多大才能保证矩形可制成呢？二、问题探究（多维思考）老师引导：此时面积有具体数值，如600、800等，为研究问题方便怎么办？用什么数学模型解决，有几种方法？学生找到解决问题方法：设面积为S ，则S=x(50－x) 可得方法1：－x 2+50x －s=0(方程思想）x 2－50x+s=0△=2500－4s ≥0才有解S ≤625此法从方程根的判别式求最值，此时学生可能还有疑惑，由此想到方法2：S=x(50－x)= －x 2+50x （函数思想）S=－(x －25)2+625∵－(x －25)2≤0 ∴S ≤625 即当x=25时，S 矩形最大为625cm 22、推及一般师问：当x=25时，矩形长宽分别为多少？此时矩形有何特殊性。

预设生答：长宽等于25cm ，是正方形。

师追问：确实是正方形，那么可以这样小结：矩形周长一定时，它的面积最大时一定是正方形呢？（课下探究）设金属丝长为Lcm ，矩形面积为Scm 2，设矩形一边长为x cm ，则 S=x(2L－x)=－x 2+2L x=－(x 2－2L x+162L )+162L =－(x －4L )2+162L∵－(x －4L )2≤0 ∴S ≤162L当x=4L 时，S 矩形最大=162Lcm ，此时矩形变成正方形。

部编数学九年级上册实际问题与二次函数专题训练(4大题型35题)2023考点题型精讲(解析版)含答案

22.3实际问题与二次函数专题训练（4大题型35题）题型1：几何问题-面积问题1．某中学课外兴趣活动小组准备围建一个矩形苗圃园（如图所示），其中一边靠墙（墙长为18m），另外三边用32m的篱笆围成．（1）令苗圃园长（平行于墙的边长）为xm，宽为ym，写出y关于x的函数关系式，并写出x的取值范围；（2）若苗圃园的面积为96m2，求垂直于墙的一边长为多少米？（3）苗圃园的面积能否达到150m2？请说明理由；并写出苗圃园的面积最大值．【分析】（1）根据篱笆的长为32米．列出y关于x的函数关系式，并根据墙长为18m，矩形的边长大于0求出x的取值范围；（2）设苗圃园的面积为Sm2，根据矩形的面积公式写出S关于x的函数解析式，令S＝96，解关于x的一元二次方程，取在x范围的解即可；（3）先令S＝150得到关于x的一元二次方程，再根据Δ＜0，可知苗圃园面积不能达到150m2；根据二次函数的性质求最值即可．【解答】解：（1）由题意得：y＝＝﹣x+16，∵，∴0＜x≤18，∴y关于x的函数关系式为y＝﹣x+16，x的取值范围为0＜x≤18；（2）设苗圃园的面积为Sm2，由（1）知，S＝xy＝x（﹣x+16）＝﹣x2+16x，令S＝96，则﹣x2+16x＝96，解得：x1＝8，x2＝24（舍去），∴平行于墙的边长8m，∴垂直于墙的边长为﹣×8+16＝12（m）；（3）由（2）知S＝﹣x2+16x，令S＝150，则﹣x2+16x＝150，整理得：x2﹣32x+300＝0，∵Δ＝（﹣32）2﹣4×1×300＝﹣176＜0，∴方程x2﹣32x+300＝0无实数解，∴苗圃园的面积不能达到150m2；∵S＝﹣x2+16x＝﹣（x﹣16）2+128，∵﹣＜0，∴当x＝16时，S有最大值，最大值为128，∴当平行于墙的边长为16m时，苗圃园的面积最大值128m2．【点评】此题考查了二次函数、一元二次方程的实际应用问题．解题的关键是根据题意构建二次函数模型，然后根据二次函数的性质求解即可．2．目前世界上有10亿多人以马铃薯为主粮，为国家粮食安全，丰富农民收入来源，某区试点马铃薯种植，给予每亩地每年发放150元补贴．年初，种植户金大伯根据以往经验，考虑各种因素，预计本年每亩的马铃薯销售收入为2000元，以及每亩种植成本y（元）与种植面积x（亩）之间的函数关系如图所示．（1）根据图象，求出y与x之间的函数关系式．（2）根据预计情况，求金大伯今年种植总收入w（元）与种植面积x（亩）之间的函数关系式．（总收入＝销售收入﹣种植成本+种植补贴）．【分析】（1）利用待定系数法即可求解；（2）分别求出销售收入、种植成本、种植补贴，再根据总收入销售收入种植成本种植补贴计算即可．【解答】（1）设函数关系式为y＝kx+b，根据图象可知，函数图象过点（200，1000），（240，880），将这两点代数函数关系式可得：，解得：，故函数关系式为：y＝﹣3x+1600；（2）销售收入：2000x；成本：y•x＝（﹣3x+1600）•x＝﹣3x2+1600x，补贴：150x；因为，总收入＝销售收入•种植成本+种植补贴，所以w＝2000x﹣（﹣3x2+1600x）+150x，整理得：w＝3x2+550x．【点评】本题主要考查一次函数的实际应用及待定系数法求解析式，解题的关键是正确解读题意，找出各个函数表达式和代数式．3．如图，学校要用一段长为36米的篱笆围成一个一边靠墙的矩形花圃，墙长为16米．（1）若矩形ABCD的面积为144平方米，求矩形的边AB的长．（2）要想使花圃的面积最大、AB边的长应为多少米？最大面积为多少平方米？【分析】（1）根据题意：矩形的面积＝AB×BC，设未知数列方程可解答；（2）设AB为x米，矩形的面积为y平方米，则BC＝（36﹣2x）米，可以得到y与x的函数关系式，在x的取值范围内求出函数的最大值即可．【解答】解：（1）设AB为x米，则BC＝（36﹣2x）米，由题意得：x（36﹣2x）＝144，解得：x1＝6，x2＝12，∵墙长为16米，36米的篱笆，∴36﹣2x≤16，2x＜36，∴10≤x＜18，∴x＝12，∴AB＝12，答：矩形的边AB的长为12米；（2）设AB为x米，矩形的面积为y平方米，则BC＝（36﹣2x）米，∴y＝x（36﹣2x）＝﹣2x2+36x＝﹣2（x﹣9）2+162，∵10≤x＜18，且﹣2＜0，故抛物线开口向下，∴当x＝10时，y有最大值是160，答：AB边的长应为10米时，有最大面积，且最大面积为160平方米．【点评】本题考查二次函数的应用、一元二次方程的应用，解题的关键是明确题意，找出所求问题需要的条件．4．数学课外活动小组进行如下操作实验，把一根长20m的铁丝剪成两段．（1）把每段首尾相连各围成一个正方形．要使这两个正方形的面积之和等于13m2，应该怎么剪这根铁丝？（2）若把剪成两段的铁丝围成两个圆，两圆面积之和的最小值是多少？【分析】（1）设剪成的较短的这段为xcm，较长的这段就为（20﹣x）cm．就可以表示出这两个正方形的面积，根据两个正方形的面积之和等于13cm2建立方程求出其解即可；（2）设两圆面积之和为Scm2，剪成较短的一短为ym，则较长的部分为（20﹣y）m，根据圆的面积公式求出两圆面积之和，再根据函数性质求最小值．【解答】解：（1）设剪成较短的一短为xm，则较长的部分为（20﹣x）m，由题意得：（）2+（）2＝13，化简得：x2﹣20x+96＝0，解得：x1＝8，x2＝12，当x＝8时，较长部分为12，答：应该把铁丝剪成8m和12m的两个部分；（2）设两圆面积之和为Scm2，剪成较短的一短为ym，则较长的部分为（20﹣y）m，由题意得：S＝π•（）2+π•（）2＝（y﹣10）2+（0≤y≤20），∵＞0，∴当y＝10时，S有最小值，最小值为．【点评】本题考查和二次函数和一元二次方程的应用，关键是根据题意列出函数关系式和一元二次方程．5．如图，用一根60厘米的铁丝制作一个“日”字型框架ABCD，铁丝恰好全部用完．（1）若所围成的矩形框架ABCD的面积为144平方厘米，则AB的长为多少厘米？（2）矩形框架ABCD面积的最大值为平方厘米．【分析】（1）设框架的长AD为xcm，则宽AB为cm，根据面积公式列出一元二次方程，解之即可；（2）在（1）的基础上，列出二次函数，再利用二次函数的性质可得出结论．【解答】解：（1）设框架的长AD为xcm，则宽AB为cm，∴x•＝144，解得x＝12或x＝18，∴AB＝12cm或AB＝8cm，∴AB的长为12厘米或8厘米；（2）由（1）知，框架的长AD为xcm，则宽AB为cm，∴S＝x•，即S＝﹣x2+20x＝﹣（x﹣15）2+150，∵﹣＜0，∴要使框架的面积最大，则x＝15，此时AB＝10，最大为150平方厘米．故答案为：150．【点评】此题考查的是二次函数在实际生活中的运用及求函数最值的方法，属较简单题目．解题的关键是用一个未知数表示出长和宽，利用面积公式来列出函数表达式后再求其最值．6．园林部门计划在某公园建一个长方形苗圃ABCD．苗圃的一面靠墙（墙最大可用长度为14米）．另三边用木栏围成，中间也用垂直于墙的木栏隔开，分成两个区域，并在如图所示的两处各留2米宽的门（门不用木栏），建成后所用木栏总长32米，设苗圃ABCD的一边CD长为x米．（1）BC长为米（包含门宽，用含x的代数式表示）；（2）若苗圃ABCD的面积为96m2，求x的值；（3）当x为何值时，苗圃ABCD的面积最大，最大面积为多少？【分析】（1）根据木栏总长32米，两处各留2米宽的门，设苗圃ABCD的一边CD长为x米，即得BC 长为（36﹣3x）米；（2）根据题意得：x•（36﹣3x）＝96，即可解得x的值；（3）w＝x•（36﹣3x）＝﹣3（x﹣6）2+108，由二次函数性质可得答案．【解答】解：（1）∵木栏总长32米，两处各留2米宽的门，设苗圃ABCD的一边CD长为x米，∴BC长为32﹣3x+4＝36﹣3x，故答案为：（36﹣3x）；（2）根据题意得：x•（36﹣3x）＝96，解得x＝4或x＝8，∵x＝4时，36﹣3x＝24＞14，∴x＝4舍去，∴x的值为8；（3）设苗圃ABCD的面积为w，则w＝x•（36﹣3x）＝﹣3x2+36x＝﹣3（x﹣6）2+108，∵﹣3＜0，∴当x＞6时，w随x的增大而减小，∵36﹣3x≤14，得x≥，∴x＝时，w最大为，答：当x为米时，苗圃ABCD的最大面积为平方米．【点评】本题考查二次函数的应用，解题得关键是读懂题意，根据已知列方程和函数关系式．7．为了提高巴中市民的生活质量，巴中市对老旧小区进行了美化改造．如图，在老旧小区改造中，某小区决定用总长27m的栅栏，再借助外墙围成一个矩形绿化带ABCD，中间用栅栏隔成两个小矩形，已知房屋外墙长9m．（1）当AB长为多少时，绿化带ABCD的面积为42m2？（2）当AB长为多少时，绿化带ABCD的面积最大，最大面积是多少？【分析】（1）根据题意和图形可知：AB•CD＝42，然后列出方程求解即可，注意CD的长不大于9m；（2）根据题意，可以写出面积与AB的长的函数关系，然后利用二次函数的性质求最值．【解答】解：（1）设AB长为xm时，绿化带ABCD的面积为42m2，x（27﹣3x）＝42，解得x1＝2，x2＝7，当x＝2时，27﹣3x＝21＞9，不合题意，舍去；当x＝7时，27﹣3x＝6，符合题意；答：当AB长为7m时，绿化带ABCD的面积为42m2；（2）设绿化带ABCD的面积为Sm2，AB长为am，S＝a（27﹣3a）＝﹣3a2+27a＝﹣3（a﹣）2+，∴该函数图象开口向下，对称轴为直线x＝，∵，解得6≤a＜9，∴当a＝6时，S取得最大值，此时S＝54，答：当AB长为6m时，绿化带ABCD的面积最大，最大面积是54 m2．【点评】本题考查二次函数的应用、一元二次方程的应用，解答本题的关键是明确题意，写出相应的方程和二次函数关系式，利用二次函数的性质求最值．8．如图，若要建一个矩形场地，场地的一面靠墙，墙长10m，另三边用篱笆围成，篱笆总长20m，设垂直于墙的一边为xm，矩形场地的面积为Sm2．（Ⅰ）S与x的函数关系式为S＝，其中x的取值范围是；（Ⅱ）若矩形场地的面积为42m2，求矩形场地的长与宽；（Ⅲ）当矩形场地的面积最大时，求矩形场地的长与宽，并求出矩形场地面积的最大值．【分析】（1）由AD＝x，可得出AB＝20﹣2x，由墙长10米，可得出关于x的一元一次不等式组，解之即可得出x的取值范围，再利用矩形的面积公式即可得出s关于x的函数关系式；（2）根据矩形场地的面积，可得出关于x的一元二次方程，解之即可得出结论；（3）把二次函数的解析式配方成顶点式，求出长与宽．【解答】解：（1）∵AD＝BC＝x，∴AB＝20﹣2x．又∵墙长10米，∴，∴5≤x＜10．∴S＝x（20﹣2x）＝﹣2x2+20x（5≤x＜10）．故答案为：﹣2x2+20x，5≤x＜10；（2）当矩形场地的面积为42m2时，﹣2x2+20x＝42，解得：x1＝3（不合题意，舍去），x2＝7，∴20﹣2x＝6．答：矩形的长为7米，宽为6米；（3）∵S＝﹣2x2+20x＝﹣2（x﹣5）2+50，∴当x＝5时，S最大是50，此时20﹣2x＝10，答：当矩形场地的面积最大时，矩形场地的长是10m，宽是5m，矩形场地面积的最大值是50m2．【点评】本题考查了一元二次方程的应用、函数关系式以及函数自变量的取值范围，解题的关键是：（1）利用矩形的面积公式，找出s关于x的函数关系式；（2）找准等量关系，正确列出一元二次方程．9．在校园嘉年华中，九年级同学将对一块长20m，宽10m的场地进行布置，设计方案如图所示．阴影区域为绿化区（四块全等的矩形），空白区域为活动区，且4个出口宽度相同，其宽度不小于4m，不大于8m．设出口长均为x（m），活动区面积为y（m2）．（1）求y关于x的函数表达式；（2）当x取多少时，活动区面积最大？最大面积是多少？（3）若活动区布置成本为10元/m2，绿化区布置成本为8元/m2，布置场地的预算不超过1850元，当x 为整数时，请求出符合预算且使活动区面积最大的x值及此时的布置成本．【分析】（1）根据活动区域的面积等于矩形的面积减去绿化区的面积，可得y与x的关系式；（2）根据二次函数的增减性可得结论；（3）根据列方程即可得到结论．【解答】解：（1）根据题意得：y＝20×10﹣4××＝200﹣（20﹣x）（10﹣x）＝200﹣200+30x﹣x2＝﹣x2+30x，∴y与x的函数关系式为y＝﹣x2+30x（4≤x≤8）；（2）由（1）知：y＝﹣x2+30x＝﹣（x﹣15）2+225，∵﹣1＜0，∵当x＜15时，y随x的增大而增大，∵4≤x≤8，∴当x＝8时，y有最大值，最大值为176，∴当x取8m时，活动区面积最大，最大面积是176m2；（3）设布置场地所用费用为w元，则w＝10（﹣x2+30x）+8[200﹣（﹣x2+30x）]＝﹣10x2+300x+1600+8x2﹣240x＝﹣2x2+60x+1600，令w＝1850，﹣2x2+60x+1600＝1850，解得：x＝25或x＝5，∵4≤x≤8，∴4≤x≤5，∵活动区域面积为y＝﹣x2+30x，﹣1＜0，对称轴为直线x＝15，∴当x＝5时，活动区面积最大，此时的布置成本为1850元．【点评】本题考查了二次函数的应用，此题关键是求得短边的长度，再利用矩形的面积求得各部分面积，进一步列不等式（组）解决问题．题型2：几何问题-动点问题10．如图，在Rt△ABC中，∠B＝90°，AB＝3cm，BC＝4cm，点P从点A出发，以1cm/s的速度沿AB运动；同时，点Q从点B出发，以2cm/s的速度沿BC运动．当点Q到达点C时，P、Q两点同时停止运动．设运动时间为t（s），四边形APQC的面积为S（cm）．（1）试写出四边形APQC的面积为S（cm）与动点运动时间t之间的函数表达式；（2）运动时间t为何值时，四边形APQC的面积最小？最小值为多少？【分析】（1）首先根据题意，表示PB＝（3﹣t）cm，BQ＝2tcm，再根据四边形APQC的面积为S＝Rt△ABC的面积﹣Rt△PBQ的面积，用t表示四边形的面积；（2）首先求出自变量的取值范围，根据二次函数的性质确定四边形APQC面积的最小值．【解答】解：（1）根据题意，得PB＝（3﹣t）cm，BQ＝2tcm，S＝﹣＝6﹣t（3﹣t）＝t2﹣3t+6；（2）S＝t2﹣3t+6（0＜t＜2），∵a＝1，∴S＝﹣＝时，S有最小值，S＝，∴当t为cm时，四边形APQC的面积最小，最小值为cm2．【点评】本题考查了二次函数的最值，掌握二次函数的性质的应用，根据题意用t表示四边形的面积是解题关键．11．如图，在矩形ABCD中，AB＝10cm，BC＝16cm，点P从点A开始沿边AB向点B以2cm/s的速度移动，点Q以点B开始沿边BC向点C以3cm/s的速度移动，如果P、Q分别从A、B同时出发，当一点到达终点时，另一个点随即停止移动．（1）经过几秒，△PBQ的面积等于18cm2？（2）在运动过程中，经过几秒时，△PBQ的面积最大？最大面积是多少？【分析】（1）根据题意表示出PB，QB的长，利用△PBQ的面积等于18列式求值即可；（2）根据三角形的面积公式列出S关于t的函数解析式，再根据函数的性质求最值即可．【解答】解：（1）设经过t（0≤t≤5）秒时间，此时PB＝10﹣2t，BQ＝3t，当△PBQ面积等于18cm2时，根据题意得：（10﹣2t）×3t＝18，解得t1＝2，t2＝3，经检验，均符合题意．∴经过2s或3s后，APBQ的面积等于18cm；（2）设运动时间为t秒，则S＝PB•BQ＝（10﹣2t）×3t＝﹣3t2+15t＝﹣3（t﹣2.5）2+，△PBQ∴当t＝2.5时，S最大，最大值为，△PBQ∴经过2.5秒时，△PBQ的面积最大，最大面积为cm2．【点评】此题考查了二次函数求最值、一元二次方程的应用，关键是找到等量关系列出函数解析式和一元二次方程．12．在长方形ABCD中，AB＝3，BC＝4，动点P从点A开始按A→B→C→D的方向运动到点D．如图，设动点P所经过的路程为x，△APD的面积为y．（当点P与点A或D重合时，y＝0）（1）写出y与x之间的函数解析式；（2）直接写出△APD的面积的最大值．【分析】（1）分三种情况：点P在AB上运动，点P在BC上运动，点P在CD上运动，分别求出y与x 之间的函数解析式即可；（2）画出函数图象，观察图象可得答案．【解答】解：（1）当点P在AB上运动时，即0≤x＜3时，y＝×AD×AP＝×4×x＝2x；当点P在BC上运动时，即3≤x＜7时，y＝×AD×AB＝×4×3＝6；当点P在CD上运动时，即7≤x≤10时，y＝×AD×PD＝×4×（10﹣x）＝﹣2x+20，综上所述，y＝；（2）函数图象如下：由图象可得，y最大为6，∴△APD的面积的最大值是6．【点评】本题考查动点问题的函数图象、三角形的面积公式等知识，解题的关键是学会分类讨论的思想方法．13．如图，在△ABC中，∠B＝90°，AB＝12cm，BC＝24cm，动点P从点A开始沿边AB向点B以2cm/s 的速度移动，动点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果P、Q两点分别从A，B两点同时出发，设运动时间为t，（1）AP＝　2tcm　，BP＝　（12﹣2t）cm　，BQ＝　4tcm　；（2）t为何值△时△PBQ的面积为32cm2？（3）t为何值时△PBQ的面积最大？最大面积是多少？【分析】（1）根据题意得出即可；（2）根据题意和三角形的面积列出方程，求出方程的解即可；（3）先列出函数解析式，再化成顶点式，最后求出最值即可．【解答】解：（1）根据题意得：AP＝2tcm，BQ＝4tcm，所以BP＝（12﹣2t）cm，故答案为：2tcm，（12﹣2t）cm，4tcm；（2）△PBQ的面积S＝＝（12﹣2t）×4t＝﹣4t2+24t＝32，解得：t＝2或4，即当t＝2秒或4秒时，△PBQ的面积是32cm2；（3）S＝﹣4t2+24t＝﹣4（t﹣3）2+36，所以当t为3时△PBQ的面积最大，最大面积是36cm2．【点评】本题考查了三角形的面积，二次函数的最值等知识点，能求出S与x的函数关系式是解此题的关键．14．如图，在Rt△ABC中，∠C＝90°，AC＝12cm，BC＝6cm，点P从点C开始沿CB向点B以1cm/s的速度移动，点Q从A开始沿AC向点C以2cm/s的速度移动，如果点P，Q同时从点C，A出发，试问：（1）出发多少时间时，点P，Q之间的距离等于？（2）出发多少时间时，△PQC的面积为6cm2？（3）△PQC面积的是否有最大值？若有是多少？此时时间是多少？【分析】（1）可设出发xs时间时，点P，Q之间的距离等于2cm，根据勾股定理列出方程求解即可；（2）可设出发ys时间时，△PQC的面积为6cm2，根据三角形的面积公式列出方程求解即可；（3）根据题意得到△PQC面积和时间t的关系式，根据关系式即可得到结论．【解答】解：（1）设出发xs时间时，点P，Q之间的距离等于2cm，依题意有x2+（12﹣2x）2＝（2）2，解得x1＝2，x2＝7.6（不合题意舍去）．答：出发2s时间时，点P，Q之间的距离等于2cm；（2）设出发ys时间时，△PQC的面积为6cm2，依题意有y（12﹣2y）＝6，解得y1＝3﹣，y2＝3+．答：出发（3﹣）s或（3+）s时间时，△PQC的面积为6cm2；＝t（12﹣2t）＝﹣（t﹣3）2+9，（3）依题意有S△PQC∵﹣1＜0，∴△PQC面积的有最大值9，此时时间是3．【点评】此题主要考查了二次函数的最值，一元二次方程的应用，熟练掌握二次函数的性质是解题关键．15．如图，在矩形ABCD中，BC＝6cm，AB＝4cm，S是AD中点，点E以每秒2cm的速度从点B出发沿折线BS﹣SD﹣DC匀速运动，同时点F以每秒1cm的速度从点C出发沿CB运动．设点E、F出发t秒（0＜t＜6）时，△EBF的面积为ycm2．（1）求y与t的函数关系式；（2）当t为何值时，y取得最大值，并求出此最大值．【分析】（1）分点E在BS上、点E在SD上和点E在DC上讨论解答即可；（2）根据（1）的结论解答即可．【解答】解：（1）点E在BS上（当0＜t≤2.5时），，点E在SD上（当2.5≤t≤4时），y＝12﹣2t；点E在DC上（当4≤t≤6时），y＝t2﹣12t+36；（2）当0＜t≤2.5时，，对称轴t＝3，y随x的增大而增大，∴t＝2.5，y的最大值为7；当2.5≤t≤4时，y＝12﹣2t，是减函数，∴t＝2.5时，y有最大值为7；当4≤t≤6时，y＝t2﹣12t+36，对称轴为t＝6，y随x的增大而减小，∴t＝4，y有最大值为4．综上所述，t＝2.5时，y有最大值为7．【点评】本题考查二次函数综合题、锐角三角函数、勾股定理、三角形面积、函数图象问题等知识，读懂图象信息是解决问题的关键，学会设未知数列方程组解决问题，把问题转化为方程去思考，是数形结合的好题目，属于中考选择题中的压轴题．16．如图，在Rt△AOB中，∠AOB＝90°，且AO＝8，BO＝6，P是线段AB上一个动点，PE⊥AO于E，PF⊥BO于F．设PE＝x，矩形PFOE的面积为S（1）求出S与x的函数关系式；（2）当x为何值时，矩形PFOE的面积S最大？最大面积是多少？【分析】（1）根据矩形的对边相等可得OF＝PE＝x，然后利用∠B的正切值求出PF，再根据矩形的面积公式列式整理即可得解；（2）把二次函数解析式整理成顶点式形式，然后根据二次函数的最值问题解答．【解答】解：（1）在矩形PFOE中，OF＝PE＝x，∵AO＝8，BO＝6，∴tan B＝＝，即＝，解得PF＝（6﹣x），∴矩形PFOE的面积为S＝PE•PF＝x•（6﹣x）＝﹣x2+8x，即S＝﹣x2+8x；（2）∵S＝﹣x2+8x＝﹣（x2﹣6x+9）+12＝﹣（x﹣3）2+12，∴当x＝3时，矩形PFOE的面积S最大，最大面积是12．【点评】本题考查了二次函数的最值问题，矩形的性质与锐角的正切的利用，（2）把二次函数的解析式转互为顶点式形式是解题的关键．17．如图，在矩形ABCD中，AB＝8，AD＝6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B 运动，点Q从点C向点D运动，且保持AP＝CQ．设AP＝x．（1）当PQ∥AD时，求x的值；（2）当线段PQ的垂直平分线与BC边相交时，求x的取值范围；（3）当线段PQ的垂直平分线与BC相交时，设交点为E，连接EP、EQ，设△EPQ的面积为S，求S 关于x的函数关系式，并写出S的取值范围．【分析】（1）根据已知条件，证明四边形APQD是矩形，再根据矩形的性质和AP＝CQ求x即可；（2）连接EP、EQ，则EP＝EQ，设BE＝y，列出等式（8﹣x）2+y2＝（6﹣y）2+x2然后根据函数的性质来求x的取值范围；（3）由图形的等量关系列出方程，再根据函数的性质来求最值．【解答】解：（1）当PQ∥AD时，则∠A＝∠APQ＝90°，∠D＝∠DQP＝90°，又∵AB∥CD，∴四边形APQD是矩形，∴AP＝QD，∵AP＝CQ，AP＝CD＝，∴x＝4．（2）如图，连接EP、EQ，则EP＝EQ，设BE＝y．∴（8﹣x ）2+y 2＝（6﹣y ）2+x 2，∴y ＝．∵0≤y ≤6，∴0≤≤6，∴≤x ≤．（3）S △BPE ＝•BE •BP ＝••（8﹣x ）＝，S △ECQ ＝＝•（6﹣）•x ＝，∵AP ＝CQ ，∴S BPQC ＝，∴S ＝S BPQC ﹣S △BPE ﹣S △ECQ ＝24﹣﹣，整理得：S ＝＝（x ﹣4）2+12（），∴当x ＝4时，S 有最小值12，当x ＝或x ＝时，S 有最大值．∴12≤S ≤．【点评】解答本题时，涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点，这是一道综合性比较强的题目，所以在解答题目时，一定要把各个知识点融会贯通，这样解题时才会少走弯路．题型3：利润问题18．某种产品按质量不同分等级，生产最低档次产品每件获利润8元，每提高一个档次，每件利润增加2元．用同样工时每天可生产最低档次产品800件，每提高一个档次将减产40件，求生产何种档次产品的利润最高？【分析】档次提高时，带来每件利润的提高，销售量下降，设生产第x档次时获得产品的利润为y元，每件利润为[8+2（x﹣1）]元，销售量为[800﹣40（x﹣1）]件，根据：利润＝每件利润×销售量列函数式，化成顶点式即可．【解答】解：设生产第x档次时获得产品的利润为y元，则∵生产最低档次产品每件获利润8元，每提高一个档次，每件利润增加2元．用同样工时每天可生产最低档次产品800件，每提高一个档次将减产40件，∴y＝[8+2（x﹣1）][800﹣40（x﹣1）]＝﹣80（x﹣9）2+11520，∵当x＝9时，y有最大值，所以，生产第九档次产品获利润最大．【点评】本题考查二次函数的实际应用，借助二次函数解决实际问题，解题的关键是能够从实际问题中抽象出二次函数模型，难度不大．19．小明在“生活中的数学”探究活动中，经过市场调查，研究了某种商品的售价、销量、利润之间的变化关系．小明整理出该商品的相关数据如下表所示．时间x（天）1≤x＜3030≤x≤50售价（元/件）x+4070每天销量（件）100﹣2x已知该商品的进价为每件10元，设销售该商品的每天利润为y元．（1）求y与x的函数关系式；（2）销售该商品第几天时，当天销售利润最大，最大利润是多少？【分析】（1）根据题意可以分别求得1≤x＜50和50≤x≤90时的y与x的函数关系式；（2）根据题意可以分别求得两段的函数的最大值，从而可以解答本题．【解答】解：（1）当1≤x＜30时，y＝（100﹣2x）（x+40﹣10）＝﹣2x2+40x+3000，当30≤x≤50时，y＝（100﹣2x）（70﹣10）＝﹣120x+6000，综上所述：y与x的函数关系式为y＝；（2）当1≤x＜30时，二次函数y＝﹣2x2+40x+3000＝﹣2（x﹣10）2+3200，∵﹣2＜0，∴当x＝10时，y＝3200，最大当30≤x≤50时，y＝﹣120x+6000中y随x的增大而减小，＝2400，∴当x＝30时，y最大综上所述，该商品第10天时，当天销售利润最大，最大利润是3200元．【点评】本题考查二次函数的应用，解题的关键是明确题意，找出所求问题需要的条件．20．“全民防控新冠病毒”期间某公司推出一款消毒产品，成本价8元/千克，经过市场调查，该产品的日销售量y（千克）与销售单价x（元/千克）之间满足一次函数关系，该产品的日销售量与销售单价几组对应值如表：销售单价x（元/千克）121620日销售量y（千克）220180140（1）求y关于x的函数关系式（不要求写出x的取值范围）；（2）设日销售利润为W，求出W与x的函数关系式；（注：日销售利润＝日销售量×（销售单价−成本单价）（3）该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象，为了保证捐赠后每天的剩余利润不低于1500元，试确定该产品销售单价的范围．【分析】（1）设y关于x的函数解析式为y＝kx+b，由待定系数法求解即可；（2）根据日销售利润＝日销售量×（销售单价﹣成本单价）写出函数关系式；（3）根据题意得﹣10x2+420x﹣2720﹣100≥1500，变形得出关于x的二次不等式，然后解一元二次方程，再根据二次函数的性质可得答案．【解答】解：（1）设y关于x的函数解析式为y＝kx+b，将（12，220），（16，180）代入得：，解得：．∴y＝﹣10x+340；（2）由题意得：W＝（﹣10x+340）（x﹣8）＝﹣10x2+420x﹣2720，∴W与x的函数关系式是W＝﹣10x2+420x﹣2720；（3）由题意得：﹣10x2+420x﹣2720﹣100≥1500，∴x2﹣42x+432≤0，当x2﹣42x+432＝0时，解得：x1＝18，x2＝24，∵函数y＝x2﹣42x+432的二次项系数为正，图象开口向上，∴当18≤x≤24时，x2﹣42x+432≤0，即﹣10x2+420x﹣2720﹣100≥1500，∴该产品销售单价的范围为18≤x≤24．【点评】本题考查了待定系数法求一次函数的解析式及二次函数在销售问题中的应用，理清题中的数量关系并明确二次函数的性质是解题的关键．21．某科技公司生产一款精密零件，每个零件的成本为80元，当每个零件售价为200元时，每月可以售出1000个该款零件，若每个零件售价每降低5元，每月可以多售出100个零件，设每个零件售价降低x元，每月的销售利润为w元．（1）求w与x之间的函数关系式；（2）为了更好地回馈社会，公司决定每销售1个零件就捐款n（0＜n≤6）元作为抗疫基金，当40≤x≤60时，捐款后每月最大的销售利润为135000元，求n的值．【分析】（1）根据销售利润＝单件利润×销售量列出函数解析式即可；（2）根据销售利润﹣捐款额列出函数解析式，再根据函数的性质结合x的取值范围求值即可．【解答】解：（1）设每个零件售价降低x元，则每个零件的实际售价为（200﹣x）元，每月的实际销售量为（1000+×100），则w＝（200﹣x﹣80）（1000+×100）＝20x2十1400x+120000，∵，∴0≤x≤120，∴w与x之间的函数关系式为w＝﹣20x2+1400x+120000（0≤x≤120）；（2）设捐款后的实际利润为p元，则p＝﹣20x2+1400x+120000﹣（1000+×100）n，整理得：p＝﹣20x2+（1400﹣20n）x+120000﹣1000n，则p是x的二次函数，其对称轴为直线x＝﹣＝，∵0＜n≤6，∴32≤＜35，∵﹣20＜0，∴函数图象开口向下，当40≤x≤60时，p随x的增大而减小，∴当x＝40时，p有最大值135000，即﹣20×402+40（1400﹣20n）+120000﹣1000n＝135000，解得：n＝5．【点评】本题考查二次函数的应用，关键是根据题意列出函数解析式．22．我市某卖场的一专营柜台，专营一种电器，每台进价60元，调查发现，当销售价80元时，平均每月能售出1000台；当销售价每涨1元时，平均每月能少售出10台；该柜台每月还需要支出20000元的其它费用．为了防止不正当竞争，稳定市场，市物价局规定：“出售时不得低于80元/台，又不得高于180元/台”，设售价为x元/台时，月平均销售量为y台，月平均利润为w元．（1）求y与x的函数关系式，w与x的函数关系式（写出x的取值范围）；（2）每台售价多少元时，月销售利润最高，最高为多少元．【分析】（2）根据题意直接得出结论；（2）根据抛物线的性质可得答案．【解答】解：（1）由题意得：y＝1000﹣10（x﹣80）＝1800﹣10x（80≤x≤180），w＝（x﹣60）（1800﹣10x）﹣20000＝﹣10x2+2400x﹣128000（80≤x≤180）；（2）w＝﹣10x2+2400x﹣128000＝﹣10（x﹣120）2+16000，∵﹣10＜0，∴抛物线开口向下，∴当每台售价120元时，月销售利润最高，最高为16000元．【点评】本题主要考查二次函数的实际应用，理解题意找到题目蕴含的相等关系是解题的关键．23．某文具店购进一批单价为12元的学习用品，按照相关部门规定其销售单价不低于进价，且不高于进价的1.5倍，通过分析销售情况，发现每天的销售量y（件）与销售单价x（元）满足一次函数关系，且当x ＝15时，y＝50；当x＝17时，y＝30．（1）求y与x之间的函数关系式；（2）这种学习用品的销售单价定为多少时，每天可获得最大利润，最大利润是多少元？【分析】（1）设y与x之间的函数关系式为y＝kx+b，然后代值求解即可；（2）设每天获得的利润为w元，由（1）可得w＝﹣10（x﹣16）2+160进而根据二次函数的性质可求解．【解答】解：（1）设y与x之间的函数关系式为y＝kx+b，由题意得：，解得：，∴y与x之间的函数关系式为y＝﹣10x+200；（2）设每天获得的利润为w元，由（1）可得：w＝（x﹣12）（﹣10x+200）＝﹣10x2+320x﹣2400＝﹣10（x﹣16）2+160，∵12≤x≤18，且﹣10＜0，∴当x＝16时，w有最大值，最大值为160．答：这种学习用品的销售单价定为16元时，每天可获得最大利润，最大利润是160元．【点评】本题主要考查一次函数与二次函数的应用，熟练掌握一次函数与二次函数的图象与性质是解题的关键．24．为扩大销售，某乡镇农贸公司在某平台新开了一家网店进行线上销售．在对一种特产（成本为10元/千克）在网店试销售期间发现每天销售量y（千克）与销售单价x（元）大致满足如图所示的函数关系（其中14≤x≤25）．（1）写出y关于x的函数解析式，并求x＝20时，农贸公司每天销售该特产的利润；（2）设农贸公司每天销售该特产的利润为W元，当销售单价x为多少元时，W最大？最大是多少元？【分析】（1）设出y关于x的函数解析式，用待定系数法求函数解析式即可；（2）根据每千克的利润×销售量＝总利润列出函数解析式，用函数的性质求最值即可．【解答】解：（1）设y关于x的函数解析式y＝kx+b（k≠0），将（14，320），（25，210）代入得，解得，∴y与x之间的函数关系式为y＝﹣10x+460；当x＝20时，y＝﹣10×20+460＝260，农贸公司每天销售该特产的利润为（20﹣10）×260＝2600（元），。

21.3 第2课时面积问题(含答案)-2021-2022学年九年级数学上册课时作业(人教版)

2021－2022学年九年级数学上册课时作业(人教版)第二十一章一元二次方程21.3实际问题与一元二次方程第2课时面积问题分点训练知识点1几何图形的面积问题1. 从一块正方形的木板上锯掉2 m宽的长方形木条，剩下的面积是48 m2，则原来这块木板的面积是( )A. 100 m2B. 64 m2C. 121 m2D. 144 m22. 公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花(如图)，原空地一边减少了1 m，另一边减少了2 m，剩余空地的面积为18 m2，求原正方形空地的边长. 设原正方形的空地的边长为x m，则可列方程为( )A. (x＋1)(x＋2)＝18B. x2－3x＋16＝0C. (x－1)(x－2)＝18D. x2＋3x＋16＝03. 餐桌桌面是长为160 cm，宽为100 cm的长方形，妈妈准备设计一块桌布，面积是桌面的2倍，且使四周垂下的边等宽，小刚设四周垂下的边宽为x cm，则应列方程是( )A. (160＋x)(100＋x)＝2×160×100B. (160＋2x)(100＋2x)＝2×160×100C. (160＋x)(100＋x)＝160×100D. 2(160x＋100x)＝160×1004. 要将一幅长90 cm，宽40 cm的风景画的四周外围镶上一条宽度相同的金色纸边，制成一幅挂图，如果要求风景画的面积占整个挂图的面积的60％，设金色边的宽度为x cm，根据题意列方程为.5. 一幅长20 cm，宽12 cm的图案，如图，其中有一横两竖的彩条，横、竖彩条的宽度比为3∶2.设竖彩条的宽度为x cm，若图案中三条彩条所占面积是图案面积的25，求横竖彩条的宽度.知识点2营销中的利润问题6. 原来商场将每件进价为80元的某商品按每件100元出售，一天可出售100件，经调查发现该商品每降低2元销售量可增加10件，设后来该商品每件降价x元，则可获利元.7. 某商场将某种商品的售价从原来的每件40元经两次调价后调至每件32.4元.若该商品两次调价的降价率相同，则这个降价率为；经调查，该商品每降价0.2元，即可多销售10件.若该商品原来每月销售500件，那么两次调价后，每月可销售商品件.8. 某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品每降价1元，那么商场每月可以多售出5件.(1)降价前商场每月销售该商品的利润是多少元?(2)要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元?强化提升9. 如图，在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分)，余下部分种植草坪.要使草坪的面积为540平方米，则道路的宽为( )A. 5米B. 3米C. 2米D. 2米或5米10. 如图，过点A(2，4)分别作x轴、y轴的垂线，垂足分别是点M，N，若点P从点O出发，沿OM做匀速运动，1分钟可到达M点，同时点Q从M点出发，沿MA做匀速运动，1分钟可到达点A，若线段PQ 的长度为2，则经过的时间为.11. 某西瓜经营户以2元/千克的价格购进一批良种西瓜，以3元/千克的价格出售，每天可售出200千克，为了促销，该经营户决定降价销售，经调查发现，这种良种西瓜每降价0.1元/千克，每天可多售出40千克，另外每天的房租等固定成本共24元，该经营户要想每天盈利200元，应将每千克良种西瓜降价多少元?12. 如图，用长为24 m的篱笆，一面利用墙(墙的最大可用长度a为10 m)围成中间隔有一道篱笆的长方形花圃.(1)现要围成面积为45 m2的花圃，则AB的长是多少米?(2)现要围成面积为48 m2的花圃，能行吗?若不能行，请说明理由.13. 在直角墙角AOB(OA∶OB，且OA，OB长度不限)中，要砌20 m长的墙，与直角墙角AOB围成地面为矩形的储仓，且地面矩形AOBC的面积为96 m2.(1)求地面矩形的长；(2)有规格为0.80×0.80和1.00×1.00(单位：m)的地板砖单价分别为55元/块和80元/块，若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙)，用哪一种规格的地板砖费用较少?14. 如图，要建造一个四边形花圃ABCD，要求AD边靠墙，CD∶AD，AD∶BC，AB∶CD＝5∶4，且三边的总长为20米.设AB的长为5x米.(1)请求出AD的长(用含字母x的式子表示)；(2)若该花圃的面积为50平方米，且周长不大于30米，求AB的长.参考答案1. B 【解析】设原来的正方形木板的边长为x ．x (x －2)＝48，x 1＝8或x 2＝－6(舍去)，8×8＝64，故选A ．2. C 【解析】设原正方形的边长为x m ，由题意得(x －1)(x －2)＝18，故选C ．3. B 【解析】依题意得，桌布面积为160×100×2，桌面的长为(160＋2x )，宽为(100＋2x )，则面积为(160＋2x )(100＋2x )＝2×160×100．故选B ．4. (90＋2x )(40＋2x )×60％＝90×40 【解析】设金色纸边的宽度为x cm ，那么挂图的面积就应该为(90＋2x )(40＋2x )，根据题意，得(90＋2x )(40＋2x )×60%＝90×40．5. 解：由题意得20×32x ＋2×12x －2×32x ·x ＝25×20×12，整理得x 2－18x ＋32＝0. 解得x 1＝2，x 2＝16＞12(舍去)，∶32x ＝3. 答：横彩条的宽度为3 cm ，竖彩条的宽度为2 cm. 6. (100－80－x )(100＋2x ·10) 7. 10％ 880 【解析】设降价率为x ，由题意列方程得40(1－x )2＝32.4，解得x 1＝0.1，x 2＝1.9(舍去)．故这个降价率为10%．500＋4032.40.2×10＝880件． 8. 解：(1)(360－280)×60＝4800(元).(2)设每件商品应降价x 元，依题意得(360－280－x )(60＋5x )＝7200，解得x 1＝8，x 2＝60，为减少库存，则x ＝60. 答：每件商品应降价60元.9. C 【解析】设道路的宽为x ，根据题意得20x ＋32x －x 2＝20×32－540，整理得(x －26)2＝576，x －26＝24或x －26＝－24，解得x 1＝50(舍去)或x 2＝2，所以道路宽为2米．10. 0.4分钟【解析】∶A (2，4)，∶OM ＝AN ＝2，AM ＝ON ＝4，∶P 点1分钟可到达M 点，Q 点1分钟可到达A 点，∶P 点的运动速度是2个单位每分钟，Q 点的运动速度是4个单位每分钟，设经过t 分钟，则PM＝2－2t，MQ＝4t，在Rt∶PQM中，PM2＋MQ2＝PQ2，即(2－2t)2＋16t2＝4，20t2－4t＝0，解得t＝0.4或0(舍去)，即经过0.4分钟，线段PQ的长度为2．11. 解：设每千克良种西瓜降价x元，则有(3－x－2)·(200＋400.1x)－24＝200，x1＝0.2，x2＝0.3，均符合题意. 答：要想每天盈利200元，应将每千克良种西瓜降价0.2元或0.3元.12. 解：(1)设AB的长为x m，依题意得(24－3x)x＝45，解得x1＝3，x2＝5，∶0＜24－3x≤10，∶143≤x＜8，∶x＝5，∶AB的长为5 m.(2)假如能行，设AB的长为y m，由题意得(24－3y)y＝48，即(y－4)2＝0，∶y1＝y2＝4. ∶143≤y＜8，∶y＝4不合题意，舍去，∶不能围成面积为48 m2的花圃.13. 解：(1)设地面矩形的长是x m，则依题意得x(20－x)＝96，解得x1＝12，x2＝8(舍去)，答：地面矩形的长是12米；(2)规格为0.80×0.80所需的费用：96÷(0.80×0.80)×55＝8250(元).规格为1.00×1.00所需的费用：96÷(1.00×1.00)×80＝7680(元).因为8250≥7680，所以采用规格为1.00×1.00所需的费用较少.14. 解：(1)作BH∶AD于H，则AH＝3x，由BC＝DH＝20－9x得AD＝AH＋HD＝20－6x.(2)由2(20－9x)＋3x＋9x≤30得x≥53，由12[(20－9x)＋(20－6x)]·4x＝50得3x2－8x＋5＝0，∶x1＝53，x2＝1(舍去)，∶5x＝253. 答：AB的长为253米.。

2017秋九年级数学上册22.3第1课时几何图形面积问题习题课件(新版)新人教版

解：(1)∵三块矩形区域的面积相等，∴矩形 AEFD 面积是矩形 BCFE 面积的 2 倍，∴AE＝2BE，设 BE＝FC＝a，则 AE＝HG＝DF＝2a， ∴DF＋FC＋HG＋AE＋EB＋EF＋BC＝80，即 8a＋2x＝80， 1 3 3 3 2 ∴a＝－ x＋10，3a＝－ x＋30，∴y＝(－ x＋30)x＝－ x ＋30x， 4 4 4 4 1 3 2 ∵a＝－ x＋10>0，∴x<40，则 y＝－ x ＋30x(0<x<40) 4 4
5 ．将一条长为 20 cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形， 12.5 2. 则这两个正方形面积之和的最小值是____cm
6．如图，已知▱ABCD 的周长为 8 cm，∠B＝30°，若边长 AB＝x cm. 1 2 2 y ＝－ x (1)▱ABCD 的面积 y(cm )与 x 之间的函数解析式为， 2 ＋2x 自变量 x 的取值范围为 0<x<4 ；
10．如图，线段AB＝6，点C是AB上一点，点D是AC的中点，分别以AD， 4 DC，CB为边作正方形，则AC＝____时，三个正方形的面积之和最小．
11．如图，正方形 ABCD 边长为 1，E，F，G，H 分别为各边上的点，且 AE＝BF＝CG＝DH，设小正方形 EFGH 的面积为 S，AE 的长为 x，则 S 1 2－2x＋1 S ＝ 2x 关于 x 的函数关系式是，当 x＝____ 2 时，S 的值最小．
2 2 ． (2)当 x 取____时，y 的值最大，最大值为____
7．用12 m长的木料做成如图的矩形窗框，则当长和宽各为多少米时，矩形窗框的面积最大？最大面积是多少？
1 解：设长为 x m，则宽为 (12－3x)＝(4－x) m， 3 则矩形窗框的面积 S＝x(4－x)＝－x2＋4x＝－(x－2)2＋4， ∴当 x＝2 m 时，矩形窗框的面积有最大值，最大值为 4 m2

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4
5
1如图，在平面直角坐标系xOy中，抛物线y＝ax2 －2ax－3a（a＜0）与x轴交于A、B两
点（点A在点B的左侧），经过点A的直线l：y＝kx＋b与y轴负半轴交于点C，与抛物线的
另一个交点为D，且CD＝4AC．
（1）直接写出点A的坐标，并求直线l的函数表达式（其中k、b用含a的式子表示）

（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为求a的
值

2如图，抛物线y＝a ＋bx＋c经过A (－1，0)、B (3，0)、C (0，3)三点，对称轴与抛物线
相交于点P、与直线BC相交于点M，连接PB．
（1）求该抛物线的解析式；
（2）抛物线上是否存在一点Q，使△QMB与△PMB的面积相等，若存在，求点Q的坐标；
若不存在，说明理由；
（3）在第一象限、对称轴右侧的抛物线上是否存在一点R，使△RPM与△RMB的面积相等，
若存在，直接写出点R的坐标；若不存在，说明理由．

x
y
O
A B

D
l

x
2
3如图，在平面直角坐标系xOy中，二次函数y=a +bx﹣4（a≠0）的图象与x轴交于A（﹣
2，0）、B（8，0）两点，与y轴交于点B，其对称轴与x轴交于点D
（1）求该二次函数的解析式；（2）如图2，若点P（m，n）是该二次函数图象上的一个动点
（其中m＞0，n＜0），连结PB，PD，BD，求△BDP面积的最大值及此时点P的坐标．

4如图，已知二次函数的图象与y轴交于点A（0，4），与x轴交于点B、
C，点C坐标为(8，0)，连接AB、AC.

（1）请直接写出二次函数的表达式；
（2）若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，
当△AMN面积最大时，求此时点N的坐标.
yxOMNCBAy

xOMNCB
A

cxaxy
2

3
2