对轻量级分组密码I-PRESENT-80和I-PRESENT-128的biclique攻击
轻量级密码算法研究与性能评估

轻量级密码算法研究与性能评估随着互联网的发展,数据的保护愈发重要,密码算法成为了各种软件、设备以及通信协议的必备部分。
而轻量级密码算法因其在资源受限的场景下优秀的性能表现,成为了广大研究者的关注重点。
本文旨在介绍轻量级密码算法的研究现状以及性能评估,为读者深入了解轻量级密码算法提供一些参考。
一、轻量级密码算法概述轻量级密码算法是指在资源受限的系统中使用的密码算法,如物联网设备、传感器等。
这类设备具有处理能力、存储空间等方面的限制,因此不能使用传统意义上的加密算法进行数据保护。
轻量级密码算法的诞生解决了这一问题,使得密码算法能够更广泛地应用于各种资源受限环境中。
轻量级密码算法通常具有以下特点:1. 算法复杂度低:轻量级密码算法的设计考虑到了受限系统的处理能力,因此通常采用的算法都具有低复杂度的特点。
2. 存储空间要求低:受限系统的存储空间往往有限,轻量级密码算法的设计通常也考虑到了这一点,尽可能地减小了算法对存储空间的需求。
3. 低功耗:在许多场景下,轻量级密码算法需要长时间持续运行,因此在设计时需要考虑功耗的问题,并尽可能地减小算法对功耗的消耗。
二、轻量级密码算法的研究现状目前,轻量级密码算法的研究可以分为两个大方向:一是继续设计新的算法,二是改进已有的轻量级密码算法。
在新算法设计方面,一些重要的轻量级密码算法如下:1. PRESENT算法:由法国研究者设计,是目前为止最流行的轻量级密码算法之一。
PRESENT的设计理念是控制流,其核心思想是采用S盒代替传统的线性运算。
2. SIMON算法:由美国研究者设计,与PRESENT算法类似,同样采用了S盒代替传统的线性运算。
SIMON算法的优势在于其可以轻松地进行扩展,适用于多种不同的加密场景。
在已有算法改进方面,主要有以下几种方法:1. 增加轮数:轻量级密码算法的常用方法是增加轮数,这可以提升算法的安全性。
但同时也会带来较大的性能开销。
2. 修改算法结构:改变算法的结构,如在ROUND函数中增加S盒、混淆公式等操作,会影响算法的性能和安全性,但难度较大。
RECTANGLE-80的相关密钥差分分析

RECTANGLE-80的相关密钥差分分析王沙沙; 张文涛; 向泽军【期刊名称】《《信息安全学报》》【年(卷),期】2019(004)004【总页数】15页(P94-108)【关键词】轻量级分组密码; RECTANGLE; 相关密钥差分分析; 自动化搜索; 差分特征【作者】王沙沙; 张文涛; 向泽军【作者单位】[1]中国科学院信息工程研究所信息安全国家重点实验室中国北京100093; [2]中国科学院大学网络空间安全学院中国北京100049【正文语种】中文【中图分类】TP309.71 引言在物联网的应用背景下, AES等密码算法不能完全适用。
特别是在资源受限的应用场景中(如RFID、物联网、智能电网等),AES等密码算法标准的实现代价过高。
因此,轻量级密码成为密码学的一个研究热点,此处的“轻量级”是指与传统密码算法相比实现代价更小、计算资源消耗更少。
近十年来,研究者对轻量级分组密码进行了大量的研究,提出了许多不同种类的轻量级分组密码算法,比如KLEIN[1],Lblock[2], PRESENT[3], RECTANGLE[4], SKINNY[5],SIMON[6],LED[7]等。
其中, PRESENT[3]算法的硬件实现代价很低,国际标准化组织(International Organization for Standardization, ISO)和国际电工委员会(International Electrotechnical Commission, IEC)于2012年将其定为轻量级分组密码标准。
随着对轻量级密码算法应用场景的进一步认识,密码学研究者们发现:对于轻量级密码算法,软件实现性能也是一个重要指标。
在一些低端微处理器上,包括AVR、MSP、ARM 等,软件实现比硬件实现更加灵活、成本更低,对算法进行修改更加容易。
2013年,美国国家安全局(National Security Agency, NSA)提出了轻量级分组密码SIMON和SPECK[6],他们宣称这两个密码算法兼顾了软件和硬件实现性能; 2014年,张文涛等人[4]提出了RECTANGLE密码算法,此算法采用比特切片技术,软件和硬件的实现性能均较好,可在多平台快速实现。
典型轻量级分组密码算法不可能差分分析研究

典型轻量级分组密码算法不可能差分分析研究轻量级分组密码算法由于其计算、存储资源开销少、且能够提供所要求的加密性能,从而被广泛应用于资源受限的环境。
随着物联网的兴起,轻量级分组密码算法成为了人们研究的热点。
不可能差分分析作为差分分析的一个变种,由Knudsen和Biham两人分别独立提出,是目前最常用的密码分析方法之一。
不可能差分分析的关键在于找出分组密码算法的最长不可能差分区分器。
不可能差分区分器轮数的上确界是衡量密码算法抵抗不可能差分分析的一个重要标准。
如果能够给出密码算法最长不可能差分区分器,则无论对密码设计者还是分析者都有重要的参考价值。
本文致力于几个典型轻量级分组密码算法在不可能差分分析下的安全性研究。
基本研究思路是,首先对密码算法或者密码模型的密码学特性进行研究。
其次,基于得到的性质,分析密码算法或者密码模型加、解密方向的差分扩散规律,并利用中间相错技术得到其不可能差分区分器的上确界。
再次,利用密码算法或者密码模型加、解密方向的差分扩散规律找出其全部最长不可能差分区分器,或者对最长不可能差分区分器进行分类。
最后,选择较优的不可能差分区分器,并结合一些攻击技术,给出密码算法的安全性评估结果。
本文取得如下成果。
1.对Midori算法在截断不可能差分分析下的安全性进行了研究。
通过分析Midori算法的加密方向与解密方向的差分扩散规律,证明了Midori算法的截断不可能差分区分器至多6轮,并对6轮截断不可能差分区分器进行了分类。
其次,根据分类结果,构造了一个6轮不可能差分区分器,并给出11轮Midori-64算法的不可能差分分析,恢复了128比特主密钥。
2.对SPECK算法在不可能差分分析下的安全性进行了研究。
首先利用徐洪等人给出的模整数加法差分扩散性质,分析SPECK系列算法的加密方向与解密方向的差分扩散规律,从而证明了在该性质下SPECK系列算法的不可能差分区分器至多6轮,并给出了所有6轮不可能差分区分器;其次,进一步给出模整数加法差分扩散的补充性质,并利用该性质构造了SPECK系列算法的7轮不可能差分区分器;此外,基于得到的SPECK系列算法6轮、7轮不可能差分区分器,给出了SPECK 2n/4n(2n=32,48,64,128)算法的10轮和11轮不可能差分分析,及SPECK 96/144算法的9轮和10不可能差分分析,恢复了全部主密钥。
3.分组密码分析

-- 25 --
-- 26 --
利用中间相错技术,在F函数是双射的条件下构造5轮 Feistel结构的不可能差分区分器。
-- 27 --
不可能差分分析的一般步骤
z 寻找r轮不可能差分a0→ ar ; z 选择满足输入差分为a0的明文对(P,P⊕a0),并进
PS: 一个结构中包含232组明文,每个结构内部能 够生成263对差分对。全部结构能够生成263+N 对 明文。因此可以获得263+N 对密文。
-- 37 --
Step 2. 在Step1生成的263+N个密文对中,保留在第 2,3,5,6,8,9,12,15这8个字节处为0的密文对,并抛弃 其余的密文对。 PS:密文满足Step2条件的概率为(2-8)8=2-64,因此, 经过Step2,剩余2N+63-64=2N-1个明密对被留下。
W 正确密钥: 一定不产生不可能差分
W 错误密钥: 一定的概率产生不可能差分
-- 23 --
加密 解密
差分分析VS不可能差分分析
差分分析: 利用密码算法的高概率差分(差分传递链),通过 统计方法来恢复密钥。
不可能差分分析: 利用概率为0的差分对正确密钥进行区分,如果用 候选密钥对一对明密文进行部分加脱密之后得到概 率为0的差分对应,那么该候选密钥必定是错误密 钥,应予以抛弃。当抛弃完所有的错误密钥之后剩 余的就为正确密钥。
?
0
0
⎟ ⎟
⎜0 0 ? ?⎟ ⎜0 0 ? ?⎟ ⎜? ? 0 0⎟ ⎜? ? 0 0⎟
⎜
⎟⎜
⎟⎜
⎟⎜
⎟
⎝? 0 0 ?⎠ ⎝? 0 0 ?⎠ ⎝? ? 0 0⎠ ⎝? ? 0 0⎠
现代密码学_第四五讲 分组密码

循环左移
D1 (28位) (56位) 置换选择2 k1 (48位)
14 3 23 16 41 30 44 46
置换方法
17 28 19 7 52 40 49 42 11 15 12 27 31 51 39 50 24 6 4 20 37 45 56 36 1 21 26 13 47 33 34 29 5 10 8 2 55 48 53 32
20
迭代的轮数
分组密码一般采用简单的、安全性弱的密码函数进行多
轮迭代运算,使得安全性增强。一般来说,分组密码迭代轮 数越多,密码分析越困难,但也不是追求迭代轮数越多越好, 过多迭代轮数会使加解密算法的性能下降,而实际的安全性 增强不明显。 决定迭代轮数的准则:密码算法分析的难度大 于简单穷举搜索攻击的难度。分组密码迭代轮数一般采用8、 10、12、16、20的居多。
循环左移
C16 (28位)
循环左移
C16 (28位) (56位) 置换选择2 k16 (48位)
注:去掉9,18,22,25,35,38, 43,54位
注:密钥各位在子密钥出现次数基本相同(12次至15次),平均次数为13.7
30
压缩替代S-盒(48位压缩到32位)
48比特
6比特 6比特 6比特 6比特 6比特 6比特 6比特 6比特
考虑,通常密钥长度t不能太大。当然,密钥长度t不能太小,
否则,难以抵抗对密钥的穷举搜索攻击。
7
分组密码的要求
分组长度要足够大 密钥量要足够大
当分组长度较小时,攻击者通过 穷举明文空间,得到密码变换规 律,难于抵御选择明文攻击。
密码变换足够复杂
加密和解密运算简单 无数据扩展或压缩
21
轻量级分组密码PRIDE的线性分析

-- 15 --
三、PRIDE密码线性分析的具体过程
例如: 偏差为2-5的2轮可迭代线性逼近
1轮 1轮 (0, 1, 0, 0; 0, 0, 0, 0; 0, 0, 0, 0; 0, 0, 0, 0) (0, 1, 0, 0; 0, 1, 0, 0; 0, 0, 0, 0; 0, 1, 0, 0) (0, 1, 0, 0; 0, 0, 0, 0; 0, 0, 0, 0; 0, 0, 0, 0)
-- 22 --
三、PRIDE密码线性分析的具体过程
I1 X1 Y1 Z1
0000 ???? 0??? 0000 0000 ???? ???? 0000 ???? ???? 0000 0000 0??? ???? 0000 0000 0000 ???? 0??? 0000 0000 ???? ???? 0000 ???? ???? 0000 0000 0??? ???? 0000 0000 0000 ??0? 0?00 0000 0000 ?0?? 00?0 0000 00?0 ?0?? 0000 0000 0?00 ??0? 0000 0000 0?00 0?00 0?00 0?00 0??0 0000 0000 ??00 0000 0??0 ??00 0000 0?00 00?0 00?0 0?00
{ | (0,?,?,?)},
中取值,其中 ? 表示该比特位置未知。
-- 20 --
三、PRIDE密码线性分析的具体过程
输入差分
1
0
0
0
输入掩码
0
?
?
?
S盒
P=1
Ɛ≠ 0
S盒
输出差分
?
0
?
?
分组密码

密码类型
01 研究历史
03 设计分析
目录
02 研究内容 04 设计原则
05 AES征集
07 技术总结
目录
06 算法要求
分组密码(block cipher)的数学模型是将明文消息编码表示后的数字(简称明文数字)序列,划分成长度为 n的组(可看成长度为n的矢量),每组分别在密钥的控制下变换成等长的输出数字(简称密文数字)序列。
研究历史
现代分组密码的研究始于 丰硕的研究成果。
对于分组密码,在早期的研究,基本上是围绕DES进行的,推出了一些类似的算法,例如:LOKI,FEAL, GOST等。进入20世纪90年代,人们对DES算法研究更加深入,特别是差分密码分析(differential cryptanalysis)和线性密码分析(linear cryptanalysis)的提出,迫使人们不得不研究新的密码结构。 IDEA密码打破了DES类密码的垄断局面,随后出现了SQUARE、SHARK、SAFER-64等采用了结构非常清晰的代替— 置换(SP)网络,每一轮由混淆层和扩散层组成,从理论上给出了最大差分特征概率和最佳线性逼近优势的界, 证明了密码对差分密码分析和线性密码分析的安全性。
谢谢观看
1997年-2000年,AES的征集掀起了分组密码研究的新高潮,15个AES候选算法反映了当前分组密码设计的水 平,也可以说是近几年研究成果的一个汇总。
目前分组密码所采用的整体结构可分为Feistel结构(例如CAST—256、DEAL、DFC、E2等)、SP网络(例如 Safer+、Serpent等)及其他密码结构(例如Frog和HPC)。加解密相似是Feistel型密码的一个实现优点,但它 在密码的扩散似乎有些慢,例如需要两轮才能改变输入的每一个比特。SP的网络结构非常清晰,S被称为混淆层 (非线性层),主要起混淆作用。P被称为扩散层,主要起扩散作用。
分组密码的主要攻击方法
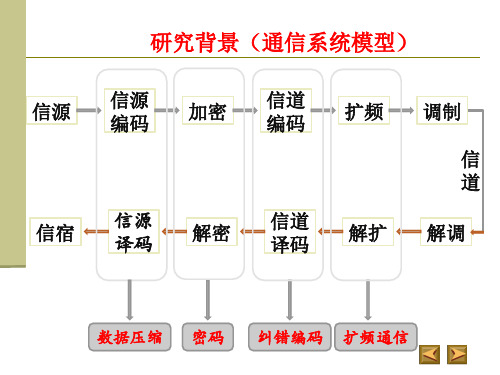
研究背景(序列密码) 研究背景(序列密码)
序列密码的主要攻击方法: 经典序列密码的攻击方法: 线性逼近攻击-非线性度 相关攻击-相关免疫度 代数攻击-代数免疫度
1 f ( x) = n 2
∑S
w∈F2n
f
( w)( −1)
wi x
布尔函数的Walsh变换 §1.2 布尔函数的 变换
第1章 布尔函数与向量值函数
☆ Walsh谱的基本性质 谱的基本性质 (1)循环Walsh谱与线性Walsh谱具有如下关系 循环Walsh谱与线性Walsh谱具有如下关系 Walsh谱与线性Walsh
第1章 布尔函数与向量值函数
●
非线性度
NL ( f ) = min d ( f , l ) = min wt ( f − l )
l∈ An l∈ An
(1) NL ( f ) = 2 (2 ) (3 ) (4)
n −1
1 − max | W f ( w) | w∈ 2 w∈F2n
n −1 2
NL ( f ) ≤ 2 n −1 − 2
定义3 为两个正整数, 定义3 设n和m为两个正整数,从F2n到F2m的映射称 和 为两个正整数 向量值函数, 为(n,m)函数,有时也称为向量值函数,多输出布 )函数,有时也称为向量值函数 尔函数或向量布尔函数. 尔函数或向量布尔函数. 向量值函数的表示方法: ☆ 向量值函数的表示方法: (1)分量函数表示法: 分量函数表示法:
4
代数攻击-代数次数 中间相遇攻击 相关密钥攻击
研究背景(序列密码) 研究背景(序列密码)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年11月Journal on CommunicationsNovember 2017第38卷第11期 通 信 学 报 V ol.38 No.11对轻量级分组密码I-PRESENT-80和 I-PRESENT-128的biclique 攻击崔杰,左海风,仲红(安徽大学计算机科学与技术学院,安徽 合肥 230039)摘 要:I-PRESENT 是一种适用于RFID 、无线传感节点等资源受限环境的代换——置换型分组密码。
利用中间筛选技术来构造I-PRESENT 的biclique 结构,首次对全轮I-PRESENT-80和I-PRESENT-128算法进行了biclique 攻击。
结果表明,biclique 对I-PRESENT-80和I-PRESENT-128攻击的数据复杂度分别为262和362个选择密文;攻击的时间复杂度分别为79.482和127.332次加密。
攻击在时间复杂度和数据复杂度上均优于穷举。
利用提出的I-PRESENT 的密钥相关性技术,攻击的时间复杂度可以进一步降低到78.612和126.482。
关键词:轻量级分组密码;PRESENT ;预计算匹配;biclique 攻击 中图分类号:TN918.1 文献标识码:ABiclique cryptanalysis on lightweight block ciphers I-PRESENT-80 and I- PRESENT-128CUI Jie, ZUO Hai-feng, ZHONG Hong(College of Computer Science and Technology, Anhui University, Hefei 230039, China)Abstract: I-PRESENT was a lightweight SPN block cipher for resource-constraint environments such as RFID tags and sensor networks. The biclique structures of I-PRESENT with sieve-in-the-middle technique was an constracted. The bic-lique cryptanalysis schemes on full-round I-PRESENT-80 and I-PRESENT-128 were proposed for the first time. The re-sults show that the data complexity of the biclique cryptanalysis on I-PRESENT-80 and I-PRESENT-128 is 262and 362chosen ciphertexts respectively ,and the time complexity on them is 79.482and 127.332encryptions respectively. The time and data complexity are better than that of the exhaustive attack. In addition, the time complexity on them can be reduced to 78.612and 126.482encryptions by using related-key technology of I-PRESENT.Key words: lightweight block cipher, PRESENT, matching-with-precomputations, biclique cryptanalysis1 引言随着射频识别标签(RFID tags)、物联网(Internet of Things)和无线传感节点(wireless sensor node)等低资源设备的发展,使轻量级密码技术逐渐成为一种热门研究领域,在该领域中寻找满足不同低资源设备安全目的的解决方案就显得尤为重要。
迄今为止,有许多的轻量级分组密码都满足低资源设备的要求,比如PRESENT [1]、the KATAN and KTANTANfamilies [2]、LBLOCK [3]、LED [4]、PRINCE [5]和theSimon and the Speck families [6]。
I-PRESENT [7]算法是一种代换——置换网络型对合的轻量级分组密码,是对PRESENT 算法的改进。
I-PRESENT 的主要优点是使用了对合函数,使加密电路和解密电路完全相同,以及密码的混淆扩散速度更迅速。
这对于需要实现2种电路的密码环境来说是一个比较大的优势。
biclique 攻击方法首次是由Khovratovich 等[8]在收稿日期:2017-05-18;修回日期:2017-08-10基金项目:国家自然科学基金资助项目(No.61502008, No.61572001);安徽省自然科学基金资助项目(No.1508085QF132)Foundation Items: The National Natural Science Foundation of China (No.61502008, No.61572001), The Natural Science Founda-tion of Anhui Province (No.1508085QF132)doi:10.11959/j.issn.1000-436x.2017214·14· 通 信 学 报 第38卷2012年提出的。
相对来说,biclique 攻击是比较新的技术。
biclique 结构就是一个完全二部图,即起始状态的每一条边都和结束状态的一条边相连。
另外,biclique 结构中的每条路径都是通过唯一的密钥相连。
如果路径中没有共享活动的非线性加密单元,敌手通过biclique 结构就可以高效地测试一系列的候选密钥。
最终会取得降低密码攻击开销的效果,或者是可以增加中间相遇攻击以及其他攻击的轮数。
biclique 攻击方法对分组密码的密钥恢复有着比较强的适用能力。
2011年,Bogdanov 等[9]对AES 进行了biclique 攻击,由于这是第一次针对单密钥模型分组密码的全轮攻击,他们的工作受到了广泛的关注。
自该攻击方法结合密码实现之后,基于biclique 结构的密钥恢复攻击被广泛应用到一系列的分组密码中,包括3D 密码[10]、SQUARE [11]、HIGHT [12]、Piccolo [13]、ARIA [14]、LBlock [15]、TWINE [16]、IDEA [17]、KLEIN [18], mCrypton [19],所有的这些工作,都是第一次对全轮轻量级分组密码的攻击。
2 I-PRESENT 算法I-PRESENT 算法结构如图1所示。
2.1 加密加密函数可以看作输入64位的明文以及32个64位的轮密钥的集合。
轮密钥由主密钥通过密钥扩展算法生成。
加密过程简单地说就是一个明文依次经过15次轮函数迭代、对合操作以及15轮的逆轮函数迭代之后输出密文。
2.2 解密解密过程与加密过程完全相同,除了解密轮密钥是加密轮密钥的逆序值,即解密轮密钥k [0]等于加密轮密钥k [31]…解密轮密钥k [31]等于加密轮密钥k [0]。
加解密算法流程如下。
I-PRESENT_Encrypt(state,subkey){ for(i =0;i <15;i ++){Mixkey(state,subkey[i ]); STrans(state); PTrans(state); }Invo(state);for(i =15;i <30;i ++){ PTransInv(state); STransInv(state);Mixkey(state,subkey[i ]); } } 2.3 轮函数轮密钥加层(Mixkey),得到的具体结果是轮密钥的值异或上当前状态的值。
S 盒层(STrans ,STransInv),输入状态分成16个4位的半字,然后对每个半字使用一个4×4的S 盒操作。
S 盒是非线性的函数,每个4位的输入对应得到一个4位的输出。
I-PRESENT 用到的S 盒的映射如表1所示,表1中均为十六进制图1 I-PRESENT 算法结构第11期 崔杰等:对轻量级分组密码I-PRESENT-80和I-PRESENT-128的biclique 攻击 ·15·值。
s 指S 盒操作用在加密阶段,其逆运算1s −用在解密阶段。
例如,s 的4位半字输入x =1,则s 的输出(1)6s =。
如果x =6是1s −的输入,则输出1(6)1s −=。
表1I-PRESENT 的S 盒映射关系x ()s x 1()s x − ˆ()s x 0 D 8 E 1 6 2 A 2 1 F 2 3 F 9 C 4 4 4 4 5 8 7 8 6 B 1 F 7 5 E D 8 0 5 5 9 3 C 9 A A A 1 B C 6 B C 9 B 3 D E 0 7 E 7 D 0 F236置换层(PTrans, PTransInv),PTrans 函数表示的是64位输入状态的置换操作。
设表达式6362063620,X x x x Y y y y ==""分别表示PTrans 函数的输入和输出状态,则00y x =,161y x =,…,4762y x =,6363y x =,PTrans 的置换规则如表2所示。
2.4 对合(Invo)对合操作中64位的输入状态被划分成了16个4位的半字,然后对每个半字进行一个44×的S 盒操作,用ˆs表示。
ˆs 映射关系参考表1。
2.5 密钥扩展I-PRESENT 支持2种长度的密钥,分别为80位和128位。
2.5.1 80位密钥设当前主密钥为79780k k k "。
第i 轮密钥63320797816iK k k k κκκ==""。
轮密钥的生成以及主密钥状态更新过程如下。
1) 当前主密钥循环左移53位,表示为79781026252827[][]k k k k k k k k =""。
表2 I-PRESENT 置换层位置变换关系x y x y x y x y 0 0 16 4 32 8 48 121 16 17 20 33 24 49 282 32 18 36 34 40 50 443 48 19 52 35 56 51 604 1 205 36 9 52 135 17 21 21 37 25 53 296 33 22 37 38 41 54 457 49 23 53 39 57 55 618 2 24 6 40 10 56 149 18 25 22 41 26 57 3010 34 26 38 42 42 58 4611 50 27 54 43 58 59 6212 3 28 7 44 11 60 1513 19 29 23 45 27 61 3114 35 30 39 46 43 62 4715 51 31 55 47 59 63 632) 当前主密钥中最左侧的4位做()s x 变换,表示为7978777679787776[][]k k k k s k k k k =,函数()s x 的映射关系如表1所示。
