线面垂直习题精选

. . . . .

线面垂直的证明中的找线技巧

◆

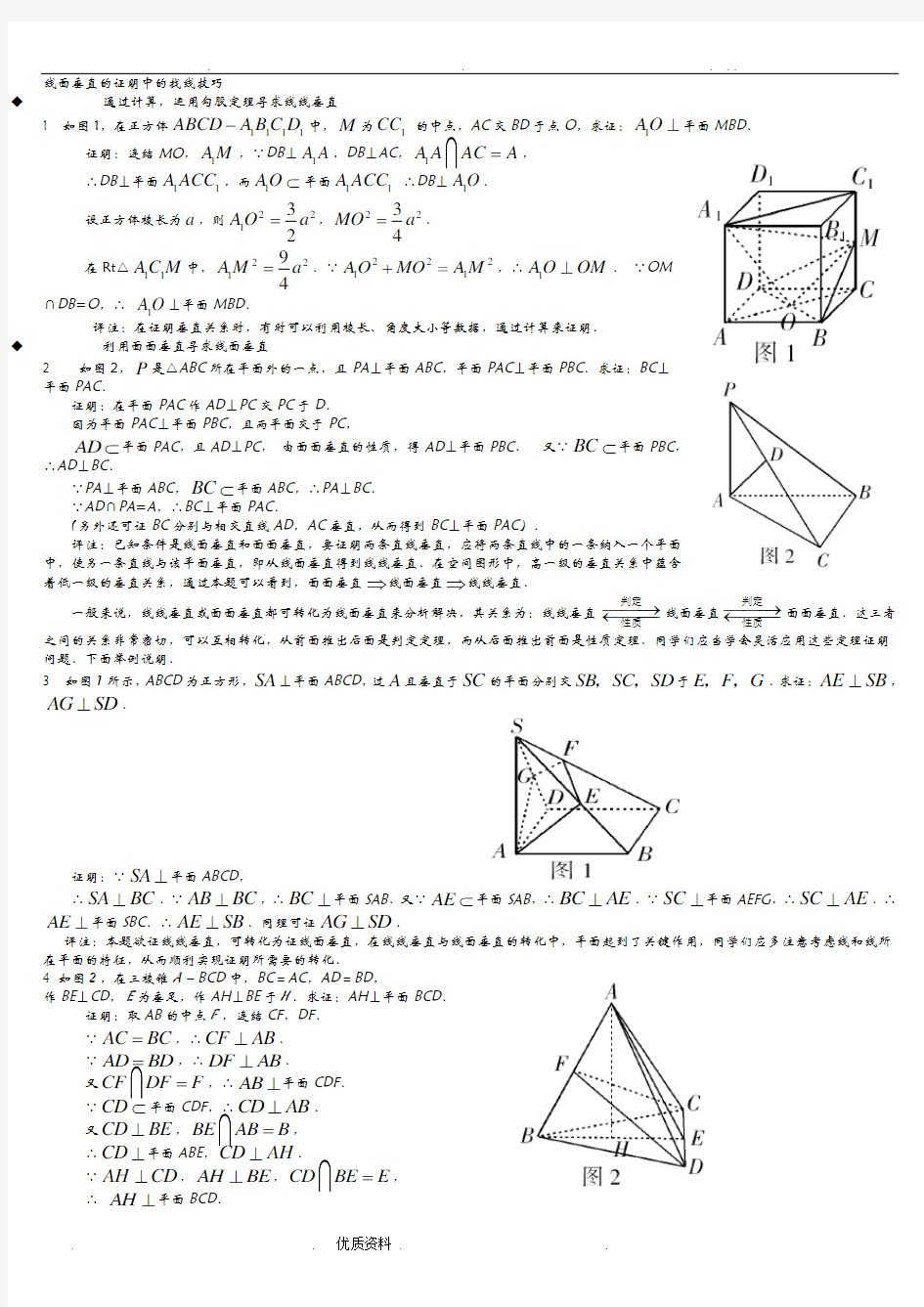
通过计算，运用勾股定理寻求线线垂直 1 如图1，在正方体

1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1A O ⊥平面MBD ．

证明：连结MO ，1A M

，∵DB ⊥

1A A ，DB ⊥AC ，1A A

AC A =，

∴DB ⊥平面

11A ACC ，而1

AO ?平面11A ACC ∴DB ⊥1A O ．设正方体棱长为a ，则22132A O a =，2

234MO a =．

在Rt △11A C M 中，2

A M a =．∵22211A O MO A M +=，∴1AO OM ⊥． ∵OM

∩DB =O ，∴ 1A O ⊥平面MBD ．

评注：在证明垂直关系时，有时可以利用棱长、角度大小等数据，通过计算来证明． ◆

利用面面垂直寻求线面垂直

2 如图2，P 是△ABC 所在平面外的一点，且PA ⊥平面ABC ，平面PAC ⊥平面PBC ．求证：BC ⊥平面PAC ．

证明：在平面PAC 作AD ⊥PC 交PC 于D ．

因为平面PAC ⊥平面PBC ，且两平面交于PC ，

AD ?平面PAC ，且AD ⊥PC ，由面面垂直的性质，得AD ⊥平面PBC ．又∵BC ?平面PBC ，

∴AD ⊥BC ．

∵PA ⊥平面ABC ，BC ?平面ABC ，∴PA ⊥BC ． ∵AD ∩PA =A ，∴BC ⊥平面PAC ．

（另外还可证BC 分别与相交直线AD ，AC 垂直，从而得到BC ⊥平面PAC ）．

评注：已知条件是线面垂直和面面垂直，要证明两条直线垂直，应将两条直线中的一条纳入一个平面中，使另一条直线与该平面垂直，即从线面垂直得到线线垂直．在空间图形中，高一级的垂直关系中蕴含着低一级的垂直关系，通过本题可以看到，面面垂直?线面垂直?线线垂直．

一般来说，线线垂直或面面垂直都可转化为线面垂直来分析解决，其关系为：线线垂直???→←???判定性质

线面垂直???→←???

判定性质

面面垂直．这三者之间的关系非常密切，可以互相转化，从前面推出后面是判定定理，而从后面推出前面是性质定理．同学们应当学会灵活应用这些定理证明

问题．下面举例说明．

3 如图１所示，ABCD 为正方形，SA ⊥平面ABCD ，过

A 且垂直于SC 的平面分别交S

B S

C S

D ，，于

G ，，．

求证：AE SB ⊥，AG SD ⊥．

证明：∵SA ⊥平面ABCD ，

∴SA BC ⊥．∵AB BC ⊥，∴BC ⊥平面SAB ．又∵AE ?平面SAB ，∴BC AE ⊥．∵SC ⊥平面AEFG ，∴SC AE ⊥．∴AE ⊥平面SBC ．∴AE SB ⊥．同理可证AG SD ⊥．

评注：本题欲证线线垂直，可转化为证线面垂直，在线线垂直与线面垂直的转化中，平面起到了关键作用，同学们应多注意考虑线和线所在平面的特征，从而顺利实现证明所需要的转化．

4 如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，

作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ．求证：AH ⊥平面BCD ．证明：取AB 的中点Ｆ，连结CF ，DF ．

∵

AC BC =，∴CF AB ⊥． ∵AD BD =，∴DF AB ⊥．

又CF DF F =，∴AB ⊥平面CDF ． ∵CD ?平面CDF ，∴CD AB ⊥．又CD BE ⊥，BE AB B =， ∴CD ⊥平面ABE ，CD AH ⊥．

∵AH CD ⊥，AH BE ⊥，CD BE E =，

∴ AH ⊥平面BCD ．

评注：本题在运用判定定理证明线面垂直时，将问题转化为证明线线垂直；而证明线线垂直时，又转化为证明线面垂直．如此反复，直到证得结论．

5 如图３，AB是圆Ｏ的直径，Ｃ是圆周上一点，PA⊥平面ABC．若AE⊥PC，Ｅ为垂足，Ｆ是PB上任意一点，求证：平面AEF⊥平面PBC．

证明：∵AB是圆Ｏ的直径，∴AC BC

⊥．

∵PA⊥平面ABC，BC?平面ABC，

∴PA BC

⊥．∴BC⊥平面APC．

∵BC?平面PBC，

∴平面APC⊥平面PBC．

∵AE⊥PC，平面APC∩平面PBC＝PC，

∴AE⊥平面PBC．

∵AE?平面AEF，∴平面AEF⊥平面PBC．

评注：证明两个平面垂直时，一般可先从现有的直线中寻找平面的垂线，即证线面垂直，而证线面垂直则需从已知条件出发寻找线线垂直的关系．

6. 空间四边形ABCD中，若AB⊥CD，BC⊥AD，求证：AC⊥BD

B O

证明：过A作AO⊥平面BCD于O

AB CD CD BO

⊥∴⊥

，

同理BC⊥DO ∴O为△ABC的垂心于是BD CO BD AC

⊥?⊥

7. 证明：在正方体ABCD－A1B1C1D1中，A1C⊥平面BC1D

D1C1

A1B1

D C

A B

证明：连结AC

BD AC

⊥

AC为A1C在平面AC上的射影

∴⊥

⊥?

?⊥

BD A C

A C BC A C BC D

1111

同理可证

平面

8. 如图，PA⊥平面ABCD，ABCD是矩形，M、N分别是AB、PC的中点，求证：MN AB

⊥

D C

A B

. 证：取PD中点E，则EN DC

//1

E N

D C

A B

?EN AM //

∴AE MN //

又平面平面平面 CD AD PA AC CD PAD AE PAD ⊥⊥????⊥???

? ?⊥?

???⊥CD AE CD AB AE MN MN AB

////

9如图在ΔABC 中， AD ⊥BC ， ED=2AE ，过E 作FG ∥BC ，且将ΔAFG 沿FG 折起，使∠A'ED=60°，求证:A'E ⊥平面A'BC

分析：

弄清折叠前后，图形中各元素之间的数量关系和位置关系。

解： ∵FG ∥BC ，AD ⊥BC

∴A'E ⊥FG ∴A'E ⊥BC

设A'E=a ，则ED=2a

由余弦定理得：

A'D 2=A'E 2+ED 2-2?A'E ?EDcos60° =3a 2

∴ED 2=A'D 2+A'E 2 ∴A'D ⊥A'E

∴A'E ⊥平面A'BC

10如图, 在空间四边形SABC 中, SA ⊥平面ABC , ∠ABC = 90?, AN ⊥SB 于N , AM ⊥SC 于M 。求证: ①AN ⊥BC; ②SC ⊥平面ANM 分析:

①要证AN ⊥BC , 转证, BC ⊥平面SAB 。

②要证SC ⊥平面ANM , 转证, SC 垂直于平面ANM 的两条相交直线, 即证SC ⊥AM , SC ⊥AN 。要证SC ⊥AN , 转证AN ⊥平面SBC , 就可以了。证明:

①∵SA ⊥平面ABC ∴SA ⊥BC 又∵BC ⊥AB , 且AB SA = A ∴BC ⊥平面SAB ∵AN 平面SAB ∴AN ⊥BC ②∵AN ⊥BC , AN ⊥SB , 且SB BC = B ∴AN ⊥平面SBC ∵SCC 平面SBC ∴AN ⊥SC 又∵AM ⊥SC , 且AM AN = A ∴SC ⊥平面ANM

11已知如图，P ?平面ABC ，PA=PB=PC ，∠APB=∠APC=60°，∠BPC=90 °求证：平面ABC ⊥平面PBC

分析：要证明面面垂直，只要在其呈平面找一条线，然后证明直线与另一平面垂直即可。显然BC 中点D ，证明AD 垂直平PBC 即可证明：取BC 中点D 连结AD 、PD ∵PA=PB ；∠APB=60° ∴ΔPAB 为正三角形

同理ΔPAC 为正三角形设PA=a 在RT ΔBPC 中，PB=PC=a

BC=

2a ∴PD=

a 在ΔABC 中 AD=

2BD AB -

A B C

F E

G A'

a∵AD2+PD2=

a=a2=AP2∴ΔAPD为直角三角形即AD⊥DP又∵AD⊥BC

∴AD⊥平面PBC

∴平面ABC⊥平面PBC

13 以AB为直径的圆在平面

α，α

⊥

PA于A，C在圆上，连PB、PC过A作AE⊥PB于E，AF⊥PC于F，试判断图中还有几组线面垂直。

A B

解：

⊥

PAC

面

为直径

⊥

?PB

PBC

AF面

面AEF ［例1］如图9—39，过S引三条长度相等但不共面的线段SA、SB、SC，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面ABC⊥平面BSC．

【证明】∵SB=SA=SC，∠ASB=∠ASC=60°∴AB=SA=AC取BC的中点O，连AO、SO，

则AO⊥BC，SO⊥BC，

∴∠AOS为二面角的平面角，设SA=SB=SC=a，又∠BSC=90°，∴BC=

2a，SO=2

a，

AO2=AC2－OC2=a2－2

a2=2

a2，∴SA2=AO2+OS2，∴∠AOS=90°，从而平面ABC⊥平面BSC．

【评述】要证两平面垂直，证其二面角的平面角为直角．这也是证两平面垂直的常用方法．［例2］如图9—40，在三棱锥S—ABC中，SA⊥平面ABC，平面SAB⊥平面SBC．

图9—40

（1）求证：AB⊥BC；（2）若设二面角S—BC—A为45°，SA=BC，求二面角A—SC—B的大小．

（1）【证明】作AH⊥SB于H，∵平面SAB⊥平面SBC．平面SAB∩平面SBC=SB，∴AH⊥平面SBC，

又SA⊥平面ABC，∴SA⊥BC，而SA在平面SBC上的射影为SB，∴BC⊥SB，又SA∩SB=S，

∴BC⊥平面SAB．∴BC⊥AB．

（2）【解】∵SA⊥平面ABC，∴平面SAB⊥平面ABC，又平面SAB⊥平面SBC，∴∠SBA为二面角S—BC—A的平面角，

∴∠SBA=45°．设SA=AB=BC=a，

作AE⊥SC于E，连EH，则EH⊥SC，∴∠AEH为二面角A—SC—B的平面角，而AH=2

a，AC=

2a，SC=3a，AE=3

a ∴sin∠AEH=2

，二面角A—SC—B为60°．

【注】三垂线法是作二面角的平面角的常用方法．

［例3］如图9—41，PA⊥平面ABCD，四边形ABCD是矩形，PA=AD=a，M、N分别是AB、PC的中点．

（1）求平面PCD 与平面ABCD 所成的二面角的大小；（2）求证：平面MND ⊥平面PCD （1）【解】PA ⊥平面ABCD ，CD ⊥AD ，

∴PD ⊥CD ，故∠PDA 为平面ABCD 与平面PCD 所成二面角的平面角，在Rt △PAD 中，PA=AD ， ∴∠PDA=45°

（2）【证明】取PD 中点E ，连结EN ，EA ，则EN 2

1CD AM ，∴四边形ENMA 是平行四边形，∴EA ∥MN ． ∵AE ⊥PD ，AE ⊥CD ，∴AE ⊥平面PCD ，从而MN ⊥平面PCD ，∵MN ?平面MND ，∴平面MND ⊥平面PCD ．

【注】证明面面垂直通常是先证明线面垂直，本题中要证MN ⊥平面PCD 较困难，转化为证明AE ⊥平面PCD 就较简单了．另外，在本题中，当AB 的长度变化时，可求异面直线PC 与AD 所成角的围．

［例4］如图9—42，正方体ABCD —A 1B 1C 1D 1中，E 、F 、M 、N 分别是A 1B 1、BC 、C 1D 1、B 1C 1的中点．

图9—42

（1）求证：平面MNF ⊥平面ENF ．（2）求二面角M —EF —N 的平面角的正切值．

（1）【证明】∵M 、N 、E 是中点，∴M C NC N B EB 1111===∴?=∠=∠45MNC ENB 11

∴?=∠90MNE 即MN ⊥EN ，又NF ⊥平面A 1C 1，11C A MN 平面?∴MN ⊥NF ，从而MN ⊥平面ENF ．∵MN ?平面MNF ，

∴平面MNF ⊥平面ENF ．

（2）【解】过N 作NH ⊥EF 于H ，连结MH ．∵MN ⊥平面ENF ，NH 为MH 在平面ENF 的射影，

∴由三垂线定理得MH ⊥EF ，∴∠MHN 是二面角M —EF —N 的平面角．在Rt △MNH 中，求得MN=

2a ，NH=

33a ，

∴tan ∠MHN=26=

MN ，即二面角M —EF —N 的平面角的正切值为26

．

［例5］在长方体ABCD —A 1B 1C 1D 1中，底面ABCD 是边长为

2的正方形，侧棱长为3，E 、F 分别是AB 1、CB 1的中点，求证：平面

D 1EF ⊥平面AB 1C ．

【证明】如图9—43，∵E 、F 分别是AB 1、CB 1的中点，

图9—43∴EF ∥AC ．∵AB 1=CB 1，O 为AC 的中点．∴B 1O ⊥AC ．故B 1O ⊥EF ．在Rt △B 1BO 中，∵BB 1=

3，BO=1．

∴∠BB 1O=30°，从而∠OB 1D 1=60°，又B 1D 1=2，B 1O 1=2

OB 1=1（O 1为BO 与EF 的交点）

∴△D 1B 1O 1是直角三角形，即B 1O ⊥D 1O 1，∴B 1O ⊥平面D 1EF ．又B 1O ?平面AB 1C ，∴平面D 1EF ⊥平面AB 1C ．

1．棱长都是2的直平行六面体ABCD —A 1B 1C 1D 1中，∠BAD=60°，则对角线A 1C 与侧面DCC 1D 1所成角的正弦值为_____．

【解】过A 1作A 1G ⊥C 1D 1于G ，由于该平行六面体是直平行六面体，∴A 1G ⊥平面D 1C ，连结CG ，∠A 1CG 即为A 1C 与侧面DCC 1D 1所成的角．

∵A 1G= A 1 D 1 ·sin ∠A 1 D 1 G=2sin60°=2·

=3而

AC=

???-+120cos 222BC AB BC AB =

32)21

(2222222=-???-+∴A 1C=

41242

21=+=+AC A A ， ∴sin ∠A 1CG=

4311=C A G A ．【答案】43

2．E 、F 分别是正方形ABCD 的边AB 和CD 的中点，EF 、BD 相交于O ，以EF 为棱将正方形折成直二面角，则∠BOD=_____．【解析】设正方形的边长为2a ．

则DO 2=a 2+a 2=2a 2OB 2=a 2+a 2=2a 2DB 2=DF 2+FB 2=a 2+4a 2+a 2=6a 2∴cos ∠DOB=21

222622222-

=??-+a

a a a a ∴∠DOB=120°

3．如图9—44，已知斜三棱柱ABC —A 1B 1C 1的各棱长均为2，侧棱与底面成3π

的角，侧面ABB 1A 1垂直于底面，

图9—44

（1）证明：B 1C ⊥C 1A ．（2）求四棱锥B —ACC 1A 1的体积．

（1）【证明】过B 1作B 1O ⊥AB 于O ，∵面ABB 1A 1⊥底面ABC ，面AB ABC A ABB 11=面 ∴B 1O ⊥面ABC ，∴∠B 1BA 是侧棱与底

面所成角，∴∠B 1BA=3π

，又各棱长均为2，∴O 为AB 的中点，连CO ，则CO ⊥AB ，而OB 1∩CO=O ，

∴AB ⊥平面B 1OC ，又B 1C ?平面OB 1C ，∴B 1C ⊥AB ，连BC 1，∵BCC 1B 1为边长为2的菱形，∴B 1C ⊥BC 1，而AB ∩BC 1=B ， ∴B 1C ⊥面ABC 1∵A 1C ?面ABC 1∴B 1C ⊥AC 1

（2）【解】在Rt △BB 1O 中，BB 1=2，BO=1，B 1O=

3，V 柱=Sh=

43·4·3=3，∴111C B A B V -=31

V 柱=1，

C C AA B V 11-=V

柱

－111C B A B V

-=3－1=2

4．如图9—45，四棱锥P —ABCD 的底面是边长为a 的正方形，PA ⊥底面ABCD ，E 为AB 的中点，且PA=AB ．

图9—45

（1）求证：平面PCE ⊥平面PCD ；（2）求点A 到平面PCE 的距离．（1）【证明】PA ⊥平面ABCD ，AD 是PD 在底面上的射影，

又∵四边形ABCD 为矩形，∴CD ⊥AD ，∴CD ⊥PD ，∵AD ∩PD=D ∴CD ⊥面PAD ，∴∠PDA 为二面角P —CD —B 的平面角， ∵PA=PB=AD ，PA ⊥AD ∴∠PDA=45°，取Rt △PAD 斜边PD 的中点F ，则AF ⊥PD ，∵AF ?面PAD ∴CD ⊥AF ，

又PD ∩CD=D ∴AF ⊥平面PCD ，取PC 的中点G ，连GF 、AG 、EG ，则GF

1CD 又AE

1CD ，

∴GF AE ∴四边形AGEF 为平行四边形∴AF ∥EG ，∴EG ⊥平面PDC 又EG ?平面PEC ， ∴平面PEC ⊥平面PCD ．

（2）【解】由（1）知AF ∥平面PEC ，平面PCD ⊥平面PEC ，过F 作FH ⊥PC 于H ，则FH ⊥平面PEC ∴FH 为F 到平面PEC 的距离，即为A 到平面PEC 的距离．在△PFH 与 △PCD 中，∠P 为公共角，

而∠FHP=∠CDP=90°，∴△PFH ∽△PCD ．∴PC PF

FH =，设AD=2，∴PF=2，PC=32482

2=+=+CD PD ， ∴FH=36

22=

?∴A 到平面PEC 的距离为

．

5．已知直四棱柱ABCD —A 1B 1C 1D 1的底面是菱形，对角线AC=2，BD=2

3，E 、F 分别为棱CC 1、BB 1上的点，且满足EC=BC=2FB ．

图9—46

（1）求证：平面AEF ⊥平面A 1ACC 1；（2）求异面直线EF 、A 1C 1所成角的余弦值．

（1）【证明】∵菱形对角线AC=2，BD=23∴BC=2，EC=2，FB=1，取AE 中点M ，连结MF ，设BD 与AC 交于点O ，MO

FB ?

平面AEF ⊥平面ACC 1A 1

（2）在AA 1上取点N ，使AN=2，连结NE ，则NE

A 1C 1

故∠NEF 为异面直线A 1C 1与EF 所成的角，连结NF ，在直角梯形NABF 中易求得NF=

5，同理求得EF=5．

在△ENF 中，cos ∠NEF=555

22543=

??-+，即EF 与A 1C 1所成角的余弦值为55．

【解题指导】在证明两平面垂直时，一般方法是先从现有的直线中寻找平面的垂线；若没有这样的直线，则可通过作辅助线来解决，而作辅助线则应有理论根据并且要有利于证明，不能随意添加．在有平面垂直时，一般要用性质定理，在一个平面作交线的垂线，使之转化为线面垂直．解决这类问题的关键是熟练掌握“线线垂直”“线面垂直”“面面垂直”间的转化条件和转化应用．

【拓展练习】一、备选题

1．如图，AB 是圆O 的直径，C 是圆周上一点，PA ⊥平面ABC ．（1）求证：平面PAC ⊥平面PBC ；

（2）若D 也是圆周上一点，且与C 分居直径AB 的两侧，试写出图中所有互相垂直的各对平面．

（1）【证明】∵C 是AB 为直径的圆O 的圆周上一点，AB 是圆O 的直径 ∴BC ⊥AC ；

又PA ⊥平面ABC ，BC ?平面ABC ， ∴BC ⊥PA ，从而BC ⊥平面PAC ． ∵BC ?平面PBC ，

∴平面PAC ⊥平面PBC ．

（2）【解】平面PAC ⊥平面ABCD ；平面PAC ⊥平面PBC ；平面PAD ⊥平面PBD ；平面PAB ⊥平面ABCD ；平面PAD ⊥平面ABCD ．

2．ABC —A ′B ′C ′是正三棱柱，底面边长为a ，D ，E 分别是BB ′，CC ′上的一点，BD ＝21

a ，EC ＝a ．

（1）求证：平面ADE ⊥平面ACC ′A ′；（2）求截面△ADE 的面积．

（1）【证明】分别取A ′C ′、AC 的中点M 、N ，连结MN ，