高二数学定积分

高二数学定积分
目标认知
学习目标:
1.了解“以直代曲”、“以不变代变”的思想方法,了解定积分的实际背景,了解定积分的基本思
想,了解定积分的概念、几何意义。
2.直观了解微积分基本定理的含义,并能用定理计算简单的定积分。
3.应用定积分解决平面图形的面积、变速直线运动的路程和变力作功等问题,在解决问题的过程中体
验定积分的价值.
教学重点:
正确计算定积分,利用定积分求面积。
教学难点:
定积分的概念,将实际问题化归为定积分问题。
知识要点梳理
知识点一:定积分的概念
如果函数在区间上连续,用分点将区间分为n个小区间,在每个小区间上任取一点(i=1,2,3…,n),作和式
,当时,上述和式无限趋近于某个常数,这个常数叫
做在区间上的定积分.记作.即=,这里,与分别叫做积分下限与积分上限,区间叫做积分区间,函数叫做被积函数,叫做积分变量,叫做被积式.
说明:
(1)定积分的值是一个常数,可正、可负、可为零;
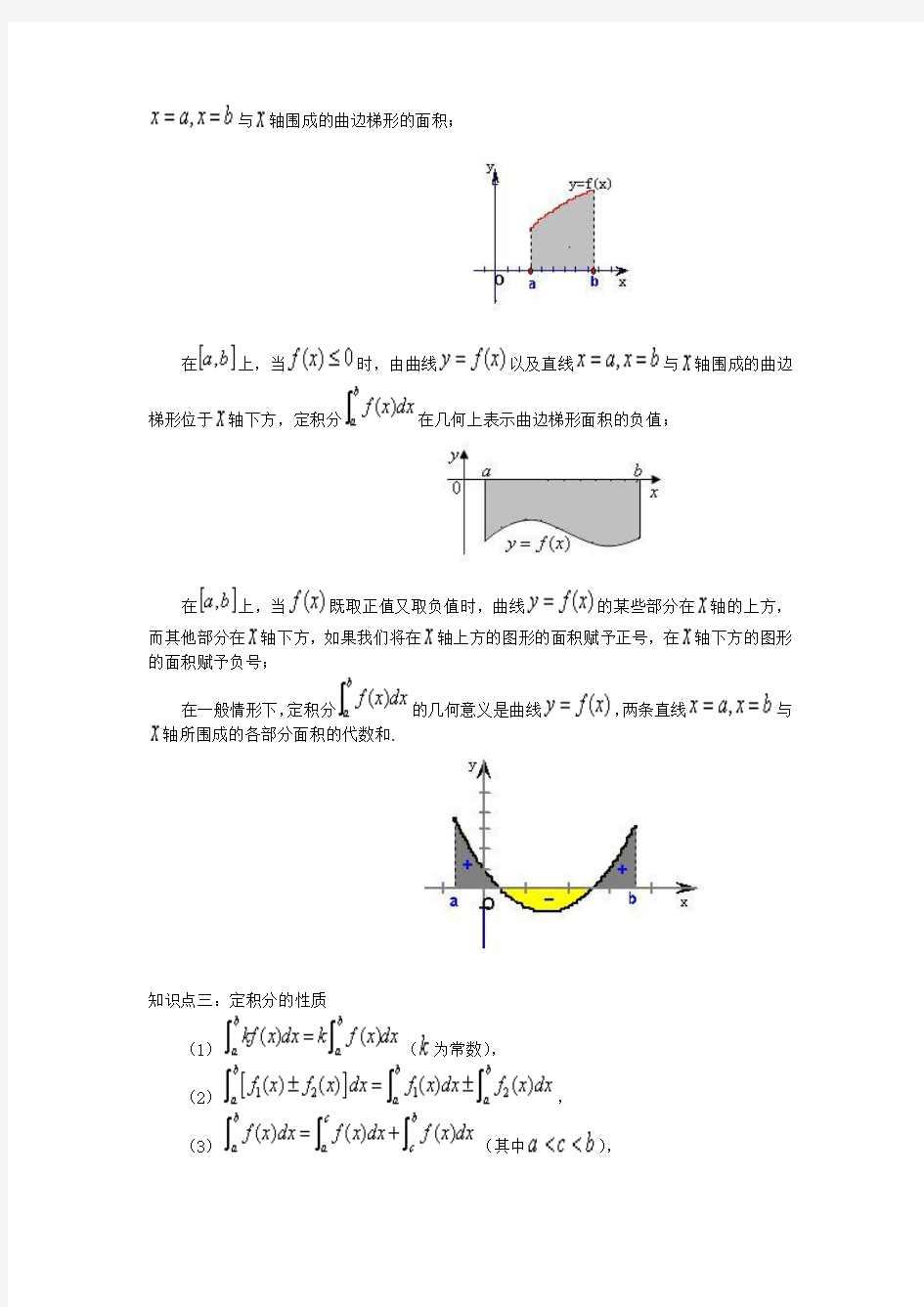
(2)用定义求定积分的四个基本步骤:①分割;②近似代替;③求和;④取极限. 知识点二:定积分的几何意义
设函数在区间上连续.
在上,当时,定积分在几何上表示由曲线以及直线
与轴围成的曲边梯形的面积;
在上,当时,由曲线以及直线与轴围成的曲边梯形位于轴下方,定积分在几何上表示曲边梯形面积的负值;
在上,当既取正值又取负值时,曲线的某些部分在轴的上方,
而其他部分在轴下方,如果我们将在轴上方的图形的面积赋予正号,在轴下方的图形的面积赋予负号;
在一般情形下,定积分的几何意义是曲线,两条直线与轴所围成的各部分面积的代数和.
知识点三:定积分的性质
(1)(为常数),
(2),
(3)(其中),
(4)利用函数的奇偶性求积分:
若函数在区间上是奇函数,则;
若函数在区间上是偶函数,则.
知识点四:微积分基本定理
如果在上连续,且,则,这个结论
叫做微积分基本定理(或牛顿-莱布尼兹公式)。其中叫做的一个原函数.由于
也是的原函数,其中c为常数.
一般地,原函数在上的改变量简记作.因此,微积分基本定
理可以写成形式:.
注意:求定积分主要是要找到被积函数的原函数,也就是说,要找到一个函数,它的导函数等于被积函数.由此,求导运算与求原函数运算互为逆运算.
知识点五:应用定积分求曲边梯形的面积
1. 如图,由三条直线,,轴(即直线)及一条曲线
()围成的曲边梯形的面积:;
2. 如图,由三条直线,,轴(即直线)及一条曲线
()围成的曲边梯形的面积:
;
高二数学定积分
高二数学定积分 目标认知 学习目标: 1.了解“以直代曲”、“以不变代变”的思想方法,了解定积分的实际背景,了解定积分的基本思 想,了解定积分的概念、几何意义。 2.直观了解微积分基本定理的含义,并能用定理计算简单的定积分。 3.应用定积分解决平面图形的面积、变速直线运动的路程和变力作功等问题,在解决问题的过程中体 验定积分的价值. 教学重点: 正确计算定积分,利用定积分求面积。 教学难点: 定积分的概念,将实际问题化归为定积分问题。 知识要点梳理 知识点一:定积分的概念 如果函数在区间上连续,用分点将区间分为n个小区间,在每个小区间上任取一点(i=1,2,3…,n),作和式 ,当时,上述和式无限趋近于某个常数,这个常数叫 做在区间上的定积分.记作.即=,这里,与分别叫做积分下限与积分上限,区间叫做积分区间,函数叫做被积函数,叫做积分变量,叫做被积式. 说明: (1)定积分的值是一个常数,可正、可负、可为零; (2)用定义求定积分的四个基本步骤:①分割;②近似代替;③求和;④取极限. 知识点二:定积分的几何意义 设函数在区间上连续. 在上,当时,定积分在几何上表示由曲线以及直线
与轴围成的曲边梯形的面积; 在上,当时,由曲线以及直线与轴围成的曲边梯形位于轴下方,定积分在几何上表示曲边梯形面积的负值; 在上,当既取正值又取负值时,曲线的某些部分在轴的上方, 而其他部分在轴下方,如果我们将在轴上方的图形的面积赋予正号,在轴下方的图形的面积赋予负号; 在一般情形下,定积分的几何意义是曲线,两条直线与轴所围成的各部分面积的代数和. 知识点三:定积分的性质 (1)(为常数), (2), (3)(其中),
定积分的方法总结
定积分的方法总结 定积分是新课标的新增内容,其中定积分的计算是重点考查的考点之一,下面例析定积分计算的几种常用方法. 一、定义法 例1、求 s i n b a x d x ? , (b a <) 解:因为函数s i n x 在],[b a 上连续,所以函数sin x 在],[b a 上可积,采用特殊的 方法作积分和.取h = n a b -,将],[b a 等分成n 个小区间, 分点坐标依次为 ?=+<<+<+高等数学定积分应用
第六章 定积分的应用 本章将应用第五章学过的定积分理论来分析和解决一些几何、物理中的问题,其目的不仅在于建立这些几何、物理的公式,而且更重要的还在于介绍运用元素法将一个量表达为定积分的分析方法。 一、教学目标与基本要求: 使学生掌握定积分计算基本技巧;使学生用所学的定积分的微元法(元素法)去解决各种领域中的一些实际问题; 掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、变力作功、引力、压力及函数的平均值等) 二、本章各节教学内容及学时分配: 第一节 定积分的元素法 1课时 第二节 定积分在几何学上的应用 3课时 第三节 定积分在物理学上的应用 2课时 三、本章教学内容的重点难点: 找出未知量的元素(微元)的方法。用元素法建立这些几何、物理的公式解决实际问题。运用元素法将一个量表达为定积分的分析方法 6.1定积分的微小元素法 一、内容要点 1、复习曲边梯形的面积计算方法,定积分的定义 面积A ?∑=?==→b a n i i i dx x f x f )()(lim 1 ξλ 面积元素dA =dx x f )( 2、计算面积的元素法步骤: (1)画出图形; (2)将这个图形分割成n 个部分,这n 个部分的近似于矩形或者扇形; (3)计算出面积元素; (4)在面积元素前面添加积分号,确定上、下限。 二、教学要求与注意点 掌握用元素法解决一个实际问题所需要的条件。用元素法解决一个实际问题的步骤。 三、作业35 6.2定积分在几何中的应用
一、内容要点 1、在直角坐标系下计算平面图形的面积 方法一 面积元素dA =dx x x )]()([12??-,面积 A = x x x b a d )]()([12??-? 第一步:在D 边界方程中解出y 的两个表达式)(1x y ?=,)(2x y ?=. 第二步:在剩下的边界方程中找出x 的两个常数值a x =,b x =;不够时由)(1x ?)(2x ?=解出, b x a ≤≤,)()(21x y x ??≤≤,面积S =x x x b a d )]()([12??-? 方法二 面积元素dA =dy y y )]()([12??-,面积 A = y y y d c d )]()([12??-? 第一步:在D 边界方程中解出x 的两个表达式)(1y x ?=,)(2y x ?=. 第二步:在剩下的边界方程中找出y 的两个常数值c y =,d y =;不够时由)(1y ?)(2y ?=解出, d y c ≤≤,)()(21y x y ??≤≤,面积S =y y y d c d )]()([12??-? 例1 求22-=x y ,12+=x y 围成的面积 解?????+=-=1 222x y x y ,1222+=-x x ,1-=x ,3=x 。当31<<-x 时1222+<-x x ,于是 面积?--=+-=--+=3 1 313223 210)331 ()]2()12[(x x x dx x x 例2 计算4,22-==x y x y 围成的面积 解 由25.0y x =,4+=y x 得,4,2=-=y y ,当42<<-y 时 45.02+ 数学选修2-2知识点总结 一、导数 1.函数的平均变化率为 =??=??x f x y x x f x x f x x x f x f ?-?+=--)()()()(111212 注1:其中x ?是自变量的改变量,可正,可负,可零。 注2:函数的平均变化率可以看作是物体运动的平均速度。 2、导函数的概念:函数)(x f y =在0x x =处的瞬时变化率是x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数,记作)(0'x f 或 0|'x x y =,即)(0'x f =x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000. 3.函数的平均变化率的几何意义是割线的斜率; 函数的导数的几何意义是切线的斜率。 4导数的背景(1)切线的斜率;(2)瞬时速度; 6、常见的导数和定积分运算公式:若() g x均可导(可积),则有: f x,() 用导数求函数单调区间的步骤: ①求函数f(x)的导数'() f x ②令'() f x>0,解不等式,得x的范围就是递增区间. ③令'() f x<0,解不等式,得x的范围,就是递减区间; [注]:求单调区间之前一定要先看原函数的定义域。 7.求可导函数f(x)的极值的步骤: (1)确定函数的定义域。 (2) 求函数f(x)的导数'() f x (3)求方程'() f x=0的根 (4) 用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格,检查/() f x在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如 常 用 积 分 公 式 (一)含有ax b +的积分(0a ≠) 1.d x ax b +? =1 ln ax b C a ++ 2.()d ax b x μ+?=11 ()(1) ax b C a μμ++++(1μ≠-) 3.d x x ax b +? =21 (ln )ax b b ax b C a +-++ 4.2d x x ax b +? =22311()2()ln 2ax b b ax b b ax b C a ?? +-++++???? 5.d () x x ax b +?=1ln ax b C b x +-+ 6.2 d () x x ax b +?=21ln a ax b C bx b x +-++ 7.2d ()x x ax b +? =21(ln )b ax b C a ax b ++++ 8.22 d ()x x ax b +?=2 31(2ln )b ax b b ax b C a ax b +-+-++ 9.2 d ()x x ax b +? = 211ln ()ax b C b ax b b x +-++ 的积分 10.x C + 11.x ?=2 2(3215ax b C a -+ 12.x x ?=2223 2 (15128105a x abx b C a -+ 13.x =22 (23ax b C a - 14.2x =2223 2(34815a x abx b C a -+ 15 . =(0) (0) C b C b ?+>< 16 . 2a b - 17 .x =b +18 .x =2a x -+ (三)含有22x a ±的积分 19.22d x x a +?=1arctan x C a a + 20.22d ()n x x a +?=2221222123d 2(1)()2(1)()n n x n x n a x a n a x a ---+-+-+? 21.22 d x x a -? =1ln 2x a C a x a -++ (四)含有2(0)ax b a +>的积分 22.2d x ax b +? =(0) (0) C b C b ?+>+< 23.2 d x x ax b +? =2 1ln 2ax b C a ++ 24.22d x x ax b +?=2d x b x a a ax b -+? 25.2d ()x x ax b +?=2 2 1ln 2x C b ax b ++ 26.22d ()x x ax b +? =21d a x bx b ax b --+? 定积分的性质与计算方法 摘要: 定积分是微积分学中的一个重要组成部分,其计算方法和技巧非常 丰富。本文主要给出定积分的定义及讨论定积分的性质和计算方法,并通过一些很有代表性的例题说明了其计算方法在简化定积分计算中的强大功能。 关键词:定积分 性质 计算方法 定积分的定义 设函数f(x) 在区间[a,b]上连续,将区间[a,b]分成n 个子区间[x 0,x 1], (x 1,x 2], (x 2,x 3], …, (x n-1,x n ],其中x 0=a ,x n =b 。可知各区间的长度依次是:△x 1=x 1-x 0, △x 2=x 2-x 1, …, △x n =x n -x n-1。在每个子区间(x i-1,x i ]中任取一点i ξ(1,2,...,n ),作和式1()n i i f x ι=ξ?∑。设λ=max{△x 1, △x 2, …, △x n }(即λ是 最大的区间长度),则当λ→0时,该和式无限接近于某个常数,这个常数叫做函数f(x) 在区间[a,b]的定积分,记为: ()b a f x dx ?。 其中:a 叫做积分下限,b 叫做积分上限,区间[a, b]叫做积分区间,函数f(x)叫做被积函数,x 叫做积分变量,f(x)dx 叫做被积表达式,∫ 叫做积分号。 对于定积分,有这样一个重要问题:函数()f x 在[a,b]上满足怎样的条件, ()f x 在[a,b]上一定可积?下面给出两个充分条件: 定理1: 设()f x 在区间[a,b]上连续,则()f x 在[a,b]上可积。 定理2: 设()f x 在区间[a,b]上有界,且只有有限个间断点,则 ()f x 在[a,b]上可积。 例:利用定义计算定积分1 20x dx ?. 解:因为被积函数2()f x x =在积分区间[0,1]上连续,而连续函数是可积的,所以积分与区间[0,1]的分法及点i ξ的取法无关。因此,为了 便于计算,不妨把区间[0,1]分成n 等份,分点为i i x n = ,1,2,,1i n =?-;这样, 高中数学-定积分的概念测试 1.定积分??0 1 1d x 的值等于 ( ) A .0 B .1 C.1 2 D .2 答案 B 2.已知??1 3 f (x )d x =56,则 ( ) A.??1 2 f (x )d x =28 B.??2 3f (x )d x =28 C.??1 22f (x )d x =56 D.??12f (x )d x +??2 3 f (x )d x =56 答案 D 3.如图所示,??a b f 1(x )d x =M ,??a b f 2(x )d x =N ,则阴影部分的面积为 ( ) A .M +N B .M C .N D .M -N 答案 D 4.不用计算,根据图形,用不等号连接下列各式 ( ) (1)??01 x d x ________??0 1x 2d x (图1); (2)??01x d x ________??1 2 x d x (图2); (3)??024-x 2d x ________??0 2 2d x (图3). 答案 (1)> (2)< (3)< 1.定积分可以表示图形的面积 从几何上看,如果在区间[a ,b ]上,函数f (x )连续且恒有f (x )≥0,那么定积分??a b f (x )d x 就表示由直线x =a ,x =b (a ≠b ),y =0和曲线y =f (x )所围成的曲边梯形的面积,这就是定积分??a b f (x )d x 的几何意义. 2.定积分表示图形面积的代数和 被积函数是正的,定积分的值也为正,如果被积函数是负的,函数曲线在x 轴之下,定积分的值就是带负号的曲边梯形的面积.当被积函数在积分区间上有正有负时,定积分就是x 轴之上的正的面积与x 轴之下的负的面积的代数和. 3.此外,定积分还有更多的实际意义,比如在物理学中,可以用定积分表示功、路程、压力、体积等. 4.定积分是一个数值(极限值),它的值仅仅取决于被积函数与积分的上、下限,而与积分变量用什么字母表示无关,即??a b f (x )d x =??a b f (u )d u =??a b f (t )d t =…(称为积分形式的不变性),另外定积分??a b f (x )d x 与积分区间[a ,b ]息息相关,不同的积分区间,所得的值也不同,例如??01(x 2+1)d x 与??0 3(x 2 +1)d x 的值就不同. 选修2-21.5.3定积分的概念 一、选择题 1.定积分??1 3(-3)d x 等于( ) A .-6 B .6 C .-3 D .3 [答案] A [解析] 由积分的几何意义可知??1 3(-3)d x 表示由x =1,x =3,y =0及y =-3所围成的矩形面积的相反数,故??1 3(-3)d x =-6. 2.定积分??a b f (x )d x 的大小( ) A .与f (x )和积分区间[a ,b ]有关,与ξi 的取法无关 B .与f (x )有关,与区间[a ,b ]以及ξi 的取法无关 C .与f (x )以及ξi 的取法有关,与区间[a ,b ]无关 D .与f (x )、区间[a ,b ]和ξi 的取法都有关 [答案] A [解析] 由定积分定义及求曲边梯形面积的四个步骤知A 正确. 3.下列说法成立的个数是( ) ①??a b f (x )d x =∑i =1 n f (ξi )b -a n ②?? a b f (x )d x 等于当n 趋近于+∞时,f (ξi )·b -a n 无限趋近的值 ③??a b f (x )d x 等于当n 无限趋近于+∞时,∑i =1 n f (ξi )b -a n 无限趋近的常 数 ④??a b f (x )d x 可以是一个函数式子 A .1 B .2 C .3 D .4 [答案] A [解析] 由??a b f (x )d x 的定义及求法知仅③正确,其余不正确.故应 选A. 4.已知??1 3f (x )d x =56,则( ) A.??1 2f (x )d x =28 B.??2 3f (x )d x =28 C.??1 22f (x )d x =56 D.??1 2f (x )d x +??2 3f (x )d x =56 [答案] D [解析] 由y =f (x ),x =1,x =3及y =0围成的曲边梯形可分拆成两个:由y =f (x ),x =1,x =2及y =0围成的曲边梯形知由y =f (x ),x =2,x =3及y =0围成的曲边梯形. ∴??1 3f (x )d x =??1 2f (x )d x +??2 3f (x )d x 即??1 2f (x )d x +??2 3f (x )d x =56. 故应选D. 5.已知??a b f (x )d x =6,则??a b 6f (x )d x 等于( ) A .6 B .6(b -a ) 1. 求 dx e x ?-2ln 01。5.解:设t e x =-1,即)1ln(2+=t x ,有dt t t dx 122+= 当0=x 时,0=t ;当2ln =x 时,1=t 。 dt t dt t t dx e x )111(21211021 0222ln 0???+-=+=- 22)1arctan 1(2)arctan (210π- =-=-=x t . 2. 求由两条曲线2x y =与2y x =围成的平面区域的面积。 .解:两条曲线的交点是)0,0(与)1,1(,则此区域的面积 31)3132()(1 0323210=-=-=?x x dx x x S 3. 求反常积分 ?+∞-+222x x dx 。 解:dx x x x x dx x x dx b b b b )2111(lim 3 12lim 222222+--=-+=-+???+∞→+∞→+∞ 4ln 3 1)4ln 21(ln lim 31)21ln(lim 312=++-=+-=+∞→+∞→b b x x b b b 5、 4. 设???≤<≤≤-+=20,02,13)(32x x x x x f ,求?-22)(dx x f 解:原式=??-+0 22 0)()(dx x f dx x f ---------5分 =14 ----------5分 6. 求由曲线32,2+==x y x y 所围成的区域绕x 轴旋转而得的旋转体体积。 解:两曲线交点为(-1,1)(3,9)-------2分 面积?--+=3122)32(dx x x S π ---------5分 =17 256 7. 计算定积分2 2π π -? 8. 设()f x 在区间[,]a b 上连续,且()1b a f x dx =?,求() b a f a b x dx +-?。 答案:解:令u a b x =+-,则当x a =时,u b =;当x b =时,u a =,且d x d u =-, 故 ()b a f a b x dx +-?=()a b f u du -? =()1b a f x dx =?。 第二节 定积分计算公式和性质 一、变上限函数 设函数在区间上连续,并且设x 为上的任一点, 于是, 在区间 上的定积分为 这里x 既是积分上限,又是积分变量,由于定积分与积分变量无关,故可将此改为 如果上限x 在区 间上任意变动,则对 于每一个取定的x 值,定积分有一个确定值与之对应,所以定积分在 上定义了一个以x 为自变量的函数,我们把 称为函数 在区间 上 变上限函数 记为 从几何上看,也很显然。因为X 是上一个动点, 从而以线段 为底的曲边梯形的面积,必然随着底数 端点的变化而变化,所以阴影部分的面积是端点x 的函数(见图5-10) 图 5-10 定积分计算公式 利用定义计算定积分的值是十分麻烦的,有时甚至无法计算。因此,必须寻求计算定积分的简便方法。 我们知道:如果物体以速度作直线运动,那么在时间区间上所经过的路程s 为 另一方面,如果物体经过的路程s 是时间t 的函数,那么物体 从t=a 到t=b 所经过的路程应该是(见图5-11) 即 由导数的物理意义可知:即 是 一个原函数,因此,为了求出定积分,应先求出被积函数 的原函数 , 再求 在区间 上的增量 即可。 如果抛开上面物理意义,便可得出计算定积分的一般 方法: 设函数在闭区间上连续, 是 的一个原函数, 即 ,则 图 5-11 这个公式叫做牛顿-莱布尼兹公式。 为了使用方便,将公式写成 牛顿-莱布尼兹公式通常也叫做微积分基本公式。它表示一个函数定积分等于这个函数的原函数在积分上、下限处函数值之差。它揭示了定积分和不定积分的内在联系,提供了计算定积分有效而简便的方法,从而使定积分得到了广泛的应用。 例1 计算 因为是的一个原函数所以 例 2 求曲线 和直线x=0、x= 及y=0所围成图形面积A(5-12) 解 这个图形的面积为 二、定积分的性质 设 、 在相应区间上连续,利用前面学过的知识,可以 得到定积分以下几个简单性质: 图 5-12 高中数学-定积分的概念练习 一、基础达标 1.下列命题不正确的是 ( ) A .若f (x )是连续的奇函数,则 B .若f (x )是连续的偶函数,则 C .若f (x )在[a ,b ]上连续且恒正,则??a b f (x )d x >0 D .若f (x )在[a ,b ]上连续且??a b f (x )d x >0,则f (x )在[a ,b ]上恒正 答案 D 2.直线x =1,x =-1,y =0及曲线y =x 3 +sin x 围成的平面图形的面积可表示为 ( ) A. B .2??0 1(x 3 +sin x )d x C . D.??0 1(x 3 +sin x )d x 答案 B 3.已知??a b [f (x )+g (x )]d x =18,??a b g (x )d x =10,则??a b f (x )d x 等于 ( ) A .8 B .10 C .18 D .不确定 答案 A 4.已知定积分??06f (x )d x =8,则f (x )为奇函数,则??-6 6f (x )d x = ( ) A .0 B .16 C .12 D .8 答案 A 5.根据定积分的几何意义,用积分表示如图所示各图的阴影部分的面积, S =________. 答案 ??a b [f 1(x )-f 2(x )]d x (两图积分式相同) 6.由定积分的几何意义,定积分sin x d x 表示________. 答案 由直线x =0,x =π 2,y =0和曲线y =sin x 围成的曲边梯形的面积 7.根据定积分的几何意义推出下列积分的值. (1) x d x ;(2) cos x d x . 解 若x ∈[a ,b ]时,f (x )≥0,则??a b f (x )d x 的几何意义是表示由直线x =a ,x=b y =0和曲线y =f (x )围成的平面图形的面积;若x ∈[a ,b ]时,f (x )≤0,则??a b f (x )d x 表示所围成的图形面积的负值. (1)如图①,x d x =-A 1+A 1=0. (2)如图②,cos x d x =A 1-A 2+A 3=0. 二、能力提升 8.和式 1n +1+1n +2+ (12) ,当n →∞时的极限值用定积分式子可表示为 ( ) A.??011x d x B.? ?0 1 1 x +1d x 高等数学之不定积分的计算方法总结不定积分中有关有理函数、三角函数有理式、简单无理函数的求法,是考研中重点考察的内容,也是考研中的难点。不定积分是计算定积分和求解一阶线性微分方程的基础,所以拿握不定积分的计算方法很重要。不定积分考查的函数特点是三角函数、简单无理函数、有理函数综合考查,考查方法是换元积分法、分部积分法的综合应用。不定积分的求法的理解和应用要多做习题,尤其是综合性的习题,才能真正掌握知识点,并应用于考研。 不定积分的计算方法主要有以下三种: (1)第一换元积分法,即不定积分的凑微分求积分法; (2)第二换元积分法 (3)分部积分法常见的几种典型类型的换元法: 樂,Q? o 金J犷- / .乍治阳必厶二如皿盒.「宀丄" 名% =a仏 找.』x二a沁沁r 年”十I '九久二严詈严妬5inx八ic5兄厶 整 I—炉 叶严 山二启虫? 常见的几种典型类型的换元法 题型一:利用第一换元积分法求不定积分 分析: 1-3 ? - IK )-忑.旦r x 二)祝成);网><可久切 二2氐化如(長)寸 a 花不直押、朱 J 、 解: 2少弋協“尤十C__ -辿迪牆H JS m 弟 R Eff 洱 ->1和弟r 直 - —7朮呻' g 丄 U P A J 齐—系卩£.§计 一 H a8~t ' J 乂 u D y " ?朮? p o r t v 卩 J (r 4 5*〉J" 卩?对渎 t-k )+c p T + T d ? g T + c m -辿」 当积分j/O心(X)不好计算容易计算时[使用分部私jf(A-)Jg(.v)二f(x)g(x)- J g(x)df(x).常见能使用分部积分法的类型: ⑴卩"“dx J x n srn xdx J尢"cos皿等,方法是把。',sin-t, cosx 稽是降低X的次数 是化夫In 尢9 arcsine arctanx. 例11: J (1 + 6-r )arctanAz/.r :解:arctan f xdx等,方法是把疋; Jx" arcsm11xdx §1.5.3定积分的概念 教学目标: 1.通过求曲边梯形的面积和汽车行驶的路程,了解定积分的背景; 2.借助于几何直观定积分的基本思想,了解定积分的概念,能用定积分定义求简单的定积分; 3.理解掌握定积分的几何意义. 教学重点:定积分的概念、用定义求简单的定积分、定积分的几何意义. 教学难点:定积分的概念、定积分的几何意义. 教学过程: 一.创设情景 复习: 1. 2二.新课讲授 1.定积分的概念 一般地,设函数()f x 在区间[ ,]a b 上连续,用分点 0121i i n a x x x x x x b -=<<<<<<<=L L 将区间[,]a b 等分成n 个小区间,每个小区间长度为x D (b a x n -D =),在每个小区间 []1,i i x x -上任取一点()1,2, ,i i n x =L ,作和式: 11 ()()n n n i i i i b a S f x f n x x ==-=D =邋 如果x D 无限接近于0(亦即n ? )时,上述和式n S 无限趋近于常数S ,那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。记为:()b a S f x dx =ò, 其中 - ò积分号,b -积分上限,a -积分下限,()f x -被积函数,x -积分变量, [,]a b -积分区间,( )f x dx -被积式。 说明:(1)定积分() b a f x dx ò是一个常数,即n S 无限趋近的常数S (n ? 时)记 为 ()b a f x dx ò,而不是n S . (2)用定义求定积分的一般方法是:①分割:n 等分区间[],a b ;②近似代替:取 点[]1,i i i x x x -?;③求和:1 ()n i i b a f n x =-?;④取极限:() 1 ()l i m n b i n a i b a f x dx f n x =-=?ò (3)曲边图形面积:()b a S f x dx = ò;变速运动路程2 1 ()t t S v t dt =ò ;变力做功 ()b a W F r dr = ò 2.定积分的几何意义 第五章 定积分 内容:定积分的概念和性质、微积分基本公式、换元积分法、分部积分法、广义积分。 要求:理解定积分的概念和性质。掌握牛顿-莱布尼兹公式、定积分的换元法和分部积分法,理解变上限的定积分作为其上限的函数及其求导定理,理解广义积分的概念和计算方法。 重点:定积分的概念和性质;微积分基本公式;换元积分法、分部积分法。 难点:定积分的概念;变上限积分函数及其导数;换元积分法、分部积分法。 §1.定积分的概念 一、实例分析 1.曲边梯形的面积 设函数)(x f y =∈C[a , b ], 且)(x f y =>0. 由曲线0,,),(====y b x a x x f y 围成的图形称为曲边梯形. 如何定义曲边梯形的面积 (1) 矩形面积=底高. (2) 预备一张细长条的纸, 其面积底高. (3) 预备一张呈曲边梯形状的纸, 将其撕成许多细长条. (4) 启示: 将曲边梯形分割为许多细长条, 分割得越细, 误差越小. 第i 个细长条面积)],,[()(11---=?∈??≈?i i i i i i i i i x x x x x x f S ξξ 曲边梯形面积: ∑=?≈ n i i i x f S 1 )(ξ 定积分概念示意图.ppt 定义: ),,2,1,max {()(lim 1 n i x x f S i n i i i Λ=?=?=∑=→λξλ y =f (x ) x =a x =b y =f (x ) a=x 0 x 1 x i-1 x i x n =b 抛开上述过程的几何意义,将其数学过程定义为定积分. 二、定积分的定义 1. 定义 设)(x f y =在[a , b ]有定义, 且有界. (1) 分割: 用分点b x x x a n =<<<=Λ10把[a , b ]分割成n 个小区间: } ,,2,1,max{,,,2,1],,[11n i x x x x n i x x i i i i i i ΛΛ=?=-=?=--λ记 (2) 取点: 在每个小区间],[1i i x x -上任取一点i , 做乘积: i i x f ?)(ξ. (3) 求和: ∑=?n i i i x f 1 )(ξ (4) 取极限: ∑=→?n i i i x f 1 )(lim ξλ 若极限存在, 则其为)(x f 在[a , b ]上的定积分, 记作: ? b a dx x f )(. 即: ∑? =→?=n i i i b a x f dx x f 1 )(lim )(ξλ [a , b ]: 积分区间;a :积分下限;b :积分上限; ∑=?n i i i x f 1 )(ξ积分和式. 问题: 定积分是极限值, 在求极限的过程中, 谁是常量, 谁是变量 注: (1) ∑ =?n i i i x f 1 )(ξ与区间的分割法x i 和取点法 i 有关; 而 ? b a dx x f )(与x i 和 i 无 关. (2) ? b a dx x f )(与a 、b 、f 有关,与x 无关,即: [][]???? ===b a b a b a b a d f du u f dt t f dx x f )()()()( 2.定积分存在定理 定理 若)(x f 在[a , b ]上有界且只有有限个间断点,则)(x f 在[a , b ]上可积. 推论 若)(x f 在[a , b ]上连续,则)(x f 在[a , b ]上可积. 例1. 求 ?1 xdx 第 1 页 定 积 分 一、定积分的概念 1、曲边梯形的面积 分割→近似取代→求和→求极限 说明:(1)常用的求和公式 )12)(1(61...3212222++=++++n n n n 223333)1(4 1...321+=++++n n n (2)在定积分理论中,这种分割是任意的,只要保证每个区间的长度都向于0.在这里“等分”与“任意分割”等价的。 2、定积分的概念 一般地,设函数()f x 在区间[,]a b 上连续,用分点 0121i i n a x x x x x x b -=<<<<<<<= 将区间[,]a b 等分成n 个小区间,每个小区间长度为x ?(b a x n -?= ),在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ= ,作和式:11()()n n n i i i i b a S f x f n ξξ==-=?=∑∑ 如果x ?无限接近于0(亦即n →+∞)时,上述和式n S 无限趋近于常数S ,那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。记为:()b a S f x dx =? 其中()f x 成为被积函数,x 叫做积分变量,[,]a b 为积分区间,b 积分上限,a 积分下限。 3、定积分的几何意义 从几何上看,如果在区间[]b a ,上函数 )(x f 连续且恒有0)(≥x f 。那么定积分?b a dx x f )(表示由直线a x = b x =,)(b a <,0=y 和曲线)(x f y =所围成的曲边梯形 的面积。 4.性质1 、 ??=b a b a dx x f k dx x kf )()( (其中k 是不为0的常数) (定积分的线性性质) 性质2、 1212[()()]()()b b b a a a f x f x dx f x dx f x dx ±=±??? (定积分的线性性质) 性质3 、 ()()()() b c b a a c f x dx f x dx f x dx a c b =+< 数学选修2-2导数及其应用(定积分)知识点必记 1.函数的平均变化率是什么? 答:平均变化率为 =??=??x f x y x x f x x f x x x f x f ?-?+=--)()()()(111212 注1:其中x ?是自变量的改变量,可正,可负,可零。 注2:函数的平均变化率可以看作是物体运动的平均速度。 2、导函数的概念是什么? 答:函数)(x f y =在0x x =处的瞬时变化率是x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数,记作)(0'x f 或0|'x x y =,即)(0'x f =x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000. 3.平均变化率和导数的几何意义是什么? 答:函数的平均变化率的几何意义是割线的斜率;函数的导数的几何意义是切线的斜率。 4导数的背景是什么? 答:(1)切线的斜率;(2)瞬时速度;(3)边际成本。 5、常见的函数导数和积分公式有哪些? 函数 导函数 不定积分 y c = 'y =0 ———————— n y x =()*n N ∈ 1'n y nx -= 1 1n n x x dx n +=+? x y a =()0,1a a >≠ 'ln x y a a = ln x x a a dx a =? x y e = 'x y e = x x e dx e =? log a y x =()0,1,0a a x >≠> 1 'ln y x a = ———————— ln y x = 1'y x = 1 ln dx x x =? sin y x = 'cos y x = cos sin xdx x =? cos y x = 'sin y x =- sin cos xdx x =-? 6、常见的导数和定积分运算公式有哪些? 学习目标 1.理解曲边梯形面积的求解思想, 掌握其方法步骤; 2.了解定积分的定义、性质及函数在上可积的充分条件; 3.明确定积分的几何意义和物理意义; 4.无限细分和无穷累积的思维方法. 学习过程 一、课前准备 (预习教材,找出疑惑之处) 复习1:函数23 (sin) y x =的导数是 复习2:若函数2 log(23) a y x x =--的增区间是(,1) -∞-,则a的取值范围是 二、新课导学 学习探究 探究任务一:曲边梯形的面积 问题:下图的阴影部分类似于一个梯形,但有一边是曲线() y f x =的一段,我们把直线x a =,x b =() a b ≠,0 y=和曲线() y f x =所围成的图形称为曲边梯形. 如何计算这个曲边梯形的面积呢? 研究特例:对于1 x=,0 y=,2 y x =围成的图形(曲边三角形)的面积如何来求呢? 新知:1.用流程图表示求曲边三角形面积的过程 分割?近似代替?求和?取极限 2.定积分的定义: 1 ()lim() n b i a n i b a f x dx f n ξ →∞ = - =∑ ? 3.定积分的几何意义: 4.定积分的性质: (1)()()b b a a kf x dx k f x dx =?? (k 为常数) (2)1212[()()]()() b b b a a a f x f x dx f x dx f x dx ±=±??? (3)()()() b c b a a c f x dx f x dx f x dx =+???(其中a c b <<) 试试:求直线0,2,0x x y ===与曲线2y x =所围成的曲边梯形的面积. 反思:在求曲边梯形面积过程中,你认为最让你感到困难的是什么?(如何分割,求和逼近是两大难点) 典型例题 例1 利用定积分的定义,计算1 30x dx ?的值 变式:计算2 30x dx ?的值,并从几何上解释这个值表示什么? 定积分计算的总结 闫佳丽 摘 要:本文主要考虑定积分的计算,对一些常用的方法和技巧进行了归纳和总结.在定积分的计算中,常用的计算方法有四种:(1)定义法、(2)牛顿—莱布尼茨公式、(3)定积分的分部积分法、(4)定积分的换元积分法. 关键词:定义、牛顿—莱布尼茨公式、分部积分、换元. 1前言 17世纪后期,出现了一个崭新的数学分支—数学分析.它在数学领域中占据着主导地位.这种新数学思想的特点是非常成功地运用了无限过程的运算即极限运算.而其中的微分和积分这两个过程,则构成系统微积分的核心.并奠定了全部分析学的基础.而定积分是微积分学中的一个重要组成部分. 2正文 那么,究竟什么是定积分呢?我们给定积分下一个定义:设函数()f x 在[],a b 有定义,任给[],a b 一个分法T 和一组{}k ξξ=,有积分和 1 (,)()n k k k T f x σξξ==?∑,若当()0l T →时,积分和(,)T σξ存在有限极限,设 ()0 ()0 1 lim (,)lim ()n k k l T l T k T f x I σξξ→→==?=∑,且数I 与分法T 无关,也与k ξ在[] 1,k k x x -的取法无关,即{}0,0,:(),k T l T εδδξξ?>?>? §1.5.3定积分的概念 【学情分析】: 前面两节(曲边梯形的面积和汽车行驶的路程)课程的学习为定积分的概念的引入做好了铺垫。学生对定积分的思想方法已有了一定的了解。 【教学目标】: (1)知识与技能:定积分的概念、几何意义及性质 (2)过程与方法:在定积分概念形成的过程中,培养学生的抽象概括能力和探索提升能力。 (3)情感态度与价值观:让学生了解定积分概念形成的背景,培养学生探究数学的兴趣. 【教学重点】: 理解定积分的概念及其几何意义,定积分的性质 【教学难点】: 对定积分概念形成过程的理解 练习与测试: (基础题) 1.函数()f x 在[] ,a b 上的定积分是积分和的极限,即 ()b a f x dx =? _________________ . 答案:0 1 lim ()n i i i f x λξ→=?∑ 2.定积分的值只与______及_______有关,而与_________的记法无关 . 答案:被积函数,积分区间,积分变量; 3.定积分的几何意义是_______________________ . 答案:介于曲线()y f x =,x 轴 ,直线,x a x b ==之间各部分面积的代数和; 4.据定积分的几何意义()a b <,则________;b a dx =?________.b a xdx =? 答案:b a - , 22 2 b a - (提高题) 5.将和式极限表示成定积分 (1). 2 1 lim (12)n n n →∞+++L 解:122 011 11 1 lim (12)lim lim n n n n n i i i n i xdx n n n n →∞→∞→∞==+++===∑∑?L (2). 2 1lim ()n i i i f x λξ→=?∑,其中{}0121,[,],n i i i i x a x x x b x x Max x ξλ-=<<<<=∈=L 解:2 20 1 lim ()()()n b b i i a a i f x g x dx f x dx λξ→=?==∑?? 6. 利用定义计算定积分 2 1 1 .dx x ? 解:在[1,2]中插入分点2 1 ,,,n q q q -L ,典型小区间为1[,]i i q q -,(1,2,,i n =L ) 小区间的长度11(1)i i i i x q q q q --?=-=-,取1 i i q ξ-=,(1,2,,i n =L ) 1 11 111 1()(1)n n n i i i i i i i i i f x x q q q ξξ--===?=?=-∑ ∑∑1 (1)(1)n i q n q ==-=-∑ 取2n q =即12n q =, 11 ()(21),n n i i i f x n ξ=?=-∑ 1 121 lim (21)lim ln 2,1 x x x x x x →+∞ →+∞--==Q 1lim (21)ln 2,n n n →∞ ∴-= 12 1 0111 lim lim (21)ln 2.n n i n i i dx x n x λξ→→∞==?=-=∑? () i g ξi x ?i ξ高中数学定积分知识点
高等数学积分公式大全
定积分的性质与计算方法
高中数学-定积分的概念测试
(完整版)高二数学定积分的概念测试题
高等数学定积分复习题
定积分计算公式和性质
高中数学-定积分的概念练习
[全]高等数学之不定积分的计算方法总结[下载全]
高中数学定积分的概念教案新人教版选修2-2
高等数学第五章定积分总结
人教版高中数学定积分概念及其运算
高中数学人教版选修2-2导数及其应用(定积分)知识点总结
(新课程)高中数学《1.5定积分的概念》导学案 新人教A版选修22
定积分计算的总结论文
人教版高中数学定积分的概念第3课时
