第2章数学建模方法论.doc

第2章 数学建模方法论

不同的实际问题，建模的模式千差万别，各不相同，这与问题的性质、建模的目的以及建模者自身的数学基础知识和专长有关。然而，还是有一些普遍适用的思想方法与思维方式，本章将从方法论的角度介绍建模时通常会采用的一般方法。

2.1 概 论

数学建模首先在学习形式上与别的数学课程有很大的差别，它不像许多人想像的那样单靠一个人、一支笔、一张纸就可以解决问题，它经常表现为一种集体性质的活动，三、五个人甚至于更多的人组成一个团队，通过个人的智慧和与别人的合作来解决一个甚至一类实际问题。因此，培养良好的交流、合作和表达能力非常重要。对于个人来讲，在整个建模过程中，应该自始至终坚持做好记录，独自思考时随时记下好的想法。再次，在进行集体讨论时借助于文字进行交流，并记下讨论要点；工作中记下方法、计划、进程和结果，以辅助我们高效地进行交流以及作为论文写作的原始资料。另外，思考时养成记录的习惯可以帮助我们整理思路，并经常可以激发我们产生出新的、创造性的思想。

其次，数学建模在思考方法和思维方式上与学习其他数学课程有很大差别。这表现在数学建模过程是一种创新过程，它需要相当高程度的观察力、想像力以及一些灵感和顿悟。数学建模讲求创新，而我们同学最缺乏的就是创新思维，创新思维是创新能力的核心与灵魂，创新思维主要有类比思维、归纳思维、逆向思维、发散思维、猜测思维等等。下面介绍几种常用的思维方法。

2.1.1发散性思维方法

发散性思维是创新思维的重要组成部分，是发明创造的一个有力的武器。遇到问题(特别是难题)时最好不要有一点想法就一条路走下去，应把自己的思路尽量打开，去寻求更佳的方案。这里介绍两种方法：一种是借助于一系列问题来展开思路；另一种是借助于下意识的联想来展开思路。

第一种方法我们称之为提问题法。当你想到什么主意或者面临什么难题时，通过提出一系列问题来导出一些想法或一个好的方案。一些常用的问题如下:

(1)这个问题和什么问题相类似?

(2)假如变动问题的某些条件将会怎样?

(3)将问题分解成若干部分再考虑会怎样?

(4)重新组合又会怎样?

对问题已有初步的想法或解决方案时，为进一步打开思路还可提出以下问题:

(5)我们还可以做些什么工作?

(6)还有没有需要进一步完善的内容?

(7)可否换一种数学工具来解决此问题?

另一种方法我们称之为关键词联想法。即抓住问题或方案的关键词，然后不受任何约束地浮想联翩，并把联想到的内容记在卡片上，再在这些卡片的激发下产生新的想法，进一步想出新的主意。经过这样一个过程后，把积攒的卡片相互搭配，形成解决问题的初步思路与步骤。

例1．A 、B 两个加油站位于同一公路旁，为在公路上行驶的汽车提供同一种汽油，彼此竞争激烈。一天，A 站推出降价销售，以吸引顾客，造成B 站的顾客被拉走。B 站决定也降价销售以拉回顾客。请你站在B 加油站的立场上为其提供决策支持。

不论是A 加油站还是B 加油站，不管他们采用什么手段，其主要目的还是为获得更多的利润。影响利润的主要因素有销售量和价格。对于B 加油站来讲，其决策需要考虑销售量和成本价格，而销售量又取决于销售价格，销售价格的确定需要考虑A 站的销售价格，B 站确定的新的销售价格以及其他加油站的销售价格。这些要素之间的关系如下：

2.1.2 从整体上把握问题的方法

价格 成本价格

利用上面拓展思路的思维方法，我们对问题和问题的解决有了一些初步的认识后，可能还是不知从何处入手解决问题，往往陷于问题的某个局部而不能自拔。这就要求我们必须努力把握住问题的全貌，而把握住问题的全貌的一个非常有效的途径便是研究问题的结构。

层次结构是一种最常见的结构。许多问题都可以分解为若干个子问题，每个子问题又可以进一步分解，如此类推。我们把各个部分用线段连接起来，便构成了一个具有层次结构的网状图。我们还可以在图上进一步分析，并标示出问题的特点和难点部分，这样我们就能对问题的整体框架一目了然。

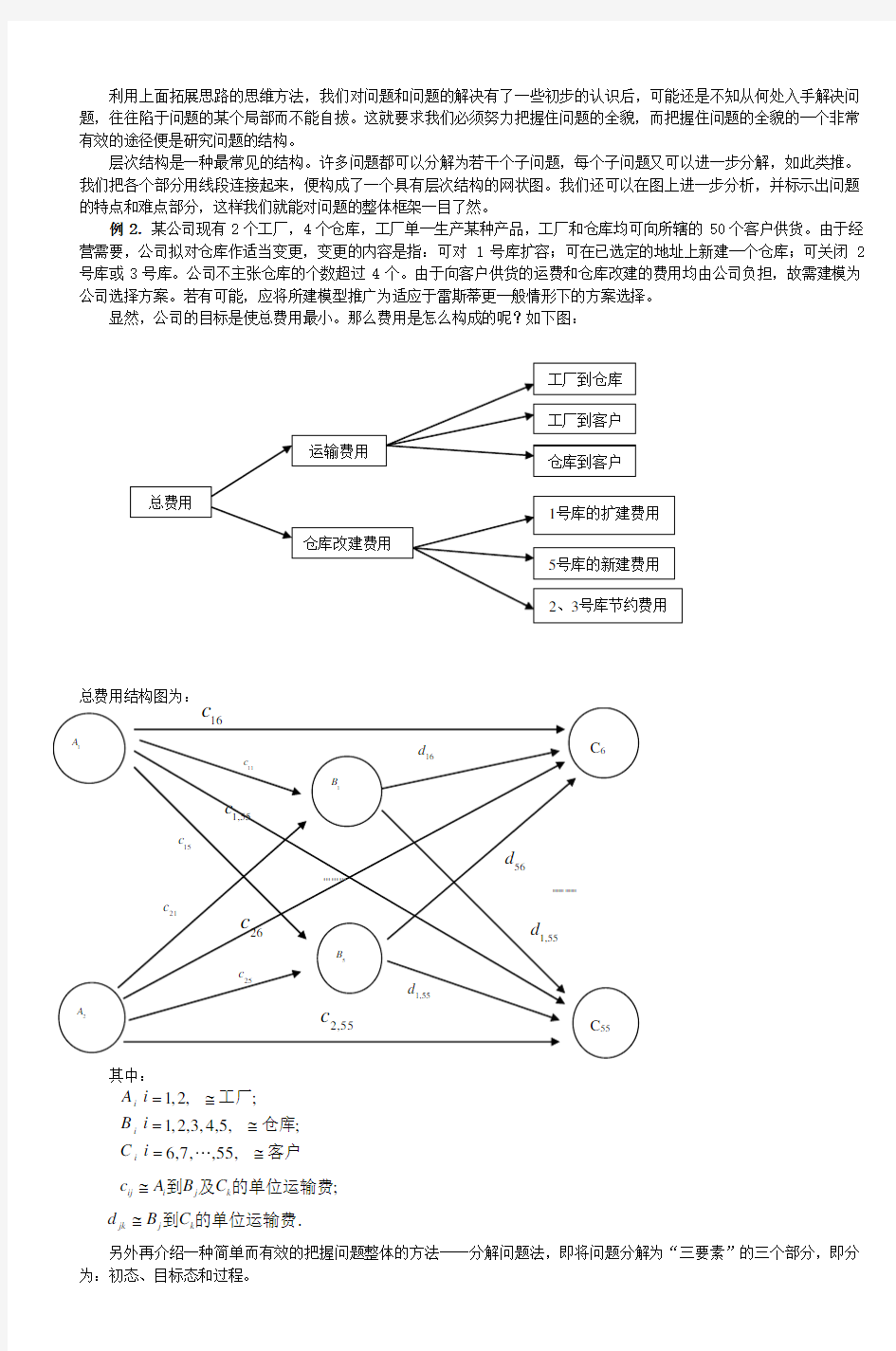
例2．某公司现有2个工厂，4个仓库，工厂单一生产某种产品，工厂和仓库均可向所辖的50个客户供货。由于经营需要，公司拟对仓库作适当变更，变更的内容是指：可对1号库扩容；可在已选定的地址上新建一个仓库；可关闭2号库或3号库。公司不主张仓库的个数超过4个。由于向客户供货的运费和仓库改建的费用均由公司负担，故需建模为公司选择方案。若有可能，应将所建模型推广为适应于雷斯蒂更一般情形下的方案选择。

显然，公司的目标是使总费用最小。那么费用是怎么构成的呢？如下图：

总费用结构图为：

其中：

另外再介绍一种简单而有效的把握问题整体的方法一一分解问题法，即将问题分解为“三要素”的三个部分，即分为：初态、目标态和过程。 1,2, ;

1,2,3,4,5, ; 6,7,,55, i i i A i B i C i =?=?=?L 工厂仓库客户;

ij i j k c A B C ?到及的单位运输费jk j k d B C ?到的单位运输费.

初态：觉察到的现在状态。

目标态：觉察到的希望目标。

过程：能在初态和目标态之间发生作用的行动。

“初态”可以理解为我们目前“有什么”，比如条件、数据等；“目标态”则往往是我们希望达到的、或想要得到什么或希望避免什么等等；“过程”则可以理解为我们要“做什么”。

例3．以例2说明。

初态：现有工厂和仓库以及运输费用和仓库改建费用。

目标态：扩容、新建或关闭。

过程：建立判断的优化管理方案及相应算法。

大家熟知的数学题目模式往往是从“已知”到“求(证)”，所以目前的教学很大程度上是致力于教会学生们在给定条件下“怎样做”以达到目标，换言之，在事先己设定好初态和目标态的情况下，教会你采用何种过程来达到目标。可是我们在解决实际问题时，通常要尽很大的努力才能分析出问题的初态和目标态。

需要避免的是，在清晰地描述出问题的初态和目标态之前，不要急于去形成并运用一个过程，即过早地进入解决问题的阶段。这样做的后果是：由于条件不清、目标不明，好比盲人摸象似的，工作很可能事倍功半。

2.1.3 小组群体思维的方法

前面已经说过，数学建模经常表现为一种集体性质的活动，它经常需要不同部门或不同专长的人们相互合作，各自发挥自己的特长，正如俗话所说“三个臭皮匠顶一个诸葛亮”。在建模活动中，经常会发生这样的事：两个合作者(尤其是青年学生)激烈地争论了很久，双方都不让步；又或者在没有搞清楚对方想法的情况下，盲目地争论否认对方的想法，在争论很久以后才发现双方的论点竟然是完全一致的。为了高效率地合作，提高交流能力，减少无谓的争辩，在建模时有必要制定一些交流、讨论的原则。

首先，良好的合作必须建立在相互平等、相互尊重和充分交流的基础上。要真正做到这一点，就必须注意一些“交流忌语”：

(1)武断的评价。轻易使用“这绝对不行”、“这根本行不通”这类语句，不仅会刺伤同伴的自尊心，往往还会束缚自己思路。

(2)回避责任。遇到问题的第一反应便是“怎么办呢?”，这是只能依靠别人时所使用的语句。而“我想这样做，你看怎么样?”这种自己也承担一部分责任的态度是很必要的。如若不然，对问题的观察和分析、对工作的适应能力就会变得越来越迟钝。

(3)无可奈何。“没办法!”，说这话只是为了回避问题，不仅使自己的能力不能充分发挥出来，而且还会压抑人们对问题的深入观察、思考和实际行动的能力。

(4)对交流失去信心。“很难听懂他说的什么”、“他简直无动于衷!”，这也反映出一种对待问题的消极态度。面对问题应采取积极的态度去分析、去解决。这里应该从说、听两个方面去检查原因：表达者是否清楚地表达了自己的意思?最好把自己的想法写出来，这样使对方有充分的时间去思考并理解你的思想，同时你在书写的时候还能更好地整理你的思路。作为倾听的一方应积极反馈，“你对哪一部分还不理解?”或“我是这样理解的，你看对不对？”。

交流中还必须注意学会倾听，首先让对方把话说完，稍加思考后再发表自己的看法。倾听的时候，努力去把握对方讲话的要点，最好做一下笔记，并用反馈的方式确认是否真正理解了对方的思路。另外，正确的身体姿态也会增强交流的效果，如目光正视对方、理解时面带微笑地点点头以鼓励对方继续下去。相反的，如果听的一方左顾右盼，或毫无表情，则会严重影响讲话者的情绪。事实上，正确的肢体语言可强化交流效果，反之，错误的肢体语言很可能造成对方的反感，致使交流失败。

一位名叫阿莱斯库·奥兹庞的美国人提出了一种集体思考法方法，这种方法是采取召开会议的形式，让大家畅所欲言地出主意、想办法。作为一条原则，就是对别人的意见不予批评，让大家自由地思考、不受约束地提出各自的方案，或借助于别人的想法进一步制定出更好的方案。总之，在一个开放的环境中，大家应充分交流、相互启发、积极吸取别人的长处.

2.2 建模方法论

在第一章中我们介绍了数学建模的一般步骤和流程，其中最为重要的五个步骤为：问题的分析、模型假设、建立模型、模型求解以及对模型的分析、检验、修改与推广。当我们面临新的建模问题时，由这五个步骤构成的流程是非常具有指导意义的。下面我们结合实例对上述流程的各个步骤作具体说明。

2.2.1问题分析（模型准备）

进行数学建模和做很多数学“应用题”具有非常显著的差别，首先，“应用题”通常有不多不少恰到好处的条件和数据，内容和方法也基本限制在该节或该章。而数学建模问题经常是由各领域的应用者提出的，因而既不可能明确提出该用什么方法，也不会给出恰到好处的条件(可能有多余的条件，也可能缺少必要的条件和数据)。更经常出现的情形是：

问题本身就是含糊不清的。问题含糊不清的产生原因很可能是来自不向领域的人们相互间的交流发生障碍，也可能是提出问题的人只是感觉到需要解决某些方面的问题，但他还不能清楚地描述这个问题，当然，也可能存在你对问题是否能准确理解的情形.所以，数学建模的第一步便是对问题的分析。为此，要充分了解问题的实际背景，明确建立模型的目的，尽可能弄清楚对象的特征，并为此搜集必需的各种信息或数据。要善于捕捉对象特征中隐含的数学因素，并将其一一列出（这时是不怕多的，只怕一个也列不出）。至此，我们便有了一个很好的开端，因而可以初步确定用哪一类模型。只有情况明确了才能保证方法对，这一步一定不能忽视。如果不经过这一步，过早地着手解决问题，往往会陷入一些意想不到的陷阱，或者偏离方向。我们看一下的例子。

例4．（方桌问题）日常生活中经常碰到这样的事情：把方桌置于地面上时，常常是只有三只脚着地而放不稳，通常需要调整几次方可将方桌放稳，试用数学语言对此问题给以表述，并用数学工具给予说明：方桌能否在地面上放稳?若能，请给予证明并给出做法，否则说明理由。

我们来看看这个似乎与数学毫无关系的实际问题怎样一步步转化为数学问题，并用数学工具给以证明的。

问题分析：所谓方桌能否在地面放稳是指方桌的四个脚能否同时着地，而四个桌脚是否同时着地是指四个桌脚与地面的距离是否同时为零。于是我们可以转而研究四个桌脚与地面的距离是否同时等于零。这个距离显然是变化的，于是可视为函数，那么作为函数，它随哪个量的改变而改变？构造这个距离函数成为主要建模目的。

为了构造函数和设定相关参数，让我们实际操作一下，从中搜集信息，弄清其特征（这也是建模中常用的策略）。要想四个桌脚同时着地，通常有两种方法，其一是将方桌搬离原地，换个位置试验，另一个做法是在原地进行旋转试验。前法需要研究的范围可能要很大，这里采取第二种做法（请读者一定做一下：沿逆时针或顺时针慢慢旋转几个小角度即可）。易得出结论：只要地面相对平坦，没有地面大起大落情况，那么随着旋转角度的不同，三只脚同时落地后，第四只脚与地面距离也不同（不仅如此，旋转中总有两个脚同时着地，而另两个脚不稳定）而最终找到一个角度，使这个距离为零。也就是说，这个距离与旋转角度有关，是旋转角度的函数，于是一个确定的函数关系找到了。我们的问题也顺其自然地转化为：是否存在一角度，使得四个距离函数同时为零？

综上分析，问题可以归结为证明函数的零点的存在性，遂决定试用函数模型予以处理。请注意上述内容中的黑体字，它实际上蕴涵了使方桌放稳的一些前提条件，而这些往往是下一步我们要做出的假设的部分内容。

例5.（走路问题）考虑如下问题：人在匀速行走时，步长多大才能最省力?

问题分析：对这样的问题，好像一时无法回答,你必须搞清楚这个问题的实质是要做什么.所谓省力是指走步所作的功最少，走步时步长过大或过小都不省力，因而必有一个合适的步长，使作功最少（作功大小应是步长的函数）。当然，所做功还与许多因素有关，譬如提高人体重心所需势能，两腿运动所需动能（可由数学公式表达）；所穿衣物多少，是否负有重物，穿的鞋子是否轻便，行走地面是否平坦、干燥，走路时腿的运动形式（可否都用数学语言表达？）等。建模目标：求一个功函数，它应该是步长的函数。

例6．（热传导问题）在比较寒冷的北方城镇，双层玻璃密封窗使用的十分普遍。这种窗户上的玻璃是双层的，两层玻璃中间有一定空隙，利用橡胶制品将中间的空气与外界隔离开制成。据说这种窗户保暖效果比过去沿用多年的单层玻璃窗要好，试建立其数学模型以描述双层玻璃密封窗的保温功能。

问题分析：1．建模目的是分析双层玻璃密封窗的保温功能。所谓窗户的保温效果是指室内的热量通过玻璃窗散发出去的量的分析，它与室内室外的温度有关系，与窗户的密封情况、玻璃材料，以及房间大门的保温情况也有关。

2．双层玻璃密封窗保温效果的优与劣自然是相对于单层玻璃窗保温效果来说的，故可以通过对比方式来研究效果。

3．关于热量扩散问题，应查阅相关物理资料以备用。

例7．（宇宙速度问题）众所周知，数值7.9km/秒与11.2km/秒被称为第一与第二宇宙速度，那么它们是怎么得到的?如此精确的数量结果恐怕除使用数学模型外的其它方法是难已获得的。

问题分析：卫星发射情形大家至少都在电视中见过：一枚运载火箭竖立于发射架上，一旦点火，火箭便腾空而起飞向太空。火箭的去向大体上有两个，其一是摆脱地球引力而飞向远方，其二是不脱离地球引力范围而沿着固定轨道绕地球运行。前者恐怕要去探测其它行星的秘密，后者便是人们所说的人造地球卫星。不论哪种情形，有两个基本原理在起着关键作用：一个是它们都属于运动模型，故应首先考虑牛顿运动定律的应用；另一个是它们的飞行均与地球引力直接相关，因此，还要考虑万有引力定律的的运用。另外，卫星质量，火箭质量及其流线形式，还有那个不可忽视的空气阻力等都应在考虑之列。

2.2．2 模型假设

模型假设是与问题分析紧密衔接的一个重要步骤。根据对象的特征和建模目的，在问题分析的基础上需要对问题进行必要的、合理的取舍简化，并使用精确的语言作出假设，这是建模至关重要的一步。这是因为，一个实际问题往往是复杂多变的，如不经过合理的简化假设，将很难转化成数学模型，即便转化成功，也可能是一个复杂的难于求解的模型从而使建模归于失败。于是，我们必须忍痛割爱，从中舍去次要因素，抓住主要因素，进行必要的筛选；如果我们认定的主要因素还是觉得多的话，为了能顺利建模，也必须，或者说至少是暂时不予以考虑而舍弃，等到最后在模型分析时再给予考虑，或者在本模型建立中根本不予考虑。当然，假设作得不合理或过分简单也同样会因为与实际相去甚远而使建模归于失败。

一般地，作出假设时要充分利用与问题相关的有关学科知识，充分发挥想象力和观察判断力，分清问题的主次，抓

住主要因素，舍弃次要因素。另一方面，在我们选定的因素里，为建模需要，也常常要进行合理的简化，诸如线性化，均匀化，理想化等近似化处理，这也是满足建模所用数学方法必须的前提条件。当然，假设不能违背实际问题主要特征和建模目的。有人说，进行假设的目的就在于在第一步列出的各种因素中选出主要因素，忽略非本质因素，既使得问题简化以便进行数学处理，又抓住了问题的本质，是不无道理的。另外，为建模顺利，写出假设时，语言要准确，就象作习题时写出已知条件一样。所有这些就是模型假设这一步要做的工作。我们结合以下例子给予说明。

1．对方桌问题来说，依前面的问题分析，我们可做出如下假设：

（1）桌子的四条腿同长（这个假设显然合理，而且避免了问题与桌腿长度有关使问题变复杂）。

（2）将方桌的桌脚与地面接触处看成是一个几何点，四脚连线为正方形（这是因为问题本身考虑的是能否四脚着地而与桌腿样式、粗细、质地等无关。像这样将问题抽象化，将易于在数学上进行处理）。

（3）地面相对平坦，即在旋转所在地面范围内，方桌在任何位置至少有三只脚同时着地（自然这是符合实际的合理假设，也是我们在问题分析中注意到了的）。

（4）地面高度连续变化，即可视地面为数学上的连续曲面（这样，所设的高度函数便成为角度的连续函数）。

π上的连续函数。若设角度为θ，则可写高度函数为在上述假设之下，我们所设的高度函数是定义在角度区间[0,2]

fθ。至于其模型建立就不在话下了。

()

2．对走路问题来说，依前面的问题分析，我们可做出如下假设：

（1）人行走时所作的功由两部份组成：抬高人体重心所需势能与两腿前后运动所需动能。暂不考虑负重（划定主要因素）。

（2）运动与所穿鞋子、衣服情况无关，地面是相对平坦而干燥的（舍弃次要因素）。

（3）人的行走可视为腿（直杆）绕腰部的转动（理想化表达）。

（4）设定下列参量：M——人的体重；m——人的腿重；H—人的腿长；v——行走速度；n——单位时间行走的步数；x——步长。

有了以上分析和假设，我们只须根据物理中的势能公式和动能公式计算出运动所做的势能和动能（他们自然是步长的函数），然后求其最小值即可。

3．对热传导问题来说，依前面的问题分析，我们可做出如下假设：

（1）两层玻璃的密封性能很好，即其中间的空气是不流动的，这样，热量的传播过程只有传导而没有对流，故此属热传导问题（抓住主要因素）。

（2）设室内温度T1 ，室外温度T2 均为常数，即沿热传导方向，单位时间通过单位面积的热量是常数。

（3）玻璃材料均匀，热传导系数为常数（此与假设2同为均匀化和理想化处理，使模型便于处理又不失合理性）。

（4）室内温度从其它途径（门等）传播情况忽略不计（忽略非主要因素影响）。

有了上述分析和假设，就可以建立两种不同玻璃窗热量传导值，从而通过比较其大小说明问题了。

4．对宇宙速度问题来说，依前面的问题分析，我们可做出如下假设：

（1）视火箭及其搭载物为一个质量为定数的物体，与火箭搭载物的形状，大小和尺寸等无关（简单化）。

（2）火箭的升天过程视为一个物体在地球表面被垂直上抛的过程（实际情况）。

（3）为使模型简单，忽略物体飞行中的空气阻力不计（理想化）。

（4）设定如下参量：

m—被垂直上抛的物体质量；

M—地球质量；

R—地球半径；

k—万有引力常数（k>0）；

v0—垂直上抛物体的初始速度。

这里，我们注意到一个似乎很不合理的假设：忽略空气阻力。事实上，空气阻力是不可避免的，而且是一个主要因素。那么，这个大胆的理想化处理的结果如何？你只需继续做下去便可见分晓：它竟然给出了第二宇宙速度。然后，你不妨再将此因素考虑进来，看看所建模型的结果，就会有新的发现和体会。

在上述分析和假设之下，建立其模型已经是水到渠成。

2.2.3 建立模型

有了问题分析和模型假设做雄厚基础，就到了建立模型这个最关键的步骤了。根据假设分析相关变量间的关系，寻求等量（不等量）关系或其它关系以建立模型时，应充分利用已知领域的已知模型或结果，通过类比联想等方法构造模型，利用图示方法等等。至于建立何种模型，要依据问题分析与模型假设的情况，更要结合自己的数学基础和使用模型的对象等具体情况，不能一概而论。这里先对上两讲所提到的几个实例进行建模。

A

B C D O A '

B '

C '

D '

x 1．建立例4的数学模型：

如图，以长方形的两条对角线的交点为

原点建立平面直角坐标系，且不妨设

A 、C 两桌脚开始时位于横轴上，则问题与旋转角度θ有关。注意到假

设3，设A 、B 两个桌脚与地面距离之和为0)(≥θf ，另外两个桌脚与地面距离之和为,0)(≥θg 则又由假设2，以上两个函数均为

旋转角度的连续函数，于是有命题：

已知,0)0(,0)0(,0)()()(),(>==?g f g f g f 且，的连续函数，对是θθθθθθ

则0θ?，使得.0)()(00==θθg f

这就是问题的数学模型。 2.建立例6的数学模型：

由物理学知道，在上述假设下，热传导过程遵从下面的物理规律：

厚度为d 的均匀介质，两侧温度差为T ?，则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为Q ，与T ?成正比，与d 成反比，即

d

T k

Q ?= （1） 其中k 为热传导系数。

（1）双层玻璃的热量流失

记双层窗内窗玻璃的外侧温度为a T ，外层玻璃的内侧温度为b T ，玻璃的热传导系数为1k ，空气的热传导系数为2k ，由（1）式单位时间单位面积的热量传导（热量流失）为：

d T T k d T T k d T T k Q b b a a 21211

-=-=-= （2） 由d T T k Q a -=11及d

T T k Q b 21-=可得1212)(k Qd T T T T b a --=- 再代入d T T k Q b a -=2

就将（2）中a T 、b T 消去，变形可得： ()d

l h k k h s s d T T k Q ==+-= , , 2)(21211 （3） （2）单层玻璃的热量流失

对于厚度为d 2的单层玻璃窗户，容易写出热量流失为：

d

T T k Q 2211-=' （4） （3） 单层玻璃窗和双层玻璃窗热量流失比较

比较（3）（4）有： 22+='s Q Q （5） 显然，Q Q '<。

2.2.4 模型求解

依据所建模型的特点和归属（哪个数学分支）寻求其求解方法，常有可能找不到相应的数学工具，这时可考虑如下方案解决：

（1）在问题允许范围内，适当修改所建模型，以方便求解；

（2）若解析解求不出，通常可在允许范围内求其近似解、数值解和图解，也可考虑用计算机模拟；

（3）若为未见过的全新模型，则需要你去发明新的算法，但一定给出严格的证明。

1．例4模型的求解：

只须证明上述命题即可。

将桌子旋转0

180)(π，则A 、B 两点与D 、C 两点恰好交换位置。由假设便有，)(,0)(ππg f >.0=又由前述假设，.0)0(,0)0(>=g f

令),()()(θθθg f h -=则有.0)(,0)0(><πh h 由于)(),(θθg f 的连续性知)(θh 也是连续函数。依据连续函数的基本性质（零点定理），必至少存在一个角度0θ，,00πθ<<

使得0)(0=θh ，即).()(00θθg f =又根据θθθ?=,0)()(g f 成立，故有.0)()(00==θθg f

2．例6模型的求解：

为了获得更具体的结果，我们需要21,k k 的数据，从有关资料可知，不流通、干燥空气的热传导系数42105.2-?=k （焦耳/厘米.秒.度），常用玻璃的热传导系数331108~10

4--??=k （焦耳/厘米.秒.度），于是 32~162

1=k k 在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时，我们作最保守的估计，即取

1621=k k ，由（3）（5）可得： d

l h h Q Q =+=' 181 （6） 比值Q Q '反映了双层玻璃窗在减少热量损失上的功效，它只与d l h =有关，下图给出了h Q Q ~'的曲线，当h 由0增加时，Q Q '迅速下降，而当h 超过一定值（比如4>h ）后Q Q '下降缓慢，可见h 不宜选得过大。

2.2.5 模型的分析、检验、修改与推广

对所得数学解答进行分析包括：

（1）变量间依赖关系或稳定性状况，诸如增减性、最值性、渐进性及数据微小变化对解的影响等；

（2）依据结果给出预报、控制或最优决策；

（3）误差分析也是常做的一项工作，这时因为所搜集的信息、数据本身具有误差，假设不合理等。

所谓检验与修改是将数学上的分析结果返回到实际问题中去，并用实际现象或数据与模型计算出的结果进行比较以检验模型的合理性和适用性，这一步工作对于建模的成败非常重要。假如有较大出入，则模型需进行必要的修改，甚至

要推倒重来。这一问题的产生通常出在模型假设上，要重新审视假设建华的合理性。

所谓推广有两层意思，一是对所建模型的优、缺点进行客观评注，二是将条件加以增减或放宽，讨论模型能够进一步适应的范围。这是一件很有意义的工作。谁不希望自己辛辛苦苦建立起来的模型能够适应更多的实际现象呢？

就例4的模型而言，由于其非常直观和简单，模型的分析、检验和修改就可以略去。不过模型还可推广为方桌的四个脚呈长方形时的情况；请读者自己证明解决。

就例6的模型而言，模型与实际是否吻合的很好呢？可能的原因是什么？请读者自己找出来。另外，双层玻璃窗通常见于北方，那么双层玻璃窗对于高热的南方的适用性如何呢？

本章从方法论的角度讨论了建立数学模型所采用的一般方法，请读者结合第10章来细细品味建立模型的过程。为更好和更快地掌握建立数学模型的方法，一方面是阅读一些优秀的建模论文，另一方面是自己试着去做一些题目，或许刚开始觉得很难，可是一旦开始做下去，你就会感到建模的乐趣。

习题2

1．某条公路的交通不太拥挤，以致人们养成“冲”过马路的习惯，不愿行走到邻近的“斑马线”。当地交通管理部门不允许任意横穿公路，为方便行人，准备在一些特殊地点增设“斑马线”，让行人可穿越马路，并且还要保证行人的等待时间不超过一定时间，比如15秒。请列出与选择设置“斑马线”的地点有关的要素。

2．一家大型食品公司的销售经理就关于应该雇多少推销员的问题征询你的意见。请就你对这个问题的理解给出你对这个问题的分析。（不需求解）

3．请试着建立本章例5和例7的模型，并求解。