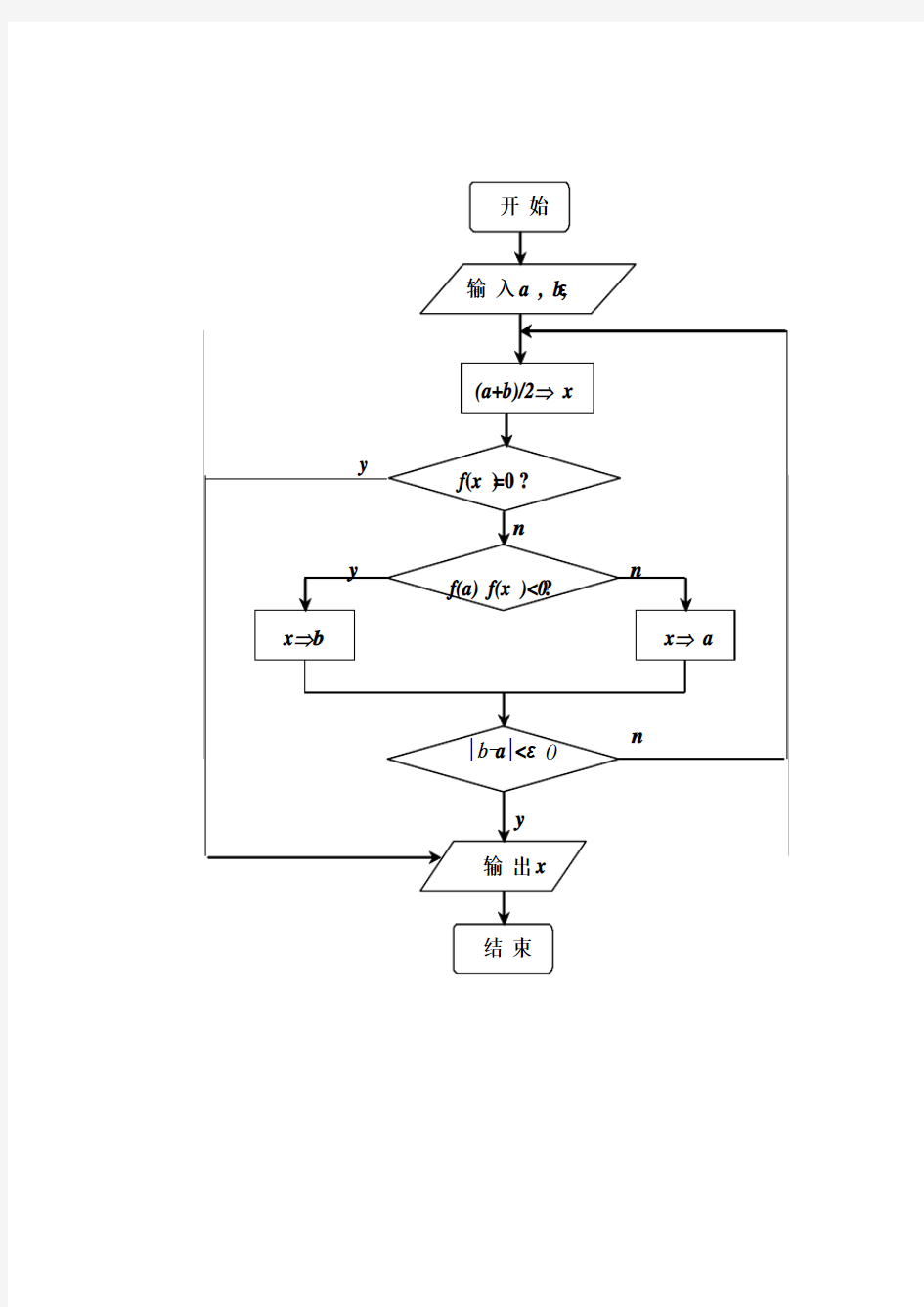
牛顿法解流程图
最优化课程设计
《最优化》课程设计 题目:牛顿法与阻尼牛顿法算法分析 学院: 数学与计算科学学院 专业:数学与应用数学 姓名学号:廖丽红 1000730105 欧艳 1000730107 骆宗元 1000730122 沈琼赞 1000730127 指导教师:李向利 日期:2012年11月08日
摘要 本文基于阻尼牛顿法在解决无约束最优化问题中的重要性,对其原理与算法予以讨论。论文主要是参阅大量数学分析和最优化理论方法,还有最优化方法课程以及一些学术资料,结合自己在平时学习中掌握的知识,并在指导老师的建议下,拓展叙述牛顿法和其改进方法——阻尼牛顿法的优缺点,同时针对阻尼牛顿法的基本思路和原理进行研究,其搜索方向为负梯度方向,改善了牛顿法的缺点,保证了下降方向。 关键词:无约束牛顿法下降方向阻尼牛顿法最优解
Abstract This thesis is based on the importance of the damping Newton's method to solve unconstrained optimization problems, we give the discussion about its principles and algorithms. We search a large number of mathematical analysis and optimization theory methods, optimization methods courses, as well as some academic information ,and at the same time combined with knowledge we have learning in peacetime and thanks to the instructor's advice, we also give an expanding narrative for the Newton's method and the improved method -- damping Newton method's advantages and disadvantages, and make a study of the basic ideas and principles for damping Newton method at the same time , we find that a negative gradient direction is for the search direction of the damping Newton method, this method improves the shortcomings of the Newton method which can ensure the descent direction. Keywords: unconstrained , Newton's method , descent direction , damping Newton's method ,optimal solution
牛顿插值法原理及应用
牛顿插值法 插值法是利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。如果这特定函数是多项式,就称它为插值多项式。当插值节点增减时全部插值基函数均要随之变化,这在实际计算中很不方便。为了克服这一缺点,提出了牛顿插值。牛顿插值通过求各阶差商,递推得到的一个公式: f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0 )...(x-xn-1)+Rn(x)。 插值函数 插值函数的概念及相关性质[1] 定义:设连续函数y-f(x) 在区间[a,b]上有定义,已知在n+1个互异的点 x0,x1,…xn上取值分别为y0,y1,…yn (设a≤ x1≤x2……≤xn≤b)。若在函数类中存在以简单函数P(x) ,使得P(xi)=yi,则称P(x) 为f(x)的插值函数. 称x1,x2,…xn 为插值节点,称[a,b]为插值区间。 定理:n次代数插值问题的解存在且唯一。
牛顿插值法C程序 程序框图#include Matlab实现数值分析插值及积分 摘要: 数值分析(numerical analysis)是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科,是数学的一个分支,它以数字计算机求解数学问题的理论和方法为研究对象。在实际生产实践中,常常将实际问题转化为数学模型来解决,这个过程就是数学建模。学习数值分析这门课程可以让我们学到很多的数学建模方法。 分别运用matlab数学软件编程来解决插值问题和数值积分问题。题目中的要求是计算差值和积分,对于问题一,可以分别利用朗格朗日插值公式,牛顿插值公式,埃特金逐次线性插值公式来进行编程求解,具体matlab代码见正文。编程求解出来的结果为:=+。 其中Aitken插值计算的结果图如下: 对于问题二,可以分别利用复化梯形公式,复化的辛卜生公式,复化的柯特斯公式编写程序来进行求解,具体matlab代码见正文。编程求解出来的结果为: 0.6932 其中复化梯形公式计算的结果图如下: 问题重述 问题一:已知列表函数 表格 1 分别用拉格朗日,牛顿,埃特金插值方法计算。 问题二:用复化的梯形公式,复化的辛卜生公式,复化的柯特斯公式计算积分,使精度小于5。 问题解决 问题一:插值方法 对于问题一,用三种差值方法:拉格朗日,牛顿,埃特金差值方法来解决。 一、拉格朗日插值法: 拉格朗日插值多项式如下: 首先构造1+n 个插值节点n x x x ,,,10 上的n 插值基函数,对任一点i x 所对应的插值基函数 )(x l i ,由于在所有),,1,1,,1,0(n i i j x j +-=取零值,因此)(x l i 有因子 )())(()(110n i i x x x x x x x x ----+- 。又因)(x l i 是一个次数不超过n 的多项式,所以只 可能相差一个常数因子,固)(x l i 可表示成: )())(()()(110n i i i x x x x x x x x A x l ----=+- 利用1)(=i i x l 得: 《MATLAB 程序设计实践》课程考核 ---第37-38页 题1 : 编程实现以下科学计算算法,并举一例应用之。(参考书籍《精 通MAT LAB科学计算》,王正林等著,电子工业出版社,2009 年) “牛顿法非线性方程求解” 弦截法本质是一种割线法,它从两端向中间逐渐逼近方程的根;牛顿法本质上是一种切线法,它从一端向一个方向逼近方程的根,其递推公式为: - =+n n x x 1) ()(' n n x f x f 初始值可以取)('a f 和)('b f 的较大者,这样可以加快收敛速度。 和牛顿法有关的还有简化牛顿法和牛顿下山法。 在MATLAB 中编程实现的牛顿法的函数为:NewtonRoot 。 功能:用牛顿法求函数在某个区间上的一个零点。 调用格式:root=NewtonRoot )(```eps b a f 其中,f 为函数名; a 为区间左端点; b 为区间右端点 eps 为根的精度; root 为求出的函数零点。 , 牛顿法的matlab程序代码如下: function root=NewtonRoot(f,a,b,eps) %牛顿法求函数f在区间[a,b]上的一个零点%函数名:f %区间左端点:a %区间右端点:b %根的精度:eps %求出的函数零点:root if(nargin==3) eps=1.0e-4; end f1=subs(sym(f),findsym(sym(f)),a); f2=subs(sym(f),findsym(sym(f)),b); if (f1==0) root=a; end if (f2==0) root=b; end if (f1*f2>0) disp('两端点函数值乘积大于0 !'); return; else tol=1; fun=diff(sym(f)); %求导数 fa=subs(sym(f),findsym(sym(f)),a); fb=subs(sym(f),findsym(sym(f)),b); dfa=subs(sym(fun),findsym(sym(fun)),a); dfb=subs(sym(fun),findsym(sym(fun)),b); if(dfa>dfb) %初始值取两端点导数较大者 root=a-fa/dfa; else root=b-fb/dfb; end while(tol>eps) r1=root; fx=subs(sym(f),findsym(sym(f)),r1); dfx=subs(sym(fun),findsym(sym(fun)),r1); %求该点的导数值 root=r1-fx/dfx; %迭代的核心公式 tol=abs(root-r1); end end 例:求方程3x^2-exp(x)=0的一根 解:在MATLAB命令窗口输入: >> r=NewtonRoot('3*x^2-exp(x)',3,4) 输出结果: X=3.7331 中南大学MATLAB程序设计实践学长有爱奉献,下载填上信息即可上交,没有下载券的自行百度。所需m文件照本文档做即可,即新建(FILE)→脚本(NEW-Sscript)→复制本文档代码→运行(会跳出保存界面,文件名默认不要修改,保存)→结果。第一题需要把数据文本文档和m文件放在一起。全部测试无误,放心使用。本文档针对做牛顿法求非线性函数题目的同学,当然第一题都一样,所有人都可以用。←记得删掉这段话 班级: ? 学号: 姓名: 一、《MATLAB程序设计实践》Matlab基础 表示多晶体材料织构的三维取向分布函数(f=f(φ1,φ,φ2))是一个非常复杂的函数,难以精确的用解析函数表达,通常采用离散 空间函数值来表示取向分布函数,是三维取向分布函数的一个实例。 由于数据量非常大,不便于分析,需要借助图形来分析。请你编写一 个matlab程序画出如下的几种图形来分析其取向分布特征: (1)用Slice函数给出其整体分布特征; " ~ (2)用pcolor或contour函数分别给出(φ2=0, 5, 10, 15, 20, 25, 30, 35 … 90)切面上f分布情况(需要用到subplot函数); (3) 用plot函数给出沿α取向线(φ1=0~90,φ=45,φ2=0)的f分布情况。 ( 备注:数据格式说明 解: (1)( (2)将文件内的数据按照要求读取到矩阵f(phi1,phi,phi2)中,代码如 下: fid=fopen(''); for i=1:18 tline=fgetl(fid); end phi1=1;phi=1;phi2=1;line=0; f=zeros(19,19,19); [ while ~feof(fid) tline=fgetl(fid); data=str2num(tline); line=line+1;数据说明部分,与 作图无关此方向表示f随着 φ1从0,5,10,15, 20 …到90的变化而 变化 此方向表示f随着φ 从0,5,10,15, 20 … 到90的变化而变化 表示以下数据为φ2=0的数据,即f(φ1,φ,0) 最优化方法结课作业 年级数学121班 学号201200144209 姓名李强 1、几种方法比较 无约束优化:不对定义域或值域做任何限制的情况下,求解目标函数的最小值。这是因为实际应用中,许多情形被抽象为函数形式后均为凸函数,对于凸函数来说局部最小值点即为全局最小值点,因此只要能求得这类函数的一个最小值点,该点一定为全局最小值。(直接法:又称数值方法,它只需计算目标函数驻点的函数数值,而不是求其倒数,如坐标轮换法,单纯型法等。间接法:又称解析法,是应用数学极值理论的解析方法。首先计算出目标函数的一阶或一阶、二阶导数,然后根据梯度及海赛矩阵提供的信息,构造何种算法,从而间接地求出目标函数的最优解,如牛顿法、最速下降法共轭梯度法及变尺度法。)在优化算法中保证整体收敛的重要方法就是线搜索法与信赖域法,这两种算法既相似又有所不同。根据不同的线搜索准则就延伸出不同的线搜索算法,譬如比较常见和经典的最速下降法,牛顿法,拟牛顿法以及共辄梯度法等。 一维搜索又称线性搜索(Line Search),就是指单变量函数的最优化,它是多变量函数最优化的基础,是求解无约束非线性规划问题的基本方法之一。 一维搜索技术既可独立的用于求解单变量最优化问题,同时又是求解多变量最优化问题常用的手段,虽然求解单变量最优化问题相对比较简单,但其中也贯穿了求解最优化问题的基本思想。由于一维搜索的使用频率较高,因此努力提高求解单变量问题算法的计算效率具有重要的实际意义。 在多变量函数的最优化中,迭代格式Xk+1=Xk+akdk其关键就是构造搜索方向dk和步长因子ak 设Φ(a)=f(xk+adk) 这样从凡出发,沿搜索方向dk,确定步长因子ak,使Φ(a)<Φ(0)的问题就是关于步长因子a 的一维搜索问题。其主要结构可作如下概括:首先确定包含问题最优解的搜索区间,然后采用某种分割技术或插值方法缩小这个区间,进行搜索求解。 一维搜索通常分为精确的和不精确的两类。如果求得ak使目标函数沿方向dk达到极小,即使得f (xk+akdk)=min f (xk+ adk) ( a>0)则称这样的一维搜索为最优一维搜索,或精确一维搜索,ak叫最优步长因子;如果选取ak使目标函数f得到可接受的下降量,即使得下降量f (xk)一f (xk+akdk)>0是用户可接受的,则称这样的一维搜索为近似一维搜索,或不精确一维搜索,或可接受一维搜索。由于在实际计算中,一般做不到精确的一维搜索,实际上也没有必要做到这一点,因为精确的一维搜索需要付出较高的代价,而对加速收敛作用不大,因此花费计算量 题目一:多项式插值 某气象观测站在8:00(AM )开始每隔10分钟对天气作如下观测,用三次多项式插值函数(Newton )逼近如下曲线,插值节点数据如上表,并求出9点30分该地区的温度(x=10)。 二、数学原理 假设有n+1个不同的节点及函数在节点上的值(x 0,y 0),……(x n ,y n ),插值多项式有如下形式: )() )(()()()(n 10n 102010n x -x )(x -x x -x x P x x x x x x -??-+??+-++=αααα (1) 其中系数i α(i=0,1,2……n )为特定系数,可由插值样条i i n y x P =) ((i=0,1,2……n )确定。 根据均差的定义,把x 看成[a,b]上的一点,可得 f(x)= f (0x )+f[10x x ,](0x -x ) f[x, 0x ]= f[10x x ,]+f[x,10x x ,] (1x -x ) …… f[x, 0x ,…x 1-n ]= f[x, 0x ,…x n ]+ f[x, 0x ,…x n ](x-x n ) 综合以上式子,把后一式代入前一式,可得到: f(x)= f[0x ]+f[10x x ,](0x -x )+ f[210x x x ,,](0x -x )(1x -x )+ …+ f[x, 0x ,…x n ](0x -x )…(x-x 1-n )+ f[x, 0x ,…x n ,x ]) (x 1n +ω= N n (x )+) (x n R 其中 N n (x )= f[0x ]+f[10x x ,](0x -x )+ f[210x x x ,,](0x -x )(1x -x )+ …+ f[x, 0x ,…x n ](0x -x )…(x-x 1-n ) (2) )(x n R = f(x)- N n (x )= f[x, 0x , (x) n ,x ]) (x 1n +ω (3) ) (x 1n +ω=(0x -x )…(x-x n ) Newton 插值的系数i α(i=0,1,2……n )可以用差商表示。一般有 f k =α[k 10x x x ??,] (k=0,1,2,……,n ) (4) 把(4)代入(1)得到满足插值条件N )() (i i n x f x =(i=0,1,2,……n )的n 次Newton 插值多项式 N n (x )=f (0x )+f[10x x ,](1x -x )+f[210x x x ,,](1x -x )(2x -x )+……+f[n 10x x x ??,](1x -x )(2x -x )…(1-n x -x ). 其中插值余项为: ) ()! () ()()()(x 1n f x N -x f x R 1n 1 n n +++==ωξ ξ介于k 10x x x ??,之间。 三、程序设计 function [y,A,C,L]=newdscg(X,Y,x,M) % y 为对应x 的值,A 为差商表,C 为多项式系数,L 为多项式 % X 为给定节点,Y 为节点值,x 为待求节点 n=length(X); m=length(x); % n 为X 的长度 for t=1:m revisenewton.m syms x1 x2 x3 xx; % f = x1*x1 +x2*x2 -x1*x2 -10*x1 -4*x2 + 60 ; % f = x1^2 + 2*x2^2 - 2*x1 *x2 -4*x1 ; f = 100 * (x1^2 - x2^2) + (x1 -1 )^2 ; hessen = jacobian(jacobian(f , [x1,x2]),[x1,x2]) ; gradd = jacobian(f , [x1,x2]) ; X0 = [0,0]' ; B = gradd' ; x1 = X0(1); x2 = X0(2); A = eval(gradd) ; % while sqrt( A(1)^2 + A(2)^2) >0.1 i=0; while norm(A) >0.1 i = i+1 ; fprintf('the number of iterations is: %d\n', i) if i>10 break; end B1 = inv(hessen)* B ; B2= eval(B1); % X1 = X0 - B2 % X0 = X1 ; f1= x1 + xx * B2(1); f2= x2 + xx* B2(2); % ff = norm(BB) ? syms x1 x2 ; fT=[subs(gradd(1),x1,f1),subs(gradd(2),x2,f2)]; ff = sqrt((fT(1))^2+(fT(2))^2); MinData = GoldData(ff,0,1,0.01); x1 = X0(1); x2 = X0(2); x1 = x1 + MinData * B2(1) x2 = x2 + MinData * B2(2) A = eval(gradd) End GoldData.m function MiniData = GoldData( f,x0,h0,eps) syms xx; MATLAB程序设计期中作业 ——编程实现牛顿插值 成员:刘川(P091712797)签名_____ 汤意(P091712817)签名_____ 王功贺(P091712799)签名_____ 班级:2009信息与计算科学 学院:数学与计算机科学学院 日期:2012年05月02日 牛顿插值的算法描述及程序实现 一:问题说明 在我们的实际应用中,通常需要解决这样的问题,通过一些已知的点及其对应的值,去估算另外一些点的值,这些数据之间近似服从一定的规律,于是,这就引入了插值法的思想。 插值法是利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。如果这特定函数是多项式,就称它为插值多项式。利用插值基函数很容易得到拉格朗日插值多项式,公式结构紧凑,在理论分析中甚为方便,但当插值节点增减时全部插值基函数均要随之变化,整个公式也将发生变化,这在实际计算中是很不方便的,为了克服这一缺点,提出了牛顿插值。 二:算法分析 newton 插值多项式的表达式如下: 010011()()()()()n n n N x c c x x c x x x x x x -=+-+???+--???- 其中每一项的系数c i 的表达式如下: 12011010 [,,,][,,,] [,,,]i i i i i f x x x f x x x c f x x x x x -???-???=???= - 即为f (x)在点01,,,i x x x ???处的i 阶差商,([]()i i f x f x =,1,2,,i n = ),由差商01[,,,]i f x x x ???的性质可知: () 010 1 [,,,]()i i i j j k j k k j f x x x f x x x ==≠???=-∑∏ 牛顿插值的程序实现方法: 第一步:计算[][][][]001012012,,,,,,,n f x f x x f x x x f x x x x 、、、 、。 第二步:计算牛顿插值多项式中01[,,,]i f x x x ???011()()()i x x x x x x ---???-,1,2,,i n = ,得到n 个多项式。 实验报告日期:2013年6月2日 一、实验概述 【实验名称】:牛顿法 【实验性质】:验证性 【实验目的及要求】:配合课堂教学,培养学生动手能力,根据牛顿法求极小值的思想设计程序。 【基本原理】:牛顿法的迭代公式:)()(12)()1(k k k k x f x f x x ??-=-+,其中)(2k x f k ?是f(x)在k x 处的Hesse 矩阵。【实施环境】: MATLAB 7.0 二、实验内容 【项目内容及要求】 用牛顿法求解以下问题: min z=(x1-1)4+x22 三、实验过程 【实验操作步骤】 function [x1k]=newton(x1,j) %x1为初始点x1=[8,8]';j=1e-10; hs=inline('(x-1)^4+y^2'); ezcontour(hs,[-1010-1010]);hold on; syms x y f=(x-1)^4+y^2; grad1=jacobian(f,[x,y]);%求梯度 grad2=jacobian(grad1,[x,y]);%求Hesse矩阵 k=0; while1 grad1z=subs(subs(grad1,x,x1(1)),y,x1(2));%求梯度值 grad2z=subs(subs(grad2,x,x1(1)),y,x1(2));%求Hesse矩阵x2=x1-inv(grad2z)*(grad1z');%牛顿迭代公式 if norm(x1-x2) 改进的牛顿迭代法求解非线性方程 摘要:牛顿法思想是将非线性方程线性化,以线性方程的解逐步逼近非线性方程的解,但是其对初值、波动和可能出现的不收敛等缺点,而牛顿下山法克服了可能出现的发散的缺点。 关键词:牛顿法、牛顿下山法、非线性方程 一、牛顿法的迭代公式 设)(x f 在其零点*x 附近一阶连续可微,且0)(≠'x f ,当*0x x →时,由Taylor 公式有: ))(()()(000x x x f x f x f -'+≈ 以方程 0))(()(000=-'+x x x f x f 近似方程0)(=x f ,其解 ) ()(0001x f x f x x '-= 可作为方程的近似解,重复上述过程,得迭代公式 ),1,0(,) ()(1 ='-=+n x f x f x x n n n n 该方法称为牛顿迭代法。 二、牛顿法的改进 由于牛顿法缺点对牛顿法进行改进,使其计算简单,无需每次迭代都去计算)(x f ',且能够更好的收敛。 2.1简化的牛顿法 牛顿法的缺点之一是每次迭代都得去计算)(k x f '。为回避该问题,常用一个固定 )(k x f '迭代若干步后再求)(k x f '。这就是简化牛顿法的基本思想。 简化牛顿法的公式为: )(1k k k x cf x x -=+ 迭代函数 )()(x cf x x -=? 若 2)(0,1)(1)(<'<<'-='x f c x f c x 即?,在根*x 附近成立,则迭代法局部收敛。 显然此法简化了计算量,却降低了收敛速度。 2.2牛顿下山法 牛顿法的缺点二是其收敛依赖与初值0x 的选取,若0x 偏离所求根*x 较远,则牛顿法可能发散。为防止迭代发散,我们对迭代过程再附加一项条件,即具有单调性: )()(1k k x f x f <+ 保证函数值稳定下降,然后结合牛顿法加快收敛速度,即可达目的。将牛顿法的计算结果 ) ()(1k k k k x f x f x x '-=+ 与前一步的近似值k x 适当加权平均作为新的改进值 k k k x x x )1(11λλ-+=++ 其中,称 )10(≤<λλ为下山因子,即为: ) ()(1k k k k x f x f x x '-=+λ 称为牛顿下山法。选择下山因子λ时,从 1=λ开始逐次将λ减半进行试算,直到条件成立为止。 三 举例说明 例1 求方程013=--x x 的根 (1)取5.10=x ,用牛顿法公式: 1 32131---=-+k k k k x x x x x 计算得:32472.1,32520.1,34783.1321===x x x 牛顿法 迭代公式:(1)2()1()[()]()k k k k x x f x f x +-=-?? Matlab 代码: function [x1,k] =newton(x1,eps) hs=inline('(x-1)^4+y^2'); 写入函数 ezcontour(hs,[-10 10 -10 10]); 建立坐标系 hold on; 显示图像 syms x y 定义变量 f=(x-1)^4+y^2; 定义函数 grad1=jacobian(f,[x,y]); 求f 的一阶梯度 grad2=jacobian(grad1,[x,y]); 求f 的二阶梯度 k=0; 迭代初始值 while 1 循环 grad1z=subs(subs(grad1,x,x1(1)),y,x1(2)); 给f 一阶梯度赋初值 grad2z=subs(subs(grad2,x,x1(1)),y,x1(2)); 给f 二阶梯度赋初值 x2=x1-inv(grad2z)*(grad1z)'; 核心迭代公式 if norm(x1-x2) end end end 优点:在极小点附近收敛快 缺点:但是要计算目标函数的hesse 矩阵 最速下降法 1. :选取初始点xo ,给定误差 2. 计算一阶梯度。若一阶梯度小于误差,停止迭代,输出 3. 取()()()k k p f x =? 4. 10 t ()(), 1.min k k k k k k k k k k t f x t p f x tp x x t p k k +≥+=+=+=+进行一维搜索,求,使得令转第二步 例题: 求min (x-2)^4+(x-2*y)^2.初始值(0,3)误差为0.1 (1)编写一个目标函数,存为f.m function z = f( x,y ) z=(x-2.0)^4+(x-2.0*y)^2; end (2)分别关于x 和y 求出一阶梯度,分别存为fx.m 和fy.m function z = fx( x,y ) z=2.0*x-4.0*y+4.0*(x-2.0)^3; end 和 function z = fy( x,y ) 6.3.5 牛顿插值法的MATLAB 综合程序 求牛顿插值多项式、差商、插值及其误差估计的MATLAB 主程序 function [y,R,A,C,L]=newdscg(X,Y,x,M) n=length(X); m=length(x); for t=1:m z=x(t); A=zeros(n,n);A(:,1)=Y'; s=0.0; p=1.0; q1=1.0; c1=1.0; for j=2:n for i=j:n A(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1)); end q1=abs(q1*(z-X(j-1)));c1=c1*j; end C=A(n,n);q1=abs(q1*(z-X(n))); for k=(n-1):-1:1 C=conv(C,poly(X(k))); d=length(C);C(d)=C(d)+A(k,k); end y(k)= polyval(C, z); end R=M*q1/c1;L(k,:)=poly2sym(C); 例6.3.6 给出节点数据00.27)00.4(=-f ,00.1)00.0(=f ,00.2)00.1(=f ,00.17)00.2(=f ,作三阶牛顿插值多项式,计算)345.2(-f ,并估计其误差. 解 首先将名为newdscg.m 的程序保存为M 文件,然后在MATLAB 工作窗口输入程序 >> syms M,X=[-4,0,1,2]; Y =[27,1,2,17]; x=-2.345; [y,R,A,C,P]=newdscg(X,Y,x,M) 运行后输出插值y )345.2(-≈f 及其误差限公式R ,三阶牛顿插值多项式P 及其系数向量C ,差商的矩阵A 如下 y = 22.3211 R = 65133/562949953421312*M (即R =2.3503*M ) A= 27.0000 0 0 0 1.0000 -6.5000 0 0 2.0000 1.0000 1.5000 0 17.0000 15.0000 7.0000 0.9167 C = 0.9167 4.2500 -4.1667 1.0000 P = 11/12*x^3+17/4*x^2-25/6*x+1 牛顿迭代法求解非线性方程组 非线性方程组如下: 221122121210801080 x x x x x x x ?-++=??+-+=?? 给定初值()00.0T x =,要求求解精度达到0.00001 1.首先建立函数()F X ,方程编程如下,将F.m 保存到工作路径中: function f=F(x) f(1)=x(1)^2-10*x(1)+x(2)^2+8; f(2)=x(1)*x(2)^2+x(1)-10*x(2)+8; f=[f(1),f(2)] ; 2.建立函数()DF X ,用于求方程的jacobi 矩阵,将DF.m 保存到工作路径中: function df=DF(x) df=[2*x(1)-10,2*x(2);x(2)^2+1,2*x(1)*x(2)-10]; %jacobi 矩阵是一阶偏导数以一定方式排列成的矩阵。 3.编程牛顿迭代法解非线性方程组,将newton.m 保存在工作路径中: clear,clc; x=[0,0]'; f=F(x); df=DF(x); fprintf('%d %.7f %.7f\n',0,x(1),x(2)); N=4; for i=1:N y=df\f'; x=x-y; f=F(x); df=DF(x); fprintf('%d %.7f %.7f\n',i,x(1),x(2)); if norm(y)<0.0000001 break; else end end ezplot('x^2-10*x+y^2+8',[-6,6,-6,6]); hold on ezplot('x*y^2+x-10*y+8',[-6,6,-6,6]); 运行结果如下: 0 0.0000000 0.0000000 1 0.8000000 0.8800000 2 0.9917872 0.9917117 3 0.9999752 0.9999685 §3.4 牛顿迭代法 牛顿迭代法也称为牛顿-拉夫森(Newton-Raphson)迭代法,它是数值分析中最重要的方法之一,它不仅适用于方程或方程组的求解,还常用于微分方程和积分方程求解。 3.4.1 牛顿迭代法 用迭代法解非线性方程时,如何构造迭代函数是非常重要的,那么怎样构造的迭代函数才能保证迭代法收敛呢?牛顿迭代法就是常用的方法之一,其迭代格式的来源大概有以下几种方式: 1设 ],[)(2b a C x f ∈,对)(x f 在点],[0b a x ∈作泰勒展开: !2))((''))((')()(2 0000x x f x x x f x f x f -+-+=ξ 略去二次项,得到)(x f 的线性近似式: ))((')()(000x x x f x f x f -+≈。 由此得到方程=)(x f 0的近似根(假定 ≠)('0x f 0),)(')(000x f x f x x -= 即可构造出迭代格式(假定≠)('k x f 0):)(') (1k k k k x f x f x x -=+ 公式(3.4.1) 这就是牛顿迭代公式,若得到的序列{k x }收敛于α,则α就是非线性方程的根。 2 牛顿迭代法也称为牛顿切线法,这是由于)(x f 的线 性化近似函数)(x l =))((')(000x x x f x f -+是曲线y = )(x f 过点))(,(00x f x 的切线而得名的,求)(x f 的零点代之 以求)(x l 的零点,即切线)(x l 与x 轴交点的横坐标,如右图 所示,这就是牛顿切线法的几何解释。实际上,牛顿迭代法 也可以从几何意义上推出。利用牛顿迭代公式,由k x 得到1+k x ,从几何图形上看,就是过点))(,(k k x f x 作函数)(x f 的切线k l ,切线k l 与x 轴的交点就是1+k x ,所以有 1)()('+-=k k k k x x x f x f ,整理后也能得出牛顿迭代公式: )(') (1k k k k x f x f x x -=+。 3 要保证迭代法收敛,不管非线性方程=)(x f 0的形式如何,总可以构造: )()()(x f x k x x x -==? )0)((≠x k ? 作为方程求解的迭代函数。因为:)(')()()('1)('x f x k x f x k x --=? 而且)('x ?在根α附近越小,其局部收敛速度越快,故可令:0)('=α? %均差牛顿插值 function [ f y f0 ] = newton1( X,Y,x0 ) if nargin<3 error('Requires at least three input arguments.'); end if length(X)==length(Y) n=length(X); else error('length must equal') end syms x s=Y(1); l=1.0; y=zeros(n); y(1:n,1)=Y'; for i=2:n for j=2:i y(i,j)=(y(i,j-1)-y(j-1,j-1))/(X(i)-X(j-1)); if i==j l=l*(x-X(i-1)); s=s+y(i,i)*l; end end end f=simple(s); f0=subs(f,x0); function [ f f0 y] = newton2( X,Y,x0 ) if nargin<3 error('Requires at least three input arguments.'); end if length(X)==length(Y) n=length(X); else error('length must equal') end syms x s=Y(1); l=1.0; y=zeros(n) y(1:n,1)=Y'; for i=2:n for j=2:i y(i,j)=(y(i,j-1)-y(i-1,j-1))/(X(i)-X(i-j+1)); if i==j l=l*(x-X(i-1)); s=s+y(i,i)*l; end end end f=simple(s); f0=subs(f,x0); 中南大学 MATLAB程序设计实践学长有爱奉献,下载填上信息即可上交,没有下载券 的自行百度。所需m文件照本文档做即可,即新建(FILE)→脚本(NEW-Sscript)→复制本文档代码→运行(会跳出 保存界面,文件名默认不要修改,保存)→结果。第 一题需要把数据文本文档和m文件放在一起。全部测 试无误,放心使用。本文档针对做牛顿法求非线性函 数题目的同学,当然第一题都一样,所有人都可以用。 ←记得删掉这段话 班级: 学号: 姓名: 一、《MATLAB程序设计实践》Matlab基础 表示多晶体材料织构的三维取向分布函数(f=f(φ1,φ,φ2))是一个非常复杂的函数,难以精确的用解析函数表达,通常采用离散空间函数值来表示取向分布函数,是三维取向分布函数的一个实例。由于数据量非常大,不便于分析,需要借助图形来分析。请你编写一个matlab程序画出如下的几种图形来分析其取向分布特征:(1)用Slice函数给出其整体分布特征; (2)用pcolor或contour函数分别给出(φ2=0, 5, 10, 15, 20, 25, 30, 35 … 90)切面上f分布情况(需要用到subplot函数); (3) 用plot函数给出沿α取向线(φ1=0~90,φ=45,φ2=0)的f分布情况。 备注:数据格式说明 解: (1)将文件内的数据按照要求读取到矩阵f(phi1,phi,phi2)中,代码如下: fid=fopen(''); for i=1:18 tline=fgetl(fid); end phi1=1;phi=1;phi2=1;line=0; f=zeros(19,19,19); while ~feof(fid) tline=fgetl(fid); data=str2num(tline); line=line+1; if mod(line,20)==1 phi2=(data/5)+1; phi=1; 数据说明部分,与作图无关 此方向表示f 随着φ1从0,5,10,15, 20 …到90的变化而变化 此方向表示f 随着φ从0,5,10,15, 20 …到90的变化而变化 表示以下数据为φ2=0的数据,即f (φ1,φ,0) 牛顿迭代法c++程序设计 求解{0=x*x-2*x-y+0.5; 0=x*x+4*y*y-4; }的方程 #include 2008-12-08 12:30 利用梯度法和牛顿法编程求最优解(matlab) f(x)=x1^2+4*x2^2 x0=[2;2] e=0.002 利用梯度法和牛顿法编程求最优解 方法一.梯度法 function y=fun(x1,x2) y=x1^2+4*x2^2; %定义fun.m函数 clc syms x1 x2 d; f=x1^2+4*x2^2; fx1=diff(f,'x1'); fx2=diff(f,'x2'); x1=2; x2=2; for n=1:100 f0=subs(f); f1=subs(fx1); f2=subs(fx2); if (double(sqrt(f1^2+f2^2)) <= 0.002) n vpa(x1) vpa(x2) vpa(f0) break; else D=fun(x1-d*f1,x2-d*f2); Dd=diff(D,'d'); dd=solve(Dd); x1=x1-dd*f1; x2=x2-dd*f2; end end %结果n=10,x1=0.2223e-3,x2=-0.1390e-4,f0=0.5021e-7. 方法二.牛顿法 clc syms x1 x2 ; f=x1^2+4*x2^2; fx1=diff(f,'x1'); fx2=diff(f,'x2'); fx1x1=diff(fx1,'x1');fx1x2=diff(fx1,'x2');fx2x1=diff(fx2,'x1');fx2x2= diff(fx2,'x2'); x1=2; x2=2; for n=1:100 f0=subs(f); f1=subs(fx1); f2=subs(fx2); if (double(sqrt(f1^2+f2^2)) <= 0.002) n x1=vpa(x1,4) x2=vpa(x2,4) f0=vpa(f0,4) break; else X=[x1 x2]'-inv([fx1x1 fx1x2;fx2x1 fx2x2]) *[f1 f2]'; x1=X[1,1]; x2=X[2,1]; end end %结果 n=2,x1=0,x2=0,f0=0. 惩罚函数法(内点法、外点法)求解约束优化问题最优值编程 matlab 1 用外点法求下列问题的最优解 方法一:外点牛顿法: clc m=zeros(1,50);a=zeros(1,50);b=zeros(1,50);f0=zeros(1,50);%a b为最优点坐标,f0为最优点函数值,f1 f2最优点梯度。 syms x1 x2 e; %e为罚因子。m(1)=1;c=10;a(1)=0;b(1)=0; %c为递增系数。赋初值。 f=x1^2+x2^2+e*(1-x1)^2;f0(1)=1; fx1=diff(f,'x1');fx2=diff(f,'x2');fx1x1=diff(fx1,'x1');fx1x2=diff(fx1 ,'x2');fx2x1=diff(fx2,'x1');fx2x2=diff(fx2,'x2');%求偏导、海森元素。for k=1:100 %外点法e迭代循环. x1=a(k);x2=b(k);e=m(k); formatlab实现数值分析报告插值及积分
牛顿法非线性方程求解
matlab程序设计实践-牛顿法解非线性方程
最优化方法,汇总
matlab牛顿插值法例题与程序
最优化方法之修正牛顿法matlab源码(含黄金分割法寻找步长)
牛顿插值MATLAB算法
matlab最优化-牛顿法
改进的牛顿迭代法
最优化牛顿法最速下降法共轭梯度法matlab代码
牛顿插值法的MATLAB综合程序
牛顿迭代法求解非线性方程组的代码
牛顿-拉夫森(Newton-Raphson)迭代法 2
均差牛顿插值MATLAB,M文件
matlab程序设计实践-牛顿法解非线性方程
c++求解非线性方程组的牛顿顿迭代法
最优化 多目标优化 惩罚函数法 梯度法 牛顿法
