插值法数值上机实验报告

插值法数值上机实验报告
实验题目:
利用下列条件做插值逼近,并与R (x) 的图像比较
考虑函数:R x y=1
1+x2
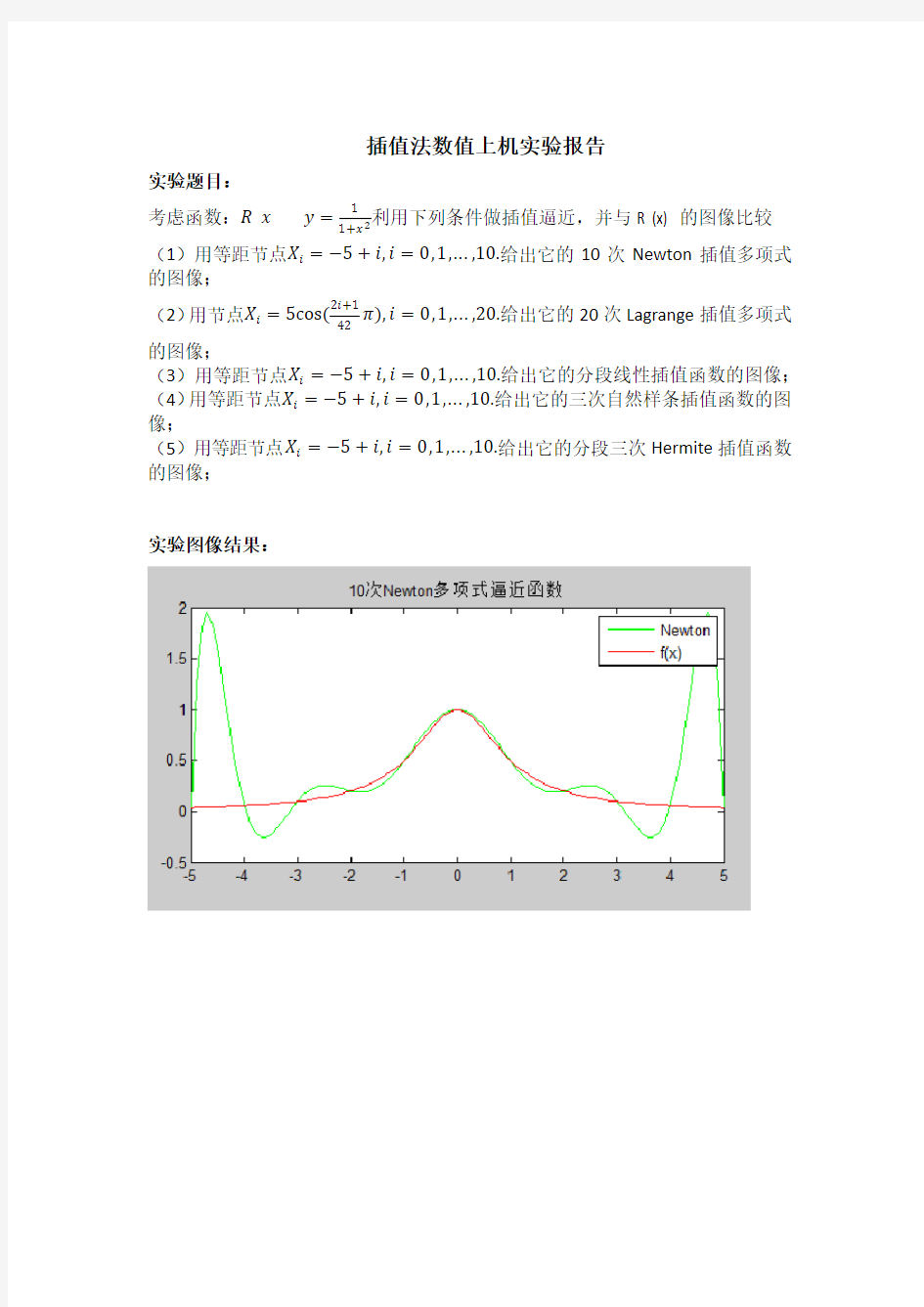
(1)用等距节点X i=?5+i,i=0,1,...,10.给出它的10次Newton插值多项式的图像;
π),i=0,1,...,20.给出它的20次Lagrange插值多项式(2)用节点X i=5cos(2i+1
42
的图像;
(3)用等距节点X i=?5+i,i=0,1,...,10.给出它的分段线性插值函数的图像;(4)用等距节点X i=?5+i,i=0,1,...,10.给出它的三次自然样条插值函数的图像;
(5)用等距节点X i=?5+i,i=0,1,...,10.给出它的分段三次Hermite插值函数的图像;
实验图像结果:
实验结果分析:
1.为了验证Range现象,我还特意做了10次牛顿插值多项式和20次牛顿插值多项式的对比图像,结果如下图(图对称,只截取一半)
可以看出,Range现象在高次时变得更加明显。这也是由于高次多项式在端点处的最值随次数的变大很明显。可以料定高次多项式在两侧端点处剧烈震荡,在更小的间距内急剧上升然后下降,Range现象非常明显。
2.分析实验(2)的结果,我们会惊讶地发现,由于取21个点逼近,原本预料的Range现象会很明显,但这里却和f(x)拟合的很好。(即下图中Lagrange p(x)的图像)。可是上图中取均匀节点的20次牛顿多项式逼近的效果在端点处却很差。料想是由于节点X i=5cos2i+1
42
π ,i=0,1,...,20 取得很好。由书上第五章的
知识,对于函数y=1
1+x ,y
1
2对应的cherbyshev多项式的根恰好为X i=
5cos2i+1
42
π ,i=0,1,...,20 。由于所学限制,未能深入分析。
(3)比较三次样条插值图像和Hermit插值图像对原函数图像的逼近情形。见下图:
初看上去,两者都逼近的很好,也都没有Range现象。
经放大后,局部来看:
在某些地方,分段三次Hermite插值比三次样条插值逼近效果更好。
分析如下:
三次样条插值函数只利用基点处的函数值,并未利用到导函数值,虽然要求二次连续可微,但这并不能保证逼近的好。而分段三次Hermite插值在每段区间上不但要求函数值相等,还要求导函数值相等,这就保证了插值函数在基点处图像与原函数相切,所以逼近效果更好。
注意到分段三次Hermite插值比三次样条插值利用了更多的条件,这也从另一个方面说明了其逼近效果理论上应该更好。
(4)分析三次自然样条插值函数的图像,我们会发现逼近的效果很好,且没有实验(1)中的Range现象。
但同时我也发现了三次自然样条方法特别依赖于选点,如果少了点,影响会很大。例如,在实现上图代码的基础上,将节点X i=?5+i,i=0,1,...,10.去除其中X=0的点,得到下面的图像:中间直接拟合的效果很差。(见下图)
是左右对称的,而恰好实验同时很依赖于节点的选取,由于这里原函数y=1
1+x2
所给的是等距左右对称的节点,所以效果才这么好,如果非等距对称节点效果会差不少。
4.对比三次Hermit插值和三次样条插值的图像:
实验中碰到的问题:
1.在编写实现第四个实验的程序时,由于不想在MATLAB中使用大量的for循环,特意使用MATLAB的向量化编程技巧。
例如:
但这里便没用到Honor算法,去算函数在作图点的值。所以此处应该还可以在优化。
2.在设计最后一题程序时,由于时间问题没有考虑优化算法,仅仅为了实现画图的功能,编的很冗杂。应该可以做大幅度的优化。
如下图:
3.初始时对Matlab运用不熟,时常有语法问题,比如“:”一不小心错用成“;”,导致运行结果故障。
程序实现:
本实验由MATLAB编程实现。
程序代码见后附文件。
说明:(共有八个函数文件)
1.Hermit_figure: 生成分段三次Hermit插值函数图形,并与原图形对比。
https://www.360docs.net/doc/1c815945.html,grange_function: 构造Lagrange插值函数,在后续Plot和Plot2中调用。
3.Newton_function: 构造Lagrange插值函数,在后续Plot和Plot2中调用。
4.Nspline_figure: 生成三次自然样条插值函数的图像,并与原图形对比。
5.Plot: 在同一个图中画Newton插值多项式图形(调用3)、Lagrange插值多项式图像(调用2)、分段线性图形、原函数图形。
6.Plot2:此文件用来在整个图像中生成前三问对应的子图(调用2和3)。
7.Plot3: 验证Range现象:比较Newton10次多项式和Newton20次多项式的图像(调用2)。
8.Plot4:生成自然三次样条插值的图形、原函数图形和Hermit插值多项式图形,并进行比较效果。
计算方法上机实验报告
《计算方法》上机实验报告 班级:XXXXXX 小组成员:XXXXXXX XXXXXXX XXXXXXX XXXXXXX 任课教师:XXX 二〇一八年五月二十五日
前言 通过进行多次的上机实验,我们结合课本上的内容以及老师对我们的指导,能够较为熟练地掌握Newton 迭代法、Jacobi 迭代法、Gauss-Seidel 迭代法、Newton 插值法、Lagrange 插值法和Gauss 求积公式等六种算法的原理和使用方法,并参考课本例题进行了MATLAB 程序的编写。 以下为本次上机实验报告,按照实验内容共分为六部分。 实验一: 一、实验名称及题目: Newton 迭代法 例2.7(P38):应用Newton 迭代法求 在 附近的数值解 ,并使其满足 . 二、解题思路: 设'x 是0)(=x f 的根,选取0x 作为'x 初始近似值,过点())(,00x f x 做曲线)(x f y =的切线L ,L 的方程为))((')(000x x x f x f y -+=,求出L 与x 轴交点的横坐标) (') (0001x f x f x x - =,称1x 为'x 的一次近似值,过点))(,(11x f x 做曲线)(x f y =的切线,求该切线与x 轴的横坐标) (') (1112x f x f x x - =称2x 为'x
的二次近似值,重复以上过程,得'x 的近似值序列{}n x ,把 ) (') (1n n n n x f x f x x - =+称为'x 的1+n 次近似值,这种求解方法就是牛顿迭代法。 三、Matlab 程序代码: function newton_iteration(x0,tol) syms z %定义自变量 format long %定义精度 f=z*z*z-z-1; f1=diff(f);%求导 y=subs(f,z,x0); y1=subs(f1,z,x0);%向函数中代值 x1=x0-y/y1; k=1; while abs(x1-x0)>=tol x0=x1; y=subs(f,z,x0); y1=subs(f1,z,x0); x1=x0-y/y1;k=k+1; end x=double(x1) K 四、运行结果: 实验二:
数据分析实验报告
数据分析实验报告 文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-
第一次试验报告 习题1.3 1建立数据集,定义变量并输入数据并保存。 2数据的描述,包括求均值、方差、中位数等统计量。 分析—描述统计—频率,选择如下: 输出: 统计量 全国居民 农村居民 城镇居民 N 有效 22 22 22 缺失 均值 1116.82 747.86 2336.41 中值 727.50 530.50 1499.50 方差 1031026.918 399673.838 4536136.444 百分位数 25 304.25 239.75 596.25 50 727.50 530.50 1499.50 75 1893.50 1197.00 4136.75 3画直方图,茎叶图,QQ 图。(全国居民) 分析—描述统计—探索,选择如下: 输出: 全国居民 Stem-and-Leaf Plot Frequency Stem & Leaf 5.00 0 . 56788 数据分析实验报告 【最新资料,WORD 文档,可编辑修改】
2.00 1 . 03 1.00 1 . 7 1.00 2 . 3 3.00 2 . 689 1.00 3 . 1 Stem width: 1000 Each leaf: 1 case(s) 分析—描述统计—QQ图,选择如下: 输出: 习题1.1 4数据正态性的检验:K—S检验,W检验数据: 取显着性水平为0.05 分析—描述统计—探索,选择如下:(1)K—S检验
结果:p=0.735 大于0.05 接受原假设,即数据来自正太总体。 (2 )W 检验 结果:在Shapiro-Wilk 检验结果972.00 w ,p=0.174大于0.05 接受原假设,即数据来自正太总体。 习题1.5 5 多维正态数据的统计量 数据:
数值分析实验报告1
实验一误差分析 实验1.1(病态问题) 实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。通过本实验可获得一个初步体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 问题提出:考虑一个高次的代数多项式 显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。现考虑该多项式的一个扰动 其中ε(1.1)和(1.221,,,a a 的输出b ”和“poly ε。 (1(2 (3)写成展 关于α solve 来提高解的精确度,这需要用到将多项式转换为符号多项式的函数poly2sym,函数的具体使用方法可参考Matlab 的帮助。 实验过程: 程序: a=poly(1:20); rr=roots(a); forn=2:21 n form=1:9 ess=10^(-6-m);
ve=zeros(1,21); ve(n)=ess; r=roots(a+ve); -6-m s=max(abs(r-rr)) end end 利用符号函数:(思考题一)a=poly(1:20); y=poly2sym(a); rr=solve(y) n
很容易的得出对一个多次的代数多项式的其中某一项进行很小的扰动,对其多项式的根会有一定的扰动的,所以对于这类病态问题可以借助于MATLAB来进行问题的分析。 学号:06450210 姓名:万轩 实验二插值法
数据库上机实验报告
数据库实验 (第三次) 题目1 实验内容: 1. 检索上海产的零件的工程名称; 2. 检索供应工程J1零件P1的供应商号SNO; 3. 检索供应工程J1零件为红色的供应商号SNO; 4. 检索没有使用天津生产的红色零件的工程号JNO; 5. 检索至少用了供应商S1所供应的全部零件的工程号JNO; 6. 检索购买了零件P1的工程项目号JNO及数量QTY,并要求对查询的结果按数 量QTY降序排列。
1 select jname from j where jno in (select jno from spj where sno in (select sno from s where city ='上海' ) ); 2 select sno from spj where jno ='j1'and pno ='p1' 3
selectdistinct sno from spj where pno in (select pno from p where color='红'and pno in (select pno from spj where jno ='j1' ) ); 4 selectdistinct jno from spj where pno notin (select pno from p where color ='红'and pno in (select pno from spj where sno in (select sno from s where city ='天津' ) ) )
5 select jno from spj where sno ='s1' 6 select jno,qty from spj where pno ='p1' orderby qty desc 四﹑思考题 1.如何提高数据查询和连接速度。 建立视图 2. 试比较连接查询和嵌套查询 有些嵌套查询是可以用连接来代替的,而且使用连接的方式,性能要比 嵌套查询高出很多 当查询涉及多个关系时,用嵌套查询逐步求解结构层次清楚,易于构造,具有结构化程序设计的优点。但是相比于连接运算,目前商用关系数据库管理系统对嵌套查询的优化做的还不够完善,所以在实际应用中,能够用连接运算表达的查询尽可能采用连接运算。
数值分析实验报告
数值分析实验报告 姓名:周茹 学号: 912113850115 专业:数学与应用数学 指导老师:李建良
线性方程组的数值实验 一、课题名字:求解双对角线性方程组 二、问题描述 考虑一种特殊的对角线元素不为零的双对角线性方程组(以n=7为例) ?????????? ?????? ? ???? ?d a d a d a d a d a d a d 766 55 44 3 32 211??????????????????????x x x x x x x 7654321=?????????? ? ???????????b b b b b b b 7654321 写出一般的n (奇数)阶方程组程序(不要用消元法,因为不用它可以十分方便的解出这个方程组) 。 三、摘要 本文提出解三对角矩阵的一种十分简便的方法——追赶法,该算法适用于任意三对角方程组的求解。 四、引言 对于一般给定的d Ax =,我们可以用高斯消去法求解。但是高斯消去法过程复杂繁琐。对于特殊的三对角矩阵,如果A 是不可约的弱对角占优矩阵,可以将A 分解为UL ,再运用追赶法求解。
五、计算公式(数学模型) 对于形如????? ?? ????? ??? ?---b a c b a c b a c b n n n n n 111 2 2 2 11... ... ...的三对角矩阵UL A =,容易验证U 、L 具有如下形式: ??????? ????? ??? ?=u a u a u a u n n U ...... 3 3 22 1 , ?? ????? ? ?? ??????=1 (1) 1132 1l l l L 比较UL A =两边元素,可以得到 ? ?? ??-== = l a b u u c l b u i i i i i i 111 i=2, 3, ... ,n 考虑三对角线系数矩阵的线性方程组 f Ax = 这里()T n x x x x ... 2 1 = ,()T n f f f f ... 2 1 = 令y Lx =,则有 f Uy = 于是有 ()?????-== --u y a f y u f y i i i i i 1 1 11 1 * i=2, 3, ... ,n 再根据y Lx =可得到
计算方法第二章方程求根上机报告
实验报告名称 班级:学号:姓名:成绩: 1实验目的 1)通过对二分法与牛顿迭代法作编程练习与上级运算,进一步体会二分法与牛顿迭代法的不同特点。 2)编写割线迭代法的程序,求非线性迭代法的解,并与牛顿迭代法。 2 实验内容 用牛顿法和割线法求下列方程的根 x^2-e^x=0; x*e^x-1=0; lgx+x-2=0; 3实验步骤 1)根据二分法和牛顿迭代法,割线法的算法编写相应的求根函数; 2)将题中所给参数带入二分法函数,确定大致区间; 3)用牛顿迭代法和割线法分别对方程进行求解; 3 程序设计 牛顿迭代法x0=1.0; N=100; k=0; eps=5e-6; delta=1e-6; while(1) x1=x0-fc1(x0)/fc2(x0); k=k+1; if k>N disp('Newmethod failed')
break end if(abs(x1-x0) 实验四数组、指针与字符串 1.实验目的 1.学习使用数组 2.学习字符串数据的组织和处理 3.学习标准C++库的使用 4.掌握指针的使用方法 5.练习通过Debug观察指针的内容及其所指的对象的内容 6.联系通过动态内存分配实现动态数组,并体会指针在其中的作用 7.分别使用字符数组和标准C++库练习处理字符串的方法 2.实验要求 1.编写并测试3*3矩阵转置函数,使用数组保存3*3矩阵。 2.使用动态内存分配生成动态数组来重新完成上题,使用指针实现函数的功能。 3.编程实现两字符串的连接。要求使用字符数组保存字符串,不要使用系统函数。 4.使用string类定义字符串对象,重新实现上一小题。 5.定义一个Employee类,其中包括姓名、街道地址、城市和邮编等属性,以及change_name()和display()等函数。Display()显示姓名、街道地址、城市和邮编等属性,change_name()改变对象的姓名属性。实现并测试这个类。 6.定义包含5个元素的对象数组,每个元素都是Employee类型的对象。 7. (选做)修改实验4中的选做实验中的people(人员)类。具有的属性如下:姓名char name[11]、编号char number[7]、性别char sex[3]、生日birthday、身份证号char id[16]。其中“出生日期”定义为一个“日期”类内嵌对象。用成员函数实现对人员信息的录入和显示。要求包括:构造函数和析构函数、拷贝构造函数、内联成员函数、聚集。在测试程序中定义people类的对象数组,录入数据并显示。 3.实验内容及实验步骤 1.编写矩阵转置函数,输入参数为3*3整形数组,使用循环语句实现矩阵元素的行列对调,注意在循环语句中究竟需要对哪些元素进行操作,编写main()函数实现输入、输出。程序名:lab6_1.cpp。 2.改写矩阵转置函数,参数为整型指针,使用指针对数组元素进行操作,在main()函数中使用new操作符分配内存生成动态数组。通过Debug观察指针的内容及其所指的对象中的内容。程序名:lab6_2.cpp。 3.编程实现两字符串的连接。定义字符数组保存字符串,在程序中提示用户输入两个字符串,实现两个字符串的连接,最后用cout语句显示输出。程序名:lab6_3.cpp。用cin实现输入,注意,字符串的结束标志是ASCII码0,使用循环语句进行字符串间的字符拷贝。 4.使用string类定义字符串对象,编程实现两字符串的连接。在string类中已重载了运算符“+=”实现字符串的连接,可以使用这个功能。程序名:lab6_4.cpp。 5.在employee.h文件中定义Employee类。Employee类具有姓名、街道地址、城市和邮编等私有数据成员,在成员函数中,构造函数用来初始化所有数据成员;display()中使用cout显示 (此文档为word格式,下载后您可任意编辑修改!) 2012级6班###(学号)计算机数值方法 实验报告成绩册 姓名:宋元台 学号: 成绩: 数值计算方法与算法实验报告 学期: 2014 至 2015 第 1 学期 2014年 12月1日课程名称: 数值计算方法与算法专业:信息与计算科学班级 12级5班 实验编号: 1实验项目Neton插值多项式指导教师:孙峪怀 姓名:宋元台学号:实验成绩: 一、实验目的及要求 实验目的: 掌握Newton插值多项式的算法,理解Newton插值多项式构造过程中基函数的继承特点,掌握差商表的计算特点。 实验要求: 1. 给出Newton插值算法 2. 用C语言实现算法 二、实验内容 三、实验步骤(该部分不够填写.请填写附页) 1.算法分析: 下面用伪码描述Newton插值多项式的算法: Step1 输入插值节点数n,插值点序列{x(i),f(i)},i=1,2,……,n,要计算的插值点x. Step2 形成差商表 for i=0 to n for j=n to i f(j)=((f(j)-f(j-1)(x(j)-x(j-1-i)); Step3 置初始值temp=1,newton=f(0) Step4 for i=1 to n temp=(x-x(i-1))*temp*由temp(k)=(x-x(k-1))*temp(k-1)形成 (x-x(0).....(x-x(i-1)* Newton=newton+temp*f(i); Step5 输出f(x)的近似数值newton(x)=newton. 2.用C语言实现算法的程序代码 #include 数值分析上机实验报告 《数值分析》上机实验报告 1.用Newton 法求方程 X 7-X 4+14=0 在(0.1,1.9)中的近似根(初始近似值取为区间端点,迭代6次或误差小于0.00001)。 1.1 理论依据: 设函数在有限区间[a ,b]上二阶导数存在,且满足条件 {}α?上的惟一解在区间平方收敛于方程所生的迭代序列 迭代过程由则对任意初始近似值达到的一个中使是其中上不变号 在区间],[0)(3,2,1,0,) (') ()(],,[x |))(),((|,|,)(||)(|.4;0)(.3],[)(.20 )()(.110......b a x f x k x f x f x x x Newton b a b f a f mir b a c x f a b c f x f b a x f b f x f k k k k k k ==- ==∈≤-≠>+ 令 )9.1()9.1(0)8(4233642)(0)16(71127)(0)9.1(,0)1.0(,1428)(3 2 2 5 333647>?''<-=-=''<-=-='<>+-=f f x x x x x f x x x x x f f f x x x f 故以1.9为起点 ?? ?? ? ='- =+9.1)()(01x x f x f x x k k k k 如此一次一次的迭代,逼近x 的真实根。当前后两个的差<=ε时,就认为求出了近似的根。本程序用Newton 法求代数方程(最高次数不大于10)在(a,b )区间的根。 1.2 C语言程序原代码: #include 实验一 误差分析 实验(病态问题) 实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。通过本实验可获得一个初步体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 问题提出:考虑一个高次的代数多项式 )1.1() ()20()2)(1()(20 1∏=-=---=k k x x x x x p 显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。现考虑该多项式的一个扰动 )2.1(0 )(19=+x x p ε 其中ε是一个非常小的数。这相当于是对()中19x 的系数作一个小的扰动。我们希望比较()和()根的差别,从而分析方程()的解对扰动的敏感性。 实验内容:为了实现方便,我们先介绍两个Matlab 函数:“roots ”和“poly ”。 roots(a)u = 其中若变量a 存储n+1维的向量,则该函数的输出u 为一个n 维的向量。设a 的元素依次为121,,,+n a a a ,则输出u 的各分量是多项式方程 01121=+++++-n n n n a x a x a x a 的全部根;而函数 poly(v)b = 的输出b 是一个n+1维变量,它是以n 维变量v 的各分量为根的多项式的系数。可见“roots ”和“poly ”是两个互逆的运算函数。 ;000000001.0=ess );21,1(zeros ve = ;)2(ess ve = ))20:1((ve poly roots + 上述简单的Matlab 程序便得到()的全部根,程序中的“ess ”即是()中的ε。 实验要求: (1)选择充分小的ess ,反复进行上述实验,记录结果的变化并分析它们。 如果扰动项的系数ε很小,我们自然感觉()和()的解应当相差很小。计算中你有什么出乎意料的发现表明有些解关于如此的扰动敏感性如何 (2)将方程()中的扰动项改成18x ε或其它形式,实验中又有怎样的现象 出现 (3)(选作部分)请从理论上分析产生这一问题的根源。注意我们可以将 方程()写成展开的形式, ) 3.1(0 ),(1920=+-= x x x p αα 同时将方程的解x 看成是系数α的函数,考察方程的某个解关于α的扰动是否敏感,与研究它关于α的导数的大小有何关系为什么你发现了什么现象,哪些根关于α的变化更敏感 思考题一:(上述实验的改进) 在上述实验中我们会发现用roots 函数求解多项式方程的精度不高,为此你可以考虑用符号函数solve 来提高解的精确度,这需要用到将多项式转换为符号多项式的函数poly2sym,函数的具体使用方法可参考Matlab 的帮助。 课题一:拉格朗日插值法 1.实验目的 1.学习和掌握拉格朗日插值多项式。 2.运用拉格朗日插值多项式进行计算。 2.实验过程 作出插值点(1.00,0.00),(-1.00,-3.00),(2.00,4.00)二、算法步骤 已知:某些点的坐标以及点数。 输入:条件点数以及这些点的坐标。 输出:根据给定的点求出其对应的拉格朗日插值多项式的值。 3.程序流程: (1)输入已知点的个数; (2)分别输入已知点的X坐标; (3)分别输入已知点的Y坐标; 程序如下: #include 插值算法*/ { int i,j; float *a,yy=0.0; /*a作为临时变量,记录拉格朗日插值多项*/ a=(float*)malloc(n*sizeof(float)); for(i=0;i<=n-1;i++) { a[i]=y[i]; for(j=0;j<=n-1;j++) if(j!=i) a[i]*=(xx-x[j])/(x[i]-x[j]); yy+=a[i]; } free(a); return yy; } int main() { int i; int n; float x[20],y[20],xx,yy; printf("Input n:"); scanf("%d",&n); if(n<=0) { printf("Error! The value of n must in (0,20)."); getch();return 1; } for(i=0;i<=n-1;i++) { printf("x[%d]:",i); scanf("%f",&x[i]); } printf("\n"); for(i=0;i<=n-1;i++) { printf("y[%d]:",i);scanf("%f",&y[i]); } printf("\n"); printf("Input xx:"); scanf("%f",&xx); yy=lagrange(x,y,xx,n); printf("x=%f,y=%f\n",xx,yy); getch(); } 举例如下:已知当x=1,-1,2时f(x)=0,-3,4,求f(1.5)的值。 计算方法实验报告 班级: 学号: 姓名: 成绩: 1 舍入误差及稳定性 一、实验目的 (1)通过上机编程,复习巩固以前所学程序设计语言及上机操作指令; (2)通过上机计算,了解舍入误差所引起的数值不稳定性 二、实验内容 1、用两种不同的顺序计算10000 21n n -=∑,分析其误差的变化 2、已知连分数() 1 01223//(.../)n n a f b b a b a a b =+ +++,利用下面的算法计算f : 1 1 ,i n n i i i a d b d b d ++==+ (1,2,...,0 i n n =-- 0f d = 写一程序,读入011,,,...,,,...,,n n n b b b a a 计算并打印f 3、给出一个有效的算法和一个无效的算法计算积分 1 041 n n x y dx x =+? (0,1,...,1 n = 4、设2 2 11N N j S j == -∑ ,已知其精确值为1311221N N ?? -- ?+?? (1)编制按从大到小的顺序计算N S 的程序 (2)编制按从小到大的顺序计算N S 的程序 (3)按两种顺序分别计算10001000030000,,,S S S 并指出有效位数 三、实验步骤、程序设计、实验结果及分析 1、用两种不同的顺序计算10000 2 1n n -=∑,分析其误差的变化 (1)实验步骤: 分别从1~10000和从10000~1两种顺序进行计算,应包含的头文件有stdio.h 和math.h (2)程序设计: a.顺序计算 #include 数据分析实验报告 【最新资料,WORD文档,可编辑修改】 第一次试验报告 习题1.3 1建立数据集,定义变量并输入数据并保存。 2数据的描述,包括求均值、方差、中位数等统计量。 分析—描述统计—频率,选择如下: 输出: 方差1031026.918399673.8384536136.444百分位数25304.25239.75596.25 50727.50530.501499.50 751893.501197.004136.75 3画直方图,茎叶图,QQ图。(全国居民) 分析—描述统计—探索,选择如下: 输出: 全国居民Stem-and-Leaf Plot Frequency Stem & Leaf 9.00 0 . 122223344 5.00 0 . 56788 2.00 1 . 03 1.00 1 . 7 1.00 2 . 3 3.00 2 . 689 1.00 3 . 1 Stem width: 1000 Each leaf: 1 case(s) 分析—描述统计—QQ图,选择如下: 输出: 习题1.1 4数据正态性的检验:K—S检验,W检验数据: 取显着性水平为0.05 分析—描述统计—探索,选择如下:(1)K—S检验 单样本Kolmogorov-Smirnov 检验 身高N60正态参数a,,b均值139.00 标准差7.064 最极端差别绝对值.089 正.045 负-.089 Kolmogorov-Smirnov Z.686 渐近显着性(双侧).735 a. 检验分布为正态分布。 b. 根据数据计算得到。 结果:p=0.735 大于0.05 接受原假设,即数据来自正太总体。(2)W检验 数值分析实验报告模板 篇一:数值分析实验报告(一)(完整) 数值分析实验报告 1 2 3 4 5 篇二:数值分析实验报告 实验报告一 题目:非线性方程求解 摘要:非线性方程的解析解通常很难给出,因此线性方程的数值解法就尤为重要。本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。利用二分法求解给定非线性方程的根,在给定的范围内,假设f(x,y)在[a,b]上连续,f(a)xf(b) 直接影响迭代的次数甚至迭代的收敛与发散。即若x0 偏离所求根较远,Newton法可能发散的结论。并且本实验中还利用利用改进的Newton法求解同样的方程,且将结果与Newton法的结果比较分析。 前言:(目的和意义) 掌握二分法与Newton法的基本原理和应用。掌握二分法的原理,验证二分法,在选对有根区间的前提下,必是收 敛,但精度不够。熟悉Matlab语言编程,学习编程要点。体会Newton使用时的优点,和局部收敛性,而在初值选取不当时,会发散。 数学原理: 对于一个非线性方程的数值解法很多。在此介绍两种最常见的方法:二分法和Newton法。 对于二分法,其数学实质就是说对于给定的待求解的方程f(x),其在[a,b]上连续,f(a)f(b) Newton法通常预先要给出一个猜测初值x0,然后根据其迭代公式xk?1?xk?f(xk) f'(xk) 产生逼近解x*的迭代数列{xk},这就是Newton法的思想。当x0接近x*时收敛很快,但是当x0选择不好时,可能会发散,因此初值的选取很重要。另外,若将该迭代公式改进为 xk?1?xk?rf(xk) 'f(xk) 其中r为要求的方程的根的重数,这就是改进的Newton 法,当求解已知重数的方程的根时,在同种条件下其收敛速度要比Newton法快的多。 程序设计: 本实验采用Matlab的M文件编写。其中待求解的方程写成function的方式,如下 function y=f(x); 实验报告一 题目:非线性方程求解 摘要:非线性方程的解析解通常很难给出,因此线性方程的数值解法就尤为重要。本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。 前言:(目的和意义) 掌握二分法与Newton法的基本原理和应用。 数学原理: 对于一个非线性方程的数值解法很多。在此介绍两种最常见的方法:二分法和Newton法。 对于二分法,其数学实质就是说对于给定的待求解的方程f(x),其在[a,b]上连续,f(a)f(b)<0,且f(x)在[a,b]内仅有一个实根x*,取区间中点c,若,则c恰为其根,否则根据f(a)f(c)<0是否成立判断根在区间[a,c]和[c,b]中的哪一个,从而得出新区间,仍称为[a,b]。重复运行计算,直至满足精度为止。这就是二分法的计算思想。 Newton法通常预先要给出一个猜测初值x0,然后根据其迭代公式 产生逼近解x*的迭代数列{x k},这就是Newton法的思想。当x0接近x*时收敛很快,但是当x0选择不好时,可能会发散,因此初值的选取很重要。另外,若将该迭代公式改进为 其中r为要求的方程的根的重数,这就是改进的Newton法,当求解已知重数的方程的根时,在同种条件下其收敛速度要比Newton法快的多。 程序设计: 本实验采用Matlab的M文件编写。其中待求解的方程写成function的方式,如下 function y=f(x); y=-x*x-sin(x); 写成如上形式即可,下面给出主程序。 二分法源程序: clear %%%给定求解区间 b=1.5; a=0; %%%误差 R=1; k=0;%迭代次数初值 while (R>5e-6) ; c=(a+b)/2; if f12(a)*f12(c)>0; a=c; else b=c; end R=b-a;%求出误差 k=k+1; end x=c%给出解 Newton法及改进的Newton法源程序:clear %%%% 输入函数 f=input('请输入需要求解函数>>','s') %%%求解f(x)的导数 df=diff(f); 实验一——插值方法 实验学时:4 实验类型:设计 实验要求:必修 一 实验目的 通过本次上机实习,能够进一步加深对各种插值算法的理解;学会使用用三种类型的插值函数的数学模型、基本算法,结合相应软件(如VC/VB/Delphi/Matlab/JAVA/Turbo C )编程实现数值方法的求解。并用该软件的绘图功能来显示插值函数,使其计算结果更加直观和形象化。 二 实验内容 通过程序求出插值函数的表达式是比较麻烦的,常用的方法是描出插值曲线上尽量密集的有限个采样点,并用这有限个采样点的连线,即折线,近似插值曲线。取点越密集,所得折线就越逼近理论上的插值曲线。本实验中将所取的点的横坐标存放于动态数组[]X n 中,通过插值方法计算得到的对应纵坐标存放 于动态数组[]Y n 中。 以Visual C++.Net 2005为例。 本实验将Lagrange 插值、Newton 插值和三次样条插值实现为一个C++类CInterpolation ,并在Button 单击事件中调用该类相应函数,得出插值结果并画出图像。CInterpolation 类为 class CInterpolation { public : CInterpolation();//构造函数 CInterpolation(float *x1, float *y1, int n1);//结点横坐标、纵坐标、下标上限 ~ CInterpolation();//析构函数 ………… ………… int n, N;//结点下标上限,采样点下标上限 float *x, *y, *X;//分别存放结点横坐标、结点纵坐标、采样点横坐标 float *p_H,*p_Alpha,*p_Beta,*p_a,*p_b,*p_c,*p_d,*p_m;//样条插值用到的公有指针,分别存放 i h ,i α,i β,i a ,i b ,i c ,i d 和i m }; 其中,有参数的构造函数为 CInterpolation(float *x1, float *y1, int n1) { //动态数组x1,y1中存放结点的横、纵坐标,n1是结点下标上限(即n1+1个结点) n=n1; N=x1[n]-x1[0]; X=new float [N+1]; x=new float [n+1]; y=new float [n+1]; 《数据库技术与应用》上机实验报告 姓名:谢优贤 学号:020******* 专业班级:安全工程1003班 通过这次上机实验,我做了学生信息管理系统数据库,通过创建表、查询、窗体、报表和宏对输入数据库中的学生的基本信息进行整理和操作,以便得到我们想要的信息。学生信息管理系统可以实现对学生的基本信息:学号、姓名、联系方式、性别、成绩等的查询,还有对教师的情况进行比较了解从而可以帮助学生更好地选课和学习,省去了纸质档案管理不方便的方面。 通过窗体的创建和美化,使我们在操作数据时有一个简洁明了美观的窗口,简化了用户的操作程序,方便用户的使用。报表的创建可以使用户想要的数据很好地呈现在纸上。使用宏命令还使数据库有了设置密码的功能,很好的保护了数据的使用权限;也可以使用宏命令打开我们希望打开的窗口。 一、主要上机内容 1. 数据库的创建: 我使用自行创建数据库的方式进行创建,数据库文件名为学生信息管理系统。数据库要实现的主要功能:学生基本信息及学习成绩情况的统计,通过窗体进行学生信息的查询、学生信息及成绩的普通查询、打印学生信息报表等。 2. 表的创建: 基本表为学生信息表、学生成绩表、教师信息表、课程信息表等均使用设计器创建表学生信息表的记录: 学生信息表结构: 在学生信息表中设置了学号为主键,为了方便输入又在学号字段中设置了掩码(如下图) 学生年龄一般不会太大或太小,于是为了防止填写信息时出错,添加了有效性规则 性别只有男和女之分,于是为了方便,选择了查询向导 同样在入学日期和电话字段也设置了输入掩码 头像属于图片类型,其数据类型为“OLE对象”,所得荣誉和自我介绍选择了“备注”类 序言 数值分析是计算数学的范畴,有时也称它为计算数学、计算方法、数值方法等,其研究对象是各种数学问题的数值方法的设计、分析及其有关的数学理论和具体实现的一门学科,它是一个数学分支。是科学与工程计算(科学计算)的理论支持。许多科学与工程实际问题(核武器的研制、导弹的发射、气象预报)的解决都离不开科学计算。目前,试验、理论、计算已成为人类进行科学活动的三大方法。 数值分析是计算数学的一个主要部分,计算数学是数学科学的一个分支,它研究用计算机求解各种数学问题的数值计算方法及其理论与软件实现。现在面向数值分析问题的计算机软件有:C,C++,MATLAB,Python,Fortran等。 MATLAB是matrix laboratory的英文缩写,它是由美国Mathwork公司于1967年推出的适合用于不同规格计算机和各种操纵系统的数学软件包,现已发展成为一种功能强大的计算机语言,特别适合用于科学和工程计算。目前,MATLAB应用非常广泛,主要用于算法开发、数据可视化、数值计算和数据分析等,除具备卓越的数值计算能力外,它还提供了专业水平的符号计算,文字处理,可视化建模仿真和实时控制等功能。 本实验报告使用了MATLAB软件。对不动点迭代,函数逼近(lagrange插值,三次样条插值,最小二乘拟合),追赶法求解矩阵的解,4RungeKutta方法求解,欧拉法及改进欧拉法等算法做了简单的计算模拟实践。并比较了各种算法的优劣性,得到了对数值分析这们学科良好的理解,对以后的科研数值分析能力有了极大的提高。 目录 序言 (1) 问题一非线性方程数值解法 (3) 1.1 计算题目 (3) 1.2 迭代法分析 (3) 1.3计算结果分析及结论 (4) 问题二追赶法解三对角矩阵 (5) 2.1 问题 (5) 2.2 问题分析(追赶法) (6) 2.3 计算结果 (7) 问题三函数拟合 (7) 3.1 计算题目 (7) 3.2 题目分析 (7) 3.3 结果比较 (12) 问题四欧拉法解微分方程 (14) 4.1 计算题目 (14) 4.2.1 方程的准确解 (14) 4.2.2 Euler方法求解 (14) 4.2.3改进欧拉方法 (16) 问题五四阶龙格-库塔计算常微分方程初值问题 (17) 5.1 计算题目 (17) 5.2 四阶龙格-库塔方法分析 (18) 5.3 程序流程图 (18) 5.4 标准四阶Runge-Kutta法Matlab实现 (19) 5.5 计算结果及比较 (20) 问题六舍入误差观察 (22) 6.1 计算题目 (22) 6.2 计算结果 (22) 6.3 结论 (23) 7 总结 (24) 附录 计算方法上机实验报告——拉格朗日插值问题 一、方法原理 n次拉格朗日插值多项式为:Ln(x)=y0l0(x)+y1l1(x)+y2l2(x)+…+ynln(x) n=1时,称为线性插值,L1(x)=y0(x-x1)/(x0-x1)+y1(x-x0)/(x1-x0)=y0+(y1-x0)(x-x0)/(x1-x0) n=2时,称为二次插值或抛物线插值,精度相对高些 L2(x)=y0(x-x1)(x-x2)/(x0-x1)/(x0-x2)+y1(x-x0)(x-x2)/(x1-x0)/(x1-x 2)+y2(x-x0)(x-x1)/(x2-x0)/(x2-x1) 二、主要思路 使用线性方程组求系数构造插值公式相对复杂,可改用构造方法来插值。 对节点xi(i=0,1,…,n)中任一点xk(0<=k<=n)作一n次多项式lk(xk),使它在该点上取值为1,而在其余点xi(i=0,1,…,k-1,k+1,…,n)上为0,则插值多项式为Ln(x)=y0l0(x)+y1l1(x)+y2l2(x)+…+ynln(x) 上式表明:n个点xi(i=0,1,…,k-1,k+1,…,n)都是lk(x)的零点。可求得lk 三.计算方法及过程:1.输入节点的个数n 2.输入各个节点的横纵坐标 3.输入插值点 4.调用函数,返回z 函数语句与形参说明 程序源代码如下: 形参与函数类型 参数意义 intn 节点的个数 doublex[n](double*x) 存放n个节点的值 doubley[n](double*y) 存放n个节点相对应的函数值 doublep 指定插值点的值 doublefun() 函数返回一个双精度实型函数值,即插值点p处的近似函数值 #includeC上机实验报告实验四
数值计算实验报告
数值分析上机实验报告
数值分析实验报告1
数值分析拉格朗日插值法上机实验报告
计算方法上机实习题大作业(实验报告).
数据分析实验报告
数值分析实验报告模板
(完整版)哈工大-数值分析上机实验报告
计算方法实验报告册
数据库上机实验报告
数值分析2016上机实验报告
计算方法上机实验报告——拉格朗日插值问题
