线性代数第1章行列式试卷及答案

第一章行列式

一、单项选择题

1.行列式D 非零的充分条件是( D )

(A) D 的所有元素非零 (B) D 至少有n 个元素非零 (C) D 的任何两行元素不成比例

(D)以D 为系数矩阵的非齐次线性方程组有唯一解 2．二阶行列式

21--k k ≠0的充分必要条件是（ C ）

A ．k ≠-1

B ．k ≠3

C ．k ≠-1且k ≠3

D ．k ≠-1或≠3 3．已知2阶行列式

1b a b a =m ,

1c b c b =n ,则

111c a b c a b ++=（ B ）

+n （m+n ）

4.设行列式==1

11103

222,1111304z y x z

y x 则行列式（ A ） A.32

D.3

8 5．下列行列式等于零的是(D )

A .100123123- B. 031010300- C ． 100003010- D ． 2

61422613-

6．行列式

101111011110------第二行第一列元素的代数余子式21A =（ B ）

A ．-2

B ．-1

C ．1

D ．2

8．如果方程组??

??=+=-=-+0404033232321kx x x x x kx x 有非零解,则 k =（ B ）

9．（考研题）行列式

0000000

b a b

d c d

=（ B ）

A.()2ad bc -

B.()

2ad bc --

C.2222a d b c -

D.2222

b c a d -

二、填空题

1.四阶行列式中带负号且含有因子12a 和21a 的项为 44332112a a a a 。

2. 行列式11

44916

中（3，2）元素的代数余子式A 32=___-2___.

3. 设7

43690211

8751----=

D ，则5A 14

A 24+A 44=_______。

解答：5A 14+A 24+A 44=

1501

3430

90211

5751-=---

4．已知行列式01

110321

2=-a ，则数a =____3______.

5．若a ,b 是实数，则当a =___且b =___时，有=---10100

a b b a 0。

解答：0)(1

0100

22=+-=--=---b a a

b b

a a

b b a a =0, b =0

6. 设1

4321322

)(+--+-+=

x x x x f ，则2x 的系数为 23 。

7. 五阶行列式=6

200357020381002

300031000___________。

解答：4232

331)1(6

200357020381002

30003100032=??

-=?

8. （考研题）多项式2

1111

)(32

3213

21321+++++=

x a a a a x a a a a x a a a a x f 的所有零

点为 01=x ，12-=x ，23-=x 。

9、（考研题）设x

c b

d x

b d

c x

b d

c b

x x f =

)(，则方程0)(=x f 的根为=x 。

【分析】 )(x f 是关于x 的四次多项式，故方程0)(=x f 应有四根，利用行列式的性质知，当d c b x ,,=时，分别会出现两行相等的情况，所以行列式为零，故d c b x ,,=是方程的三个根。

再将后三列均加到第一列上去可以提取一个公因子为

d c b x +++，所以当)(d c b x ++-=时，满足0)(=x f ，所以得方程的

第四根)(d c b x ++-=。

故方程的四个根分别是：)(,,,d c b d c b ++-。二、计算题

1、计算000100

0200020120002013000

002014

D =

。

【分析】方法一：此行列式刚好只有n 个非零元素

nn n n n a a a a ,,,,112211--- ，故非零项只有一项：

nn n n n t a a a a 112211)1(---- ，其中2

)

2)(1(--=

n n t ，

因此 (20141)(20142)

(1)

2014!2014!D --=-=

方法二：按行列展开的方法也行。

2、计算行列式 3

214214314324

321=

D 。

分析：如果行列式的各行（列）数的和相同时，一般首先采用的是将各列（行）加到第一列（行），提取第一列（行）的公因子(简称列（行)加

法).

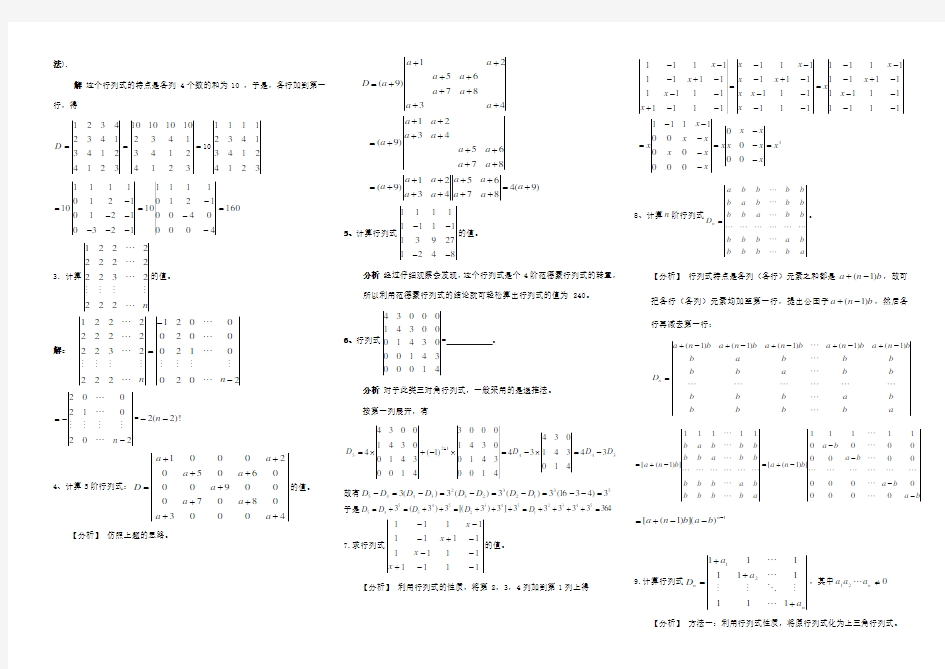
解这个行列式的特点是各列4个数的和为10 ，于是，各行加到第一行，得

===

421431432101010103214214314324321D 10

1111234134124123

1111012

110

210321

-=-----1604

004

001210111110=---=

3．计算n 22223222

2222

221的值。

解： 2

0200

120

00200021222232222222

221--=n n

02012002--

=)!2(2--n

4、计算5阶行列式：4

700

9000605020001

+++++++++=

a a a a a a a a a D 的值。

【分析】仿照上题的思路。

56(9)

(9)

5678

1256(9)

4(9)

3478

a a a a D a a a a a a a a a a a a a a a a a a a a a a a a ++++=+++++++++=+++++++++=+=+++++

5、计算行列式

111

1111

927

1248

----的值。

分析经过仔细观察会发现，这个行列式是个4阶范德蒙行列式的转置，所以利用范德蒙行列式的结论就可轻松算出行列式的值为240。

6、行列式4

100034100034100

03410

0034= 。

分析对于此类三对角行列式，一般采用的是递推法。

按第一列展开，有

344125344

103410

34344

100341003410

003)1(4

1003410034100344D D D D -=?-=?

-+?

故有5

123

232

34453)4316(3)(3)(3)(3=--=-=-=-=-D D D D D D D D

于是36433333]3)3[(3)3(35

43215432543545=++++=+++=++=+=D D D D D

7.求行列式

111111111111

--+---+---x x x x 的值。

【分析】利用行列式的性质，将第2，3，4列加到第1列上得

400000

000011111

11111111

11111

1111111

1111

1111111111

1111x x

x x x

x x

x x x

x x x x

x x x x x

x x x x x x =---=-----=-----+---=-----+---=

--+---+---

8、计算n 阶行列式

b a b b b b b a b b b

b b b b a D n

。【分析】行列式特点是各列（各行）元素之和都是b n a )1(-+，故可把各行（各列）元素均加至第一行，提出公因子b n a )1(-+，然后各行再减去第一行：

b a b b b b b a b b b b b a b

n a b n a b n a b n a b n a D n

)1()1()1()1()1(-+-+-+-+-+=

a b

a b a b a b n a a

b b

b a b b b b b a b b b b b a b

b n a -----+=-+=0

00000000000011111]

)1([11111]

)1([

1)]()1([---+=n b a b n a

9.计算行列式n

n a a a D +++=

11111121

，其中021≠n a a a

【分析】方法一：利用行列式性质，将原行列式化为上三角行列式。

)11(00001

100

1112121111

211

∑∑==+=++=

--+=

i i

n n

i i

n a a a a a a a a a a a a a a D

方法二：利用加边的方法

1112

11121

21111

111101111000111100011

1110

111110001(1)0000

n n

i i

n i i

a a D a a a a a a a a a a a a +==+-=+=-+-+=

=+∑

∑

10.计算行列式4

4442

1111

d c b a d

d c b a D =

的值。

【分析】利用范作范德蒙行列式4

3333322222

111111

x d c b a x d c b a x d c b a x

d c b a

D =，则行列式D 就是行列式1D 元素3

x 的余子式45M ，即45M D =

又))()()()()()()()()((1a b b c a c c d b d a d d x c x b x a x D ----------=

此式3

x 的系数是

))()()()()()((a b b c a c c d b d a d d c b a ------+++-也为1D 中

元素3

x 的代数余子式45A ，因为4545A M -=

所以，

))()()()()()((11114

4442

a b b c a c c d b d a d d c b a d c b a d

d c b a D ------+++==

。

线性代数期末考试试题

《线性代数》重点题一．单项选择题 1.设A 为3阶方阵，数 = 3，|A | =2，则 | A | =（）. A ．54； B ．-54； C ．6； D ．-6. 解. .54227)3(33-=?-=-==A A A λλ 所以填: B. 2、设A 为n 阶方阵，λ为实数，则|λA |=（） A 、λ|A |； B 、|λ||A |； C 、λn |A |； D 、|λ|n |A |. 解. |λA |=λn |A |.所以填: C. 3.设矩阵()1,2,12A B ?? ==- ??? 则AB =（）. 解. ().24121,221???? ??--=-???? ??=AB 所以填: D. A. 0； B. ()2,2-； C. 22?? ?-??； D. 2142-?? ?-?? . 4、123,,a a a 是3维列向量，矩阵123(,,)A a a a =.若|A |=4，则|-2A |=（）. A 、-32； B 、-4； C 、4； D 、32. 解. |-2A |=(-2)3A =-8?4=-32. 所以填: D. 5.以下结论正确的是（）. A .一个零向量一定线性无关； B .一个非零向量一定线性相关； C .含有零向量的向量组一定线性相关； D .不含零向量的向量组一定线性无关. 解. A .一个零向量一定线性无关；不对,应该是线性相关. B .一个非零向量一定线性相关；不对,应该是线性无关. C .含有零向量的向量组一定线性相关；对. D .不含零向量的向量组一定线性无关. 不对, 应该是:不能判断. 所以填: C. 6、 1234(1,1,0,0),(0,0,1,1),(1,0,1,0),(1,1,1,1),αααα====设则它的极大无关组为( ) A 、 12,; αα B 、 123,, ;ααα C 、 124,, ;ααα D 、1234,, ,αααα

线性代数考试题库及答案(五)

线性代数考试题库及答案一、单项选择题（共5小题，每题2分，共计10分） 1.在111 ()111111 x f x x x -+=-+-展开式中，2x 的系数为（） (A) -1 (B) 0 (C) 1 (D) 2 2.A 是m ×n 矩阵，(),r A r B =是m 阶可逆矩阵，C 是m 阶不可逆矩阵，且 ()r C r <，则（） (A) BAX O =的基础解系由n-m 个向量组成 (B) BAX O =的基础解系由n-r 个向量组成 (C) CAX O =的基础解系由n-m 个向量组成 (D) CAX O =的基础解系由n-r 个向量组成 3.设n 阶矩阵,A B 有共同的特征值，且各自有n 个线性无关的特征向量，则（） (A) A B = (B) ,0A B A B ≠-=但 (C) A B (D) A B 与不一定相似，但 A B = 4.设,,A B C 均为n 阶矩阵，且AB BC CA E ===，其中E 为n 阶单位阵，则 222A B C ++= （） (A) O (B) E (C) 2E (D) 3E 5．设1010,0203A B ???? == ? ????? ，则A B 与（） (A)合同，且相似 (B)不合同，但相似 (C)合同，但不相似（D ）既不合同，又不相似

二、填空题（共二、填空题（共10小题，每题 2分，共计 20 分） 1．已知11 122 233 30a b c a b c m a b c =≠，则1111 22223333 232323a b c c a b c c a b c c ++=+ 。 2．设 1 010 2010 1A ?? ?= ? ?? ? ，若三阶矩阵Q 满足2,AQ E A Q +=+则Q 的第一行的行向量是。 3．已知β为n 维单位列向量， T β为β的转置，若T C ββ= ，则 2C = 。 4．设12,αα分别是属于实对称矩阵A 的两个互异特征值12,λλ的特征向量，则 12T αα= 。 5．设A 是四阶矩阵，A * 为其伴随矩阵，12,αα是齐次方程组0AX =的两个线性无关解，则()r A *= 。 6．向量组1 23(1,3,0,5,0),(0,2,4,6,0),(0,3,0,6,9)T T T ααα===的线性关系是。 7．已知三阶非零矩阵B 的每一列都是方程组1231231 23220 2030 x x x x x x x x x λ+-=?? -+=??+-=?的解，则 λ= 。 8．已知三维向量空间3R 的基底为123(1,1,0),(1,0,1),(0,1,1)T T T ααα===，则向量 (2,0,0)T β=在此基底下的坐标是。 9．设21110012100,112004A a a ?? ?? ? ?== ? ? ? ????? 则。 10．二次型2 2 2 123123121323(,,)222222f x x x x x x x x x x x x =++++-的秩为。

线性代数行列式算与性质

线性代数行列式的计算与性质行列式在数学中，是一个函数，其定义域为的矩阵，取值为一个标量，写作或。行列式可以看做是有向面积或体积的概念在一般的欧几里得空间中的推广。或者说，在维欧几里得空间中，行列式描述的是一个线性变换对“体积”所造成的影响。无论是在线性代数、多项式理论，还是在微积分学中（比如说换元积分法中），行列式作为基本的数学工具，都有着重要的应用。行列式概念最早出现在解线性方程组的过程中。十七世纪晚期，关孝和与莱布尼茨的著作中已经使用行列式来确定线性方程组解的个数以及形式。十八世纪开始，行列式开始作为独立的数学概念被研究。十九世纪以后，行列式理论进一步得到发展和完善。矩阵概念的引入使得更多有关行列式的性质被发现，行列式在许多领域都逐渐显现出重要的意义和作用，出现了线性自同态和矢量组的行列式的定义。行列式的特性可以被概括为一个多次交替线性形式，这个本质使得行列式在欧几里德空间中可以成为描述“体积”的函数。矩阵 A 的行列式有时也记作 |A|。绝对值和矩阵范数也使用这个记法，有可能和行列式的记法混淆。不过矩阵范数通常以双垂直线来表示（如：），且可以使用下标。此外，矩阵的绝对值是没有定义的。因此，行列式经常使用垂直线记法（例如：克莱姆法则和子式）。例如，一个矩阵： A= ? ? ? ? ? ? ? i h g f e d c b a ，行列式也写作，或明确的写作： A= i h g f e d c b a ，即把矩阵的方括号以细长的垂直线取代行列式的概念最初是伴随着方程组的求解而发展起来的。行列式的提出可以追溯到十七世纪，最初的雏形由日本数学家关孝和与德国数学家戈特弗里德·莱布尼茨各自独立得出，时间大致相同。

线性代数期末考试试卷答案合集

线性代数期末考试试卷答案合集文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]

三、单项选择题 (每小题仅有一个正确答案，将正确答案题号填入括号内。每小题2 分，共10分) 1. 设A 为n 阶矩阵，且2=A ，则=T A A （）。 ① n 2 ② 12-n ③ 12+n ④ 4 2. n 维向量组 s ααα，，， 21（3 s n ）线性无关的充要条件是（）。 ① s ααα，，， 21中任意两个向量都线性无关 ② s ααα，，， 21中存在一个向量不能用其余向量线性表示 ③ s ααα，，， 21中任一个向量都不能用其余向量线性表示 ④ s ααα，，， 21中不含零向量 3. 下列命题中正确的是( )。 ① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关 4. 设A ，B 均为n 阶方阵，下面结论正确的是( )。 ① 若A ，B 均可逆，则B A +可逆 ② 若A ，B 均可逆，则 A B 可逆 ③ 若B A +可逆，则 B A -可逆 ④ 若B A +可逆，则 A ，B 均可逆 5. 若4321νννν，，，是线性方程组0=X A 的基础解系，则4321νννν+++是0=X A 的（） ① 解向量 ② 基础解系 ③ 通解 ④ A 的行向量四、计算题 ( 每小题9分，共63分) 1. 计算行列式 x a b c d a x b c d a b x c d a b c x d ++++。

(完整word版)线性代数考试题及答案解析

WORD 格式整理 2009－2010学年第一学期期末考试《线性代数》试卷答卷说明：1、本试卷共6页，五个大题，满分100分，120分钟完卷。 2、闭卷考试。评阅人:_____________ 总分人：______________ 一、单项选择题。(每小题3分,共24分) 【】1.行列式=----3111131111311113 (A)0 (B) 1 (C) 2 (D)3 【】2.设A 为3阶方阵，数2-=λ，3=A ，则=A λ (A) 24 (B) 24- (C) 6 (D) 6- 【】3.已知,,B A 为n 阶方阵，则下列式子一定正确的是 (A)BA AB = (B)2222B)(A B AB A ++=+ (C)BA AB = (D) 22))((B A B A B A -=-+ 【】4.设A 为3阶方阵, 0≠=a A ，则=*A (A) a （B) 2a (C) 3a (D) 4a __ __ ___ __ __ ___ __ __ 系_ __ __ ___ __ 专业_ __ __ ___ __ _班级姓名_ __ ___ __ __ ___ __ 学号__ ___ __ __ ___ __ _ ………… … … … … … … … … （密） … … … … … … … … … … … … （封） … … … …… … … … … … … … （线） … … … … … … … … … … … …

(A) )()(B R A R < (B) )()(B R A R > (C) )()(B R A R = (D) 不能确定)(A R 和)(B R 的大小【】6.设n 元齐次线性方程组0=Ax 的系数矩阵A 的秩为r ，则0=Ax 有非零解的充分必要条件是 (A) n r = (B) n r ≥ (C) n r < (D) n r > 【】7. 向量组)2(,,,21≥m a a a m 线性相关的充分必要条件是 (A) m a a a ,,,21 中至少有一个零向量 (B) m a a a ,,,21 中至少有两个向量成比例 (C) m a a a ,,,21 中每个向量都能由其余1-m 个向量线性表示 (D) m a a a ,,,21 中至少有一个向量可由其余1-m 个向量线性表示【】8. n 阶方阵A 与对角阵相似的充分必要条件是 (A)n A R =)( (B)A 有n 个互不相同的特征值 (C)A 有n 个线性无关的特征向量 (D)A 一定是对称阵二、填空题。(每小题3分,共15分) 1.已知3阶行列式D 的第2行元素分别为1,2,1-，它们的余子式分别为2,1,1-，则=D 。 2.设矩阵方程??????-=???? ??12640110X ，则=X 。 3.设*=ηx 是非齐次线性方程组b Ax =的一个特解，21,ξξ为对应齐次线性方程组 0=Ax 的基础解系，则非齐次线性方程组b Ax =的通解为 . 4.设n m ?矩阵A 的秩r A R =)(，则n 元齐次线性方程组0=Ax 的解集S 的最大无关组S 的秩=R 。

考研数学线性代数行列式的计算方法

考研数学线性代数行列式的计算方法考研数学线性代数行列式的计算方法一、基本内容及历年大纲要求。本章内容包括行列式的定义、性质及展开定理。从整体上来看，历年大纲要求了解行列式的概念，掌握行列式的性质，会应用行列式的性质及展开定理计算行列式。不过要想达到大纲中的要求还需要考生理解排列、逆序、余子式、代数余子式的概念，以及性质中的相关推论是如何得到的。二、行列式在线性代数中的地位。行列式是线性代数中最基本的运算之一,也是考生复习考研线性代数必须掌握的基本技能之一(另一项基本技能是求解线性方程组)，另外，行列式还是解决后续章节问题的一个重要工具，不论是后续章节中出现的重要概念还是重要定理、解题方法等都与行列式有着密切的联系。三、行列式的计算。由于行列式的计算贯穿整个学科，这就导致了它不仅计算方法灵活，而且出题方式也比较多变，这也是广大考生在复习线性代数时面临的第一道关卡。虽然行列式的计算考查形式多变，但是从本质上来讲可以分为两类：一是数值型行列式的计算;二是抽象型行列式的计算。 1.数值型行列式的计算主要方法有： (1)利用行列式的定义来求，这一方法适用任何数值型行列式的计算，但是它计算量大，而且容易出错;

(2)利用公式，主要适用二阶、三阶行列式的计算; (3)利用展开定理，主要适用出现零元较多的行列式计算; (4)利用范德蒙行列式，主要适用于与它具有类似结构或形式的行列式计算; (5)利用三角化的思想，主要适用于高阶行列式的计算，其主要思想是找1，化0，展开。 2.抽象型行列式的计算主要计算方法有： (1)利用行列式的性质，主要适用于矩阵或者行列式是以列向量的形式给出的; (2)利用矩阵的运算，主要适用于能分解成两个矩阵相乘的'行列式的计算; (3)利用矩阵的特征值，主要适用于已知或可以间接求出矩阵特征值的行列式的计算; (4)利用相关公式，主要适用于两个矩阵相乘或者是可以转化为两个矩阵相乘的行列式计算; (5)利用单位阵进行变形，主要适用于既不能不能利用行列式的性质又不能进行合并两个矩阵加和的行列式计算。我们究竟该做多少年的真题? 建议大家在刚开始复习的时候，不要去做真题，因为以你刚开始复习的程度还不足以支撑起真题的难度和深度。我们做真题的时间是在我们的强化阶段结束之后，也就是提高阶段和冲刺模考去做真题。应该怎么样去做真题? 第一：练习重质不重量

线性代数02198自考历年试题及答案

2009年7月高等教育自学考试全国统一命题考试线性代数试题课程代码：02198 试卷说明：在本卷中，A T 表示矩阵A 的转置矩阵；A * 表示A 的伴随矩阵；R （A ）表示矩阵 A 的秩；|A |表示A 的行列式；E 表示单位矩阵。一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。错选、多选或未选均无分。 1．设A ，B ，C 为同阶方阵，下面矩阵的运算中不成立．．．的是（） A ．（A +B ）T =A T +B T B ．|AB |=|A ||B | C ．A （B +C ）=BA +CA D ．（AB ）T =B T A T 2．已知3332 31 232221 131211 a a a a a a a a a =3，那么33 32 31 23222113 12 11222222a a a a a a a a a ---=（） A ．-24 B ．-12 C ．-6 D ．12 3．若矩阵A 可逆，则下列等式成立的是（） A ．A = | |1A A * B ．|A |=0 C ．（A 2）-1=（A -1）2 D ．（3A ）-1=3A -1 4．若 A =?? ????-25 1 21 3 ，B =??? ? ????-12 32 14 ，C =?? ???? --21 312 ，则下列矩阵运算的结果为3×2的矩阵的是（） A ．ABC B ．AC T B T C ．CBA D ．C T B T A T 5．设有向量组A ：4321,,,αααα，其中α1，α2，α3线性无关，则（） A ．α1，α 3线性无关 B ．α1，α2，α3，α4线性无关 C ．α1，α2，α3，α4线性相关 D ．α2，α3，α 4线性无关 6．若四阶方阵的秩为3，则（） A ．A 为可逆阵 B ．齐次方程组Ax =0有非零解 C ．齐次方程组Ax =0只有零解 D ．非齐次方程组Ax =b 必有解 7．已知方阵A 与对角阵B =??? ? ????---20 020 00 2 相似，则A 2 =（） A ．-64E B ．-E

线性代数测试试卷及答案

线性代数（A 卷）一﹑选择题(每小题3分,共15分) 1. 设A ﹑B 是任意n 阶方阵,那么下列等式必成立的是( ) (A)AB BA = (B)222()AB A B = (C)222()2A B A AB B +=++ (D)A B B A +=+ 2. 如果n 元齐次线性方程组0AX =有基础解系并且基础解系含有()s s n <个解向量,那么矩阵A 的秩为( ) (A) n (B) s (C) n s - (D) 以上答案都不正确 3.如果三阶方阵33()ij A a ?=的特征值为1,2,5,那么112233a a a ++及A 分别等于( ) (A) 10, 8 (B) 8, 10 (C) 10, 8-- (D) 10, 8-- 4. 设实二次型11212222(,)(,)41x f x x x x x ?? ??= ? ?-???? 的矩阵为A ,那么( ) (A) 2331A ??= ?-?? (B) 2241A ??= ?-?? (C) 2121A ??= ? -?? (D) 1001A ?? = ??? 5. 若方阵A 的行列式0A =，则( ) (A) A 的行向量组和列向量组均线性相关 (B)A 的行向量组线性相关,列向量组线性无关 (C) A 的行向量组和列向量组均线性无关 (D)A 的列向量组线性相关,行向量组线性无关二﹑填空题(每小题3分,共30分) 1 如果行列式D 有两列的元对应成比例,那么该行列式等于； 2. 设100210341A -?? ? =- ? ?-?? ，*A 是A 的伴随矩阵，则*1()A -= ； 3. 设α,β是非齐次线性方程组AX b =的解,若λαμβ+也是它的解, 那么λμ+= ； 4. 设向量(1,1,1)T α=-与向量(2,5,)T t β=正交,则t = ； 5. 设A 为正交矩阵,则A = ；

线性代数试题及答案。。

第一部分选择题(共28分) 一、单项选择题（本大题共14小题，每小题2分，共28分）在每小题列出的四个选项中只有一个是符合题目要求的，请将其代码填在题后的括号内。错选或未选均无分。 1.设行列式a a a a 1112 2122 =m， a a a a 1311 2321 =n，则行列式 a a a a a a 111213 212223 + + 等于（） A. m+n B. -(m+n) C. n-m D. m-n 2.设矩阵A= 100 020 003 ? ? ? ? ? ? ? ，则A-1等于（） A. 1 3 00 1 2 001 ? ? ? ? ? ? ? ? ? ? B. 100 1 2 00 1 3 ? ? ? ? ? ? ? ? ? ? C. 1 3 00 010 00 1 2 ? ? ? ? ? ? ? ?? D. 1 2 00 1 3 001 ? ? ? ? ? ? ? ? ? ? 3.设矩阵A= 312 101 214 - - - ? ? ? ? ? ? ? ，A*是A的伴随矩阵，则A *中位于（1，2）的元素是（） A. –6 B. 6 C. 2 D. –2 4.设A是方阵，如有矩阵关系式AB=AC，则必有（） A. A =0 B. B≠C时A=0 C. A≠0时B=C D. |A|≠0时B=C 5.已知3×4矩阵A的行向量组线性无关，则秩（A T）等于（） A. 1 B. 2 C. 3 D. 4 6.设两个向量组α1，α2，…，αs和β1，β2，…，βs均线性相关，则（） A.有不全为0的数λ1，λ2，…，λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λsβs=0 B.有不全为0的数λ1，λ2，…，λs使λ1（α1+β1）+λ2（α2+β2）+…+λs（αs+βs）=0 C.有不全为0的数λ1，λ2，…，λs使λ1（α1-β1）+λ2（α2-β2）+…+λs（αs-βs）=0 D.有不全为0的数λ1，λ2，…，λs和不全为0的数μ1，μ2，…，μs使λ1α1+λ2α2+…+ λsαs=0和μ1β1+μ2β2+…+μsβs=0 7.设矩阵A的秩为r，则A中（） A.所有r-1阶子式都不为0 B.所有r-1阶子式全为0 C.至少有一个r阶子式不等于0 D.所有r阶子式都不为0 8.设Ax=b是一非齐次线性方程组，η1，η2是其任意2个解，则下列结论错误的是（） A.η1+η2是Ax=0的一个解 B.1 2η1+1 2 η2是Ax=b的一个解 C.η1-η2是Ax=0的一个解 D.2η1-η2是Ax=b的一个解 9.设n阶方阵A不可逆，则必有（）

线性代数期末考试试卷+答案合集

×××大学线性代数期末考试题一、填空题（将正确答案填在题中横线上。每小题2分，共10分） 1. 若02 2 1 50 1 31 =---x ，则=χ__________。 2．若齐次线性方程组??? ??=++=++=++0 00321 321321x x x x x x x x x λλ只有零解，则λ应满足。 3．已知矩阵n s ij c C B A ?=)(，，，满足CB AC =，则A 与B 分别是阶矩阵。 4．矩阵??? ? ? ??=32312221 1211 a a a a a a A 的行向量组线性。 5．n 阶方阵A 满足032 =--E A A ，则=-1A 。二、判断正误（正确的在括号内填“√”，错误的在括号内填“×”。每小题2分，共10分） 1. 若行列式D 中每个元素都大于零，则0?D 。（） 2. 零向量一定可以表示成任意一组向量的线性组合。（） 3. 向量组m a a a ，，， 21中，如果1a 与m a 对应的分量成比例，则向量组s a a a ，，， 21线性相关。（） 4. ? ? ??? ???? ???=010********* 0010 A ，则A A =-1。（） 5. 若λ为可逆矩阵A 的特征值，则1 -A 的特征值为λ。 ( ) 三、单项选择题 (每小题仅有一个正确答案，将正确答案题号填入括号内。每小题2分，共10分) 1. 设A 为n 阶矩阵，且2=A ，则=T A A （）。 ① n 2 ② 1 2 -n ③ 1 2 +n ④ 4 2. n 维向量组 s ααα，，， 21（3 ≤ s ≤ n ）线性无关的充要条件是（）。 ① s ααα，，， 21中任意两个向量都线性无关 ② s ααα，，， 21中存在一个向量不能用其余向量线性表示 ③ s ααα，，， 21中任一个向量都不能用其余向量线性表示

#线性代数技巧行列式的计算方法

计算n 阶行列式的若干方法举例 n 阶行列式的计算方法很多，除非零元素较多时可利用定义计算（①按照某一列或某一行展开②完全展开式）外，更多的是利用行列式的性质计算，特别要注意观察所求题目的特点，灵活选用方法，值得注意的是，同一个行列式，有时会有不同的求解方法。下面介绍几种常用的方法，并举例说明。 1．利用行列式定义直接计算例1 计算行列式 0010020010000 00n D n n = - 解 D n 中不为零的项用一般形式表示为 112211!n n n nn a a a a n ---=. 该项列标排列的逆序数t （n －1 n －2…1n ）等于 (1)(2) 2 n n --，故 (1)(2) 2 (1) !.n n n D n --=- 2．利用行列式的性质计算例2 一个n 阶行列式 n ij D a =的元素满足 ,,1,2, ,,ij ji a a i j n =-= 则称D n 为反对称行列式，证明：奇数阶反对称行列式为零. 证明：由i j j i a a =-知i i i i a a =-，即 0,1,2, ,ii a i n ==

故行列式D n 可表示为 1213112 23213 2331230000 n n n n n n n a a a a a a D a a a a a a -=----- 由行列式的性质A A '= 1213112 23213 2331230000 n n n n n n n a a a a a a D a a a a a a -----=- 1213112 23213 23312300(1)0 n n n n n n n a a a a a a a a a a a a -=------ (1)n n D =- 当n 为奇数时，得D n =－D n ，因而得D n = 0. 3．化为三角形行列式若能把一个行列式经过适当变换化为三角形，其结果为行列式主对角线上元素的乘积。因此化三角形是行列式计算中的一个重要方法。例3 计算n 阶行列式 a b b b b a b b D b b a b b b b a = 解：这个行列式的特点是每行（列）元素的和均相等，根据行列式的性质，把第2，3，…，

历年自考线性代数试题真题及答案分析解答

全国2010年度4月高等教育自学考试线性代数（经管类）试题答案一、单项选择题（本大题共10小题，每小题2分，共20分） 1．已知2阶行列式 m b b a a =2 1 21， n c c b b =2 1 21，则 =++2 21 121c a c a b b （ B ） A ．n m - B ．m n - C ．n m + D ．)(n m +- 2．设A , B , C 均为n 阶方阵，BA AB =，CA AC =，则=ABC （ D ） A ．ACB B ．CAB C ．CBA D ．BCA 3．设A 为3阶方阵，B 为4阶方阵，且1||=A ，2||-=B ，则行列式||||A B 之值为（ A ） A ．8- B ．2- C ．2 D ．8 4．??? ? ? ??=3332 312322 211312 11a a a a a a a a a A ，????? ??=3332312322 211312 11333a a a a a a a a a B ，????? ??=100030001P ，??? ? ? ??=100013001Q ，则=B （ B ） A ．PA B ．AP C ．QA D ．AQ 5．已知A 是一个43?矩阵，下列命题中正确的是（ C ） A ．若矩阵A 中所有3阶子式都为0，则秩(A )=2 B ．若A 中存在2阶子式不为0，则秩(A )=2 C ．若秩(A )=2，则A 中所有3阶子式都为0 D ．若秩(A )=2，则A 中所有2阶子式都不为0 6．下列命题中错误．．的是（ C ） A ．只含有1个零向量的向量组线性相关 B ．由3个2维向量组成的向量组线性相关 C ．由1个非零向量组成的向量组线性相关 D ．2个成比例的向量组成的向量组线性相关 7．已知向量组321,,ααα线性无关，βααα,,,321线性相关，则（ D ）

线性代数期末考试试题含答案

线性代数期末考试试题含答案 The final edition was revised on December 14th, 2020.

江西理工大学《线性代数》考题一、填空题（每空3分，共15分） 1. 设矩阵??????????=333222 111 c b a c b a c b a A ,??????????=333 222111d b a d b a d b a B 且4=A ,1=B 则=+B A ______ 2. 二次型233222213214),,(x x tx x x x x x f +-+=是正定的，则t 的取值范围__________ 3. A 为3阶方阵，且2 1=A ，则=--*12)3(A A ___________ 4. 设n 阶矩阵A 的元素全为1，则A 的n 个特征值是___________ 5. 设A 为n 阶方阵，n βββ ,,21为A 的n 个列向量，若方程组0=AX 只有零解，则向量组(n βββ ,,21)的秩为 _____ 二、选择题（每题3分，共15分） 6. 设线性方程组?????=+=+--=-032231 3221ax cx bc bx cx ab ax bx ，则下列结论正确的是（） (A)当c b a ,,取任意实数时，方程组均有解 (B)当a ＝0时，方程组无解 (C) 当b ＝0时，方程组无解 (D)当c ＝0时，方程组无解 7. 同为n 阶方阵，则（）成立 (A) B A B A +=+ (B) BA AB = (C) BA AB = (D) 111)(---+=+B A B A 8. 设??????????=333231232221 131211 a a a a a a a a a A ，??????????+++=331332123111131211232221a a a a a a a a a a a a B ,??????????=1000010101P , ???? ??????=1010100012P 则（）成立 (A)21P AP (B) 12P AP (C) A P P 21 (D) A P P 12 9. A ,B 均为n 阶可逆方阵，则AB 的伴随矩阵=*)(AB （） (A) **B A (B) 11--B A AB (C) 11--A B (D)**A B 10. 设A 为n n ?矩阵，r A r =)(＜n ，那么A 的n 个列向量中（）

线性代数期末考试试卷答案

线性代数期末考试题样卷一、填空题（将正确答案填在题中横线上。每小题2分，共10分） 1. 若02 2 1 50 1 31 =---x ，则=χ__________。 2．若齐次线性方程组??? ??=++=++=++0 00321 321321x x x x x x x x x λλ只有零解，则λ应满足。 3．已知矩阵n s ij c C B A ?=)(，，，满足CB AC =，则A 与B 分别是阶矩阵。 4．矩阵??? ? ? ??=32312221 1211 a a a a a a A 的行向量组线性。 5．n 阶方阵A 满足032 =--E A A ，则=-1A 。二、判断正误（正确的在括号内填“√”，错误的在括号内填“×”。每小题2分，共10分） 1. 若行列式D 中每个元素都大于零，则0?D 。（） 2. 零向量一定可以表示成任意一组向量的线性组合。（） 3. 向量组m a a a ，，，Λ21中，如果1a 与m a 对应的分量成比例，则向量组s a a a ，，，Λ21线性相关。（） 4. ? ? ??? ???? ???=010********* 0010 A ，则A A =-1。（） 5. 若λ为可逆矩阵A 的特征值，则1 -A 的特征值为λ。 ( ) 三、单项选择题 (每小题仅有一个正确答案，将正确答案题号填入括号内。每小题2分，共10分) 1. 设A 为n 阶矩阵，且2=A ，则=T A A （）。 ① n 2 ② 1 2 -n ③ 1 2 +n ④ 4 2. n 维向量组 s ααα，，，Λ21（3 ≤ s ≤ n ）线性无关的充要条件是（）。 ① s ααα，，，Λ21中任意两个向量都线性无关 ② s ααα，，，Λ21中存在一个向量不能用其余向量线性表示 ③ s ααα，，，Λ21中任一个向量都不能用其余向量线性表示

线性代数-特殊行列式及行列式计算方法总结

特殊行列式及行列式计算方法总结一、几类特殊行列式 1. 上（下）三角行列式、对角行列式（教材P7例5、例6） 2. 以副对角线为标准的行列式 111121 12,1221222,11,21,1 1,1 12 ,1 (1)2 12,1 1 000000000000000 00 (1) n n n n n n n n n n n nn n n n n n nn n n n n n a a a a a a a a a a a a a a a a a a a a a a ---------= ==- 3. 分块行列式（教材P14例10）一般化结果： 00n n m n n m n m m n m m n m A C A A B B C B ????==? 0(1)0n m n n m n mn n m m m n m m n A C A A B B C B ????==-? 4. 范德蒙行列式（教材P18例12）注：4种特殊行列式的结果需牢记！以下几种行列式的特殊解法必须熟练掌握！！！二、低阶行列式计算二阶、三阶行列式——对角线法则（教材P2、P3）三、高阶行列式的计算【五种解题方法】 1) 利用行列式定义直接计算特殊行列式； 2) 利用行列式的性质将高阶行列式化成已知结果的特殊行列式；

3) 利用行列式的行（列）扩展定理以及行列式的性质，将行列式降阶进行计算——适用于行列式的某一行或某一列中有很多零元素，并且非零元素的代数余子式很容易计算； 4) 递推法或数学归纳法； 5) 升阶法（又称加边法）【常见的化简行列式的方法】 1. 利用行列式定义直接计算特殊行列式例1 （2001年考研题） 0001000200019990002000000 002001 D = 分析：该行列式的特点是每行每列只有一个元素，因此很容易联想到直接利用行列式定义进行计算。解法一：定义法 (1,2,...,2,1,)012...19990(1)2001!(1)2001!2001!n n n D τ--+++++=-=-= 解法二：行列式性质法利用行列式性质2把最后一行依次与第n -1,n -2,…,2,1行交换（这里n =2001），即进行2000次换行以后，变成副对角行列式。 2001(20011) 20011 20011 2 000020010 001000200(1) (1) (1)2001!2001!019990002000 00 D ?---=- =--=

线性代数期末考试试题(含答案)

江西理工大学《线性代数》考题一、填空题（每空3分，共15分） 1. 设矩阵??????????=333222 111 c b a c b a c b a A ,??????????=333 222111d b a d b a d b a B 且4=A ,1=B 则=+B A ______ 2. 二次型233222213214),,(x x tx x x x x x f +-+=是正定的，则t 的取值范围__________ 3. A 为3阶方阵，且2 1=A ，则=--*12)3(A A ___________ 4. 设n 阶矩阵A 的元素全为1，则A 的n 个特征值是___________ 5. 设A 为n 阶方阵，n βββ ,,21为A 的n 个列向量，若方程组0=AX 只有零解，则向量组(n βββ ,,21)的秩为 _____ 二、选择题（每题3分，共15分） 6. 设线性方程组?????=+=+--=-032231 3221ax cx bc bx cx ab ax bx ，则下列结论正确的是（） (A)当c b a ,,取任意实数时，方程组均有解 (B)当a ＝0时，方程组无解 (C) 当b ＝0时，方程组无解 (D)当c ＝0时，方程组无解 7. A.B 同为n 阶方阵，则（）成立 (A) B A B A +=+ (B) BA AB = (C) BA AB = (D) 111)(---+=+B A B A 8. 设??????????=333231232221 131211 a a a a a a a a a A ，??????????+++=331332123111131211232221a a a a a a a a a a a a B ,??????????=1000010101P , ???? ??????=1010100012P 则（）成立 (A)21P AP (B) 12P AP (C) A P P 21 (D) A P P 12 9. A ,B 均为n 阶可逆方阵，则AB 的伴随矩阵=*)(AB （） (A) **B A (B) 11--B A AB (C) 11--A B (D)**A B 10. 设A 为n n ?矩阵，r A r =)(＜n ，那么A 的n 个列向量中（）（A ）任意r 个列向量线性无关

上海财经大学《线性代数》课程考试卷(B)及答案

诚实考试吾心不虚，公平竞争方显实力，考试失败尚有机会，考试舞弊前功尽弃。上海财经大学《线性代数》课程考试卷（B ）闭卷课程代码 105208 课程序号姓名学号班级一、单选题(每小题2分，共计20分) 1. 当=t 3 时，311244s t a a a a 是四阶行列式中符号为负的项。 2. 设A 为三阶方阵，3A = ，则* 2A -=__-72__。 3. 设矩阵01000 01000010 00 0A ????? ?=?????? ，4k ≥,k 是正整数，则=k P 0 。 4. 设A 是n 阶矩阵，I 是n 阶单位矩阵,若满足等式2 26A A I +=，则 () 1 4A I -+= 2 2A I - 。 5. 向量组()()()1,2,6,1,,3,1,1,4a a a +---的秩为1，则 a 的取值为__1___。 6. 方程组1243400x x x x x ++=??+=? 的一个基础解系是 ???? ? ? ? ??--??????? ??-1101,0011 。 7. 设矩阵12422421A k --?? ?=-- ? ?--??，500050004A ?? ? = ? ?-?? ，且A 与B 相似，则=k 4 。 …………………………………………………………… 装订线…………………………………………………

8. 123,,ααα是R 3 的一个基,则基312,,ααα到基12,αα,3α的过渡矩阵为 ???? ? ??001100010 。 9. 已知413 1 210,32111 a A B A A I -===-+-, 则B 的一个特征值是 2 。 10. 设二次型222 12312132526f x x x tx x x x =++++为正定, 则t 为 5 4||< t 。二．选择题（每题3分，共15分） 1. 设A 为n 阶正交方阵，则下列等式中 C 成立。 (A) *A A =; (B)1*A A -= (C)()1T A A -=; (D) *T A A = 2. 矩阵 B 合同于145-?? ? - ? ??? (A) 151-?? ? ? ??? ; （B ）????? ??--321;（C ）???? ? ??112;（D ）121-?? ? - ? ?-?? 3. 齐次线性方程组AX O =有唯一零解是线性方程组B AX =有唯一解的（ C ）。（A ）充分必要条件；（B ）充分条件；（C ）必要条件；（D ）无关条件。 4．设,A B 都是n 阶非零矩阵，且AB O =，则A 和B 的秩（ B ）。（A ）必有一个等于零；（B ）都小于n ；（C ）必有一个等于n ；（D ）有一个小于n 。 5．123,,ααα是齐次线性方程组AX O =的基础解系，则__B___也可作为齐次线性方程组 AX O =的基础解系。 (A) 1231231222,24,2αααααααα-+-+--+ （B ）1231212322,2,263αααααααα-+-+-+

线性代数第1章行列式试卷及答案

最新线性代数试题精选与精解(含完整试题与详细答案-考研数学基础训练)

线性代数期末考试试题

线性代数考试题库及答案(五)

线性代数行列式算与性质

线性代数期末考试试卷答案合集

(完整word版)线性代数考试题及答案解析

考研数学线性代数行列式的计算方法

线性代数02198自考历年试题及答案

线性代数测试试卷及答案

线性代数试题及答案。。

线性代数期末考试试卷+答案合集

#线性代数技巧行列式的计算方法

历年自考线性代数试题真题及答案分析解答

线性代数期末考试试题含答案

线性代数期末考试试卷答案

线性代数-特殊行列式及行列式计算方法总结

线性代数期末考试试题(含答案)

上海财经大学《 线性代数 》课程考试卷(B)及答案

上海财经大学《线性代数》课程考试卷(B)及答案