数据统计与预测模型与MATLAB实现

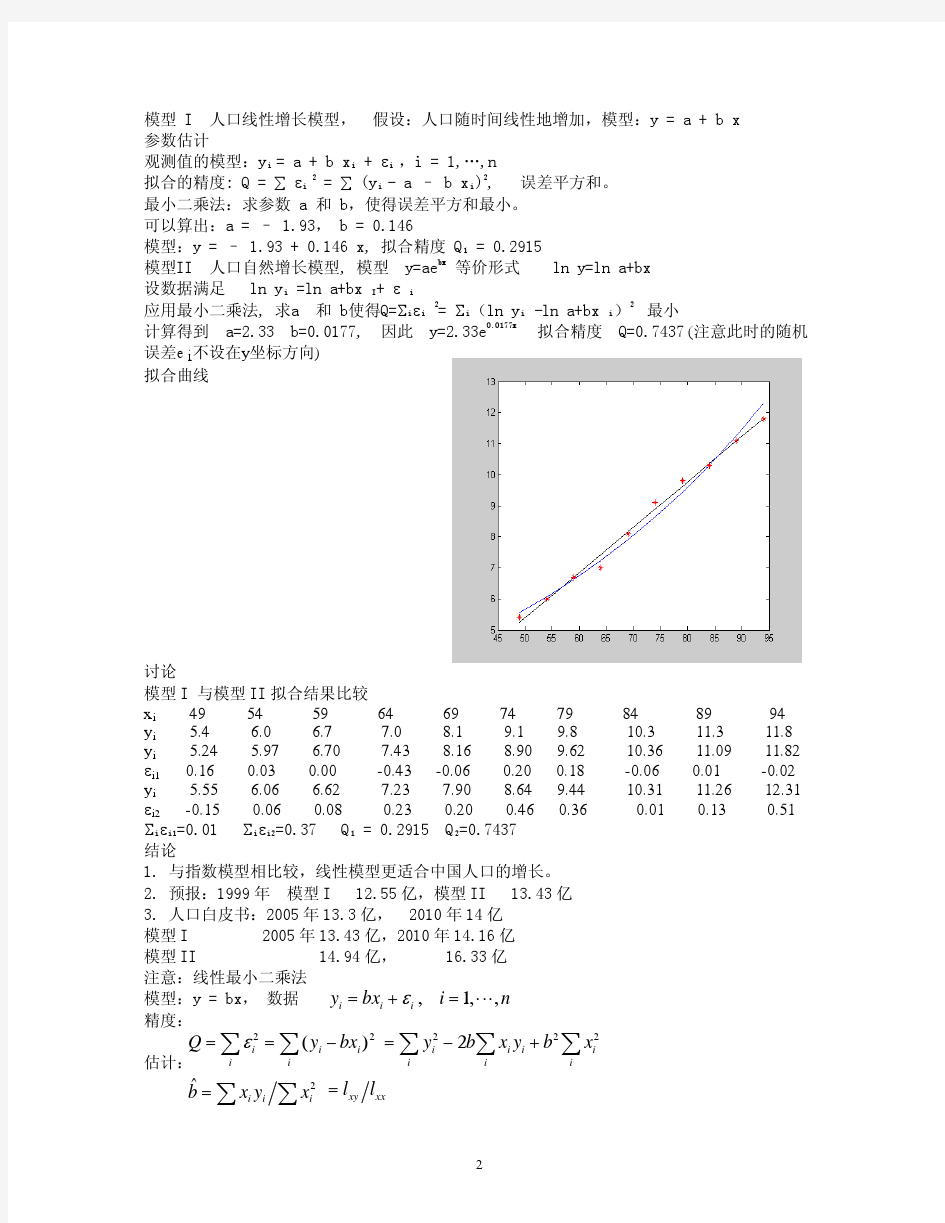
matlab曲线拟合人口增长模型及其数量预测
实验目的 [1] 学习由实际问题去建立数学模型的全过程; [2] 训练综合应用数学模型、微分方程、函数拟合和预测的知识分析和解决实际问题; [3] 应用matlab 软件求解微分方程、作图、函数拟合等功能,设计matlab 程序来求解 其中的数学模型; [4] 提高论文写作、文字处理、排版等方面的能力; 通过完成该实验,学习和实践由简单到复杂,逐步求精的建模思想,学习如何建立反映人口增长规律的数学模型,学习在求解最小二乘拟合问题不收敛时,如何调整初值,变换函数和数据使优化迭代过程收敛。 应用实验(或综合实验) 一、实验内容 从1790—1980年间美国每隔10年的人口记录如表综2.1所示: 表综2.1 用以上数据检验马尔萨斯(Malthus)人口指数增长模型,根据检验结果进一步讨论马尔萨斯人口模型的改进,并利用至少两种模型来预测美国2010年的人口数量。 二、问题分析 1:Malthus 模型的基本假设是:人口的增长率为常数,记为 r 。记时刻t 的人口为x (t ),(即x (t )为模型的状态变量)且初始时刻的人口为x 0,于是得到如下微分方程: ?????==0 )0(d d x x rx t x 2:阻滞增长模型(或Logistic 模型) 由于资源、环境等因素对人口增长的阻滞作用,人 口增长到一定数量后,增长率会下降,假设人口的增长率为x 的减函数,如设r(x)=r(1-x/x m ),其中r 为固有增长率(x 很小时),x m 为人口容量(资源、环境能容纳的最大数量),于是得到如下微分方程: ?? ???=-=0)0()1(d d x x x x rx t x m
Matlab与统计分析
Matlab 与统计分析 一、 回归分析 1、多元线性回归 1.1 命令 regress( ), 实现多元线性回归,调用格式为 [b,bint,r,rint,stats]=regress(y,x,alpha) 其中因变量数据向量Y 和自变量数据矩阵x 按以下排列方式输人 ????? ???????=????????????=n nk n n k k y y y y x x x x x x x x x x 21212222111211,111 对一元线性回归,取k=1即可。alpha 为显著性水平(缺省时设定为0.05),输出向量b ,bint 为回归系数估计值和它们的置信区间,r ,rint 为残差及其置信区间,stats 是用于检验回归模型的统计量,有三个数值,第一个是2 R , 其中R 是相关系数,第二个是F 统计量值,第三个是与统计量F 对应的概率P ,当α
人口预测 matlab
数学建模第一次实验报告 一.实验目的 学习有关人口预测的模型,了解有关混沌的基本理论,建立人口预报模型,并完成人口总量的预报,能够用软件完成数据计算。 二.实验内容 1.下表为我国自1949年至2000年的人口数据,请根据人口模型,预测出2010、2015 年我国的人口总数,并根据中国统计局的全国人口普查公报的1%调查数据,计
2. 谈谈你所认识的混沌 三. 实验步骤 1. 查阅资料选择模型 通过查阅资料,发现在考虑算法复杂度以及预测效果等综合因素时,阻滞增长 模型(Logistic 模型)要优于其他模型,所以我们选用阻滞增长模型进行本次实验。 2. 建立模型 阻滞增长模型(Logistic 模型)是考虑到自然资源、环境条件等因素对人口增长的阻滞作用,对指数增长模型的基本假设进行修改后得到的。阻滞作用体现在对人口增长率r 的影响上,是的r 随着人口数量x 的增加而下降。若将r 表示为x 的函数 ()r x ,则它应是减函数,于是有: ()()0,0dx r x x x x dt == (1) 对于()r x 的一个最简单的假设是()r x 为x 的线性函数,即:
()(),0,0r x r sx r s =->> (2) 设自然资源和环境所能容纳的最大人口数量为m x ,当m x x =时人口不在增长,即增长率()0m r x =,代入(2)式可得m r s x = ,所以有: ()(1)m r r x r x =- (3) 将(3)式代入(1)式得: ()0(1)0m dx r rx dt x x x ?=-?? ?=? (4) 解(4)可得(5)式: ()0 1(1)e m rt m x x t x x -= +- (5) 3. 根据模型原理进行编程 程序见第五部分。 4. 运行结果 采用1949年到2000年的人口调查结果作为数据,计算得到的模型参数()r x 和 m x 为:()0.0296r x =,()204.5537m x =千万人。 1949年到2000年的预测结果与人口调查结果对比图如图1所示。
统计学原理-回归分析案例0204192330
美国各航空公司业绩的统计数据公布在《华尔街日报1998年鉴》(The Wall Street Journal Almanac 1998)上,有关航班正点到达的比率和每10万名乘客投诉的次数的数据如下: 航空公司名称航班正点率(%)投诉率(次/10万名乘客)西南(Southwest)航空公司81.8 0.21 大陆(Continental) 航空公司76.6 0.58 西北(Northwest)航空公司76.6 0.85 美国(US Airways)航空公司75.7 0.68 联合(United)航空公司73.8 0.74 美洲(American)航空公司72.2 0.93 德尔塔(Delta)航空公司71.2 0.72 70.8 1.22 美国西部(America West)航空公 司 环球(TWA)航空公司68.5 1.25 a. 画出这些数据的散点图 b. 根据再(a)中作出的散点图,表明二变量之间存在什么关系? c. 求出描述投诉率是如何依赖航班按时到达正点率的估计的回归方程 d. 对估计的回归方程的斜率作出解释 e. 如何航班按时到达的正点率是80%,估计每10万名乘客投诉的次数是多少?
1)作散点图: 2)根据散点图可知,航班正点率和投诉率成负直线相关关系。 3)作简单直线回归分析: SUMMARY OUTPUT 回归统计 Multiple R0.882607 R Square0.778996 Adjusted R Square0.747424 标准误差0.160818 观测值9 方差分析 df SS MS F Significance F 回归分析10.6381190.63811924.673610.001624残差70.1810370.025862 总计80.819156 Coefficient s标准误差t Stat P-value Lower 95%Upper 95%下限95.0%上限95.0% Intercept 6.017832 1.05226 5.7189610.000721 3.5296358.506029 3.5296358.506029 X Variable 1-0.070410.014176-4.967250.001624-0.10393-0.03689-0.10393-0.03689 4)y = -0.0704x + 6.0178
Matlab+灰色预测模型模型GM(1,1)
GM(1,1)灰色预测模型 Introduction Initial 给定原始序列: x(0) =(x(0)(1), x(0)(2), x(0)(3)…, x(0)(n)) Step 1 一次AGO(1-AGO)生成序列,以弱化原始序列的随机性和波动性:x(1) =(x(1)(1), x(1)(2), x(1)(3)…, x(1)(n)) Matlab Program clear syms a b; c=[a b]'; fid=fopen('.\Grey Model\test.txt'); x0=fscanf(fid,'%f');x0=x0'; fclose(fid); x1=cumsum(x0); %原始数据累加 n=length(x0); for i=1:(n-1) z(i)=(x1(i)+x1(i+1))/2; %生成累加矩阵end %计算待定参数的值 Y=x0;Y(1)=[]; Y=Y'; B=[-z;ones(1,n-1)];B=B'; c=inv(B'*B)*B'*Y; c=c'; a=c(1);b=c(2); %预测后续数据 %预测之后10个时间单位的数据 xx1=[];xx1(1)=x0(1); for i=2:(n+10) xx1(i)=(x0(1)-b/a)/exp(a*(i-1))+b/a; end xx0=[];xx0(1)=x0(1);
Step 2 (1) dx (1) dt +ax1t=u,式中a, u为待定系数。 灰微分方程模型为: x0k+az1k=u,z为背景值 z1k=1/2(x1k+x1k?1) (2) 构造矩阵B和数据向量Y n Y n=Ba Y n=x02 x03 ? x0n , B= ?1/2(x11+x12), ?1/2(x12+x13), ? ?1/2(x1n?1+x1n), 1 1 ? 1 a=a u=(B T B)?1B T Y n Step 3 模型响应函数 x1k+1= x01?u e?ak+ u x0k+1=x1k+1?x1k Step 4 检验和判断GM(1,1)模型的精度(1) 残差检验for i=2:(n+10) xx0(i)=xx1(i)-xx1(i-1); end %关联度检验 for i=1:n e(i)=abs(x0(i)-xx0(i)); end mmax=max(e); for i=1:n ee(i)=0.5*mmax/(e(i)+0.5*mmax); end r=sum(ee)/n; %后验差检验 x0bar=sum(x0)/n; s1=0; for i=1:n s1=s1+(x0(i)-x0bar)^2; end s1=sqrt(s1/n); s2=0; ebar=sum(e)/n; for i=1:n s2=s2+(e(i)-ebar)^2; end s2=sqrt(s2/n); C=s2/s1; p=0; for i=1:n if abs(e(i)-ebar)<0.6745*s1
中国人口预测模型(精)
中国人口预测模型 天津师范大学数学科学学院 1003班 刘瑶(10505135)周丽(10505110) 2013年6月17日星期一
中 国 人 口 预 测 模 型 摘 要 为了加快中国的经济建设进程,全面落实科学的发展观,按照构建社会主义和谐社会的要求,实现人口与经济社会资源环境的协调和可持续发展。我们确定人口发展战略,必须既着眼于人口本身的问题,又处理好人口与经济社会资源环境之间的相互关系,构建社会主义和谐社会,统筹解决人口数量、素质、结构、分布等问题。 本文是以《中国人口统计年鉴》公布的部分人口数据为基准(其他部分数据通过网站查询得到),通过合理的假设和数学模型得到了对于中国人口增长预测的统计模型。对Leslie 人口模型改进,构建了反映生育率和死亡率变化率负指数函数。基于leslie 的改 进模型: (t)X B B B +(t)X A A A =t)▽n +X(t 22) -(n 3 2112) -(n 3 21 此模型考虑到了生育率的变化,并是针对总人口分布处理的,克服了leslie 模型的不足,很适合做长期预测。得到结论:人口数量先增大后减小,峰值出现在2040年,届时人口数量将达到最大,为15.869亿。 关键词: 人口预测, Leslie 人口模型改进 , 长期预测 一 问题的背景 中国是世界上人口最多的发展中国家,人口多,底子薄,耕地少,人均占有资源相对不足,是我国的基本国情,人口问题一直是制约中国经济发展的首要因素。新中国成立50多年来,我国人口发展经历了前30年高速增长和后20年低速增长两大阶段:从建国初期到上世纪70年代初,中国人口再生产由旧中国的高出生、高死亡率进入高出生、低死亡率的人口高增长时期,1950-1975年人口出生率始终保持在30‰以上, 最高达到37‰(附录1)。70年代以后,人口过快增长的势头得到迅速扭转,人口出生率、自然增长率、妇女总和生育率有了明显下降,人口出生率由70年代初的33‰大幅度下降到80年代的21‰, 妇女总和生育率也由6下降到2.3左右。90年代以来,随着我国经济高速发展,人民文化和健康水平逐步提高,计划生育工作的不断深入,在20-29岁生育旺盛人数年均超过1亿的情况下, 人口出生率依然呈现大幅下降的趋势,到2000年底人口出生率从1990年的21.06‰下降到14.03‰,自然增长率由1990年的14.39‰下降到7.58‰, 妇女总和生育率也下降到2以下。进入90年代末期, 我国人口再生产实现了低出生、低死亡、低增长的历史性转变,我国用20多年时间完成了国外近200年的历程。到2000年底全国总人口为12.6743亿, 成功实现了“九五”计划将人口控制在13亿的奋斗目标。 中国政府自1980年在全国城乡实行计划生育基本国策以来成果卓著,据国家计生委“计划生育投入与效益研究”课题组的研究成果,20年共少生2.5亿个孩子。若从70年代算起,至今至少少生3亿人口,这有效地控制了人口的快速增长,为中国现代化建设、全面实现小康打下坚实的基础, 这同时也是对世界人口的增长和控制做出了杰出贡献。但是由于中国人口基数大,人口增长问题依然十分严峻,1990-1999年每年平均净增人口约1300万,这仍然对我国社会和经济产生巨大的压力。在我国现代化进程中,必须实现人口与经济、社会、
SPSS多元线性回归分析实例操作步骤
SPSS 统计分析 多元线性回归分析方法操作与分析 实验目的: 引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。 实验变量: 以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。 实验方法:多元线性回归分析法 软件: 操作过程: 第一步:导入Excel数据文件 1.open data document——open data——open;
2. Opening excel data source——OK. 第二步: 1.在最上面菜单里面选中Analyze——Regression——Linear ,Dependent(因变量)选择商品房平均售价,Independents(自变量)选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率;Method 选择Stepwise.
进入如下界面: 2.点击右侧Statistics,勾选Regression Coefficients(回归系数)选项组中的Estimates;勾选Residuals(残差)选项组中的Durbin-Watson、Casewise diagnostics默认;接着选择Model fit、Collinearity diagnotics;点击Continue.
3.点击右侧Plots,选择*ZPRED(标准化预测值)作为纵轴变量,选择DEPENDNT(因变量)作为横轴变量;勾选选项组中的Standardized Residual Plots(标准化残差图)中的Histogram、Normal probability plot;点击Continue.
灰色预测模型的Matlab程序及检验程序(精)
灰色预测模型的Matlab 程序及检验程序 %灰色预测模型程序 clear syms a b; c=[a b]'; A=[46.2 32.6 26.7 23.0 20.0 18.9 17.5 16.3];% 原始序列 B=cumsum(A);%累加n=length(A); for i=1:(n-1) C(i)=(B(i)+B(i+1))/2; end %计算待定参数 D=A; D(1)=[]; D=D'; E=[-C; ones(1,n-1)]; c=inv(E*E')*E*D; c=c'; a=c(1); b=c(2); %预测往后预测5个数据 F=[];F(1)=A(1); for i=2:(n+5) F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a; end G=[];G(1)=A(1); for i=2:(n+5) G(i)=F(i)-F(i-1); end t1=2002:2009; t2=2002:2014; G plot(t1,A,'o',t2,G) %灰色预测模型检验程序 function [ q,c,p ] = checkgm( x0,x1 ) %GM 检验函数 %x0 原始序列
%x1 预测序列 %·返回值 % q –- 相对误差 % c -- ·方差比 % p -- 小误差概率 e0=x0-x1; q=e0/x0; s1=var(x0); %qpa=mean(e0); s2=var(e0); c=s2/s1; len=length(e0); p=0; for i=1:len if(abs(e0(i)) < 0.6745*s1) p=p+1; end end p=p/len; end
灰色系统新陈代谢模型源码(matlab)
function g(x); %定义函数gm(x) for j=1:10 clc; %清屏,以使计算结果独立显示 format long; %设置计算精度 if length(x(:,1))==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换x=x'; end; n=length(x); %取输入数据的样本量 z=0; for i=1:n %计算累加值,并将值赋与矩阵be z=z+x(i,:); be(i,:)=z; end for i=2:n %对原始数列平行移位 y(i-1,:)=x(i,:); end for i=1:n-1 %计算数据矩阵B的第一列数据 c(i,:)=-0.5*(be(i,:)+be(i+1,:)); end for j=1:n-1 %计算数据矩阵B的第二列数据 e(j,:)=1; end for i=1:n-1 %构造数据矩阵B B(i,1)=c(i,:); B(i,2)=e(i,:); end alpha=inv(B.'*B)*B.'*y; %计算参数α、μ矩阵 for i=1:n+1 %计算数据估计值的累加数列,如改n+1为n+m可预测后m-1个值ago(i,:)=(x(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1,:)*(i-1))+alpha(2,:)/alpha(1,:); end var(1,:)=ago(1,:) for i=1:n %如改n为n+m-1,可预测后m-1个值 var(i+1,:)=ago(i+1,:)-ago(i,:); %估计值的累加数列的还原,并计算出下一预测值end for i=1:n error(i,:)=var(i,:)-x(i,:); %计算残差 end c=std(error)/std(x); %调用统计工具箱的标准差函数计算后验差的比值c ago %显示输出预测值的累加数列 alpha %显示输出参数α、μ数列 var %显示输出预测值 error %显示输出误差 c %显示后验差的比值c var=fix(var);
MATLAB回归预测模型
MATLAB---回归预测模型 Matlab统计工具箱用命令regress实现多元线性回归,用的方法是最小二乘法,用法是:b=regress(Y,X) [b,bint,r,rint,stats]=regress(Y,X,alpha) Y,X为提供的X和Y数组,alpha为显着性水平(缺省时设定为0.05),b,bint为回归系数估计值和它们的置信区间,r,rint为残差(向量)及其置信区间,stats是用于检验回归模型的统计量,有四个数值,第一个是R2,第二个是F,第三个是与F对应的概率 p ,p <α拒绝 H0,回归模型成立,第四个是残差的方差 s2 。 残差及其置信区间可以用 rcoplot(r,rint)画图。 例1合金的强度y与其中的碳含量x有比较密切的关系,今从生产中收集了一批数据如下表 1。 先画出散点图如下: x=0.1:0.01:0.18; y=[42,41.5,45.0,45.5,45.0,47.5,49.0,55.0,50.0]; plot(x,y,'+') 可知 y 与 x 大致上为线性关系。 设回归模型为y =β 0+β 1 x
用regress 和rcoplot 编程如下: clc,clear x1=[0.1:0.01:0.18]'; y=[42,41.5,45.0,45.5,45.0,47.5,49.0,55.0,50.0]'; x=[ones(9,1),x1]; [b,bint,r,rint,stats]=regress(y,x); b,bint,stats,rcoplot(r,rint) 得到 b =27.4722 137.5000 bint =18.6851 36.2594 75.7755 199.2245 stats =0.7985 27.7469 0.0012 4.0883 即β 0=27.4722 β 1 =137.5000 β 的置信区间是[18.6851,36.2594], β 1 的置信区间是[75.7755,199.2245]; R2= 0.7985 , F = 27.7469 , p = 0.0012 , s2 =4.0883 。可知模型(41)成立。
统计学多元回归分析实例
某农场负责人认为早稻收获量(y:单位为kg/公顷)与春季降雨(x i:单位为mm)和春季温度(X2:单位为C )有一定的联系,通过7组试验获得了相关的数据。利用Excel得到下面的回归结果(a =0.1): 方差分析表 (1)将方差分析表中的所缺数值补齐。 (2 )写出早稻收获量与春季降雨量、春季温度的多元线性回归方程,并解释各回归系数的意义。 (3 )检验回归方程的线性关系是否显著? (4)检验各回归系数是否显著? 2 (5)计算判定系数R,并解释它的实际意义。 (6)计算估计标准误差Se,并解释它的实际意义。 (每个空格为0.5分) 2、设总体回归模型为Y= 口+ P 1X^^ 2X2+ & ?x^ ?x2,由EXCEL输出结果可知,?= -0.39 14.92x1估计回归方程为? = ? 218.45x2,回归系数 ?的意义指在温度不变的条件下,当降雨量每增加1mm早稻收获量平均增加 14.92 kg/公顷;回归系数:?的意义指在降雨量不变的条件下, 2 当温度增加1C,早稻收获量平均增加218.45 kg/公顷。---5 分 3、由于p值=0.000075 < a =0.05,则拒绝原假设,即表明回归方程的线性关系是显著的。
4、由于各回归系数的P值均小于a ( 0.05 ),所以各回归系数是显著的。 ---2 分5、2二§臾二1387849567二0.99,表示早稻收获量的总变异中有99%的部分可以由降 R SST 14000000 雨量、温度的联合变动来解释。---4 分 6、S =」SS E =V MST = J30376.08 =174.29(k为自变量个数),是总体回归模型 e n - k -1 中随机扰动项&的标准差的无偏估计量,用来衡量回归方程拟合程度的分析指标,S e越大,拟合程度越低;S e越小,拟合程度越高? —4 分
matlab多元线性回归模型
云南大学数学与统计学实验教学中心 实验报告 一、实验目的 1.熟悉MATLAB的运行环境. 2.学会初步建立数学模型的方法 3.运用回归分析方法来解决问题 二、实验内容 实验一:某公司出口换回成本分析 对经营同一类产品出口业务的公司进行抽样调查,被调查的13家公司,其出口换汇成本与商品流转费用率资料如下表。试分析两个变量之间的关系,并估计某家公司商品流转费用率是6.5%的出口换汇成本. 实验二:某建筑材料公司的销售量因素分析 下表数据是某建筑材料公司去年20个地区的销售量(Y,千方),推销开支、实际帐目数、同类商品
竞争数和地区销售潜力分别是影响建筑材料销售量的因素。1)试建立回归模型,且分析哪些是主要的影响因素。2)建立最优回归模型。 提示:建立一个多元线性回归模型。
三、实验环境 Windows 操作系统; MATLAB 7.0. 四、实验过程 实验一:运用回归分析在MATLAB 里实现 输入:x=[4.20 5.30 7.10 3.70 6.20 3.50 4.80 5.50 4.10 5.00 4.00 3.40 6.90]'; X=[ones(13,1) x]; Y=[1.40 1.20 1.00 1.90 1.30 2.40 1.40 1.60 2.00 1.00 1.60 1.80 1.40]'; plot(x,Y,'*'); [b,bint,r,rint,stats]=regress(Y,X,0.05); 输出: b = 2.6597 -0.2288 bint = 1.8873 3.4322 -0.3820 -0.0757 stats = 0.4958 10.8168 0.0072 0.0903 即==1,0?6597.2?ββ,-0.2288,0?β的置信区间为[1.8873 3.4322],1,?β的置信区间为[-0.3820 -0.0757]; 2r =0.4958, F=10.8168, p=0.0072 因P<0.05, 可知回归模型 y=2.6597-0.2288x 成立. 1 1.5 2 2.5 散点图 估计某家公司商品流转费用率是6.5%的出口换汇成本。将x=6.5代入回归模型中,得到 >> x=6.5; >> y=2.6597-0.2288*x y = 1.1725
统计学案例——相关回归分析
《统计学》案例——相关回归分析 案例一质量控制中的简单线性回归分析 1、问题的提出 某石油炼厂的催化装置通过高温及催化剂对原料的作用进行反应,生成各种产品,其中液化气用途广泛、易于储存运输,所以,提高液化气收率,降低不凝气体产量,成为提高经济效益的关键问题。 通过因果分析图和排列图的观察,发现回流温度是影响液化气收率的主要原因,因此,只有确定二者之间的相关关系,寻找适当的回流温度,才能达到提高液化气收率的目的。经认真分析仔细研究,确定了在保持原有轻油收率的前提下,液化气收率比去年同期增长1个百分点的目标,即达到12.24%的液化气收率。 2、数据的收集
目标值确定之后,我们收集了某年某季度的回流温度与液化气收率的30组数据(如上表),进行简单直线回归分析。 3.方法的确立 设线性回归模型为εββ++=x y 10,估计回归方程为x b b y 10?+= 将数据输入计算机,输出散点图可见,液化气收率y 具有随着回流温度x 的提高而降低的趋势。因此,建立描述y 与x 之间关系的模型时,首选直线型是
合理的。 从线性回归的计算结果,可以知道回归系数的最小二乘估计值 b 0=21.263和b 1=-0.229,于是最小二乘直线为 x y 229.0263.21?-= 这就表明,回流温度每增加1℃,估计液化气收率将减少0.229%。 (3)残差分析 为了判别简单线性模型的假定是否有效,作出残差图,进行残差分析。
从图中可以看到,残差基本在-0.5—+0.5左右,说明建立回归模型所依赖的假定是恰当的。误差项的估计值s=0.388。 (4)回归模型检验 a.显著性检验 在90%的显著水平下,进行t 检验,拒绝域为︱t ︱=︱b 1/ s b1︱>t α/2=1.7011。 由输出数据可以找到b 1和s b1,t=b 1/ s b1=-0.229/0.022=-10.313,于是拒绝原假设,说明液化气收率与回流温度之间存在线性关系。 b.拟合度检验 判定系数r 2=0.792。这意味着液化气收率的样本变差大约有80%可以由它与回流温度的线性关系来解释。 2r r ==-0.89 这样,r 值为y 与x 之间存在中高度的负线性关系提供了进一步的证据。 由于n ≥30,我们近似确定y 的90%置信区间为: s z y )(?2 α±=21.263-0.229x ±1.282×0.388 = 21.263-0.229x ± 0.497
灰色预测模型matlab程序精确版
灰色预测模型matlab程序 %下面程序是灰色模型GM(1,1)程序二次拟合和等维新陈代谢改进预测程序,mat lab6.5 ,使用本程序请注明,程序存储为gm1.m %x = [5999,5903,5848,5700,7884];gm1(x); 测试数据 %二次拟合预测GM(1,1)模型 function gmcal=gm1(x) sizexd2 = size(x,2); %求数组长度 k=0; for y1=x k=k+1; if k>1 x1(k)=x1(k-1)+x(k); %累加生成 z1(k-1)=-0.5*(x1(k)+x1(k-1)); %z1维数减1,用于计算B yn1(k-1)=x(k); else x1(k)=x(k); end end %x1,z1,k,yn1 sizez1=size(z1,2); %size(yn1); z2 = z1'; z3 = ones(1,sizez1)'; YN = yn1'; %转置 %YN B=[z2 z3]; au0=inv(B'*B)*B'*YN; au = au0'; %B,au0,au
ufor = au(2); ua = au(2)./au(1); %afor,ufor,ua %输出预测的 a u 和 u/a的值 constant1 = x(1)-ua; afor1 = -afor; x1t1 = 'x1(t+1)'; estr = 'exp'; tstr = 't'; leftbra = '('; rightbra = ')'; %constant1,afor1,x1t1,estr,tstr,leftbra,rightbra strcat(x1t1,'=',num2str(constant1),estr,leftbra,num2str(afor1),tstr,r ightbra,'+',leftbra,num2str(ua),rightbra) %输出时间响应方程 %****************************************************** %二次拟合 k2 = 0; for y2 = x1 k2 = k2 + 1; if k2 > k else ze1(k2) = exp(-(k2-1)*afor); end end %ze1 sizeze1 = size(ze1,2); z4 = ones(1,sizeze1)'; G=[ze1' z4]; X1 = x1'; au20=inv(G'*G)*G'*X1; au2 = au20'; %z4,X1,G,au20
统计学多元回归分析实例
某农场负责人认为早稻收获量(y :单位为kg/公顷)与春季降雨(x 1:单位为mm )和春季温度(x 2:单位为℃)有一定的联系,通过7组试验获得了相关的数据。利用Excel 得到下面的回归结果(α=0.1): 方差分析表 (2)写出早稻收获量与春季降雨量、春季温度的多元线性回归方程,并解释各回归系数的意义。 (3)检验回归方程的线性关系是否显著? (4)检验各回归系数是否显著? (5)计算判定系数2 R ,并解释它的实际意义。 (6)计算估计标准误差Se ,并解释它的实际意义。 (每个空格为0.5分) -----3分 2、设总体回归模型为Y =1 2 1 2 x x αεββ+ ++ 估计回归方程为y ?=1 2 1 2 ???x x αββ++,由EXCEL 输出结果可知,y ?=120.3914.92218.45-++x x ,回归系数1 ?β 的意义指在温度不变的条件下,当降雨量每增加1mm ,早稻收获量平均增加14.92kg/公顷;回归系数 2 ?β 的意义指在降雨量不变的条件下, 当温度增加1℃,早稻收获量平均增加218.45kg/公顷。 ---5分
3、由于p 值=0.000075<α=0.05,则拒绝原假设,即表明回归方程的线性关系是显著的。 ---2分 4、由于各回归系数的P 值均小于α(0.05),所以各回归系数是显著的。 ---2分 5、 2 13878495.67 0.9914000000 = ==SSR SST R ,表示早稻收获量的总变异中有99%的部分可以由降雨量、温度的联合变动来解释。 ---4分 6、 174.29= ===e S (k 为自变量个数) ,是总体回归模型中随机扰动项ε的标准差的无偏估计量,用来衡量回归方程拟合程度的分析指标,e S 越大, 拟合程度越低;e S 越小,拟合程度越高. ---4分
灰色预测模型matlab程序精确版
%x=[1019,1088,1324,1408,1601];gm1(x); 测试数据%二次拟合预测GM(1,1)模型 function gmcal=gm1(x) if nargin==0 x=[1019,1088,1324,1408,1601] end format long g sizex=length(x); %求数组长度 k=0; for y1=x k=k+1; if k>1 x1(k)=x1(k-1)+x(k); %累加生成 z1(k-1)=-0.5*(x1(k)+x1(k-1)); %z1维数减1,用于计算B yn1(k-1)=x(k); else x1(k)=x(k); end end %x1,z1,k,yn1 sizez1=length(z1); %size(yn1); z2 = z1'; z3 = ones(1,sizez1)'; YN = yn1'; %转置 %YN B=[z2 z3]; au0=inv(B'*B)*B'*YN; au = au0'; %B,au0,au afor = au(1); ufor = au(2); ua = au(2)./au(1); %afor,ufor,ua %输出预测的 a u 和 u/a的值 constant1 = x(1)-ua; afor1 = -afor; x1t1 = 'x1(t+1)'; estr = 'exp'; tstr = 't'; leftbra = '(';
rightbra = ')'; %constant1,afor1,x1t1,estr,tstr,leftbra,rightbra strcat(x1t1,'=',num2str(constant1),estr,leftbra,num2str(afor1),tstr,rightbra,'+ ',leftbra,num2str(ua),rightbra) %输出时间响应方程 %****************************************************** %二次拟合 k2 = 0; for y2 = x1 k2 = k2 + 1; if k2 > k else ze1(k2) = exp(-(k2-1)*afor); end end %ze1 sizeze1=length(ze1); z4 = ones(1,sizeze1)'; G=[ze1' z4]; X1 = x1'; au20=inv(G'*G)*G'*X1; au2 = au20'; %z4,X1,G,au20 Aval = au2(1); Bval = au2(2); %Aval,Bval %输出预测的 A,B的值 strcat(x1t1,'=',num2str(Aval),estr,leftbra,num2str(afor1),tstr,rightbra,'+',lef tbra,num2str(Bval),rightbra) %输出时间响应方程 nfinal = sizex-1 + 1;(其中+1可改为+5等其他数字,即可预测更多的数字) %决定预测的步骤数5 这个步骤可以通过函数传入 %nfinal = sizexd2 - 1 + 1; %预测的步骤数 1 for k3=1:nfinal x3fcast(k3) = constant1*exp(afor1*k3)+ua; end %x3fcast %一次拟合累加值 for k31=nfinal:-1:0 if k31>1 x31fcast(k31+1) = x3fcast(k31)-x3fcast(k31-1); else if k31>0
多元回归分析matlab剖析
回归分析MATLAB 工具箱 一、多元线性回归 多元线性回归:p p x x y βββ+++=...110 1、确定回归系数的点估计值: 命令为:b=regress(Y , X ) ①b 表示???? ?? ????????=p b βββ?...??10 ②Y 表示????????????=n Y Y Y Y (2) 1 ③X 表示??? ??? ????? ???=np n n p p x x x x x x x x x X ...1......... .........1 (12) 1 22221 11211 2、求回归系数的点估计和区间估计、并检验回归模型: 命令为:[b, bint,r,rint,stats]=regress(Y ,X,alpha) ①bint 表示回归系数的区间估计. ②r 表示残差. ③rint 表示置信区间. ④stats 表示用于检验回归模型的统计量,有三个数值:相关系数r 2、F 值、与F 对应的概率p. 说明:相关系数2 r 越接近1,说明回归方程越显著;)1,(1-->-k n k F F α时拒绝0H ,F 越大,说明回归方程越显著;与F 对应的概率p α<时拒绝H 0,回归模型成立. ⑤alpha 表示显著性水平(缺省时为0.05) 3、画出残差及其置信区间. 命令为:rcoplot(r,rint) 例1.如下程序. 解:(1)输入数据. x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; X=[ones(16,1) x]; Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]'; (2)回归分析及检验. [b,bint,r,rint,stats]=regress(Y ,X) b,bint,stats 得结果:b = bint =
matlab与统计回归分析 (1)
一Matlab作方差分析 方差分析是分析试验(或观测)数据的一种统计方法。在工农业生产和科学研究中,经常要分析各种因素及因素之间的交互作用对研究对象某些指标值的影响。在方差分析中,把试验数据的总波动(总变差或总方差)分解为由所考虑因素引起的波动(各因素的变差)和随机因素引起的波动(误差的变差),然后通过分析比较这些变差来推断哪些因素对所考察指标的影响是显著的,哪些是不显著的。 【例1】(单因素方差分析)一位教师想要检查3种不同的教学方法的效果,为此随机地选取水平相当的15位学生。把他们分为3组,每组5人,每一组用一种方法教学,一段时间以后,这位教师给15位学生进行统考,成绩见下表1。问这3种教学方法的效果有没有显著差异。 表1 学生统考成绩表 方法成绩 甲75 62 71 58 73 乙71 85 68 92 90 丙73 79 60 75 81 Matlab中可用函数anova1(…)函数进行单因子方差分析。 调用格式:p=anova1(X) 含义:比较样本m×n的矩阵X中两列或多列数据的均值。其中,每一列表示一个具有m 个相互独立测量的独立样本。 返回:它返回X中所有样本取自同一总体(或者取自均值相等的不同总体)的零假设成立的概率p。
解释:若p值接近0(接近程度有解释这自己设定),则认为零假设可疑并认为至少有一个样本均值与其它样本均值存在显著差异。 Matlab程序: Score=[75 62 71 58 73;81 85 68 92 90;73 79 60 75 81]’; P=anova1(Score) 输出结果:方差分析表和箱形图 ANOVA Table Source SS df MS F Prob>F Columns 604.9333 2 302.4667 4.2561 0.040088 Error 852.8 12 71.0667 Total 1457.7333 14 由于p值小于0.05,拒绝零假设,认为3种教学方法存在显著差异。 例2(双因素方差分析)为了考察4种不同燃料与3种不同型号的推进器对火箭射程(单位:海里)的影响,做了12次试验,得数据如表2所示。 表2 燃料-推进器-射程数据表 推进器1 推进器2 推进器3 燃料1 58.2 56.2 65.3 燃料2 49.1 54.1 51.6 燃料3 60.1 70.9 39.2 燃料4 75.8 58.2 48.7 在Matlab中利用函数anova2函数进行双因素方差分析。 调用格式:p=anova2(X,reps)
spss多元回归分析案例
企业管理 对居民消费率影响因素的探究 ---以湖北省为例改革开放以来,我国经济始终保持着高速增长的趋势,三十多年间综合国力得到显著增强,但我国居民消费率一直偏低,甚至一直有下降的趋势。居民消费率的偏低必然会导致我国内需的不足,进而会影响我国经济的长期健康发展。 本模型以湖北省1995年-2010年数据为例,探究各因素对居民消费率的影响及多元关系。(注:计算我国居民的消费率,用居民的人均消费除以人均GDP,得到居民的消费率)。通常来说,影响居民消费率的因素是多方面的,如:居民总收入,人均GDP,人口结构状况1(儿童抚养系数,老年抚养系数),居民消费价格指数增长率等因素。 总消费(C:亿元) 总GDP(亿元)消费率(%) 1995 1095.97 2109.38 51.96 1997 1438.12 2856.47 50.35 2000 1594.08 3545.39 44.96 2001 1767.38 3880.53 45.54 2002 1951.54 4212.82 46.32 2003 2188.05 4757.45 45.99 1.人口年龄结构一种比较精准的描述是:儿童抚养系数(0-14岁人口与 15-64岁人口的比值)、老年抚养系数(65岁及以上人口与15-64岁人口的比值〉或总抚养系数(儿童和老年抚养系数之和)。0-14岁人口比例与65岁及以上人口比例可由《湖北省统计年鉴》查得。
(注:数据来自《湖北省统计年鉴》) 一、计量经济模型分析 (一)、数据搜集 根据以上分析,本模型在影响居民消费率因素中引入6个解释变量。X1:居民总收入(亿元),X2:人口增长率(‰),X3:居民消费价格指数增长率,X4:少儿抚养系数,X5:老年抚养系数,X6:居民消费占收入比重(%)。 Y :消费率(%) X1:总收入 (亿元) X2:人口 增长率 (‰) X3:居民 消费价格指数增长率 X4:少儿抚养系数 X5:老年 抚养系数 X6:居民 消费比重(%) 1995 51.96 1590.75 9.27 17.1 45.3 9.42 68.9 1997 50.35 2033.68 8.12 2.8 41.1 9.44 70.72 2000 44.96 2247.25 3.7 0.4 39 9.57 70.93 2004 2452.62 5633.24 43.54 2005 2785.42 6590.19 42.27 2006 3124.37 7617.47 41.02 2007 3709.69 9333.4 39.75 2008 4225.38 11328.92 37.30 2009 4456.31 12961.1 34.38 2010 5136.78 15806.09 32.50
